О градиентных методах и сопряженных задачах при идентификации теплофизических параметров
О
градиентных методах и сопряжённых задачах при идентификации теплофизических
параметров
В.К.
Толстых, (доктор ф.-м. наук., доц., ДонНУ)
Н.А.
Володин (канд. ф.-м. наук, доц. ДонНТУ)
В.Е.
Бодряга (зав. лаб., ДонНУ)
Вступление
Решается задача идентификации коэффициента
температуропроводности непрерывнолитого стального цилиндрического слитка.
Температуропроводность представляется полиномиальной зависимостью от
температуры процесса с весовыми коэффициентами. Задача рассматривается как оптимизационная.
Минимизация целевой функции осуществляется методом сопряженных градиентов.
Рассматриваются методы поиска градиента функции с помощью сопряженной задачи и
численного дифференцирования. Приводятся сравнительный анализ расчётов задачи
идентификации для обоих методов.
Идентификация, оптимизация,
градиент, непрерывный слиток.
При идентификации параметров в задачах
теплофизики приходится численно минимизировать функционалы от состояния системы
- критерии качества идентификации. Наиболее часто здесь используются
градиентные алгоритмы [1, 2]. Если искомые параметры являются пространственными
или временными функциями, то градиент критерия качества также является
пространственно-временной функцией и находится через решение сопряжённой
задачи, например, - [3,4]. Если искомые параметры является функциями состояния
системы, то их представляют различными рядами относительно состояния с
множеством коэффициентов. Такие коэффициенты образуют вектор идентифицируемых
параметров, и здесь градиент критерия качества превращается в вектор
сопряжённого пространства, например, - [4]. При этом градиент для вектора
искомых параметров может быть получен и без сопряжённой задачи, а численным
дифференцированием критерия качества идентификации, как это было реализовано в
[5]. Возникает ряд вопросов, в каком случае следует использовать технику
сопряжённых задач, а в каком - численное дифференцирование, что эффективнее,
проще в реализации? Именно поиску ответов на данные вопросы, применительно к
задачам параметрической идентификации в теплофизических, возможно нелинейных
системах, посвящена настоящая работа.
Постановка задачи
В работе рассматривается проблема
математического моделирования процессов затвердевания слитков, в частности, - в
машинах непрерывного литья заготовок (МНЛЗ). Точность моделирования, в
основном, определяется точностью задания параметров, входящих в уравнения
конвекции и тепломассопереноса. Такие уравнения довольно громоздки, при
численном решении требуют значительных ресурсов компьютеров и не гарантируют желаемой
точности. Значительное снижение вычислительных затрат может быть достигнуто
введением эффективных коэффициентов теплопроводности и диффузии, что позволяет
отказаться от расчета уравнений конвекции и существенно снизить число
определяемых параметров [2, 5]. Естественно, что достоверные значения этих
параметров могут быть получены только из решения задач параметрической
идентификации.
Математическая модель установившегося теплового
процесса в цилиндрическом непрерывном слитке может быть представлена следующим
квазилинейным параболическим уравнением [2]:
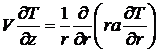 ,
, 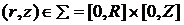 , (1)
, (1)
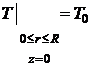 ,
,  ,
,
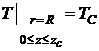 ,
, 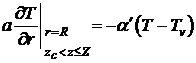 , (2)
, (2)
где 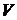 - скорость литья,
- скорость литья, 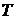 -
температура слитка,
-
температура слитка, 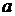 -
эффективный коэффициент температуропроводности,
-
эффективный коэффициент температуропроводности, 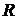 - эффективный радиус слитка,
- эффективный радиус слитка, 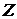 - длина вертикальной
части МНЛЗ,
- длина вертикальной
части МНЛЗ, 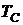 -
температура слитка в зоне кристаллизатора,
-
температура слитка в зоне кристаллизатора, 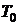 - температура заливаемого в
установку металла,
- температура заливаемого в
установку металла, 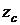 - нижняя
граница кристаллизатора,
- нижняя
граница кристаллизатора, 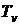 -
температура охладителя в зоне вторичного охлаждения (ЗВО),
-
температура охладителя в зоне вторичного охлаждения (ЗВО), 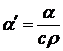 ,
, 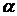 -
коэффициент теплоотдачи в ЗВО,
-
коэффициент теплоотдачи в ЗВО, 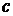 - теплоемкость,
- теплоемкость, 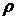 -
плотность. На рис. 1 схематично изображена часть МНЛЗ с затвердевающим слитком.
-
плотность. На рис. 1 схематично изображена часть МНЛЗ с затвердевающим слитком.
Предположим, что все теплофизические
параметры модели (1)-(2) заданы точно, за исключением эффективного коэффициента
температуропроводности 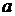 .
.
Рис. 1. Принципиальная схема затвердевающего
слитка в МНЛЗ вертикального литья:
- кристаллизатор, 2 - слиток, 3 - вторичный охладитель
Качество идентификации эффективного
коэффициента 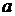 будем
оценивать интегральным расхождением модельной
будем
оценивать интегральным расхождением модельной 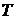 и экспериментально наблюдаемой
и экспериментально наблюдаемой  температурами
по объёму слитка:
температурами
по объёму слитка:
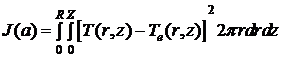 (3)
(3)
В работе [4] показано, что
идентификация эффективного коэффициента температуропроводности 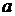 традиционными
полиномами в общем случае невозможна, однако удается получить хорошее решение
при использовании полинома вида:
традиционными
полиномами в общем случае невозможна, однако удается получить хорошее решение
при использовании полинома вида:
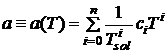 (4)
(4)
где 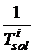 - коэффициент масштабирования,
- коэффициент масштабирования, 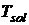 -
температура затвердевания металла,
-
температура затвердевания металла, 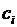 - коэффициенты полинома. При этом
задача идентификации модели (1)-(2) сводится к задаче параметрической
идентификации вектора
- коэффициенты полинома. При этом
задача идентификации модели (1)-(2) сводится к задаче параметрической
идентификации вектора 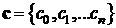 размерности
размерности
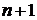 , а
минимизируемый функционал (3) превращается функцию
, а
минимизируемый функционал (3) превращается функцию 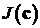 .
.
Минимизацию 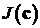 будем
осуществлять методом сопряженных градиентов:
будем
осуществлять методом сопряженных градиентов:
 ,
, 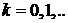 (5)
(5)
где  ,
,
а число  рассчитывалось
с использованием метода Вульфа [6].
рассчитывалось
с использованием метода Вульфа [6].
Для оценки эффективности методов
идентификации вектора 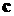 по
алгоритму (5) градиент
по
алгоритму (5) градиент 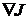 в
в 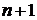 мерном
пространстве будем рассчитывать двумя способами: численным дифференцированием и
с использованием сопряженной задачи.
мерном
пространстве будем рассчитывать двумя способами: численным дифференцированием и
с использованием сопряженной задачи.
При численном дифференцировании
градиент целевой функции 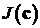 рассчитывался
по формуле [6]:
рассчитывался
по формуле [6]:
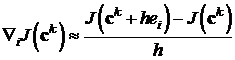 ,
, 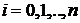 , (6)
, (6)
где число 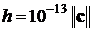 ,
, 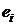 - единичный
вектор вдоль оси
- единичный
вектор вдоль оси 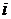 в
пространстве оптимизируемых параметров
в
пространстве оптимизируемых параметров 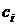 .
.
Для расчета вторым способом градиент
целевой функции 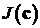 находился
модифицированным методом множителей Лагранжа [1]:
находился
модифицированным методом множителей Лагранжа [1]:
 , (7)
, (7)
где 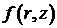 удовлетворяет сопряженной задаче:
удовлетворяет сопряженной задаче:
 , (8)
, (8)
 ,
, 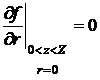 ,
, 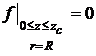 ,
, 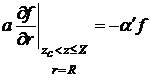 , (9)
, (9)
Тестирование алгоритмов
производилось следующим образом. Задавалось тестовое значение 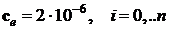 и начальное
приближение
и начальное
приближение 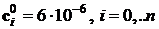 .
Квазилинейная задача (1), (2), (4) аппроксимировалась неявной
конечно-разностной схемой и решалась методом прогонки с подитерациями для учёта
нелинейности [7]. В частности, для данной задачи было подобрано наилучшее число
подитераций
.
Квазилинейная задача (1), (2), (4) аппроксимировалась неявной
конечно-разностной схемой и решалась методом прогонки с подитерациями для учёта
нелинейности [7]. В частности, для данной задачи было подобрано наилучшее число
подитераций 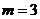 . В
результате решения прямой задачи (1), (2), (4) определялось поле температур,
которое принималось как экспериментальное
. В
результате решения прямой задачи (1), (2), (4) определялось поле температур,
которое принималось как экспериментальное  . Далее решалась обратная задача
идентификации вектора
. Далее решалась обратная задача
идентификации вектора 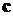 по критерию
(3) методом (5), где градиент вычислялся либо по формуле (6), либо по формуле
(7) с использованием линейной сопряжённой задачи (8), (9). Последняя решалась
обычным методом прогонки, не требующим подитераций.
по критерию
(3) методом (5), где градиент вычислялся либо по формуле (6), либо по формуле
(7) с использованием линейной сопряжённой задачи (8), (9). Последняя решалась
обычным методом прогонки, не требующим подитераций.
Условием завершения итераций метода
сопряжённых градиентов (5), было изменение критерия качества менее чем на 0,1%.
Эффективность методов идентификации оценивалось не только по степени
минимизации критерия 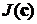 , но и по
степени приближения искомого вектора к точному значению -
, но и по
степени приближения искомого вектора к точному значению - 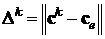 . Расчёты
проводились при следующих значениях:
. Расчёты
проводились при следующих значениях: 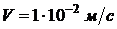 ,
, 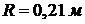 ,
, 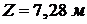 ,
, 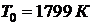 ,
, 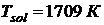 ,
, 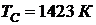 ,
, 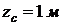 ,
, 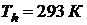 ,
, 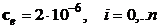 ,
, 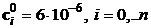 . Величина
. Величина 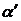 в расчетах
принималась равной
в расчетах
принималась равной 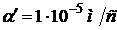 .
.
Анализ результатов вычислений
В таблице 1 приведены результаты
идентификации вектора 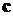 при расчете
градиента посредством численного дифференцирования, а в таблице 2 - при расчете
градиента с использованием сопряженной задачи.
при расчете
градиента посредством численного дифференцирования, а в таблице 2 - при расчете
градиента с использованием сопряженной задачи.
Таблица 1. Результаты идентификации
коэффициента температуропроводности при расчете градиента 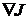 посредством
численного дифференцирования
посредством
численного дифференцирования
Видно, что в первом случае (таб. 1)
удаётся существенно лучше восстановить вектор 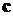 , он приближается к точному значению
, он приближается к точному значению
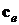 на
несколько порядков ближе, чем во втором случае (таблица 2).
на
несколько порядков ближе, чем во втором случае (таблица 2).
Таблица 2. Результаты идентификации
коэффициента температуропроводности при расчете градиента 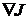 посредством
сопряжённой задачи
посредством
сопряжённой задачи
Однако при этом затрачивается в
несколько раз больше итераций 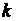 . В тоже время необходимо отметить,
что с точки зрения практических результатов идентификации коэффициента
теплопроводности, для МНЛЗ оба метода дают достаточно высокую точность
моделирования.
. В тоже время необходимо отметить,
что с точки зрения практических результатов идентификации коэффициента
теплопроводности, для МНЛЗ оба метода дают достаточно высокую точность
моделирования.
Если оценивать вычислительные
затраты в обеих методах, то мы получим следующее. Метод численного
дифференцирования (6) на каждой итерации требует 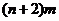 решений дифференциального уравнения
(1) с учётом внутренних подитераций для преодоления нелинейности задачи, а
метод с линейной сопряжённой задачей требует всего
решений дифференциального уравнения
(1) с учётом внутренних подитераций для преодоления нелинейности задачи, а
метод с линейной сопряжённой задачей требует всего 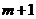 решений:
дифференциальное уравнение (1) и сопряжённое дифференциальное уравнение (8) на
каждой итерации. В нижних строках таблиц 1 и 2 приведено результирующее
количество решений дифференциальных уравнений в каждом случае. Мы видим, что
метод численного дифференцирования, обладающий относительно высокой точность
при малых размерностях вектора
решений:
дифференциальное уравнение (1) и сопряжённое дифференциальное уравнение (8) на
каждой итерации. В нижних строках таблиц 1 и 2 приведено результирующее
количество решений дифференциальных уравнений в каждом случае. Мы видим, что
метод численного дифференцирования, обладающий относительно высокой точность
при малых размерностях вектора 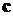 , с ростом размерности теряет
точность и требует значительно возрастающих вычислительных затрат. В то же
время метод с сопряжённой задачей оказывается не чувствительным к размерности
искомого вектора
, с ростом размерности теряет
точность и требует значительно возрастающих вычислительных затрат. В то же
время метод с сопряжённой задачей оказывается не чувствительным к размерности
искомого вектора 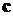 .
.
Выводы
температуропроводность слиток
тепловой градиент
Таким образом, при идентификации градиентными
методами теплофизических векторов-параметров небольшой размерности
целесообразно использовать численное дифференцирование целевой функции,
которое, к тому же, относительно просто реализуется. При большой размерности, и
тем более бесконечной, когда искомый параметр - функция, необходимо
использовать сопряжённую задачу для расчёта градиента.
Список литературы
1. Толстых
В. К. Прямой экстремальный подход для оптимизации систем с распределенными
параметрами / Виктор Константинович Толстых. - Донецк: Юго-Восток, 1997. - 178
с.
2. Прямая
оптимизация теплофизических процессов/ [Огурцов А. П., Недопекин Ф. В., Толстых
В. К., Володин Н. А.]. - Донецк: Юго-Восток, 1997. - 150 с.
. Бородин
В.С. Идентификация параметров в моделях формирования отливок / В. С. Бородин,
Н. А. Володин, В. К. Толстых // Процессы литья. - 1995. - №1. - с. 96 - 101.
. Толстых
В.К. Идентификация теплофизических параметров в виде полиномов, зависящих от
температуры / Недопекин Ф. В., Бодряга В. Е. //
Технічна теплофізика та
промислова теплоенергетика. - 2009. -
Випуск
№1. - С. 193-199.
5. Недопекин
Ф.В. Математическое моделирование гидродинамики и тепломассопереноса в слитках
/ Федор Викторович Недопекин. - Ижевск: Из-во Удмуртского университета, 1995. -
236 с.
6. Jorge
Nocedal Numerical Optimization / Jorge Nocedal, Stephan J. Wright. - Springer,
1999. - 636 p.
7. Тихонов
А.Н. Уравнения математической физики/ Тихонов А., Самарский А. - М.: Наука,
1966. - 724 с.