Высшая математика
Задание 1
Даны три комплексных числа 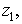
 и
и 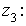
) выполните действия над ними в
алгебраической, тригонометрической и показательной формах;
) найдите расстояние между точками 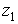 и
и 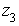 на
комплексной плоскости.
на
комплексной плоскости.
2. 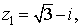
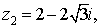
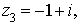
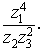
Решение:
1) Найдем значение 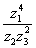 в
алгебраической форме
в
алгебраической форме
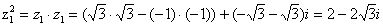
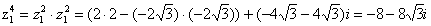
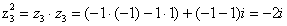
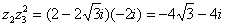
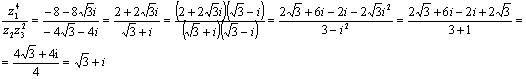
Найдем значение 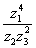 в
тригонометрической форме
в
тригонометрической форме
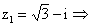

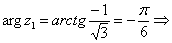
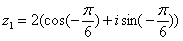
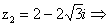
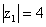
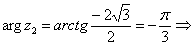
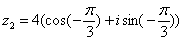
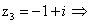
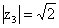
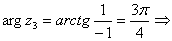
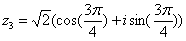
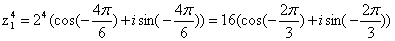
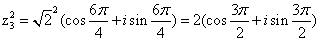
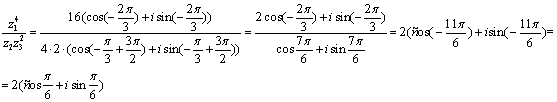
Вычислим значение 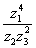 в
показательной форме
в
показательной форме
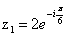
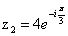
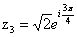
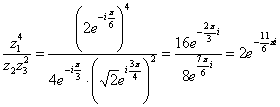
2)Найдем расстояние между точками 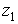 и
и 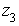 на
комплексной плоскости:
на
комплексной плоскости:
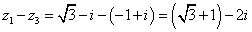
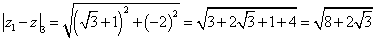
Задание 2
Решите уравнение на множестве комплексных чисел
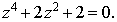
Решение.
Сделаем замену z2=t, получим
уравнение:
t2+2t+2=0
t1=-1-i
t2=-1+i
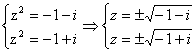
Приведем числа к тригонометрической
форме
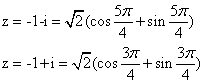
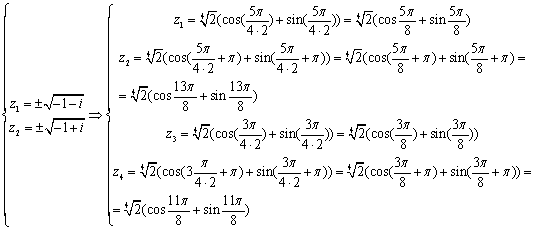
Задания 3
Решите систему уравнений тремя способами:
) методом Крамера;
) методом обратной матрицы;
) методом Гаусса.
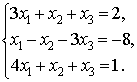
Решение.
)Для решения системы по правилу
Крамера найдем следующие определители:
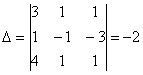
Так как данный определитель не равен
нулю, то данная система имеет единственное решение, а значит система совместна.
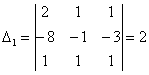
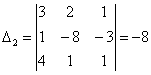
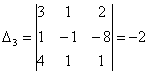
Тогда решение системы находим по
формулам:
х1 = 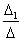 = -1; х2
=
= -1; х2
= 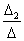 = 4; х3
=
= 4; х3
= 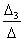 =1
=1
2) Решим систему линейных уравнений
матричным методом.
Обозначим A = 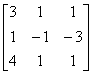 , X =
, X =  , B =
, B = 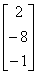 . Тогда
данную систему можно записать в виде: АХ=В. Т.к. матрица невырожденная (Δ=-2), то X = A-1B.
. Тогда
данную систему можно записать в виде: АХ=В. Т.к. матрица невырожденная (Δ=-2), то X = A-1B.
Вычислим обратную матрицу
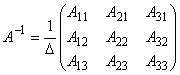 .
.
Определитель
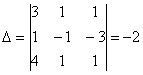
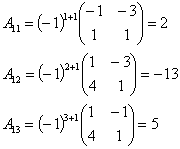
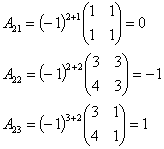
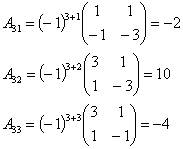
Тогда A-1 = 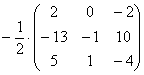
Получим X = A-1B =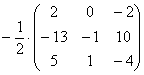
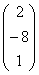 =
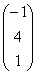
= 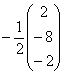 =
=
)Для решения системы методом Гаусса
приведем матрицу к треугольному виду
Рассмотрим расширенную матрицу
системы и приведем ее к треугольному виду:
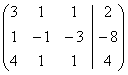 = [поменяем местами первую и вторую
строчки] =
= [поменяем местами первую и вторую
строчки] =
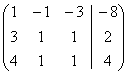 = [умножаем первую строчку на -3 и
складываем со второй, умножаем первую на -4 и складываем с третьей] =
= [умножаем первую строчку на -3 и
складываем со второй, умножаем первую на -4 и складываем с третьей] = 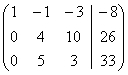 = умножаем
вторую строку на -
= умножаем
вторую строку на -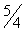 и
складываем с третьей] =
и
складываем с третьей] = 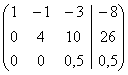
Получаем систему:
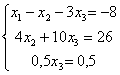
Ответ: х1=-1, х2=4,
х3=1
Задание 4
Даны три вектора 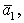
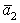 и
и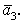 Докажите, что векторы
Докажите, что векторы 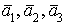 образуют
базис, и определите, какая это тройка векторов: правая или левая.
образуют
базис, и определите, какая это тройка векторов: правая или левая.
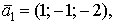
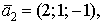
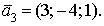
Решение.
Векторы a,b,c
образуют базис в пространстве R3
в том случае, если равенство aa+
bb+ gc=
0 выполняется лишь тогда, когда a = b
= g= 0.
Рассмотрим это условие:
a(1;-1;-2) + b(2;1;-1)
+ g(3;-4;1)= (0;0;0) или
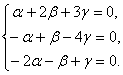
Рассмотрим матрицу данной системы и
приведем ее к треугольному виду:
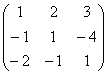
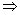 Умножим первую строку на 2 и сложим
с третьей, сложим первую строку со второй;
Умножим первую строку на 2 и сложим
с третьей, сложим первую строку со второй;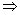
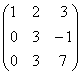
 Умножим вторую строку на -1 и
сложим с третьей
Умножим вторую строку на -1 и
сложим с третьей 
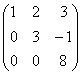
Так как число ненулевых строк в треугольной
матрице равно числу переменных, то система имеет единственное решение, а именно
a
= b = g= 0. Значит,
векторы a,b,c
образуют базис.
Найдем смешанное произведение векторов
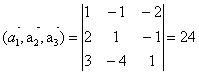
Cмешанное
произведение векторов не равно 0, то 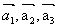 образуют базис, и так как
образуют базис, и так как 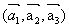 >0, то
тройка векторов является правой.
>0, то
тройка векторов является правой.
Задание 5
комплексный число плоскость
матрица
Даны координаты вершин треугольной
пирамиды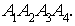 Найдите:
Найдите:
) угол между ребрами 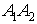 и
и 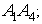
) площадь грани 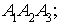
) длину высоты, опущенной из вершины
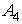 на грань
на грань 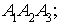
) уравнение прямой, проходящей через
ребро 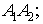
) уравнение плоскости, которой
принадлежит грань 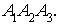
) массу материальной треугольной
пирамиды 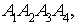 изготовленной
из меди плотностью
изготовленной
из меди плотностью 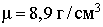 (считая,
что 1 масштабная единица в системе координат равна 1 см).
(считая,
что 1 масштабная единица в системе координат равна 1 см).
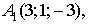
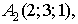
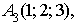
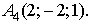
) Известно, что косинус угла
меду двумя векторами 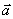 и
и 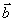 определяется
по формуле
определяется
по формуле 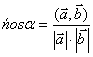
Координаты вектора 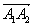 (-1; 2;4) ,
(-1; 2;4) , 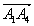 (-1; -3; 4)
(-1; -3; 4)
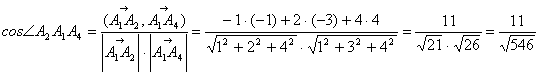
) площадь треугольника,
построенного на векторах 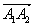 и
и 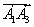 вычисляется
по формуле
вычисляется
по формуле 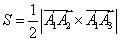 .
.
А1А2 (-1; 2; 4),
А1А3 (1-3; 2-1; 3-(-3))
А1А3 (-2; 1; 6)
Векторное произведение векторов
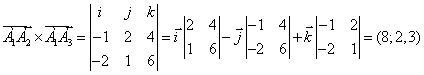
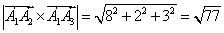
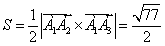 (ед. кв.)
(ед. кв.)
)Найдем уравнение плоскости А1А2А3
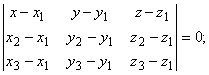 или
или 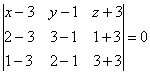
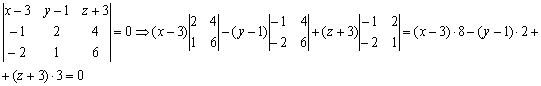
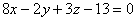 -уравнение плоскости основания А1А2А3
-уравнение плоскости основания А1А2А3
)Расстояние от т.А4(2;-2;1)
до плоскости А1А2А3 находится по формуле
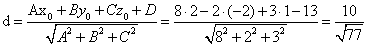
5) Уравнение прямой А1А2
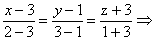
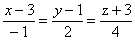 искомое уравнение
искомое уравнение
) Вычислим объем пирамиды А1А2А3А4
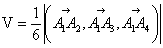
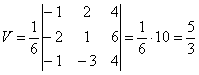 (ед3)
(ед3)
Масса материальной треугольной
пирамиды 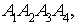 изготовленной
из меди плотностью
изготовленной
из меди плотностью 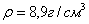
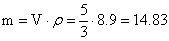 г.
г.
Задания 6
Изобразите геометрическое место
точек, заданных уравнением:
) на плоскости;
) в пространстве.
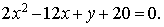
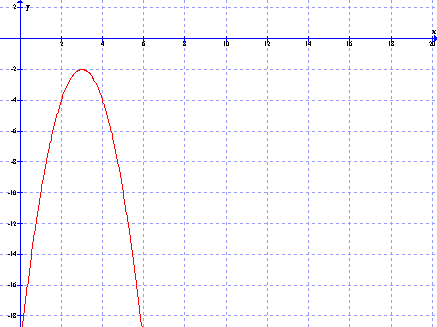
) Преобразуем выражение 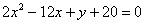 к виду
к виду
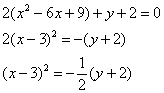
Это уравнение задает параболу с осью
симметрии параллельную Оу и вершиной в точке (3;-2).
2) В пространстве 3то уравнение параболического
цилиндра