Моделирование систем

Оглавление

Введение

. Задание

. Этап конструирования и описания модели

.1 Структурная схема модели

.2 Описание элементов модели

.3 Описание задачи

.3.1 Блок Vxod

.3.2 Блок tip klienta

.3.3 Блоки klient 1, ... , klient 5

.3.4 Блоки kassa 1, ... , kassa 8

.3.5 Блок Vyxod

. Развитие концепций: дополнительные методы

.1 Календарь событий

. Этап проведения компьютерного эксперимента с моделью

.1 Запуск модели

.2 Остановка модели

.3 Сбор результатов компьютерного эксперимента

.4 Определение параметров прогона модели

.5 Структуры файлов результатов

Заключение

Список используемой литературы

Введение

На сегодняшний день большое число задач оптимизации сложных систем из различных областей науки и техники не могут быть решены с помощью аналитического моделирования. Во многих случаях единственным методом решения является метод имитационного моделирования. Задача оптимизации на основе имитационного моделирования формулируется следующим образом: необходимо найти значения входных переменных (факторов), оптимизирующих основной выходной показатель системы (отклик). При этом предполагается, что функция отклика не может быть вычислена аналитически, но может быть рассчитана с помощью имитационного моделирования, т.е. с помощью проведения имитационного эксперимента с моделью сложной системы.

Эта технология появилась в 60-х г. XX в., и на протяжении многих лет она не только остается одной из основных в исследовании операций, но и бурно развивается в области реинжиниринга бизнес-процессов и новых направлений искусственного интеллекта (онтология предприятий, клеточные автоматы, мультиагентные системы и др.).

Основу этой технологии составляет компьютерный имитационный эксперимент, связанный с воспроизведением динамических процессов функционирования исследуемой системы. В процессе такого воспроизведения осуществляется наблюдение за функционированием модели и выявление "узких мест" в организации деятельности. Основными достоинствами этого метода являются:

§  возможность воспроизведения реальной системы с практически любым уровнем детальности;

§  повторяемость эксперимента;

§  возможность произвольной фрагментации и структуризации системы.

Оптимизация на основе имитационного моделирования заключается в совместном использовании имитационной модели (ИМ) сложной системы и алгоритма оптимизации. С помощью ИМ рассчитывается значения отклика для различных комбинаций значений факторов, которые предлагает алгоритм оптимизации. Поисковый алгоритм оптимизации, в свою очередь, используя значения отклика, пытается улучшить решение.

Имитационное моделирование - один из видов компьютерного моделирования, использующий методологию системного анализа, центральной процедурой которого является построение обобщенной модели, отражающей все факторы реальной системы, в качестве же методологии исследования выступает вычислительный эксперимент.

Имитационная модель строится строго целенаправленно, поэтому для нее характерно адекватное отображение исследуемого объекта, логико-математическая модель системы представляет собой программно реализованный алгоритм функционирования системы. При имитационном моделировании структура моделируемой системы адекватно отображается в модели, а процесс ее функционирования имитируется на построенной модели. Под имитацией понимают проведение на компьютерах различных серий экспериментов с моделями, которые представлены в качестве некоторого набора (комплекса) компьютерных программ. Сравнение характеристик (конструкций, управлений) моделируемого объекта осуществляется путем вариантных просчетов. Особую роль имеет возможность многократного воспроизведения моделируемых процессов с последующей их статистической обработкой, позволяющая учитывать случайные внешние воздействия на изучаемый объект. На основе набираемой в ходе компьютерных экспериментов статистики делаются выводы в пользу того или иного варианта функционирования или конструкции реального объекта или сущности явления.

В ряде случаев формировать решения с помощью формальных методов не удается - эксперт должен быть включен в процесс принятия решения. Он становится активным компонентом информационной системы; детализирует проблему и модель, осуществляет постановку направленного вычислительного эксперимента на модели, генерацию и ранжирование альтернатив, выбор критериев для принятия решений, а также формирует рациональный вариант управления с помощью базы знаний. Принятие решений в условиях риска, например, требует ведения диалоговых процедур формирования статистически достоверных результатов и поэтапного сопоставления их с функцией цены риска. Необходимо осуществлять прямое участие эксперта в формировании оптимального множества вариантов решений и в процедурах вариантного синтеза.

Таким образом, имитационное моделирование значительно расширяет возможности и эффективность работы лиц, принимающих решения (ЛПР), предоставляя им удобный инструмент и средства для достижения поставленных целей. Имитационное моделирование реализует итерационный характер разработки модели системы, поэтапный характер детализации моделируемых подсистем, что позволяет постепенно увеличивать полноту оценки принимаемых решений по мере выявления новых проблем и получения новой информации.

Имитационная модель не дает оптимального решения подобно классическому решению задач оптимизации, но она является удобным для системного аналитика вспомогательным средством для поиска решения определенной проблемы. Область применения имитационных моделей практически не ограничена, это могут быть задачи: исследования структур сложных систем и их динамики, анализа узких мест, прогнозирования и планирования и т.д. Главным преимуществом имитационного моделирования является то, что эксперт может ответить на вопрос: "Что будет, если … ", т.е. с помощью эксперимента на модели вырабатывать стратегию развития.

Таким образом, в сфере современных информационных технологий имитационное моделирование приобретает в мировых научных исследованиях и практической деятельности крайне весомое значение. С помощью имитационного моделирования эффективно решаются задачи самой широкой проблематики, - в области стратегического планирования, бизнес-моделирования, менеджмента (моделирование различного рода финансовых проектов, управление производством), реинжиниринга, проектирования (актуально применение имитационного моделирования в области инвестиционно-технологического проектирования), а также моделирования и прогнозирования социально-экономического развития региональных и городских систем.

Наиболее важными свойствами, которыми должны обладать системы оптимизации на основе имитационного моделирования, являются: качество получаемых решений (хотя его трудно определить на практике, поскольку истинный оптимум не известен) и время поиска, необходимое для их получения. Время поиска решения зависит от количества конфигураций системы, которые необходимо моделировать, а также от времени прогона одной конфигурации системы.

Необходимо отметить, что применение в качестве алгоритма оптимизации точных математических методов оптимизации, обеспечивающих нахождение оптимального решения, не всегда целесообразно, поскольку имитационная модель является копией реальной системы с некоторой степенью точности. При этом использование точных методов, как правило, требует значительных вычислительных затрат, что во многих случаях является критичным или вовсе недопустимо. Поэтому в большинстве случаев в качестве алгоритма поисковой оптимизации лучше использовать методы, которые не обязательно гарантируют достижение точного оптимума, а находят близкие к оптимальным решениям и при этом обеспечивают быструю поисковую сходимость алгоритма.

На сегодняшний день существует несколько программных пакетов оптимизации имитационного моделирования, которые используют средства имитационного моделирования совместно с различными методами поиска решений.

Одной из наиболее простых и адекватных задач исследования систем операционного и производственного менеджмента является технология имитационного моделирования на основе использования системы Micro Saint. Отличительными особенностями ее являются концептуальная завершенность, целостность и простота использования даже для исследования весьма сложных систем.

1.     
Задание

Распределение времени между приходами клиентов в банк описывается экспоненциальным распределением со средним значением 18 сек. В течение рабочего дня открыто 8 окошек кассиров. Каждый кассир выполняет только одну из пяти возможных операций, при этом в очередь к нему встают только те клиенты, которые нуждаются в выполнении соответствующей операции. Время выполнения каждой из операций имеет экспоненциальное распределение. Вероятности обслуживания клиента с выполнением определенной операции и соответствующие средние времена выполнения операций приведены в таблице.

Таблица 1

Вид обслуживания	Вероятность обслуживания	Среднее время выполнения операции
1	0,10	45
2	0,19	75
3	0,32	100
4	0,24	150
5	0,15	300

Приведенная ниже таблица содержит один из возможных вариантов распределения кассиров по операциям.

Таблица 2

Окно кассира, в котором выполняется операция	1	2	3	4	5	6	8
Вид обслуживания (кассовая операция)	1	2	3	3	4	4	5	5

Ни один из клиентов не требует выполнения более чем одной кассовой операции за один визит в банк. Попытайтесь найти такой вариант распределения кассовых операций по кассирам, при котором ожидание клиентов было бы минимальным.

2. Этап конструирования и описания модели

 

2.1 Структурная схема модели

Модель исследуемой системы должна быть представлена в виде сетевой структуры.

Овалы изображают блоки действий, стрелки - пути перемещения динамических объектов (тэгов), ромбы - разветвления таких путей, таблички изображают очереди тэгов, а маленький треугольник рядом с первым блоком определяет точку ввода тэгов в модель.

В общем случае сетевая структура модели может быть представлена как на одном (нулевом, верхнем) уровне, так и на нескольких уровнях. При этом нулевой уровень определяет основную модель, составленную из компонент, каждая из которых в свою очередь может рассматриваться как модель первого, второго и т. д. уровня.

Модель системы обслуживания в банке представлена на рисунке 1, в котором блоки имеют следующее назначение:

§  vxod и vyxod - символизируют приход/уход очередного клиента;

§  tip klienta - позволяет классифицировать клиентов по типу обслуживания;

§  klient 1, ... , klient 5 - блоки распределения клиентов по кассам;

§  kassa 1, ... , kassa 8 - блоки выполнения операций.

Рис.1 Модель системы обслуживания в банке

 

2.2 Описание элементов модели

Описание элементов модели связано с понятием переменной. Любая переменная используется для описания какой-либо характеристики системы, например, узел может находиться в одном из двух состояний:

§  занят (участвует в операции сборки детали),

§  свободен (не участвует в операции сборки детали).

Во многих случаях перечислить все значения переменной трудно (или невозможно), поэтому в таких ситуациях переменную характеризуют типом, определяющим ее возможные значения.

В процессе имитации исследуемой системы переменные модели будут изменять свои значения, поэтому перед запуском модели всем переменным необходимо назначить исходные начальные значения (Initial Value), которые будут определять исходное состояние системы.

Все переменные модели должны быть внесены в список переменных.

Рис. 2 Окно списка переменных (Name - имя, Value - значение переменной)

В таблице 3 представлен список с описанием всех переменных модели. В этом списке представлены системные переменные. Такие переменные используются в любой модели: переменная clock - модельное время и tag (тэг) - индивидуальный номер динамического объекта.

Кроме системных переменных в модели присутствуют переменные, которые определяются непосредственно пользователем применительно к его модели.

Таблица 3

Имя переменной	Смысловое содержание	Тип переменной	Начальное значение
clock	Системная переменная	Real	0
duration	Системная переменная	Real	0
objective	Системная переменная	Real	0
run	Системная переменная	Integer	1
seed	Системная переменная	Integer	1
tag	Системная переменная	Integer	0
k	Сигнал прихода очередного клиента в банк	Integer	0
Status[ ]	Сигнальная переменная для входа тэга в блок	Array of Integers	0
q[ ]	Количество клиентов в очереди, ожидающих обслуживания	0
M1-M8	Среднее время выполнения операции	Array of Integers

 

2.3 Описание задачи

Окно описания задачи открывается после двойного клика на соответствующем блоке сетевой многоуровневой структуры модели.

 

2.3.1 Блок Vxod

Блок Vxod имитирует поступление клиентов в банк. В данном блоке задается время между приходами клиентов - 18, тип распределения - Exponential.

Поля Time Distribution, Mean Time и Standard Deviation используются для задания интервала времени между приходами клиентов. В списке Time Distribution содержатся различные законы распределения вероятностей. Экспоненциальное распределение (Exponential Distribution) связано с моделированием простейших потоков. В таких потоках время между событиями распределено по экспоненциальному закону. Это распределение характеризуется единственным параметром - средним значением.

Поле Release Condition в общем случае содержит условие возможности входа тэга в соответствующий блок. Если в этом поле присутствует любое число, большее 0, вход в блок открыт.

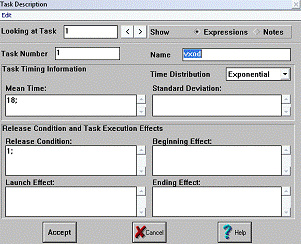
Рис. 3 Окно описания блока Vxod

Разветвитель типа Multiple используется для организации потока клиентов. Тэг, попадая в разветвитель, раздваивается: одна копия тэга поступает в блок tip klienta (при условии, если переменная k=0), вторая - на вход этого же блока (обратная связь).

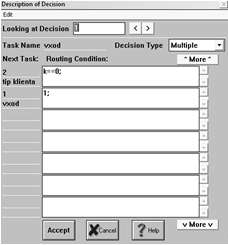
Рис. 4 Описание разветвителя

2.3.2 Блок tip klienta

Блок tip klienta является вспомогательным в структуре модели, необходим для организации прихода клиентов в банк по очереди - переменная k организует вход в блок только одного тэга.

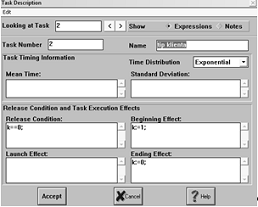
Рис. 5 Описание блока tip klienta

Разветвитель, стоящий после данного блока, распределяет всех пришедших клиентов в соответствии с заданной вероятностью, направляя их тем самым в разные очереди.

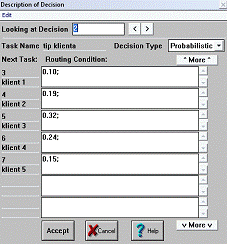
Рис. 6 Описание разветвителя

Разветвитель может использовать один из трех типов разветвления (Decision Type): Multiple, Probabilistic и Tactical. Тип Probabilistic определяет стохастический (случайный) механизм выбора тэгом направления дальнейшего движения. Для такого выбора в полях Routing Condition задаются вероятности переходов по выбранному направлению (их сумма должна быть равна 1).

2.3.3 Блоки klient 1, ... , klient 5

Блоки-клиенты организуют поступление посетителей в соответствующие очереди и особо необходимы для тех случаев, когда разные кассы выполняют одну и ту же операцию. При этом дополнительно используются разветвители, которые указывают клиенту направление движения в сторону свободной кассы. Описание блоков klient 1,…,5 представлено на рисунке 7,8,9,10,11.

блок компьютерный модель файл

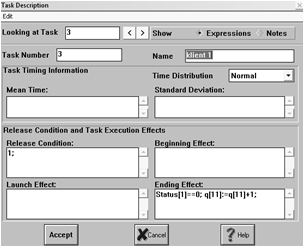
Рис. 7 Описание блока klient 1

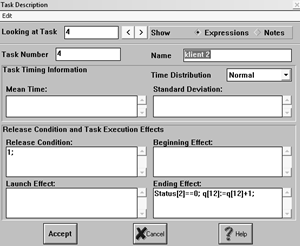
Рис. 8 Описание блока klient 2

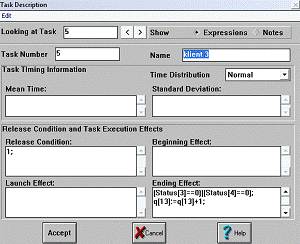
Рис. 9 Описание блока klient 3

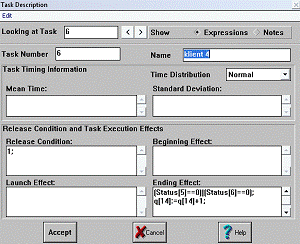
Рис. 10 Описание блока klient 4

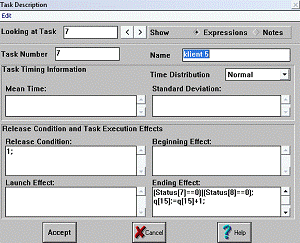
Рис. 11 Описание блока klient 5

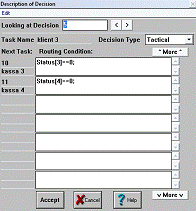
Рис. 12 Описание разветвителя после блоков klient 3, klient 4, klient 5

Тип Tactical использует поля Routing Condition для записи выражений, значения которых определяют направление дальнейшего движения тэга. Тэг, проходящий через разветвитель типа Tactical, будет направлен в ту задачу, для которой выражение, записанное в соответствующем поле Routing Condition, примет (в момент перехода) максимальное значение.

2.3.4 Блоки kassa 1, ... , kassa 8

Блоки kassa 1, ... , kassa 8 имитируют 8 окошек кассиров в банке. Перед данными блоками находятся очереди для учета количества клиентов, ожидающих обслуживания. Каждый вновь пришедший клиент встает в очередь перед кассой, если в момент своего прихода кассир занят для обслуживания другого клиента, и учитывается переменной q[i].

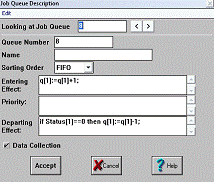
Рис. 13 Окно описания регистратора очереди в kassa 8

Когда кассир освобождается, переменная q[i] уменьшает свое значение на 1, тэг входит в блок, и переменная Status[i] меняет свое значение на 1, что говорит о занятости кассира. После выполнения операции переменная Status снова примет значение 0 (касса свободна).

На рисунках 14,15,16,17,18,19,20,21 приведено описание для блоков kassa 1, kassa 2, kassa 3, kassa 4, kassa 5, kassa 6, kassa 7, kassa 8.

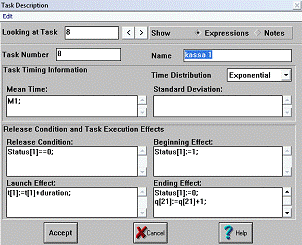
Рис. 14 Окно описания блока kassa 1

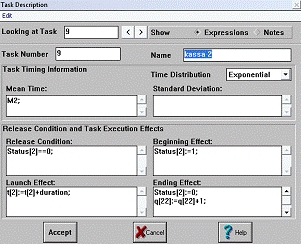
Рис. 15 Окно описания блока kassa 2

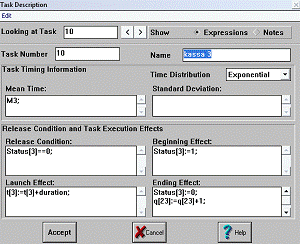
Рис. 16 Окно описания блока kassa 3

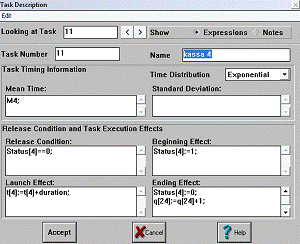
Рис. 17 Окно описания блока kassa 4

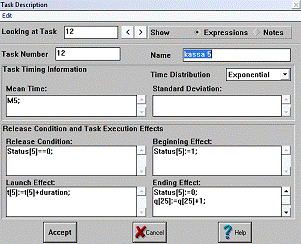
Рис. 18 Окно описания блока kassa 5

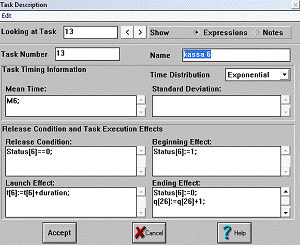
Рис. 19 Окно описания блока kassa 6

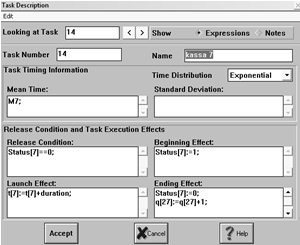
Рис. 20 Окно описания блока kassa 7

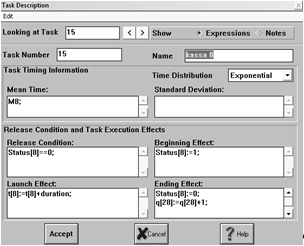
Рис. 21 Окно описания блока kassa 8

2.3.5 Блок Vyxod

В силу того, что ни один клиент не требует выполнения более чем одной кассовой операции за один визит в банк, после обслуживания на кассе он выходит из банка, что соответствует направления движения из блоков касс на блок Vyxod.

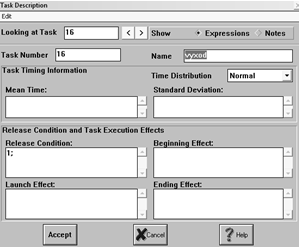
Рис. 22 Блок Vyxod

3. Развитие концепций: дополнительные методы

 

3.1 Календарь событий

Модельное время - это системная переменная, имитирующая ход часов реального времени, в котором "живет" и развивается исследуемая система. Имитация хода реального времени основывается на концепции событий, которые связаны с изменениями состояния модели. Такие события упорядочены по времени их возникновения в специальной структуре - календаре (расписании) событий. Пересчет модельного времени связан с выбором ближайшего по времени события из календаря и "переводом стрелок часов" модельного времени на момент возникновения этого события. Такая схема предполагает, что события могут следовать одно за другим через интервалы времени разной величины, включая и ноль (одновременно происходящие события).

Таким образом, календарь событий представляет собой своеобразный сценарий моделирования. Каждое событие такого сценария связано с выполнением определенного набора действий, которые должны произойти в тот или иной момент времени, по тому или иному условию. Сценарий содержит события двух типов:

1.      события, связанные с изменением текущего состояния системы (например, выход активного тэга из очереди, вход тэга в тот или иной блок и т. п.);

2.      запланированные события, специально введенные в календарь пользователем для управления процессом выполнения модели.

События первого типа полностью определяются структурой модели и описанием ее элементов, события второго типа управляют компьютерным экспериментом. Такое управление может быть связано с остановкой модели, установкой новых значений переменных в процессе моделирования, выполнением дополнительных вычислений по окончании этапа моделирования и т. п.

Планирование событий в календаре обычно используется для обработки промежуточных результатов компьютерного эксперимента и внесения необходимых изменений в динамике интерпретации модели.

В моем примере использования календаря событий (рис.23) для управления экспериментом привела планирование события остановки модели.

Рис. 23 Календарь событий

В поле Perform at Time назначается время наступления события (28801 единиц модельного времени (ЕМВ), 1 ЕМВ=1 мин.), в поле Expression определяется оператор, который должен быть выполнен в назначенное время. Нажатие кнопки Accept приводит к появлению в календаре событий соответствующей строки - уведомления о событии (см. рис.24). Внесение в календарь такого уведомления приведет к остановке модели в момент времени clock=28801 в реальном времени.

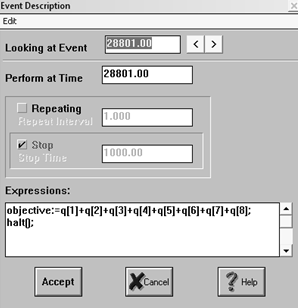
Рис. 24 Окно описания события

 

4. Этап проведения компьютерного эксперимента с моделью

 

4.1 Запуск модели

После составления описаний всех элементов модели она может быть запущена для выполнения задач. Для запуска и управления процессом выполнения модели используется правая часть средней панели инструментов (рис.25).

Рис. 25 Панель управления моделированием

 

4.2 Остановка модели

Существует два основных способа остановки модели: "вручную" (меню Execute, оператор Halt) и по определенному условию (достижение в модели определенного состояния).

Второй способ связан с размещением оператора остановки halt() в определенных полях описания модели. Например, размещение опера тора halt() в поле Entering Effect очереди приведет к тому, что, когда первый тэг войдет в очередь и произойдет вычисление этого эффекта, модель будет остановлена.

 

4.3 Сбор результатов компьютерного эксперимента

Целью любого компьютерного эксперимента является сбор информации о значениях переменных модели, наблюдаемых в процессе проведения эксперимента, и состояниях очередей, возникающих в процессе моделирования. Переменные, которые могут наблюдаться в эксперименте, составляют коллекцию переменных. Для одной и той же модели могут быть определены несколько разных коллекций, отличающихся друг от друга составом переменных и условиями, при которых осуществляется регистрация их значений. Список коллекций в моем примере: (рис.26).

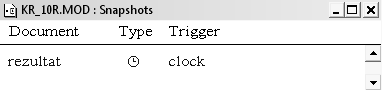
Рис. 26 Список коллекций переменных

В поле Document Name указывается имя коллекции (rezultat), в поле Variables to Store - имена переменных, которые мы включаем в коллекцию. Кроме того, в этом же окне указываются условия, при которых будут регистрироваться значения переменных коллекции (рис.27).

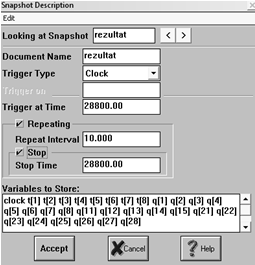
Рис. 27 Описание коллекции переменных

 

4.4 Определение параметров прогона модели

Перед запуском модели необходимо определить, в каком режиме будет проходить моделирование (выполняться прогон модели) (рис.28).

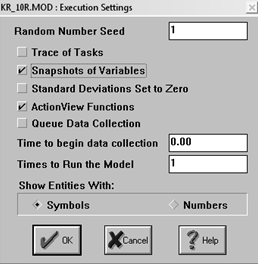
Рис. 28 Установка параметров прогона

В этом окне отмечаются функции, которые будут реализованы в процессе прогона модели.

1.       Trace of Tasks (трассировка задач).

2.  Snapshots of Variables (сбор значений переменных).

3.      Standard Deviations Set to Zero (не используется для простых задач).

4.      Action View Functions (анимация).

5.      Queue Data Collection (сбор данных о состояниях очередей).

6.      Time to begin Data Collection (модельное время начала сбора данных).

7.      Times to Run the Model (номер прогона модели).

.        Show Entities With (форма показа динамических объектов - тэгов, символами или их количеством, обычно символами).

Второй и пятый из этих пунктов необходимы для сбора результатов, остальные реализуют вспомогательные функции. После установки этих позиций при запуске модели система запросит вас о файлах, в которых вы предполагаете собирать информацию.

4.5 Структуры файлов результатов

На рис.29 - файл KR_10R.QUE, в котором собрана информация о состоянии очередей в течение прогона программы модели.

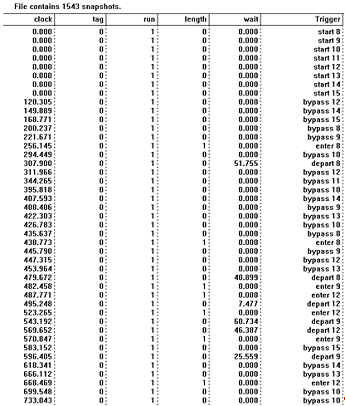
Рис. 29 Файл KR_10R.QUE

Файл содержит 6 полей:

1.         Clock (момент времени, в который изменилось состояние очереди);

2.      Tag (номер объекта-тэга, который был активен в этот момент времени). Напомним, что активный тэг - это тэг, который в текущий момент времени передвигается по структуре модели и меняет ее состояние;

3.      Run (номер прогона программы модели, он для нас не информативен);

4.      Length (длина очереди тэгов в момент Clock);

5.      Wait (время ожидания в очереди активного тэга);

6.      Trigger (характер изменения состояния очереди).

В поле Trigger встречаются записи четырех видов:

1.         Start (старт для работы с очередью);

2.      Enter (вход тэга в очередь);

3.      Depart (выход тэга из очереди);

4.      Bypass (проход тэга через очередь без задержки, т. е. через пустую очередь).

Решаем поставленную задачу с помощью целевой функции оптимизации objective, которая является суммой значений клиентов находящихся в очереди перед кассой. Используя в качестве изменяемой переменной время выполнения операции и минимизировав значение целевой функции, получим искомое решение:

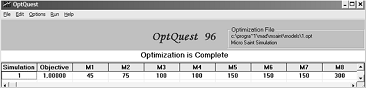
Рис. 30 Результаты моделирования

В результате был найден такой вариант распределения кассовых операций по кассирам, при котором ожидание клиентов становится минимальным. Для наилучшей организации обслуживания клиентов в банке необходимо следующее распределение:

Таблица 4

Окно кассира, в котором выполняется операция	1	2	3	4	5	6	7	8
Вид обслуживания (кассовая операция)	1	2	3	3	4	4	4	5

Заключение

Итак, моделирование позволяет заранее предвидеть ход событий и тенденции развития, присущие управляемой системе, выяснить условия ее существования и установить режим деятельности с учетом влияния разных факторов. При этом на первый взгляд, может показаться, что чем большее количество факторов учтено в модели, тем лучше сама модель. На самом деле детализированная модель не всегда целесообразна, так как это излишне усложняет модель и представляет трудность для ее анализа.

Совершенствование процесса принятия управленческих решений и соответственно повышение качества принимаемых решений достигается за счет использования научного подхода, моделей и методов принятия решений. Модель является представлением системы, идеи или объекта. Необходимо использовать модели из-за сложности организаций, невозможности проводить эксперименты в реальном мире, необходимости заглядывать в будущее. Основные типы моделей: физические, аналоговые и математические (символические). Общими проблемами моделирования являются недостоверные предпосылки, информационные ограничения, плохое использование результатов и чрезмерные расходы.

Сама по себе имитационная модель очень редко является целью проекта. Для конечного пользователя важно решение конкретной задачи, например: оптимизировать количество персонала, определиться с планированием территории, управлением парком транспортных средств, политикой закупок, процесс сборки изделий и т.д. И естественно, модель одного и того же объекта будет выглядеть совершенно по-разному при разных целях моделирования. А иногда при анализе задачи становится ясно, что изначально планировавшееся ИМ вовсе не необходимо, и можно обойтись более простыми методами (например, линейным программированием). Это важно отследить в самом начале проекта.

При имитационном моделировании динамические процессы системы-оригинала подменяются процессами, имитируемыми в абстрактной модели, но с соблюдением основных правил (режимов, алгоритмов) функционирования оригинала. В процессе имитации фиксируются определенные события и состояния или измеряются выходные воздействия, по которым вычисляются характеристики качества функционирования системы. Имитационное моделирование позволяет рассматривать процессы, происходящие в системе, практически на любом уровне детализации. При этом в имитационной модели можно реализовать практически любой алгоритм управленческой деятельности или поведения системы. Кроме того, модели, которые допускают исследование аналитическими методами, также могут анализироваться имитационными методами. Все это служит причиной того, что имитационные методы моделирования в настоящее время становятся основными методами исследования сложных систем.

Результаты имитационного моделирования могут быть оформлены в виде графиков или таблиц, в которых каждому варианту значений параметров исследуемого объекта поставлены в соответствие определенные значения показателей , оценивающих функционирование объекта. Однако зависимости между теми же величинами в аналитическом виде с помощью имитационной модели не могут быть получены Все имитационные модели представляют собой модели типа так называемого черного ящика. Это означает, что они обеспечивают выдачу выходных параметров системы, если на ее взаимодействующие подсистемы поступают входные воздействия. Поэтому для получения необходимой информации или результатов следует осуществить "прогон" (реализацию, "репетицию") моделей, а не "решать" их. Имитационные модели не способны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются экспериментатором. Этот кажущейся на первый взгляд недостаток, на самом деле является главным достоинством имитационного моделирования вследствие того, что целесообразность применения имитационного моделирования становится очевидной при наличии любого из следующих условий:

Ø  не существует законченной математической постановки задачи, либо еще не разработаны аналитические методы решения сформулированной математической модели

Ø  кроме оценки определенных параметров, желательно осуществить на имитационной модели наблюдение за ходом процесса в течение некоторого времени

Ø  имитационное моделирование может оказаться единственной возможностью вследствие трудностей постановки экспериментов и наблюдения явлений в реальных условиях.

В итоге можно сделать вывод: к методу имитационного моделирования обращаются тогда и только тогда, когда аналитическое решение задачи исследования данного объекта затруднено или невозможно.

Список используемой литературы

1.         Лекции по предмету "Моделирование систем";

2.      М. А. Кораблин "Информатика поиска управленческих решений", Москва, "СОЛОН-Пресс", 2003.