Моделирование работы системы и определение ее оптимальной структуры

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Казанский государственный технический университет

им. А.Н. Туполева

Кафедра КС

Курсовой проект по дисциплине

"Моделирование"

Выполнила:

Оценка: __________________________

Подпись руководителя: _____________

Руководитель проекта:

Захаров В.М. а

Дата защиты: «____»_______________2009 г.

Казань, 2009

Оглавление

1. Концептуальная модель (задание на курсовую работу)

. Формализация концептуальной модели

2.1 Построение формальной схемы функционирования системы

.2 Определение параметров и переменных модели, единицы модельного времени

.3 Определение закона функционирования системы

. Алгоритмизация модели и ее машинная реализация

.1 Выбор технических и программных средств моделирования

.2 Составление алгоритма моделирующей программы

.3 Описание моделирующей программы для детерминированного варианта модели

.4 Верификация (тестирование) программы

.5 Моделирование случайных воздействий

.5.1 Моделирование случайных воздействий, имеющих равномерное распределение

.5.1.1 Аппаратный способ

.5.1.2 Программный способ

.5.1.3 Выбор генератора равномерно распределенных ПСЧ

.5.2 Моделирование случайных воздействий, имеющих неравномерное распределение

.6 Описание моделирующей программы для стохастической модели

.7 Описание моделирующей программы для стохастической модели на языке GPSS

. Получение и интерпретация результатов моделирования

.1 Планирование машинного эксперимента

.2 Проведение прогонов модели

.3 Анализ результатов моделирования

. Заключение

Список литературы

1. Концептуальная модель (задание на курсовую работу)

программа моделирование алгоритм

Задание №121.

В систему через каждые 1.5 ± 0.5 мин. поочередно поступают задания 4-х типов, которые затем обрабатываются на ЭВМ. Время выполнения зависит от типа задания и распределено следующим образом: для задания 1 типа - по экспоненциальному закону с m = 0.7 мин; 2 типа - по нормальному закону с m = 3 мин., σ = 1; 3 типа по Гамма закону с σ = 1; 4 типа - по равномерному в интервале 2 - 6 мин. Если ЭВМ занята, задания поступают на накопители емкостью 1, причем для каждого задания в системе имеется свой накопитель.

Смоделировать 10 часов работы системы. Определить количество выполняемых запросов второго типа.

.        Варьируя параметрами системы, определить ее оптимальную структуру, обеспечивающую минимальное время простоя обслуживания.

2. Формализация концептуальной модели

.1 Построение формальной схемы функционирования системы

Моделируемая система представляет собой систему массового обслуживания с непрерывно - стохастическим законом функционирования. Следовательно, в качестве аппарата формализации процессов функционирования рассматриваемой системы, будем использовать типовую Q - схему. Построим структурную схему системы, используя стандартные

обозначения элементов Q-схемы (рис.1).

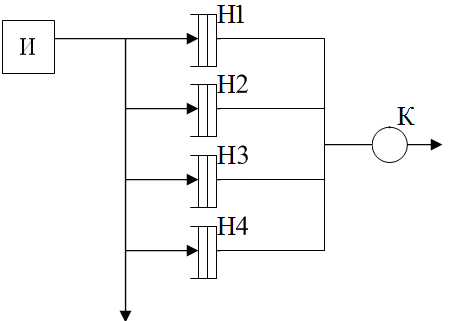
Рис. 1

В данной схеме использованы обозначения: И - источник заявок, Н1 - накопитель для задания 1, Н2 - накопитель для задания 2, Н3 - накопитель для задания 3, Н4 - накопитель для задания 4, К - ЭВМ.

2.2 Определение параметров и переменных модели, единицы модельного времени

Определим множество внешних воздействий, внутренних параметров, характеристик, существенных для анализа функционирования системы:- время между приходом заявок, tm2, tm3, tm4 - время обработки на ЭВМ- текущее время между приходом заявок, tektm2, tektm3, tektm4 - текущее время обработки на ЭВМ, tv2, tv3, tv4 - текущее время обработки, нужно для накопителей

t_stop, t_stop_percent - время простоя (также и в процентах)- активность ЭВМ- тип заявки, kr2, kr3, kr4 - количество выполненных заявок, kn2, kn3, kn4 - заявок осталось на накопителе, ko2, ko3, ko4 - количество отказов, kt2, kt3, kt4 - общее количество- время работы системы- наличие заявки на входе, n2, n3, n4 - накопители

За единицу модельного времени (емв) примем 0.1 минуты.

.3 Определение закона функционирования системы

С использованием временных диаграмм (в приложении 1) опишем работу системы следующим образом: через определенное время приходит задание и обрабатывается на ЭВМ в течение определенного времени в зависимости от типа. Если ЭВМ занята, заявка оседает на одноместном накопителе (для каждого типа задания свой). В случае, если накопитель занят, задание не выполняется - происходит отказ в обслуживании. На начальном этапе построения модели будем рассматривать детерминированный вариант модели. Для этого при создании детерминированной модели заданной вычислительной системы заменим стохастические потоки их математическими ожиданиями: время между приходом пользователей - 1.5 мин.; время обработки задания 1 - го типа - 0.7 мин.; время обработки задания 2 - го типа - 3 мин.; время обработки задания 3 - го типа - 2 мин.; время обработки задания 4 - го типа - 4 мин. С поступлением заявки в систему, она начинает обрабатываться, если свободна ЭВМ. Итак, после прихода первого задания, оно обрабатывается 0.7 мин. Второе задание обрабатывается в течение 3 мин. К приходу третьего задания ЭВМ занята, и задание отправляется на накопитель. К приходу 4-го задания ЭВМ освобождается, но на ней обрабатывается задание 3, а 4-е отправляется на свой накопитель. Несмотря на довольно плотный поток заданий, в работе ЭВМ наблюдаются простои, которые периодически повторяются. Из диаграммы видно, что, подав на вход системы 400 заявок, мы получим следующие результаты:

Время простоя канала в емв: 20.000000

В процентах: 0.003333

Выполнено заданий (по типам):

1. 51

2. 25

3. 73

4. 75

Осталось на накопителе:

1. 1

2. 1

3. 1

4. 0

Отказ в обслуживании:

1. 48

2. 74

3. 26

4. 25

3. Алгоритмизация модели и ее машинная реализация

.1 Выбор технических и программных средств моделирования

В качестве технических и программных средств для выполнения курсовой работы по моделированию можно использовать ПВЭМ IBM РС, принтер, в качестве программных средств - пакет Turbo C и разработанные на кафедре ЭВМ КГТУ им. А.Н. Туполева автоматизированную информационную систему формирования последовательностей псевдослучайных чисел (ПСЧ) с равномерным распределением (GENER) и автоматизированную систему статистического анализа информации (STAN). Для статистического анализа и отображения результатов можно использовать также интегрированные пакеты MATHLAB, MATHCAD.

.2 Составление алгоритма моделирующей программы

3.3 Описание моделирующей программы для детерминированного варианта модели

Представим листинг моделирующей программы:

#include <stdio.h>

#include <conio.h>

#define EMV_MAX 6000

tps, // время между приходом заявок

tm1, tm2, tm3, tm4, // время обработки на ЭВМ

tektps, // текущее время между приходом заявок

tektm1, tektm2, tektm3, tektm4, // текущее время обработки на ЭВМ

tv1, tv2, tv3, tv4, // время выполнения. нужно для накопителей

t_stop, t_stop_percent; // время простоя, // ЭВМ, // тип заявки1, kr2, kr3, kr4, // количество выполненных заявок

kn1, kn2, kn3, kn4, // осталось на накопителе

ko1, ko2, ko3, ko4, // количество отказов

kt1, kt2, kt3, kt4, // общее количество

t; // время работы системы

bool

ns, // наличие заявки на входе

n1, n2, n3, n4; // накопителиmain()

{

// предустановки

ns = false;

ts = 0; // заявок еще нет, с приходом первой тип будет равен 1

sm = 0;= 0; kr2 = 0; kr3 = 0; kr4 = 0;= 0; kn2 = 0; kn3 = 0; kn4 = 0;= 0; ko2 = 0; ko3 = 0; ko4 = 0;= 0; kt2 = 0; kt3 = 0; kt4 = 0;= 0;= 0; tektm2 = 0; tektm3 = 0; tektm4 = 0;= 0; tv2 = 0; tv3 = 0; tv4 = 0;= false; n2 = false; n3 = false; n4 = false; // пустые("tps (default: 15) = "); scanf("%f", &tps); // 1.5("tm1 (default: 7) = "); scanf("%f", &tm1); // 0.7("tm2 (default: 30) = "); scanf("%f", &tm2); // 3("tm3 (default: 20) = "); scanf("%f", &tm3); // 2("tm4 (default: 40) = "); scanf("%f", &tm4); // 2 ~ 6. avg = 4(t = 0; t < EMV_MAX; t++)

{

if (++tektps >= tps) // поступила заявка

{

ns = true;= 0;++;(ts == 5) ts = 1; // циклично(ts)

{1:++;;2:++;;3:++;;4:++;;

}

}(sm == 1)

{(n1) tv1++; else tektm1++;(n1) if (tv1 >= tm1) //заявка выполнена

{= 0;= 0;++;= false;

}if (tektm1 >= tm1) //заявка выполнена

{= 0;= 0;++;

}

}if (sm == 2)

{(n2) tv2++; else tektm2++;(n2) if (tv2 >= tm2) //заявка выполнена

{= 0;= 0;++;= false;

}if (tektm2 >= tm2) //заявка выполнена

{= 0;= 0;++;

}

}if (sm == 3)

{(n3) tv3++; else tektm3++;(n3) if (tv3 >= tm3) //заявка выполнена

{= 0;= 0;++;= false;

}if (tektm3 >= tm3) //заявка выполнена

{= 0;= 0;++;

}

}if (sm == 4)

{(n4) tv4++; else tektm4++;(n4) if (tv4 >= tm4) //заявка выполнена

{= 0;= 0;++;= false;

}if (tektm4 >= tm4) //заявка выполнена

{= 0;= 0;++;

}

}if (sm == 0) // ЭВМ свободна

{

if (ns) // есть заявка на входе

{

if (!(n1 && n2 && n3 && n4)) // все накопители свободны

switch (ts) // тип заявки

{1: = 1; // занимаем ЭВМ

break;

case 2:

sm = 2; // занимаем ЭВМ

break;3:= 3; // занимаем ЭВМ;4:= 4; // занимаем ЭВМ;:("--ERROR-- Unknown type");1;

}goto m;= false;

}

else // нет заявки на входе (выполняем с накопителя)

{:;(n1)

{= 1;++;

}if (n2)

{= 2;++;

}if (n3)

{= 3;++;

}if (n4)

{

sm = 4;

tv4++;

}

else t_stop++; // если не занята ЭВМ и нечего выполнять с накопителя... т.е. тупо стоим на месте

}

}

if (((t == 0) || (t % (int)tps == 0)) && (sm != 0)) // по приходу следующего задания и если занята ЭВМ

{(ts)

{1:(!n1) n1 = true;ko1++;;2:(!n2) n2 = true;ko2++;;3:(!n3) n3 = true;ko3++;;4:(!n4) n4 = true;ko4++;;

}

}

} // for_stop_percent = t_stop / EMV_MAX;= n1 ? 1 : 0;= n2 ? 1 : 0;= n3 ? 1 : 0;= n4 ? 1 : 0;("Idle time %f, %f in percent\n", t_stop, t_stop_percent);("Success: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", kr1, kr2, kr3, kr4);("Accumulated: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", kn1, kn2, kn3, kn4);("Denied: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", ko1, ko2, ko3, ko4);("Total: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", kt1, kt2, kt3, kt4);();

return 0;

}

.4 Верификация (тестирование) программы

Протокол работы моделирующей программы

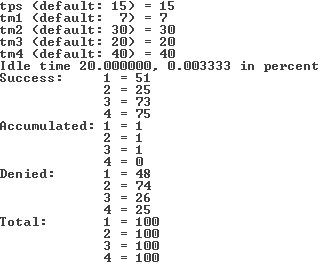
Результаты работы моделирующей программы совпадают с рассчитанными теоретически, следовательно, программа написана и работает правильно.

.5 Моделирование случайных воздействий.

.5.1 Моделирование случайных воздействий, имеющих равномерное распределение.

.5.1.1 Аппаратный способ

Для формирования файлов ПСЧ воспользуемся автоматизированной системой GENERATO, разработанной на кафедре ЭВМ. Данная система моделирует работу генератора псевдослучайных чисел (ГПСЧ), построенного на основе регистра сдвига. Запустив файл с системой GENERATO, пользователь работает в диалоговом режиме с ПЭВМ: определяет структуру генератора: разрядность регистра сдвига, количество и номера подключенных в цепь обратной связи, разрядность и количество генерируемых чисел и др. Сформируем данным способом файл равномерно распределённых ПСЧ. Определим структуру ГПСЧ для создания файла ПСЧ.

Данные:

·   Число разрядов - 20;

·   Число подключений в обратную связь - 10;

·   Номера подключенных разрядов - 2, 3, 5, 7, 9, 11, 13, 15, 17, 18;

·   Количество генерируемых ПСЧ - 30000;

·   Разрядность ПСЧ - 30;

·   Число сдвигов - 15;

·   Исходное состояние ГПСЧ - 11100111001110011100.

С помощью одной из систем статистического анализа, например, STAN определим характеристики полученных файлов:

Тест на равномерность

Тест комбинаций:

На основании проведенного теста проверенную последовательность чисел можно считать равномерной с доверительной вероятностью

0.001

Тест пар:

Результаты проведенного теста показывают, что распределение 10 старших разрядов случайного числа можно считать равномерным с доверительной вероятностью (по разрядам):

Разряд : > 1 ***** дов. вер. = 0.700

Разряд : > 2 ***** дов. вер. = 0.800

Разряд : > 3 ***** дов. вер. = 0.950

Разряд : > 4 ***** дов. вер. = 0.950

Разряд : > 5 ***** дов. вер. = 0.950

Разряд : > 6 ***** дов. вер. = 0.700

Разряд : > 7 ***** дов. вер. = 0.800

Разряд : > 8 ***** дов. вер. = 0.900

Разряд : > 9 ***** дов. вер. = 0.990

Разряд : >10 ***** дов. вер. = 0.990

Тест многомерной равномерности:

На основании проведенного теста, можно считать проверяемую выборку чисел равномерной с доверительной вероятностью не более 0.800

Тест максимального из t:

Проверяемую выборку чисел можно считать равномерной с доверительной вероятностью не более 0.999

Тест на независимость

Тест корреляции:

На основании исследования корреляционной зависимости чисел проверяемой последовательности данную последовательность можно считать случайной с доверительной вероятностью 0.20

Тест на случайность

Тест монотонности:

На основании исследования монотонности чисел, проверяемую последовательность можно считать случайной с доверительной вероятностью по не убыванию 0.8

********** по не возрастанию 0.9

Тест серий:

На основании проведенного теста последовательность можно считать случайной с доверительной вероятностью 0.8

Тест на периодичность

Период не обнаружен.

Гистограмма распределения

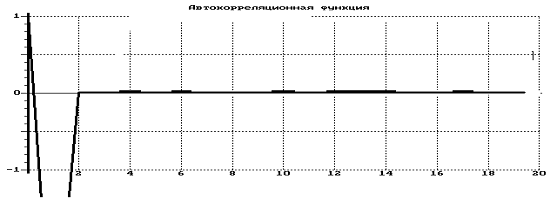
Количественное расхождение равномерного статистического распределения от теоретического определим по критериям согласия Хи-квадрат и Колмогорова, пользуясь STAN.

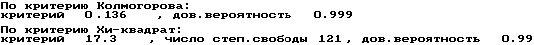
.5.1.2 Программный способ

Создадим процедуру для генерации последовательности псевдослучайных чисел.

Процедура для генерации времени прихода заявок:

#include <stdio.h>unirand(void);long dummy;

/* L'Ecuyer algorithm for uniform random generator with practically endless period. */

#define EPS 1.2e-7

#define RNMX (1.0-EPS)

#define NTAB 32

#define IM1 2147483563

#define IM2 2147483399

#define NWUP 8

#define AM (1./IM1)

#define IMM1 (IM1-1)

#define IA1 40014

#define IA2 40692

#define IQ1 53668

#define IQ2 52774

#define IR1 12211

#define IR2 3791

#define NDIV (1+IMM1/NTAB)unirand(void)

{j;k;long dummy2=123456789;long iy=0;long iv[NTAB];temp;

/* initialize the random sequence (first set of coefficients, theclose to that in the function above */(dummy<=0 || !iy)

{

/* avoid negative or zero seed */(dummy<0) dummy=-dummy;if (dummy==0) dummy=1;=dummy;

/* after NWUP warmups, initialize shuffle table */(j=NTAB+NWUP-1;j>=0;j--)

{=dummy/IQ1;((dummy=IA1*(dummy-k*IQ1)-IR1*k)<0) dummy+=IM1;(j<NTAB) iv[j]=dummy;

}

/* first specimen from the table */=iv[0];

}

/* regular work: generate 2 sequences. */=dummy/IQ1;((dummy=IA1*(dummy-k*IQ1)-IR1*k)<0) dummy+=IM1;=dummy2/IQ2;((dummy2=IA2*(dummy2-k*IQ2)-IR2*k)<0) dummy2+=IM2;

/* shuffle output combining 2 sequences */=iv[j=iy/NDIV]-dummy2;[j]=dummy;(iy<1) iy+=IMM1;

/* return the result, as in the previous function */((temp=AM*iy)>RNMX) return(RNMX);return(temp);

}main()

{*pResult = fopen("result.txt", "w");(int i = 0; i < 5000; i++) fprintf(pResult,"%f\n", unirand());(pResult);0;

}

В процедуре используется т.н. «Алгоритм Л'Экюера». Считается одним из наиболее «чистых» генераторов. Впрочем, это нужно подтвердить анализом.

С помощью системы статистического анализа STAN определим характеристики полученного файла.

Числовые характеристики:

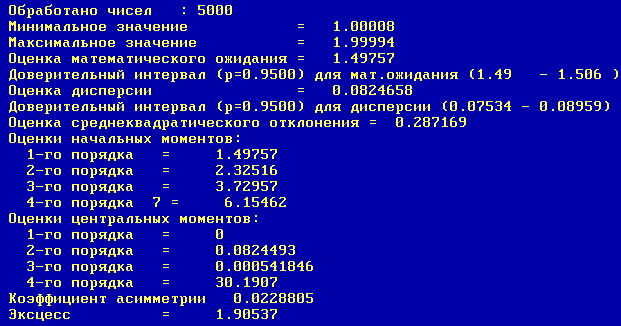
Тест на равномерность.

Тест комбинаций:

На основании проведенного теста проверенную последовательность чисел можно считать равномерной с доверительной вероятностью

.001

Тест пар:

Результаты проведенного теста показывают, что распределение 10 старших разрядов случайного числа можно считать равномерным с доверительной вероятностью (по разрядам):

Разряд : > 1 ***** дов. вер. = 0.001

Разряд : > 2 ***** дов. вер. = 0.700

Разряд : > 3 ***** дов. вер. = 0.500

Разряд : > 4 ***** дов. вер. = 0.500

Разряд : > 5 ***** дов. вер. = 0.300

Разряд : > 6 ***** дов. вер. = 0.700

Разряд : > 7 ***** дов. вер. = 0.950

Разряд : > 8 ***** дов. вер. = 0.500

Разряд : > 9 ***** дов. вер. = 0.800

Разряд : >10 ***** дов. вер. = 0.700

Тест многомерной равномерности:

На основании проведенного теста, можно считать проверяемую выборку чисел равномерной с доверительной вероятностью не более 0.001

Тест максимального из t:

Проверяемую выборку чисел можно считать равномерной с доверительной вероятностью не более 0.001

Тест на независимость.

Тест корреляции:

На основании исследования корреляционной зависимости чисел проверяемой последовательности данную последовательность можно считать случайной с доверительной вероятностью 0.493

Тест на случайность.

Тест монотонности:

На основании исследования монотонности чисел, проверяемую последовательность можно считать случайной с доверительной вероятностью по не убыванию 0.2

************* по не возрастанию 0.2

Тест серий:

На основании проведенного теста последовательность можно считать случайной с доверительной вероятностью 0.8

Тест на периодичность.

Период не обнаружен

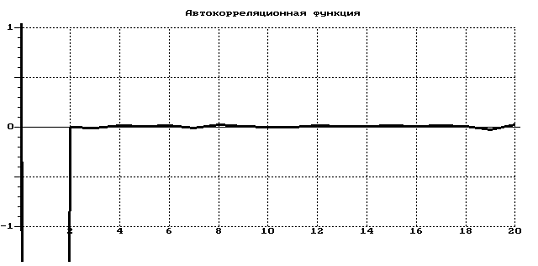
Гистограмма распределения и график автокорреляционной функции ()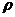

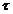3.5.1.. Выбор генератора равномерно распределенных ПСЧ.

В качестве генератора ПСЧ для дальнейшего использования в качестве источника равномерно распределенных случайных чисел возьмем генератор, полученный программным способом.

.5.2 Моделирование случайных воздействий, имеющих неравномерное распределение.

В данной системе согласно заданию требуется сформировать стохастические потоки чисел, распределенные по экспоненциальному, нормальному и Гамма закону. Сформируем файлы с соответствующими законами, по следующим алгоритмам:

a) алгоритм для экспоненциального закона распределения (для m = 0.7):

 ,

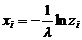где 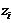 - равномерно распределенное число из интервала (0, 1);

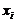 - очередное число последовательности;

Листинг программы по вышеуказанному алгоритму:

#include<stdio.h>

#include<conio.h>

#include<math.h>

#include<stdlib.h>main()

{*f;xi=0, z=0,=0.7;l;k=0;=1/m;=fopen ("exponent.dat", "w");(k=1; k<=5000; k++)

{=(float)rand()/32765;=-(1/l)*log(z);(f, "%f\n", xi);

}

fclose(f);

getch();

}

б) алгоритм для нормального закона распределения (для m = 3, σ = 1):

,

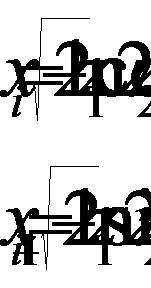где 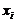 - очередное число последовательности;

Листинг программы по вышеуказанному алгоритму:

#include<stdio.h>

#include<math.h>

#include<stdlib.h>

#include<stdlib.h>main(void)

{j;x1,x2, z1,z2,a1,a2;*f=fopen("norm_zak.dat","w");(j=0;j<2500;j++)

{=(float)rand()/RAND_MAX;=(float)rand()/RAND_MAX;=sqrt(-2*log(z1))*cos(2*3.14*z2);=sqrt(-2*log(z1))*sin(2*3.14*z2);=sqrt(1)*x1+3;=sqrt(1)*x2+3;(f,"%f\n",a1);(f,"%f\n",a2);

}

fclose(f);

}

в) алгоритм для Гамма закона распределения (для m = 2, σ = 1)

где xi - очередное число последовательности.

Листинг программы по вышеуказанному алгоритму:

#include <stdio.h>

#include <math.h>

#include <stdlib.h>main()

{*f=fopen("gam.txt","w");x, alfa=1, beta=2, s = 0;(int n=0;n<=5000; n++)

{(int i=0;i<=alfa;i++) s+=log((double)rand()/RAND_MAX);=beta*s;=0;(f,"%f\n",x);

}(f);0;

}

3.5.2.1 Оценка качества чисел, имеющих экспоненциальный закон распределения

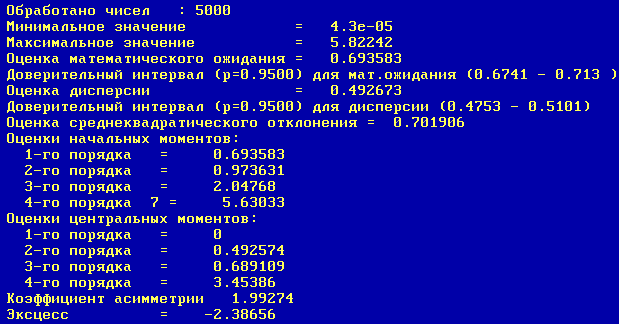
В таблице 1 определены числовые характеристики данных ПСЧ.

Плотность распределения для экспоненциального закона распределения имеет вид:

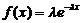
Область значений случайной величины: .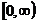

Параметры закона: ,, .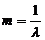

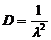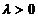Таблица 1

С помощью системы статистического анализа STAN дадим анализ последовательности случайных чисел, полученной программным путем по алгоритму из п. 3.5.2.

Тест на равномерность

Тест комбинаций:

На основании проведенного теста проверенную последовательность чисел можно считать равномерной с доверительной вероятностью

0.001

Тест пар:

Результаты проведенного теста показывают, что распределение 10 старших разрядов случайного числа можно считать равномерным с доверительной вероятностью (по разрядам):

Разряд : > 1 ***** дов. вер. = 0.001

Разряд : > 2 ***** дов. вер. = 0.001

Разряд : > 3 ***** дов. вер. = 0.001

Разряд : > 4 ***** дов. вер. = 0.001

Разряд : > 5 ***** дов. вер. = 0.001

Разряд : > 6 ***** дов. вер. = 0.001

Разряд : > 7 ***** дов. вер. = 0.100

Разряд : > 8 ***** дов. вер. = 0.700

Разряд : > 9 ***** дов. вер. = 0.100

Разряд : >10 ***** дов. вер. = 0.500

Тест многомерной равномерности :

На основании проведенного теста, можно считать проверяемую выборку чисел равномерной с доверительной вероятностью не более 0.001

Тест максимального из t:

Проверяемую выборку чисел можно считать равномерной с доверительной вероятностью не более 0.001

Тест на независимость

Тест корреляции:

На основании исследования корреляционной зависимости чисел проверяемой последовательности данную последовательность можно считать случайной с доверительной вероятностью 0.12

Тест на случайность

Тест монотонности:

На основании исследования монотонности чисел, проверяемую последовательность можно считать случайной с доверительной вероятностью по не убыванию 0.05

******************** по не возрастанию 0.001

Тест серий:

На основании проведенного теста последовательность можно считать случайной с доверительной вероятностью 0.999

Тест на периодичность

Период не обнаружен.

График автокорелляционной функции

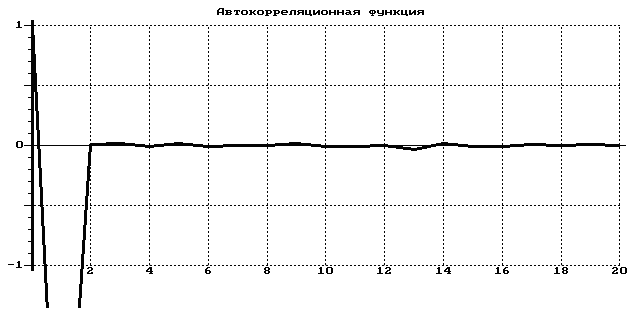
Гистограмма распределения

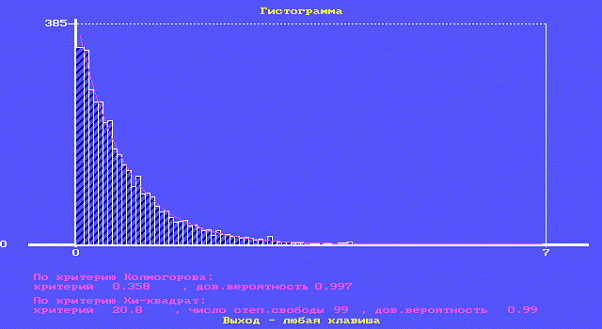
Полученная нами последовательность ПСЧ, имеющая экспоненциальный закон распределения, удовлетворяет предъявленным требованиям по качеству и может быть использована в стохастической моделирующей программе.

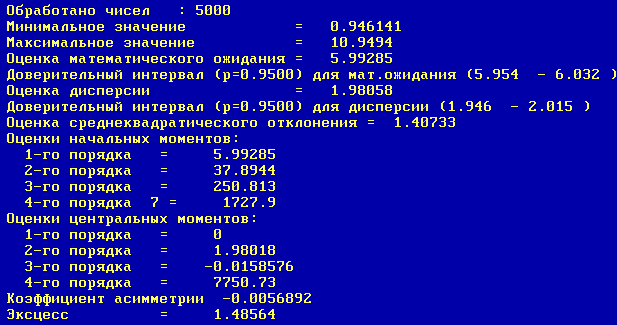
3.5.2.2 Обработка файла чисел, имеющих нормальный закон распределения.

В таблице 2 определены числовые характеристики данных ПСЧ.

Плотность распределения для нормального закона распределения имеет вид:

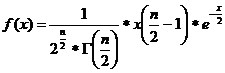
Область значений случайной величины: 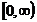. Параметры закона n = 1, 2, 3, …; m=n; D=2*n.

Таблица 2

С помощью системы статистического анализа STAN дадим анализ последовательности случайных чисел, полученной программным путем по алгоритму из п. 3.5.2.

Тест на равномерность.

Тест комбинаций:

На основании проведенного теста проверенную последовательность чисел можно считать равномерной с доверительной вероятностью

.001

Тест пар:

Результаты проведенного теста показывают, что распределение 10 старших разрядов случайного числа можно считать равномерным с доверительной вероятностью (по разрядам):

Разряд : > 1 ***** дов. вер. = 0.001

Разряд : > 2 ***** дов. вер. = 0.001

Разряд : > 3 ***** дов. вер. = 0.001

Разряд : > 4 ***** дов. вер. = 0.001

Разряд : > 5 ***** дов. вер. = 0.800

Разряд : > 6 ***** дов. вер. = 0.050

Разряд : > 7 ***** дов. вер. = 0.500

Разряд : > 8 ***** дов. вер. = 0.900

Разряд : > 9 ***** дов. вер. = 0.100

Разряд : >10 ***** дов. вер. = 0.100

Тест многомерной равномерности:

На основании проведенного теста, можно считать проверяемую выборку чисел равномерной с доверительной вероятностью не более 0.001

Тест максимального из t:

Проверяемую выборку чисел можно считать равномерной с доверительной вероятностью не более 0.001

Тест на независимость.

Тест корреляции:

На основании исследования корреляционной зависимости чисел проверяемой последовательности данную последовательность можно считать случайной с доверительной вероятностью 0.5

Тест на случайность.

Тест монотонности:

На основании исследования монотонности чисел, проверяемую последовательность можно считать случайной с доверительной вероятностью по неубыванию 0.001

********* по невозрастанию 0.5

Тест серий:

На основании проведенного теста последовательность можно считать случайной с доверительной вероятностью 0.999

Тест на периодичность.

Период не обнаружен

Гистограмма распределения и график автокорреляционной функции ()

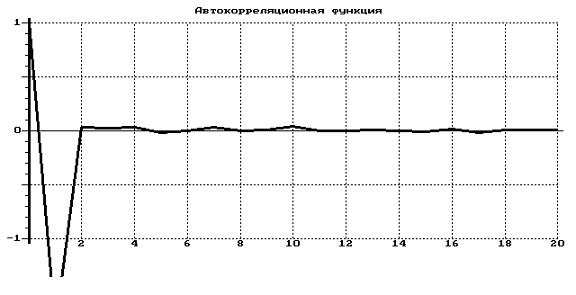
Полученная нами последовательность ПСЧ, имеющая нормальный закон распределения, удовлетворяет предъявленным требованиям по качеству и может быть использована в стохастической моделирующей программе.

3.5.2.3.Обработка файла чисел, имеющих Гамма закон распределения.

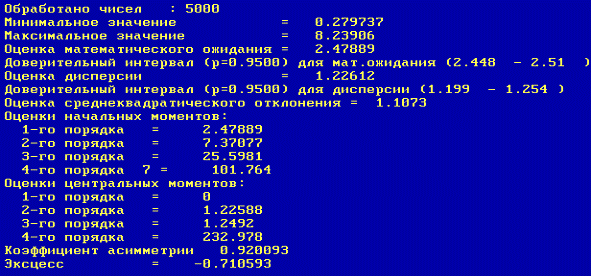
В таблице 3 определены числовые характеристики данных ПСЧ.

Плотность распределения для Гамма закона распределения имеет вид:

Область значений случайной величины: 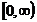. Параметры закона m=α-β; D=α-β2.

Таблица 3

С помощью системы статистического анализа STAN дадим анализ последовательности случайных чисел, полученной программным путем по алгоритму из п. 3.5.2.

Тест на равномерность.

Тест комбинаций:

На основании проведенного теста проверенную последовательность чисел можно считать равномерной с доверительной вероятностью

.001

Тест пар:

Результаты проведенного теста показывают, что распределение 10 старших разрядов случайного числа можно считать равномерным с доверительной вероятностью (по разрядам):

Разряд : > 1 ***** дов. вер. = 0.001

Разряд : > 2 ***** дов. вер. = 0.001

Разряд : > 3 ***** дов. вер. = 0.001

Разряд : > 4 ***** дов. вер. = 0.001

Разряд : > 5 ***** дов. вер. = 0.800

Разряд : > 6 ***** дов. вер. = 0.050

Разряд : > 7 ***** дов. вер. = 0.500

Разряд : > 8 ***** дов. вер. = 0.900

Разряд : > 9 ***** дов. вер. = 0.100

Разряд : >10 ***** дов. вер. = 0.100

Тест многомерной равномерности:

На основании проведенного теста, можно считать проверяемую выборку чисел равномерной с доверительной вероятностью не более 0.001

Тест максимального из t:

Проверяемую выборку чисел можно считать равномерной с доверительной вероятностью не более 0.001

Тест на независимость.

Тест корреляции:

На основании исследования корреляционной зависимости чисел проверяемой последовательности данную последовательность можно считать случайной с доверительной вероятностью 0.5

Тест на случайность.

Тест монотонности:

На основании исследования монотонности чисел, проверяемую последовательность можно считать случайной с доверительной вероятностью по неубыванию 0.001

********* по невозрастанию 0.5

Тест серий:

На основании проведенного теста последовательность можно считать случайной с доверительной вероятностью 0.999

Тест на периодичность.

Период не обнаружен

Гистограмма распределения и график автокорреляционной функции ()

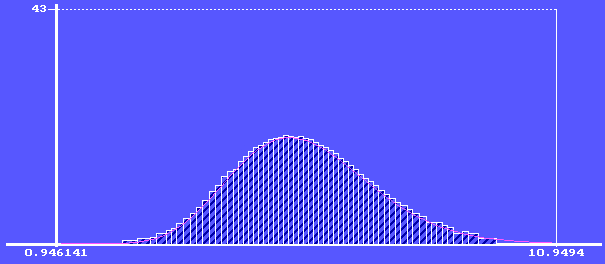
Полученная нами последовательность ПСЧ, имеющая Гамма закон распределения, удовлетворяет предъявленным требованиям по качеству и может быть использована в стохастической моделирующей программе.

.6 Описание моделирующей программы для стохастической модели

В моделирующую программу с вероятностным законом функционирования внесем в первую некоторые изменения: детерминированные параметры заменим стохастическими потоками чисел, формирующимися по указанным в задании законам. Листинг моделирующей программы со стохастическими потоками чисел представлен ниже.

#include <stdio.h>

#include <stdlib.h> // for atof

#include <conio.h> // for getch

#define EMV_MAX 6000

float

tps, // время между приходом заявок

tm1, tm2, tm3, tm4, // время обработки на ЭВМ

tektps, // текущее время между приходом заявок

tektm1, tektm2, tektm3, tektm4, // текущее время обработки на ЭВМ

tv1, tv2, tv3, tv4, // время выполнения. нужно для накопителей

t_stop, t_stop_percent; // время простоя, // ЭВМ, // тип заявки1, kr2, kr3, kr4, // количество выполненных заявок

kn1, kn2, kn3, kn4, // осталось на накопителе

ko1, ko2, ko3, ko4, // количество отказов

kt1, kt2, kt3, kt4, // общее количество

t; // время работы системы

bool

ns, // наличие заявки на входе

n1, n2, n3, n4; // накопители

FILE

*f0 = fopen("ra0.txt", "r"),

*f1 = fopen("exp.txt", "r"),

*f2 = fopen("nor.txt", "r"),

*f3 = fopen("gam.txt", "r"),

*f4 = fopen("rav.txt", "r");stohread(FILE *stream);main()

{

// предустановки

ns = false;

ts = 0; // заявок еще нет, с приходом первой тип будет равен 1

sm = 0;= 0; kr2 = 0; kr3 = 0; kr4 = 0;= 0; kn2 = 0; kn3 = 0; kn4 = 0;= 0; ko2 = 0; ko3 = 0; ko4 = 0;= 0; kt2 = 0; kt3 = 0; kt4 = 0;= 0;= 0; tektm2 = 0; tektm3 = 0; tektm4 = 0;= 0; tv2 = 0; tv3 = 0; tv4 = 0;(f0, SEEK_SET, 0);(f1, SEEK_SET, 0);(f2, SEEK_SET, 0);(f3, SEEK_SET, 0);(f4, SEEK_SET, 0);= false; n2 = false; n3 = false; n4 = false; // пустые= 10 * stohread(f0);= 10 * stohread(f1);= 10 * stohread(f2);= 10 * stohread(f3);= 10 * stohread(f4);(t = 0; t < EMV_MAX; t++)

{

if (++tektps >= tps) // поступила заявка

{

ns = true;= 0;++;(ts == 5) ts = 1; // циклично(ts)

{1:++;;2:++;;3:++;;4:++;;

}= 10 * stohread(f0);

}(sm == 1)

{(n1) tv1++; else tektm1++;(n1) if (tv1 >= tm1) //заявка выполнена

{= 0;= 0;++;= false;= 10 * stohread(f1);

}if (tektm1 >= tm1) //заявка выполнена

{= 0;= 0;++;= 10 * stohread(f1);

}

}if (sm == 2)

{(n2) tv2++; else tektm2++;(n2) if (tv2 >= tm2) //заявка выполнена

{= 0;= 0;++;= false;= 10 * stohread(f2);

}if (tektm2 >= tm2) //заявка выполнена

{= 0;= 0;++;= 10 * stohread(f2);

}

}if (sm == 3)

{(n3) tv3++; else tektm3++;(n3) if (tv3 >= tm3) //заявка выполнена

{= 0;= 0;++;= false;= 10 * stohread(f3);

}if (tektm3 >= tm3) //заявка выполнена

{= 0;= 0;++;= 10 * stohread(f3);

}

}if (sm == 4)

{(n4) tv4++; else tektm4++;(n4) if (tv4 >= tm4) //заявка выполнена

{= 0;= 0;++;= false;= 10 * stohread(f4);

}if (tektm4 >= tm4) //заявка выполнена

{= 0;= 0;++;= 10 * stohread(f4);

}

}if (sm == 0) // ЭВМ свободна

{

if (ns) // есть заявка на входе

{

if (!(n1 && n2 && n3 && n4)) // все накопители свободны

switch (ts) // тип заявки

{1: = 1; // занимаем ЭВМ

break;

case 2:

sm = 2; // занимаем ЭВМ

break;3:= 3; // занимаем ЭВМ;4:= 4; // занимаем ЭВМ;:("--ERROR-- Unknown type");1;

}goto m;= false;

}

else // нет заявки на входе (выполняем с накопителя)

{:;(n1)

{= 1;++;

}if (n2)

{= 2;++;

}if (n3)

{= 3;++;

}if (n4)

{

sm = 4;

tv4++;

}

else t_stop++; // если не занята ЭВМ и нечего выполнять с накопителя... т.е. тупо стоим на месте

}

}

if (((t == 0) || (t % (int)tps == 0)) && (sm != 0)) // по приходу следующего задания и если занята ЭВМ

{(ts)

{1:(!n1) n1 = true;ko1++;;2:(!n2) n2 = true;ko2++;;3:(!n3) n3 = true;ko3++;;4:(!n4) n4 = true;ko4++;;

}

}

} // for(f0);(f1);(f2);(f3);(f4);_stop_percent = t_stop / EMV_MAX;= n1 ? 1 : 0;= n2 ? 1 : 0;= n3 ? 1 : 0;= n4 ? 1 : 0;("Idle time %f, %f in percent\n", t_stop, t_stop_percent);("Success: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", kr1, kr2, kr3, kr4);("Accumulated: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", kn1, kn2, kn3, kn4);("Denied: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", ko1, ko2, ko3, ko4);("Total: 1 = %d\n 2 = %d\n 3 = %d\n 4 = %d\n", kt1, kt2, kt3, kt4);();0;

}stohread(FILE *stream)

{buf[8];(&buf, sizeof(buf)+1, 1, stream); atof(buf);

}

.7 Описание моделирующей программы для стохастической модели на языке GPSS

Применение универсальных языков программировании при реализации имитационных моделей позволяет исследователю достигнуть гибкости при разработке, отладке и испытании модели. Однако языки моделирования, ориентированные на определенную предметную область, являются языками более высокого уровня, поэтому дают возможность с меньшими затратами создавать программы моделей для исследования сложных систем. GPSS как раз является таким «специализированным» языком.

Листинг моделирующей представлен ниже.

XPDIS FUNCTION RN1,C24

.0,0.0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.83/.88,2.12/.9,2.3/.92,2.52

.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9/.99,4.6/.995,5.3

.998,6.2/.999,7.0/.9997,8.0FUNCTION RN1,C25

.0,5.0/.00003,4/.00135,3/.00621,2.5/.02275,2

.06681,1.5/.11507,1.2/.15866,1/.21186,.8/.27425,.6

.34458,.4/.42074,.2/.5,0/.57926,2/.65542,.4

.72575,.6/.78814,.8/.84134,1/.88493,1.2/.93319,1.5

.97725,2/.99379,2.5/.99865,3/.99997,4/1.0,5.0FUNCTION RN1,C14

,0/.1,.5/.15,.754/.2,1/.3,1.16/.4,1.2/.5,1.5

.6,1.64/.65,1.697/.8,1.74/.9,1.88/.92,1.860/.96,1.87/1,2X$TASKNO,01.5,0.5TASKNO+,1G X$TASKNO,4,NEXTTASKNO,1TEST L X$TASKNO,4,TYPE4L X$TASKNO,3,TYPE3L X$TASKNO,2,TYPE2TEST L Q$OCHERED_1,1,UDALOCHERED_1EVMOCHERED_10.7,FN$XPDISEVM,OUTTEST L Q$OCHERED_2,1,UDALOCHERED_2EVMOCHERED_21.4,FN$NORMEVM,OUTTEST L Q$OCHERED_3,1,UDALOCHERED_3EVMOCHERED_3FN$GAMMEVM,OUTTEST L Q$OCHERED_4,1,UDALOCHERED_4EVMOCHERED_42,.1EVM,OUTSAVEVALUE UDALEN+,1 TERMINATE

GENERATE 600

TERMINATE 1

Результат работы программы представлен ниже:

GPSS World Simulation Report - mod.2.1, December 13, 2008 12:43:10TIME END TIME BLOCKS FACILITIES STORAGES

.000 600.000 39 1 0VALUE10014.00010004.0005.00010002.000_1 10012.000_2 10016.000_3 10017.000_4 10018.00037.00010006.0008.00015.00022.00029.00036.00010019.00010000.000LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

GENERATE 397 0 0

SAVEVALUE 397 0 0

TEST 397 0 0

SAVEVALUE 99 0 05 TEST 397 0 0

TEST 298 0 0

TEST 199 0 08 TEST 100 0 0

QUEUE 99 0 0

SEIZE 99 0 0

DEPART 99 0 0

ADVANCE 99 0 0

RELEASE 99 0 0

TRANSFER 99 0 015 TEST 99 0 0

QUEUE 99 0 0

SEIZE 99 0 0

DEPART 99 0 0

ADVANCE 99 0 0

RELEASE 99 0 0

TRANSFER 99 0 022 TEST 99 0 0

QUEUE 99 0 0

SEIZE 99 0 0

DEPART 99 0 0

ADVANCE 99 0 0

RELEASE 99 0 0

QUEUE 99 0 0

SEIZE 99 0 0

DEPART 99 0 0

ADVANCE 99 0 0

RELEASE 99 0 0

TRANSFER 99 0 036 SAVEVALUE 1 0 037 TERMINATE 397 0 0

GENERATE 1 0 0

TERMINATE 1 0 0ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY396 0.873 1.323 1 0 0 0 0 0MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY_1 1 0 99 1 0.262 1.588 1.604 0_2 1 0 99 40 0.172 1.045 1.753 0_3 1 0 99 43 0.179 1.087 1.921 0_4 1 0 99 39 0.178 1.079 1.780 0RETRY VALUE0 1.0000 1.000XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

399 0 600.393 399 0 1

0 1200.000 400 0 38

4. Получение и интерпретация результатов моделирования

.1 Планирование машинного эксперимента

Условимся считать некоторую систему оптимальной, если она в процессе работы удовлетворяет следующим условиям:

имеет минимальное время простоя оборудования;

не имеет очередей заявок;

имеет минимальное количество отказов.

Для сокращения времени простоя оборудования следует увеличить интенсивность поступления заявок в систему. Для уменьшения количества отказов системы, а также заявок в буфере требуется обеспечить ЭВМ минимальным временем обработки задания.

.2 Проведение прогонов модели

Результаты прогонов модели представлены в таблице 3 и 4.

Таблица 3

Таблица 4

4.3 Анализ результатов моделирования

Значения выходных характеристик, полученные при прогонах модели с различными случайными воздействиями, будут отличны друг от друга. Усредненное по многим прогонам модели значение выходной характеристики незначительно отличается от соответствующей детерминированной величины, что подтверждает правильность работы модели.

Из результатов в п.4.2. видно, что в системе некоторое количество заданий не обрабатываются (уходят в отказ). Следует увеличить время прихода заданий до 20 минут.

Результат приведен на рисунке ниже:

5. Заключение

Как видно из результатов, после оптимизации работы программы, количество отказов снизилось до нуля. Однако, увеличился на несколько тысячных процент простоя канала ко времени работы. В целом процент простоя составляет не более 0,005% к суммарному времени. Оптимизацию можно счесть удачной.

Список литературы

1. Советов Б. Я., Яковлев С. Я. Моделирование систем: Курсовое проектирование: Учеб. Пособие для вузов по спец. АСУ.-М: Высш. шк., 1988.-135 с.

2. Глова В. И., Захаров В. М., Маврина Л. Н. Моделирование: Учебное пособие к курсовому проектированию: Казан. Гос. Техн. Университет; Казань, 1997.-42с.

3. Живетина Т. М., Маврина Л. Н., Песошин В. А. Моделирование вычислительных систем: Лабораторный практикум. - Казань: Изд. КГТУ, 1995.-70 с.