Моделирование многомерной системы управления реактором
Курсовая
работа по дисциплине «Моделирование систем»
Тема:
“Моделирование многомерной системы управления реактором”
Содержание
Введение
. Краткая характеристика объекта
.1. Принципиальная схема объекта
моделирования
.2 .Исходные данные
. Разработка математической модели
аппарата
.1. Стехиометрический анализ и
модель кинетики
.2. Математическая модель динамики
объекта
.3. Математическая модель статики
объекта
.4. Синтез формализованной модели
объекта
. Исследование статики и динамики
объекта
. Оптимизация режима работы аппарата
. Моделирование системы управления
нелинейного объекта с использованием линейных типовых регуляторов
.1. Получение кривых разгона
.2. Идентификация объекта управления
.3. Оценка параметров настроек
регулятора
. Моделирование линеаризованной
системы
Заключение
Список литературы
Реферат
В курсовой работе по исходной модели объекта
управления:
разработка математической модели объекта;
получение статических характеристик объекта по
уравнениям динамики;
нахождение переходных функций;
Для решения поставленных задач разрабатывается
программа моделирования объекта в среде пакета MathCAD
с использованием встроенных функций. Суть метода заключается в моделировании на
ЭВМ режима запуска и вывода аппарата на нужный режим.
проведена оптимизация модели объекта;
проведена идентификация модели объекта типовыми
звеньями;
проведено моделирование системы управления
линеаризованного объекта с линейными регуляторами (ПИ-закон регулирования);
Работа содержит:
58 страниц;
13 рисунков;
2 структурные схемы;
1 таблица.
Использовано 4 литературных источника.
Введение
Моделирование-это исследование каких-либо
явлений, процессов или систем путём построения и изучения их моделей с целью
определения и уточнения характеристик этих систем.
Математическое моделирование - это исследование
объектов и систем путём построения их математических моделей, изучения их
свойств и характеристик объектов на этих моделях.
В данной курсовой работе объектом исследования
является химический реактор емкостного типа, снабжённый механической мешалкой.
Химические реакторы являются важнейшими аппаратами химической технологии, т.к.
именно в них в результате химических превращений из исходного сырья получают
необходимые продукты. Многообразие химических реакций обуславливает большое
число типов реакторов, отличающихся конструкцией, режимом работы (непрерывный,
периодический), агрегатным состоянием компонентов (жидкое, газообразное,
плазмохимическое), тепловым режимом (изотермический, адиабатический,
политропический), режимом движения фаз и их количеством (гетерогенные,
гомогенные). В общем случае реакторы являются сложной физико-химической
системой, в которой протекают все типовые процессы.
Химическое взаимодействие веществ на
молекулярном уровне сопровождается отводом или подводом тепла (теплоперенос),
транспортированием компонентов из одной фазы в другую (массоперенос), движением
фаз в зоне реакции, определяемым структурой гидродинамических потоков. Поэтому
модели химических реакторов строятся на основе блочного принципа.
Перечисленные типовые процессы и явления,
протекающие в реакторах, можно разделить на явления микро и макро уровня.
Микроуровень - это взаимодействие молекул
химических веществ.
Макроуровень характеризуется явлениями и
процессами, происходящими на уровне локальных объемов аппаратов и реактора в
целом.
Основу модели любого реактора составляет модель
кинетики и модель гидродинамики, определяющее распределение времени пребывания
компонентов в аппарате.
Целью курсовой работы являются закрепление и
углубление знаний по дисциплине «Моделирование систем управления», а также
развитие практических навыков исследования динамики и статики объектов
химической технологии и систем управления.
1.
Краткая характеристика объекта
.1
Принципиальная схема объекта моделирования
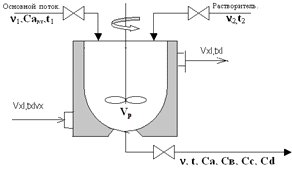
Рис 1. Принципиальная
схема объекта моделирования.
В реакторе емкостного типа объемом Vp,
снабженном механической мешалкой, проводятся экзотермические реакции:
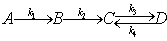
Реагент с концентрацией 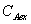 подаётся в
потоке
подаётся в
потоке 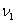 . Поток
. Поток 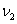 служит для
разбавления реакционной смеси. Смесь из реактора забирается насосом, величина
потока может регулироваться клапаном. Благодаря интенсивному перемешиванию
структура потоков в реакторе может быть описана моделью идеального смешения.
Аппарат работает в политропическом режиме.
служит для
разбавления реакционной смеси. Смесь из реактора забирается насосом, величина
потока может регулироваться клапаном. Благодаря интенсивному перемешиванию
структура потоков в реакторе может быть описана моделью идеального смешения.
Аппарат работает в политропическом режиме.
Выходные переменные объекта:
Объём (уровень) реакционной смеси - Vp;
концентрации компонентов в выходном потоке - 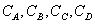 ; температура смеси в аппарате - t;
температура жидкости в рубашке -
; температура смеси в аппарате - t;
температура жидкости в рубашке - 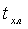 .
.
Входные переменные объекта:
Расходы потоков на входе и выходе из
аппарата -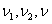 ;
концентрация вещества А во входном потоке - СА; температуры входных потоков-t1,t2,tхлвх; расход
хладагента на входе в рубашку -vхл
;
концентрация вещества А во входном потоке - СА; температуры входных потоков-t1,t2,tхлвх; расход
хладагента на входе в рубашку -vхл
1.2
Исходные данные
Таблица 1.
Исходные данные.
|
№
|
Наименование
|
Единицы
измерения
|
Численное
значение
|
Обозначение
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
Теплоемкость
вещества в аппарате и входных потоках.
|
КДж/кгК
|
4,19
|
Ср
|
|
Теплоемкость
хладагента.
|
|
|
Cхл
|
|
2
|
Плотность
вещества в аппарате и входных потоках.
|
Кг/л
|
1,2
|
r
|
|
Плотность
насыщенного хладагента.
|
|
0,978
|
pхл
|
|
3
|
Тепловой
эффект реакции
|
КДж/моль
|
400
|
DН
|
|
4
|
Предэкспонентциальный
множитель константы скорости
|
1/мин
|
20
1 10 2
|
К10
К20 К30 К40
|
|
5
|
Энергия
активации
|
КДж/моль
|
20000
25000 20000 20000
|
Е1
Е2 Е3 Е4
|
|
6
|
Концентрация
компонента А на входе
|
моль/л
|
1.1
|
Савх
|
|
7
|
Расход
на входе в реактор (основной поток)
|
л/мин
|
1.5
|
n1
|
|
8
|
Расход
на входе в реактор (растворитель)
|
л/мин
|
0.5
|
n2
|
|
9
|
Температура
хладагента
|
0С
|
30
|
tхл
|
|
10
|
Температура
на входе в реактор (основной поток)
|
0С
|
30
|
t1
|
|
11
|
Температура
на входе в реактор (растворитель)
|
0С
|
40
|
t2
|
|
12
|
Коэффициент
теплопередачи
|
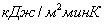 10 10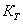
|
|
|
|
13
|
Расход
хладагента
|
л/мин
|
0.5
|
nхл
|
2.
Разработка математической модели аппарата
Описание полной математической модели объекта -
довольно сложная, а нередко просто невыполнимая задача. Учёт всех особенностей
функционирования объекта необходим лишь в редких случаях, когда точность
модели, описывающей объект, имеет первостепенное значение. Поэтому на практике
обычно ограничиваются теми свойствами объекта, которые играют наиболее важную
роль в процессе его эксплуатации, пренебрегая малосущественными факторами, лишь
усложняющими модель.
2.1
Стехиометрический анализ и модель кинетики

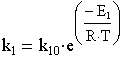
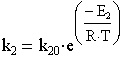
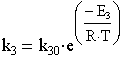
Скорость реакции для каждой стадии:
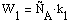
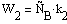
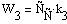
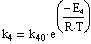
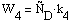
С учётом стехиометрии получим:
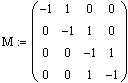
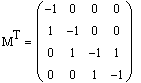
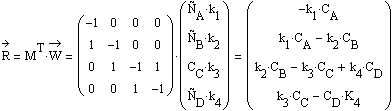
Полученная система кинетических
уравнений полностью определяет динамику превращений компонентов реакции.
2.2
Математическая модель динамики объекта
Допущения:
Структура потоков в аппарате описывается моделью
идеального смешения.
Физико-химические параметры реакционной смеси и
хладагента не зависят от температуры и концентрации компонентов, т. е. являются
постоянными. моделирование
кинетика аппарат программа
Потери тепла в окружающую среду отсутствуют.
Стенки аппарата тепла не аккумулируют.
Транспортным запаздыванием при изменении входных
переменных пренебрегаем.
Считаем тепловой эффект реакции приведенным к
первой стадии.
Изменение подачи хладагента не влияет на его
уровень в рубашке.
Расход хладагента на входе и на выходе одинаков.
Температура хладагента одинакова во всём объёме
рубашки.
Математическая модель динамики объекта
записывается в виде дифференциальных уравнений, выражающих баланс вещества,
энергии с учётом принятых допущений и упрощений.
В данном случае математическая модель динамики
реактора идеального смешения состоит из общего уравнения баланса по жидкости,
уравнений материального баланса по каждому компоненту в реакторе, уравнения
теплового баланса реакционной смеси и хладагента в рубашке.
.Общее уравнение материального баланса и по
компонентам:
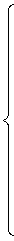
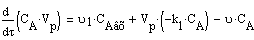
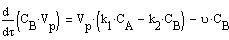
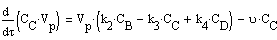
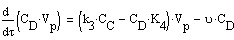
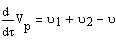
. Уравнение теплового баланса для реакционной
смеси:
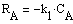
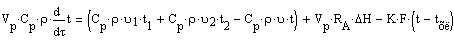
. Уравнение теплового баланса для рубашки:
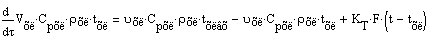
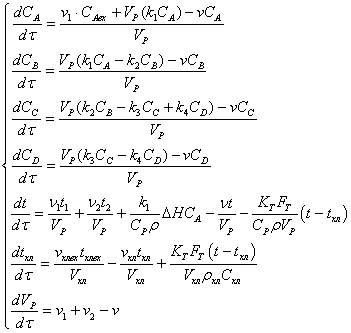
В качестве начальных условий для
решения уравнений динамики выступают значения выходных переменных в статике.
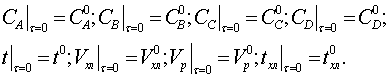
2.3
Математическая модель статики
Математическая модель статики объекта
записывается в виде конечных уравнений и отражает зависимость между входными и
выходными переменными в установившемся состоянии. Отсюда следует простой способ
составления этой модели: производные в левых частях дифференциальной модели
динамики заменяются нулями, а остальным переменным добавляют индекс «0»,
показывая тем самым, что значения переменных в этих уравнениях берутся в
состоянии покоя системы.
Для исследуемой нами модели система уравнений
статики объекта запишется следующим образом:
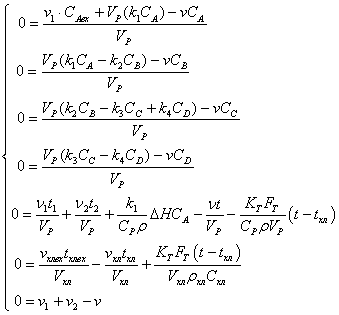
Полученная математическая модель
статики объекта представляет собой систему нелинейных алгебраических уравнений.
2.4
Синтез формализованной модели объекта
В предыдущем разделе было получено
математическое описание модели объекта в виде системы обыкновенных
дифференциальных уравнений. Однако, эта система обладает нелинейностью, которую
вносят коэффициенты скорости реакций, а также произведения переменных.
Использование линеаризованных математических моделей обусловлено тем фактом,
что среди всего многообразия дифференциальных уравнений общие методы решения
имеют лишь линейные дифференциальные уравнения.
Формализованной моделью будем считать модель
объекта, полученную путем линеаризации исходной системы в окрестности рабочей
точки статической характеристики, Линеаризацию проводим путём разложения всех
функций и переменных, входящих в систему в ряд Тейлора. При этом будем
пренебрегать членами второго порядка малости. Текущие значения переменных
выражаются следующим образом:
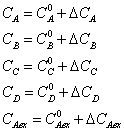
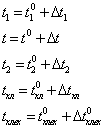
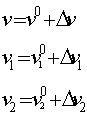
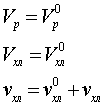
Уравнения динамики запишутся
следующим образом:
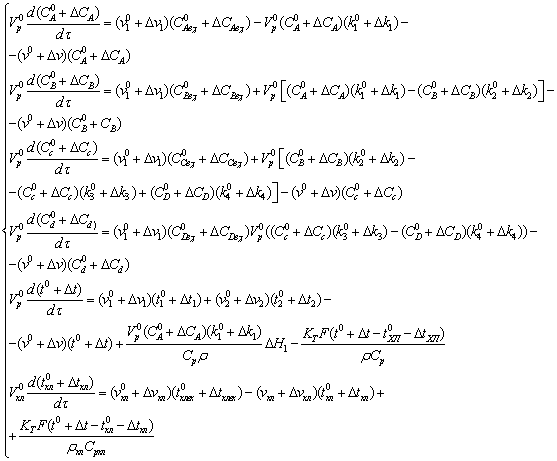
Вычтем из полученных уравнений
уравнения статики и используя выражение 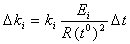 преобразуем уравнения:
преобразуем уравнения:
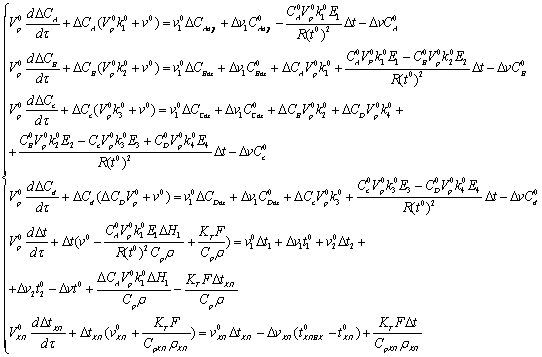
Упростим систему:
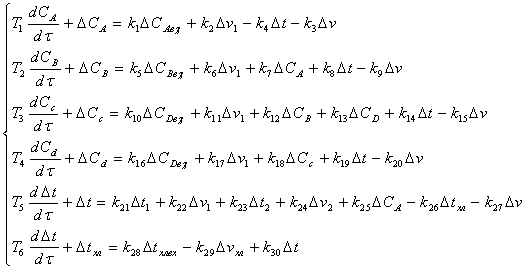
Значения параметров формализованной
модели
Таблица 2.
Параметры линеаризованной модели.
|
№
|
Расчетные
формулы
|
Численные
значения
|
Ед. измерения
|
|
1
|
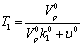 0.0499Мин. 0.0499Мин.
|
|
|
|
2
|
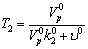 0.996Мин. 0.996Мин.
|
|
|
|
3
|
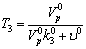 0.09996Мин. 0.09996Мин.
|
|
|
|
4
|
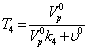 0.499Мин. 0.499Мин.
|
|
|
|
5
|
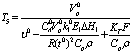 2.9*10-4Мин. 2.9*10-4Мин.
|
|
|
|
6
|
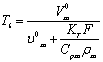 31.46Мин. 31.46Мин.
|
|
|
|
7
|
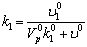 0.000005Безразм. 0.000005Безразм.
|
|
|
8 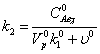 9,99*10-6Моль*мин
9,99*10-6Моль*мин
9 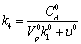 0,5999Моль*мин
0,5999Моль*мин
10 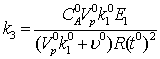 0,6898Моль
0,6898Моль
|
Л
С
|
|
|
|
|
11
|
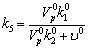 1,59*10-6Безразм 1,59*10-6Безразм
|
|
|
12 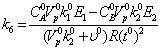 7,499*10-6Моль
7,499*10-6Моль
13 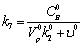 1,999*10-6Моль*мин
1,999*10-6Моль*мин
|
Л
|
|
|
|
|
14
|
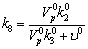 0,99999Безразм. 0,99999Безразм.
|
|
|
15 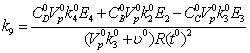 1,5561Моль
1,5561Моль
|
Л
С
|
|
|
|
|
16
|
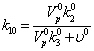 7,578*10-6Безразм. 7,578*10-6Безразм.
|
|
|
17 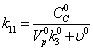 2,143*10-6Моль*мин
2,143*10-6Моль*мин
|
Л
|
|
|
|
|
18
|
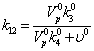 5,714*10-8Безразм. 5,714*10-8Безразм.
|
|
|
19 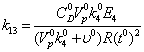 0,11428Моль
0,11428Моль
20 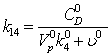 0,211495Моль*мин
0,211495Моль*мин
|
Л
|
|
|
|
|
21
|
 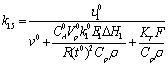 4,114*10-8Безразм 4,114*10-8Безразм
|
|
|
22 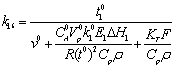 0,75 0
0,75 0
мин
* С
|
Л.
|
|
|
|
|
23
|
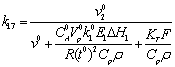 0,002Безразм 0,002Безразм
|
|
|
24 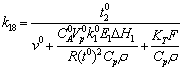 350000 0
350000 0
мин
* С
25 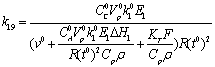 12603,05 0
12603,05 0
Л
* С
|
МИН.
|
|
|
|
|
26
|
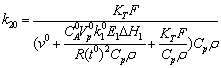 0,00875Безразм 0,00875Безразм
|
|
|
27 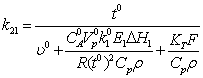 7,289*10-70
7,289*10-70
мин
* С
|
Л.
|
|
|
|
|
28
|
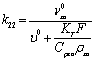 2,187*10-5Безразм. 2,187*10-5Безразм.
|
|
|
29 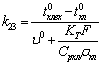 1,822*10-70
1,822*10-70
мин
* С
|
Л.
|
|
|
|
|
30
|
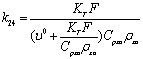 2,916*10-5Безразм. 2,916*10-5Безразм.
|
|
|
С целью упрощения задачи построения
структурной схемы объекта обозначим правые части в уравнениях системы: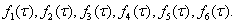 Тогда
система запишется в виде:
Тогда
система запишется в виде:
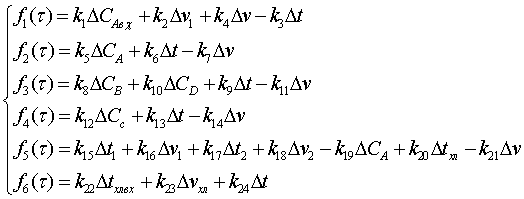
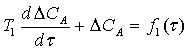
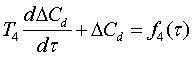
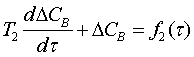
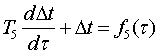
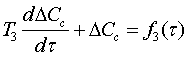
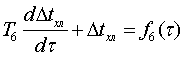
Преобразовав по Лапласу систему
уравнений, получим выражения для передаточных функций:
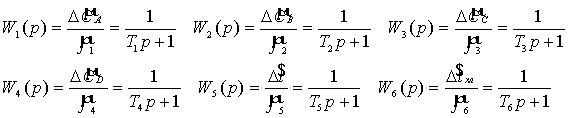
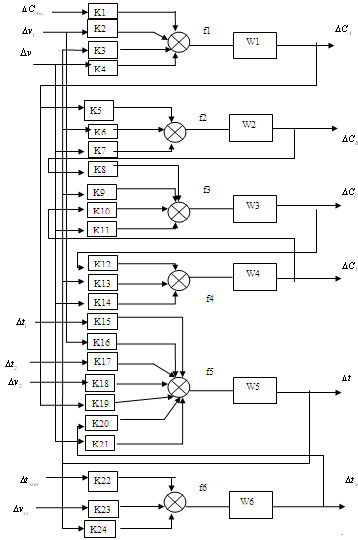
Рис.2. Структурная схема объекта.
3.
Оптимизация режима работы аппарата
В реакторе осуществляется
экзотермическая реакция последовательного типа. Пусть целевым условием
эффективности максимизации является степень превращения вещества А: 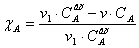 . Поставим
задачу оптимизации: при заданном составе исходного сырья и температурной
зависимости констант скоростей определить среднее время пребывания и
температуру в аппарате, обеспечивающие максимум степени превращения вещества А.
Ввиду того, что нагрузка на аппарат задана (
. Поставим
задачу оптимизации: при заданном составе исходного сырья и температурной
зависимости констант скоростей определить среднее время пребывания и
температуру в аппарате, обеспечивающие максимум степени превращения вещества А.
Ввиду того, что нагрузка на аппарат задана (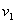 и
и 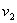 ), время пребывания определяется
рабочим объемом аппарата - Vp. Аппарат работает в
политропическом режиме, поэтому необходимо найти только оптимальный объем
аппарата. В математической форме задача имеет вид:
), время пребывания определяется
рабочим объемом аппарата - Vp. Аппарат работает в
политропическом режиме, поэтому необходимо найти только оптимальный объем
аппарата. В математической форме задача имеет вид:
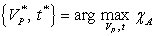 , где
, где 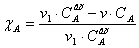 ;
;
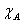 - степень превращения вещества А, Vp*, t* -
оптимальное значение объема аппарата и температуры. В результате оптимизации
варьировался объем аппарата в диапазоне 200
- степень превращения вещества А, Vp*, t* -
оптимальное значение объема аппарата и температуры. В результате оптимизации
варьировался объем аппарата в диапазоне 200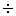 1000 литров и температура в
диапазоне 40
1000 литров и температура в
диапазоне 40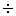 900С. В
качестве оптимальных значений варьируемых переменных выбраны значения:Vp=550 литров,
t=82.7790С,
которые обеспечивают
900С. В
качестве оптимальных значений варьируемых переменных выбраны значения:Vp=550 литров,
t=82.7790С,
которые обеспечивают 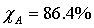
Решим эту задачу с помощью метода
покоординатного спуска. Листинг программы приведен ниже.
Листинг программы моделирования
вывода аппарата на статический режим
Аппарат работает в политропическом
режиме, реакция - экзотермическая (хладагент жидкость)
.Исходные данные:
теплоёмкость вещества, кдж/кгградК
теплоёмкость хладагента, кдж/кг
градК
плотность вещества в аппарате и
входных потоках, кг/л
плотность хладагента, кг/л
коэффициент теплопередачи, кдж / м
мин градК
тепловой эффект реакции, кдж/моль
универсальная газовая постоянная,
дж/моль градК
концентрация компонента А на входе,
моль/л
расход на выходе из реактора V,
л/мин
расход на входе в реактор V2, л/мин
расход на входе в реактор V1, л/мин
расход хладагента, л/мин
температура на входе в реактор t1,
градС
температура на входе в реактор t2,
градС
температура хладагента на входе,
градС
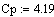
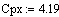
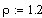
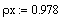
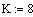
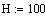
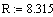
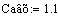
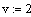
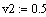
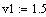
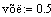
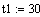
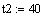
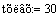
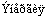
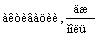
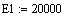
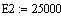
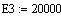
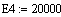
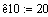
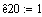
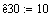
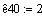
. Постоянные коэффициенты
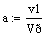
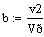
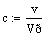
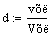
. Константа скорости
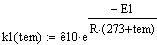
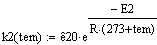
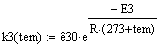
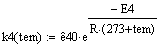
. Вектор-функция правых частей
дифференциальных уравнений модели
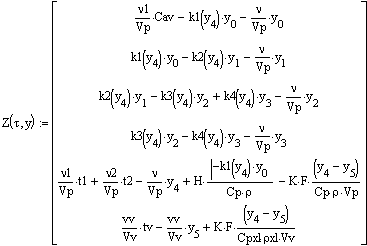
. Начальные условия и условия
интегрирования
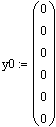
. Решение дифференциальных уравнений
модели
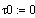
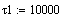
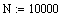
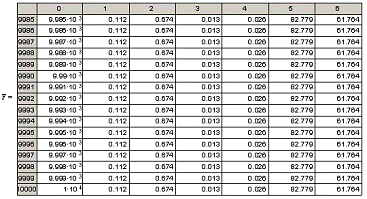
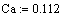 концентрация компонента А
концентрация компонента А
Vp*=550 объем
реактора
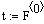
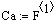
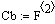
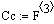
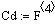
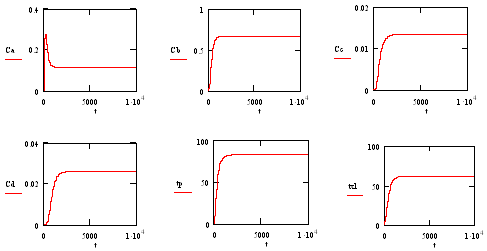
Рис. 3. Процесс вывода аппарата на
статический режим
а) изменение концентрации компонента
А
б) изменение концентрации компонента
В
в) изменение концентрации компонента
С
г) изменение концентрации компонента
D
д) изменение температуры в реакторе
е) изменение температуры хладагента
При значении величины объема реактора Vp*=550
литров, оптимальное значение температуры t*
= 82.7790C
Приняв полученные значения параметров,
полученных в ходе оптимизации, в качестве начальных условий системы уравнений
(Листинг 1), получили кривые разгона в виде прямых линий, таким образом,
убедились, что оптимизация проведена корректно.
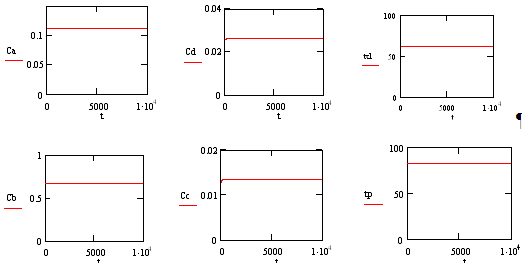
Рис 3. Процесс вывода аппарата на статический
режим
а) изменение концентрации компонента А
б) изменение концентрации компонента В
в) изменение концентрации компонента С
г) изменение концентрации компонента D
д) изменение температуры в реакторе
е) изменение температуры хладагента
4.
Моделирование системы управления нелинейного объекта с использованием линейных
типовых регуляторов (ПИ-закон регулирования)
В большинстве случаев промышленные объекты, в
том числе и рассматриваемый тип реактора, являются многомерными. Их состояние
характеризуется несколькими величинами, значения которых определяются
значениями входных переменных (ряд этих переменных являются возмущениями,
другая часть может выступать в качестве регулирующих воздействий). Из всей
совокупности переменных состояния измерению, контролю и регулированию подлежит
только определенная часть. Эти переменные называются выходными. Регулирование
многомерных объектов может быть НЕСВЯЗАННЫМ и СВЯЗАННЫМ. В первом случае каждая
выходная переменная регулируется одним регулятором, воздействующим только на
«свой» регулирующий орган; во втором случае каждый регулятор воздействует не
только на свой регулирующий орган, но и на регулирующие органы других
регулируемых величин.
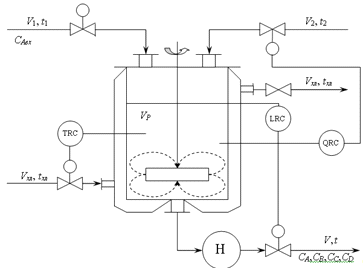
Рис. 4. Функциональная схема автоматизации
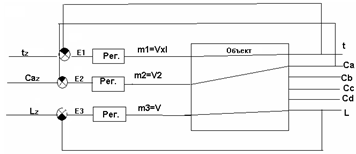
Рис. 5. Структурная схема системы несвязного
регулирования многомерного одноконтурного объекта.
4.1
Получение кривых разгона
Получим кривые разгона, применив ступенчатое
воздействие к вышеописанным каналам управления. Используем следующую программу
(Листинг 2):
Исходные данные:
Канал управления: расход разбавителя -
концентрация в аппарате:
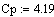
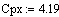
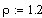
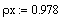
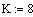
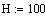
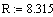
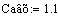
v:=2.1
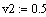 +0.1
+0.1
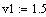
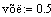
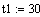
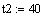
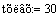
теплоёмкость вещества, кдж/кгградК
теплоёмкость хладагента, кдж/кг градК
плотность вещества в аппарате и входных потоках,
кг/л
плотность хладагента, кг/л
коэффициент теплопередачи, кдж / м мин градК
поверхность теплообмена, м
тепловой эффект реакции, кдж/моль
универсальная газовая постоянная, дж/моль градК
концентрация компонента А на входе, моль/л
расход на выходе из реактора V, л/мин
расход на входе в реактор V2, л/мин
расход на входе в реактор V1, л/мин
расход хладагента, л/мин
температура на входе в реактор t1, градС
температура на входе в реактор t2, градС
температура хладагента на входе, градС
Vp:=550 -
объем реактора
Vv:=200 -
объем рубашки
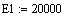
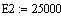
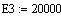
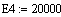
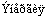
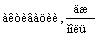
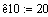
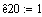
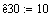
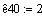
. Постоянные коэффициенты
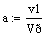
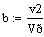
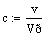
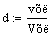
. Константа скорости
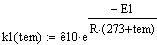
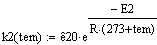
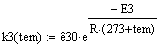
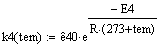
. Вектор-функция правых частей дифференциальных
уравнений модели
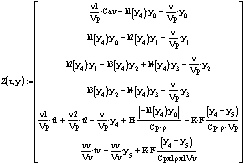
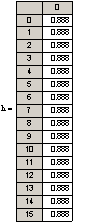
. Начальные условия и условия
интегрирования
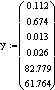
Ca
6. Решение дифференциальных
уравнений модели
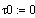
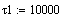
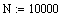
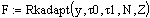
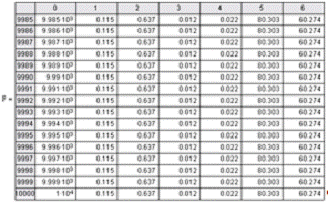
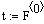
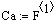
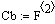
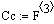
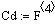
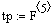
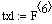
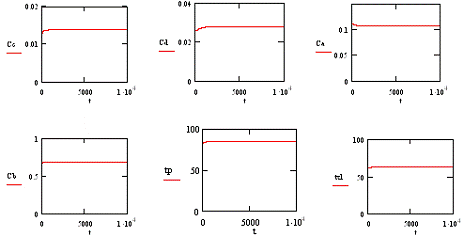
Рис 6. Реакция на изменение расхода разбавителя v2
(Δv2=0.1 литр/мин).
а) изменение концентрации компонента А
б) изменение концентрации компонента В
в) изменение концентрации компонента С
г) изменение концентрации компонента D
д) изменение температуры в реакторе
е) изменение температуры хладагента
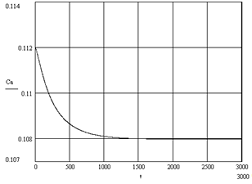
Рис. 7. Кривая разгона по каналу расход
разбавителя - концентрация в аппарате
Канал управления: расход хладагента -
температура в аппарате:
Исходные данные:
теплоёмкость вещества, кдж/кгградК
теплоёмкость хладагента, кдж/кг градК
плотность вещества в аппарате и входных потоках,
кг/л
плотность хладагента, кг/л
коэффициент теплопередачи, кдж / м мин градК
поверхность теплообмена, м
тепловой эффект реакции, кдж/моль
универсальная газовая постоянная, дж/моль градК
концентрация компонента А на входе, моль/л
расход на выходе из реактора V, л/мин
расход на входе в реактор V2, л/мин
расход на входе в реактор V1, л/мин
расход хладагента, л/мин
температура на входе в реактор t1, градС
температура на входе в реактор t2, градС
температура хладагента на входе, градС
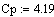
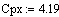
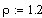
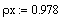
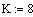
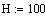
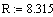
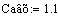
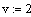
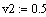
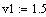
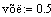 +0.1
+0.1
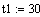
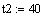
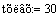
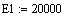
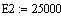
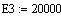
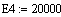
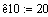
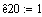
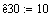
. Постоянные коэффициенты
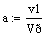
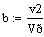
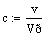
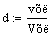
. Константа скорости
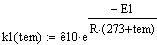
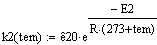
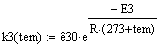
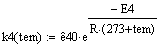
. Вектор-функция правых частей дифференциальных
уравнений модели
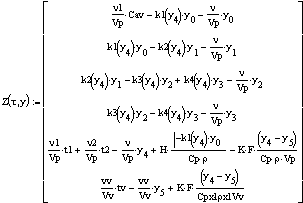
. Начальные условия и условия интегрирования
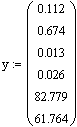
Ca
6. Решение дифференциальных уравнений модели
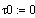
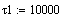
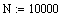
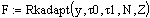
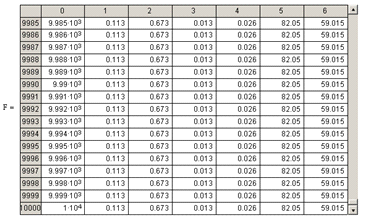
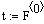
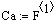
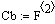
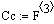
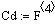
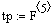
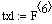
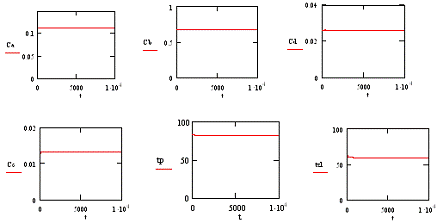
Рис 8. Реакция на изменение расхода
хладагента vхл (Δvхл=0.1
литр/мин).
а) изменение концентрации компонента А
б) изменение концентрации компонента В
в) изменение концентрации компонента С
г) изменение концентрации компонента D
д) изменение температуры в реакторе
е) изменение температуры хладагента
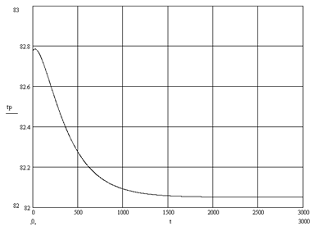
Рис. 9. Кривая разгона по каналу расход
хладагента - температура в аппарате
Канал управления: расход на выходе из реактора-
уровень в реакторе:
Исходные данные:
теплоёмкость вещества, кдж/кгградК
теплоёмкость хладагента, кдж/кг градК
плотность вещества в аппарате и входных потоках,
кг/л
плотность хладагента, кг/л
коэффициент теплопередачи, кдж / м мин градК
поверхность теплообмена, м
тепловой эффект реакции, кдж/моль
универсальная газовая постоянная, дж/моль градК
концентрация компонента А на входе, моль/л
расход на выходе из реактора V, л/мин
расход на входе в реактор V2, л/мин
расход на входе в реактор V1, л/мин
расход хладагента, л/мин
температура на входе в реактор t1, градС
температура на входе в реактор t2, градС
температура хладагента на входе, градС
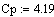
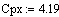
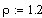
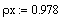
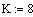
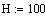
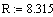
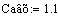
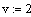 -0.1
-0.1
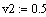
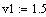
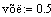
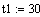
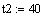
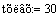
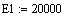
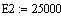
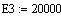
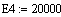
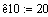
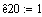
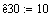
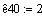
. Постоянные коэффициенты
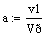
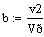
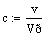
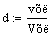
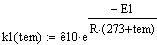
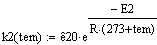
. Константа скорости
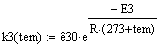
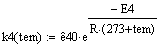
4. Вектор-функция правых частей дифференциальных
уравнений модели
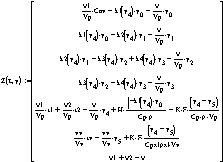
. Начальные условия и условия
интегрирования
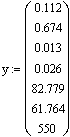
6. Решение дифференциальных
уравнений модели
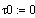
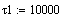
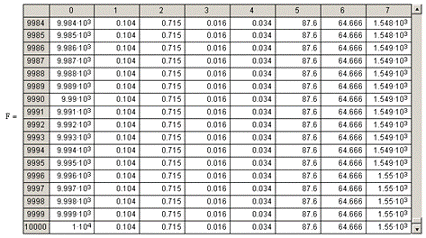
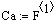
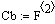
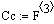
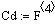
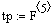
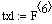
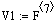
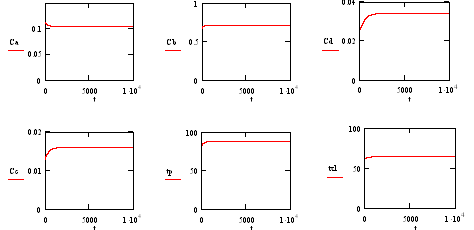
Рис 10. Реакция на изменение расхода
на выходе v (Δv=-0.1
литр/мин).
а) изменение концентрации компонента А
б) изменение концентрации компонента В
в) изменение концентрации компонента С
г) изменение концентрации компонента D
д) изменение температуры в реакторе
е) изменение температуры хладагента
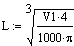
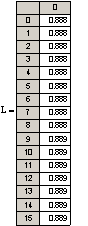
L0=0.888, L10000=1.254
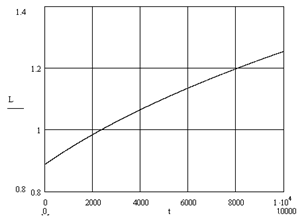
Рис. 11. Кривая разгона по каналу расход на
выходе из реактора - уровень в реакторе
4.2
Идентификация объекта управления
Получили следующие кривые разгона:
. Кривая разгона по каналу: расход разбавителя -
концентрация в реакторе, представлена на рисунке 1 (v2
- Ca)
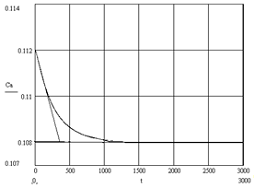
Рис. 12. Кривая разгона по каналу расход
разбавителя - концентрация в аппарате
Определим передаточную функцию по этому каналу.
Коэффициент передачи найдем из соотношения:
K01=(0.108-0.112)/0.1=-0.04
Постоянную времени объекта найдём, проведя
касательную к кривой разгона: Т01=380 мин.
Таким образом, передаточная функция будет иметь
вид:
W1(p)=k/(Tp+1)=-0.04/(380p+1)
. Кривая разгона по каналу: расход на хладагента
- температура в реакторе, представлен на рисунке 2 (Vxl
- tp)
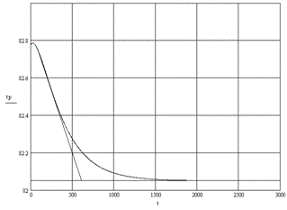
Рис. 13. Кривая разгона по каналу расход
хладагента - температура в аппарате
Определим передаточную функцию по этому каналу.
Коэффициент передачи найдем из соотношения:
K02=(82.05-82.779)/0.1=-7.29
Постоянную времени объекта найдём, проведя
касательную к кривой разгона: Т02=600 мин.
Таким образом, передаточная функция будет иметь
вид:
W2(p)=k/(Tp+1)=-7.29/(600p+1)
. Кривая разгона по каналу: расход на выходе из
реактора- уровень в реакторе, представлена на рисунке 3 (v
- L)
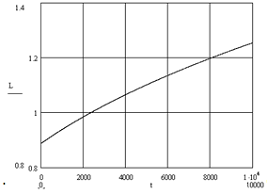
Рис. 14. Кривая разгона по каналу расход на
выходе из реактора- уровень в реакторе
Определим передаточную функцию по этому каналу.
Коэффициент передачи найдем из соотношения:
K03=(1.254-0.888)/10000=0.000036
Таким образом, передаточная функция будет иметь
вид:
W3(p)=k/p=0.000036/p
4.3
Оценка параметров настроек регулятора
Поскольку объект по каналам регулирования
характеризуется малым запаздыванием и является устойчивым, то целесообразно
использовать ПИ-алгоритм регулирования:
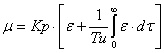 .
.
При решении задач моделирования
систем управления на ЭВМ необходимо иметь математическое описание объекта и
регулятора, представленных в одинаковой форме - в виде обыкновенных
дифференциальных уравнений. Преобразуем уравнение для регулятора в
дифференциальную форму:
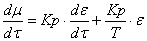 ,
,
где 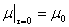 - значение регулирующего воздействия
в статике. Подставляя в данное уравнение значение ошибки регулирования из
уравнения сумматора, получим уравнения работы регуляторов:
- значение регулирующего воздействия
в статике. Подставляя в данное уравнение значение ошибки регулирования из
уравнения сумматора, получим уравнения работы регуляторов:
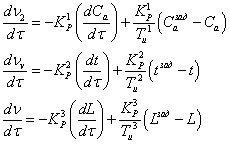
Найдем настройки регулятора по
методу Циглера-Никольса для канала 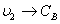 :
:
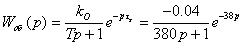
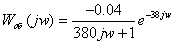
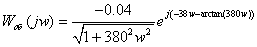
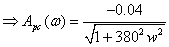
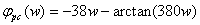
Построим фазочастотную
характеристику:
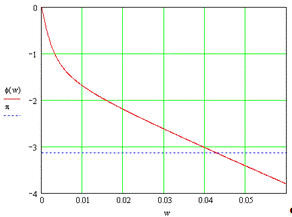
Рис. 15. Фазочастотная
характеристика.
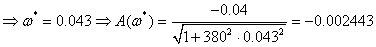
Определим настройки ПИ-регулятора:
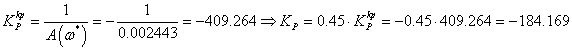
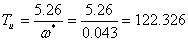
Аналогично найдем настройки для
канала 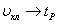 :
:
Получили:
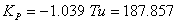
Настройки регулятора уровня примем
такими же, как и регулятора концентрации вещества А.
4.4
Моделирование несвязанной системы управления на ЭВМ
При решении задачи на ЭВМ необходимо учитывать,
что знак Kp будет
противоположен знаку коэффициента передачи объекта по каналу регулирования
благодаря наличию единичной обратной отрицательной связи в структуре системы
управления.
Исходные данные:
теплоёмкость вещества, кдж/кгградК
теплоёмкость хладагента, кдж/кг градК
плотность вещества в аппарате и входных потоках,
кг/л
плотность хладагента, кг/л
коэффициент теплопередачи, кдж / м мин градК
поверхность теплообмена, м
тепловой эффект реакции, кдж/моль
универсальная газовая постоянная, дж/моль градК
концентрация компонента А на входе, моль/л
расход на выходе из реактора V, л/мин
расход на входе в реактор V2, л/мин
расход на входе в реактор V1, л/мин
расход хладагента, л/мин
температура на входе в реактор t1, градС
температура на входе в реактор t2, градС
температура хладагента на входе, градС
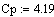
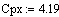
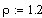
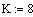
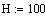
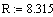
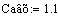
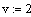
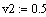
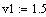
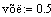
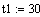
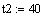
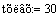
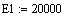
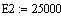
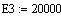
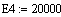
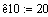
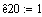
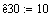
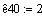
. Постоянные коэффициенты
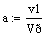
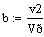
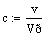
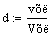
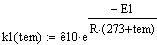
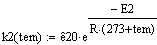
. Константа скорости
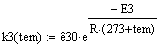
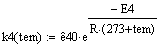
. Вектор-функция правых частей дифференциальных
уравнений модели
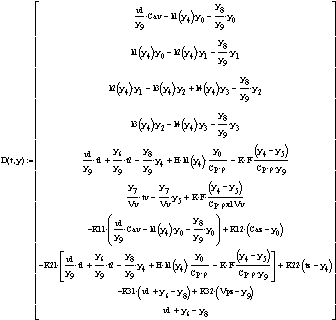
. Начальные условия и условия интегрирования
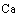
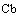
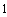
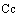
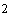
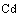
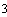
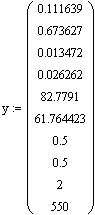
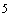
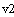

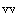
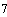

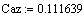
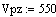
. Решение дифференциальных уравнений модели
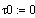
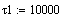
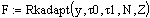
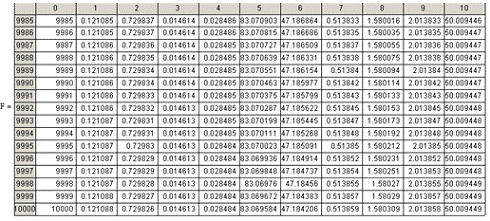
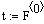
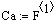
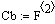
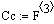
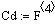
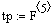
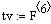
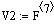
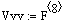
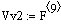
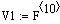
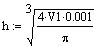
Подставим в записанные уравнения начальные
условия из статики (полученные в ходе оптимизации)
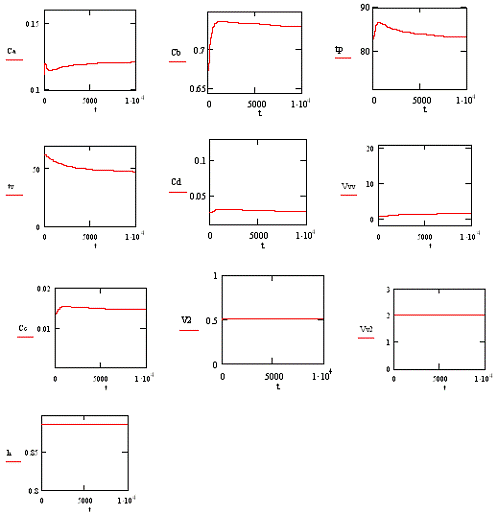
При моделировании несвязной системы
регулирования на ЭВМ была составлена системы уравнений, но в процессе расчетов
было выяснено, что из-за совокупности исходных данных мы не имеем возможности
подавать воздействия на регуляторы и определять качество регулирования из-за
несовершенства техники.
Оценивают качество процесса
регулирования по трем параметрам: время регулирования (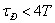 ),
статическая
),
статическая 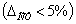 и
динамическая ошибка
и
динамическая ошибка 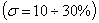 .
Статическая ошибка будет равна нулю, т.к. используется ПИ регулятор.
.
Статическая ошибка будет равна нулю, т.к. используется ПИ регулятор.
5.
Моделирование системы управления линеаризованного объекта с использованием
аппроксимирующей модели
Проведем моделирование линеаризованной системы в
окрестности рабочей точки. Для этого примем передаточные функции, полученные
при идентификации объекта управления и настройки регулятора, полученные при
оценке параметров настроек регулятора.
Передаточная функция по каналу управления расход
разбавителя - концентрация в реакторе имеет вид: W1(p)=k/(Tp+1)=-0.04/(380p+1),
по каналу управления расход хладагента - температура в реакторе имеет вид: W2(p)=k/(Tp+1)=-7.29/(600p+1),
по каналу управления расход на выходе из реактора - уровень в реакторе имеет
вид: W3(p)=k/p=0.000036/p
.
Моделирование возможно только по каналам
управления, так как по каналам возмущения нет передаточных функций.
Моделирование проведем в среде MatLAB.
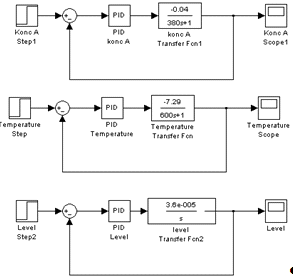
Рис. 16. Схема моделирования
Получим результаты моделирования, и оценим
параметры качества регулирования:
Примем 50%-е изменение задания регулятору.
. Процесс регулирования концентрации вещества B
при изменении задания регулятору (CА=
0.112 моль/литр, Δ CА
=0.056 моль/литр).
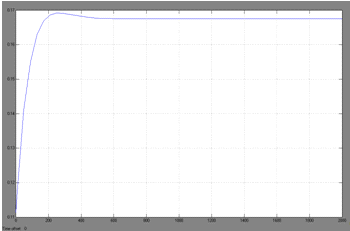
Рис. 17. Процесс регулирования концентрации
вещества А при изменении задания регулятору (CА=
0.112 моль/литр, Δ CА
=0.056 моль/литр).
Динамическая ошибка σ
= 0.89%,
время регулирования τр=600 мин.
. Процесс регулирования концентрации вещества B
при изменении задания регулятору (CА=
0.112 моль/литр, Δ CА
=-0.056 моль/литр).
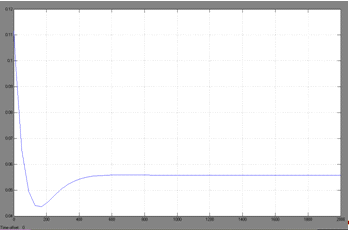
Рис.18. Процесс регулирования концентрации
вещества А при изменении задания регулятору (CА=
0.112 моль/литр, Δ CА
=-0.056 моль/литр).
Динамическая ошибка σ
= 1.56%,
Время регулирования τр=850 мин.
. Процесс регулирования температуры в ректоре
при изменении задания регулятору (t0=82.7790С,
Δt0= 41.389 °C)
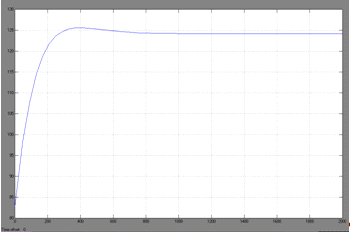
Рис.19. Процесс регулирования температуры в
ректоре при изменении задания регулятору (t0=82.7790С,
Δt0= 41.389 °C).
Динамическая ошибка σ
= 0.76%,
Время регулирования τр=1000 мин.
. Процесс регулирования температуры в ректоре
при изменении задания регулятору (t0=82.7790С,
Δt0= -41.389 °C)
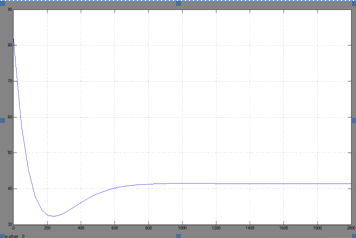
Рис.20. Процесс регулирования температуры в
ректоре при изменении задания регулятору (t0=82.7790С,
Δt0= -41.389 °C).
Динамическая ошибка σ
= 21.89%,
Время регулирования τр=1200 мин.
. Процесс регулирования уровня в ректоре при
изменении задания регулятору (L=0.889
м, ΔL=
0.4445 м)
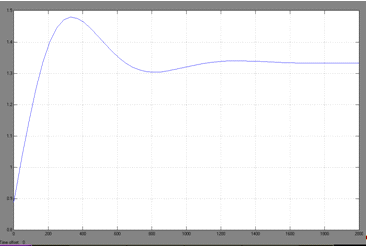
Рис.21. Процесс регулирования уровня в ректоре
при изменении задания регулятору (L=0.889
м, ΔL=
0.4445 м).
Динамическая ошибка σ
= 11.15%,
Время регулирования τр=1620 мин.
. Процесс регулирования уровня в ректоре при
изменении задания регулятору (L=0.889
м, ΔL=-
0.4445 м)
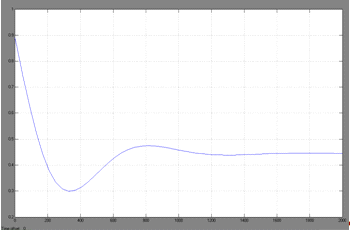
Рис.22. Процесс регулирования уровня в ректоре
при изменении задания регулятору (L=0.889
м, ΔL=
-0.4445 м).
Анализ переходных процессов показывает, что при
50%-х возмущениях выбранные настройки параметров регулятора обеспечивают
удовлетворительное качество регулирования.
Заключение
В данной курсовой работе мы провели
стехиометрический анализ и рассмотрели модель кинетики. Разработали
математическую модель динамики объекта управления (получили систему уравнений
материальных и тепловых балансов). Получили математическую модель статики
объекта управления.
Затем провели синтез формализованной модели
объекта и рассчитали все параметры системы, которая описывает данную модель.
Математическая модель объекта представляет собой систему нелинейных,
обыкновенных дифференциальных уравнений, т.к. объект не линеен, что
подтверждается характером и видом статических характеристик по различным
каналам. Исследовали статику и динамику объекта по всем каналам управления
Список
использованной литературы
1. Лабутин А. Н. Моделирование на
ЭВМ объектов и систем управления, учебное пособие, Иваново - 1989
2. Ротач В. Я. Теория
автоматического управления теплоэнергетическими процессами. М.:
Энергоиздат,1985
. Лабутин А. Н., Ерофеева Е.
В. Моделирование на ЭВМ объектов и систем управления, методические указания к
выполнению курсовой работы, Иваново - 1995
. Кафаров В.В. Методы
кибернетики в химической технологии М.: Химия , 1974