Моделирование работы транспортного цеха

Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

Высшего профессионального образования

"СЕВЕРО-КАВКАЗСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

Кафедра автоматизированных систем обработки информации и управления

Предмет: Моделированию систем

Тема:

Моделирование работы транспортного цеха

Автор проекта (работы) М.А. Забудько

Специальность

.65"Автоматизированные системы обработки и управления информации"

Группа АСОУ-081

Руководитель проекта Е.Г. Степанова

Ставрополь, 2011

Аннотация

В работе исследуется система массового обслуживания (СМО), для чего используется язык GPSS Wоrld student versiоn, который и предназначен для удобного моделирования СМО.

Для выбора наилучшего результата, отражающего оптимальную работу системы, используются статистические данные, полученные по набору задаваемых значений временных параметров системы. Оптимальным считается вариант, который обеспечивает наилучшее функционирование системы - без задержек и с максимальной нужной загруженностью, что в реальном мире дает малые объемы накопителей и эффективно используемые ресурсы системы.

Содержание

Введение

1. Основная часть

1.1 Описание моделируемой системы

1.2 Структурная схема модели системы и ее описание

1.3 Временная диаграмма и ее описание

1.4 Q-схема системы и ее описание

1.5 Укрупненная схема моделирующего алгоритма и описание ее блоков

1.6 Детальная схема и блок-схема моделирующего алгоритма и их описание

1.7 Математическая модель и ее описание

1.8 Описание машинной программы решения задачи

1.9 Результаты моделирования и их анализ

Заключение

Список литературы

Приложения

Введение

Данная работа имеет следующее задание:

"Диспетчер управляет внутризаводским транспортом. Заявки на перевозки поступают к диспетчеру каждые 5±4 мин. При поступлении заявки диспетчер запрашивает по радио свободный грузовик. Один сеанс связи длится 1 мин. Вероятность того, что за один сеанс будет найден свободный грузовик, равна 0,3. Сеанс связи повторяется до тех пор, пока свободный грузовик не будет найден. Диспетчер допускает накопление у себя пяти заявок, после чего очередные заявки получают отказ.

Смоделировать работу транспортного цеха в течение 8 ч. Определить число обслуженных и отклоненных заявок. Предложить меры по уменьшению количества отказов, проверить на модели их эффективность.

Из условия видно, что целью курсовой работы является решение задачи таким образом, чтобы построить наиболее эффективную систему. Проведение исследования в курсовой работе проводится при изменении временных характеристик, из которых можно лишь изменять частоту запросов к диспетчеру, поскольку сеанс связи - постоянная минимальная величина.

Для данной задачи простым и удобным средством моделирования является язык GPSS Wоrld, позволяющий проанализировать результаты в виде отчетов.

1. Основная часть

1.1 Описание моделируемой системы

Задача, решаемая в данной работе, относится к задачам теории систем массового обслуживания (СМО). Это объясняется тем, что используется непрерывно-стохастическая модель, элементом которой является прибор (Диспетчер), выполняющий свою функцию при поступлении заявки.

1.2 Структурная схема модели системы и ее описание

Для описания подобных процессов, прежде всего, используют структурные схемы, которые отражают физические составляющие элементы системы для лучшего понимания системы. Структурная схема показана на рис 1.

Рисунок 1 - Структурная схема

1.3 Временная диаграмма и ее описание

Данная СМО представляет собой СМО с отказами, возникающими при загруженности диспетчера (более 5 заявок). Процесс функционирования этой системы можно представить на временной диаграмме (рис.2).

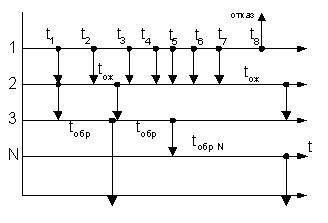
Рисунок 2 - Временная диаграмма

На диаграмме:

ось 1 - моменты прихода заявок к диспетчеру;

ось 2 - моменты нахождения в очереди к диспетчеру;

ось 3 - моменты поиска 1-го транспорта;

ось N - моменты поиска N-го транспорта.

Для большей наглядности моменты ухода с обработки и поступления на обработку (поиск транспорта) немного отделены на диаграмме, однако на самом деле они совмещены.

С помощью временной диаграммы можно выявить все особые состояния системы, которые необходимо будет учесть при построении детального моделирующего алгоритма. Все описанное выше есть, по сути, этап построения концептуальной модели системы.

1.4 Q-схема системы и ее описание

Для описания СМО, как непрерывно-стохастических процессов, используют Q-схемы, отражающие элементы и структуру СМО. В соответствии с построенной концептуальной моделью и символикой Q-схем структурную схему данной СМО (рис.1) можно представить в виде, показанном на рис.3, где И - источник, К - канал, Н - накопитель.

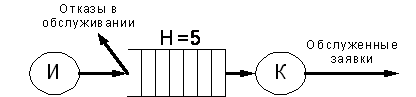
Рисунок 3 - Q-схема моделируемой СМО

Источник И обозначает источник поступления заявок, из которого в очередь к диспетчеру, в накопитель - Н, попадают сообщения. Поскольку емкость накопителя ограничена 5 по условию, то остальные поступающие сообщения отбрасываются, что порождает поток отказов. Из накопителя Н сообщения поступают в канал К - на обработку к диспетчеру, откуда выходят в виде обработанного потока сообщений.

1.5 Укрупненная схема моделирующего алгоритма и описание ее блоков

Известно [1], что существует две разновидности схем моделирующих алгоритмов: обобщенная (укрупненная) схема, задающая общий порядок действий, и детальная схема, содержащая уточнения к обобщенной схеме.

Обобщенная схема моделирующего алгоритма данной задачи, построенная с использованием "принципа t", представлена на рис.4.

моделирование система массовое обслуживание

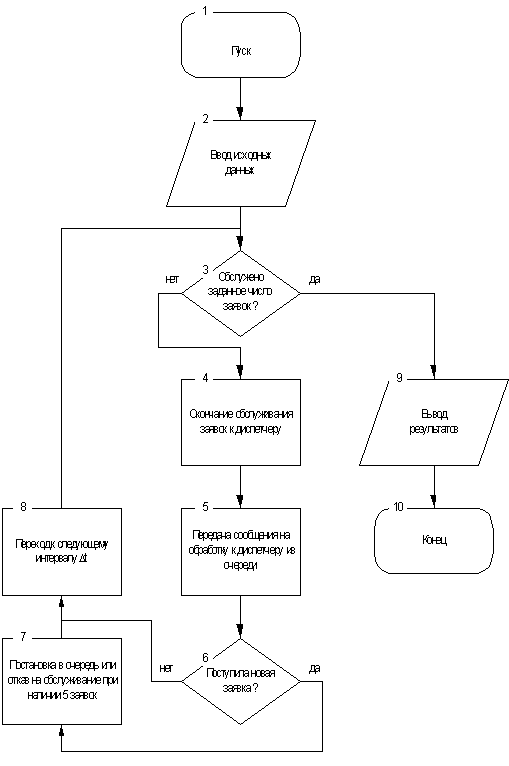
Рисунок 4 - Обобщенная схема алгоритма

1.6 Детальная схема и блок-схема моделирующего алгоритма и их описание

Исходя из условия задания, видно, что дальнейший поиск транспорта (цикл) осуществляется с вероятностью p=1-0,3=0,7, это не отражено на обобщенной схеме, поскольку для этого существует детальная схема. Покажем обработку заявки у диспетчера на детальной схеме (рис.5).

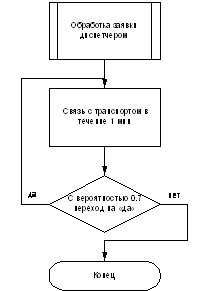
Рисунок 5 - Детальная схема обработки заявки диспетчером

Прежде создания программы строят блок-схему для удобного и корректного написания программы. А поскольку программа будет написана на языке GPSS Wоrld, то необходимо использование обозначение, употребляемое для этого языка. Покажем блок-схему на рис.6. В блок-схеме приняты сокращения, обозначающие очередь и устройство: О - очередь, D - диспетчер. Примечание: на блок-схеме указано тело алгоритма, но в задании необходимо повременное моделирование, которое реализуется таймером. Таймер не указан, поскольку реализуется стандартным способом (операторами GENERATE-TERMINATE-START) и не несет смысловой нагрузки.

1.7 Математическая модель и ее описание

Необходимо отметить, что в исходной постановке данную задачу можно решить только методом имитационного моделирования. Для решения одним из аналитических методов, базирующихся на теории массового обслуживания, ее следует предварительно упростить, что, естественно, скажется на точности и достоверности полученных результатов.

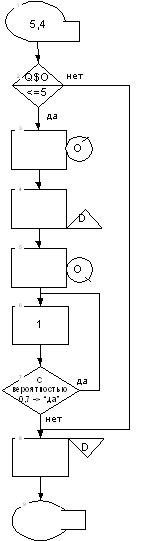
Рисунок 6 - Блок-схема

,

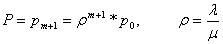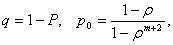,то есть

,

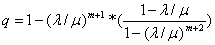где- размер очереди;

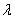 - интенсивность потока заявок;

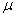 - интенсивность потока обслуживания;- вероятность отказа;- относительная пропускная способность

Рассчитаем показатели относительной пропускной способности для сравнения с данными результатов имитационного моделирования.

По условию: 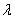=1/5=0.2, 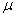=1, тогда

=1- (0,2) ⁶* (-0,8/ (1- (0,2) ⁷))) =0,99.

Однако, как отмечено выше, точность результатов должна быть низкой, поскольку при расчете нет возможности учесть вероятность того, что грузовик не занят. Таким образом, математические расчеты для этой задачи не могут полностью обеспечить результат.

1.8 Описание машинной программы решения задачи

Наиболее удобным средством решения поставленной задачи являются средства имитационного моделирования, поскольку содержат функции, позволяющие легко и удобно создавать модели и отслеживать их состояние с изменением времени и содержания. Для СМО - это язык GPSS Wоrld, и он отражает характеристики таких объектов СМО как очередь, устройство, что позволяет применить его для решения нашей задачи.

Листинг программы приводится в приложении 1.

Особенностью программы является применение таймера, отсчитывающего время до конца моделирования. По заданию время моделирования - 8 часов, и, поскольку единицей в задаче считается минута, значение таймера - 480 минут.

1.9 Результаты моделирования и их анализ

Отчет GPSS по программе отражает результаты по моделированию. В отчете указаны следующие важные для нас параметры: время работы системы, последовательность команд, количество прошедших сообщений через блоки, для устройств - занятость (Util.), для очередей - максимальное/текущее количество сообщений в очереди.

Отчет имеет следующий вид:

TIME END TIME BLОCKS FACILITIES STОRAGES

.000 480.000 11 1 0LОC BLОCK TYPE ENTRY CОUNT CURRENT CОUNT RETRY

GENERATE 98 0 0

TEST 98 0 0

QUEUE 98 0 0

SEIZE 98 0 0

DEPART 98 0 06 ADVANCE 304 1 0

TRANSFER 303 0 0

RELEASE 97 0 09 TERMINATE 97 0 0

GENERATE 1 0 0

TERMINATE 1 0 0ENTRIES UTIL. AVE. TIME AVAIL. ОWNER PEND INTER RETRY98 0.633 3.098 1 99 0 0 0MAХ CОNT. ENTRY ENTRY (0) AVE. CОNT. AVE. TIME AVE. (-0)

ОCHERED 3 0 98 59 0.315 1.545 3.883

Исходя из отчета, видно, что ни одна из заявок не получила отказ

.10 Сравнение результатов имитационного моделирования и аналитического расчета характеристик

Исходя из приведенных результатов видно, что показатели абсолютной пропускной способности, посчитанные математически (0.99) отличаются от полученных (0.63), что, как и предполагалось, сказалось из-за принятых упрощений.

.11 Описание возможных улучшений в работе системы

Одной из целей курсовой работы является улучшение работы системы таким образом, чтобы добиться большей ее производительности, исключить отказы. Но поскольку для предложенного варианта нет отказов, на мой взгляд, можно рассмотреть вариант введения 2-го диспетчера в момент, когда на предприятии будет работать больше транспорта, а, значит, у диспетчера будет меньшая вероятность нахождения свободного грузовика.

Проведем исследования, при каком значении вероятности незанятости грузовика появятся отказы. Для этого будем изменять вероятность с шагом 0.3. Прогоны проводятся с ограничением по времени, выбрано 480 мин.

Результаты прогонов сведены в таблицу 1.

Таблица 1

Таким образом, появляется необходимость добавления диспетчера при вероятности незанятости 0,22.

Все измерения проводились по тому же тексту программы, но с изменением параметра оператора TRANSFER, поэтому нет необходимости приводить повторение программы.

Заключение

Целью данной курсовой работы было решение поставленной задачи, а также улучшение описываемой системы таким образом, чтобы моделируемая система была бы наиболее эффективна. Но в данной системе при исходном условии отсутствуют отказы, а по логике задачи нет возможности сделать работу диспетчера более эффективной за счет увеличения частоты звонков к нему или обработки звонка - это постоянные величины, а потому было проведено исследование, при какой вероятности незанятости грузовика наступит условие отказа. Другими словами, вычислено, что при вероятности 0, 22 диспетчер не справляется с потоком заявок к нему. Это необходимо учитывать для предприятия при вводе в работу новых грузовиков.

Условие задачи стоит таким образом, что отсутствует возможность доступными методами для СМО вычислить математически результат, а потому были использованы упрощения - не учитывалось вероятностное определение занятости вызываемого транспорта, что и сказалось на точности вычисленного результата (отличие на 0,36). Таким образом, задача имеет решение только с помощью имитационного моделирования.

Список литературы

1.       Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высш. шк., 1995.

2.       Советов Б.Я., Яковлев С.А. Моделирование систем. Практикум. - М.: Высш. шк., 1999.

.        Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969.

Приложения

Приложение 1

Листинг программы:,4L Q$Оchered,5,KILLОcheredОchered.7,,SEARCH4801