Кинематика точки и вращательное движение тела
Задание 1.
Кинематика точки
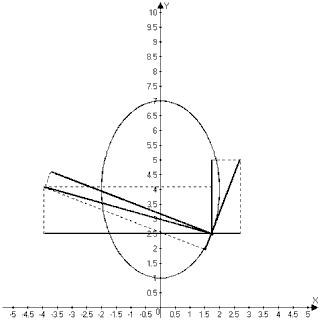
По заданным уравнениям движения точки М установить вид её траектории и
для момента времени t=t1(с) найти положение точки на траектории, её скорость,
полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Дано:
|
Уравнения движения
|
t1, с
|
|
x=x(t), см
|
y=y(t), см
|
|
|
-4t2 +1
|
-3t
|
1
|
1.
Уравнение траектории. Для определения
уравнения траектории точки исключим время 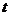 из
заданных уравнений движения.
из
заданных уравнений движения.
Воспользуемся
свойством тригонометрических функций
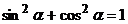 .
.
Тогда
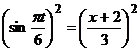 ,
, 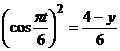
и
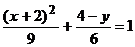
и
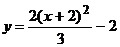 .
.
Это
уравнение параболы.
2.
Скорость точки. Скорость найдем по ее
проекциям на координатные оси:
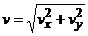 , где
, где
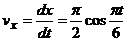 ,
, 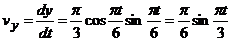 . При
. При 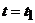 =1 с
=1 с
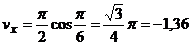 (см/с),
(см/с), 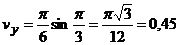 (см/с),
(см/с),
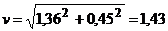 (см/с).
(см/с).
.
Ускорение точки. Находим аналогично:
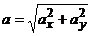 ,
,
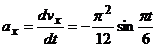 ,
, 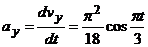
и
при 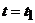 =1 с
=1 с
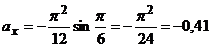 (см/с2),
(см/с2),
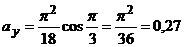 (см/с2),
(см/с2),
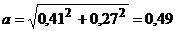 (см/с2).
(см/с2).
4. Касательное ускорение. Найдем, дифференцируя равенство
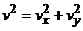 .
.
Получим
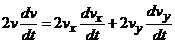 ,
,
откуда
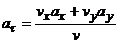
и
при 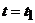 =1 с
=1 с
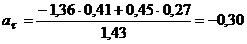 (см/с2).
(см/с2).
.
Нормальное ускорение.
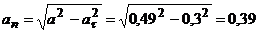 (см/с2).
(см/с2).
.
Радиус кривизны траектории.
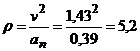 (см).
(см).
|
v
|
a
|
at
|
an
|
r
|
|
см/с
|
см/с2
|
см
|
|
1,43
|
0,49
|
-0,3
|
0,39
|
5,2
|
Задание 2.
Вращательное движение тела
Вал электродвигателя, связанный со шкивом 1 ременной передачи, вращается
равноускоренно в течение t
секунд. Найти передаточные числа передач, угловые скорости и угловые ускорения
звеньев, скорость и ускорения точки М для момента времени t1.
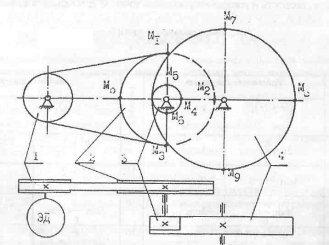
Кинематические пары механизма:
O(0-1);
A(1-2); B(2-3);B(3-4);
C(0-3); E(4-5);К(0-5) - вращательные пары 5 класса;
Число всех звеньев механизма:
m = 6.
Число подвижных звеньев механизма:
n = 5.
Число степеней свободы механизма:
W = 3×n - 2×P5 - P4= 3×5 - 2×7 - 0 = 1,
где P5 - число пар 5-го класса (низшие пары);
P4 - число пар 4-го класса (высшие
пары).
Разложим
механизм на группы Ассура
Рассмотрим группу (4-5)
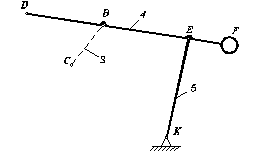
К(0-5)
- возможная пара;
Е(4-5)
- действительная пара;
В(3-4)
- возможная пара.
Wгр = 3×n - 2×P5 = 3×2 - 2×3 = 0,
где
Wгр -
степень свободы группы;
n - число
подвижных звеньев группы;
Р5
- число пар 5-го класса, входящих в группу.
Формула
группы:
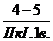
Рассмотрим
группу (2-3)
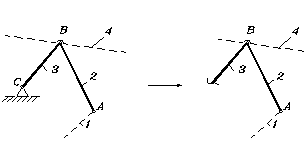
n = 2
А(1-2) - возможная пара;
В(2-3) - действительная пара;
В(3-4) - возможная пара.
Wгр
= 3×n - 2×P5 = 3×2 - 2×3 = 0,
Формула группы:
Рассмотрим
начальный механизм
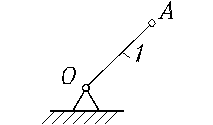
n = 1;
W = 3×n - 2×P5 - P4;
O(0-1) -
действительная пара
W = 3×1 - 2×1 = 1.
Формула механизма
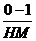
Структурная формула механизма:
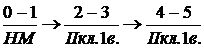
Механизм
II класса 1 вида.
Планы
скоростей строим повернутыми на 90о графо-аналитическим методом, решая
системы векторных уравнений.
Определяем
скорость точки М0 механизма:
VA = ω1×lAO =
15×0,06 = 0,9 м/с,
где
VA - скорость точки А, м/с;
lAO -
длина звена, м.
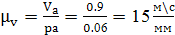
где
mV
- масштабный коэффициент плана скоростей, 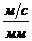 ;
;
Найдем
скорость точки.
Точка
принадлежит звеньям 2 и 3. Её положение на плане скоростей определяется как
точка пересечения линий действия соответствующих векторов скоростей.
Так
как точка С неподвижна, то:
Определим
скорость точки Е, принадлежащей звеньям 4 и 5:
Точка
К является неподвижной опорой:
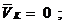
где
V - линейная скорость точки или звена, м/с;
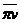 - вектор
скорости точки, или звена.
- вектор
скорости точки, или звена.
VB = pb × μV
= 66,6 × 0,0198 = 1,32 м/с;
VE = pe × μV
= 59,3× 0,0198 = 1,17 м/с;
VD = pd × μV
= 96,2 × 0,0198 = 1,9 м/с;
VF = pf × μV
= 117,7 × 0,0198 = 2,33 м/с;
VAB =
ab × μV
= 45,7 × 0,0198 = 0,9 м/с;
VDF =
df × μV
= 182,4 × 0,0198 = 3,61 м/с.
Угловые
скорости звеньев определяются по формуле:
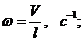
где
w - угловая скорость звена, с-1;- скорость
звена, м/с;- длина звена, м.
Массы
звеньев 1, 2, 3, 5 не заданы, поэтому их силы тяжести не учитываем. Приведенный
момент Mп представим в виде пары сил Pп с плечом AB.
Приведение произведем с помощью “Рычага Жуковского”. Одна из составляющих пары
сил Pп не будут иметь момента относительно полюса плана скоростей,
поэтому ее не показываем. Величину и направление Pп определим из
равенства - по величине и направлению - момента силы Pп сумме
моментов сил GШ и GF относительно полюса.
Для
положения 1:
где
pa, 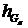 ,
, 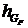 - плечи сил (снимаются с планов скоростей), мм;
- плечи сил (снимаются с планов скоростей), мм;
Pпр - приведенная сила, Н;
Для
положения 2:
Для
положения 3:
Для
положения 4:
Для
положения 5:
Для положения 6:
Для положения 7:
Для положения 8:
Для положения 9:
Для положения 10:
Для положения 11:
Для положения 12:
Приведенный момент будем определять по формуле:
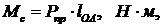
где
Мс - приведенный момент сил сопротивления, Н×м.
Для
расчетного положения:
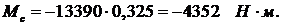
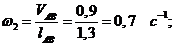
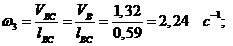
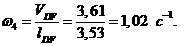
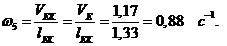
Строим
план ускорений для расчётного положения.
Ускорения
точек звеньев будем определять по формуле:
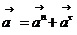 ,
,
где
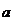 - полное ускорение точки,
- полное ускорение точки, 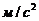 ;
;
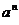 -
нормальное ускорение точки,
-
нормальное ускорение точки, 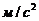 ;
;
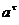 -
тангенциальное (касательное) ускорение точки,
-
тангенциальное (касательное) ускорение точки, 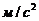 ;
;
Так
как угловая скорость кривошипа постоянна, то 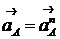 .
.
Из
произвольно выбранного полюса 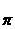 откладываем
вектор
откладываем
вектор 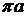 . Найдём масштабный коэффициент плана ускорений:
. Найдём масштабный коэффициент плана ускорений:
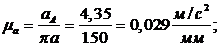
Для
нахождения ускорений точек звеньев используем графоаналитический метод.
Точка B принадлежит звеньям 2 и 3. Её
положение на плане ускорений определяется как точка пересечения линий действия
соответствующих векторов ускорений:
Точка
b находится на пересечении линий действия 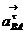 ,
,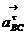 .
.
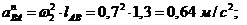
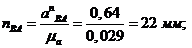 (
(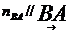 );
);
Так
как стойка неподвижна, то ac=0.
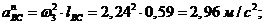
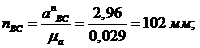 (
(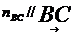 );
);
Точка
Е принадлежит звеньям 4 и 5:
Точка
e находится на пересечении линий действия 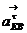 ,
, 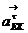 .
.
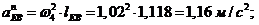
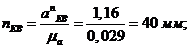 (
(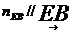 )
)
Положение
точек на плане ускорений определим исходя из пропорциональности отношений длин
звеньев c учетом обхода точек.
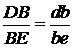
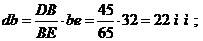
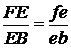
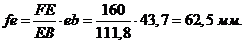
Ускорения
точек и звеньев:
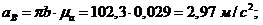
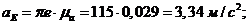
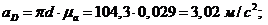
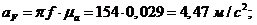
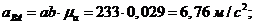
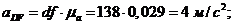
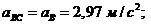
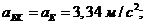
Тангенциальные
ускорения:
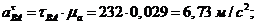
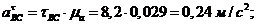
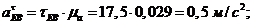
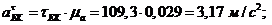
Угловые
ускорения звеньев:
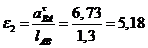 ,
,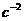 ;
;
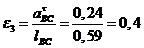 ,
, 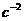
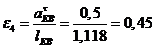 ,
, 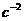
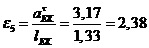 ,
, 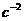
Силы
инерции:
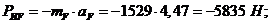
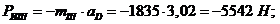
“-“
показывает направление силы инерции. Сила инерции направлена противоположно
ускорению.
Приведенные
моменты инерции:
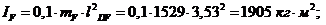
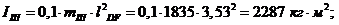
Момент
инерции звеньев:
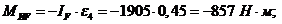
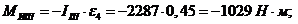
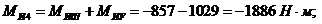
Момент
инерции направлен противоположно угловому ускорению.
Рассмотрим
группу Ассура 4-5.
Тангенциальные
реакции определим аналитически из уравнений моментов относительно точки Е звена
4:
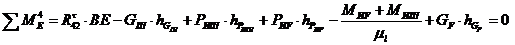 ;
;
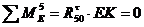 ;
;
где
BF, EK,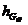 ,
,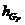 ,
,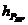 ,
,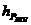 - плечи соответствующих сил, снятые с плана положений,
мм;
- плечи соответствующих сил, снятые с плана положений,
мм;
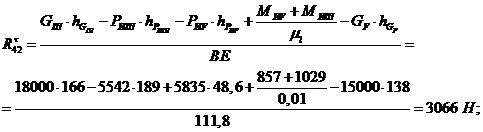
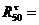 0;
0;
Реакции
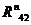 (
(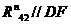 ) и
) и 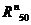 (
(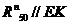 ) определим графически через сумму всех сил для всей
группы:
) определим графически через сумму всех сил для всей
группы:
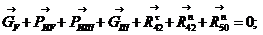
Определим
масштабный коэффициент плана сил:
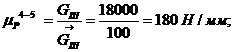
где
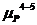 - масштабный коэффициент группы 4-5, Н/мм;
- масштабный коэффициент группы 4-5, Н/мм;
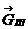 - вектор
силы GШ,
принятый равным 100, мм;
- вектор
силы GШ,
принятый равным 100, мм;
Задание 3.
Кинематика твердого тела
ускорение точка вал ползунный
Для внецентренного кривошипно-ползунного механизма выполнить
кинематический анализ с использованием аналитического и графоаналитического
способа.
Дано:
Заданы следующие параметры кривошипно-ползунного механизма
Yb =- 0,003 м
угловая скорость кривошипа ω1 = 240 с-1 = const. Направление движения кривошипа
против часовой стрелки
m3 = m2, где m3 - масса ползуна 3; m2 - масса шатуна 2
Р
= 2F1, где F1 - сила инерции кривошипа 1;
q = 10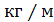 - масса одного метра длинны звена
- масса одного метра длинны звена

Построение плана 12 положений механизма
Определяем масштабный коэффициент длин, представляющий собой отношение
действительной длины в метрах к длине отрезка на чертеже в миллиметрах.
Изображаем длину кривошипа lОА на
чертеже отрезком l′ОА,
равным 51 мм. Тогда масштабный коэффициент будет иметь величину:
μl = 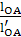 =
= 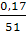 = 0,00333
= 0,00333 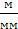
Остальные длины звеньев, изображенные на чертеже, будут иметь следующие
значения:
l′АВ
= 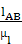 =
= 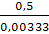 = 150
= 150 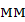 ,
,
l′ВС
= 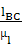 =
= 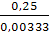 = 75
= 75 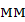 ,
,
е′ = 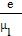 =
= 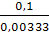 = 30
= 30 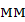
Из произвольной точки О откладываем отрезок lОА = 51 мм. Далее проводим
горизонтальную прямую Х, отстоящую от точки О по вертикали на
величину е′. Из точки А раствором циркуля, равным l′АВ, на оси Х
делаем засечку, получая точку В. На продолжении линии АВ
откладываем расстояние l′ВС
и отмечаем точку С. Указываем положение центров масс S1, S2, S3,(для положений механизма 2 и 7) которые находятся в
серединах отрезков ОА, АС, и в точке В. Аналогичным образом
строим и другие положения механизма, которые отличаются величинами угла φ1. Получаем план 12 положений
механизма. Положение механизма 2 и 7 выделяем толстыми линиями.
Построение плана скоростей положения механизма №2
Отдельно вычерчиваем положение механизма №2
Определяем скорость точки А.
VA = ω1∙ lОА = 12 ∙ 0,17 = 2,04 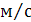 .
.
Находим масштабный коэффициент скоростей, для чего полученную величину
делим на длину вектора этой скорости, выбранную равной ра = 150 мм.
μV = 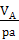 =
= 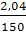 = 0,0136
= 0,0136 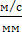
Из произвольной точки р (полюса скоростей) проводим вектор 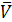 A длиной 150 мм, который
перпендикулярен кривошипу ОА и направлен в сторону его вращения.
Скорость точки В находим графически, используя векторные уравнения:
A длиной 150 мм, который
перпендикулярен кривошипу ОА и направлен в сторону его вращения.
Скорость точки В находим графически, используя векторные уравнения:
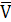 B =
B = 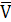 A +
A + 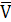 BA,
BA,
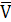 B =
B = 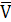 B′ +
B′ + 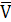 BB′
BB′
Здесь точка В′ принадлежит стойке Х.
Так как скорости точек О и В′ равны нулю, то точки о
и b′ помещаем в полюсе. Уравнения
решаются так. Из точки а проводим линию, перпендикулярную шатуну АВ,
а из полюса - прямую, параллельную стойке Х. На пересечении ставим стрелки, получая
векторы скоростей 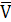 B и
B и 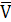 BA.
Для нахождения положения точки с используем отношение:
BA.
Для нахождения положения точки с используем отношение:
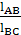 =
= 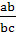 , bc =
, bc = 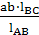 =
= 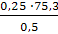 = 37,6 мм
= 37,6 мм
Откладываем эту величину на продолжении линии аb. Полученную точку соединяем с полюсом, получая вектор
скорости 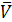 C. Численные значения скоростей
получаем путем замер каждого вектора и умножения полученной величины на μV.
C. Численные значения скоростей
получаем путем замер каждого вектора и умножения полученной величины на μV.
VB = pb ∙ μ V = 135,5 ∙ 0,0136 = 1,8 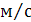
VВА
= ba ∙ μ V = 75,5 ∙ 0,0136 = 1 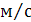
VC = pc ∙ μ V = 145,5 ∙ 0,0136 = 2 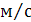
Находим угловую скорость ω2 шатуна:
ω2 = 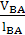 =
= 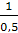 = 2
= 2 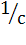
Направление этой скорости можно найти, поместив вектор 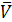 BA в точку В и посмотрев, куда
повернется шатун АВ относительно точки В. В данном случае - по
часовой стрелке. Циркулем обозначим дуговую стрелку скорости ω2, ставя ножку циркуля в точку А.
BA в точку В и посмотрев, куда
повернется шатун АВ относительно точки В. В данном случае - по
часовой стрелке. Циркулем обозначим дуговую стрелку скорости ω2, ставя ножку циркуля в точку А.
Угловая скорость ω3 ползуна равна нулю.
Построение плана ускорений положения механизма №2
Ускорение точки А в общем случае складывается из двух
составляющих:
āА = 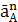 +
+ 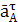
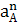 =
= 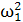 ∙ lОА = 122 ∙ 0,17 = 24,5
∙ lОА = 122 ∙ 0,17 = 24,5
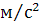 ;
;
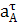 = ε1 ∙ lОА = 0, т.к.
ε1 =
= ε1 ∙ lОА = 0, т.к.
ε1 = 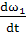 = 0
= 0
Следовательно, аА = 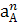 = 24,5
= 24,5 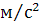
Масштабный коэффициент ускорений можно найти путем деления этой величины
на длину πа вектора
āА на чертеже, равную 150 мм.
μА = 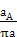 =
= 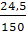 = 0,163
= 0,163 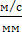
Ускорение точки А направлено параллельно кривошипу ОА от
точки А к центру О. Из произвольной точки π (полюса ускорений) проводим вектор āА длиной 150 мм. Ускорение
точки В находим графоаналитически, решая систему векторных уравнений:
āВ = āА + 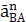 +
+ 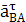 , āВ = āВ′ +
, āВ = āВ′ + 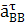
Ускорения ā0 и āВ′ равны нулю, поэтому точки 0 и
b′ помещаем в полюсе.
Определяем ускорение 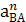 :
:
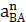 =
= 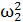 ∙ lВА = 22 ∙ 0,5 = 2
∙ lВА = 22 ∙ 0,5 = 2 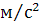
Это ускорение направлено параллельно шатуну ВА от точки В к
точке А. Длина вектора этого ускорения:
ат = 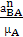 =
= 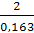 = 12,3 мм
= 12,3 мм
В конце вектора 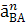 проводим прямую, перпендикулярную шатуну АВ. Из
полюса π направляем
луч, параллельный стойке Х. На пересечении ставим стрелки, получая
векторы
проводим прямую, перпендикулярную шатуну АВ. Из
полюса π направляем
луч, параллельный стойке Х. На пересечении ставим стрелки, получая
векторы 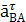 и āВ. Точка а и b соединяем и на продолжении от точки b откладываем отрезок bc, получаемый из соотношения:
и āВ. Точка а и b соединяем и на продолжении от точки b откладываем отрезок bc, получаемый из соотношения:
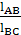 =
= 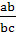 , bc =
, bc = 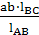 =
= 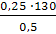 = 65 мм
= 65 мм
Точку с соединяем с полюсом, получая вектор āС. В серединах отрезков оа и са
находим положения точек s1 и s2, соединяя которые с полюсом, находим
векторы ускорений āS1 и āS2. Вектор ускорения āS3 совпадает с вектором āВ.
Замеряя длины векторов неизвестных ускорений, находим их численные
значения:
аB = 𝜋b ∙ μ А = 75 ∙ 0,163 = 12,2 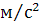 ,
,
аС = 𝜋с ∙ μ А = 99 ∙ 0,163 = 16,1 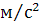 ,
,
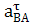 =
bт ∙ μ А = 129 ∙ 0,163 = 21
=
bт ∙ μ А = 129 ∙ 0,163 = 21 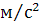 ,
,
aS1 = 𝜋 s1 ∙ μ А = 75 ∙ 0,163 = 12,2 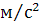 ,S2 = 𝜋 s2 ∙ μ А = 82 ∙ 0,163 = 13,4
,S2 = 𝜋 s2 ∙ μ А = 82 ∙ 0,163 = 13,4 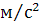 ,S3 = 𝜋 s3 ∙ μ А = 75 ∙ 0,163 = 12,2
,S3 = 𝜋 s3 ∙ μ А = 75 ∙ 0,163 = 12,2 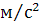
Определяем угловое ускорение:
𝜀2 = 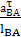 =
= 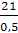 = 42
= 42 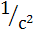
Переносим вектор 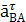 в точку В механизма и находим, что угловое ускорение
направлено против часовой стрелки. Угловое ускорение 𝜀3 ползуна равно нулю.
в точку В механизма и находим, что угловое ускорение
направлено против часовой стрелки. Угловое ускорение 𝜀3 ползуна равно нулю.
Аналитическое исследование положения механизма №2
Для проверки точности результатов построения планов скоростей и ускорений
найдем линейные и угловые скорости и ускорения аналитическим методом.
Представим звенья механизма в виде векторов, а углы их наклона укажем от
положительного направления оси Х против хода часовой стрелки. Определим
угол φ2 следующим образом.
Из треугольника АВЕ находим угол α
α = arcsin 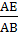 .
.
Но АЕ = AD - DE.
Величину AD найдем из
треугольника OAD:
AD = OA ∙ sinφ1 = lОА ∙ sinφ1
Т.к. DE = e, то получим:
α = arcsin 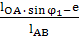 = arcsin
= arcsin 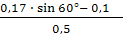 = 5,4°
= 5,4°
Следовательно, φ2 = 360° - 5,4° =
354,6°
Угловую скорость ω2 шатуна определим по формуле:
ω2 = - ω1 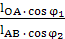 = - 12
= - 12 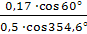 = - 2,04
= - 2,04 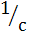
В этой формуле скорость ω1 подставляется со своим знаком. Знак
минус указывает, что скорость ω2 направлена по часовой стрелке.
Угловое ускорение 𝜀2 шатуна находим по
формуле:
𝜀2 = 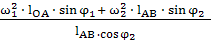 =
= 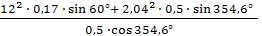 = 42,2
= 42,2 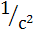
Скорость ползуна определится следующим образом:
VB = ω1 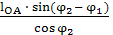 = 12
= 12 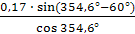 = - 1,87
= - 1,87 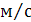
Знак минус говорит о том, что скорость направлена в сторону, обратную
направлению оси Х.
Ускорение ползуна вычисляем по формуле:
аВ = - 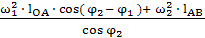 = -
= - 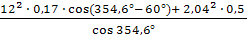 =
=
= -12,28 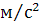
Отрицательное значение указывает на то, что оно направлено влево.
Сравнение результатов, полученных различными способами, говорит о том,
что построения выполнены с высокой точностью.
Отдельно вычерчиваем положение механизма №2
Определяем скорость точки А.
VA = ω1∙ lОА = 12 ∙ 0,17 = 2,04 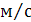 .
.
Находим масштабный коэффициент скоростей, для чего полученную величину
делим на длину вектора этой скорости, выбранную равной ра = 150 мм.
μV = 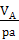 =
= 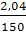 = 0,0136
= 0,0136 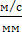
Из произвольной точки р (полюса скоростей) проводим вектор 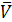 A длиной 150 мм, который
перпендикулярен кривошипу ОА и направлен в сторону его вращения.
Скорость точки В находим графически, используя векторные уравнения:
A длиной 150 мм, который
перпендикулярен кривошипу ОА и направлен в сторону его вращения.
Скорость точки В находим графически, используя векторные уравнения:
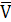 B =
B = 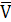 A +
A + 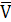 BA,
BA, 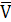 B =
B = 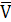 B′ +
B′ + 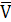 BB′
BB′
Здесь точка В′ принадлежит стойке Х.
Так как скорости точек О и В′ равны нулю, то точки о
и b′ помещаем в полюсе. Уравнения
решаются так. Из точки а проводим линию, перпендикулярную шатуну АВ,
а из полюса- прямую, параллельную стойке Х. На пересечении ставим
стрелки, получая векторы скоростей 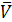 B и
B и 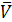 BA. Для нахождения положения точки с используем
отношение:
BA. Для нахождения положения точки с используем
отношение:
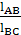 =
= 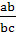 , bc =
, bc = 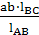 =
= 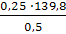 = 70 мм
= 70 мм
Откладываем эту величину на продолжении линии аb. Полученную точку соединяем с полюсом, получая вектор
скорости 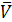 C. Численные значения скоростей
получаем путем замер каждого вектора и умножения полученной величины на μV.
C. Численные значения скоростей
получаем путем замер каждого вектора и умножения полученной величины на μV.
VB = pb ∙ μ V = 23,3 ∙ 0,0136 = 0,3 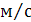
VВА
= ba ∙ μ V = 139,8 ∙ 0,0136 = 1,9 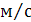
VC = pc ∙ μ V = 65 ∙ 0,0136 = 0,9 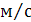
Находим угловую скорость ω2 шатуна:
ω2 = 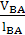 =
= 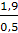 = 3,8
= 3,8 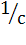
Направление этой скорости можно найти, поместив вектор 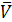 BA в точку В и посмотрев, куда
повернется шатун АВ относительно точки В. В данном случае -
против часовой стрелки. Циркулем обозначим дуговую стрелку скорости ω2, ставя ножку циркуля в точку А.
BA в точку В и посмотрев, куда
повернется шатун АВ относительно точки В. В данном случае -
против часовой стрелки. Циркулем обозначим дуговую стрелку скорости ω2, ставя ножку циркуля в точку А.
Угловая скорость ω3 ползуна равна нулю.
Построение плана ускорений положения механизма №7
Ускорение точки А в общем случае складывается из двух
составляющих:
āА = 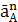 +
+ 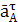
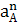 =
= 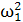 ∙ lОА = 122 ∙ 0,17 = 24,5
∙ lОА = 122 ∙ 0,17 = 24,5
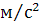 ;
;
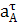 = ε1 ∙ lОА = 0, т.к.
ε1 =
= ε1 ∙ lОА = 0, т.к.
ε1 = 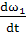 = 0
= 0
Следовательно, аА = 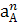 = 24,5
= 24,5 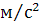
Масштабный коэффициент ускорений можно найти путем деления этой величины
на длину πа вектора
āА на чертеже, равную 150 мм.
μА = 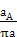 =
= 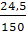 = 0,163
= 0,163 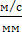
Ускорение точки А направлено параллельно кривошипу ОА от
точки А к центру О. Из произвольной точки π (полюса ускорений) (рис. 2.7) проводим вектор āА длиной 150 мм. Ускорение точки
В находим графоаналитически, решая систему векторных уравнений:
āВ = āА + 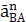 +
+ 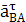 , āВ = āВ′ +
, āВ = āВ′ + 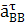
Ускорения ā0 и āВ′ равны нулю, поэтому точки 0 и
b′ помещаем в полюсе.
Определяем ускорение 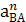 :
:
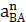 =
= 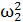 ∙ lВА = 3,82 ∙ 0,5 = 7,2
∙ lВА = 3,82 ∙ 0,5 = 7,2 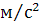
Это ускорение направлено параллельно шатуну ВА от точки В к
точке А. Длина вектора этого ускорения:
ат = 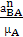 =
= 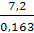 = 44,2 мм
= 44,2 мм
В конце вектора 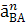 проводим прямую, перпендикулярную шатуну АВ. Из
полюса π направляем
луч, параллельный стойке Х. На пересечении ставим стрелки, получая
векторы
проводим прямую, перпендикулярную шатуну АВ. Из
полюса π направляем
луч, параллельный стойке Х. На пересечении ставим стрелки, получая
векторы 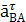 и āВ. Точка а и b соединяем и на продолжении от точки b откладываем отрезок bc, получаемый из соотношения:
и āВ. Точка а и b соединяем и на продолжении от точки b откладываем отрезок bc, получаемый из соотношения:
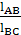 =
= 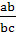 , bc =
, bc = 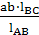 =
= 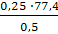 = 38,7 мм
= 38,7 мм
Точку с соединяем с полюсом, получая вектор āС. В серединах отрезков оа и са
находим положения точек s1 и s2, соединяя которые с полюсом, находим
векторы ускорений āS1 и āS2. Вектор ускорения āS3 совпадает с вектором āВ.
Замеряя длины векторов неизвестных ускорений, находим их численные
значения:
аB = 𝜋b ∙ μ А = 110,5 ∙ 0,163 = 18 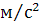 ,
,
аС = 𝜋с ∙ μ А = 107,7 ∙ 0,163 = 17,5 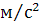 ,
,
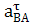 =
bт ∙ μ А = 62,6 ∙ 0,163 = 10,2
=
bт ∙ μ А = 62,6 ∙ 0,163 = 10,2 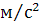 ,
,
aS1 = 𝜋 s1 ∙ μ А = 75 ∙ 0,163 = 12,2 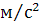 ,S2 = 𝜋 s2 ∙ μ А = 117 ∙ 0,163 = 19
,S2 = 𝜋 s2 ∙ μ А = 117 ∙ 0,163 = 19 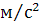 ,S3 = 𝜋 s3 ∙ μ А = 110,5 ∙ 0,163 = 18
,S3 = 𝜋 s3 ∙ μ А = 110,5 ∙ 0,163 = 18 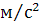
Определяем угловое ускорение:
𝜀2 = 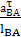 =
= 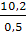 = 20,4
= 20,4 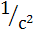
Переносим вектор 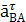 в точку В механизма и находим, что угловое ускорение
направлено по часовой стрелке. Угловое ускорение 𝜀3 ползуна равно нулю.
в точку В механизма и находим, что угловое ускорение
направлено по часовой стрелке. Угловое ускорение 𝜀3 ползуна равно нулю.
Аналитическое исследование положения механизма №7
Для проверки точности результатов построения планов скоростей и ускорений
найдем линейные и угловые скорости и ускорения аналитическим методом.
Представим звенья механизма в виде векторов, а углы их наклона укажем от
положительного направления оси Х против хода часовой стрелки. Определим
угол φ2 следующим образом.
α = arcsin 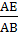 .
.
Но АЕ = AD + DE
Величину AD найдем из
треугольника OAD:
AD = OA ∙ sin(φ1 - 180°) = lОА ∙ sin(210° - 180°) = lОА ∙ sin30°
Т.к. DE = e, то получим:
α = arcsin 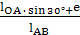 = arcsin
= arcsin 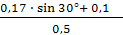 = 21,7°
= 21,7°
Следовательно, φ2 = α = 21,7°
Угловую скорость ω2 шатуна определим по формуле:
ω2 = - ω1 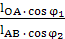 = - 12
= - 12 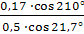 = 3,8
= 3,8 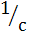
В этой формуле скорость ω1 подставляется со своим знаком. Знак
плюс указывает, что скорость ω2 направлена против часовой стрелки.
Угловое ускорение 𝜀2 шатуна находим по
формуле:
𝜀2 =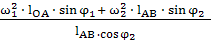 =
= 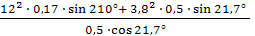 =
=
= - 20,6 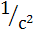
Скорость ползуна определится следующим образом:
VB = ω1 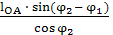 = 12
= 12 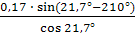 = 0,3
= 0,3 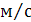
Знак плюс говорит о том, что скорость направлена по направлению оси Х.
Ускорение ползуна вычисляем по формуле:
аВ = - 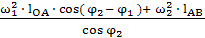 = -
= - 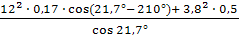 =
=
= 18,3 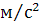
Положительное значение указывает на то, что оно направлено вправо.
Сравнение результатов, полученных различными способами, говорит о том,
что построения выполнены с высокой точностью.
Изображаем механизм в положении №2 с обозначением масштабного
коэффициента μl = 0,00333 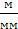 . На механизм действуют следующие
силы:
. На механизм действуют следующие
силы:
. Сила полезного сопротивления 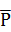 , указываемая в задании. Она
проложена в точке В ползуна 3 и направлена горизонтально.
, указываемая в задании. Она
проложена в точке В ползуна 3 и направлена горизонтально.
. Силы тяжести 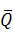 , определяемые через массы звеньев, которые можно условно
найти по формуле m = q ∙ l, где q - единицы длины звена, l - длина звена:
, определяемые через массы звеньев, которые можно условно
найти по формуле m = q ∙ l, где q - единицы длины звена, l - длина звена:
m1 = q ∙ l1 = 10 ∙ 0,17 = 1,7 кг
m2 = q ∙ l2 = 10 ∙ 0,75 = 7,5 кг
m3 = m2 = 7,5 кг
Следовательно,
Q1 = m1 ∙ g =
1,7 ∙ 9,8 = 16,7 H
Q2 = m2∙ g =
7,5 ∙ 9,8 = 73,5 H
Q3 = m3 ∙ g =
7,5 ∙ 9,8 = 73,5 H
Силы тяжести прикладываются в центрах масс S1, S2, S3 и направлены вертикально вниз.
. Силы инерции звеньев 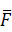 , определяемые по формуле F = m ∙ as
, определяемые по формуле F = m ∙ as
F1
= m1 ∙ 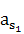 = 1,7 ∙ 12,2 = 24,7 H
= 1,7 ∙ 12,2 = 24,7 H
F2
= m2 ∙ 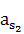 = 7,5 ∙ 13,4 = 100,5 H
= 7,5 ∙ 13,4 = 100,5 H
F3 = m3 ∙ 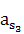 = 7,5 ∙ 12,2 = 91,5 H
= 7,5 ∙ 12,2 = 91,5 H
Эти силы прикладываются в центрах масс и направлены они в стороны,
обратные ускорениям 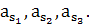
4. Моменты сил инерции М, которые можно найти по формуле
М = Is ∙
ε, где
Is - моменты инерции звеньев относительно центральных осей
М1 = 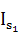 ∙ ε1 = 0, т.к. ε1 = 0
∙ ε1 = 0, т.к. ε1 = 0
М2 = 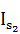 ∙ ε2
∙ ε2
М3 = 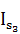 ∙ ε3 = 0, т.к. ε3 = 0
∙ ε3 = 0, т.к. ε3 = 0
Моменты инерции звеньев определяем по формуле
Is = 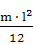
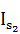 =
= 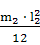 =
= 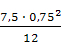 = 0,35 кгм2
= 0,35 кгм2
Следовательно,
М2 = 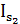 ∙ ε2 = 0,35 ∙ 42,2 = 14,77 Нм
∙ ε2 = 0,35 ∙ 42,2 = 14,77 Нм
Моменты сил инерции направлены в стороны, обратные угловым ускорениям.
. Уравновешивающая сила 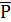 у, прикладываемая в точке А кривошипа 1 и на - правленная перпендикулярно
ему. В нашем случае она направлена вверх.
у, прикладываемая в точке А кривошипа 1 и на - правленная перпендикулярно
ему. В нашем случае она направлена вверх.
Изображаем отдельно структурную группу, состоящую из шатуна 2 и ползуна
3. Реакцию 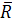 12 направляем произвольно, а реакцию
12 направляем произвольно, а реакцию 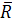 03 - вертикально. Пусть она направлена
вверх. Рассматриваем равновесие группы и записываем уравнение моментов
относительно точки А. Для этого сначала из точки А проводим
перпендикуляры ко всем силам, замеряем их длины в миллиметрах и умножаем на μl, получая их величины:
03 - вертикально. Пусть она направлена
вверх. Рассматриваем равновесие группы и записываем уравнение моментов
относительно точки А. Для этого сначала из точки А проводим
перпендикуляры ко всем силам, замеряем их длины в миллиметрах и умножаем на μl, получая их величины:
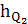 =
=
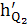 ∙ μl = 112 ∙ 0, 00333 = 0,37 м
∙ μl = 112 ∙ 0, 00333 = 0,37 м
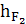 =
=
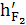 ∙ μl = 54,2 ∙ 0, 00333 = 0,18 м
∙ μl = 54,2 ∙ 0, 00333 = 0,18 м
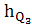 =
=
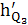 ∙ μl = 149,3 ∙ 0, 00333 = 0,5 м
∙ μl = 149,3 ∙ 0, 00333 = 0,5 м
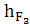 =
=
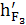 ∙ μl = 14,2 ∙ 0, 00333 = 0,05 м
∙ μl = 14,2 ∙ 0, 00333 = 0,05 м
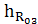 =
=
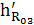 ∙ μl = 149,3 ∙ 0, 00333 = 0,37 м
∙ μl = 149,3 ∙ 0, 00333 = 0,37 м
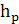 =
=
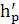 ∙ μl = 14,2 ∙ 0, 00333 = 0,05 м
∙ μl = 14,2 ∙ 0, 00333 = 0,05 м
Уравнение равновесия будет иметь вид:
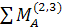 = - Q2 ∙
= - Q2 ∙
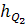 + F2 ∙
+ F2 ∙ 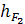 - Q3 ∙
- Q3 ∙ 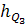 + F3 ∙
+ F3 ∙ 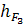 + R03 ∙
+ R03 ∙ 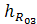 + P ∙
+ P ∙ 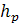 -
-
M2 = 0
R03 = 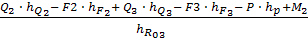 03 =
03 = 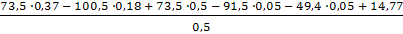 = 107,16 H
= 107,16 H
Используя графическое условие равновесия группы 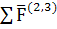 = 0, составляем силовой многоугольник
(рис. 3.3) в масштабе μF = 1
= 0, составляем силовой многоугольник
(рис. 3.3) в масштабе μF = 1 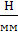 .
.
Вычисляем длины векторов сил:
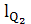 =
= 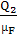 =
=
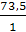 = 73,5 мм
= 73,5 мм
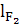 =
= 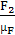 =
=
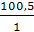 = 73,5 мм
= 73,5 мм
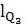 =
= 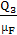 =
=
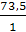 = 73,5 мм
= 73,5 мм
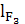 =
= 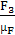 =
=
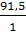 = 91,5 мм
= 91,5 мм
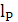 =
=  =
=
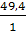 = 49,4 мм
= 49,4 мм
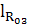 =
= 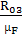 =
=
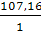 = 107,16 мм
= 107,16 мм
Сначала строим силы одного звена, а затем силы действующие на другое
звено. Начало первой силы (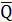 2) обозначаем точкой. Соединяем конец последней силы (
2) обозначаем точкой. Соединяем конец последней силы (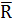 03) с начало первой, получая вектор
03) с начало первой, получая вектор 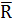 12, который направлен в начало силы
12, который направлен в начало силы 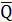 2. Замеряем длину этого вектора в миллиметрах и
умножаем на μF,
получая величину силы
2. Замеряем длину этого вектора в миллиметрах и
умножаем на μF,
получая величину силы 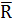 12.
12.
R12 = 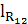 ∙ μF = 233,1 ∙ 1 = 233,1 H
∙ μF = 233,1 ∙ 1 = 233,1 H
Вектор 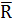 12 перечеркиваем и направляем его так, как он идет в многоугольнике.
12 перечеркиваем и направляем его так, как он идет в многоугольнике.
Чтобы получить реакцию в шарнире В, нужно рассмотреть равновесие второго
звена. Для этого начало силы 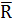 12 нужно соединить с концом силы
12 нужно соединить с концом силы 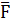 2. Получаем вектор
2. Получаем вектор 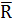 32, который идет в начало силы
32, который идет в начало силы 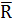 12. Замеряем длину этого вектора и
умножаем на μF, получая значение силы
12. Замеряем длину этого вектора и
умножаем на μF, получая значение силы 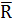 32.
32.
R32 = 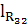 ∙ μF = 145 ∙ 1 = 145 H
∙ μF = 145 ∙ 1 = 145 H
Изображаем отдельно кривошип 1 со всеми силами, причем реакцию 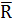 01 направляем пока произвольно, а сила
01 направляем пока произвольно, а сила 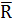 21 направлена в сторону, обратную силе
21 направлена в сторону, обратную силе 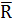 12, т.е.
12, т.е. 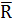 21 = -
21 = - 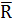 12. Из точки О проводим перпендикуляры
ко всем силам, замеряем их и умножаем на μl. Получаем длины плеч сил.
12. Из точки О проводим перпендикуляры
ко всем силам, замеряем их и умножаем на μl. Получаем длины плеч сил.
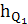 =
=
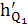 ∙ μl = 12,7 ∙ 0, 00333 = 0,04 м
∙ μl = 12,7 ∙ 0, 00333 = 0,04 м
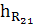 =
=
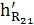 ∙ μl = 44,2 ∙ 0, 00333 = 0,15 м
∙ μl = 44,2 ∙ 0, 00333 = 0,15 м
Рассматривая равновесие кривошипа, записываем уравнение моментов
относительно точки О.
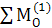 = - Q1
∙
= - Q1
∙ 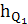 - R21
∙
- R21
∙ 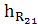 + Pу ∙ lОА = 0
+ Pу ∙ lОА = 0
Откуда
Ру = 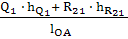 =
= 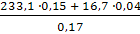 = 209,6 H
= 209,6 H
Используя графическое условие равновесия кривошипа 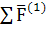 = 0, составляем силовой многоугольник
в масштабе μF = 2
= 0, составляем силовой многоугольник
в масштабе μF = 2 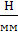 .
.
Находим длины векторов:
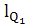 =
= 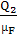 =
=
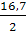 = 8,35 мм
= 8,35 мм
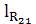 =
= 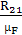 =
=
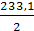 = 116,5 мм
= 116,5 мм
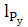 =
= 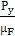 =
=
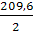 = 104,8 мм
= 104,8 мм
Соединяем начало первой силы 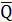 1 и конец последней
1 и конец последней 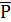 у, получаем вектор
у, получаем вектор 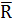 01, который направлен в начало силы
01, который направлен в начало силы 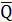 1. Находим величину этой силы:
1. Находим величину этой силы:
R01 = 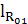 ∙ μF = 68,7 ∙ 2 = 137,4 H
∙ μF = 68,7 ∙ 2 = 137,4 H
Вектор 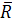 01 перечеркиваем и направляем так, как он идет в многоугольнике.
01 перечеркиваем и направляем так, как он идет в многоугольнике.
Для проверки точности расчетов и построений найдем уравновешивающую силу
по методу Жуковского. Момент силы инерции второго звена М2 заменяем
парой сил 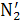 и
и 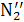 (рис. 3.1), действующих в точках А и С и направленных
перпендикулярно шатуну АС. При этом направление пары сил совпадает с
направлением момента М2.
(рис. 3.1), действующих в точках А и С и направленных
перпендикулярно шатуну АС. При этом направление пары сил совпадает с
направлением момента М2.
Найдем величины этих сил:
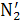 =
= 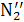 =
= 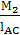 =
=
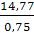 = 19,7 H
= 19,7 H
Переносим с первого листа курсовой работы план скоростей, на который
помещаем все внешние силы (рис. 3.6), проложив их в соответствующие точки и
повернув на 90° по часовой стрелке. Из полюса скоростей р проводим к
силам перпендикуляры, которые являются плечами сил. Замеряем длины
перпендикуляров и записывает уравнение моментов относительна полюса р.
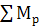 = Q1∙
= Q1∙ 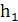 + F2
∙
+ F2
∙ 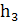 + Q2 ∙
+ Q2 ∙ 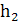 +
F3 ∙ pb + P ∙ pb -
+
F3 ∙ pb + P ∙ pb - 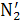 ∙
∙ 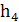 - Pу
∙ pа -
- Pу
∙ pа - 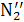 ∙
∙ 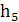 = 0
= 0
Ру = 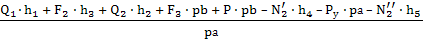
Pу
= 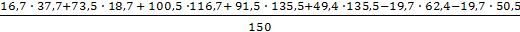 =
=
= 107,16 H
Сравнение результатов, полученных двумя способами, говорит о том, что
погрешность вычислений и построений незначительна.
Задача 1.
Статика
Дано:
P1=1kH1=28kH=1kH/mA RB
RCD RE -?
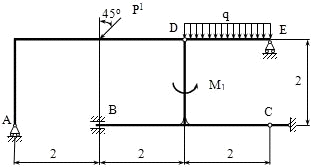
(1) ΣFkx=XD1-P1*Sin45o=0
(2) ΣFky=RA+YD1-P1*Cos45o=0
(3) ΣMD(Fk)=-RA*4+P1*2*Sin45o=0
(1)=>XD1=P1*Sin45o≈5.66(kH)
(3)=>RA=(2P1*Sin45o)/4≈2.83(kH)
(2)=>YD1=P1*Cos45o-RA≈2.83(kH)
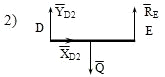
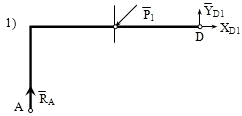
(4) ΣFkx=XD2=0
(5) ΣFky=YD2+RE-Q=0
(6) ΣMD(Fk)=-Q*1+RE*2=0=q*2=2(kH)
(4)=>XD2=0(kH)
(6)=>RE=Q/2=1(kH)
(5)=>YD2=Q-RE=1(kH)
) 
(7) ΣFkx=XD3+RC=0
(8) ΣFky=RBYD3=0
(9) ΣMB(Fk)=MB+M1+YD3*2-XD3*2=0
(10) XD1+XD2+XD3=0
(11) YD1+YD2+YD3=0
(10)=>XD3= -XD1-XD2=
-5.66(kH)
(11)=>YD3= -YD1-YD2=
-3.83(kH)
(7)=>RC= - XD3=5.66(kH)
(8)=>RB= - YD3=3.83(kH)
(9)=>MB= -M1-2*YD3+2*XD3=
-31.66(kHm)
Проверка:
ΣFKX= -P1*Sin45O+RC=
-5.66+5.66=0
ΣFKY=RA-P1*Cos45O+RE-Q+RB=2.83-8*Cos45O+1-2+3.83=0
ΣMD(FK)= -RA*4+P1*2*
Sin45O-Q*1+RE*2+M1+MB-RB*2+RC*2=
- 4*2.83+16* Sin45O-2+2*1+28-31.66-2*3.83+2*5.66=0
Ответ:
|
MB
|
RA
|
RB
|
RC
|
XD1
|
XD2
|
XD3
|
YD1
|
YD2
|
YD3
|
RE
|
|
-
|
+
|
+
|
+
|
+
|
|
-
|
+
|
+
|
-
|
+
|
|
31.66
|
2.83
|
3.83
|
5.66
|
5.66
|
0
|
5.66
|
2.83
|
1
|
3.83
|
|
|
kHm
|
kH
|
kH
|
kH
|
kH
|
kH
|
kH
|
kH
|
kH
|
kH
|
kH
|
Задача 2.
Статика
Дано: М=100 Нм, 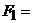 10 Н,
10 Н, 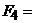 40 Н, l==0,5 м.
40 Н, l==0,5 м.
Найти: Реакции связей в т. А и В
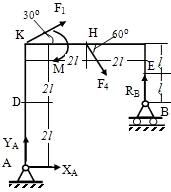
РЕШЕНИЕ:
Рассмотрим
равновесие жесткой рамы. На раму действуют силы: силы 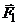 и
и 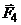 , пара
сил с моментом М и реакции связей
, пара
сил с моментом М и реакции связей 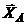 ,
, 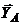 ,
, 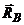 .
.
Неизвестны
реакции связей 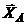 ,
, 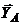 ,
, 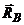 .
.
Для
полученной плоской системы сил составим три уравнения равновесия:
уравнение
моментов относительно т.А
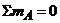 ,
,
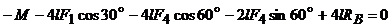 , отсюда
, отсюда
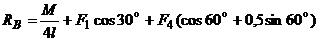 =
=
=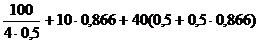 = 96 (Н);
= 96 (Н);
уравнения
проекций на оси координат
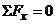 ,
, 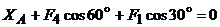 , отсюда
, отсюда
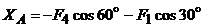 =
=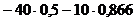 = -28,7 (Н)
= -28,7 (Н)
действительное
направление реакции противоположно принятому на рисунке;
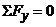 ,
, 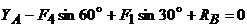 , отсюда
, отсюда
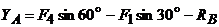 =
=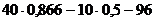 = -66,4 (кН)
= -66,4 (кН)
действительное
направление реакции противоположно принятому на рисунке.