Особенности изучения квадратичной функции и её приложений в школьном курсе математики
МОСКОВСКИЙ
ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра
математического анализа и методики его преподавания
Дипломная работа
по теме: «ОСОБЕННОСТИ
ИЗУЧЕНИЯ КВАДРАТИЧНОЙ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ»
Введение
Функциональная линия школьного курса математики
является одной из ведущих, определяющих стиль изучения многих тем и разделов
курса алгебры. Изучение функций в средней школе позволяет раскрыть внутренние
связи между понятием функции и другими понятиями школьного курса математики,
осуществить межпредметные связи.
В школе учащиеся овладевают понятиями функции,
ее графика и способов задания; изучают элементарные функции, знакомятся с
такими свойствами функций, как область определения, область значения,
монотонность, четность и нечетность и другие; учатся применять знания о
функциях к изучению разнообразных процессов и явлений.
Изучение квадратичной функции расширяет
представление учащихся о функции, ее свойствах и графике. Изучение свойств
функций имеет огромное развивающее значение для учащихся: они учатся
вырабатывать алгоритм действий при решении задач, на основе исследований делать
выводы, строить зависимости между величинами. Исследование свойств функции
применяется для решения широкого спектра задач.
Целью дипломной работы является обзор приложений
квадратичной функции к решению различных задач школьного курса математики и
составление соответствующих методических рекомендаций.
Для достижения данной цели, были поставлены
следующие задачи:
изучение психолого-педагогической, методической
и учебной литературы;
подбор задачного материала;
выделение типовых задач в каждом разделе и
составление решения к ним;
составление методических комментариев к решениям
задач.
Решение поставленных задач определило структуру
дипломной работы. Она состоит из двух глав, введения, заключения и
библиографии. Первая глава посвящена психолого-педагогическим и методическим
аспектам изучения квадратичной функции. Особое внимание здесь отводится роли
наглядности в обучении вообще и при изучении функциональной линии в частности.
Первая глава также содержит сравнительный анализ учебной литературы по теме
«Квадратичная функция».
Вторая часть дипломной работы посвящена
приложениям квадратичной функции к решению различных задач школьного курса
математики по следующим направлениям:
. Построение и чтение графика квадратичной
функции.
. Решение уравнений и их систем.
. Решение квадратных уравнений с параметрами, в
том числе, поиск параметра в зависимости от свойств корней уравнения.
. Решение квадратных неравенств с параметрами.
К каждому разделу подобраны задачи, некоторые из
них представлены с решениями и методическими рекомендациями.
Глава 1. Психолого-педагогические и
методические особенности изучения темы «Квадратичная функция»
.1 Психолого-педагогические
особенности подросткового возраста (11-15 лет)
. Возрастные психологические особенности
Подростковый возраст представляет собой сложный
процесс личностного развития, отличающийся разноуровневыми характеристиками
социального созревания. Уровень возможностей подростка, условия и скорость его
социального развития связаны с осмыслением подростком себя и своей
принадлежности к обществу, степенью выраженности прав и обязанностей, степенью
овладения миром социальных вещей и отношений, насыщенностью дальних и ближних
связей, их дифференциацией. По мере взросления у подростка изменяются характер
и особенности видения себя в обществе, восприятие общества, иерархии
общественных связей, изменяются его мотивы и степень их адекватности
общественным потребностям.
В 12-13 лет, наряду с общим принятием себя
сохраняется и ситуативно-отрицательное отношение ребенка к себе, обнаруживающее
зависимость от оценок окружающих, прежде всего сверстников. В то же время
критическое отношение подростка к себе, переживание недовольства собой
сопровождается актуализацией потребности в самоуважении, общем положительном
отношении к себе как личности.
В 14-15 лет возникает «оперативная самооценка»,
определяющая отношение подростка к себе и в настоящее время. Эта самооценка
основывается на сопоставлении подростком своих личностных особенностей, форм
поведения с определенными нормами, которые выступают для него как идеальные
формы его личности [27].
Другим важным механизмом самосознания выступает
личностная рефлексия, представляющая собой форму осознания подростком как
своего внутреннего мира, так и понимания внутреннего мира других людей. Ведущее
место занимает рассмотрение черт своего характера и особенностей
взаимоотношений с людьми. В это время происходит своеобразный скачок в развитии
личностной рефлексии, что выступает как серьезный стимул для самовоспитания
подростка. Возрастает критичность детей по отношению к особенностям своей
личности, что типично для 35% подростков.
Поуровневые изменения на протяжении
подросткового периода онтогенеза претерпевает и наиболее заметная
характерологическая особенность 10-15-летнего ребенка, проявляющаяся в
обостренном стремлении утвердить себя в обществе, добиться от взрослых
признания своих прав и возможностей.
Особенно зримо прослеживаются изменения в мотивах
общественно полезной деятельности подростков. Если у младших подростков
преобладают мотивы эмоционального отношения («я хочу заниматься общественно
полезной работой, потому что это доставляет мне удовольствие»), то у детей
14-15 лет развиваются и начинают доминировать моральные мотивы, такие, как
социальная взаимопомощь, ответственность перед коллективом, удовлетворенность
от приносимой людям пользы.
Характерно, что с возрастом увеличивается
количество подростков с ярко выраженными коллективистическими мотивами, которые
к 14-15 годам отличаются зрелостью, стремлением «видеть» себя среди других,
понять свою роль и определить свое место среди сверстников. Причем
коллективистические мотивы, развиваясь в процессе специально организуемой
деятельности, приближаются к мотивам, адекватным общественно значимому смыслу
труда. В то же время мотивы групповой солидарности, которые не приобретают
коллективистический характер, к старшему подростковому возрасту превращаются в
индивидуалистические.
. Особенности развития мышления подростка
Для человека свойственен высший познавательный
процесс, название которому - мышление. В житейской практике мышление может
ассоциироваться со здравым смыслом, интуицией. В действительности, оно не имеет
ничего общего ни с тем, ни с другим. Оно представляет собой способность
учиться, решать поставленную задачу. Мышление представляет собой порождение
нового знания, активную форму творческого отражения и преобразования человеком
действительности. Оно порождает такой результат, какого ни в самой
действительности, ни у субъекта на данный момент времени не существует.
Мышление (в элементарных формах оно имеется и у животных) также можно понимать
как получение новых знаний, творческое преобразование имеющихся представлений.
Мышление в отличие от восприятия выходит за
пределы чувственно данного, расширяет границы познания. В мышлении на основе
сенсорной информации делаются определенные теоретические и практические выводы.
Оно отражает бытие не только в виде отдельных вещей, явлений и их свойств, но и
определяет связи, существующие между ними, которые чаще всего непосредственно,
в самом восприятии человеку не даны. Свойства вещей и явлений, связи между ними
отражаются в мышлении в обобщенной форме, в виде законов, сущностей. На
практике мышление как отдельный психический процесс не существует, оно незримо
присутствует во всех других познавательных процессах: в восприятии, внимании,
воображении, памяти, речи. Высшие формы этих процессов обязательно связаны с
мышлением, и степень его участия в этих познавательных процессах определяет их
уровень развития.
В многообразных явлениях мышления различаются:
мыслительная деятельность, мыслительные действия, мыслительные операции, формы
мышления, виды мышления, индивидуально-типологические особенности мышления,
мышление как процесс решения творческих, нестандартных задач.
Мыслительная деятельность - система мыслительных
действий, направленная на решение какой-либо проблемы. Отдельные мыслительные
действия связаны с решением промежуточных задач, составных частей общей
проблемы.
Мыслительные действия - совокупность
мыслительных операций, направленных на выявление непосредственно не данных,
скрытых свойств и отношений объектов реального мира. Каждый мыслительный акт
основан на системе операций.
К мыслительным операциям относятся сравнение,
обобщение, абстрагирование, классификация и конкретизация.
Все мыслительные операции связаны с анализом и
синтезом. Анализ и синтез - это две неразрывные стороны всего процесса познания
(в том числе и чувственного этапа).
Продукт мыслительных действий - определенные
познавательные результаты, которые выражаются в трех формах мышления.
Формами мышления являются: 1) суждение; 2)
умозаключение; 3) понятие. Закономерности взаимоотношений между этими формами
мышления изучает логика. Изучая формы мышления, логика отвлекается от
конкретного содержания мыслей, заключенных в этих формах, она устанавливает
общие законы и принципы достижения истинности тех знаний, которые выводятся из
других достоверных знаний. Психология же изучает закономерности творческого
мышления, приводящего к новым познавательным результатам, к открытию новых
знаний.
Для подростка большое значение приобретает
теоретическое мышление, способность устанавливать максимальное количество
связей в окружающем мире - в системе исторически обусловленной реальности
существования. Он психологически погружен в реальности предметного мира,
образно-знаковых систем, природы и социального пространства. Подросток,
погружаясь в социальную среду, непрестанно трансформирует свои высшие
психические функции и присваиваемую систему знаков. Это обстоятельство изменяет
мышление. Ж. Пиаже писал, что «социальная жизнь трансформирует интеллект через
воздействие трех посредников: языка (знаки), содержания взаимодействия субъекта
с объектами (интеллектуальные ценности) и правил, предписанных мышлению
(коллективные логические и дологические нормы). В этом случае присваиваемые
социальные отношения вырабатывают новые возможности мышления».
То, насколько быстро подросток способен выйти на
уровень теоретического мышления, определяет глубину постижения им учебного
материала и развитие его интеллектуального потенциала. В отрочестве престижно
быть преуспевающим в интеллектуальной деятельности [26].
Математическое мышление - это система,
направленная на решение математических задач, в которой как в целостности
представлены интеллектуальные, деятельностные, эмоционально-личностные и
творческие составляющие.
В качестве интеллектуальной составляющей
подразумеваются математические знания, интуиция и логика. Эмоционально-личностными
компонентами математического мышления принято считать совокупность таких
качеств личности, как самоконтроль, самокритика, способность получать
эстетическое удовольствие от процесса и результата решения математической
задачи. К творческой составляющей математического мышления, можно отнести:
«беглость» - способность продуцировать большое
количество идей;
«гибкость» - способность применять разнообразные
стратегии при решении проблем;
«оригинальность» - способность продуцировать
необычные, нестандартные идеи;
«разработанность» - способность детально
разрабатывать возникшие идеи;
«абстрагирование» - способность выделять
главное, способность понимать суть проблемы;
«сопротивление замыканию» - способность
длительное время оставаться открытым новизне и разнообразию идей, достаточно
долго откладывать принятие окончательного решения для того, чтобы совершить
мыслительный скачок и создать оригинальные идеи.
Деятельностной составляющей являются
математические умения и навыки.
Эффективное школьное образование - это такое
образование, при котором ученик постепенно начинает сам организовывать процесс
своего обучения.
Умение решать задачи является наиболее яркой
характеристикой уровня математического мышления учеников. Зная возможности
задач, нетрудно подобрать почти к каждой теме системы задач, решения которых
совершенствуют конкретные операции и приемы мышления. Например, практические
задачи стимулируют операцию конкретизации, а также понимание взаимосвязи и
зависимости между различными областями знаний, и в частности, между
математическими и физическими знаниями. Задачи с неполным или избыточным
составом условия; задачи, данные которых противоречат друг другу; так
называемые нереальные задачи (их данные противоречат научному или здравому
смыслу) развивают умение анализировать, выделять существенное, критически
оценивать условия, конкретизировать теоретические положения, предупреждают
случаи неправомерного обобщения явлений.
В процессе решения математических задач решающую
роль играют определенные «эвристические методы», которые обусловливают
возникновение следующих друг за другом стадий решения.
Одним из них является умение
«переструктурировать», изменить ситуацию. При этом изменяются не только те или
иные части ситуации, но и сама структура. Части и моменты ситуации, которые
раньше совсем не осознавались, вдруг выделяются, становятся главной темой.
Решающие моменты в процессах мышления, моменты внезапного понимания,
возникновения чего-то нового, всегда являются моментами, когда происходит
переструктурирование мыслимого материала. Умение посмотреть на проблему с новой
точки зрения, сместить акценты, является следствием достигшей в мышлении
децентрации - способности сменить систему отсчета.
Сознательное манипулирование системой отсчета
требует от подростка специальных умений. В своей работе «Как приходят новые
идеи» Г. Гельмгольц пишет: «Каждый раз мне приходилось всячески переворачивать
мою задачу на все лады так, чтобы все ее изгибы и сплетения залегли прочно в
голове и могли быть пройдены наизусть» [11].
К. Дункер в своей работе «Психология
продуктивного мышления» рассматривает процессы решения математических задач.
«Решение, - отмечает К. Дункер, - возникает из рассмотрения исходных данных
задач под углом зрения требуемого, из ряда переструктурирований ситуации,
вследствие чего и возникают моменты внезапного понимания» [14]. Свойствами
мышления, которые являются условием успешности решения математических задач, К.
Дункер считает широту и гибкость мышления и способность абстрагироваться от
конкретного содержания.
Для развития мышления в математике полезна
визуализация - включение наглядных образов. Чувственно-наглядные образы лежат в
основе мысленных (воображаемых) моделей. Важнейшей функцией такой модели
является наглядное представление чувственно-невоспринимаемых явлений. Развитие
математического мышления школьника предполагает необходимость развития умения
конструировать модели существующего явления в рамках целостности с целью его
опосредованного изучения.
1.2 Роль дидактических принципов в
обучении математике
. Принципы обучения
Принципы обучения - это исходные положения,
определяющие деятельность педагога и характер познавательной деятельности
учащихся. Принципы обучения выражают определенные закономерности обучения.
Незнание принципов или их неумелое применение
тормозит успешность обучения, затрудняет усвоение знаний, формирование качеств
личности ребенка.
Совокупность принципов позволяет характеризовать
весь учебный процесс, все стороны деятельности учителя и познавательной
деятельности детей.
Содержание учебного материала и методы его
изучения должны быть научными. Иначе дети не смогут овладеть основами научных
знаний. Отсюда следует необходимость соблюдения принципа научности обучения как
исходного положения, определяющего связь обучения с наукой.
Знания в опыте человечества находятся в
определенной системе. Их нельзя усваивать хаотично, в беспорядке. Эту сторону
обучения отражает принцип систематичности. Иногда его называют принципом
систематичности и последовательного обучения, понимая под последовательностью
расположение материала в соответствии с возрастными возможностями развития
детей.
Учебный процесс теряет смысл, если его
содержание будет недоступным для усвоения. Отсюда вытекает принцип доступности
учебного материала.
Чувственные образы, представления детей об
окружающем мире являются необходимыми компонентами всякого обучения. Эта
сторона учебного процесса привела к обоснованию принципа наглядности.
Знания должны быть осознаны детьми, а для этого
необходима высокая познавательная активность. В противном случае материал
быстро забывается. Отсюда необходимость принципа сознательности и активности
обучения детей.
Знания, умения и навыки должны быть прочными,
что бы обеспечить высокое общее развитие. Принцип прочности обучения раскрывает
эту сторону развития детей.
Индивидуальный подход повышает эффективность
обучения, что давно замечено в практической деятельности учителей. Эта
особенность педагогического процесса нашла отражение в принципе
индивидуализации развития детей [28].
Остановимся подробнее на принципе наглядности.
Принцип наглядности является связующим звеном
между принципом научности и принципом доступности, между которыми имеется
некоторый «разрыв». Материал, преподаваемый учащимся, может быть объяснен
научный языком, но таком случае, многим учащимся он может оказаться
недоступным, либо доступным, но не в полной мере. Этот пробел можно
ликвидировать за счет соблюдения принципа наглядности. После изображения этого
же материала на «картинке», он становится для учащихся доступным и более понятным.
И наоборот, материал может быть объяснен доступно, но не научно. И снова
помогает принцип наглядности.
. Роль наглядности в обучении.
Многолетний опыт обучения и специальные
психолого-педагогические исследования давно показали, что эффективность обучения
зависит от степени привлечения к восприятию всех органов чувств человека. Чем
более разнообразны чувственные восприятия учебного материала, тем более прочно
он усваивается. Эта закономерность нашла свое выражение в дидактическом
принципе наглядности. При этом сама наглядность в дидактике понимается более
широко, чем непосредственное зрительное восприятие. Она включает в себя и
восприятие через моторные, тактильные ощущения.
Впервые теоретически обосновал данный принцип
чешский педагог Я.А. Коменский, который выдвинул требование учить людей
познавать сами вещи, а не только чужие свидетельства о них, по следующим
правилам: «от близкого к далекому», «от простого к сложному», «от более
простого к более трудному», «от известного к неизвестному».
Наглядное обучение, по словам русского педагога
К. Д. Ушинского, "строится не на отвлеченных представлениях и словах, а на
конкретных образах, непосредственно воспринятых ребенком". Наглядность
обогащает круг представлений ребенка, делает обучение более доступным,
конкретным и интересным, развивает наблюдательность и мышление. Он указывал,
что наглядность отвечает психологическим особенностям детей, мыслящих
"формами, звуками, красками, ощущениями".
Любая наглядность связана с чувственным
отражением действительности. Существует три формы чувственного отражения:
ощущения, восприятия, представления. При этом следует обратить внимание, что
даже простые ощущения появляются не в рецепторах, а коре головного мозга.
Ощущения несут информацию о тех или иных
объективно существующих и меняющихся свойствах предметов. Именно в этом смысле
нужно понимать «сходство» ощущений со свойствами вещей. Все ощущения в той или
иной мере информируют о внешних или внутренних объектах и их состоянии, но не
являются их изобразительным слепком.
Используя любую наглядность в учебном процессе,
мы не должны упускать из вида, что «образу» свойственно не совпадение с
объектом, а лишь его соответствие объекту. «Образ» - это не зеркальная копия
вещи, а нечто, соответствующее ей, согласующееся с ней и не более того.
Рассудок анализирует ощущения как определенный объект; ощущения отражаются в
рациональном, абстрактном мышлении.
Поэтому наглядность не должна сводиться к
какому-то автоматизму, к механическому отражению внешних предметов (иллюстрация
предметов и явлений). Она должна включаться в познавательную систему головного
мозга, являясь «пищей для ума», и в процессе обработки информации давать в той
или иной степени содержательные знания об исследуемом объекте.
Классическая дидактика установила принцип
наглядности, исходя из предположения, что успешным оказывается только такое
обучение, которое начинается с рассмотрения предметов, процессов, явлений
окружающей действительности. Ф. А. Дистерверг при этом отмечал, что люди
достигают знаний только путем наглядности.
Принцип наглядности вытекает из сущности
процесса восприятия, осмысления и обобщения учащимися изучаемого материала. Он
означает, что в обучении необходимо, следуя логике процесса усвоения знаний, на
каждом этапе обучения найти его исходное начало в фактах и наблюдениях
единичного или в аксиомах, научных понятиях, теориях, после чего определить
закономерный переход от восприятия единичного, конкретного предмета к общему,
абстрактному или, наоборот, от общего, абстрактного к единичному, конкретному.
Таким образом, дидактика исходит из единства чувственного и логического,
считает, что наглядность обеспечивает связь между конкретным и абстрактным,
содействует развитию абстрактного мышления, во многих случаях служит его
опорой.
Однако характер и степень использования
наглядности различны на разных этапах обучения, излишнее увлечение наглядностью
в обучении может привести к нежелательным результатам. Конкретная наглядность
(например, рассмотрение моделей геометрических тел) должна постепенно уступать место
абстрактной наглядности (рассмотрению плоских чертежей).
Роль наглядности в обеспечении познавательного
процесса весьма значительна: наглядность является главным каналом, который
непосредственно связывает человека с внешним миром; наглядность способствует
активизации мышления учащихся в процессе обучения; рациональное в большой
степени базируется на анализе материала, который дает нам наблюдение;
регулирование предметной деятельностью осуществляется прежде всего с помощью
информации, получаемой в процессе наглядного обучения.
По характеру отражения окружающей
действительности различают следующие виды наглядности:
натуральная (естественная) наглядность,
представляющая собой реальные предметы или процессы (объекты и явления,
раздаточный материал и др.);
изобразительная наглядность (фотографии,
художественные картины, рисунки, учебные картины и др.) применяется, когда
показ натурального предмета затруднен, а созерцание конкретного образа
необходимо;
символическая наглядность (чертежи, графики,
схемы, таблицы, диаграммы) по существу является своеобразным языком, а потому
должна специально изучаться, чтобы стать понятной. Например, при изучении
свойств функций (возрастание, убывание, максимум, минимум и др.) целесообразно
их аналитическую запись переводить на язык графиков и на этой основе
тренировать учащихся "читать" графики функций.
В обучении математике наглядность определяют,
как совокупность материальных, материализованных, идеальных действий,
совершаемых как обучающим, так и обучаемым в ходе реализации дидактической цели
наглядного обучения.
В обучении математике выделяют следующие виды
наглядности:
. Оперативная наглядность - процесс формирования
модели в учебной деятельности, базирующийся на опорных внешних действиях. К
оперативной наглядности относится демонстрационная наглядность и технические
средства обучения. Применение оперативной наглядности расширяет число каналов
передачи и получения информации, ускоряя и углубляя восприятие изучаемого
материала. В то же время применение оперативной наглядности может служить
мотивацией творческой деятельности учащихся, позволяет увидеть процессы в
динамике, способствует установлению межпредметных связей, расширяет область
практического применения изучаемых вопросов.
. Формализованная наглядность - процесс формирования
модели в учебной деятельности, базирующийся на структурных внешних действиях,
процесс формирования "внешней" структуры, структуры обозначения,
выделения и размещения текста на доске или в учебном пособии. К этому виду
наглядности относится форматирование текста, выделение формул, использование
цвета. Это вид наглядности способствует лучшему восприятию, осмыслению и
запоминанию материала.
. Структурная наглядность - процесс формирования
модели учебной деятельности, базирующийся на структурных внешних действиях,
процесс формирования "внутренней" структуры. К этому виду наглядности
относится выделение основного материала, построение модели с опорой на
устойчивые ассоциации, характеризующиеся полнотой изложения основных понятий,
методов, теорем, доведение изучаемого материала до узнаваемости объекта
восприятия, построение системы непрерывного хранения информации (составление
контролирующих программ для компьютера). Структурная наглядность активизирует
мыслительную деятельность в процессе восприятия, учит логически мыслить,
выделять существенное.
. Фоновая наглядность - процесс моделирования
специфических особенностей данного организованного набора знаний, носящий
мотивированный сквозной характер, обеспечивающий лучшее восприятие и усвоение.
Фоновая наглядность характеризуется длительностью, неодномоментностью,
“ненавязчивостью” побочно применяемых действий. Примером применения наглядности
этого вида могут служить приемы создания фона настроения, создания пониженного
фона интенсивности вокруг опорной информации, привлечение исторического
материала, применение мнемонических эффектов. Целевая установка, мотивация,
внешнее ненавязчивое побуждение учителя к внутренним действиям ученика,
адекватным поставленным целям - составляющие компоненты фоновой наглядности.
Особое значение этот вид наглядности приобретает в условиях профильной
дифференциации. Фоновая наглядность - это тот фактор, который позволяет
проводить воспитательную работу в процессе обучения.
. Дистрибутивная наглядность характеризуется
структурными внешними действиями при изучении сформированной модели в процессе
учебной деятельности. К этому виду наглядности относится структура размещения
материала, выделение базовых определений, порций материала, классификацию
методов доказательств. Этот вид наглядности широко используют авторы учебников
и учебных пособий. Использование этого вида наглядности позволяет расставить
акценты на изучаемом материале, делает его более доступным для восприятия и
усвоения, учит логически мыслить, анализировать, выделять главное и
устанавливать связи между изучаемыми понятиями, уметь ориентироваться в большом
объеме информации, воспитывает критическое отношение, учит быть собранным.
. Наглядность преемственности характеризуется
опорностью ассоциативных связей внутри раздела, предмета и межпредметных. Сюда
относится структура взаимосвязей, методы изложения, пропедевтика, опорные
мотивационные исторические задачи, циклы задач исследовательского характера.
Применение этого вида наглядности зависит от того, насколько глубоко учитель
владеет материалом, от творческого использования им методов изложения
материала, от его эрудиции, общей культуры, заинтересованности в результатах
своего труда.
Различные виды наглядности выполняют различные
функции. Одни содействуют оживлению представлений (картины, предметы жизни),
другие являются опорой для отвлеченного мышления.
Наглядность применяется и как средство познания
нового, и для иллюстрации мысли, и для развития наблюдательности, и для лучшего
запоминания материала. Средства наглядности используются на всех этапах
процесса обучения: при объяснении нового материала учителем, при закреплении
знаний, формировании умений и навыков, при выполнении домашних заданий, при
контроле усвоения учебного материала.
Применение наглядных пособий в обучении
подчинено ряду правил:
ориентировать учащихся на всестороннее
восприятие предмета с помощью разных органов чувств;
обращать внимание учащихся на самые важные,
существенные признаки предмета;
показать предмет (по возможности) в его
развитии;
предоставить учащимся возможность проявлять
максимум активности и самостоятельности при рассмотрении наглядных пособий;
использовать средства наглядности ровно столько,
сколько это нужно, не допускать перегрузки обучения наглядными пособиями, не
превращать наглядность в самоцель.
Следовательно, умелое применение средств
наглядности в обучении всецело находится в руках учителя. Учитель в каждом
отдельном случае должен самостоятельно решать, когда и в какой мере надо
применять наглядность в процессе обучения, ибо от этого в определенной степени
зависит качество знаний учащихся. Вредным является как недостаточное, так и
избыточное применение средств наглядности. Их недостаток приводит к формальным
знаниям, а избыток может затормозить развитие логического мышления, пространственного
представления и воображения [12].
Так, при изучении квадратичной функции в 7-9
классах формируется представление о свойствах функции и ее графике, умение по
графику считывать свойства данной функции, формируется навык элементарного
преобразования графика квадратичной функции и использования графика
квадратичной функции для графического решения уравнений и неравенств. Для этого
непосредственно необходимо выполнения принципа наглядности.
Понятие «функция» порой учащимся трудно для
восприятия, поэтому очень важна опора на наглядность. В такой ситуации работают
оба полушария головного мозга ученика: правое, отвечающее за образы, и левое,
отвечающее за формально-логическое мышление. В 7-8 классах учащиеся работают на
наглядно-интуитивном уровне. В частности, в учебнике А. Г. Мордковича и др.
такие свойства функции, как область определения, наибольшее и наименьшее
значения функции на промежутке, монотонность, непрерывность рассматривается в 7
классе только на наглядно-интуитивном уровне [22].
Приведем примеры использования наглядности для
решения некоторых задач курса алгебры.
. Решить уравнение:
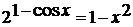

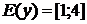
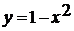
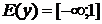
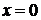 - единственное
решение уравнения.
- единственное
решение уравнения.
Здесь используется такое свойство функции, как
множество ее значений. При решении этой задачи следует обратить внимание
учащихся на то, что для левой части достаточно построить не сам график, а
схему, изображающую только существенное для решения этой задачи свойство -
график расположен в полосе между прямыми 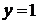 и
и
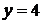 .
.
. При каких значениях параметра а график функции
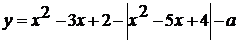 пересекает
ось абсцисс менее чем в трех различных точках?
пересекает
ось абсцисс менее чем в трех различных точках?
Построим график функции 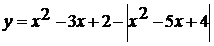
) 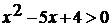
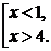
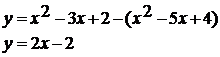
) 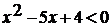
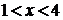
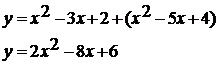
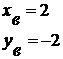
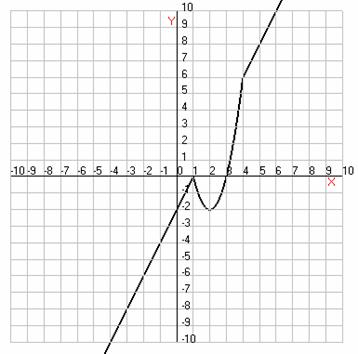
В данном примере параметр - это число, значит
его изменение ведет к движению графика заданной функции.
Т.о. получаем ответ:
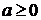 - движение вниз
- движение вниз
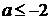 - движение вверх
- движение вверх
Данная задача взята из пробного ЕГЭ для 11
класса 2009/10 учебный год. Она явно демонстрирует применение принципа
наглядности при решении.
) При каких значениях параметра а корни уравнения
 положительны?
положительны?
Решение:
способ.
) 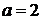 .
Тогда получим уравнение:
.
Тогда получим уравнение:
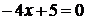
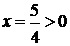 - удовлетворяет
условию задачи.
- удовлетворяет
условию задачи.
2) 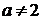 .
Тогда получим квадратное уравнение.
.
Тогда получим квадратное уравнение.
Решим его:
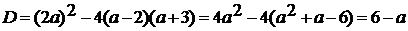
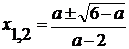
Если 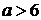 ,
то
,
то 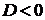 ,
тогда уравнение решений не имеет.
,
тогда уравнение решений не имеет.
Если 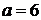 ,
то
,
то 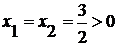 и
и
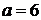 является
решением задачи
является
решением задачи
Если 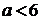 (кроме
a=2), то
(кроме
a=2), то

неравенство:
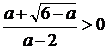
) 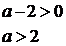
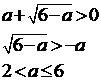
) 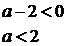
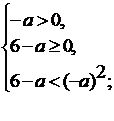
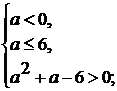
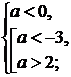
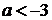 .
.
неравенство:
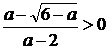
) 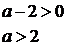
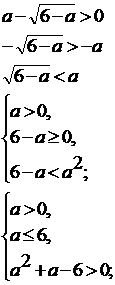
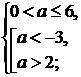
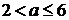 .
.
2) 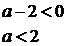
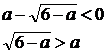
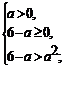
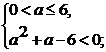
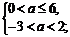
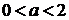 .
.
Ответ: 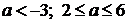 .
.
способ.
) 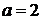 -
решение.
-
решение.
) 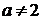 .
Перейдем к уравнению:
.
Перейдем к уравнению:
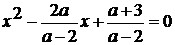
Рассмотрим квадратичную функцию:
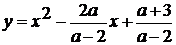 .
.
Графиком данной функции является парабола, ветви
направлены вверх. Т.к. по условию задачи корни уравнения положительны, то
парабола пересекает ось х в двух точках правой полуплоскости.
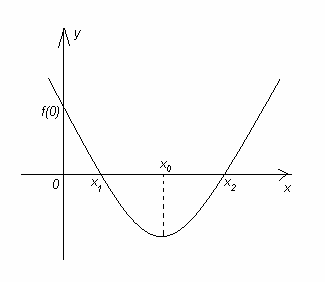
Т.к. уравнение имеет решения, то 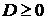 ,
т.е.
,
т.е. 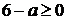 .
.
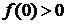 , т.е.
, т.е. 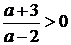
Вершина параболы расположена в правой
полуплоскости, значит, ее абсцисса положительна.
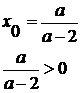
Получим систему неравенств:
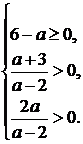
Ответ: 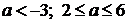 .
.
Последний представленный способ гораздо легче.
При этом мы пользуемся наглядностью.
дидактический математика
квадратичный функция
1.3 Анализ учебного материала по
теме «Квадратичная функция» в учебниках по алгебре 7-9 классов
Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.
Суворова
класс.
В данном учебнике изучение темы «Квадратичная
функция» начинается с 3 главы «Степень с натуральным показателем». Перед этим
ученики знакомятся с понятиями функции и ее графика, рассматривается линейная
функция и прямая пропорциональность.
Функция  рассматривается
на основе зависимости площади квадрата от его стороны. Далее авторы предлагают
построить график функции
рассматривается
на основе зависимости площади квадрата от его стороны. Далее авторы предлагают
построить график функции  по точкам. Для
чего составляется таблица значений функции.
по точкам. Для
чего составляется таблица значений функции.
Далее описываются некоторые свойства
рассматриваемой функции:
График функции проходит через начало координат;
все точки графика функции, кроме (0; 0), расположенных выше оси х; точки
графика, имеющие противоположные координаты, симметричны относительно оси у.
В заключении данного параграфа дается система
упражнений на нахождение по графику функции значения х по заданному значению у
и наоборот, на нахождение значения y по заданному значению х.
Также в 7 классе авторы учебника рассматривают
абсолютную погрешность, взяв для рассмотрения график функции  .
По графику определяются приближенные значения функции при заданных значениях х.
Затем значения х подставляются в формулу. Получается второй результат. После
этого высчитывается погрешность.
.
По графику определяются приближенные значения функции при заданных значениях х.
Затем значения х подставляются в формулу. Получается второй результат. После
этого высчитывается погрешность.
класс
В 8 классе работа с квадратичной функцией
начинается во второй главе «Квадратные корни».
Учащимся даются понятия: квадратный корень,
арифметический квадратный корень, вводится обозначение арифметического
квадратного корня и понятие подкоренного выражения.
Авторы подводят учащихся к решению уравнения 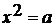 ,
где a - произвольное число. Говорится, что если
,
где a - произвольное число. Говорится, что если 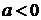 ,
то уравнение
,
то уравнение 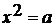 не имеет корней, а
вот если
не имеет корней, а
вот если 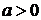 ,
то уравнение
,
то уравнение 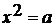 имеет два корня.
Проверяется наличие корней графическим методом, используя квадратичную функцию.
имеет два корня.
Проверяется наличие корней графическим методом, используя квадратичную функцию.
Далее изучается функция 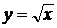 и
ее график. Сначала рассматривается задача: зависимость площади квадрата от его
стороны. Выводится формула
и
ее график. Сначала рассматривается задача: зависимость площади квадрата от его
стороны. Выводится формула 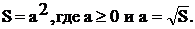
Построение осуществляется по точкам (точно также
как и функция  ). Говорится, что
графики функций
). Говорится, что
графики функций  (при
(при 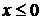 )
и
)
и 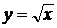 симметричны
относительно прямой y = x.
симметричны
относительно прямой y = x.
класс
В 9 классе данный коллектив авторов
рассматривает квадратичную функцию в общем виде. Сначала изучается частный
случай квадратичной функции - функция 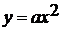 .
При
.
При 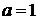 получаем
функцию
получаем
функцию  ,
при
,
при 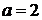 -
-
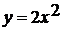 .
Составляется таблица значений функции
.
Составляется таблица значений функции 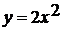 и
строится ее график. Затем делается вывод, что при любом
и
строится ее график. Затем делается вывод, что при любом 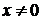 значение
функции
значение
функции 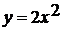 больше
соответствующего значения функции
больше
соответствующего значения функции  в
2 раза. График функции
в
2 раза. График функции  можно получить из
параболы
можно получить из
параболы  растяжением
от оси х в 2 раза.
растяжением
от оси х в 2 раза.
Аналогично рассматривается функция 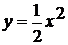 .
И отсюда следует вывод, что график функции
.
И отсюда следует вывод, что график функции 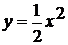 можно
получить из параболы
можно
получить из параболы  сжатием к оси х в
2 раза.
сжатием к оси х в
2 раза.
Затем авторы акцентируют свое внимание на то,
что график функции 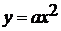 можно получить из
параболы
можно получить из
параболы  растяжением
от оси х в а раз, если
растяжением
от оси х в а раз, если 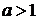 , и сжатием к оси х
в
, и сжатием к оси х
в  раз,
если
раз,
если  .
.
Далее аналогично строится график функции 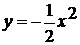 и
сравнивается с графиком функции
и
сравнивается с графиком функции 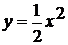 . График функции
. График функции 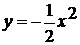 может
быть получен из графика функции
может
быть получен из графика функции 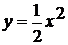 с помощью
симметрии относительно оси х.
с помощью
симметрии относительно оси х.
Далее авторы, подводя итог, говорят, что графики
функций 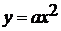 и
и
 (при
(при
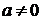 )
симметричны относительно оси х.
)
симметричны относительно оси х.
В конце этого параграфа говорится, что
построение графика, симметричного данному относительно оси х, растяжение
графика от оси х или сжатие к оси х - различные виды преобразования графиков
функций. Преобразования графиков, рассмотренные для функции 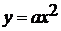 ,
применимы к любой функции.
,
применимы к любой функции.
Система упражнений на закрепление этой темы
состоит из упражнений на построение графиков функций.
Затем авторы рассматривают графики функций вида  и
и
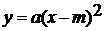 .
В качестве примеров берутся другие частные случаи квадратичной функции.
.
В качестве примеров берутся другие частные случаи квадратичной функции.
Далее делается вывод: график функции  является
параболой, которую можно получить из графика функции
является
параболой, которую можно получить из графика функции 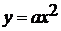 с
помощью параллельного переноса вдоль оси у на n единиц вверх, если
с
помощью параллельного переноса вдоль оси у на n единиц вверх, если 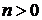 ,
или на -n единиц вниз, если
,
или на -n единиц вниз, если 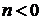 ; график функции
; график функции 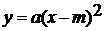 является
параболой, которую можно получить из графика функции
является
параболой, которую можно получить из графика функции 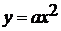 с
помощью параллельного переноса вдоль оси х на m единиц вправо, если
с
помощью параллельного переноса вдоль оси х на m единиц вправо, если 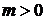 ,
или на -m единиц влево, если
,
или на -m единиц влево, если  .
.
Полученные выводы позволяют понять, что
представляет собой график функции 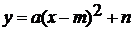 .
Рассматривается очередной пример (
.
Рассматривается очередной пример (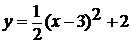 )
и после этого делается вывод, что график функции
)
и после этого делается вывод, что график функции 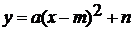 является
параболой, которую можно получить из графика функции
является
параболой, которую можно получить из графика функции 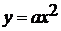 с
помощью двух параллельных переносов. Замечается, что производить параллельные
переносы можно в любом порядке: сначала выполнить параллельный перенос вдоль
оси х, а затем вдоль оси y или наоборот.
с
помощью двух параллельных переносов. Замечается, что производить параллельные
переносы можно в любом порядке: сначала выполнить параллельный перенос вдоль
оси х, а затем вдоль оси y или наоборот.
Далее в учебнике рассматривается построение
графика квадратичной функции в общем виде. Вводится квадратичная функция 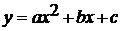 и
из трехчлена
и
из трехчлена 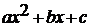 выделяют квадрат двучлена.
После некоторых преобразований авторы получают
выделяют квадрат двучлена.
После некоторых преобразований авторы получают 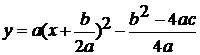 .
Получается формула вида
.
Получается формула вида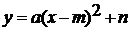 , где
, где 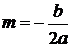 ,
,
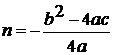 .
Авторы акцентируют внимание на том, что график функции
.
Авторы акцентируют внимание на том, что график функции 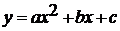 есть
парабола, которую можно получить из графика функции
есть
парабола, которую можно получить из графика функции 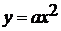 с
помощью двух параллельных переносов - сдвига вдоль оси х и сдвига вдоль оси у.
с
помощью двух параллельных переносов - сдвига вдоль оси х и сдвига вдоль оси у.
Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров, Н.Е.
Федорова, М.И. Шабунин
класс
В 7 классе рассматривается прямоугольная система
координат, понятие функции, линейная функция и ее график.
класс
В данном учебнике изучение квадратичной функции
начинается в 5 главе после изучения квадратных корней и квадратных уравнений.
Сначала рассматриваются примеры из разных
областей науки и техники, где встречаются квадратичные функции.
После этого вводится определение квадратичной
функции, и рассматриваются примеры квадратичных функций и задачи.
Найти значение функции 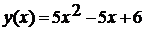 при
при
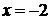
При каких значениях х квадратичная функция 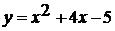 принимает
значение, равное 7;
принимает
значение, равное 7;
Найти нули функции 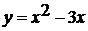 .
.
Авторы предлагают решать такие задачи
аналитически: подстановкой заданного значения в формулу.
Только после этого начинается рассмотрение
непосредственно квадратичной функции, ее некоторых свойств и графика.
Функция  вводится
как частный случай функции
вводится
как частный случай функции 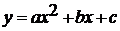 при а=1, b=c=0.
Для построения графика этой функции составляется таблица ее значений, строятся
указанные в таблице точки, соединяют плавной линией. Кривая, являющаяся
графиком функции
при а=1, b=c=0.
Для построения графика этой функции составляется таблица ее значений, строятся
указанные в таблице точки, соединяют плавной линией. Кривая, являющаяся
графиком функции  , называется
параболой.
, называется
параболой.
После этого рассматривается функция 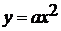 .
.
Приводится пример построения графика функции 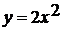 ,
зная график функции
,
зная график функции  . Для построения
составляется таблица значений функции
. Для построения
составляется таблица значений функции 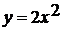 .
Говорят, что график функции
.
Говорят, что график функции 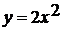 получается
растяжением графика функции
получается
растяжением графика функции  от оси Ox вдоль
оси Oy в два раза.
от оси Ox вдоль
оси Oy в два раза.
Аналогичным образом, на примере, авторы
демонстрируют сжатие графика. График функции 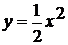 получается
сжатием графика функции
получается
сжатием графика функции  к оси Ox вдоль оси
Oy в два раза.
к оси Ox вдоль оси
Oy в два раза.
Затем рассматриваются функции  и
и
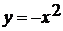 .
График функции
.
График функции 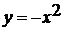 можно получить
симметрией относительно оси Ох графика функции
можно получить
симметрией относительно оси Ох графика функции  .
.
Далее авторами рассматривается функция 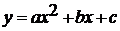 .
В начале параграфа рассматривается задача: построить график функции
.
В начале параграфа рассматривается задача: построить график функции 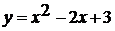 и
сравнить его с графиком функции
и
сравнить его с графиком функции  .
.
Как и для функции 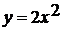 сначала
составляется таблица значений функции
сначала
составляется таблица значений функции 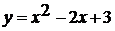 .
Найденные точки отмечаются на координатной прямой и соединяются плавной линией.
Первая часть задачи решена. Далее сравниваются функции
.
Найденные точки отмечаются на координатной прямой и соединяются плавной линией.
Первая часть задачи решена. Далее сравниваются функции 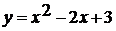 и
и
 .
Сначала преобразуется формула
.
Сначала преобразуется формула 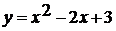 , используя метод
выделения полного квадрата. Затем сравниваются графики частями. Сначала -
функции
, используя метод
выделения полного квадрата. Затем сравниваются графики частями. Сначала -
функции  и
и
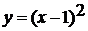 .
Отсюда делается вывод, что графиком функции
.
Отсюда делается вывод, что графиком функции 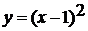 является
парабола, полученная из параболы
является
парабола, полученная из параболы  сдвигом
(параллельным переносом) вправо на единицу.
сдвигом
(параллельным переносом) вправо на единицу.
После этого сравниваются функции 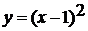 и
и
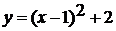 .
Получается, что графиком функции
.
Получается, что графиком функции 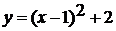 является
парабола, полученная сдвигом параболы
является
парабола, полученная сдвигом параболы 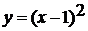 вверх
на две единицы.
вверх
на две единицы.
Из всего этого следует, что графиком функции 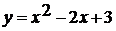 является
парабола, получаемая сдвигом параболы
является
парабола, получаемая сдвигом параболы  на
единицу вправо и на две единицы вверх.
на
единицу вправо и на две единицы вверх.
Далее авторы обобщают ранее объясненное.
Задачи, предлагаемые для закрепления данного
материала выглядят так:
. С помощью шаблона параболы  построить
график функции
построить
график функции 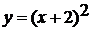 .
.
. Записать уравнение параболы, полученной из
параболы 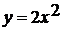 сдвигом
вдоль оси Ох на 3 единицы вправо.
сдвигом
вдоль оси Ох на 3 единицы вправо.
Также в 8 классе решаются квадратные неравенства
с помощью графика квадратичной функции. Их решение сводится к отысканию нулей
квадратичной функции и промежутков, на которых квадратичная функция принимает
положительные или отрицательные значения. В конце дается подробный алгоритм
решения неравенств графическим методом.
В качестве дополнительного более сложного
материала производится исследование квадратичной функции на основе теорем:
. Если 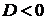 ,
то при всех действительных значениях х знак квадратичной функции
,
то при всех действительных значениях х знак квадратичной функции 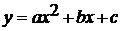 совпадает
со знаком числа
совпадает
со знаком числа 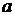 .
.
. Если 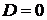 ,
то при всех действительных значения х, кроме
,
то при всех действительных значения х, кроме 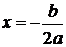 ,
знак квадратичной функции
,
знак квадратичной функции 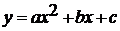 совпадает со
знаком числа а; при
совпадает со
знаком числа а; при 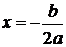 значение
квадратичной функции равно нулю.
значение
квадратичной функции равно нулю.
. Если 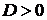 ,
то знак квадратичной функции
,
то знак квадратичной функции 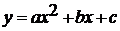 совпадает со
знаком числа
совпадает со
знаком числа 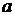 для всех х, лежащих
вне отрезка
для всех х, лежащих
вне отрезка 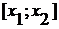 , т. е. при
, т. е. при 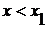 и
при
и
при 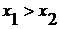 ,
где
,
где 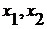 -
нули функции, знак квадратичной функции противоположен знаку числа а при
-
нули функции, знак квадратичной функции противоположен знаку числа а при 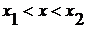 .
.
класс.
Квадратичная функция не рассматривается в 9
классе.
С.М. Никольский, М.К. Потапов, Н.Н. Решетников,
А.В. Шевкин
класс
В 7 классе данный коллектив авторов функцию не
рассматривает.
класс
В 8 классе авторы вводят понятие функции,
графика функции. После этого рассматриваются линейная, квадратичная функции и
обратная пропорциональность.
При изучении квадратичной функции сначала
рассматриваются ее свойства.
После формулировки каждого свойства даются
пояснения.
Затем рассматривается график функции  и
определяются ранее обозначенные свойства функции
и
определяются ранее обозначенные свойства функции  .
Также дается определение параболы.
.
Также дается определение параболы.
Далее рассматривается понятие квадратного корня,
опираясь на график функции  .
.
После этого вводится понятие арифметического
квадратного корня из данного неотрицательного числа. Его определение
производится по графику функции  .
.
Далее авторы рассматривают функцию 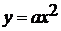 .
Сравниваются две функции
.
Сравниваются две функции  и
и 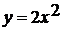 и
делается вывод, что график функции
и
делается вывод, что график функции 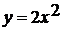 получается
из графика функции
получается
из графика функции  растяжением
последнего в 2 раза вдоль оси Оу. Рассуждая аналогично, можно показать, что
график функции
растяжением
последнего в 2 раза вдоль оси Оу. Рассуждая аналогично, можно показать, что
график функции 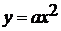 , если
, если 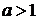 ,
получается из графика функции
,
получается из графика функции  растяжением
последнего в а раз вдоль оси у; если же
растяжением
последнего в а раз вдоль оси у; если же 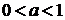 ,
то сжатием последнего в
,
то сжатием последнего в  раз.
раз.
Далее рассматривается функция 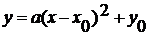 .
При этом изучаются 2 функции: сначала
.
При этом изучаются 2 функции: сначала 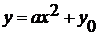 ,
а затем
,
а затем 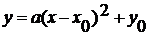 .
.
Затем авторы рассматривают график функции 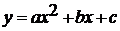 .
Приведена теорема: Графиком квадратичной функции является парабола с вершиной в
точке
.
Приведена теорема: Графиком квадратичной функции является парабола с вершиной в
точке 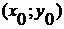 ,
полученная параллельным переносом параболы
,
полученная параллельным переносом параболы 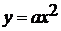 ,
где
,
где 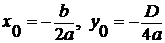 .
Эта теорема приводится с доказательством. На закрепление данного материала
учащимся предлагаются задания на построение графика квадратичной функции.
.
Эта теорема приводится с доказательством. На закрепление данного материала
учащимся предлагаются задания на построение графика квадратичной функции.
класс
В 9 классе квадратичная функция данным
коллективом авторов не рассматривается.
А.Г. Мордкович и др.
класс
В 7 классе квадратичная функция изучается после
линейной функции. Поэтому перед ее изучением автор приводит веские аргументы
для чего «она нужна». Затем учащимся предлагается подставить в формулу  целые
числа (-3, -2, -1, 0, 1, 2, 3). Из полученных значений составляется таблица. На
координатной плоскости располагают получившиеся точки и соединяют их линией,
которая называется параболой.
целые
числа (-3, -2, -1, 0, 1, 2, 3). Из полученных значений составляется таблица. На
координатной плоскости располагают получившиеся точки и соединяют их линией,
которая называется параболой.
После этого описываются геометрические свойства
параболы (ось симметрии, ветви параболы, вершина параболы) и свойства функции  .
.
Затем рассматриваются примеры применения свойств
функции (найдите наибольшее и наименьшее значения функции  на
отрезке [1, 3]).
на
отрезке [1, 3]).
В качестве совета, автор предлагает учащимся
вырезать из бумаги шаблон параболы.
Система упражнений направлена на построение
графика квадратичной функции и определению по нему ее свойств.
класс
В 8 классе продолжается рассмотрение
квадратичной функции. В 7 классе изучалась функция  .
Теперь же учащимся предлагается сначала изучить функцию
.
Теперь же учащимся предлагается сначала изучить функцию 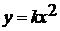 .
Для этого рассматриваются 2 функции
.
Для этого рассматриваются 2 функции 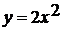 и
и
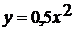 .
Составляется таблица значений функций, и строятся графики. Затем делается
вывод: от величины коэффициента k зависит «скорость устремления» ветвей
параболы вверх или, как еще говорят, «степень крутизны» параболы.
.
Составляется таблица значений функций, и строятся графики. Затем делается
вывод: от величины коэффициента k зависит «скорость устремления» ветвей
параболы вверх или, как еще говорят, «степень крутизны» параболы.
После этого рассматривается функция 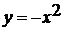 и
сравнивается с функцией
и
сравнивается с функцией  . После этого
рассмотрения делается общий вывод: График функции
. После этого
рассмотрения делается общий вывод: График функции 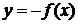 симметричен
графику функции
симметричен
графику функции 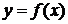 относительно оси
абсцисс.
относительно оси
абсцисс.
Затем рассматривается графики функции 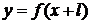 ,
,
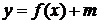 и
и
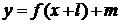 и
алгоритмы их построения.
и
алгоритмы их построения.
Далее говорится, что график любой квадратичной
функции 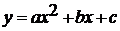 можно
получить из параболы
можно
получить из параболы 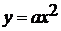 параллельным
переносом.
параллельным
переносом.
Для доказательства этого факта используется
метод выделения полного квадрата.
В следующей главе рассматривается функция 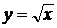 .
Говорится, что ранее было получено, что график функции
.
Говорится, что ранее было получено, что график функции 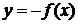 получается
из графика функции
получается
из графика функции 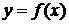 с помощью
преобразования симметрии относительно оси х. Воспользовавшись этим, строится
график функции
с помощью
преобразования симметрии относительно оси х. Воспользовавшись этим, строится
график функции 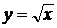 и отражается
симметрично оси х. Это и будет график функции
и отражается
симметрично оси х. Это и будет график функции  .
.
Система упражнений состоит из заданий на
определение свойств квадратичной функции по ее графику. Также большое внимание
уделено преобразованиям графика функций. Имеется достаточно много систем
уравнений для графического их решения. Делается акцент на решение задач с
параметрами.
класс
В данном учебнике квадратичная функция в 9
классе не рассматривается.
К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев
класс
Изучение квадратичной функции в данном учебнике
начинается только в 8 классе и ведется на двух языках - алгебраическом и
геометрическом.
На геометрическом языке строится график функции  .
Говорится также, что построить график «целиком» невозможно, и поэтому строят
только такую его часть, которая отражает важнейшие его свойства.
.
Говорится также, что построить график «целиком» невозможно, и поэтому строят
только такую его часть, которая отражает важнейшие его свойства.
Строится таблица значений функции. Отмечаются
полученные точки и соединяются плавной линией. Получившийся график представляет
собой бесконечную непрерывную кривую, которая называется параболой.
Затем авторы приводят сравнительную таблицу
свойств квадратичной функции на алгебраическом и геометрическом языках.
Далее на основе графика функции  рассматривается
уравнение
рассматривается
уравнение 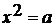 .
.
Также вводится понятие арифметического
квадратного корня из числа а и его обозначение.
Система упражнений дана на построение графика
функции  и
отыскание с помощью него точек, которые принадлежат и не принадлежат графику.
и
отыскание с помощью него точек, которые принадлежат и не принадлежат графику.
класс
В 9 классе данный коллектив авторов функциям
выделяет 2 главы.
Вначале рассказывается про квадратичную функцию 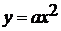 .
Напоминаются основные ранее изученные свойства функции
.
Напоминаются основные ранее изученные свойства функции  ,
говорится про ось симметрии, и на этой основе рассматриваются различные
квадратичные функции такие, как
,
говорится про ось симметрии, и на этой основе рассматриваются различные
квадратичные функции такие, как 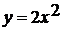 ,
, 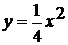 и
и
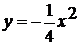 .
После каждого из этих примеров делаются выводы о преобразованиях, применимых
для графика функции
.
После каждого из этих примеров делаются выводы о преобразованиях, применимых
для графика функции  , которые приводят
к получению графика заданной функции.
, которые приводят
к получению графика заданной функции.
Упражнения, данные после этого параграфа
включают в себя:
. Постройте график функции:
1) 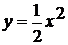 2)
2)
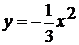 3)
3)
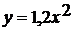 4)
4)
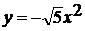
. Изготовьте из картона или плотной бумаги
шаблоны парабол:
 ,
, 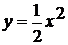 ,
,
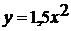 ,
,
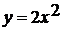
Также имеются контрольные вопросы:
Как получить график функции 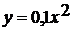 из
графика функции
из
графика функции  ?
?
Далее рассматривается функция 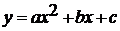 .
Выделяют полный квадрат из выражения
.
Выделяют полный квадрат из выражения 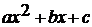 и
получают функцию
и
получают функцию 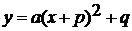 , где p и q -
некоторые числа.
, где p и q -
некоторые числа.
Приводятся примеры, рассматривается как
изменяется график в зависимости от чисел p и q и затем делается вывод, что
график функции 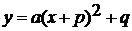 получается из
графика функции
получается из
графика функции 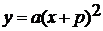 сдвигом
параллельно оси ординат на q единиц вверх при
сдвигом
параллельно оси ординат на q единиц вверх при 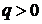 и
на |q| единиц вниз при
и
на |q| единиц вниз при 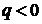 . Далее говорится,
что тем же приемом - сдвигом вдоль осей координат графика произвольной функции
. Далее говорится,
что тем же приемом - сдвигом вдоль осей координат графика произвольной функции 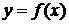 можно
получить графики функций
можно
получить графики функций 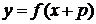 и
и 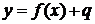 .
Именно,
.
Именно,
График функции 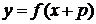 получается
из графика функции
получается
из графика функции 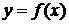 сдвигом
параллельно оси абсцисс на p единиц влево при
сдвигом
параллельно оси абсцисс на p единиц влево при 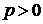 и
на -p единиц вправо при
и
на -p единиц вправо при 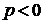 .
.
График функции 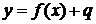 получается
из графика функции
получается
из графика функции 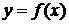 сдвигом
параллельно оси абсцисс на q единиц вверх при
сдвигом
параллельно оси абсцисс на q единиц вверх при 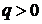 и
на -q единиц вниз при
и
на -q единиц вниз при 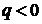 .
.
Изучение квадратичной функции в
проанализированных учебниках начинается в 7 (Ю.Н. Макарычев и др., А.Г.
Мордкович и др.) и 8 (С.М. Никольский и др., Ш.А. Алимов и др., Г.В. Дорофеев и
др.) классах. В учебниках А.Г. Мордковича и др., Ю.Н. Макарычева и др., Ш.А.
Алимова и др. изложение материала ведется доступным языком. Прослеживается нить
«от простого к сложному». В остальных же учебниках теоретический материал
изложен на более научном уровне. Во всех учебниках рассматриваются приложения
квадратичной функции (решение уравнений, неравенств, систем уравнений,
построение графиков функций, задачи с параметрами). Отличие лишь в том, какое
внимание уделяется тому или иному разделу. Задачи с параметрами наиболее ярко
отражены только в учебнике А.Г. Мордковича и др.
В учебнике Г.В. Дорофеева и др. изучение
квадратичной функции ведется в 8 и 9 классах на двух языках - алгебраическом и
геометрическом. Уделяется большое внимание преобразованиям графиков функций. Вся
теория изложена «строго по делу», без отступлений.
В учебниках А.Г. Мордковича и др. функциональная
линия является ведущей. Автор выделяет в системе упражнений по изучению того
или иного класса функций инвариантное ядро, универсальное для любого класса функций,
которое состоит из шести направлений:
графическое решение уравнений;
отыскание наибольшего и наименьшего значений
функции на заданном промежутке;
преобразование графиков;
функциональная символика;
кусочная функция;
чтение графика.
Это шесть элементов, с помощью которых, функция
становится привлекательной, понятной и привычной [22].
В учебнике Ш.А. Алимова и др. квадратичной
функции и ее приложениям посвящен практически весь учебник 8 класса. Блоком
рассматривается квадратичная функция и ее свойства, и затем квадратные
неравенства и задачи с параметрами, решаемые с помощью построения графика
квадратичной функции.
В учебнике Ю.Н. Макарычева определение
квадратичной функции дается в 9 классе предлагается учащимся сразу, затем
рассматриваются частные случаи квадратичной функции и после непосредственно
общий вид квадратичной функции. Только после этого авторы обращают внимание на
решение квадратных уравнений и систем уравнений (в частности, графический
метод), опираясь на свойства квадратичной функции. Задачам с параметрами
уделяется крайне мало внимания.
Глава 2. Методическая разработка по
теме «Квадратичная функция и ее приложения»
Квадратичная функция в школьном курсе изучается
с 7-го (в некоторых учебниках с 8-го) класса. Приложениям квадратичной функции
уделяется особое внимание. Очень важно, чтобы ученики при получении знаний,
впоследствии могли применять их на практике.
В данной главе рассматриваются приложения
квадратичной функции по 4 разделам:
. Построение и чтение графика квадратичной
функции.
. Решение уравнений и их систем.
. Решение квадратных уравнений с параметрами, в
том числе, поиск параметра в зависимости от свойств корней уравнения.
. Решение квадратных неравенств с параметрами.
К каждому разделу подобраны (частично взяты из
сборников, остальные составлены самостоятельно нами) задачи. К некоторым
наиболее типичным заданиям приведены решения и комментарии. Также имеются
задачи для самостоятельного решения с ответами.
Данная разработка носит обучающий характер и
может быть применима учителем, на уроке, факультативе, при дифференцированном
обучении, в качестве домашних заданий, в том числе индивидуальных.
. Построение и чтение графика квадратичной
функции.
Использование на уроках алгебры кусочных функций
позволяет учителю разнообразить урок, сделать его творческим и интересным.
Ученики сами могут составлять свои примеры. Более того, кусочные функции
реализовывают наше представление о реальном мире.
. Постройте график функции 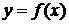 ,
где
,
где
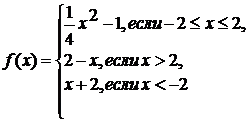
Укажите промежутки возрастания функции.
Решение:
. 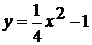
|
x
|
-2
|
-1
|
0
|
1
|
2
|
|
y
|
0
|
-0,75
|
-1
|
-0,75
|
0
|
. 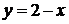
. 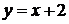
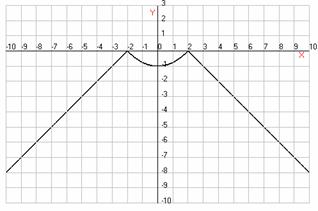
Функция 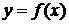 возрастает
при
возрастает
при 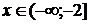 и
при
и
при 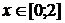 .
.
Ответ: 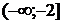 ;
;
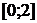
. Известно, что график квадратичной функции 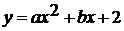 симметричен
относительно прямой
симметричен
относительно прямой 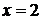 и проходит через
точку К (-2;-4). Постройте этот график.
и проходит через
точку К (-2;-4). Постройте этот график.
Решение:
Подставим координаты точки К в уравнение 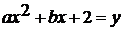 .
.
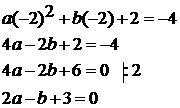
Графиком функции 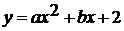 является
парабола. Т. к. известно, что график заданной функции симметричен относительно
прямой
является
парабола. Т. к. известно, что график заданной функции симметричен относительно
прямой 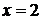 ,
то вершина параболы имеет координаты
,
то вершина параболы имеет координаты 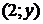 .
.
Координаты вершины:
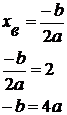
Составим систему уравнений:
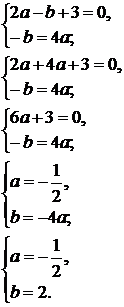
Получили функцию:
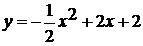
Построим график этой функции.
|
x
|
-2
|
0
|
2
|
4
|
6
|
|
y
|
-4
|
2
|
4
|
2
|
-4
|
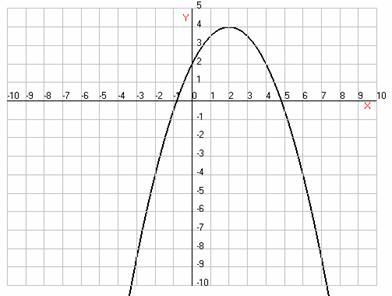
3. Постройте график функции 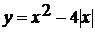 .
Сколько общих точек может иметь с этим графиком прямая
.
Сколько общих точек может иметь с этим графиком прямая 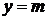 ?
(Для каждого случая укажите соответствующее значение m).
?
(Для каждого случая укажите соответствующее значение m).
Решение:
Рассмотрим 2 случая:
. Если 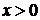 ,
тогда
,
тогда 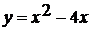
Графиком функции 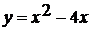 является
парабола, ветви направлены вверх.
является
парабола, ветви направлены вверх.
Нули функции:

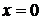 или
или 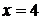
Координаты вершины:
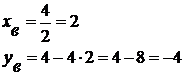
. Если 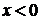 ,
тогда
,
тогда 
Графиком функции  является
парабола, ветви направлены вверх.
является
парабола, ветви направлены вверх.
Нули функции:
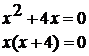
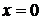 или
или 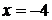
Координаты вершины:
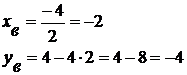
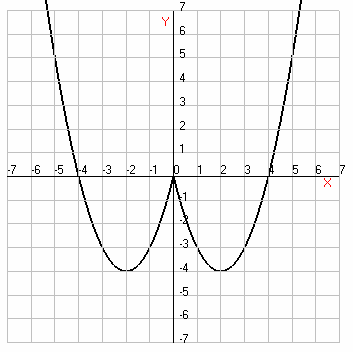
Возможны 4 случая:
нет общих точек - при 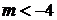
общие точки - при 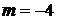 и
при
и
при 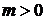
общие точки - при 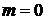
общие точки - при 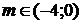
Задачи для самостоятельного решения
. Построить графики функций в одной системе
координат:
=x2x є [-2 ; 2]=-x2 + 4x є [-1 ; 1]= - (x + 2)2
+ 4x є [-2 ; -1]= - (x - 2)2 + 4x є [1 ; 2]= - (x - 1.5)2 - 3x є [0 ; 1.5]= -
(x + 1.5)2 - 4x є [-1.5 ; 0]=x2 - 6x є [-1.4 ; 0]=x2 - 5x є [0 ; 1.4]
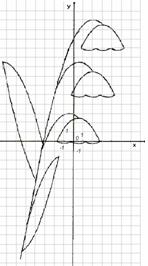
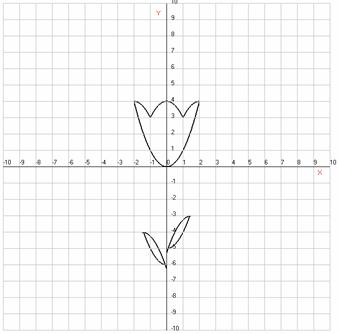
. По графикам функций, изображенным на рисунке,
восстановите аналитическую запись функций, если известно, что все эти графики
получены из графика функции 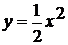 только с помощью
движений и симметрии. Указание: в случае необходимости используйте шаблон
графика функции
только с помощью
движений и симметрии. Указание: в случае необходимости используйте шаблон
графика функции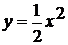 .
.
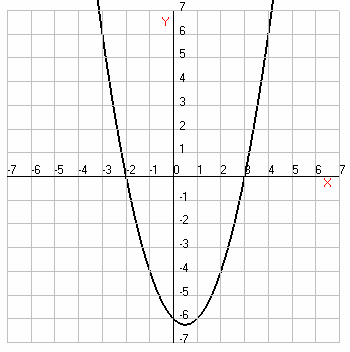
3. На рисунке изображен график функции 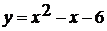 .
Используя график, решите неравенство
.
Используя график, решите неравенство 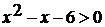
. С помощью графиков функций, вычислите
координаты точек пересечения парабол:
А) 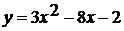 и
и
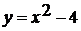
Б)  и
и
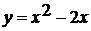
. Постройте график функции 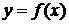 ,
где
,
где  .
Укажите промежутки возрастания функции.
.
Укажите промежутки возрастания функции.
. Постройте график функции 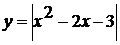 .
Сколько общих точек может иметь с этим графиком прямая
.
Сколько общих точек может иметь с этим графиком прямая 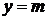 ?
(Для каждого случая укажите соответствующее значение m).
?
(Для каждого случая укажите соответствующее значение m).
. Парабола 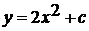 пересекает
ось х в точке
пересекает
ось х в точке 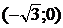 . Найдите значение
с и определите, пересекает ли эта парабола прямую
. Найдите значение
с и определите, пересекает ли эта парабола прямую 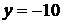 .
.
. При каких значениях а парабола  пересекает
ось х в двух точках и ее ветви направлены вниз?
пересекает
ось х в двух точках и ее ветви направлены вниз?
. При каких положительных значениях k, парабола 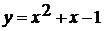 и
прямая
и
прямая 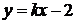 не
пересекаются?
не
пересекаются?
. При каких значениях n парабола 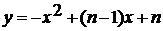 целиком
расположена ниже прямой
целиком
расположена ниже прямой 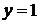 ?
?
Ответы:
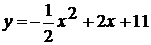
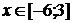
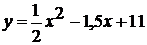
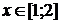
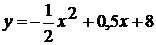
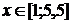
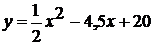
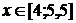
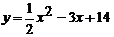
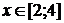
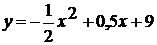
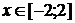
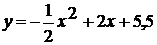
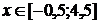
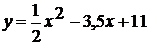
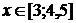
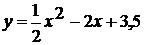
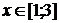
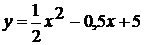
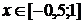
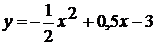
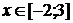
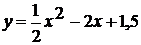
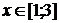
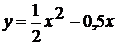
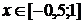
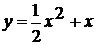
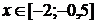
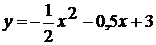
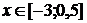
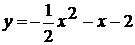
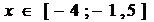
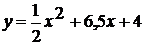

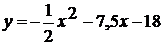
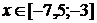
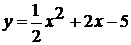
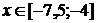
. 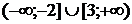
. (0,3;-3,8); (3,7;10,5)
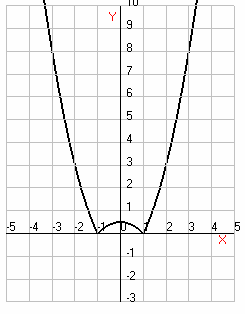
Функция возрастает на промежутках 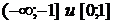
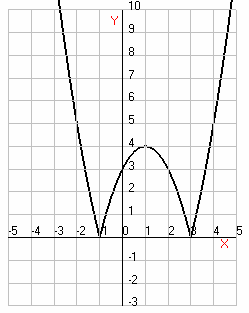
нет общих точек - при 
общие точки - при 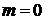 и
при
и
при 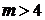
общие точки - при 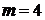
общие точки - при 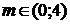
. с=18(3;0)
8. 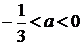
. 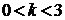
. 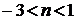
. Решение квадратных уравнений и систем
уравнений.
При решении следующих заданий удобно применить
функционально-графический метод решения. Суть этого метода состоит в том, что
для уравнения вида  , нужно построить в
одной системе координат графики функций
, нужно построить в
одной системе координат графики функций 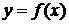 и
и
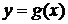 .
Затем найти точки их пересечения: абсциссы точек пересечения будут являться
корнями заданного уравнения. Этот метод позволяет определить количество решений
уравнения.
.
Затем найти точки их пересечения: абсциссы точек пересечения будут являться
корнями заданного уравнения. Этот метод позволяет определить количество решений
уравнения.
. Выясните, имеет ли корни уравнение:
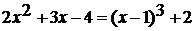
Решение:
Чтобы решить данное уравнение, построим графики
функций левой и правой частей уравнения:
. 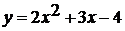
. 
. Графиком функции 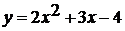 является
парабола. Ветви направлены вверх.
является
парабола. Ветви направлены вверх.
Координаты вершины:
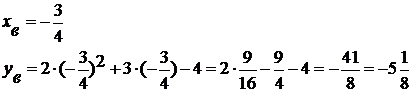
|
х
|
-2,75
|
-1,75
|
|
0
|
0,75
|
|
у
|
2,875
|
-3,125
|
|
-4
|
-0,625
|
. 
|
х
|
-1
|
-0.5
|
0
|
0.5
|
1
|
|
у
|
-6
|
-1.375
|
1
|
1.875
|
2
|
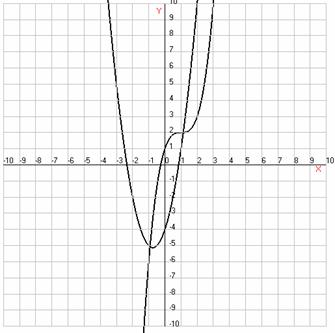
Ответ: уравнение имеет корни.
. Сколько решений имеет система уравнений 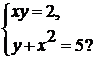
Решение:
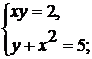
Построим графики функций:
. Графиком функции 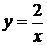 является
гипербола, расположенная в I и III четвертях.
является
гипербола, расположенная в I и III четвертях.
|
х
|
1
|
2
|
4
|
-1
|
-2
|
-4
|
|
у
|
2
|
1
|
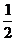
|
-2
|
-1
|
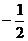
|
. Графиком функции 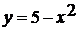 является
парабола, ветви направлены вниз.
является
парабола, ветви направлены вниз.
Координаты вершины:
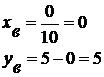
|
х
|
-2
|
-1
|
0
|
1
|
2
|
|
у
|
1
|
4
|
5
|
4
|
1
|
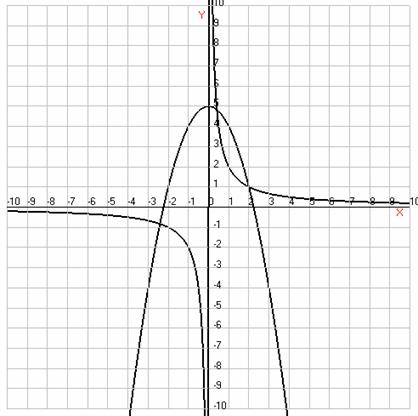
Ответ: система имеет 3 решения.
Данная система методом подстановки не решается,
т.к. получается кубическое уравнение.
Задачи для самостоятельного решения
. Выясните, имеет ли корни уравнение:

. Решите уравнение:
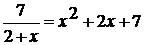
. Решите уравнение:
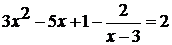
. Решите уравнение:
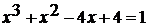
. Сколько решений имеет система уравнений:
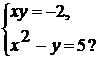
Ответы:
Имеет;
,8;
,07; 1,5;
,8;
Решение уравнений и неравенств с параметрами
довольно трудоемкое занятие и зачастую вызывают трудности в решении у учащихся.
Здесь требуется применение ранее полученных знаний не только алгоритмов решения
уравнения (неравенства), но и определенных свойств функций. Такими задачами
проверяется понимание материала учащимися.
. Решение квадратных уравнений с параметрами, в
том числе, поиск параметра в зависимости от свойств корней уравнения.
. При каком наибольшем значении параметра а,
уравнение 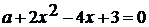 имеет хотя бы одно
решение?
имеет хотя бы одно
решение?
Решение:
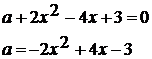
Рассмотрим функцию 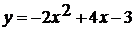 и
построим ее график.
и
построим ее график.
Графиком квадратичной функции 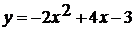 является
парабола, ветви направлены вниз (т.к. -2<0).
является
парабола, ветви направлены вниз (т.к. -2<0).
Координаты вершины:
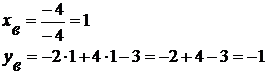
|
х
|
-1
|
0
|
1
|
2
|
3
|
|
у
|
-9
|
-3
|
-1
|
-3
|
-9
|
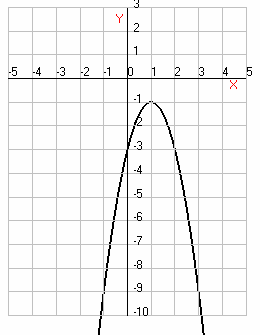
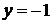 - наибольшее
значение функции.
- наибольшее
значение функции.
Значит, 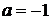 -
наибольшее значение, при котором уравнение имеет решение.
-
наибольшее значение, при котором уравнение имеет решение.
Ответ: -1.
. При каких значениях а уравнение 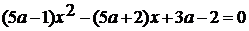 имеет
один корень?
имеет
один корень?
Решение:
Рассмотрим функцию 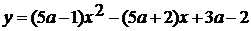 .
.
) Если 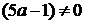 ,
то функция является квадратичной.
,
то функция является квадратичной.
Уравнение 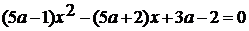 имеет
один корень, если
имеет
один корень, если 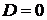 .
.

) Если 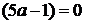 ,
(т.е.
,
(т.е. 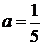 )
то функция является линейной, а уравнение принимает вид
)
то функция является линейной, а уравнение принимает вид 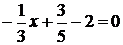 .
Это уравнение имеет один корень.
.
Это уравнение имеет один корень.
Ответ: 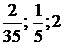
. При каких значениях p уравнение 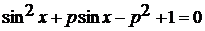 (1)
имеет решение?
(1)
имеет решение?
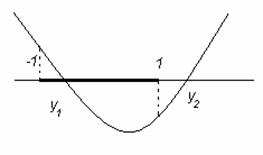
Решение:
Это уравнение квадратное относительно 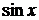 и
чтобы ответить на вопрос задачи, нужно найти значение p, при которых корни
уравнения
и
чтобы ответить на вопрос задачи, нужно найти значение p, при которых корни
уравнения 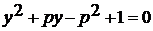 удовлетворяют
условию
удовлетворяют
условию 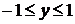 .
.
Зададим функцию 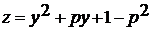 .
.
Графиком является парабола, ветви направлены
вверх.
Рассмотрим 4 случая:
) Только больший корень лежит в интервале 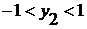

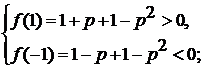
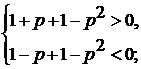
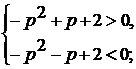
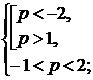
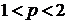 .
.
) Только меньший корень трехчлена лежит в
интервале 
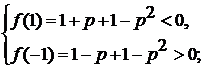
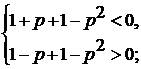
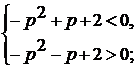
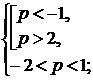
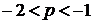 .
.
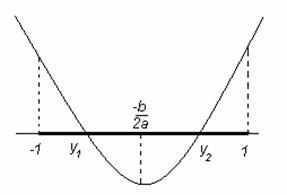
) Оба корня трехчлена лежат в интервале 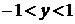
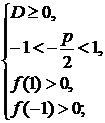
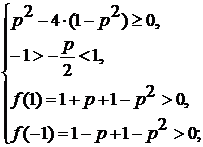
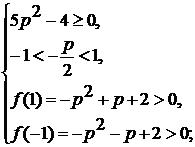
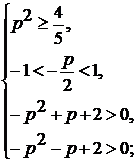
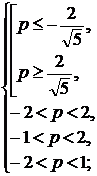
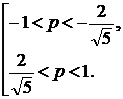
4) Число 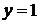 является
корнем трехчлена, если
является
корнем трехчлена, если 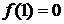 , т.е. если
, т.е. если 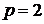 и
и
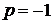 .
Число
.
Число 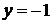 будет
корнем трехчлена, если
будет
корнем трехчлена, если 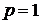 и
и 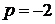 .
.
Итак, все значения 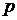 ,
при которых уравнение (1) имеет решение, определяются неравенством :
,
при которых уравнение (1) имеет решение, определяются неравенством : 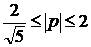 .
.
Ответ: 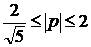
. Для каждого действительного числа а решить
уравнение: 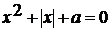 (1).
(1).
Решение:
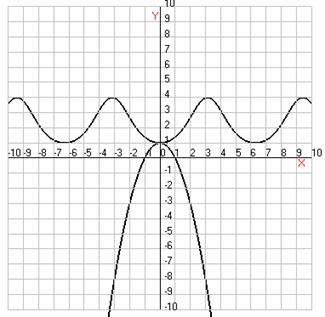
Представим уравнение (1) в виде 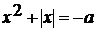 (2)
и построим график функции
(2)
и построим график функции 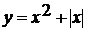 .
.
Для построения графика функции можно
использовать свойство четности. Данный график сначала строится для 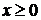 ,
функция в этом случае принимает вид
,
функция в этом случае принимает вид 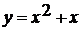 .
Далее график симметрично отображается относительно оси Оу.
.
Далее график симметрично отображается относительно оси Оу.
Графиком функции 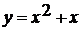 является
парабола, ветви которой направлены вниз.
является
парабола, ветви которой направлены вниз.
Координаты вершины:
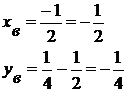
|
х
|
-2
|
-1
|
-0,5
|
0
|
1
|
|
у
|
2
|
0
|
-0,25
|
0
|
2
|
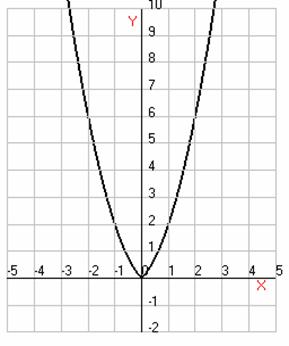
Решением уравнения (2) для различных значений
параметра а представляются абсциссы точек пересечения графика функции 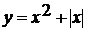 и
графика прямой
и
графика прямой 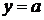 .
.
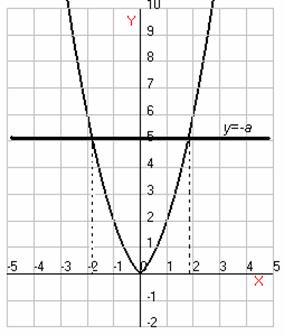
Отсюда при 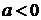 получаем
2 системы:
получаем
2 системы:
1) 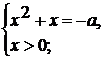 2)
2)
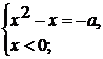
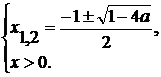
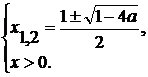
Ответ: при 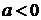
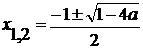 ;
;
при 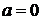
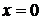 ;
;
при 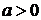 уравнение
(1) не имеет корней.
уравнение
(1) не имеет корней.
Задачи для самостоятельного решения
. При каких значениях а, уравнение 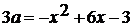 имеет
решения?
имеет
решения?
. При каких значениях параметра a, уравнение  имеет
решения?
имеет
решения?
. При каких значениях параметра z, уравнение 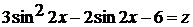 не
имеет решений?
не
имеет решений?
. При каком значении m уравнения 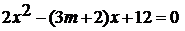 и
и
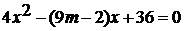 имеют
общий корень?
имеют
общий корень?
. Определить число а так, чтобы один из корней
уравнения 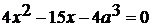 был квадратом
другого.
был квадратом
другого.
. При каких значениях k уравнение 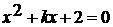 имеет
корни? Приведите пример положительного значения k, при котором выполняется это
условие.
имеет
корни? Приведите пример положительного значения k, при котором выполняется это
условие.
. При каких значениях m уравнение  имеет
корни, отношение которых равно 2?
имеет
корни, отношение которых равно 2?
. При каких значениях m уравнение  имеет
различные корни?
имеет
различные корни?
. В уравнении 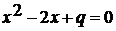 квадрат
разности корней равен 16. Определить свободный член уравнения.
квадрат
разности корней равен 16. Определить свободный член уравнения.
. При каком значении m сумма квадратов корней
уравнения 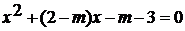 минимальна?
минимальна?
. Найти все значения параметра а, при которых
оба корня квадратного уравнения 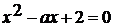 принадлежат
промежутку (0;3).
принадлежат
промежутку (0;3).
. Найти все значения параметра а, при которых
корни уравнения 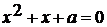 больше а?
больше а?
Ответы:
. 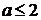
. [0;8]
.  и
и
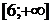
. 3
. 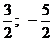
. 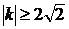
. -2; 1
. m - любое
. -3
. 1
. 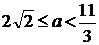
. 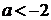
. Решение квадратных неравенств с параметрами.
. При каких значениях m неравенство 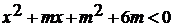 (1)
выполняется при всех
(1)
выполняется при всех 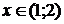 ?
?
Решение:
Чтобы неравенство (1) выполнялось для всех 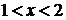 ,
нужно, чтобы квадратный трехчлен
,
нужно, чтобы квадратный трехчлен 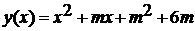 (график
- парабола, ветви направлены вверх) при всех указанных x был отрицателен.
(график
- парабола, ветви направлены вверх) при всех указанных x был отрицателен.
Для этого нужно, чтобы интервал (1;2) целиком
лежал между корнями параболы.
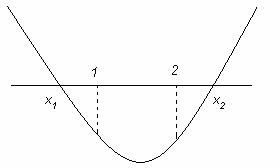
Составим систему:
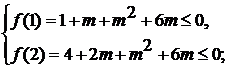
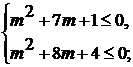
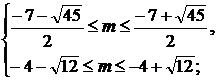
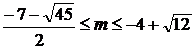 .
.
Ответ: 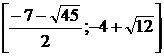 .
.
2. При каких значениях k верно следующее
утверждение: «неравенство 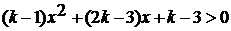 (1) выполняется
хотя бы при одном
(1) выполняется
хотя бы при одном 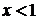 (2)»?
(2)»?
Решение:
) При 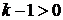 утверждение
верно, например, для точки
утверждение
верно, например, для точки 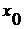 :
:
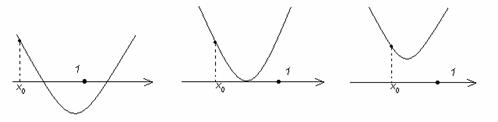
) При 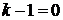 (т.е.
при
(т.е.
при 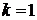 )
утверждение верно, т.к. в этом случае неравенство принимает вид:
)
утверждение верно, т.к. в этом случае неравенство принимает вид:
 ,
,
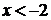 ,
,
т.е. 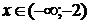 ,
например,
,
например, 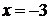 удовлетворяет
неравенству (1) и неравенству (2).
удовлетворяет
неравенству (1) и неравенству (2).
) 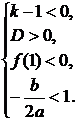
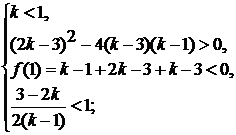
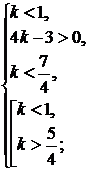
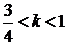 .
.
Ответ: 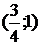 .
.
Задачи для самостоятельного решения
. Для каждого значения параметра, а решить
неравенство 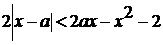 .
.
. Найти все значения а, для которых при всех х,
не превосходящих по модулю единицы, справедливо неравенство 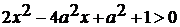
. Найти все значения k, при каждом из которых существует
хотя бы одно общее решение неравенств 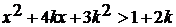 и
и
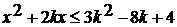 .
.
. При каких значениях p вершины парабол 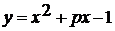 и
и
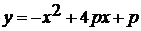 расположены
по разные стороны от оси х?
расположены
по разные стороны от оси х?
. При каких значениях m из неравенства  следует
следует
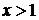 ?
?
. При каких значениях а, неравенство 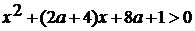 выполняется
при всех значениях х?
выполняется
при всех значениях х?
Ответы:
. При 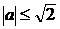 неравенство
решений не имеет
неравенство
решений не имеет
При 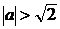
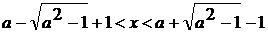 ;
;
. 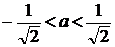
. 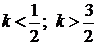
. 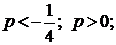
. Ни при каких m;
. 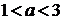
Заключение
Цель данной дипломной работы - обзор приложений
квадратичной функции к решению различных задач школьного курса математики и
составление соответствующих методических рекомендаций.
В ходе выполнения дипломной работы была проанализирована
психолого-педагогическая, методическая и учебная литература, подобран задачный
материал, выделены типовые задачи в каждом разделе и предоставлены решения к
ним, составлены комментарии к решениям задач.
Функционально-графические методы применимы для
решения широкого спектра задач школьной программы, однако, как показал анализ
учебной литературы им не всегда уделяется должное внимание.
Вторая глава дипломной работы содержит банк
задач, для решения которых так или иначе используются свойства квадратичной
функции. Условно задачи были поделены на следующие блоки:
. Построение и чтение графика квадратичной
функции.
. Решение квадратных уравнений и систем
уравнений.
. Решение квадратных уравнений с параметрами, в
том числе, поиск параметра в зависимости от свойств корней уравнения.
. Решение квадратных неравенств с параметрами.
К некоторым задачам мы привели решения и
методические рекомендации. Также имеются задачи для самостоятельного решения с
ответами. Они расположены по уровню сложности.
Имеются творческие задания, а также задачи, к
решению которых применим только функционально-графический метод.
Представленная разработка может послужить
дополнением к традиционным урокам, для работы на факультативах, для
дифференцированного обучения, а также в качестве домашних заданий, в том числе
индивидуальных.
Библиография
1. Алгебра:
сборник заданий для подготовки к итоговой аттестации в 9 кл. [Текст]: Итоговая
аттестация / Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Л.О. Рослова.- М.:
Просвещение, 2006.- 192 с.
2. Алгебра
[Текст]: Учеб. для 7 кл. общеобразоват. учреждений / С.М. Никольский, М.К.
Потапов, Н.Н. Решетников и др.- 2-е изд.- М.: Просвещение, 2008.- 285 с.
. Алгебра
[Текст]: Учеб. для 7 кл. общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин,
Ю.В. Сидоров и др.- 8-е изд.- М.: Просвещение, 2008.- 207 с.
. Алгебра
[Текст]: Учеб. для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г.
Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского.- 9-е изд.- М.:
Просвещение, 2008.- 223 с.
. Алгебра
[Текст]: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К.
Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2007.- 287 с.
. Алгебра
[Текст]: Учеб. для 8 кл. общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин,
Ю.В. Сидоров и др.- 44-е изд.- М.: Просвещение: Моск. учеб.», 2008.- 255 с.:
ил.
. Алгебра
[Текст]: Учеб. для 8 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г.
Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского.- 3-е изд.- М.:
Просвещение, 2006.- 239 с.
. Алгебра
[Текст]: Учеб. для 9 кл. общеобразоват. учреждений / С.М. Никольский, М.К.
Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2008.- 255 с.
. Алгебра
[Текст]: Учеб. Для 9 кл. общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин,
Ю.В. Сидоров и др.- 10-е изд.- М.: Просвещение: Моск. учеб., 2006.- 255 с.
. Алгебра
[Текст]: Учеб. для 9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г.
Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского.- 3-е изд.- М.:
Просвещение, 2006.- 271 с.
. Гиппенрейтер
Ю.Б. Хрестоматия по общей психологии. Психология мышления [Текст] / Ю.Б.
Гиппенрейтер, В.В. Петухова.- М.: Моск. университет, 1981.- 400 с.
. Занков
Л.В. Наглядность в обучении [Текст] / Л.В. Занков // Пед. энциклопедия: В 4 т.
/ Гл. ред. И.А. Конров.- Т. 3.- М.: Сов. энциклопедия, 1966.
. Крамор
В.С. Примеры с параметрами и их решение [Текст]: Пособие для поступающих в вузы
/ В.С. Крамор.- М.: АРКТИ, 2008.- 48 с.: ил.- Методическая библиотека.
. Крутецкий
В.А. Психология математических способностей школьников [Текст] / В.А. Крутецкий;
под ред. Н.И. Чуприковой.- М.: Ин. практич. психологии, 2008.- 416 с.
. Локоть
В.В. Задачи с параметрами. Линейные и квадратные уравнения, неравенства,
системы [Текст]: Учебное пособие / В.В. Локоть.- М.: АРКТИ, 2006.- 96 с.
. Мордкович
А.Г. Алгебра [Текст]: 7 кл.: Учеб. для общеобразоват. учреждений / А.Г.
Мордкович.- 3-е изд., доработ.- М.: Мнемозина, 2008.- 160 с.
. Мордкович
А.Г. Алгебра [Текст]: 8 кл.: Учеб. для общеобразоват. учреждений / А.Г.
Мордкович.- 3-е изд., доработ.- М.: Мнемозина, 2008.- 210 с.
. Мордкович
А.Г. Алгебра [Текст]: 9 кл.: Учеб. для общеобразоват. учреждений / А.Г.
Мордкович.- 3-е изд., испр.- М.: Мнемозина, 2006.- 192 с.
. Мордкович
А.Г. Алгебра [Текст]: 7 кл.: Задачник для общеобразоват. учреждений / А.Г.
Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.- 3-е изд., доработ.- М.:
Мнемозина, 2007.- 160 с.
. Мордкович
А.Г. Алгебра [Текст]: 8 кл.: Задачник для общеобразоват. учреждений / А.Г.
Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.- 3-е изд., испр.- М.: Мнемозина,
2008.- 239 с.
. Мордкович
А.Г. Алгебра [Текст]: 9 кл.: Задачник для общеобразоват. учреждений / А.Г.
Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.- 3-е изд., испр.- М.: Мнемозина,
2006.- 143 с.
. Мордкович
А.Г. Беседы с учителями математики [Текст]: Учеб.-метод. пособие / А.Г.
Мордкович.- 2-е изд., доп. и перераб.- М.: Оникс 21 век, 2006.- 336 с.
. Муравин
К.С. Алгебра [Текст]: 7 кл.: Учеб. для общеобразоват. учеб. заведений / К.С.
Муравин, Г.К. Муравин, Г.В. Дорофеев.- 2-е изд., испр. и доп.- М.: Дрофа,
2008.- 240 с.
. Муравин
К.С. Алгебра [Текст]: 8 кл.: Учеб. для общеобразоват. учеб. заведений / К.С.
Муравин, Г.К. Муравин, Г.В. Дорофеев.- 3-е изд., стереотип.- М.: Дрофа, 2006.-
208 с.
. Муравин
К.С. Алгебра [Текст]: 9 кл.: Учеб. для общеобразоват. учеб. заведений / К.С.
Муравин, Г.К. Муравин, Г.В. Дорофеев.- М.: Дрофа, 2006.- 240 с.
. Мухина
В.С. Возрастная психология: феноменология развития, детство, отрочество
[Текст]: Учебник для студ. вузов / В.С. Мухина.- 7-е изд., стереотип.- М.:
Академия, 2006.- 456 с.
. Формирование
личности в переходный период от подросткового к юношескому возрасту / под ред.
И.В. Дубровиной.- М.: Педагогика, 2007.
. Хон
Р.Л. Педагогическая психология. Принципы обучения [Текст]: Учеб. пособие для
высшей шк. / Р.Л. Хон.- М.: Академический проект, 2009.