Формации конечных групп
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
имени Франциска Скорины»
Математический факультет
Кафедра алгебры и геометрии
Допущена к защите
Зав.
кафедрой Шеметков Л.А.
«
» 2007 г.
Об
одной проблеме теории
Формации конечных групп
Курсовая работа
Исполнитель:
студент
группы М-51 А.И. Рябченко
Научный
руководитель:
к.ф.-
м.н., старший преподаватель В.Г. Сафонов
Гомель 2007
Оглавление
Введение
Вспомогательные
факты
Основные
результаты
Заключение
ЛИТЕРАТУРА
Введение
Все рассматриваемые в работе группы предполагаются
конечными. Кроме общепринятой терминологии [1–3], нам потребуются некоторые
определения и обозначения работы [4].
Пусть  –
некоторое непустое подмножество множества всех простых чисел;
–
некоторое непустое подмножество множества всех простых чисел; 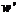 – дополнение к
– дополнение к  во
множестве всех простых чисел. Формация
во
множестве всех простых чисел. Формация  называется
называется
 -насыщенной, если ей принадлежит всякая
группа
-насыщенной, если ей принадлежит всякая
группа 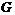 , удовлетворяющая условию
, удовлетворяющая условию 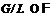 , где
, где 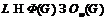 .
Всякая формация считается 0-кратно
.
Всякая формация считается 0-кратно  -насыщенной. При
-насыщенной. При  формация
формация  называется
называется
 -кратно
-кратно  -насыщенной
[4], если
-насыщенной
[4], если 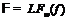 , где все непустые значения
, где все непустые значения  -локального спутника
-локального спутника 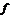 являются
являются  -кратно
-кратно
 -насыщенными формациями.
-насыщенными формациями.
Для любых двух  -кратно
-кратно
 -насыщенных формаций
-насыщенных формаций  и
и 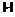 полагают
полагают
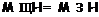 , а
, а 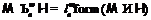 ,
где
,
где 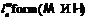 – пересечение всех
– пересечение всех  -кратно
-кратно  -насыщенных
формаций, содержащих
-насыщенных
формаций, содержащих  . Через
. Через  обозначают решетку
обозначают решетку  -кратно
-кратно  -насыщенных
формаций, заключенных между
-насыщенных
формаций, заключенных между 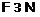 и
и  . Длину решетки
. Длину решетки 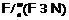 обозначают
обозначают
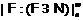 и называют
и называют  -дефектом
формации
-дефектом
формации  .
.  -Кратно
-Кратно
 -насыщенную формацию
-насыщенную формацию  называют
называют  -приводимой,
если она может быть представлена в виде решеточного объединения некоторых своих
собственных
-приводимой,
если она может быть представлена в виде решеточного объединения некоторых своих
собственных  -кратно
-кратно  -насыщенных
подформаций в решетке
-насыщенных
подформаций в решетке  . В противном случае формацию
. В противном случае формацию  называют
называют  -неприводимой.
-неприводимой.
Группа 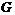 называют
критической, если
называют
критической, если 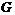 – группа минимального порядка
из
– группа минимального порядка
из 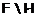 для некоторых формаций
для некоторых формаций  и
и 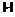 .
Критическая группа
.
Критическая группа  называется
называется 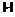 -базисной, если у формации, ею
порожденной, имеется лишь единственная максимальная подформация
-базисной, если у формации, ею
порожденной, имеется лишь единственная максимальная подформация  , причем
, причем  .
.
В работе [4] А.Н. Скибой и Л.А. Шеметковым
была поставлена задача описания  -кратно
-кратно  -насыщенных формаций
-насыщенных формаций  -дефекта
-дефекта  (вопрос
5, [4]). Полученные нами теоремы 1–3 завершают описание
(вопрос
5, [4]). Полученные нами теоремы 1–3 завершают описание  -кратно
-кратно
 -насыщенных формаций такого типа. В
частности, теорема 1 и теорема 2 позволяют классифицировать
-насыщенных формаций такого типа. В
частности, теорема 1 и теорема 2 позволяют классифицировать  -приводимые
-приводимые  -кратно
-кратно
 -насыщенные формации, имеющие
-насыщенные формации, имеющие  -дефект
-дефект  , а в
теореме 3 получено описание конечных групп, порождающих
, а в
теореме 3 получено описание конечных групп, порождающих  -неприводимые
формации
-неприводимые
формации  -дефекта 2 (
-дефекта 2 (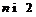 ). Отметим,
что при
). Отметим,
что при 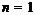 решение данной задачи получено в работе
[5].
решение данной задачи получено в работе
[5].
Вспомогательные
факты
Следствием теоремы 3.4.3 работы [6]
является
Лемма 1. Пусть  –
–  -кратно
-кратно  -насыщенная
ненильпотентная формация. Тогда в
-насыщенная
ненильпотентная формация. Тогда в  имеется по крайней
мере одна минимальная
имеется по крайней
мере одна минимальная  -кратно
-кратно  -насыщенная ненильпотентная подформация.
-насыщенная ненильпотентная подформация.
Доказательство следующей леммы аналогично
доказательству леммы 20.4 [2].
Лемма 2. Пусть  ,
, 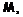
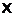 и
и 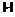 –
–  -кратно
-кратно
 -насыщенные формации, причем
-насыщенные формации, причем 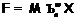 . Тогда если
. Тогда если 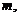
 и
и 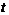 соответственно
соответственно
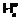 -дефекты формаций
-дефекты формаций 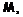
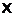 и
и  и
и 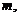
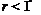 , то
, то 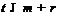 .
.
Лемма 3 [4]. Для всех 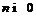 решетка
решетка
 модулярна.
модулярна.
Аналогично лемме 14 [7] доказывается
Лемма 4. Пусть 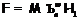 , где
, где  – некоторая
– некоторая  -кратно
-кратно
 -насыщенная нильпотентная подформация
формации
-насыщенная нильпотентная подформация
формации  ,
, 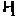 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная подформация формации
-насыщенная
ненильпотентная подформация формации  . Тогда в формации
. Тогда в формации  не существует минимальных
не существует минимальных  -кратно
-кратно  -насыщенных
ненильпотентных формаций, отличных от
-насыщенных
ненильпотентных формаций, отличных от 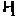 .
.
Лемма 5. Пусть  ,
,  и
и 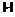 –
–  -насыщенная формации и
-насыщенная формации и 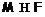 . Тогда
. Тогда 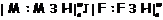 .
.
Доказательство аналогично лемме
20.3 [2].
Лемма 6 [8]. При 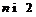 всякая
всякая  -кратно насыщенная формация, имеющая
-кратно насыщенная формация, имеющая  -дефект 2, приводима.
-дефект 2, приводима.
Лемма 7 [4]. Пусть –
–  -кратно
-кратно  -насыщенная
формация
-насыщенная
формация 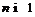 . Тогда спутник
. Тогда спутник 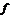 является
является
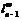 -значным.
-значным.
Лемма 8 [9]. Пусть 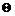 –
такая полная решетка формаций, что
–
такая полная решетка формаций, что 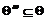 . Пусть
. Пусть 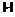 –
– 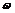 -локальная
формация с каноническим
-локальная
формация с каноническим 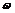 -локальным спутником
-локальным спутником 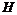 ,
,  –
– 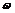 -локальная формация с минимальным
-локальная формация с минимальным 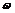 -локальным
-локальным 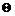 -значным
спутником
-значным
спутником 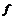 . Тогда в том и только в том случае
. Тогда в том и только в том случае  –
– 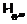 -критическая
формация, когда
-критическая
формация, когда 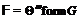 , где
, где 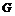 –
такая монолитическая группа с монолитом
–
такая монолитическая группа с монолитом 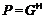 , что
либо
, что
либо 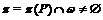 ,
, 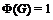 и
и 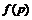 –
– 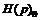 -критическая
формация для всех
-критическая
формация для всех 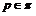 , либо
, либо 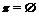 и
и
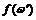 –
– 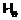 -критическая
формация.
-критическая
формация.
Лемма 9 [4]. Пусть 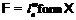 , где
, где
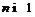 , и пусть
, и пусть 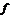 –
минимальный
–
минимальный  -значный спутник формации
-значный спутник формации  . Тогда справедливы следующие
утверждения: 1)
. Тогда справедливы следующие
утверждения: 1) 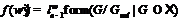 ; 2)
; 2) 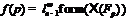 для
всех
для
всех 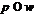 ; 3)
; 3) 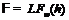 ,
спутник
,
спутник 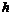 является
является 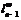 -значным
и
-значным
и 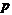 – некоторый фиксированный элемент из
– некоторый фиксированный элемент из  , то
, то 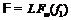 , где
, где
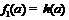 для всех
для всех 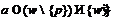 ,
, 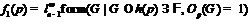 и, кроме того,
и, кроме того, 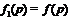 ;
4)
;
4) 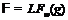 , где
, где 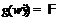 и
и 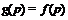 для всех
для всех 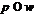 .
.
Лемма 10 [4]. Пусть 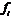 такой
внутренний
такой
внутренний  -кратно
-кратно  -локальный
спутник формации
-локальный
спутник формации 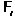 , что
, что 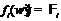 ,
,
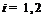 . Тогда
. Тогда 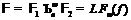 ,
где
,
где 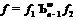 .
.
Лемма 11 [10]. Тогда и только тогда  является
минимальной
является
минимальной  -кратно
-кратно  -насыщенной
ненильпотентной формацией, когда
-насыщенной
ненильпотентной формацией, когда 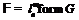 , где
, где 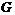 – такая монолитическая группа с цоколем
– такая монолитическая группа с цоколем
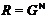 , что либо
, что либо 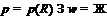 ,
либо
,
либо 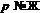 и выполняется одно из следующих условий:
и выполняется одно из следующих условий:
1) 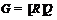 –
группа Шмидта с
–
группа Шмидта с 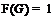 , где
, где 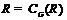 –
абелева
–
абелева 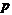 -группа,
-группа, 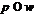 и
и 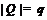 – простое число;
– простое число;
2) 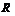 –
неабелева
–
неабелева 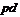 -группа,
-группа, 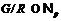 , где
, где
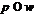 , причем, если
, причем, если 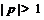 ,
то
,
то 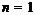 и
и 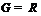 –
простая неабелева группа.
–
простая неабелева группа.
Лемма 12 [6]. Пусть 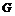 –
монолитическая группа с неабелевым монолитом
–
монолитическая группа с неабелевым монолитом 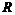 .
Тогда если простое число
.
Тогда если простое число 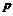 делит порядок группы
делит порядок группы
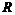 , то
, то 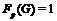 .
.
Лемма 13 [1, с. 26]. Пусть  –
произвольная непустая формация и пусть у каждой группы
–
произвольная непустая формация и пусть у каждой группы 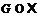
 -корадикал
-корадикал 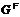 не
имеет фраттиниевых
не
имеет фраттиниевых 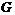 -главных факторов. Тогда если
-главных факторов. Тогда если 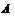 – монолитическая группа из
– монолитическая группа из 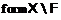 , то
, то 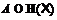 .
.
Лемма 14 [2, с.168]. Пусть  и
и 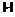 – формации, причем
– формации, причем 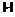 – локальна и
– локальна и 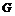 –
группа минимального порядка из
–
группа минимального порядка из 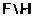 . Тогда
. Тогда 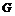 монолитична, ее монолит совпадает с
монолитична, ее монолит совпадает с 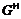 и если
и если 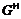 –
– 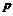 -группа, то
-группа, то 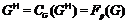 .
.
Лемма 15 [2, с.171]. Если в группе 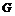 имеется
лишь одна минимальная нормальная подгруппа и
имеется
лишь одна минимальная нормальная подгруппа и 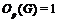 (
(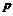 – некоторое простое число), то
существует точный неприводимый
– некоторое простое число), то
существует точный неприводимый 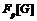 -модуль, где
-модуль, где 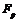 – поле из
– поле из 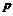 элементов.
элементов.
Лемма 16 [4]. Пусть  –
–  -насыщенная формация и
-насыщенная формация и 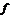 – ее
– ее  -локальный
спутник. Если
-локальный
спутник. Если  , то
, то 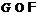 .
.
Лемма 17 [4]. Пусть 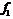 и
и 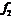 – минимальные
– минимальные  -локальные
-локальные
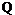 -значные спутники формаций
-значные спутники формаций 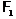 и
и 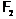 соответственно.
Тогда
соответственно.
Тогда 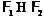 в том и только в том случае, когда
в том и только в том случае, когда 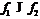 .
.
Лемма 18 [10]. Пусть 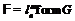 (
(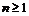 ), где
), где 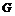 –
такая монолитическая группа с неабелевым монолитом
–
такая монолитическая группа с неабелевым монолитом 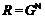 , что
, что
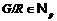 и
и 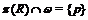 .
Тогда
.
Тогда  имеет единственную максимальную
имеет единственную максимальную 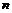 -кратно
-кратно 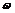 -насыщенную
подформацию
-насыщенную
подформацию  , причем
, причем 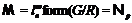 .
.
Основные результаты
Теорема 1. Пусть  –
–  -кратно
-кратно  -насыщенная
формация. Тогда в том и только в том случае
-насыщенная
формация. Тогда в том и только в том случае  -дефект
формации
-дефект
формации  равен 1, когда
равен 1, когда 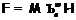 ,
где
,
где  –
–  -кратно
-кратно
 -насыщенная нильпотентная подформация
формации
-насыщенная нильпотентная подформация
формации  ,
, 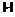 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная подформация формации
-насыщенная
ненильпотентная подформация формации  , при этом: 1) всякая
, при этом: 1) всякая
 -кратно
-кратно  -насыщенная
нильпотентная подформация из
-насыщенная
нильпотентная подформация из  входит в
входит в 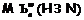 ; 2) всякая
; 2) всякая  -кратно
-кратно
 -насыщенная ненильпотентная подформация
-насыщенная ненильпотентная подформация 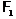 из
из  имеет
вид
имеет
вид 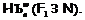
Доказательство. Необходимость. Пусть  -дефект формации
-дефект формации  равен 1. Так как
равен 1. Так как  не является нильпотентной
формацией, то по лемме 1 в
не является нильпотентной
формацией, то по лемме 1 в  входит некоторая
минимальная
входит некоторая
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная подформация
-насыщенная
ненильпотентная подформация 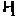 . По условию
. По условию 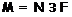 – максимальная
– максимальная  -кратно
-кратно
 -насыщенная подформация в
-насыщенная подформация в  . Значит,
. Значит, 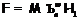 .
.
Достаточность. Пусть 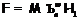 , где
, где
 –
–  -кратно
-кратно
 -насыщенная нильпотентная подформация
формации
-насыщенная нильпотентная подформация
формации  ,
, 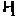 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная подформация
-насыщенная
ненильпотентная подформация  . Понятно, что
. Понятно, что 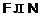 . Пусть
. Пусть  -дефекты
-дефекты
 -кратно
-кратно  -насыщенных
формаций
-насыщенных
формаций  ,
,  и
и 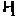 равны соответственно
равны соответственно 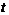 ,
, 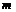 и
и  . Поскольку
. Поскольку  –
–  -кратно
-кратно  -насыщенная
нильпотентная подформация формации
-насыщенная
нильпотентная подформация формации  ,
то
,
то 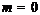 . Так как
. Так как 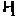 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная формация, то ее
-насыщенная
ненильпотентная формация, то ее  -дефект
-дефект  равен 1. В силу леммы 2 имеет место
неравенство
равен 1. В силу леммы 2 имеет место
неравенство 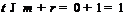 . Если
. Если 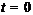 , то
, то  – нильпотентная формация, что
противоречит условию
– нильпотентная формация, что
противоречит условию 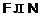 . Таким образом,
. Таким образом,  -дефект формации
-дефект формации  равен 1.
равен 1.
Докажем теперь справедливость
утверждения 1) второй части теоремы. Так как 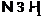 –
максимальная
–
максимальная  -кратно
-кратно  -насыщенная
подформация в
-насыщенная
подформация в 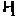 , то, в силу леммы 3, имеет
место решеточный изоморфизм
, то, в силу леммы 3, имеет
место решеточный изоморфизм
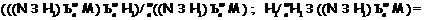
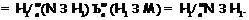
Следовательно, 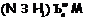 – максимальная
– максимальная  -кратно
-кратно
 -насыщенная подформация в
-насыщенная подформация в  . Тогда, поскольку
. Тогда, поскольку 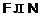 , то всякая
, то всякая  -кратно
-кратно
 -насыщенная нильпотентная подформация из
-насыщенная нильпотентная подформация из
 входит в
входит в 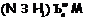 .
.
Докажем утверждение 2). Используя
лемму 4, получаем, что в формации  нет минимальных
нет минимальных  -кратно
-кратно  -насыщенных
ненильпотентных подформаций, отличных от
-насыщенных
ненильпотентных подформаций, отличных от 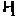 .
.
Пусть теперь 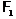 –
произвольная
–
произвольная  -кратно
-кратно  -насыщенная
ненильпотентная подформация из
-насыщенная
ненильпотентная подформация из  . Тогда в силу
уже доказанного и леммы 4 получаем, что
. Тогда в силу
уже доказанного и леммы 4 получаем, что 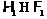 .
Следовательно, применяя лемму 3, получаем
.
Следовательно, применяя лемму 3, получаем 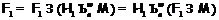 .
Теорема доказана.
.
Теорема доказана.
Теорема 2. Пусть  –
–  -приводимая формация,
-приводимая формация, 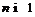 . Тогда и только тогда
. Тогда и только тогда  -дефект формации
-дефект формации  равен
2, когда
равен
2, когда  удовлетворяет одному из следующих
условий: 1)
удовлетворяет одному из следующих
условий: 1) 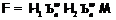 , где
, где 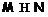 ,
,  и
и  –
различные минимальные
–
различные минимальные  -кратно
-кратно  -насыщенные ненильпотентные формации; 2)
-насыщенные ненильпотентные формации; 2)
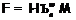 , где
, где  ,
,  –
–  -неприводимая
формация
-неприводимая
формация  -дефекта 2,
-дефекта 2,  , причем
если
, причем
если 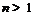 , то
, то 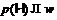 .
.
Доказательство. Заметим, что при 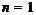 , справедливость утверждения теоремы
вытекает из теоремы 1.1 [5], а также теоремы 1 работы [11]. Поэтому мы можем считать,
что
, справедливость утверждения теоремы
вытекает из теоремы 1.1 [5], а также теоремы 1 работы [11]. Поэтому мы можем считать,
что 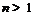 .
.
Необходимость. Пусть  -дефект
формации
-дефект
формации  равен 2,
равен 2, 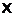 –
такая максимальная
–
такая максимальная  -кратно
-кратно  -насыщенная подформация формации
-насыщенная подформация формации  , что
, что  -дефект
формации
-дефект
формации 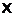 равен 1. По теореме 1 получаем
равен 1. По теореме 1 получаем 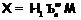 , где
, где 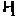 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная формация, а
-насыщенная
ненильпотентная формация, а 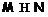 . Если в формации
. Если в формации  имеется еще одна минимальная
имеется еще одна минимальная  -кратно
-кратно  -насыщенная
ненильпотентная подформация
-насыщенная
ненильпотентная подформация 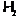 , отличная от
, отличная от 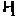 , то, в силу леммы 4,
, то, в силу леммы 4, 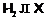 . Значит,
. Значит,
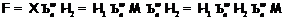
Пусть теперь в формации  нет отличных от
нет отличных от 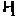 минимальных
минимальных  -кратно
-кратно
 -насыщенных ненильпотентных подформаций.
Поскольку
-насыщенных ненильпотентных подформаций.
Поскольку  –
–  -приводимая
формация, то в
-приводимая
формация, то в 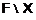 найдется такая группа
найдется такая группа 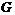 , что
, что 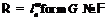 .
Понятно, что
.
Понятно, что 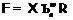 . Ввиду леммы 5
. Ввиду леммы 5  -дефект
формации
-дефект
формации  меньше или равен 2. Поскольку
меньше или равен 2. Поскольку 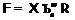 и
и  -дефект
формации
-дефект
формации 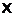 равен 1, то
равен 1, то  -дефект
формации
-дефект
формации  не равен 0. Допустим, что
не равен 0. Допустим, что  -дефект формации
-дефект формации  равен
1. Тогда по теореме 1 и предположению о единственности
равен
1. Тогда по теореме 1 и предположению о единственности 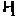 получаем,
что
получаем,
что 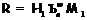 , где
, где 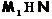 . Значит,
. Значит,
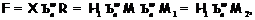 где
где  . Но
тогда в силу леммы 2
. Но
тогда в силу леммы 2  -дефект формации
-дефект формации  равен 1. Противоречие. Поэтому
равен 1. Противоречие. Поэтому  -дефект формации
-дефект формации  равен
2. Тогда
равен
2. Тогда  , так как иначе
, так как иначе 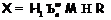 ,
что противоречит максимальности формации
,
что противоречит максимальности формации  в
формации
в
формации  . Таким образом,
. Таким образом, 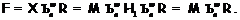
Предположим, что  –
–  -неприводимая
формация. Заметим, что если
-неприводимая
формация. Заметим, что если 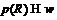 и
и  –
–  -насыщенная
формация, то
-насыщенная
формация, то  является насыщенной формацией.
Действительно, из
является насыщенной формацией.
Действительно, из  -насыщенности формации
-насыщенности формации  получаем, что для любой группы
получаем, что для любой группы 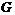 из условия
из условия 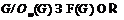 следует,
что
следует,
что 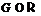 . Но
. Но 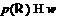 .
Значит,
.
Значит, 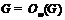 . Тогда получаем, что из условия
. Тогда получаем, что из условия 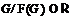 следует, что
следует, что 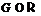 .
Таким образом,
.
Таким образом,  является насыщенной
формацией. Ввиду леммы 6 всякая
является насыщенной
формацией. Ввиду леммы 6 всякая  -кратно насыщенная
формация, имеющая нильпотентный дефект 2, приводима. В этом случае
-кратно насыщенная
формация, имеющая нильпотентный дефект 2, приводима. В этом случае  – приводимая
– приводимая  -кратно
насыщенная формация. Противоречие. Поэтому
-кратно
насыщенная формация. Противоречие. Поэтому 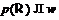 .
Тогда получаем, что формация
.
Тогда получаем, что формация  удовлетворяет
условию 2).
удовлетворяет
условию 2).
Пусть теперь  –
–
 -приводимая формация. Воспользуемся
индукцией по числу разрешимых
-приводимая формация. Воспользуемся
индукцией по числу разрешимых  -кратно
-кратно  -насыщенных подформаций однопорожденной
формации
-насыщенных подформаций однопорожденной
формации  .
.
Обозначим через 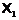 максимальную
максимальную  -кратно
-кратно
 -насыщенную подформацию формации
-насыщенную подформацию формации  , имеющую
, имеющую  -дефект,
равный 1. Так как
-дефект,
равный 1. Так как  –
–  -приводимая
формация, то в
-приводимая
формация, то в 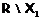 существует такая группа
существует такая группа 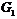 , что
, что 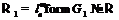 .
Ввиду максимальности формации
.
Ввиду максимальности формации 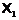 в формации
в формации  справедливо
справедливо 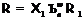 . По
теореме 1 и предположению единственности
. По
теореме 1 и предположению единственности 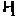 получаем,
что
получаем,
что 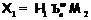 , где
, где 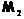 –
некоторая нильпотентная
–
некоторая нильпотентная  -кратно
-кратно  -насыщенная подформация формации
-насыщенная подформация формации 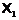 .
.
Тогда 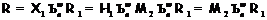 .
Заметим, что повторяя приведенные выше рассуждения для
.
Заметим, что повторяя приведенные выше рассуждения для  ,
получаем, что либо формация
,
получаем, что либо формация 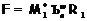 (где
(где 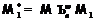 ) удовлетворяет условию 2), и
необходимость доказана, либо формация
) удовлетворяет условию 2), и
необходимость доказана, либо формация 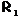 является
является
 -приводимой формацией
-приводимой формацией  -дефекта 2. Понятно, что
-дефекта 2. Понятно, что 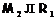 , так как иначе
, так как иначе 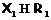 ,
что противоречит максимальности формации
,
что противоречит максимальности формации 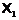 в
в 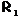 .
.
Поскольку 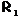 –
собственная
–
собственная  -кратно
-кратно  -насыщенная
подформация формации
-насыщенная
подформация формации  , то число разрешимых подформаций
формации
, то число разрешимых подформаций
формации 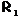 меньше чем у
меньше чем у  .
Ввиду замечания 3 [4] в однопорожденной формации
.
Ввиду замечания 3 [4] в однопорожденной формации  имеется
лишь конечное множество разрешимых
имеется
лишь конечное множество разрешимых  -кратно
-кратно  -насыщенных подформаций. Поэтому,
повторяя описанные выше действия, через конечное число шагов мы придем к
ситуации, когда либо формация
-насыщенных подформаций. Поэтому,
повторяя описанные выше действия, через конечное число шагов мы придем к
ситуации, когда либо формация 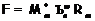 (где
(где 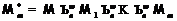 ) удовлетворяет условию 2) и
необходимость доказана, либо
) удовлетворяет условию 2) и
необходимость доказана, либо 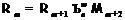 , где
, где 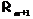 –
–  -приводимая
формация
-приводимая
формация  -дефекта 2,
-дефекта 2, 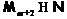 –
наименьшая неединичная разрешимая подформация формации
–
наименьшая неединичная разрешимая подформация формации  ,
такая что
,
такая что 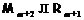 .
.
Обозначим через 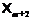 максимальную
максимальную  -кратно
-кратно
 -насыщенную подформацию формации
-насыщенную подформацию формации 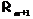 , имеющую нильпотентный
, имеющую нильпотентный  -дефект, равный 1. Так как
-дефект, равный 1. Так как 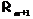 –
–  -приводимая
формация, то в
-приводимая
формация, то в 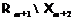 существует такая группа
существует такая группа 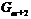 , что
, что 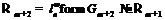 .
Ввиду максимальности формации
.
Ввиду максимальности формации 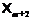 в формации
в формации 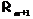 справедливо
справедливо 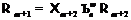 . По
теореме 1 и предположению единственности
. По
теореме 1 и предположению единственности 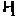 получаем,
что
получаем,
что 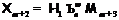 , где
, где 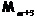 –
некоторая нильпотентная
–
некоторая нильпотентная  -кратно
-кратно  -насыщенная подформация формации
-насыщенная подформация формации 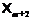 . Тогда
. Тогда
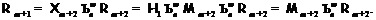
Но 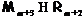 по
предположению индукции. Следовательно, формация
по
предположению индукции. Следовательно, формация 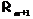 не
может быть
не
может быть  -приводимой формацией. Значит,
-приводимой формацией. Значит, 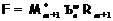 , где
, где 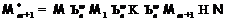 ,
, 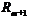 –
–  -неприводимая
формация
-неприводимая
формация  -дефекта 2. Необходимость доказана.
-дефекта 2. Необходимость доказана.
Достаточность. Пусть 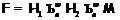 ,
где
,
где 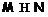 ,
, 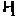 и
и 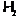 – различные минимальные
– различные минимальные  -кратно
-кратно  -насыщенные
ненильпотентные формации. Пусть
-насыщенные
ненильпотентные формации. Пусть 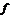 ,
, 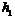 ,
, 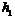 и
и 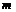
 -дефекты
формаций
-дефекты
формаций  ,
, 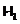 ,
, 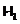 и
и  соответственно.
Тогда по лемме 2
соответственно.
Тогда по лемме 2  -дефект формации
-дефект формации  не превосходит
не превосходит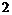 .
С другой стороны по лемме 5
.
С другой стороны по лемме 5  -дефект формации
-дефект формации  больше либо равен
больше либо равен 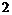 . Таким образом,
. Таким образом,  -дефект
формации
-дефект
формации  равен 2.
равен 2.
Аналогично рассматривается случай,
когда 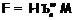 , где
, где 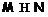 ,
, 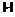 –
–  -неприводимая
формация
-неприводимая
формация  -дефекта 2. Теорема доказана.
-дефекта 2. Теорема доказана.
Теорема 3. Пусть  –
–  -кратно
-кратно  -насыщенная
формация
-насыщенная
формация 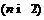 . Тогда и только тогда формации
. Тогда и только тогда формации  –
–  -неприводимая
формация
-неприводимая
формация  -дефекта 2, когда
-дефекта 2, когда 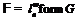 , где
, где 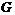 –
такая монолитическая группа с цоколем
–
такая монолитическая группа с цоколем 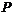 , что
выполняется одно из следующих условий:
, что
выполняется одно из следующих условий:
1) 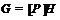 , где
, где
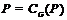 –
– 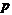 -группа,
-группа,
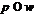 , а
, а  –
группа, удовлетворяющая одному из следующих условий:
–
группа, удовлетворяющая одному из следующих условий:
1.1) циклическая примарная группа
порядка 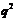
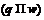 ;
;
1.2) неабелева группа порядка 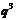 простой нечетной экспоненты
простой нечетной экспоненты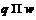 ;
;
1.3) монолитическая группа с цоколем 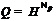 и
и 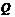 –
– 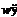 -группа;
-группа;
2) 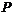 –
неабелева группа,
–
неабелева группа, 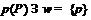 , а группа
, а группа 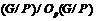 удовлетворяет одному из следующих
условий:
удовлетворяет одному из следующих
условий:
2.1) 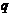 -группа,
где
-группа,
где 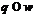 ;
;
2.2) элементарная абелева 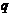 -группа,
-группа, 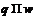 ;
;
2.3) подпрямое произведение групп
изоморфных 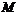 , где
, где 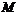 –
такая монолитическая группа с цоколем
–
такая монолитическая группа с цоколем  , что
, что
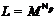 – неабелева группа,
– неабелева группа, 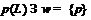 ;
;
3) 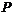 –
– 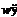 -группа, формация
-группа, формация  имеет
имеет  -дефект 1,
-дефект 1, 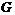 –
–  -базисная
группа, где
-базисная
группа, где 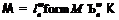 ,
, 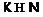 , а
, а 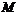 – такая монолитическая группа с цоколем
– такая монолитическая группа с цоколем
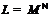 , что выполнено одно из следующих
условий:
, что выполнено одно из следующих
условий:
3.1) 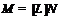 –
группа Шмидта с
–
группа Шмидта с 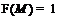 , где
, где 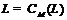 –
абелева
–
абелева 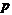 -группа,
-группа, 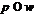 и
и 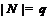 – простое число,
– простое число,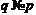 ;
;
3.2) 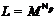 –
неабелева группа, причем
–
неабелева группа, причем 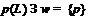 ;
;
3.3)  –
– 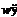 -группа.
-группа.
Доказательство.
Необходимость. Пусть
 –
–  -неприводимая
формация
-неприводимая
формация  -дефекта 2,
-дефекта 2,  –
максимальная
–
максимальная  -кратно
-кратно  -насыщенная
подформация формации
-насыщенная
подформация формации  с каноническим спутником
с каноническим спутником 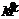 . Заметим, что ввиду леммы 7 спутник
. Заметим, что ввиду леммы 7 спутник 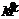 является
является  -кратно
-кратно
 -локальным. Тогда
-локальным. Тогда  является минимальной
является минимальной  -кратно
-кратно  -насыщенной
не
-насыщенной
не  -формацией. Пусть
-формацией. Пусть 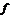 и
и 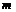 –
минимальные
–
минимальные  -кратно
-кратно  -локальные
спутники формаций
-локальные
спутники формаций  и
и  соответственно.
В силу замечания 2 [4] имеем
соответственно.
В силу замечания 2 [4] имеем 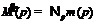 , для всех
, для всех 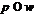 .
.
Применяя лемму 8, получим,
что 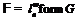 , где
, где 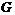 –
такая монолитическая группа с цоколем
–
такая монолитическая группа с цоколем 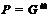 , что
либо
, что
либо  (,
(, 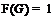 и
и 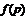 –
– 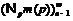 -критическая
формация для всех
-критическая
формация для всех 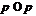 , либо
, либо 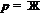 и
и
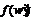 –
– 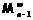 -критическая
формация. По теореме 1
-критическая
формация. По теореме 1 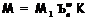 , где
, где 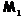 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
ненильпотентная подформация формации
-насыщенная
ненильпотентная подформация формации  ,
, 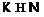 .
.
Предположим, что 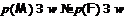 . Тогда найдется простое число
. Тогда найдется простое число 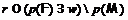 . Пусть
. Пусть 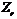 –
группа порядка
–
группа порядка  . Тогда
. Тогда 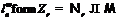 . Так как
. Так как  –
максимальная
–
максимальная  -кратно
-кратно  -насыщенная
подформация формации
-насыщенная
подформация формации  и
и 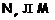 , то
, то 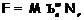 . Но формация
. Но формация  является
является
 -неприводимой по условию теоремы.
Противоречие. Следовательно,
-неприводимой по условию теоремы.
Противоречие. Следовательно, 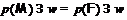 .
.
Пусть 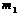 и
и 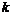 –
минимальные
–
минимальные  -кратно
-кратно  -локальные
спутники формаций
-локальные
спутники формаций 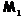 и
и 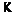 соответственно.
По лемме 9 формации
соответственно.
По лемме 9 формации 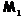 и
и 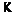 имеют
такие внутренние
имеют
такие внутренние  -кратно
-кратно  -локальные спутники
-локальные спутники  и
и 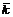 ,
принимающие соответственно значения
,
принимающие соответственно значения 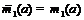 , при
, при 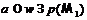 ,
, 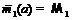 , при
, при
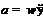 ,
, 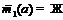 , при
, при
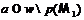 , и
, и 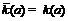 , при
, при
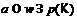 ,
,  , при
, при
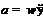 ,
, 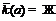 , при
, при
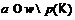 . Ввиду леммы 10 справедливо равенство
. Ввиду леммы 10 справедливо равенство 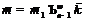 .
.
В силу леммы 11 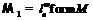 , где
, где 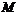 –
такая монолитическая группа с цоколем
–
такая монолитическая группа с цоколем 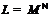 , что
либо
, что
либо 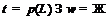 , либо
, либо 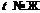 и
выполняется одно из следующих условий:
и
выполняется одно из следующих условий:
(1) 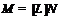 –группа Шмидта с
–группа Шмидта с 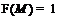 , где
, где 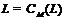 –
абелева
–
абелева 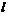 -группа,
-группа, 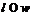 и
и 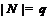 – простое число;
– простое число;
(2)  – неабелева
– неабелева 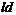 -группа
-группа
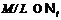 , где
, где 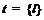 .
.
Заметим, что если 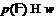 , то любая
, то любая  -насыщенная
подформация из
-насыщенная
подформация из  является насыщенной.
Следовательно, любая
является насыщенной.
Следовательно, любая  -кратно
-кратно  -насыщенная подформация формации
-насыщенная подформация формации  является
является  -кратно
насыщенной. По лемме 6 при
-кратно
насыщенной. По лемме 6 при 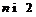 всякая
всякая  -кратно насыщенная формация с
-кратно насыщенная формация с  -дефектом 2 приводима. Поэтому при
-дефектом 2 приводима. Поэтому при 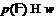 формация
формация  не
может быть
не
может быть  -неприводимой формацией,
что противоречит условию. Таким образом,
-неприводимой формацией,
что противоречит условию. Таким образом, 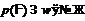 .
.
Допустим, что 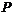 – неабелев цоколь группы
– неабелев цоколь группы 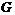 . Пусть
. Пусть  и
и 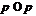 . Тогда по лемме 12 имеем
. Тогда по лемме 12 имеем 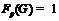 . Значит,
. Значит, 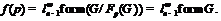
Пусть для формации 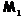 выполнено условие (1). Предположим, что
выполнено условие (1). Предположим, что
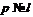 . Так как
. Так как 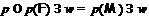 , то
имеем
, то
имеем 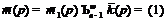 . Тогда
. Тогда 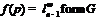 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
не
-насыщенная
не 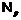 -формация. Значит,
-формация. Значит, 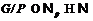 ,
, 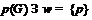 и
и  -дефект формации
-дефект формации  равен
1 по лемме 11. Противоречие. Поэтому
равен
1 по лемме 11. Противоречие. Поэтому 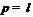 .
Используя лемму 9, имеем
.
Используя лемму 9, имеем
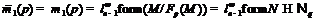 .
.
Следовательно, 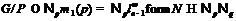 .
.
Покажем, что 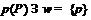 . Действительно, если
. Действительно, если 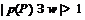 , то найдется такое
, то найдется такое 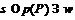 , что
, что 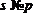 .
Поскольку
.
Поскольку 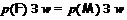 , то
, то 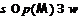 . Тогда
. Тогда
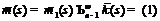 . Так как
. Так как 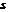 делит
порядок
делит
порядок 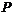 , то по лемме 12 имеем
, то по лемме 12 имеем 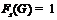 . Тогда
. Тогда 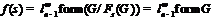 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
не
-насыщенная
не 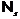 -формация. Поскольку
-формация. Поскольку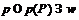 и
и 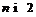 , то
, то 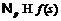 . Так как при этом
. Так как при этом 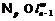 и
и 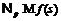 , то
, то 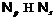 . Но
. Но 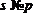 .
Противоречие. Поэтому
.
Противоречие. Поэтому 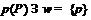 .
.
По лемме 9 имеем 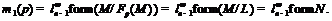 Следовательно,
Следовательно, 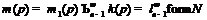 и
и
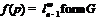 является минимальной
является минимальной  -кратно
-кратно  -насыщенной
не
-насыщенной
не 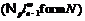 -формацией.
-формацией.
Ясно также, что 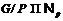 , поскольку в противном случае
, поскольку в противном случае  -дефект формации
-дефект формации  равен
1 в силу леммы 11.
равен
1 в силу леммы 11.
Если 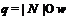 , то
, то 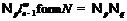 .
Значит,
.
Значит, 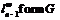 является минимальной
является минимальной  -кратно
-кратно  -насыщенной
не
-насыщенной
не 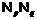 -формацией. Поэтому
-формацией. Поэтому 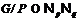 . Значит,
. Значит, 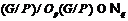 , и
формация
, и
формация  удовлетворяет условию 2.1) теоремы.
удовлетворяет условию 2.1) теоремы.
Если 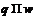 , то
, то 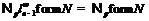 .
Тогда
.
Тогда 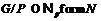 . Так как
. Так как 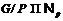 , то
, то 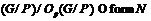 , т.е.
, т.е. 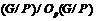 является
элементарной абелевой
является
элементарной абелевой 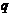 -группой, и формация
-группой, и формация  удовлетворяет условию 2.2) теоремы.
удовлетворяет условию 2.2) теоремы.
Пусть для формации 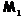 выполнено условие (2). Покажем, что
выполнено условие (2). Покажем, что 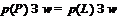 . Предположим, что существует
. Предположим, что существует 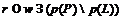 . Тогда
. Тогда 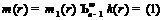 .
Значит,
.
Значит, 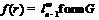 – минимальная
– минимальная  -кратно
-кратно
 -насыщенная не
-насыщенная не 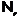 -формация.
Последнее невозможно, так как
-формация.
Последнее невозможно, так как 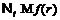 . Поэтому
. Поэтому 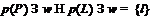 . Но
. Но 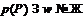 .
Следовательно,
.
Следовательно, 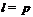 .
.
Ввиду леммы 12, 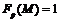 . Так как
. Так как 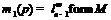 , то
, то
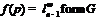 – минимальная не
– минимальная не 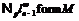 -формация. Значит,
-формация. Значит, 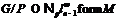 . Но, как нетрудно показать,
. Но, как нетрудно показать, 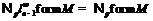 . Если
. Если 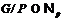 , то
по лемме 11
, то
по лемме 11  -дефект формации
-дефект формации  равен
1. Противоречие. Следовательно,
равен
1. Противоречие. Следовательно, 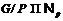 и
и 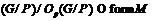 . Но тогда
. Но тогда 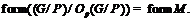 Так
как при этом группа
Так
как при этом группа 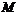 является монолитической
группой с неабелевым цоколем
является монолитической
группой с неабелевым цоколем  , то применяя лемму 13
получим, что
, то применяя лемму 13
получим, что 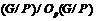 – подпрямое произведение групп
изоморфных группе
– подпрямое произведение групп
изоморфных группе 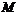 . Таким образом, группа
. Таким образом, группа 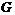 удовлетворяет условию 2.3) теоремы.
удовлетворяет условию 2.3) теоремы.
Пусть теперь 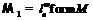 – такая формация, что
– такая формация, что 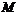 – монолитическая группа с цоколем
– монолитическая группа с цоколем 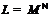 ,
, 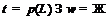 .
Так как
.
Так как 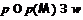 , то
, то 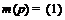 . Но
тогда
. Но
тогда 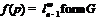 – минимальная
– минимальная  -кратно
-кратно
 -насыщенная не
-насыщенная не 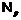 -формация.
Значит,
-формация.
Значит, 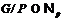 и по лемме 11 получаем, что
и по лемме 11 получаем, что  -дефект формации
-дефект формации  равен
1. Противоречие. Таким образом, данный случай невозможен.
равен
1. Противоречие. Таким образом, данный случай невозможен.
Пусть 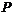 – абелева
– абелева 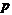 -группа,
-группа,
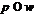 . Тогда по лемме 14 имеем
. Тогда по лемме 14 имеем 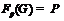 . Пусть формация
. Пусть формация 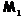 удовлетворяет
условию (1).
удовлетворяет
условию (1).
Предположим, что 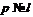 . Тогда
. Тогда 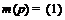 .
Значит,
.
Значит, 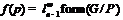 – минимальная
– минимальная  -кратно
-кратно
 -насыщенная не
-насыщенная не 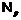 -формация.
Пусть
-формация.
Пусть  – группа минимального порядка из
– группа минимального порядка из 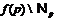 . Тогда
. Тогда  является
монолитической группой с цоколем
является
монолитической группой с цоколем 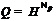 . Ясно, что
. Ясно, что 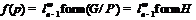 и
и 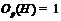 .
Применяя лемму 15, получаем, что существует точный неприводимый
.
Применяя лемму 15, получаем, что существует точный неприводимый 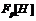 -модуль
-модуль 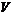 .
Обозначим через
.
Обозначим через 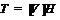 . Ввиду леммы 16 группа
. Ввиду леммы 16 группа 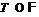 . Так как
. Так как 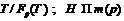 , то
, то
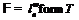 . Поскольку
. Поскольку  и
формация
и
формация  разрешима, то
разрешима, то 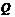 –
абелева
–
абелева  -группа для некоторого простого числа
-группа для некоторого простого числа 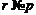 . Но
. Но 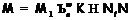 .
Если
.
Если 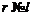 , то группа
, то группа  нильпотентна.
Поскольку
нильпотентна.
Поскольку 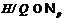 , то
, то 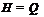 –
группа простого порядка
–
группа простого порядка  . Но тогда по лемме
11 получаем, что
. Но тогда по лемме
11 получаем, что  -дефект формации
-дефект формации  равен 1. Противоречие. Поэтому
равен 1. Противоречие. Поэтому 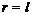 . Так как при этом
. Так как при этом 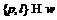 , то
, то 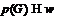 , что
невозможно. Поэтому
, что
невозможно. Поэтому 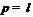 .
.
Но тогда 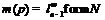 и
и 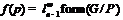 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
не
-насыщенная
не 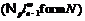 -формация.
-формация.
Рассмотрим группу 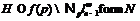 . Тогда
. Тогда  является
монолитической группой с цоколем
является
монолитической группой с цоколем 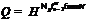 . Поскольку
. Поскольку 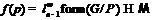 и формация
и формация  разрешима,
то
разрешима,
то 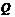 – абелева
– абелева  -группа
для некоторого простого числа
-группа
для некоторого простого числа  . Ясно, что
. Ясно, что 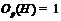 . Применяя лемму 15, получаем, что существует
точный неприводимый
. Применяя лемму 15, получаем, что существует
точный неприводимый 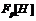 -модуль
-модуль 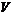 . Обозначим через
. Обозначим через 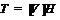 . Ввиду леммы 16 группа
. Ввиду леммы 16 группа 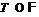 . Так как
. Так как 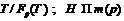 , то
, то
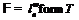 . Но
. Но 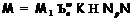 .
Значит,
.
Значит, 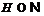 . Но
. Но  – монолитическая
группа. Значит,
– монолитическая
группа. Значит,  –
–  -группа.
Если
-группа.
Если 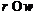 , то
, то 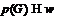 , что
невозможно. Значит,
, что
невозможно. Значит, 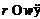 . Если
. Если 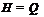 ,
то по лемме 11
,
то по лемме 11  -дефект формации
-дефект формации  равен 1. Противоречие. Следовательно,
равен 1. Противоречие. Следовательно, 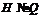 . Поскольку
. Поскольку 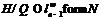 , то
, то
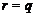 . Таким образом,
. Таким образом, 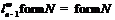 и
и
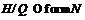 . Тогда
. Тогда 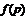 –
минимальная не
–
минимальная не 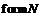 -формация. Поскольку группа
-формация. Поскольку группа  нильпотентна, то любая собственная
подгруппа из
нильпотентна, то любая собственная
подгруппа из  принадлежит
принадлежит 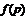 .
Таким образом,
.
Таким образом,  – минимальная не
– минимальная не 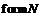 -группа. Так как при этом
-группа. Так как при этом  –
– 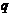 -группа,
то
-группа,
то  либо циклическая примарная группа
порядка
либо циклическая примарная группа
порядка 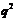 , либо неабелева группа порядка
, либо неабелева группа порядка 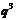 простой нечетной экспоненты
простой нечетной экспоненты 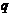 . Но тогда группа
. Но тогда группа 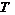 удовлетворяет условию 1.1) или 1.2) теоремы.
удовлетворяет условию 1.1) или 1.2) теоремы.
Пусть для формации 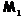 выполнено условие (2). Допустим, что
выполнено условие (2). Допустим, что 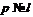 . Тогда
. Тогда 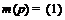 . Значит,
. Значит,
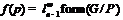 – минимальная
– минимальная  -кратно
-кратно
 -насыщенная не
-насыщенная не 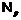 -формация.
Поскольку
-формация.
Поскольку 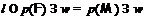 , то
, то 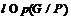 . Так
как при этом
. Так
как при этом 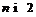 , то
, то 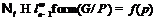 .
Если
.
Если 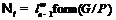 , то
, то 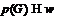 , что
невозможно. Значит,
, что
невозможно. Значит, 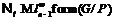 . Но
. Но 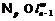 .
Следовательно,
.
Следовательно, 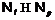 . Противоречие. Таким образом,
. Противоречие. Таким образом,
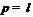 .
.
Тогда 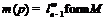 и
и 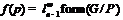 –
минимальная
–
минимальная  -кратно
-кратно  -насыщенная
не
-насыщенная
не 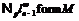 -формация. Выберем в
-формация. Выберем в 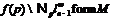 группу
группу  минимального
порядка. Тогда
минимального
порядка. Тогда  – монолитическая группа с
цоколем
– монолитическая группа с
цоколем 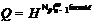 и
и 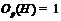 .
Применяя лемму 15, получаем, что существует точный неприводимый
.
Применяя лемму 15, получаем, что существует точный неприводимый 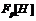 -модуль
-модуль 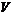 .
Обозначим через
.
Обозначим через 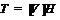 . Ввиду леммы 16 группа
. Ввиду леммы 16 группа 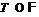 . Так как
. Так как 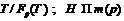 , то
, то
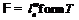 . Предположим, что
. Предположим, что 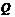 – неабелев цоколь группы
– неабелев цоколь группы  . Ввиду того, что
. Ввиду того, что 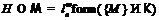 и
и
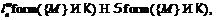 то
то
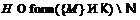 . Следовательно, по лемме 13 имеем
. Следовательно, по лемме 13 имеем 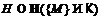 . Поскольку
. Поскольку 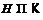 и
и 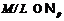 , то группа
, то группа  изоморфна
группе
изоморфна
группе 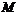 . Но тогда
. Но тогда 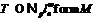 .
Однако
.
Однако  . Поэтому
. Поэтому 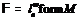 и
и  -дефект формации
-дефект формации  равен
1. Противоречие. Следовательно,
равен
1. Противоречие. Следовательно, 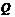 – абелева
– абелева 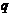 -группа, для некоторого простого числа
-группа, для некоторого простого числа 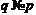 . Допустим, что
. Допустим, что 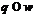 .
Пусть
.
Пусть 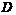 – группа порядка
– группа порядка 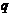 . Тогда
. Тогда 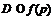 .
Пусть
.
Пусть 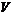 – точный неприводимый
– точный неприводимый 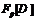 -модуль и
-модуль и 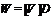 .
Применяя лемму 16, получим
.
Применяя лемму 16, получим 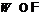 . Ввиду леммы 11
формация
. Ввиду леммы 11
формация 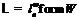 имеет
имеет  -дефект
1. Поскольку
-дефект
1. Поскольку 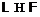 и
и 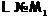 , то
мы получаем противоречие с леммой 5. Значит,
, то
мы получаем противоречие с леммой 5. Значит, 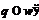 . Поскольку
. Поскольку
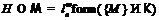 и
и
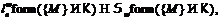 то
то
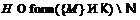 . Следовательно, по лемме 13 имеем
. Следовательно, по лемме 13 имеем 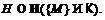 Так как
Так как 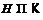 и
и 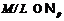 , то группа
, то группа  изоморфна
группе
изоморфна
группе 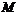 . Но
. Но  – неабелева
– неабелева
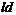 -группа. Противоречие. Следовательно, данный
случай невозможен.
-группа. Противоречие. Следовательно, данный
случай невозможен.
Пусть формация 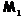 такая, что
такая, что 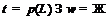 .
Так как
.
Так как 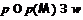 , то
, то 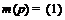 . Но
тогда
. Но
тогда 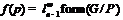 – минимальная
– минимальная  -кратно
-кратно
 -насыщенная не
-насыщенная не 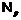 -формация.
Пусть
-формация.
Пусть  – группа минимального порядка из
– группа минимального порядка из 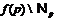 . Тогда
. Тогда  является
монолитической группой с цоколем
является
монолитической группой с цоколем 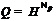 . Понятно, что
. Понятно, что 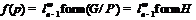 и
и 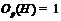 .
Применяя лемму 15 получаем, что существует точный неприводимый
.
Применяя лемму 15 получаем, что существует точный неприводимый 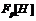 -модуль
-модуль 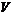 .
Обозначим через
.
Обозначим через 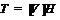 . Ввиду леммы 16 группа
. Ввиду леммы 16 группа 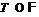 . Так как
. Так как 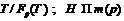 , то
, то
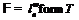 .
.
Пусть 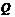 – абелева
– абелева 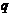 -группа
для некоторого простого числа
-группа
для некоторого простого числа 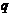 . Если
. Если 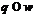 , то
, то 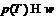 .
Противоречие. Значит,
.
Противоречие. Значит, 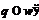 . Кроме того, понятно, что
. Кроме того, понятно, что 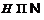 . Так как в противном случае
. Так как в противном случае 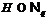 и по лемме 11 формация
и по лемме 11 формация 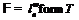 имеет
имеет  -дефект
1, что невозможно. Поскольку
-дефект
1, что невозможно. Поскольку 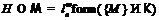 и
и 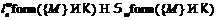 , то
, то 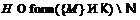 .
Тогда по лемме 13 получим, что
.
Тогда по лемме 13 получим, что 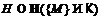 . Так как
. Так как 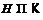 и
и 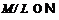 , то
группа
, то
группа  изоморфна группе
изоморфна группе 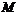 .
.
Пусть 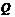 – неабелев цоколь группы
– неабелев цоколь группы  . Тогда так как
. Тогда так как 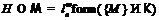 и
и
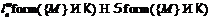 , то
, то 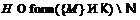 .
Применяя теперь лемму 13, заключаем, что
.
Применяя теперь лемму 13, заключаем, что 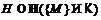 .
Так как
.
Так как  и
и 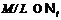 получаем,
ввиду монолитичности
получаем,
ввиду монолитичности  , что группы
, что группы  и
и 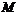 изоморфны.
изоморфны.
Кроме того, заметим, что 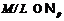 . Поскольку иначе найдется группа
. Поскольку иначе найдется группа 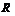 простого порядка
простого порядка 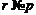 , такая, что
, такая, что 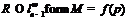 .
Пусть
.
Пусть 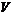 – точный неприводимый
– точный неприводимый 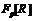 -модуль и
-модуль и 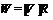 .
Применяя лемму 16, получим
.
Применяя лемму 16, получим 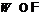 . Ввиду леммы 11
формация
. Ввиду леммы 11
формация 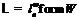 имеет
имеет  -дефект
1. Поскольку
-дефект
1. Поскольку 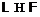 и
и 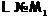 , то
мы получаем противоречие с леммой 5. Значит,
, то
мы получаем противоречие с леммой 5. Значит, 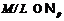 .
Таким образом, группа
.
Таким образом, группа 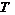 удовлетворяет условию 1.3) теоремы.
удовлетворяет условию 1.3) теоремы.
Пусть теперь 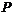 –
– 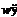 -группа
и пусть формация
-группа
и пусть формация 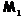 удовлетворяет условию (1) или
(2). Тогда
удовлетворяет условию (1) или
(2). Тогда 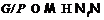 или, соответственно,
или, соответственно,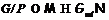 . Если
. Если  , то
, то  или
или  . Но
. Но  –
– 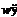 -группа.
Значит,
-группа.
Значит, 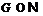 . Противоречие. Поэтому
. Противоречие. Поэтому 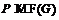 . Но тогда
. Но тогда 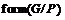 –
единственная максимальная подформация
–
единственная максимальная подформация  и
и 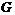 –
–  -базисная
группа. Если
-базисная
группа. Если 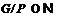 , то по лемме 11 формация
, то по лемме 11 формация  имеет
имеет  -дефект
1. Противоречие. Значит,
-дефект
1. Противоречие. Значит, 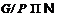 . Так как при этом,
. Так как при этом, 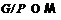 , то
, то  -дефект
формации
-дефект
формации 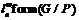 равен 1. Значит,
равен 1. Значит, 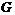 удовлетворяет условию 3.1) или 3.2)
теоремы.
удовлетворяет условию 3.1) или 3.2)
теоремы.
Пусть теперь для формации
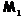 выполняется условие
выполняется условие 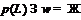 . Тогда по лемме 8
. Тогда по лемме 8 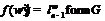 – минимальная
– минимальная  -кратно
-кратно
 -насыщенная не
-насыщенная не  -формация.
Снова применяя лемму 8, получим, что
-формация.
Снова применяя лемму 8, получим, что 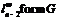 –
– 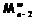 -критическая формация, …,
-критическая формация, …,  – минимальная не
– минимальная не  -формация и
-формация и 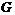 –
–  -базисная группа. Если
-базисная группа. Если 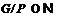 , то по лемме 11 формация
, то по лемме 11 формация  имеет
имеет  -дефект
1. Противоречие. Значит,
-дефект
1. Противоречие. Значит, 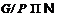 . Так как при этом,
. Так как при этом, 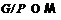 , то
, то  -дефект
формации
-дефект
формации 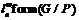 равен 1. Таким образом, группа
равен 1. Таким образом, группа 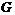 удовлетворяет условию 3.3) теоремы.
удовлетворяет условию 3.3) теоремы.
Достаточность. Пусть для формации  выполнено условие 1) теоремы и
выполнено условие 1) теоремы и  – циклическая примарная группа порядка
– циклическая примарная группа порядка 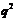 ,
, 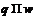 .
Пусть
.
Пусть 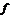 – минимальный
– минимальный  -кратно
-кратно
 -локальный спутник формации
-локальный спутник формации  . По лемме 14 имеем
. По лемме 14 имеем 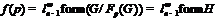 . Так как
. Так как 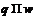 , то
, то 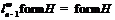 . Заметим, что
. Заметим, что 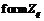 является
единственной максимальной подформацией формации
является
единственной максимальной подформацией формации 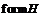 , где
, где
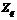 – группа порядка
– группа порядка 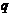 .
.
Построим  -кратно
-кратно  -локальный
спутник
-локальный
спутник 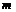 , принимающий следующие значения
, принимающий следующие значения 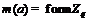 , при
, при 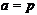 ,
, 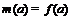 , при
, при 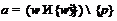 . Рассмотрим
. Рассмотрим
 -кратно
-кратно  -насыщенную
формацию
-насыщенную
формацию 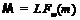 . Пусть
. Пусть 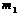 –
минимальный
–
минимальный  -кратно
-кратно  -локальный
спутник формации
-локальный
спутник формации  . Тогда так как
. Тогда так как 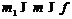 , то, ввиду леммы 17,
, то, ввиду леммы 17, 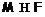 .
.
Пусть 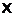 – произвольная собственная
– произвольная собственная  -кратно
-кратно  -насыщенная
подформация формации
-насыщенная
подформация формации  . И пусть
. И пусть 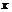 – минимальный
– минимальный  -кратно
-кратно
 -локальный спутник формации
-локальный спутник формации 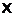 . Если
. Если 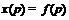 , то
так как
, то
так как 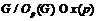 , получаем
, получаем 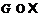 .
Следовательно,
.
Следовательно, 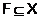 . Противоречие. Значит,
. Противоречие. Значит, 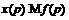 . Тогда, так как
. Тогда, так как 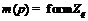 –
единственная максимальная подформация
–
единственная максимальная подформация 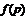 , то
, то 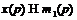 и
и 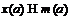 для
для 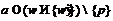 , т.е.
, т.е. 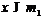 . По
лемме 17 получаем, что
. По
лемме 17 получаем, что 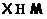 . Таким образом,
. Таким образом,  – единственная максимальная
– единственная максимальная  -кратно
-кратно  -насыщенная
подформация формации
-насыщенная
подформация формации  , т.е.
, т.е.  является
является
 -неприводимой формацией.
-неприводимой формацией.
Поскольку 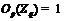 , то ввиду леммы 15 существует точный
неприводимый
, то ввиду леммы 15 существует точный
неприводимый 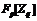 -модуль
-модуль 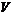 , где
, где
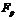 – поле из
– поле из 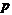 элементов.
Пусть
элементов.
Пусть 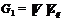 . Тогда, так как
. Тогда, так как 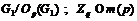 ,
то, ввиду леммы 16,
,
то, ввиду леммы 16, 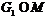 . Если предположить, что
. Если предположить, что 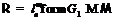 , то по лемме 17 получаем
, то по лемме 17 получаем 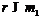 , где
, где  –
минимальный
–
минимальный  -кратно
-кратно  -насыщенный
спутник формации
-насыщенный
спутник формации  . Но тогда
. Но тогда 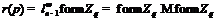 . Противоречие. Значит,
. Противоречие. Значит, 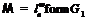 , т.е. формация
, т.е. формация  порождается
группой Шмидта и имеет нильпотентный
порождается
группой Шмидта и имеет нильпотентный  -дефект 1. Но тогда
-дефект 1. Но тогда  -дефект формации
-дефект формации  равен
2.
равен
2.
Случаи, когда  – неабелева группа порядка
– неабелева группа порядка 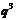 простой нечетной экспоненты
простой нечетной экспоненты 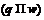 , и
, и  –
монолитическая группа с цоколем
–
монолитическая группа с цоколем 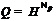 , где
, где 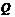 –
– 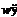 -группа,
рассматриваются аналогично.
-группа,
рассматриваются аналогично.
Пусть для формации  выполнено условие 2) теоремы. Построим
выполнено условие 2) теоремы. Построим  -значный
-значный  -локальный
спутник
-локальный
спутник 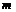 , принимающий следующие значения:
, принимающий следующие значения: 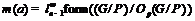 , при
, при 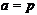 ,
, 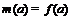 , при
, при 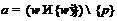 . Ясно,
что
. Ясно,
что 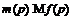 .
.
Рассмотрим  -кратно
-кратно  -насыщенную
формацию
-насыщенную
формацию  , порожденную спутником
, порожденную спутником 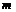 . Пусть
. Пусть 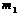 –
минимальный
–
минимальный  -кратно
-кратно  -локальный
спутник формации
-локальный
спутник формации  . Тогда так как
. Тогда так как 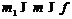 , то, ввиду леммы 17,
, то, ввиду леммы 17, 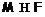 .
.
Пусть 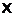 – произвольная собственная
– произвольная собственная  -кратно
-кратно  -насыщенная
подформация формации
-насыщенная
подформация формации  ,
, 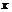 – ее
минимальный
– ее
минимальный 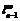 -значный
-значный  -локальный
спутник. Тогда
-локальный
спутник. Тогда 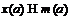 для любого
для любого 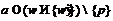 . Кроме того, как нетрудно показать,
имеет место включение
. Кроме того, как нетрудно показать,
имеет место включение
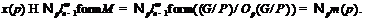
Поэтому 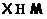 . Таким образом,
. Таким образом,  –
единственная максимальная
–
единственная максимальная  -кратно
-кратно  -насыщенная подформация формации
-насыщенная подформация формации  , т.е.
, т.е.  является
является
 -неприводимой формацией.
-неприводимой формацией.
В силу леммы 11  -дефект
-дефект  -кратно
-кратно
 -насыщенной формации
-насыщенной формации  равен 1. Но тогда
равен 1. Но тогда  -дефект
-дефект  -неприводимой
формации
-неприводимой
формации  равен 2.
равен 2.
Дано решение проблемы описания  -кратно
-кратно  -насыщенных
формаций
-насыщенных
формаций  -дефекта 2, поставленной А.Н.
Скибой и Л.А. Шеметковым в работе «Кратно
-дефекта 2, поставленной А.Н.
Скибой и Л.А. Шеметковым в работе «Кратно  -локальные
формации и классы Фиттинга конечных групп» (Матем. Труды. – 1999. – Т.2, №2. –
С. 114-147, проблема 5). В частности, установлено внутреннее решеточное
строение
-локальные
формации и классы Фиттинга конечных групп» (Матем. Труды. – 1999. – Т.2, №2. –
С. 114-147, проблема 5). В частности, установлено внутреннее решеточное
строение  -приводимых формаций
-приводимых формаций  -дефекта
-дефекта 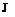 2;
получено описание конечных групп, порождающих
2;
получено описание конечных групп, порождающих  -неприводимые
формации
-неприводимые
формации  -дефекта 2.
-дефекта 2.
ЛИТЕРАТУРА
1.
Шеметков Л.А.
Формации конечных групп. – М., 1978. – 267 с.
2.
Шеметков Л.А.,
Скиба А.Н. Формации алгебраических систем. – М., 1989. – 256 с.
3.
Скиба А.Н.
Алгебра формаций. – Мн.: Беларуская навука, 1997. – 240 c.
4.
Скиба А.Н.,
Шеметков Л.А. Кратно 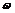 -локальные формации и классы
Фиттинга конечных групп // Матем. труды. –1999. – Т.2, №2. – С. 114–147.
-локальные формации и классы
Фиттинга конечных групп // Матем. труды. –1999. – Т.2, №2. – С. 114–147.
5.
Частично
локальные формации с заданными системами подформаций: отчет о НИР
(заключительный): ГБЦМ 20-07 / УО «Гомельский государственный университет имени
Ф.Скорины»; рук. В.Г.Сафонов; исполн.: В.М.Селькин, В.В.Аниськов. – Гомель,
2001. – 69 с. – Библиогр.: с. 66-69. – № ГР 2000419.
6.
Шаблина И.П.
Модулярные и алгебраические решетки 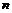 -кратно
-кратно 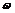 -насыщенных формаций конечных групп:
Дис. … канд. физ.-мат. наук. – Гомель, 2003. – 92 с.
-насыщенных формаций конечных групп:
Дис. … канд. физ.-мат. наук. – Гомель, 2003. – 92 с.
7.
Рябченко А. И О
частично насыщенных формациях с 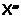 -дефектом 1 // Изв. НАН
Беларуси. Сер. физ.-мат. наук. – 2008. – № 1 .– С.28–34.
-дефектом 1 // Изв. НАН
Беларуси. Сер. физ.-мат. наук. – 2008. – № 1 .– С.28–34.
8.
Сафонов В.Г. О
минимальных кратно локальных не 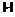 -формациях конечных
групп // Вопросы алгебры. Гомель: Изд-во Гом-го ун-та, 1995. – Вып. 8. – С. 109–138.
-формациях конечных
групп // Вопросы алгебры. Гомель: Изд-во Гом-го ун-та, 1995. – Вып. 8. – С. 109–138.
9.
Селькин В.М.,
Скиба А.Н. О 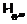 -критических формациях // Вопросы
алгебры. – Гомель: Изд-во ГГУ им. Ф.Скорины, 1999. – Вып. 14. – С. 127–131.
-критических формациях // Вопросы
алгебры. – Гомель: Изд-во ГГУ им. Ф.Скорины, 1999. – Вып. 14. – С. 127–131.
10.
Рябченко А. И. О
минимальных 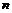 -кратно
-кратно 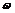 -насыщенных
ненильпотентных формациях // Вестник Полоцкого государственного университета.
Сер. С. – 2008. – №5. – C. 41–46.
-насыщенных
ненильпотентных формациях // Вестник Полоцкого государственного университета.
Сер. С. – 2008. – №5. – C. 41–46.
11.
Рябченко А. И. К
теории частично насыщенных формаций // Изв. Гом.гос.унив.им.Ф.Скорины. – 2008.
– №6(51). Ч.2.– С. 153–160.