Классы конечных групп F, замкнутые относительно произведения обобщенно субнормальных F-подгрупп
Министерство образования Республики Беларусь
Учреждение образования
"Гомельский государственный университет им. Ф.
Скорины"
Математический факультет
Кафедра алгебры и геометрии
КЛАССЫ КОНЕЧНЫХ ГРУПП  ,
ЗАМКНУТЫЕ ОТНОСИТЕЛЬНО ПРОИЗВЕДЕНИЯ ОБОБЩЕННО СУБНОРМАЛЬНЫХ
,
ЗАМКНУТЫЕ ОТНОСИТЕЛЬНО ПРОИЗВЕДЕНИЯ ОБОБЩЕННО СУБНОРМАЛЬНЫХ  -ПОДГРУПП
-ПОДГРУПП
Курсовая работа
Исполнитель:
Студентка
группы М-43 МОКЕЕВА О. А.
Научный
руководитель:
доктор
ф-м наук, профессор Семенчук В.Н.
Гомель 2008
Содержание
Перечень
условных обозначений
Введение
1
Некоторые базисные леммы
2
Критерий принадлежности факторизуемой группы
классическим
классам конечных групп
3
Сверхрадикальные формации
Заключение
Список
использованных источников
Рассматриваются
только конечные группы. Вся терминология заимствована из [44, 47].
 --- множество всех натуральных чисел;
--- множество всех натуральных чисел;
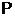 --- множество всех простых чисел;
--- множество всех простых чисел;
 --- некоторое множество простых чисел,
т. е.
--- некоторое множество простых чисел,
т. е. 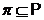 ;
;
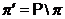 ---
---
дополнение
к  во множестве всех простых чисел; в
частности,
во множестве всех простых чисел; в
частности, 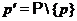 ;
;
примарное
число --- любое число вида 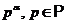 .
.
Буквами
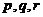 обозначаются простые числа.
обозначаются простые числа.
Пусть
 --- группа. Тогда:
--- группа. Тогда:
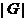 --- порядок группы
--- порядок группы  ;
;
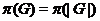 ---
---
множество
всех простых делителей порядка группы  ;
;
 -группа --- группа
-группа --- группа  , для которой
, для которой 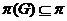 ;
;
 -группа --- группа
-группа --- группа  , для которой
, для которой 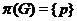 ;
;
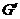 --- коммутант группы
--- коммутант группы  , т. е. подгруппа, порожденная
коммутаторами всех элементов группы
, т. е. подгруппа, порожденная
коммутаторами всех элементов группы  ;
;
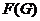 --- подгруппа Фиттинга группы
--- подгруппа Фиттинга группы  , т. е. произведение всех нормальных
нильпотентных подгрупп группы
, т. е. произведение всех нормальных
нильпотентных подгрупп группы  ;
;
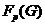 --- наибольшая нормальная
--- наибольшая нормальная  -нильпотентная подгруппа группы
-нильпотентная подгруппа группы  ;
;
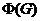 --- подгруппа Фраттини группы
--- подгруппа Фраттини группы  , т. е. пересечение всех максимальных
подгрупп группы
, т. е. пересечение всех максимальных
подгрупп группы  ;
;
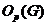 --- наибольшая нормальная
--- наибольшая нормальная  -подгруппа группы
-подгруппа группы  ;
;
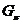 ---
---  -холлова
подгруппа группы
-холлова
подгруппа группы  ;
;
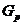 --- силовская
--- силовская  -подгруппа
группы
-подгруппа
группы  ;
;
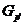 --- дополнение к силовской
--- дополнение к силовской  -подгруппе в группе
-подгруппе в группе  , т. е.
, т. е. 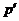 -холлова
подгруппа группы
-холлова
подгруппа группы  ;
;
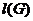 --- нильпотентная длина группы
--- нильпотентная длина группы  ;
;
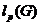 ---
---  -длина
группы
-длина
группы  ;
;
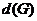 --- минимальное число порождающих
элементов группы
--- минимальное число порождающих
элементов группы  ;
;
 --- цоколь группы
--- цоколь группы  , т. е. подгруппа, порожденная всеми
минимальными нормальными подгруппами группы
, т. е. подгруппа, порожденная всеми
минимальными нормальными подгруппами группы  ;
;
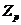 --- циклическая группа порядка
--- циклическая группа порядка  .
.
Если
 и
и 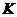 ---
подгруппы группы
---
подгруппы группы  , то :
, то :
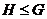 ---
---  является
подгруппой группы
является
подгруппой группы  ;
;
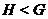 ---
---  является
собственной подгруппой группы
является
собственной подгруппой группы  ;
;
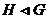 ---
---  является
нормальной подгруппой группы
является
нормальной подгруппой группы  ;
;
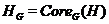 --
--
-
ядро подгруппы  в группе
в группе  , т. е. пересечение всех подгрупп,
сопряженных с
, т. е. пересечение всех подгрупп,
сопряженных с  в
в  ;
;
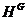 --- нормальное замыкание подгруппы
--- нормальное замыкание подгруппы  в группе
в группе  , т.
е. подгруппа, порожденная всеми сопряженными с
, т.
е. подгруппа, порожденная всеми сопряженными с  подгруппами
группы
подгруппами
группы  ;
;
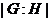 --- индекс подгруппы
--- индекс подгруппы  в группе
в группе  ;
;
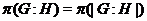 ;
;
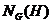 --- нормализатор подгруппы
--- нормализатор подгруппы  в группе
в группе  ;
;
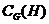 --- централизатор подгруппы
--- централизатор подгруппы  в группе
в группе  ;
;
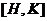 --- взаимный коммутант подгрупп
--- взаимный коммутант подгрупп  и
и 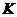 ;
;
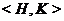 --- подгруппа, порожденная подгруппами
--- подгруппа, порожденная подгруппами  и
и 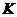 .
.
Минимальная
нормальная подгруппа группы 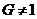 --- неединичная
нормальная подгруппа группы
--- неединичная
нормальная подгруппа группы  , не содержащая
собственных неединичных нормальных подгрупп группы
, не содержащая
собственных неединичных нормальных подгрупп группы  ;
;
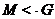 ---
--- 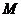 является
максимальной подгруппой группы
является
максимальной подгруппой группы  .
.
Если
 и
и  ---
подгруппы группы
---
подгруппы группы  , то:
, то:
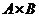 --- прямое произведение подгрупп
--- прямое произведение подгрупп  и
и  ;
;
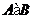 --- полупрямое произведение нормальной
подгруппы
--- полупрямое произведение нормальной
подгруппы  и подгруппы
и подгруппы  ;
;
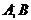 ---
---  и
и  изоморфны;
изоморфны;
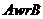 --- регулярное сплетение подгрупп
--- регулярное сплетение подгрупп  и
и  .
.
Подгруппы
 и
и  группы
группы
 называются перестановочными, если
называются перестановочными, если 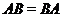 .
.
Группу
 называют:
называют:
 -замкнутой, если силовская
-замкнутой, если силовская  -подгруппа группы
-подгруппа группы  нормальна в
нормальна в  ;
;
 -нильпотентной, если
-нильпотентной, если 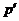 -холлова подгруппа группы
-холлова подгруппа группы  нормальна в
нормальна в  ;
;
 -разрешимой, если существует нормальный
ряд, факторы которого либо
-разрешимой, если существует нормальный
ряд, факторы которого либо  -группы, либо
-группы, либо 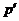 -группы;
-группы;
 -сверхразрешимой, если каждый ее главный
фактор является либо
-сверхразрешимой, если каждый ее главный
фактор является либо 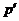 -группой, либо циклической
группой;
-группой, либо циклической
группой;
нильпотентной,
если все ее силовские подгруппы нормальны;
разрешимой,
если существует номер  такой, что
такой, что 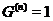 ;
;
сверхразрешимой,
если она обладает главным рядом, все индексы которого являются простыми
числами.
Монолитическая
группа --- неединичная группа, имеющая единственную минимальную нормальную
подгруппу.
 -замкнутая группа --- группа, обладающая
нормальной холловской
-замкнутая группа --- группа, обладающая
нормальной холловской  -подгруппой.
-подгруппой.
 -специальная группа --- группа,
обладающая нильпотентной нормальной холловской
-специальная группа --- группа,
обладающая нильпотентной нормальной холловской  -подгруппой.
-подгруппой.
 -разложимая группа --- группа,
являющаяся одновременно
-разложимая группа --- группа,
являющаяся одновременно  -специальной и
-специальной и 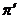 -замкнутой.
-замкнутой.
Группа
Шмидта --- это конечная ненильпотентная группа, все собственные группы которой
нильпотентны.
Добавлением
к подгруппе 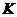 группы
группы  называется
такая подгруппа
называется
такая подгруппа  из
из  ,
что
,
что 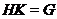 .
.
Цепь
--- это совокупность вложенных друг в друга подгрупп.
Ряд
подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через
единицу.
Ряд
подгрупп 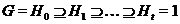 называется:
называется:
субнормальным,
если 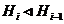 для любого
для любого 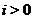 ;
;
нормальным,
если 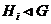 для любого
для любого 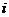 ;
;
главным,
если 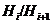 является минимальной нормальной
подгруппой в
является минимальной нормальной
подгруппой в 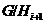 для всех
для всех 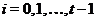 .
.
Класс
групп --- совокупность групп, содержащая с каждой своей группой  и все ей изоморфные группы.
и все ей изоморфные группы.
 -группа --- группа, принадлежащая классу
групп
-группа --- группа, принадлежащая классу
групп  .
.
Формация
--- класс групп, замкнутый относительно факторгрупп и подпрямых произведений.
Если
 --- класс групп, то:
--- класс групп, то:
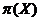 --- множество всех простых делителей
порядков всех групп из
--- множество всех простых делителей
порядков всех групп из  ;
;
 --- множество всех тех простых чисел
--- множество всех тех простых чисел  , для которых
, для которых 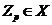 ;
;
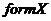 --- формация, порожденная классом
--- формация, порожденная классом  ;
;
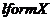 --- насыщенная формация, порожденная
классом
--- насыщенная формация, порожденная
классом  ;
;
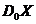 --- класс всех групп
--- класс всех групп  , представимых в виде
, представимых в виде
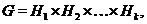
где
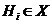 ,
, 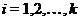 ;
;
 ;
;
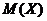 --- класс всех минимальных не
--- класс всех минимальных не  -групп, т. е. групп не принадлежащих
-групп, т. е. групп не принадлежащих  , но все собственные подгруппы которых
принадлежат
, но все собственные подгруппы которых
принадлежат  ;
;
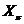 --- класс всех
--- класс всех  -групп
из
-групп
из  ;
;
 --- класс всех конечных групп;
--- класс всех конечных групп;
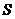 --- класс всех разрешимых конечных
групп;
--- класс всех разрешимых конечных
групп;
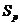 --- класс всех
--- класс всех  -групп;
-групп;
 --- класс всех разрешимых
--- класс всех разрешимых 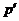 -групп;
-групп;
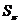 --- класс всех разрешимых
--- класс всех разрешимых  -групп;
-групп;
 --- класс всех нильпотентных групп;
--- класс всех нильпотентных групп;
 --- класс всех разрешимых групп с
нильпотентной длиной
--- класс всех разрешимых групп с
нильпотентной длиной 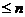 .
.
Если
 и
и  ---
классы групп, то:
---
классы групп, то:
 .
.
Если
 --- класс групп и
--- класс групп и  --- группа, то:
--- группа, то:
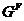 --- пересечение всех нормальных
подгрупп
--- пересечение всех нормальных
подгрупп  из
из  таких,
что
таких,
что 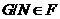 ;
;
 --- произведение всех нормальных
--- произведение всех нормальных  -подгрупп группы
-подгрупп группы  .
.
Если
 и
и  ---
формации, то:
---
формации, то:
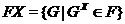 --- произведение формаций;
--- произведение формаций;
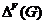 --- пересечение всех
--- пересечение всех  -абнормальных максимальных подгрупп
группы
-абнормальных максимальных подгрупп
группы  .
.
Если
 --- насыщенная формация, то:
--- насыщенная формация, то:
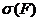 --- существенная характеристика
формации
--- существенная характеристика
формации  .
.
 -абнормальной называется максимальная
подгруппа
-абнормальной называется максимальная
подгруппа 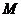 группы
группы  ,
если
,
если 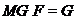 , где
, где  ---
некоторая непустая формация.
---
некоторая непустая формация.
 -гиперцентральной подгруппой в
-гиперцентральной подгруппой в  называется разрешимая нормальная
подгруппа
называется разрешимая нормальная
подгруппа  группы
группы  ,
если
,
если  обладает субнормальным рядом
обладает субнормальным рядом 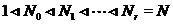 таким, что
таким, что
(1)
каждый фактор 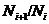 является главным фактором
группы
является главным фактором
группы  ;
;
(2)
если порядок фактора 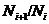 есть степень простого числа
есть степень простого числа 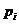 , то
, то 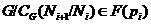 .
.
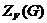 ---
---  -гиперцентр
группы
-гиперцентр
группы  , т. е. произведение всех
, т. е. произведение всех  -гиперцентральных подгрупп группы
-гиперцентральных подгрупп группы  .
.
Введение
Вопросы,
посвященные факторизации групп, в теории конечных групп занимают важное место.
Под факторизацией конечной группы понимается представление ее в виде произведения
некоторых еe подгрупп, взятых в определенном порядке, или попарно
перестановочных. Исследуются как способы факторизации заданной группы, так и
свойства групп, допускающих ту или иную заданную факторизацию.
Начало
исследований по факторизации конечных групп восходит к классическим работам Ф.
Холла [62, 63], посвященных изучению строения разрешимых групп. Как известно,
Ф. Холлом было доказано [63], что конечная разрешимая группа допускает
факторизацию при помощи некоторых своих перестановочных силовских подгрупп
различных порядков (составляющих так называемую силовскую базу разрешимой
группы).
Следующий
важный шаг в данном направлении был сделан С.А.Чунихиным, которым был
исследован ряд важных арифметических свойств конечных групп [43]. Вопросами
факторизации конечных групп занималось много математиков, и развитию данного
направления посвящено много научных работ известных математиков.
Кегель
и Виландт [68, 75] установили, что конечная группа, факторизуемая двумя
нильпотентными подгруппами разрешима. Теорема Кегеля --- Виландта послужила
источником многочисленных обобщений и стимулировала дальнейшее развитие ряда
вопросов, связанных с факторизациями конечных групп.
Cреди
дальнейших исследований, посвященных факторизации групп, выделяются работы Л.С.
Казарина [6, 7, 67], Л.А. Шеметкова [45, 46], В.С. Монахова [13, 14], А.Н.
Скибы [12, 61], В.Н. Тютянова [38] и др.
Важную
роль для дальнейшего строения факторизуемых групп оказала идея Гашюца о том
[59], что внутреннее строение конечной группы удобно исследовать по отношению к
некоторому фиксированному классу групп, названному Гашюцем насыщенной
формацией.
Напомним,
что насыщенной формацией конечных групп называется класс конечных групп,
замкнутый относительно гомоморфных образов, подпрямых произведений и фраттиниевых
расширений. Такой подход к изучению строения конечных групп привлек внимание
многих специалистов по алгебре и исследования, связанные с насыщенными
формациями, составили одно из доминирующих направлений современной теории
классов групп.
Эффективность
метода Гашюца проявилась прежде всего в том, что многие коренные свойства
конечных групп имеют инвариантный характер при переходе от одной насыщенной
формации к другой.
Известно,
что класс нильпотентных групп  замкнут относительно
произведения нормальных подгрупп. В работе [64] Хоуксом была поставлена задача
об описании наследственных разрешимых формаций Фиттинга, т. е. формаций
замкнут относительно
произведения нормальных подгрупп. В работе [64] Хоуксом была поставлена задача
об описании наследственных разрешимых формаций Фиттинга, т. е. формаций  , замкнутых относительно произведения
нормальных
, замкнутых относительно произведения
нормальных  -подгрупп. Брайс и Косси в работе [53]
доказали, что любая разрешимая наследственная формация Фиттинга является
насыщенной. Полное решение проблемы Хоукса было получено В.Н. Семенчуком в
работах [27, 30].
-подгрупп. Брайс и Косси в работе [53]
доказали, что любая разрешимая наследственная формация Фиттинга является
насыщенной. Полное решение проблемы Хоукса было получено В.Н. Семенчуком в
работах [27, 30].
Развивая
подход Хоукса, Л.А. Шеметков предложил изучать формации  ,
замкнутые относительно произведения
,
замкнутые относительно произведения  -подгрупп, обладающих
некоторыми заданными свойствами. В настоящее время данная тематика активно
развивается математиками Испании, Китая, Беларуси.
-подгрупп, обладающих
некоторыми заданными свойствами. В настоящее время данная тематика активно
развивается математиками Испании, Китая, Беларуси.
В
теории классов конечных групп естественным обобщением понятия субнормальности
является понятие  -субнормальности и
-субнормальности и  -достижимости. В дальнейшем такие
подгруппы будем нызывать обобщенно субнормальными.
-достижимости. В дальнейшем такие
подгруппы будем нызывать обобщенно субнормальными.
Одной
из первых классификационных проблем данного направления является проблема Л.А.
Шеметкова об описании наследственных насыщенных сверхрадикальных формаций, т.
е. формаций  с тем свойством, что любая группа
с тем свойством, что любая группа  , где
, где  и
и  --
--  -субнормальные
-субнормальные
 -подгруппы, принадлежит
-подгруппы, принадлежит  .
.
Данная
проблема сразу привлекла пристальное внимание специалистов по теории классов
конечных групп. В работе [28] В.Н. Семенчуком в классе конечных разрешимых
групп получено полное решение данной проблемы. Л.А. Шеметковым и В.Н.
Семенчуком в работе [33] найдены серии произвольных наследственных насыщенных
сверхрадикальных формаций.
Известно,
что формация всех сверхразрешимых групп не замкнута относительно произведения
нормальных сверхразрешимых подгрупп, но замкнута относительно произведения
нормальных сверхразрешимых подгрупп взаимно простых индексов. В связи с этим
возникает задача об описании наследственных насыщенных формаций  , замкнутых относительно произведения
обобщенно субнормальных (
, замкнутых относительно произведения
обобщенно субнормальных ( -субнормальных,
-субнормальных,  -достижимых)
-достижимых)  -подгрупп,
индексы которых взаимно просты.
-подгрупп,
индексы которых взаимно просты.
Классифицировать
наследственные насыщенные формации  с тем свойством, что
любая группа
с тем свойством, что
любая группа  , где
, где  и
и  ---
---  -субнормальные
-субнормальные
 -подгруппы взаимно простых индексов,
принадлежит
-подгруппы взаимно простых индексов,
принадлежит  .
.
В
1996 году В.Н. Тютянов в работе [38] доказал, что любая конечная группа вида  , где
, где  и
и  ---
---  -нильпотентные
подгруппы и индексы
-нильпотентные
подгруппы и индексы 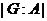 ,
, 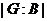 не
делятся на некоторое простое число
не
делятся на некоторое простое число  , является
, является  -нильпотентной группой.
-нильпотентной группой.
Естественно
возникает задача об описании наследственных насыщенных формаций  , замкнутых относительно произведения
, замкнутых относительно произведения  -подгрупп, индексы которых не делятся на
некоторое фиксированное простое число.
-подгрупп, индексы которых не делятся на
некоторое фиксированное простое число.
В
попытках решения этих и других классификационных проблем выявилась особая роль критических
групп формации  ( минимальных не
( минимальных не  -групп), т. е. групп, не принадлежащих
некоторому классу групп
-групп), т. е. групп, не принадлежащих
некоторому классу групп  , но все собственные
подгруппы которых принадлежат
, но все собственные
подгруппы которых принадлежат  . Еще в 1933 году
С.А. Чунихин [40] поставил задачу изучения строения группы, в зависимости от
свойств ее критических подгрупп. Развивая данную идею С.А. Чунихина, Л.А.
Шеметков на восьмом (Сумы, 1982 г.) и девятом (Москва, 1984 г.) Всесоюзных
симпозиумах по теории групп отметил особую роль критических групп при изучении
не только отдельной группы, но и при описании классов групп.
. Еще в 1933 году
С.А. Чунихин [40] поставил задачу изучения строения группы, в зависимости от
свойств ее критических подгрупп. Развивая данную идею С.А. Чунихина, Л.А.
Шеметков на восьмом (Сумы, 1982 г.) и девятом (Москва, 1984 г.) Всесоюзных
симпозиумах по теории групп отметил особую роль критических групп при изучении
не только отдельной группы, но и при описании классов групп.
Таким
образом, задача классификации наследственных насыщенных формаций  , замкнутых относительно произведения
, замкнутых относительно произведения  -подгрупп, обладающих заданными
свойствами, занимает важное место в современной теории классов групп. На
реализацию этой актуальной задачи и направлено данное диссертационное
исследование.
-подгрупп, обладающих заданными
свойствами, занимает важное место в современной теории классов групп. На
реализацию этой актуальной задачи и направлено данное диссертационное
исследование.
В
теории конечных групп одним из основных понятий является понятие
субнормальности подгрупп, введенное Виландтом в работе [73].
Напомним,
что подгруппа  называется субнормальной
подгруппой группы
называется субнормальной
подгруппой группы  , если существует цепь
подгрупп
, если существует цепь
подгрупп
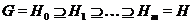
такая,
что для любого 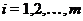 подгруппа
подгруппа 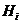 нормальна в
нормальна в 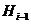 .
.
Естественным
обобщением понятия субнормальности является понятие  -субнормальности,
которое для произвольных конечных групп впервые введено Л.А. Шеметковым в
монографии [44].
-субнормальности,
которое для произвольных конечных групп впервые введено Л.А. Шеметковым в
монографии [44].
Пусть
 --- непустая формация. Подгруппу
--- непустая формация. Подгруппу  группы
группы  называют
называют
 -субнормальной, если либо
-субнормальной, если либо 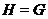 , либо существует максимальная цепь
, либо существует максимальная цепь
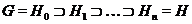
такая,
что 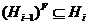 для всех
для всех 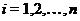 .
.
Несколько
другое понятие  -субнормальности введено
Кегелем в работе [69]. Фактически оно объединяет понятие субнормальности и
-субнормальности введено
Кегелем в работе [69]. Фактически оно объединяет понятие субнормальности и  -субнормальности в смысле Шеметкова.
-субнормальности в смысле Шеметкова.
Подгруппу
 называют
называют  -субнормальной
в смысле Кегеля или
-субнормальной
в смысле Кегеля или  -достижимой, если существует
цепь подгрупп
-достижимой, если существует
цепь подгрупп
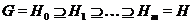
такая,
что для любого 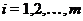 либо подгруппа
либо подгруппа 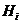 нормальна в
нормальна в 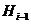 ,
либо
,
либо 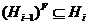 .
.
Для
любой непустой формации  множество всех
множество всех  -достижимых подгрупп произвольной группы
-достижимых подгрупп произвольной группы
 содержит множество всех субнормальных
подгрупп группы
содержит множество всех субнормальных
подгрупп группы  и множество всех
и множество всех  -субнормальных подгрупп группы
-субнормальных подгрупп группы  . Если же
. Если же  ---
непустая нильпотентная формация, то множество всех
---
непустая нильпотентная формация, то множество всех  -достижимых
подгрупп в точности совпадает с множеством всех субнормальных подгрупп для
любой группы
-достижимых
подгрупп в точности совпадает с множеством всех субнормальных подгрупп для
любой группы  .
.
В
Коуровской тетради [10] Л.А. Шеметковым была поставлена проблема классификации
сверхрадикальных формаций.
Напомним,
что формация  называется сверхрадикальной, если она
удовлетворяет следующим требованиям:
называется сверхрадикальной, если она
удовлетворяет следующим требованиям:
1)
 --- нормально наследственная формация;
--- нормально наследственная формация;
2)
любая группа  , где
, где  и
и  ---
---  -субнормальные
-субнормальные
 -подгруппы из
-подгруппы из  ,
принадлежит
,
принадлежит  .
.
В.Н.
Семенчуком в работе [28] в классе конечных разрешимых групп было получено
полное решение данной проблемы.
В
данной главе получено полное решение проблемы Шеметкова для наследственных
насыщенных формаций, критические группы которых разрешимы
В
данном разделе приводятся некоторые свойства критических групп (минимальных не  -групп) и обобщенно субнормальных (
-групп) и обобщенно субнормальных ( -субнормальных и
-субнормальных и  -достижимых)
подгрупп, которые будут использоваться при доказательстве основных результатов
диссертации.
-достижимых)
подгрупп, которые будут использоваться при доказательстве основных результатов
диссертации.
Напомним,
что критической группой формации  ( минимальной не
( минимальной не  -группой) называется группа, не
принадлежащая
-группой) называется группа, не
принадлежащая  , все собственные подгруппы
которой принадлежат
, все собственные подгруппы
которой принадлежат  . Множество всех таких групп
обозначают
. Множество всех таких групп
обозначают 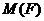 . Через
. Через 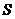 обозначают
множество всех разрешимых групп, а через
обозначают
множество всех разрешимых групп, а через  ---
множество всех групп, у которых
---
множество всех групп, у которых  -корадикал
-корадикал 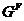 разрешим.
разрешим.
1.1
Лемма.
Пусть  --- насыщенная формация,
--- насыщенная формация,  --- наследственная насыщенная формация.
Если
--- наследственная насыщенная формация.
Если 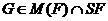 и
и 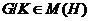 , где
, где
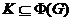 , то
, то 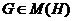 .
.
Доказательство.
Пусть 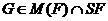 . По теореме 2.2.1,
. По теореме 2.2.1, 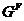 ---
---  -группа.
Очевидно, что
-группа.
Очевидно, что 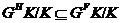 . По лемме 2.2.2,
. По лемме 2.2.2, 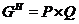 , где
, где 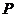 ---
---  -группа,
-группа, 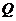 ---
--- 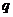 -группа и
-группа и 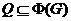 . Так
как
. Так
как  и
и  , то
, то
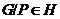 . Следовательно,
. Следовательно, 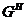 ---
---
 -группа. Пусть
-группа. Пусть 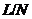 ---
---
 -главный фактор
-главный фактор 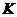 .
Если
.
Если 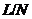 ---
--- 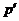 -группа,
то
-группа,
то 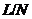
 -централен.
-централен.
Пусть
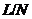 ---
---  -группа.
По теореме 2.2.3,
-группа.
По теореме 2.2.3, 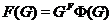 . Пусть
. Пусть 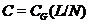 и
и 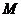 ---
произвольная
---
произвольная  -абнормальная максимальная подгруппа
группы
-абнормальная максимальная подгруппа
группы  . Тогда
. Тогда 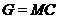 . Так
как
. Так
как 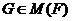 , то, по теореме 2.2.4,
, то, по теореме 2.2.4, 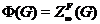 . Следовательно,
. Следовательно, 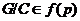 .
Поскольку
.
Поскольку
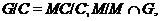
то
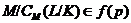 . Учитывая, что
. Учитывая, что 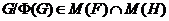 ,
по теореме 2.2.5, имеем
,
по теореме 2.2.5, имеем
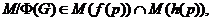
где
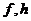 --- максимальные внутренние локальные
экраны, соответственно
--- максимальные внутренние локальные
экраны, соответственно  и
и  .
Если
.
Если 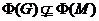 , то
, то 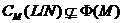 .
Отсюда и из того, что
.
Отсюда и из того, что
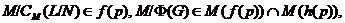
следует
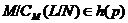 . А это значит, что
. А это значит, что 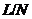
 -централен.
-централен.
Пусть
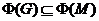 . Так как
. Так как  ---
насыщенная формация и
---
насыщенная формация и 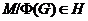 , то
, то  .
Следовательно,
.
Следовательно, 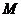 ---
---  -нормализатор
группы
-нормализатор
группы  . В силу того, что
. В силу того, что 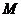 покрывает
покрывает 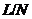 , то
, то 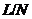
 -централен.
Следовательно,
-централен.
Следовательно, 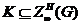 . По теореме 2.2.4,
. По теореме 2.2.4, 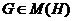 . Лемма доказана.
. Лемма доказана.
1.2
Лемма.
Пусть  --- непустая наследственная формация.
Если
--- непустая наследственная формация.
Если  ---
---  -субнормальная
подгруппа, то
-субнормальная
подгруппа, то 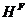 --- субнормальная подгруппа.
--- субнормальная подгруппа.
Доказательство.
Пусть  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Если
. Если 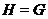 ,
то лемма очевидна. Пусть
,
то лемма очевидна. Пусть 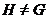 . Тогда
. Тогда  содержится в максимальной
содержится в максимальной  -нормальной подгруппе
-нормальной подгруппе 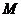 группы
группы  . По
индукции,
. По
индукции, 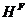 --- субнормальная подгруппа из
--- субнормальная подгруппа из 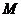 . Так как
. Так как 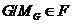 и
и  --- наследственная формация, то
--- наследственная формация, то 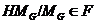 . Следовательно,
. Следовательно, 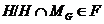 ,
значит,
,
значит, 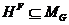 . Поскольку
. Поскольку 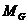 ---
нормальная подгруппа группы
---
нормальная подгруппа группы  , то
, то 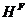 --- субнормальная подгруппа
--- субнормальная подгруппа  . Лемма доказана.
. Лемма доказана.
1.3
Лемма. Пусть
 --- наследственная насыщенная формация,
--- наследственная насыщенная формация,
 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  такая, что
такая, что 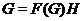 . Тогда
. Тогда 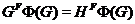 .
.
Доказательство.
Пусть 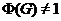 . Очевидно,
. Очевидно,
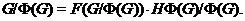
Так
как 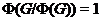 , то по индукции
, то по индукции 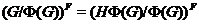 .
Следовательно,
.
Следовательно,
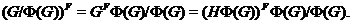
Отсюда,
согласно лемме 2.2.6,
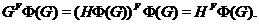
Пусть
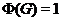 . Тогда
. Тогда 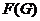 ---
цоколь группы
---
цоколь группы  . По лемме 3.1.2,
. По лемме 3.1.2, 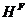 --- субнормальная подгруппа группы
--- субнормальная подгруппа группы  . По теореме 2.2.7,
. По теореме 2.2.7, 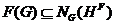 . Следовательно,
. Следовательно, 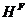 ---
нормальная подгруппа группы
---
нормальная подгруппа группы  . Тогда
. Тогда
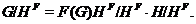
По
теореме 2.2.8, 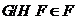 . Отсюда следует, что
. Отсюда следует, что 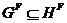 . Так как
. Так как 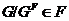 и
и  --- наследственная формация, то
--- наследственная формация, то 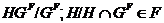 . Получаем
. Получаем 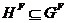 , т.
е.
, т.
е. 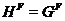 . Лемма доказана.
. Лемма доказана.
В
следующих леммах приводятся основные свойства  -субнормальных
подгрупп.
-субнормальных
подгрупп.
1.4
Лемма. Пусть
 --- непустая наследственная формация.
Тогда справедливы следующие утверждения:
--- непустая наследственная формация.
Тогда справедливы следующие утверждения:
1)
если  --- подгруппа группы
--- подгруппа группы  и
и 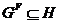 , то
, то  ---
---  -субнормальная
(
-субнормальная
( -достижимая) подгруппа группы
-достижимая) подгруппа группы  ;
;
2)
если  ---
---  -субнормальная
(
-субнормальная
( -достижимая) подгруппа группы
-достижимая) подгруппа группы  , то
, то 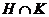 ---
---  -субнормальная (
-субнормальная ( -достижимая)
подгруппа
-достижимая)
подгруппа 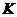 для любой подгруппы
для любой подгруппы 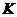 группы
группы  ;
;
3)
если  ---
---  -субнормальная
(
-субнормальная
( -достижимая) подгруппа
-достижимая) подгруппа 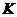 и
и 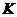 ---
---  -субнормальная (
-субнормальная ( -достижимая)
подгруппа группы
-достижимая)
подгруппа группы  , то
, то  ---
---
 -субнормальная (
-субнормальная ( -достижимая)
подгруппа группы
-достижимая)
подгруппа группы  ;
;
4)
если  и
и 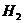 ---
---  -субнормальные (
-субнормальные ( -достижимые)
подгруппы группы
-достижимые)
подгруппы группы  , то
, то 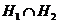 ---
---
 -субнормальная (
-субнормальная ( -достижимая)
подгруппа группы
-достижимая)
подгруппа группы  ;
;
5)
если все композиционные факторы группы  принадлежат
формации
принадлежат
формации  , то каждая субнормальная подгруппа
группы
, то каждая субнормальная подгруппа
группы 
 -субнормальна
в
-субнормальна
в  ;
;
6)
если  ---
---  -субнормальная
(
-субнормальная
( -достижимая) подгруппа группы
-достижимая) подгруппа группы  , то
, то 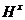
 -субнормальна (
-субнормальна ( -достижима)
в
-достижима)
в  для любых
для любых 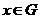 .
.
Доказательство.
1) Пусть  --- подгруппа группы
--- подгруппа группы  и
и 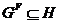 . Так
как
. Так
как 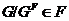 и
и  ---
наследственная формация, то подгруппа
---
наследственная формация, то подгруппа 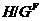 является
является
 -субнормальной подгруппой группы
-субнормальной подгруппой группы 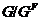 . Отсюда, согласно определению
. Отсюда, согласно определению  -субнормальной подгруппы, существует
максимальная цепь
-субнормальной подгруппы, существует
максимальная цепь
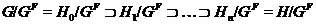
такая,
что 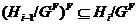 для всех
для всех 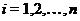 .
Отсюда, с учетом леммы 2.2.6 получаем, что в группе
.
Отсюда, с учетом леммы 2.2.6 получаем, что в группе  существует
максимальная цепь
существует
максимальная цепь
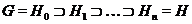
такая,
что 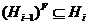 для всех
для всех 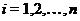 .
.
А
это значит, что  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  .
.
Пусть
 --- подгруппа группы
--- подгруппа группы  , содержащая
, содержащая 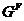 ,
тогда
,
тогда  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . А так как любая
. А так как любая  -субнормальная подгруппа группы
-субнормальная подгруппа группы  является
является  -достижимой
в
-достижимой
в  , то
, то  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
2)
Пусть  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Тогда, по определению,
существует максимальная цепь подгрупп
. Тогда, по определению,
существует максимальная цепь подгрупп
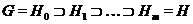
такая,
что для любого 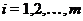
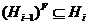 .
.
Пусть
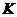 --- некоторая подгруппа из
--- некоторая подгруппа из  . Рассмотрим цепь подгрупп
. Рассмотрим цепь подгрупп
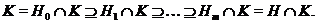
Так
как 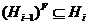 и формация
и формация  наследственна,
то из
наследственна,
то из 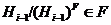 следует, что
следует, что
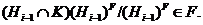
Теперь,
ввиду изоморфизма,
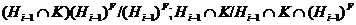
имеем
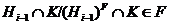 . Значит,
. Значит,  .
Так как
.
Так как 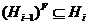 , то
, то  .
Итак,
.
Итак,  . Отсюда, по определению,
. Отсюда, по определению, 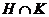 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы 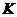 .
.
Пусть
 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы  . Тогда, по определению,
существует цепь подгрупп
. Тогда, по определению,
существует цепь подгрупп
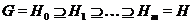
такая,
что для любого 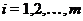 либо подгруппа
либо подгруппа 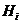 нормальна в
нормальна в 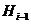 ,
либо
,
либо 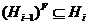 .
.
Пусть
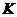 --- некоторая подгруппа из
--- некоторая подгруппа из  . Рассмотрим цепь подгрупп:
. Рассмотрим цепь подгрупп:
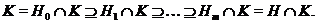
Если
подгруппа 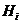 нормальна в
нормальна в 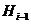 , то
подгруппа
, то
подгруппа 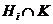 нормальна в
нормальна в 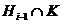 .
Пусть
.
Пусть 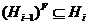 . Так как формация
. Так как формация  наследственна, то из
наследственна, то из 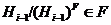 следует, что
следует, что
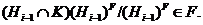
Теперь,
ввиду изоморфизма,
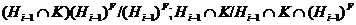
имеем
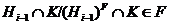 . Значит,
. Значит,  .
Так как
.
Так как 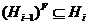 , то
, то  .
Итак, для каждого
.
Итак, для каждого 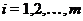 либо подгруппа
либо подгруппа 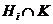 нормальна в
нормальна в 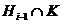 ,
либо
,
либо  . Отсюда, по определению,
. Отсюда, по определению, 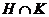 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы 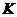 .
.
Утверждение
3) следует непосредственно из определения  -субнормальной
(
-субнормальной
( -достижимой) подгруппы.
-достижимой) подгруппы.
Утверждение
4) следует теперь из утверждений 2) и 3).
5)
Пусть все композиционные факторы группы  принадлежат
формации
принадлежат
формации  , и пусть
, и пусть  ---
субнормальная подгруппа группы
---
субнормальная подгруппа группы  . Тогда в группе
. Тогда в группе  существует цепь подгрупп
существует цепь подгрупп
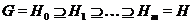
такая,
что для любого 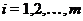 подгруппа
подгруппа 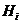 нормальна в
нормальна в 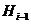 .
.
Согласно
условию, 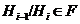 , отсюда следует, что
, отсюда следует, что 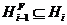 . А это значит, что подгруппа
. А это значит, что подгруппа 
 -субнормальна
в группе
-субнормальна
в группе  .
.
Утверждение
6) следует непосредственно из определения  -субнормальной
(
-субнормальной
( -достижимой) подгруппы. Лемма доказана.
-достижимой) подгруппы. Лемма доказана.
1.5
Лемма.
Пусть  --- непустая формация,
--- непустая формация,  и
и  ---
подгруппы группы
---
подгруппы группы  , причем
, причем  нормальна в
нормальна в  .
Тогда:
.
Тогда:
1)
если 
 -субнормальна
(
-субнормальна
( -достижима) в
-достижима) в  ,
то
,
то 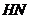
 -субнормальна
(
-субнормальна
( -достижима) в
-достижима) в  и
и
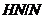
 -субнормальна
(
-субнормальна
( -достижима) в
-достижима) в 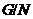 ;
;
2)
если 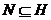 , то
, то 
 -субнормальна (
-субнормальна ( -достижима)
в
-достижима)
в  тогда и только тогда, когда
тогда и только тогда, когда 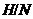
 -субнормальна
(
-субнормальна
( -достижима) в
-достижима) в 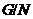 .
.
Доказательство.
Пусть  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Тогда, по определению,
существует максимальная цепь подгрупп
. Тогда, по определению,
существует максимальная цепь подгрупп
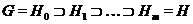
такая,
что для любого 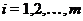
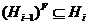 .
.
Рассмотрим
следующую цепь подгрупп
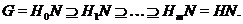
Так
как 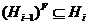 , то ввиду леммы 2.2.6,
, то ввиду леммы 2.2.6,  . Отсюда следует, что
. Отсюда следует, что
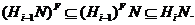
Итак,
для каждого 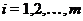
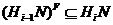 .
Отсюда, по определению,
.
Отсюда, по определению, 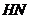 ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Ввиду
леммы 2.2.6,
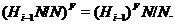
Поэтому
для любого 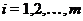
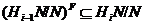 .
Значит,
.
Значит, 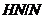 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы 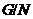 .
.
Пусть
 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы  . Тогда, по опрeделению,
существует цепь подгрупп
. Тогда, по опрeделению,
существует цепь подгрупп
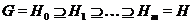
такая,
что для любого 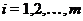 либо
либо 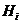 нормальна
в
нормальна
в 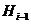 , либо
, либо 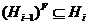 .
Рассмотрим следующую цепь подгрупп
.
Рассмотрим следующую цепь подгрупп
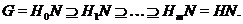
Если
подгруппа 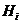 нормальна в
нормальна в 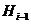 , то
подгруппа
, то
подгруппа 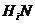 нормальна в
нормальна в 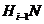 .
Пусть
.
Пусть 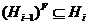 . Тогда ввиду леммы 2.2.6,
. Тогда ввиду леммы 2.2.6,  . Отсюда следует, что
. Отсюда следует, что 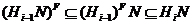 . Итак, для каждого
. Итак, для каждого 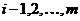 либо подгруппа
либо подгруппа 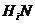 нормальна
в
нормальна
в 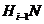 , либо
, либо 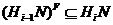 .
Отсюда, по определению,
.
Отсюда, по определению, 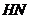 ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
Ввиду
леммы 2.2.6, 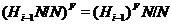 . Поэтому для любого
. Поэтому для любого 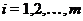 либо подгруппа
либо подгруппа 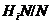 нормальна
в
нормальна
в  , либо
, либо 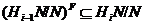 .
Значит,
.
Значит, 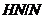 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы 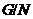 .
.
Утверждение
2) следует из 1) и леммы 2.2.6. Лемма доказана.
В
работе [3] А.Ф. Васильевым была предложена задача об описании наследственных
насыщенных формаций, замкнутых относительно произведения подгрупп  и
и  , у которых
любая силовская подгруппа
, у которых
любая силовская подгруппа  -субнормальна в
-субнормальна в 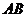 . В этой же работе было получено
описание таких формаций в классе конечных разрешимых групп. Развитию данного
направления были посвящены работы [4, 16].
. В этой же работе было получено
описание таких формаций в классе конечных разрешимых групп. Развитию данного
направления были посвящены работы [4, 16].
В
данном разделе найдены серии наследственных насыщенных формаций, не входящих в
класс конечных разрешимых групп, обладающих отмеченным выше свойством.
В
теории классов групп важную роль играет класс всех  -групп
(
-групп
( --- некоторое множество простых чисел),
который обозначается через
--- некоторое множество простых чисел),
который обозначается через 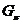 . Большинство
важнейших классов групп можно построить из классов вида
. Большинство
важнейших классов групп можно построить из классов вида 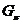 с
помощью операций пересечения и произведения классов.
с
помощью операций пересечения и произведения классов.
Напомним,
что произведением классов групп  и
и  называется класс групп
называется класс групп 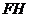 , который состоит из всех групп
, который состоит из всех групп  , таких, что в
, таких, что в  найдется
нормальная
найдется
нормальная  -подгруппа
-подгруппа  с
условием
с
условием  .
.
Пусть
 --- множество всех натуральных чисел.
Обозначим через
--- множество всех натуральных чисел.
Обозначим через 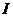 некоторое подмножество из
некоторое подмножество из 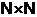 . Пусть
. Пусть 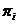 ,
, 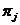 --- некоторые множества простых чисел,
а
--- некоторые множества простых чисел,
а 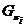 ,
, 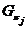 ---
классы всех
---
классы всех 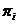 -групп и
-групп и 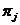 -групп
соответственно. В дальнейшем рассматриваем формации вида:
-групп
соответственно. В дальнейшем рассматриваем формации вида:
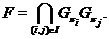
Напомним,
что группа  называется
называется  -замкнутой
(
-замкнутой
(  -нильпотентной), если ее силовская
-нильпотентной), если ее силовская  -подгруппа (силовское
-подгруппа (силовское  -дополнение) нормальна в
-дополнение) нормальна в  . Группа
. Группа  называется
называется
 -разложимой, если она одновременно
-разложимой, если она одновременно  -замкнута и
-замкнута и  -нильпотентна.
-нильпотентна.
Через
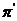 обозначим дополнение к
обозначим дополнение к  во множестве всех простых чисел, если
во множестве всех простых чисел, если  , то вместо
, то вместо 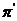 будем
просто писать
будем
просто писать  . Тогда
. Тогда 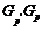 --- класс всех
--- класс всех  -нильпотентных
групп,
-нильпотентных
групп, 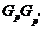 --- класс всех
--- класс всех  -замкнутых
групп,
-замкнутых
групп, 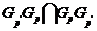 --- класс всех
--- класс всех  -разложимых
групп,
-разложимых
групп, 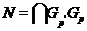 --- класс всех нильпотентных групп, где
--- класс всех нильпотентных групп, где
 пробегает все простые числа.
пробегает все простые числа.
Группа
 называется
называется  -нильпотентной
(
-нильпотентной
(  -разложимой), если она
-разложимой), если она  -нильпотентна (
-нильпотентна ( -разложима)
для любого простого числа
-разложима)
для любого простого числа  из
из  . Классы всех
. Классы всех  -нильпотентных
(
-нильпотентных
( -разложимых) групп можно записать в виде
-разложимых) групп можно записать в виде
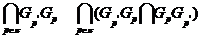
Группа
 называется
называется  -замкнутой,
если она имеет нормальную
-замкнутой,
если она имеет нормальную  -холлову подгруппу.
Тогда
-холлову подгруппу.
Тогда 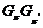 --- класс всех
--- класс всех  -замкнутых
групп.
-замкнутых
групп.
2.1
Лемма.
Пусть  --- наследственная формация. Если
--- наследственная формация. Если  ---
---  -субнормальная
-субнормальная
 -подгруппа группы
-подгруппа группы  , то композиционные факторы группы
, то композиционные факторы группы  содержатся среди композиционных
факторов групп из
содержатся среди композиционных
факторов групп из  .
.
Доказательство.
Если 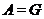 , то лемма верна. Пусть
, то лемма верна. Пусть 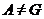 . Тогда
. Тогда  содержится
в
содержится
в  -нормальной максимальной подгруппе
-нормальной максимальной подгруппе 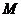 группы
группы  . По
индукции,
. По
индукции, 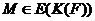 . Так как
. Так как 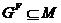 , то
, то  . Отсюда, и из
. Отсюда, и из 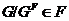 ,
получаем
,
получаем 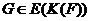 . Лемма доказана.
. Лемма доказана.
2.2
Лемма.
Пусть 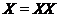 --- наследственная формация,
--- наследственная формация,  --- класс всех групп. Тогда формация
--- класс всех групп. Тогда формация 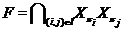 совпадает с формацией
совпадает с формацией 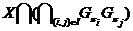 .
.
Доказательство
леммы осуществляется непосредственной проверкой.
2.3
Теорема
[10-A, 13-A]. Пусть 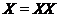 --- наследственная формация.
Тогда всякая формация
--- наследственная формация.
Тогда всякая формация  , представимая в виде
, представимая в виде 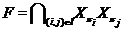 , содержит любую группу
, содержит любую группу  , у которой
, у которой 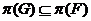 и
силовские подгруппы из подгрупп
и
силовские подгруппы из подгрупп  и
и 
 -субнормальны
в
-субнормальны
в  .
.
Доказательство.
Пусть  --- формация указанного вида и
--- формация указанного вида и  --- такая группа, что
--- такая группа, что  , где
, где 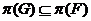 и
любая силовская подгруппа из
и
любая силовская подгруппа из  и
и 
 -субнормальна
в
-субнормальна
в  . Индукцией по порядку
. Индукцией по порядку  докажем, что
докажем, что 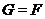 .
Рассмотрим сначала случай, когда
.
Рассмотрим сначала случай, когда 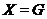 --- класс всех
групп.
--- класс всех
групп.
Пусть
 --- минимальная нормальная подгруппа из
--- минимальная нормальная подгруппа из
 . Ясно, что любая силовская подгруппа из
. Ясно, что любая силовская подгруппа из
 и
и 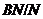 имеет
вид
имеет
вид 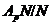 ,
, 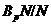 , где
, где
 и
и 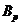 ---
силовские подгруппы из
---
силовские подгруппы из  и
и  соответственно.
Согласно лемме 3.1.5,
соответственно.
Согласно лемме 3.1.5, 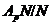 и
и 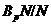 ---
---  -субнормальные подгруппы фактор-группы
-субнормальные подгруппы фактор-группы 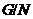 . По индукции,
. По индукции, 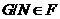 .
Так как
.
Так как  --- формация, то отсюда следует, что
--- формация, то отсюда следует, что  имеет единственную минимальную нормальную
подгруппу
имеет единственную минимальную нормальную
подгруппу  . Очевидно, что
. Очевидно, что 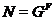 .
Так как
.
Так как  --- насыщенная формация, то нетрудно
показать, что
--- насыщенная формация, то нетрудно
показать, что 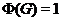 .
.
Пусть
 --- силовская подгруппа из
--- силовская подгруппа из  . Покажем, что
. Покажем, что 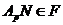 .
.
Пусть
 --- абелева группа. Так как
--- абелева группа. Так как  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  , то, согласно теореме 2.2.8,
, то, согласно теореме 2.2.8, 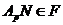 .
.
Пусть
 --- неабелева группа. В этом случае
--- неабелева группа. В этом случае 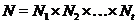 есть прямое произведение изоморфных
неабелевых простых групп и
есть прямое произведение изоморфных
неабелевых простых групп и 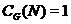 .
.
Рассмотрим
подгруппу 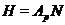 . Согласно лемме 3.1.5,
. Согласно лемме 3.1.5, 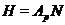 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Пусть
. Пусть 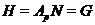 . Так как
. Так как 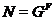 и
и  --- собственная
--- собственная  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  , то равенство
, то равенство 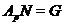 невозможно. Итак,
невозможно. Итак, 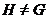 .
.
Так
как 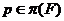 и
и  ---
насыщенная формация, то
---
насыщенная формация, то  . Отсюда следует, что
. Отсюда следует, что
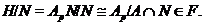
А
это значит, что 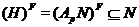 . Если
. Если  ,
то
,
то 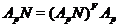 . Последнее равенство невозможно, так
как
. Последнее равенство невозможно, так
как  согласно лемме 3.1.4 --- собственная
согласно лемме 3.1.4 --- собственная  -субнормальная подгруппа
-субнормальная подгруппа 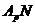 .
.
Итак,
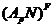 --- собственная подгруппа
--- собственная подгруппа  . Если
. Если 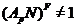 , то
, то
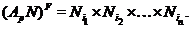
Так
как 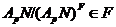 и
и  ---
наследственная формация, то
---
наследственная формация, то 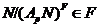 . Но тогда нетрудно
заметить, что
. Но тогда нетрудно
заметить, что 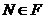 .
.
Так
как 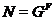 , то согласно лемме 3.1.4,
, то согласно лемме 3.1.4,  ---
---  -субнормальная
подгруппа. Так как
-субнормальная
подгруппа. Так как 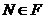 и
и  ---
наследственная формация, то любая силовская подгруппа
---
наследственная формация, то любая силовская подгруппа 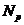
 -субнормальна в
-субнормальна в  .
Согласно лемме 3.1.4,
.
Согласно лемме 3.1.4, 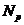 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . По индукции,
. По индукции,  . Отсюда следует, что
. Отсюда следует, что 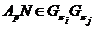 для любой
для любой 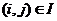 .
.
Аналогичным
образом доказывается, что 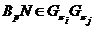 для любой
для любой 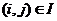 , где
, где 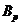 ---
любая силовская подгруппа из
---
любая силовская подгруппа из  . Из того, что
. Из того, что 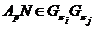 , следует
, следует  .
.
Рассмотрим
два случая:  и
и 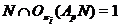 .
.
Пусть
 . Покажем, что
. Покажем, что 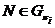 .
.
Если
 --- абелева, то
--- абелева, то  ---
примарная
---
примарная  -группа, где
-группа, где 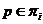 .
Отсюда следует, что
.
Отсюда следует, что 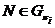 .
.
Если
 --- неабелева, то
--- неабелева, то 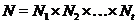 есть прямое произведение изоморфных
неабелевых простых групп.
есть прямое произведение изоморфных
неабелевых простых групп.
Так
как 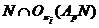 --- нормальная подгруппа из
--- нормальная подгруппа из  , то
, то
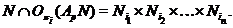
Так
как 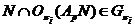 , то очевидно, что
, то очевидно, что 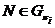 . Так как
. Так как 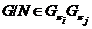 , то
, то
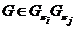 для любой
для любой 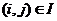 .
Следовательно,
.
Следовательно, 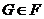 .
.
Пусть
теперь 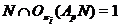 . Если
. Если  ---
неабелева, то
---
неабелева, то 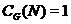 . Тогда
. Тогда 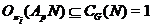 . Отсюда следует, что
. Отсюда следует, что 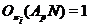 . А это значит, что
. А это значит, что  . Отсюда следует, что
. Отсюда следует, что 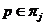 , где
, где  ---
любое простое число из
---
любое простое число из 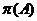 .
.
Рассмотрим
подгруппу 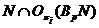 , где
, где 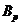 ---
любая силовская подгруппа из
---
любая силовская подгруппа из  .
.
Если
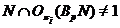 , то, как и выше, получаем, что
, то, как и выше, получаем, что 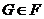 .
.
Если
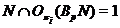 , то, как и выше, получаем, что
, то, как и выше, получаем, что 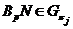 . Отсюда следует, что
. Отсюда следует, что 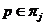 , где
, где  ---
любое простое число из
---
любое простое число из 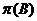 . Согласно лемме 2.2.9, любая
силовская подгруппа
. Согласно лемме 2.2.9, любая
силовская подгруппа 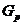 группы
группы  есть
есть 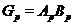 , где
, где
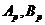 --- силовские подгруппы из
--- силовские подгруппы из  и
и  соответственно.
Отсюда следует, что любое простое число
соответственно.
Отсюда следует, что любое простое число  из
из 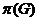 принадлежит
принадлежит 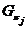 .
Следовательно,
.
Следовательно, 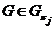 . А это значит, что
. А это значит, что 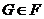 .
.
Пусть
 --- абелева группа, то
--- абелева группа, то 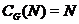 . Но тогда
. Но тогда 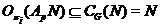 .
.
Ввиду
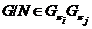 , получаем, что
, получаем, что 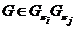 для
любой
для
любой 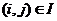 . А это значит, что
. А это значит, что 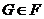 .
.
Пусть
теперь  --- произвольная наследственная
формация и
--- произвольная наследственная
формация и 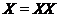 . По лемме 3.2.1, композиционные факторы
группы
. По лемме 3.2.1, композиционные факторы
группы  содержатся среди композиционных
факторов групп из
содержатся среди композиционных
факторов групп из  . Это значит, что
. Это значит, что  принадлежит
принадлежит  .
.
Пусть
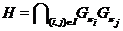 . Так как
. Так как 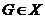 , то
ввиду леммы 3.2.2, силовские подгруппы из
, то
ввиду леммы 3.2.2, силовские подгруппы из  и
и 
 -субнормальны
в
-субнормальны
в  . По доказанному,
. По доказанному, 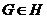 . Так как
. Так как 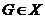 , то,
по лемме 3.2.2,
, то,
по лемме 3.2.2, 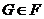 . Теорема доказана.
. Теорема доказана.
2.4
Следствие (В.Н. Семенчук, Л.А. Шеметков [33]). Пусть 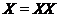 --- наследственная формация. Тогда
всякая формация вида
--- наследственная формация. Тогда
всякая формация вида 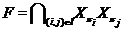 является сверхрадикальной.
является сверхрадикальной.
Доказательство.
Пусть  , где
, где  и
и  ---
---  -субнормальные
-субнормальные
 -подгруппы группы
-подгруппы группы  . Так как
. Так как  ---
наследственная формация, то согласно лемме 3.1.4, любая силовская подгруппа из
---
наследственная формация, то согласно лемме 3.1.4, любая силовская подгруппа из  (из
(из  )
)  -субнормальна в
-субнормальна в  (соответственно
в
(соответственно
в  ). Отсюда, согласно лемме 3.1.4, любая
силовская подгруппа из
). Отсюда, согласно лемме 3.1.4, любая
силовская подгруппа из  и из
и из 
 -субнормальна в
-субнормальна в  .
Теперь требуемый результат следует из теоремы 3.2.3.
.
Теперь требуемый результат следует из теоремы 3.2.3.
2.5
Следствие (В.Н. Семенчук, Л.А. Шеметков [33]). Формация вида 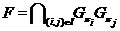 является сверхрадикальной.
является сверхрадикальной.
2.6
Следствие. Пусть  --- формация всех
--- формация всех  -нильпотентных групп. Тогда
-нильпотентных групп. Тогда  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальные
подгруппы группы
-субнормальные
подгруппы группы  , принадлежащие
, принадлежащие  .
.
2.7
Следствие. Пусть  --- формация всех
--- формация всех  -замкнутых групп. Тогда
-замкнутых групп. Тогда  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальные
подгруппы группы
-субнормальные
подгруппы группы  , принадлежащие
, принадлежащие  .
.
2.8
Следствие. Пусть  --- формация всех
--- формация всех  -разложимых групп. Тогда
-разложимых групп. Тогда  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальные
подгруппы группы
-субнормальные
подгруппы группы  , принадлежащие
, принадлежащие  .
.
2.9
Следствие [10-A, 13-A]. Пусть 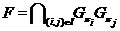 .
Тогда формация
.
Тогда формация  содержит любую группу
содержит любую группу  , у которой
, у которой 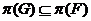 и
силовские подгруппы из подгрупп
и
силовские подгруппы из подгрупп  и
и 
 -субнормальны
в
-субнормальны
в  .
.
2.10
Следствие [10-A, 13-A]. Пусть  ---
формация всех
---
формация всех  -нильпо- тентных групп. Тогда
-нильпо- тентных групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из
подгрупп
, у которой силовские подгруппы из
подгрупп  и
и 
 -субнормальны в
-субнормальны в  .
.
2.11
Следствие [10-A, 13-A]. Пусть  ---
формация всех
---
формация всех  -замкнутых групп. Тогда
-замкнутых групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из
подгрупп
, у которой силовские подгруппы из
подгрупп  и
и 
 -субнормальны в
-субнормальны в  .
.
2.12
Следствие [10-A, 13-A]. Пусть  ---
формация всех
---
формация всех  -разложимых групп. Тогда
-разложимых групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из
подгрупп
, у которой силовские подгруппы из
подгрупп  и
и 
 -субнормальны в
-субнормальны в  .
.
2.13
Лемма.
Пусть  --- непустая наследственная формация.
Пусть все композиционные факторы группы
--- непустая наследственная формация.
Пусть все композиционные факторы группы  принадлежат
принадлежат
 . Тогда следующие утверждения
эквивалентны:
. Тогда следующие утверждения
эквивалентны:
1)
 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  ;
;
2)
 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы  .
.
Доказательство.
Пусть  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Тогда, по определению,
. Тогда, по определению,  ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы  .
.
Пусть
 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы  . Тогда существует цепь
. Тогда существует цепь
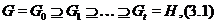
в
которой для любого 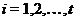 либо
либо  нормальна
в
нормальна
в 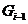 , либо
, либо 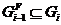 .
.
Пусть
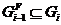 . Уплотним участок от
. Уплотним участок от  до
до 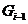 цепи
цепи
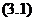 до максимальной
до максимальной 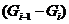 -цепи.
-цепи.
Ввиду
утверждения 1) леммы 3.1.4, все подгруппы 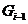 ,
содержащие
,
содержащие  ,
,  -субнормальны
в
-субнормальны
в 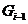 . Пусть теперь
. Пусть теперь  нормальна
в
нормальна
в 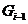 . Можно считать, что
. Можно считать, что  --- максимальная нормальная подгруппа
--- максимальная нормальная подгруппа 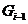 (в противном случае уплотняем участок
от
(в противном случае уплотняем участок
от  до
до 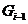 до
композиционной
до
композиционной 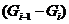 -цепи). Ввиду условия леммы
-цепи). Ввиду условия леммы  , т. е.
, т. е. 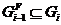 .
Пришли к рассматриваемому выше случаю. Теперь, ввиду утверждения 1) леммы
3.1.4, подгруппа
.
Пришли к рассматриваемому выше случаю. Теперь, ввиду утверждения 1) леммы
3.1.4, подгруппа 
 -субнормальна
в
-субнормальна
в  . Лемма доказана.
. Лемма доказана.
2.14
Лемма.
Пусть  --- наследственная насыщенная формация.
Тогда следующие утверждения эквивалентны:
--- наследственная насыщенная формация.
Тогда следующие утверждения эквивалентны:
1)
любая группа  , где
, где 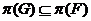 и
любые силовские подгруппы из подгрупп
и
любые силовские подгруппы из подгрупп  и
и 
 -субнормальны
в
-субнормальны
в  , принадлежит
, принадлежит  ;
;
2)
любая группа  , где
, где 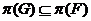 и
любые силовские подгруппы из подгрупп
и
любые силовские подгруппы из подгрупп  и
и 
 -достижимы
в
-достижимы
в  , принадлежит
, принадлежит  .
.
Доказательство.
Покажем, что из 1) следует 2). Доказательство проведем индукцией по порядку
группы  .
.
Пусть
 --- минимальная нормальная подгруппа
группы
--- минимальная нормальная подгруппа
группы  . Очевидно, что
. Очевидно, что 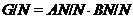 .
Пусть
.
Пусть  --- произвольная
--- произвольная  -силовская подгруппа из
-силовская подгруппа из  . Ясно, что
. Ясно, что 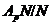 ---
---  -силовская подгруппа из
-силовская подгруппа из  . По лемме 3.1.5,
. По лемме 3.1.5, 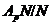 ---
---  -достижимая
подгруппа группы
-достижимая
подгруппа группы 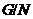 . Аналогичным образом
доказыватся, что любая силовская подгруппа из
. Аналогичным образом
доказыватся, что любая силовская подгруппа из 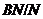
 -достижима в
-достижима в 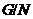 . Так
как
. Так
как 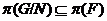 , то по индукции,
, то по индукции, 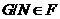 . Предположим, что
. Предположим, что 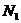 и
и 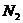 ---
две различные минимальные нормальные подгруппы группы
---
две различные минимальные нормальные подгруппы группы  .
Выше показано, что
.
Выше показано, что 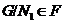 ,
, 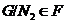 . Так
как
. Так
как  --- формация, то
--- формация, то 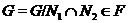 . Итак,
. Итак,  имеет
единственную минимальную нормальную подгруппу
имеет
единственную минимальную нормальную подгруппу  .
.
Покажем,
что 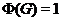 . Предположим противное. Тогда, как и
выше, с учетом индукции можно показать, что
. Предположим противное. Тогда, как и
выше, с учетом индукции можно показать, что 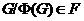 . Так
как
. Так
как  --- наследственная формация, то
--- наследственная формация, то 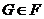 . Итак,
. Итак, 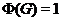 .
.
Рассмотрим
следующие два случая.
1)
Пусть  --- абелева, тогда
--- абелева, тогда  --- примарная группа. Так как
--- примарная группа. Так как  --- насыщенная формация и
--- насыщенная формация и 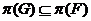 , то
, то 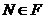 . Как
и выше, с учетом индукции можно показать, что
. Как
и выше, с учетом индукции можно показать, что 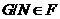 .
Теперь, с учетом леммы 3.2.13 и условия следует, что
.
Теперь, с учетом леммы 3.2.13 и условия следует, что 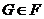 .
.
2)
Пусть  --- неабелева группа. В этом случае
--- неабелева группа. В этом случае
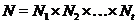
есть
прямое произведение изоморфных неабелевых простых групп и 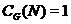 .
.
Рассмотрим
подгруппу 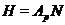 . Согласно лемме 3.1.5,
. Согласно лемме 3.1.5, 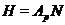 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Пусть
. Пусть 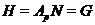 . Так как
. Так как 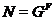 и
и  --- собственная
--- собственная  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  , то равенство
, то равенство 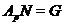 невозможно. Итак,
невозможно. Итак, 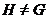 .
.
Так
как 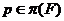 и
и  ---
насыщенная формация, то
---
насыщенная формация, то  . Отсюда следует, что
. Отсюда следует, что
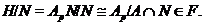
А
это значит, что 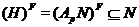 . Если
. Если  ,
то
,
то 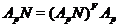 . Последнее равенство невозможно, так
как
. Последнее равенство невозможно, так
как  , согласно лемме 3.1.4, собственная
, согласно лемме 3.1.4, собственная  -субнормальная подгруппа
-субнормальная подгруппа 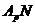 .
.
Итак,
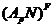 --- собственная подгруппа
--- собственная подгруппа  . Если
. Если 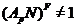 , то
, то
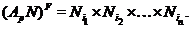
Так
как 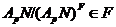 и
и  ---
наследственная формация, то
---
наследственная формация, то 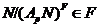 . Но тогда нетрудно
заметить, что
. Но тогда нетрудно
заметить, что 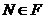 .
.
Согласно
индукции, группа 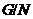 принадлежит формации
принадлежит формации  . Согласно лемме 3.2.13, любая
. Согласно лемме 3.2.13, любая  -достижимая подгруппа является
-достижимая подгруппа является  -субнормальной подгруппой. Согласно
условию получаем, что группа
-субнормальной подгруппой. Согласно
условию получаем, что группа  принадлежит
принадлежит  .
.
Непосредственно
из определения  -субнормальности и
-субнормальности и  -достижимости из 2) следует 1). Лемма
доказана.
-достижимости из 2) следует 1). Лемма
доказана.
Непосредственно
из данной леммы и теоремы 3.2.3 следует следующая теорема.
2.15
Теорема.
Пусть 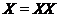 --- наследственная формация. Тогда
всякая формация
--- наследственная формация. Тогда
всякая формация  , представимая в виде
, представимая в виде 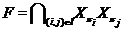 , содержит любую группу
, содержит любую группу  , у которой
, у которой 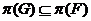 и
силовские подгруппы из подгрупп
и
силовские подгруппы из подгрупп  и
и 
 -достижимы
в
-достижимы
в  .
.
2.16
Следствие. Пусть 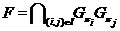 . Тогда формация
. Тогда формация  содержит любую группу
содержит любую группу  , у которой
, у которой 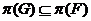 и
силовские подгруппы из подгрупп
и
силовские подгруппы из подгрупп  и
и 
 -достижимы
в
-достижимы
в  .
.
2.17
Следствие. Пусть  --- формация всех
--- формация всех  -нильпотентных групп. Тогда
-нильпотентных групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из
подгрупп
, у которой силовские подгруппы из
подгрупп  и
и 
 -достижимы в
-достижимы в  .
.
2.18
Следствие. Пусть  --- формация всех
--- формация всех  -замкнутых групп. Тогда
-замкнутых групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из
подгрупп
, у которой силовские подгруппы из
подгрупп  и
и 
 -достижимы в
-достижимы в  .
.
2.19
Следствие. Пусть  --- формация всех
--- формация всех  -разложимых групп. Тогда
-разложимых групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из
подгрупп
, у которой силовские подгруппы из
подгрупп  и
и 
 -достижимы в
-достижимы в  .
.
В
теории формаций конечных групп одной из известных проблем является проблема
Шеметкова об описании сверхрадикальных формаций.
В.Н.
Семенчуком в работе [28] получено полное решение проблемы Л.А. Шеметкова в
классе конечных разрешимых групп. Оказалось, что все такие формации имеют
следующее строение: 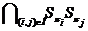 , где
, где 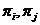 ---
некоторые множества простых чисел, а
---
некоторые множества простых чисел, а 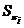 --- множество всех
разрешимых
--- множество всех
разрешимых 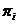 -групп.
-групп.
В
данном разделе приводится описание наследственных насыщенных сверхрадикальных
формаций, критические группы которых разрешимы.
Приведем
примеры сверхрадикальных формаций.
3.1
Пример.
Формация всех  -групп
-групп 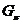 ,
где
,
где  --- некоторое множество простых чисел
является сверхрадикальной формацией.
--- некоторое множество простых чисел
является сверхрадикальной формацией.
Действительно.
Пусть  , где
, где  и
и  ---
---  -группы,
-группы,
 и
и  ---
--- 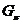 -субнормальные подгруппы группы
-субнормальные подгруппы группы  . Так как формация
. Так как формация 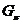 замкнута относительно расширений, то,
очевидно, что
замкнута относительно расширений, то,
очевидно, что  ---
---  -группа.
-группа.
3.2
Пример.
Формации  ,
, 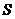 ---
сверхрадикальные формации.
---
сверхрадикальные формации.
Действительно,
если  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  , то
, то  ---
субнормальная подгруппа из
---
субнормальная подгруппа из  . Очевидно, что любая
группа
. Очевидно, что любая
группа  , где
, где  и
и  --- нильпотентные субнормальные
подгруппы из
--- нильпотентные субнормальные
подгруппы из  , нильпотентна.
, нильпотентна.
Если
 --- разрешимая
--- разрешимая 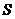 -субнормальная
подгруппа из
-субнормальная
подгруппа из  , то
, то  разрешима.
Следовательно,
разрешима.
Следовательно, 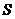 --- сверхрадикальная
формация.
--- сверхрадикальная
формация.
Следующая
лемма устанавливает связь между сверхрадикальными формациями и формациями
Фиттинга.
Напомним,
что формациями Фиттинга  называются формации,
которые замкнуты относительно взятия субнормальных подгрупп и произведения
нормальных
называются формации,
которые замкнуты относительно взятия субнормальных подгрупп и произведения
нормальных  -подгрупп.
-подгрупп.
3.3
Лемма.
Пусть  --- наследственная сверхрадикальная
формация, тогда
--- наследственная сверхрадикальная
формация, тогда  --- формация Фиттинга.
--- формация Фиттинга.
Доказательство.
Пусть  , где
, где  и
и  --- нормальные
--- нормальные  -подгруппы
группы
-подгруппы
группы  . Так как
. Так как
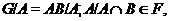
то
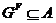 . Аналогичным образом,
. Аналогичным образом, 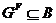 . Согласно лемме 3.1.4,
. Согласно лемме 3.1.4,  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  . Так как
. Так как  ---
сверхрадикальная формация, то
---
сверхрадикальная формация, то 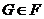 . Итак,
. Итак,  --- формация Фиттинга. Лемма доказана.
--- формация Фиттинга. Лемма доказана.
3.4
Лемма. Пусть
 --- непустая наследственная формация.
Если
--- непустая наследственная формация.
Если  содержит любую группу
содержит любую группу  , где для любого
, где для любого  из
из
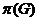 силовские
силовские  -подгруппы
-подгруппы
 и
и 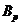 принадлежат
принадлежат
 и
и  -субнормальные
подгруппы в
-субнормальные
подгруппы в  , то
, то  ---
сверхрадикальная формация.
---
сверхрадикальная формация.
Доказательство.
Пусть  --- непустая наследственная формация,
удовлетворяющая условию леммы. Покажем, что
--- непустая наследственная формация,
удовлетворяющая условию леммы. Покажем, что  ---
сверхрадикальная формация. Пусть
---
сверхрадикальная формация. Пусть  , где
, где  и
и  ---
---  -субнормальные
-субнормальные  -подгруппы
группы
-подгруппы
группы  . Пусть
. Пусть  ---
произвольное простое число из
---
произвольное простое число из 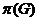 , а
, а  и
и 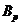 ---
силовские
---
силовские  -подгруппы из
-подгруппы из  и
и
 соответственно. Так как
соответственно. Так как  и
и  принадлежат
принадлежат
 и
и  ---
наследственная формация, то
---
наследственная формация, то  и
и 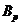 принадлежат
принадлежат  и,
и,  и
и 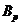
 -субнормальны в
-субнормальны в  и
и
 соответственно. Так как
соответственно. Так как  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  , то согласно лемме 3.1.4,
, то согласно лемме 3.1.4,  и
и 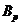
 -субнормальны в группе
-субнормальны в группе  . Согласно условию леммы,
. Согласно условию леммы,  принадлежит
принадлежит  . А
это значит, что
. А
это значит, что  --- сверхрадикальная
формация. Лемма доказана.
--- сверхрадикальная
формация. Лемма доказана.
3.5
Лемма. Пусть
 --- наследственная насыщенная
разрешимая формация. Тогда следующие утверждения эквивалентны:
--- наследственная насыщенная
разрешимая формация. Тогда следующие утверждения эквивалентны:
1)
 --- сверхрадикальная формация;
--- сверхрадикальная формация;
2)
 --- содержит любую группу
--- содержит любую группу  , где
, где 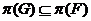 и
для любого простого числа
и
для любого простого числа  из
из 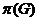 силовские
силовские  -подгруппы
-подгруппы
 и
и 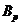
 -субнормальны в
-субнормальны в  .
.
Доказательство.
Покажем, что из 1) следует 2).
Пусть
 --- сверхрадикальная формация и пусть
--- сверхрадикальная формация и пусть  , где
, где 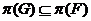 и
для любого простого числа
и
для любого простого числа  из
из 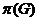
 и
и 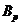 ---
---  -субнормальные
подгруппы группы
-субнормальные
подгруппы группы  . Так как
. Так как  --- насыщенная формация и
--- насыщенная формация и 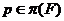 , то
, то  и
и 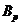 принадлежат
принадлежат  . Так
как
. Так
как  --- разрешимая формация и
--- разрешимая формация и  ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  , то отсюда нетрудно показать,
что
, то отсюда нетрудно показать,
что  --- разрешимая группа. А это значит,
что
--- разрешимая группа. А это значит,
что  и
и  разрешимы.
разрешимы.
Согласно
теореме Ф. Холла [63], 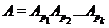 , где
, где 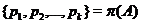 . Так как
. Так как  ---
сверхрадикальная формация, то
---
сверхрадикальная формация, то 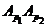 принадлежит
принадлежит  . Так как
. Так как  и
и 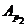 ---
---  -субнормальные
подгруппы группы
-субнормальные
подгруппы группы  , то согласно теореме 2.2.10,
, то согласно теореме 2.2.10, 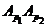 ---
---  -субнормальная
подгруппа группы
-субнормальная
подгруппа группы  . Так как
. Так как 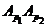 принадлежит
принадлежит  и
и  --- сверхрадикальная формация, то
подгруппа
--- сверхрадикальная формация, то
подгруппа 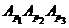 принадлежит
принадлежит  .
Продолжая в аналогичном порядке получаем, что
.
Продолжая в аналогичном порядке получаем, что  принадлежит
принадлежит
 . Аналогичным образом можем доказать,
что
. Аналогичным образом можем доказать,
что  принадлежит
принадлежит  . Так
как
. Так
как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то 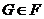 .
.
Тот
факт, что из 2) следует 1) вытекает из леммы 3.3.4. Лемма доказана.
В
следующей теореме получено решение проблемы Шеметкова о классификации
сверхрадикальных формаций для наследственных насыщенных формаций, критические
группы которых разрешимы.
3.6
Теорема
[20-A]. Пусть  --- наследственная насыщенная
формация такая, что
--- наследственная насыщенная
формация такая, что 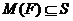 . Тогда следующие утверждения
эквивалентны:
. Тогда следующие утверждения
эквивалентны:
1)
 --- сверхрадикальная формация;
--- сверхрадикальная формация;
2)
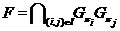 , где
, где 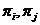 ---
некоторые множества простых чисел.
---
некоторые множества простых чисел.
Доказательство.
Пусть  --- сверхрадикальная формация. Вначале
докажем, что любая минимальная не
--- сверхрадикальная формация. Вначале
докажем, что любая минимальная не  -группа является либо
группой простого порядка, либо группой Шмидта.
-группа является либо
группой простого порядка, либо группой Шмидта.
Пусть
 --- произвольная минимальная не
--- произвольная минимальная не  -группа. Согласно условию теоремы,
-группа. Согласно условию теоремы,  разрешима. Если
разрешима. Если  ,
то нетрудно заметить, что
,
то нетрудно заметить, что  --- группа простого
порядка
--- группа простого
порядка 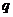 , где
, где 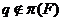 .
.
Рассмотрим
случай, когда 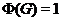 . Согласно теореме 2.2.5,
. Согласно теореме 2.2.5, 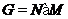 , где
, где  ---
единственная минимальная нормальная подгруппа из
---
единственная минимальная нормальная подгруппа из  ,
,  ---
---  -группа,
-группа,
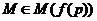 ,
, 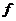 ---
максимальный внутренний локальный экран формации
---
максимальный внутренний локальный экран формации  .
Очевидно, что
.
Очевидно, что 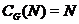 .
.
Покажем,
что  является примарной циклической
подгруппой. Предположим противное. Поскольку
является примарной циклической
подгруппой. Предположим противное. Поскольку 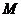 ---
разрешимая группа, то в
---
разрешимая группа, то в 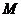 существуют
максимальные подгруппы
существуют
максимальные подгруппы 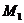 и
и 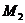 такие,
что
такие,
что 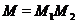 . Так как
. Так как 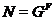 , то
очевидно, что
, то
очевидно, что 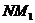 и
и 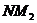 ---
---  -нормальные максимальные
-нормальные максимальные  -подгруппы группы
-подгруппы группы  . Но тогда
. Но тогда 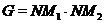 .
Так как
.
Так как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то 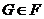 . Противоречие. Итак,
. Противоречие. Итак, 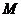 имеет единственный класс максимальных
сопряженных подгрупп. Следовательно,
имеет единственный класс максимальных
сопряженных подгрупп. Следовательно, 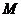 --- циклическая
--- циклическая 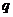 -подгруппа. Поскольку
-подгруппа. Поскольку  --- насыщенная формация и
--- насыщенная формация и 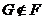 , имеем
, имеем 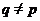 .
.
Покажем,
что  . Предположим противное. Пусть
. Предположим противное. Пусть 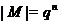 , где
, где  .
Пусть
.
Пусть  и
и 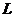 ---
циклические группы соответственно порядков
---
циклические группы соответственно порядков 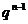 и
и 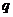 . Обозначим через
. Обозначим через  регулярное сплетение
регулярное сплетение 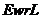 . Пусть
. Пусть 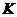 ---
база сплетения, т. е.
---
база сплетения, т. е. 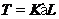 . Так как некоторая подгруппа
группы
. Так как некоторая подгруппа
группы  изоморфна
изоморфна 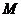 , то
, то 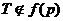 . Очевидно, подгруппы
. Очевидно, подгруппы 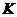 ,
, 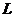 принадлежат
формации
принадлежат
формации 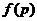 .
.
Пусть
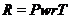 , где
, где 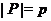 .
Обозначим через
.
Обозначим через 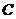 базу сплетения
базу сплетения 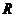 . Тогда
. Тогда 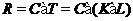 .
.
Так
как 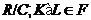 , то
, то 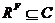 ,
значит, что подгруппы
,
значит, что подгруппы 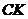 и
и 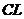
 -субнормальны в
-субнормальны в 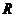 .
Легко видеть, что
.
Легко видеть, что  ,
, 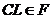 .
.
Так
как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то 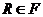 . Но
. Но 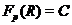 , и
поэтому
, и
поэтому 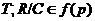 .
.
Полученное
противоречие показывает, что 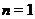 . Итак,
. Итак, 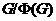 --- группа Шмидта. Теперь из леммы
3.1.1 следует, что
--- группа Шмидта. Теперь из леммы
3.1.1 следует, что  --- группа Шмидта.
--- группа Шмидта.
Пусть
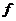 --- максимальный внутренний локальный
экран формации
--- максимальный внутренний локальный
экран формации  . Покажем, что формация
. Покажем, что формация  имеет полный локальный экран
имеет полный локальный экран 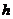 такой, что
такой, что 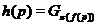 , для
любого
, для
любого  из
из  .
Действительно, пусть
.
Действительно, пусть 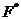 --- такая формация, у которой
есть локальный экран
--- такая формация, у которой
есть локальный экран 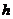 . Покажем, что
. Покажем, что  .
.
С
учетом того, что 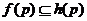 для любого простого
для любого простого  из
из  ,
получим
,
получим 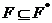 .
.
Покажем
обратное включение. Пусть  --- группа
наименьшего порядка из
--- группа
наименьшего порядка из 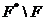 . Так как
. Так как  --- наследственная формация, то
формация
--- наследственная формация, то
формация 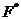 также является наследственной, значит,
также является наследственной, значит, 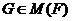 . Так как
. Так как  ---
насыщенная формация, то нетрудно показать, что
---
насыщенная формация, то нетрудно показать, что 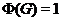 .
.
Выше
показано, что  --- либо группа простого
порядка, либо группа Шмидта. Пусть
--- либо группа простого
порядка, либо группа Шмидта. Пусть  --- группа простого
порядка и
--- группа простого
порядка и 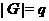 . Нетрудно показать, что
. Нетрудно показать, что 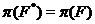 . Так как
. Так как 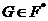 ,
имеем
,
имеем 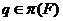 . Отсюда следует, что
. Отсюда следует, что 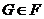 . Противоречие.
. Противоречие.
Пусть
теперь  --- группа Шмидта. Поскольку
--- группа Шмидта. Поскольку 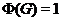 , то из свойств группы Шмидта следует
, то из свойств группы Шмидта следует 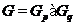 , где
, где 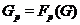 и
и 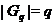 . Так как
. Так как 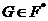 , то
, то 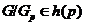 . Из того, что
. Из того, что 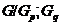 ,
следует
,
следует 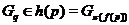 . Так как
. Так как 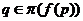 и
и 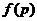 --- наследственная формация, то
--- наследственная формация, то 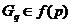 . Теперь из того, что
. Теперь из того, что 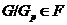 , где
, где 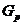 ---
единственная минимальная нормальная подгруппа группы
---
единственная минимальная нормальная подгруппа группы  и
и
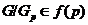 , следует что
, следует что 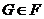 .
Получили противоречие. Итак,
.
Получили противоречие. Итак, 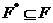 , значит,
, значит,  .
.
Так
как 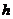 --- локальный экран формации
--- локальный экран формации  , имеем
, имеем
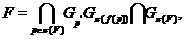
следовательно,
 --- формация из 2).
--- формация из 2).
Пусть
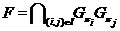 . Тогда из следствия 3.2.5 следует, что
. Тогда из следствия 3.2.5 следует, что  --- сверхрадикальная формация. Теорема
доказана.
--- сверхрадикальная формация. Теорема
доказана.
Покажем,
что в теореме 3.3.6 условие наследственной насыщенной формации  можно отбросить, в случае, когда
можно отбросить, в случае, когда  --- разрешимая формация.
--- разрешимая формация.
3.7
Лемма.
Пусть  --- разрешимая нормально наследственная
формация. Если
--- разрешимая нормально наследственная
формация. Если 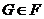 и
и 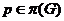 , то
, то 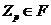 .
.
Доказательство.
Пусть 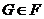 и
и 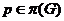 .
Если
.
Если 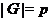 , то утверждение леммы очевидно. Пусть
, то утверждение леммы очевидно. Пусть 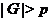 . Пусть
. Пусть 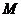 ---
нормальная максимальная подгруппа группы
---
нормальная максимальная подгруппа группы  .
Если
.
Если 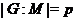 , то
, то 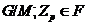 .
.
Пусть
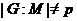 . Ясно, что
. Ясно, что 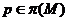 . Так
как
. Так
как 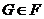 и
и  ---
нормально наследственная формация, то
---
нормально наследственная формация, то  .
Индукцией по порядку группы
.
Индукцией по порядку группы  получаем, что
получаем, что 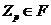 . Лемма доказана.
. Лемма доказана.
Если
 --- произвольный класс групп, то через
--- произвольный класс групп, то через  обозначим наибольший по включению
наследственный подкласс класса
обозначим наибольший по включению
наследственный подкласс класса  . Более точно
. Более точно

3.8
Лемма.
Всякая разрешимая сверхрадикальная формация является наследственной формацией.
Доказательство.
Пусть  --- разрешимая сверхрадикальная формация.
Как и в теореме 3.3.6 нетрудно показать, что любая разрешимая минимальная не
--- разрешимая сверхрадикальная формация.
Как и в теореме 3.3.6 нетрудно показать, что любая разрешимая минимальная не  -группа является группой Шмидта, либо
группой простого порядка.
-группа является группой Шмидта, либо
группой простого порядка.
Покажем,
что  , где
, где 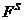 ---
максимальная наследственная подформация из
---
максимальная наследственная подформация из  .
Допустим, что множество
.
Допустим, что множество 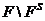 непусто и выберем в
нем группу
непусто и выберем в
нем группу  наименьшего порядка. В силу леммы
2.2.11, формация
наименьшего порядка. В силу леммы
2.2.11, формация 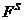 является насыщенной. Поэтому
является насыщенной. Поэтому 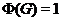 . Очевидно, что группа
. Очевидно, что группа  имеет единственную минимальную
нормальную подгруппу
имеет единственную минимальную
нормальную подгруппу  и
и 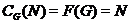 .
Так как
.
Так как 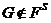 , то в
, то в  найдется
минимальная не
найдется
минимальная не 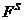 -группа
-группа  . Из нормальной наследственности
формации
. Из нормальной наследственности
формации  следует, что
следует, что 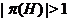 .
Ясно, что
.
Ясно, что  является также минимальной не
является также минимальной не  -группой.
-группой.
По
условию,  --- группа Шмидта. В этом случае
--- группа Шмидта. В этом случае 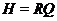 , где
, где 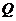 ---
нормальная силовская
---
нормальная силовская 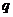 -подгруппа, а
-подгруппа, а 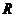 --- циклическая
--- циклическая  -подгруппа
группы
-подгруппа
группы  ,
, 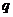 и
и  --- различные простые числа.
--- различные простые числа.
Если
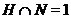 , то
, то
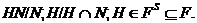
Получили
противоречие с выбором  . Остается принять, что
. Остается принять, что  . Отсюда и из
. Отсюда и из 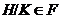 получаем,
что
получаем,
что 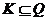 , а значит,
, а значит,  ---
--- 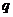 -группа. Рассмотрим
-группа. Рассмотрим 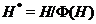 . Тогда группу
. Тогда группу  можно
представить в виде
можно
представить в виде

где
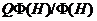 --- элементарная абелева
--- элементарная абелева 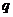 -группа, а
-группа, а 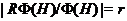 .
Так как
.
Так как  не входит в
не входит в  , то
по лемме 2.2.12
, то
по лемме 2.2.12 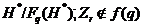 , где
, где 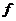 ---
максимальный внутренний локальный экран формации
---
максимальный внутренний локальный экран формации  . Так
как
. Так
как 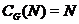 и
и 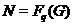 , то
, то 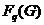 является
является 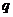 -группой.
Отсюда следует, что
-группой.
Отсюда следует, что 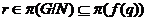 . Из нормальной
наследственности формации
. Из нормальной
наследственности формации  , по теореме 2.2.13,
следует, что
, по теореме 2.2.13,
следует, что 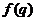 является нормально наследственной
формацией. Тогда, по лемме 3.3.7,
является нормально наследственной
формацией. Тогда, по лемме 3.3.7, 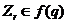 . Получили
противоречие. Таким образом,
. Получили
противоречие. Таким образом,  . Лемма доказана.
. Лемма доказана.
Напомним,
что формация  называется формацией Шеметкова, если
любая минимальная не
называется формацией Шеметкова, если
любая минимальная не  -группа является либо группой
Шмидта, либо группой простого порядка.
-группа является либо группой
Шмидта, либо группой простого порядка.
3.9
Теорема
[16-A]. Пусть  --- наследственная насыщенная
формация. Тогда следующие утверждения эквивалентны:
--- наследственная насыщенная
формация. Тогда следующие утверждения эквивалентны:
1)
 --- формация Шеметкова;
--- формация Шеметкова;
2)
формация  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -достижимые
-достижимые
 -подгруппы из
-подгруппы из  и
и
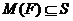 ;
;
3)
 --- сверхрадикальная формация и
--- сверхрадикальная формация и 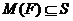 ;
;
4)
формация  такая, что для любой группы
такая, что для любой группы  и для любых ее перестановочных
и для любых ее перестановочных  -субнормальных подгрупп
-субнормальных подгрупп  и
и 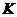 подгруппа
подгруппа

 -субнормальна
в
-субнормальна
в  и
и 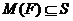 ;
;
5)
формация  такая, что для любой группы
такая, что для любой группы  и для любых ее перестановочных
и для любых ее перестановочных  -достижимых подгрупп
-достижимых подгрупп  и
и 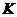 подгруппа
подгруппа

 -достижима
в
-достижима
в  и
и 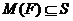 ;
;
6)
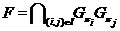 , где
, где 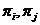 ---
некоторые множества простых чисел и
---
некоторые множества простых чисел и 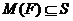 .
.
Доказательство
следует из теорем 2.2.14, 2.2.15 и теоремы 3.3.6.
3.10
Теорема [3-A,
5-A]. Пусть  --- наследственная насыщенная формация
такая, что
--- наследственная насыщенная формация
такая, что 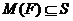 . Тогда следующие утверждения
эквивалентны:
. Тогда следующие утверждения
эквивалентны:
1)
формация  содержит любую группу
содержит любую группу  , где
, где  и
и 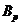 ---
---  -субнормальны
в G и
-субнормальны
в G и 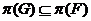 ;
;
2)
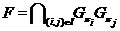 , где
, где 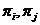 ---
некоторые множества простых чисел.
---
некоторые множества простых чисел.
Доказательство.
Покажем, что из 1) следует 2).
Пусть
 --- формация, удовлетворяющая
утверждению 1). Покажем, что она является сверхрадикальной формацией. Пусть
--- формация, удовлетворяющая
утверждению 1). Покажем, что она является сверхрадикальной формацией. Пусть  --- любая группа такая, что
--- любая группа такая, что  , где
, где  и
и  ---
---  -субнормальные
подгруппы группы
-субнормальные
подгруппы группы  , принадлежащие
, принадлежащие  . Пусть
. Пусть  и
и 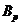 произвольные
произвольные  -силовские
подгруппы из
-силовские
подгруппы из  и
и  соответственно.
Так как
соответственно.
Так как 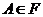 ,
, 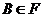 и
и  --- наследственная формация, то
--- наследственная формация, то  и
и 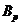
 -субнормальны соответственно в
-субнормальны соответственно в  и
и  . Так
как
. Так
как  и
и 
 -субнормальны в
-субнормальны в  ,
то по лемме 3.1.4,
,
то по лемме 3.1.4,  и
и 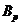
 -субнормальны в группе
-субнормальны в группе  . Отсюда следует, что
. Отсюда следует, что 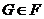 . Следовательно,
. Следовательно,  ---
сверхрадикальная формация.
---
сверхрадикальная формация.
Теперь,
согласно теореме 3.3.6, получаем, что 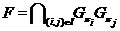 .
.
Обратное
утверждение следует из следствия 3.2.16. Теорема доказана.
Из
леммы 3.3.5 следует, что в классе конечных разрешимых групп класс всех
наследственных насыщенных сверхрадикальных формаций совпадает с классом всех
наследственных насыщенных формаций, замкнутых относительно произведения
подгрупп  и
и  ,
силовские подгруппы которых обобщенно субнормальны в
,
силовские подгруппы которых обобщенно субнормальны в 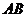 .
.
Как
следует из теоремы 3.3.10, аналогичное утверждение верно для всех
наследственных насыщенных формаций, критические группы которых разрешимы.
Однако для произвольной наследственной насыщенной формации данный вопрос
остается открытым.
В
главе 1 приведены некоторые свойства критических групп и обобщенно
субнормальных подгрупп, необходимые для доказательства основных результатов
глав2 и 3.
В
главе 2 найдены серии наследственных насыщенных формаций  , замкнутых относительно произведения
подгрупп
, замкнутых относительно произведения
подгрупп  и
и  , у
которых любая силовская подгруппа
, у
которых любая силовская подгруппа  -субнормальна в
-субнормальна в 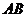 , теорема 2.3 [10-A,13-A].
, теорема 2.3 [10-A,13-A].
В
главе 3 получено описание наследственных насыщенных сверхрадикальных формаций,
критические группы которых разрешимы, теорема 3.6 [20-A].
Основные
научные результаты работы
В
данной работе проведено изучение строения наследственных насыщенных формаций  , замкнутых относительно произведения
, замкнутых относительно произведения  -подгрупп, обладающих заданными
свойствами.
-подгрупп, обладающих заданными
свойствами.
1.
Найдены серии произвольных наследственных насыщенных формаций  , замкнутых относительно произведения
подгрупп
, замкнутых относительно произведения
подгрупп  и
и  , у
которых любая силовская подгруппа
, у
которых любая силовская подгруппа  -субнормальна в
-субнормальна в 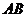 [10-A, 13-A].
[10-A, 13-A].
2.
Получено описание наследственных насыщенных сверхрадикальных формаций,
критические группы которых разрешимы [20-A].
3.
В классе конечных разрешимых групп получено описание наследственных насыщенных
формаций  , замкнутых относительно произведения
обобщенно субнормальных
, замкнутых относительно произведения
обобщенно субнормальных  -подгрупп взаимно
простых индексов [18-A].
-подгрупп взаимно
простых индексов [18-A].
4.
Доказано, что любая разрешимая 2-кратно насыщенная формация  , замкнутая относительно произведения
обобщенно субнормальных
, замкнутая относительно произведения
обобщенно субнормальных  -подгрупп, индексы
которых взаимно просты является сверхрадикальной [18-A].
-подгрупп, индексы
которых взаимно просты является сверхрадикальной [18-A].
5.
Получено описание наследственных насыщенных  -формаций
Шеметкова [14-A, 21-A].
-формаций
Шеметкова [14-A, 21-A].
6.
Получено описание наследственных насыщенных 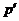 -формаций
Шеметкова [14-A, 21-A].
-формаций
Шеметкова [14-A, 21-A].
7.
В классе конечных разрешимых групп получено описание наследственных формаций
Фиттинга  , замкнутых относительно произведения
, замкнутых относительно произведения  -подгрупп, индексы которых не делятся на
некоторое фиксированное простое число [14-A, 21-A].
-подгрупп, индексы которых не делятся на
некоторое фиксированное простое число [14-A, 21-A].
Полученные
результаты могут найти приложение в вопросах классификации классов конечных групп,
в дальнейшем развитии теории обобщенно субнормальных подгрупп, а также при
изучении строения непростых конечных групп по заданным свойствам её обобщенно
субнормальных и критических подгрупп.
Решенные
в диссертации задачи позволяют подойти к ещё нерешенным проблемам: задаче об
описании наследственных сверхрадикальных формаций; задаче об описании
наследственных насыщенных формаций  , замкнутых
относительно произведений обобщенно субнормальных
, замкнутых
относительно произведений обобщенно субнормальных  -подгрупп,
индексы которых взаимно просты.
-подгрупп,
индексы которых взаимно просты.
Результаты
диссертации могут быть использованы в учебном процессе при чтении спецкурсов
для студентов математических специальностей в высших учебных заведениях,
написании курсовых, дипломных проектов и диссертаций.
1. Васильев, А.Ф. О
максимальной наследственной подформации локальной формации / А.Ф. Васильев //
Вопросы алгебры: межведомств. сб. / Мин-во народного обр. БССР, Гомельский гос.
ун-т; редкол.: Л.А. Шеметков [и др.]. -- Минск: Университетское, 1990. -- Вып.
5. -- С. 39--45.
2. Васильев, А.Ф. О
решетках подгрупп конечных групп / А.Ф. Васильев, С.Ф. Каморников, В.Н.
Семенчук // Бесконечные группы и примыкающие алгебраические системы / Ин-т
математики Акад. Украины; редкол.: Н.С. Черников [и др.]. -- Киев, 1993. -- С.
27--54.
3. Васильев, А.Ф. О
влиянии примарных  -субнормальных подгрупп на
строение группы / А.Ф. Васильев // Вопросы алгебры: межведомств. сб. / Мин-во
обр. и науки Республики Беларусь, Гомельский гос. ун-т им. Ф. Скорины; редкол.:
Л.А. Шеметков [и др.]. -- Гомель, 1995. -- Вып. 8. -- С. 31--39.
-субнормальных подгрупп на
строение группы / А.Ф. Васильев // Вопросы алгебры: межведомств. сб. / Мин-во
обр. и науки Республики Беларусь, Гомельский гос. ун-т им. Ф. Скорины; редкол.:
Л.А. Шеметков [и др.]. -- Гомель, 1995. -- Вып. 8. -- С. 31--39.
4. Васильева, Т.И. О
конечных группах с  -достижимыми силовскими
подгруппами / Т.И. Васильева, А.И. Прокопенко. -- Гомель, 2006. -- 18 с. --
(Препринт / Гомельский гос. ун-т им. Ф. Скорины; № 4).
-достижимыми силовскими
подгруппами / Т.И. Васильева, А.И. Прокопенко. -- Гомель, 2006. -- 18 с. --
(Препринт / Гомельский гос. ун-т им. Ф. Скорины; № 4).
5. Ведерников, В.А. О
локальных формациях конечных групп / В.А. Ведерников // Матем. заметки. --
1989. -- Т. 46, № 3. -- С. 32--37.
6. Казарин, Л.С.
Признаки непростоты факторизуемых групп / Л.С. Казарин // Известия АН СССР. --
1980. -- Т. 44, № 2. -- С. 288--308.
7. Казарин, Л.С. О
произведении конечных групп / Л.С. Казарин // ДАН СССР. -- 1983. -- Т. 269, №
3. -- С. 528--531.
8. Каморников, С.Ф. О
некоторых свойствах формаций квазинильпотентных групп / С.Ф. Каморников //
Матем. заметки. -- 1993. -- Т. 53, № 2. -- С. 71--77.
9. Каморников, С.Ф. О
двух проблемах Л.А. Шеметкова / С.Ф. Каморников // Сибир. мат. журнал. -- 1994.
-- Т. 35, № 4. -- С. 801--812.
10. Коуровская тетрадь
(нерешенные вопросы теории групп) // Институт математики СО АН СССР. -- Новосибирск,
1992. -- 172 с.
11. Коуровская тетрадь
(нерешенные вопросы теории групп) // Институт математики СО РАН. --
Новосибирск, 1999. -- 146 с.
12. Легчекова, Е.В.
Конечные группы с заданными слабо квазинормальными подгруппами / Е.В.
Легчекова, А.Н. Скиба, О.В. Титов // Доклады НАН Беларуси. -- 2007. -- Т. 51, №
1. -- С. 27--33.
13. Монахов, В.С.
Произведение конечных групп, близких к нильпотентным / В.С. Монахов // Конечные
группы. -- 1975. -- С. 70--100.
14. Монахов, В.С. О
произведении двух разрешимых групп с максимальным пересечением факторов / В.С.
Монахов // Вопросы алгебры: межведомств. сб. / Мин-во высш. и ср. спец. обр.
БССР, Гомельский гос. ун-т; редкол.: Л.А. Шеметков [и др.]. -- Минск:
Университетское, 1985. -- Вып. 1. -- С. 54--57.
15. Мокеева, С.А.
Конечные группы с перестановочными  -субнормальными (
-субнормальными ( -достижимыми) подгруппами / С.А.
Мокеева. -- Гомель, 2003. -- 25 с. -- (Препринт / Гомельский гос. ун-т им. Ф.
Скорины; № 56).
-достижимыми) подгруппами / С.А.
Мокеева. -- Гомель, 2003. -- 25 с. -- (Препринт / Гомельский гос. ун-т им. Ф.
Скорины; № 56).
16. Прокопенко, А.И. О
конечных группах с  -достижимыми силовскими
подгруппами / А.И. Прокопенко // Известия Гомельского гос. ун-та им. Ф.
Скорины. -- 2004. -- № 6 (27). -- С. 101--103.
-достижимыми силовскими
подгруппами / А.И. Прокопенко // Известия Гомельского гос. ун-та им. Ф.
Скорины. -- 2004. -- № 6 (27). -- С. 101--103.
17. Семенчук, В.Н. О
минимальных не  -группах / В.Н. Семенчук //
ДАН БССР. -- 1978. -- № 7. -- С. 596--599.
-группах / В.Н. Семенчук //
ДАН БССР. -- 1978. -- № 7. -- С. 596--599.
18. Семенчук, В.Н. Конечные
группы с заданными свойствами подгрупп / В.Н. Семенчук // ДАН БССР. -- 1979. --
№ 1. -- С. 11--15.
19. Семенчук, В.Н.
Минимальные не  -группы / В.Н. Семенчук //
Алгебра и логика. -- 1979. -- Т. 18, № 3. -- С. 348--382.
-группы / В.Н. Семенчук //
Алгебра и логика. -- 1979. -- Т. 18, № 3. -- С. 348--382.
20. Семенчук, В.Н.
Конечные группы с системой минимальных не  -подгрупп
/ В.Н. Семенчук // Подгрупповое строение конечных групп: Тр. / Ин-т математики
АН БССР. -- Минск: Наука и техника, 1981. -- С. 138--149.
-подгрупп
/ В.Н. Семенчук // Подгрупповое строение конечных групп: Тр. / Ин-т математики
АН БССР. -- Минск: Наука и техника, 1981. -- С. 138--149.
21. Семенчук, В.Н.
Минимальные не 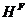 -группы / В.Н. Семенчук //
Исследование нормального и подгруппового строения конечных групп: Тр. / Ин-т
математики АН БССР. -- Минск: Наука и техника, 1984. -- С. 170--175.
-группы / В.Н. Семенчук //
Исследование нормального и подгруппового строения конечных групп: Тр. / Ин-т
математики АН БССР. -- Минск: Наука и техника, 1984. -- С. 170--175.
22. Семенчук, В.Н.
Характеризация локальных формаций  по заданным
свойствам минимальных не
по заданным
свойствам минимальных не  -групп / В.Н.
Семенчук, А.Ф. Васильев // Исследование нормального и подгруппового строения
конечных групп: Тр. / Ин-т математики АН БССР. -- Минск: Наука и техника, 1984.
-- С. 175--181.
-групп / В.Н.
Семенчук, А.Ф. Васильев // Исследование нормального и подгруппового строения
конечных групп: Тр. / Ин-т математики АН БССР. -- Минск: Наука и техника, 1984.
-- С. 175--181.
23. Семенчук, В.Н.
Описание разрешимых минимальных не  -групп для
произвольной тотально локальной формации / В.Н. Семенчук // Матем. заметки. --
1988. -- Т. 43, № 4. -- С. 251--260.
-групп для
произвольной тотально локальной формации / В.Н. Семенчук // Матем. заметки. --
1988. -- Т. 43, № 4. -- С. 251--260.
24. Семенчук, В.Н. О
разрешимых минимальных не  -группах / В.Н.
Семенчук // Вопросы алгебры. -- Минск: Университетское, 1987. -- Вып. 3. -- С.
16--21.
-группах / В.Н.
Семенчук // Вопросы алгебры. -- Минск: Университетское, 1987. -- Вып. 3. -- С.
16--21.
25. Семенчук, В.Н. Роль
минимальных не  -групп в теории формаций /
В.Н. Семенчук // Матем. заметки. -- 1991. -- Т. 98, № 1. -- С. 110--115.
-групп в теории формаций /
В.Н. Семенчук // Матем. заметки. -- 1991. -- Т. 98, № 1. -- С. 110--115.
26. Семенчук, В.Н.
Конечные группы с  -абнормальными или
-абнормальными или  -субнормальными подгруппами / В.Н.
Семенчук // Матем. заметки. -- 1994. -- Т. 56, № 6. -- С. 111--115.
-субнормальными подгруппами / В.Н.
Семенчук // Матем. заметки. -- 1994. -- Т. 56, № 6. -- С. 111--115.
27. Семенчук, В.Н.
Разрешимые тотально локальные формации / В.Н. Семенчук // Сибир. мат. журн. --
1995. -- Т. 36, № 4. -- С. 861--872.
28. Семенчук, В.Н.
Разрешимые  -радикальные формации / В.Н. Семенчук //
Матем. заметки. -- 1996. -- Т. 59, № 2. -- С. 261--266.
-радикальные формации / В.Н. Семенчук //
Матем. заметки. -- 1996. -- Т. 59, № 2. -- С. 261--266.
29. Семенчук, В.Н. Об
одной проблеме в теории формаций / В.Н. Семенчук // Весцi АН Беларусi. -- 1996.
-- № 3. -- С. 25--29.
30. Семенчук, В.Н. О
разрешимых тотально локальных формациях / В.Н. Семенчук // Вопросы алгебры. --
1997. -- № 11. -- С. 109--115.
31. Семенчук, В.Н.,
Поляков Л.Я. Характеризация минимальных не  -групп
/ В.Н. Семенчук // Известия высших учебных заведений. -- 1998. -- № 4 (431). --
С. 1--4.
-групп
/ В.Н. Семенчук // Известия высших учебных заведений. -- 1998. -- № 4 (431). --
С. 1--4.
32. Семенчук, В.Н.
Классификация локальных наследственных формаций критические группы которых
бипримарны / В.Н. Семенчук // Известия Гомельского гос. ун-та им. Ф. Скорины.
-- 1999. -- № 1 (15). -- С. 153--162.
33. Семенчук, В.Н.
Сверхрадикальные формации / В.Н. Семенчук, Л.А. Шеметков // Доклады НАН
Беларуси. -- 2000. -- Т. 44, № 5. -- С. 24--26.
34. Семенчук, В.Н.
Конечные группы, факторизуемые  -достижимыми
подгруппами / В.Н. Семенчук, С.А. Мокеева // Известия Гомельского гос. ун-та
им. Ф. Скорины. -- 2002. -- № 5 (14). -- С. 47--49.
-достижимыми
подгруппами / В.Н. Семенчук, С.А. Мокеева // Известия Гомельского гос. ун-та
им. Ф. Скорины. -- 2002. -- № 5 (14). -- С. 47--49.
35. Скиба, А.Н. Об
одном классе локальных формаций конечных групп / А.Н. Скиба // ДАН БССР. --
1990. -- Т. 34, № 11. -- С. 382--385.
36. Скиба, А.Н. Алгебра
формаций / А.Н. Скиба. -- Минск: Беларуская навука, 1997. -- 240 с.
37. Старостин, А.И. О
минимальных группах, не обладающих данным свойством / А.И. Старостин // Матем.
заметки. -- 1968. -- Т. 3, № 1. -- С. 33--37.
38. Тютянов, В.Н.
Факторизации  -нильпотентными сомножителями / В.Н.
Тютянов // Матем. сб. -- 1996. -- Т. 187, № 9. -- С. 97--102.
-нильпотентными сомножителями / В.Н.
Тютянов // Матем. сб. -- 1996. -- Т. 187, № 9. -- С. 97--102.
39. Чунихин, С.А. О
специальных группах / С.А. Чунихин // Матем. сб. -- 1929. -- Т. 36, № 2. -- С.
135--137.
40. Чунихин, С.А. О
специальных группах / С.А. Чунихин // Матем. сб. -- 1933. -- Т. 40, № 1. -- С.
39--41.
41. Чунихин, С.А. О
группах с наперед заданными подгруппами / С.А. Чунихин // Матем. сб. -- 1938.
-- Т. 4 (46), № 3. -- С. 521--530.
42. Чунихин, С.А. О
существовании подгрупп у конечной группы / С.А. Чунихин // Труды семинара по
теории групп. -- ГОНТИ, М.--Л. -- 1938. -- С. 106--125.
43. Чунихин, С.А.
Подгруппы конечных групп / С.А. Чунихин. -- Минск: Наука и техника, 1964. --
158 с.
44. Шеметков, Л.А.
Формации конечных групп / Л.А. Шеметков. -- М.: Наука, 1978. -- 272 с.
45. Шеметков, Л.А.
Экраны произведения формаций / Л.А. Шеметков // ДАН БССР. -- 1981. -- Т. 25, №
8. -- С. 677--680.
46. Шеметков, Л.А. О
произведении формаций / Л.А. Шеметков // ДАН БССР. -- 1984. -- Т. 28, № 2. --
С. 101--103.
47. Шеметков, Л.А.
Формации алгебраических систем / Л.А. Шеметков, А.Н. Скиба. -- М.: Наука, 1989.
-- 256 с.
48. Шмидт, О.Ю. Группы,
все подгруппы которых специальные / О.Ю. Шмидт // Матем. сб. -- 1924. -- Т. 31,
№ 3. -- С. 366--372.
49.
Ballester-Bolinches, A. On the lattice of  -subnormal
subgroups / A. Ballester-Bolinches, К. Doerk, M.D. Perez-Ramos // J. Algebra.
-- 1992. -- Vol. 148, № 2. -- P. 42--52.
-subnormal
subgroups / A. Ballester-Bolinches, К. Doerk, M.D. Perez-Ramos // J. Algebra.
-- 1992. -- Vol. 148, № 2. -- P. 42--52.
50. Ballester-Bolinches,
A. On  -critical groups / A.
Ballester-Bolinches, M.D. Perez-Ramos // J. Algebra. -- 1995. -- Vol. 174. --
P. 948--958.
-critical groups / A.
Ballester-Bolinches, M.D. Perez-Ramos // J. Algebra. -- 1995. -- Vol. 174. --
P. 948--958.
51.
Ballester-Bolinches, A. Two questions of L.A. Shemetkov on critical groups / A.
Ballester-Bolinches, M.D. Perez-Ramos // J. Algebra. -- 1996. -- Vol. 179. --
P. 905--917.
52.
Ballester-Bolinches, A. Classes of Finite Groups / A. Ballester-Bolinches, L.M.
Ezquerro. -- Springer, 2006. -- 385 p.
53. Bryce, R.A. Fitting
formations of finite soluble groups / R.A. Bryce, J. Cossey // Math. Z. --
1972. -- Bd. 127, № 3. -- S. 217--233.
54. Carter, R.O. The  -normalizers of a finite soluble group /
R. Carter, T. Hawkes // J. Algebra. -- 1967. -- Vol. 5, № 2. -- Р. 175--202.
-normalizers of a finite soluble group /
R. Carter, T. Hawkes // J. Algebra. -- 1967. -- Vol. 5, № 2. -- Р. 175--202.
55. Carter, R. Extreme
classes of a finite soluble groups / R. Carter, B. Fisсher, T. Hawkes // J.
Algebra. -- 1968. -- Vol. 9, № 3. -- P. 285--313.
56. Doerk, K. Minimal
nicht Uberauflosbare, endliche Gruppen / K. Doerk // Math. Z. -- 1966. -- Vol.
91. -- P. 198--205.
57. Doerk, K. Finite
soluble groups / K. Doerk, T. Hаwkes. -- Berlin -- New York: Walter de Gruyter,
1992. -- 891 p.
58. Fisman, E. On
product of two finite solvable groups / E. Fisman // J. Algebra. -- 1983. --
Vol. 80, № 2. -- P. 517--536.
59. Gaschutz, W. Zur
Theorie der endlichen auflosbaren Gruppen // Math. Z. -- 1963. -- Vol. 80, № 4.
-- P. 300--305.
60. Guo, W. The Theory
of Classes of Groups / W. Guo. -- Dordrecht -- Boston -- London: Kluwer
Academic Publishers, 2000. -- 257 p.
61. Guo, W.
X-semipermutable subgroups of finite groups / W. Guo, K.P. Shum, A.N. Skiba //
J. Algebra. -- 2007. -- Vol. 315. -- P. 31--41.
62. Hall, P. A note on
soluble groups / P. Hall // Proc. London Math. Soc. -- 1928. -- Vol. 3. -- P.
98--105.
63. Hall, P. On the
Sylow systems of a soluble group / P. Hall // Proc. London Math. Soc. -- 1937.
-- Vol. 43. -- P. 316--323.
64. Hawkes, T. On
Fitting formations / T. Hawkes // Math. Z. -- 1970. -- Vol. 117. -- P.
177--182.
65. Huppert, B.
Normalteiler und maximal Untergruppen endlichen Gruppen / B. Huppert // Math.
Z. -- 1954. -- Vol. 60. -- P. 409--434.
66. Ito, N. Note on
(LN)-groups of finite order / N. Ito // Kodai Math. Seminar Report. -- 1951. --
Vol. 1--2. -- P. 1--6.
67. Kazarin, L.S.
Product of two solvable subgroups / L.S. Kazarin // Comm. Algebra. -- 1986. --
Vol. 14, № 6. -- P. 1001--1066.
68. Kegel, O.H.
Produkte nilpotenter Gruppen // Arch. Math. -- 1961. -- Vol. 12, № 2. -- P.
90--93.
69. Kegel, O.H.
Untergruppenverbande endlicher Gruppen, die Subnormalteilerverband echt
enthalten / O.H. Kegel // Arch. Math. -- 1978. -- Bd. 30, № 3. -- S. 225--228.
70. Miller, G.A.
Nonabelian groups in which every subgroup is abelian / G.A. Miller, H.C. Moreno
// Trans. Amer. Math. Soc. -- 1903. -- Vol. 4. -- P. 398--404.
71. Semenchuk, V.N.
Finite groups with permutable  -subnormal and
-subnormal and  -accessible subgroups / V.N. Semenchuk,
S.A. Mokeeva // 4th International Algebraic Conference in Ukraine. Abstracts,
August 4--9. -- 2003. -- P. 153--154.
-accessible subgroups / V.N. Semenchuk,
S.A. Mokeeva // 4th International Algebraic Conference in Ukraine. Abstracts,
August 4--9. -- 2003. -- P. 153--154.
72. Thompson, J.G.
Nonsolvable finite groups all of whose local subgroups are solvable / J.G.
Thompson // Bull. Amer. Math. Soc. -- 1968. -- Vol. 74. -- P. 383--437.
73. Wielandt, H. Eine
Verallgemeinerung der invarianten Untergruppen // H. Wielandt // Math. Z. --
1939. -- Bd. 45. -- S. 209--244.
74. Wielandt, H. Uber
den Normalisator der subnormalen Untergruppen // H. Wielandt // Math. Z. --
1958. -- Bd. 69, № 8. -- S. 463--465.
75. Wielandt, H. Uber
das Produkt von nilpotenten Gruppen / H. Wielandt // Illinois Journ. -- 1958.
-- Vol. 2, № 4B. -- P. 611--618.