Построение цифровых моделей рельефа
1 Создание цифровых моделей рельефа и их виды.
Применение и задачи, решаемые с использованием ЦМР
С помощью новой
технологии географических информационных систем (ГИС), в отличие от аналога -
обычных "бумажных" карт, возможно обработать полученные цифровые
данные и создать максимально приближенную к действительности пространственную
трёхмерную модель или по-другому цифровую модель рельефа (ЦМР).
Цифровая модель рельефа
- это математическое представление участка земной поверхности, полученное путем
обработки материалов топографической съемки. Такая модель позволяет не просто
посмотреть положение одного объекта относительно другого, но и уточнить
структуру исследуемого объекта, а также просчитать объект путем интерполяции,
аппроксимации или экстраполяции [5].
Как следует из самого
понятия ЦМР создаётся на базе математического аппарата с использованием
компьютерной техники и информации ГИС. Для правильности пересчёта и
оптимальности затрат ресурсов необходимо чтобы математический аппарат был
адекватно подобран и способен обработать информацию правильно в кратчайшие
сроки и с минимально возможным использованием компьютерной памяти.
Для создания цифровых
моделей рельефа необходима обработка имеющихся топографических данных:
вычисление некоторой точки производится с использованием алгоритма интерполяции
(значения, получаемые в исходных точках, совпадают с истинными абсолютно точно)
или аппроксимации (значения, получаемые в исходных точках, совпадают с истинными
с некоторой степенью точности). Также точность воспроизведения особенностей
рельефа местности в ЦМР зависит от выбора метода расчёта. Для обработки может
быть использована одна приближённая формула для всей территории, так называемый
глобальный алгоритм, или применение разных формул для разных участков
моделируемой местности, так называемый кусочно-локальный алгоритм.
Оптимальность выбора в этом случае определяется качеством исходных данных: не
имеет смысла решать сложную интерполяционную задачу при низком качестве данных;
и знаниях о рельефообразующих процессах: если рельеф территории образовался
преимущественно под действием одного процесса или нескольких тесно связанных
имеет смысл использовать глобальный алгоритм, если имели место несколько
малосвязанных процессов, то кусочно-локальный алгоритм [6].
Различают следующие
виды цифровых моделей рельефа [7]:
-
регулярные;
-
структурные;
-
нерегулярные.
Для регулярных моделей
рельефа характерно расположение точек с известными пространственными
координатами в вершинах сетки квадратов (рисунок 2 а), прямоугольников, равносторонних
треугольников (рисунок 2 б) или других правильных фигур (шестиугольник на
рисунке 2 в). Либо особенные ЦМР с системой поперечных профилей, проведенных
через определенные расстояния вдоль заданной линии (например, оси трассы). В
случае линейной ЦМР положение любой точки по высоте определяется линейной
интерполяцией высот внутри заданной ячейки пространственной сетки (квадрата,
прямоугольника или треугольника). Основным недостатком такой модели рельефа
является то, что расположение точек на местности получается неоптимальным,
поскольку на некоторых участках нужна большая точность и соответственно большее
количество точек, на прочих наоборот имеющееся количество точек излишне. Отсюда
и второй недостаток - увеличенные трудозатраты при разбивке местности узловыми
точками. Основное применение регулярных ЦМР - составление моделей повышенной
точности. Весьма эффективными их можно считать при проектировании планировки
различных инженерных объектов, аэропортов и улиц городов на равнинных участках
рельефа.
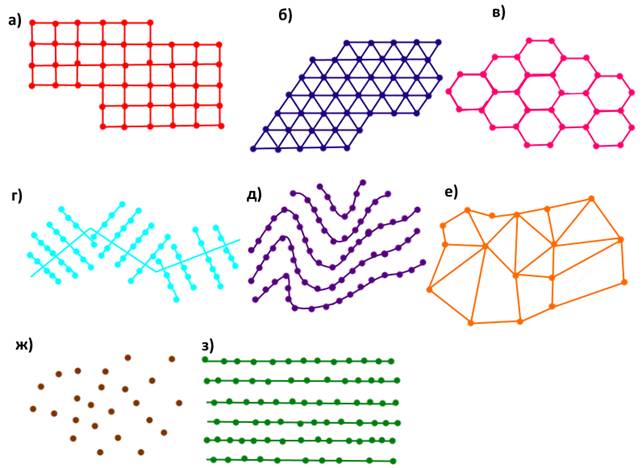
Рисунок 2 - Виды ЦМР: а - в узлах
правильных прямоугольных сеток; б - в узлах треугольных сеток; в - в узлах
шестиугольных сеток (регулярные); г - структурные - на поперечниках к
магистральному ходу; д - на горизонталях; е – нерегулярные на структурных
линиях; ж - статистическая; з - на линиях, параллельных оси фотограмметрических
координат.
Структурные ЦМР
предполагают размещение узловых точек с известными пространственными
координатами на структурных линиях рельефа (рисунок 2 г, д), местах изменения
углов наклона склонов, на характерных линиях дороги, урезах рек и тому подобное.
В этом случае отметки вдоль структурной линии меняются в соответствии с полиномиальной
зависимостью. Структурной ЦМР требуется меньшая плотность точек, чем
регулярной. При линейной интерполяции структурная модель рельефа показывает
высокую эффективность, например, для описания поверхности городских дорог. Кроме
того, такую ЦМР можно составить и при низком качестве исходных данных, их
низкой автоматизации ,в том числе при ручной обработке снимков, топографических
планов и тому подобного материала.
В нерегулярных ЦМР
точки располагаются без использования какой-либо определённой системы, но с
одинаковой заданной плотностью (рисунок 2 е, ж, з). Эта особенность обеспечила
нерегулярным цифровым моделям универсальность и в этой связи наибольшую
распространённость в настоящее время.
ЦМР возможно применять
как для цифровых вычислений различных характеристик местности, так и для
трёхмерной визуализации территории, что крайне полезно, например, для создания
виртуальных моделей местности . Также ЦМР можно использовать
для решения множества других задач [8]:
·
для
вычисления уклонов и экспозиции склонов, а также других геометрических параметров
рельефа местности, что очень важно не только при строительстве дорог и различного
рода трубопроводов, но и для правильного планирования засева полей в сельском
хозяйстве и некоторых других отраслях;
·
для
анализа видимости с целью прокладки сетей коммуникации, решения военных задач
или в других отраслях;
·
а
также для анализа освещённости территории и ветрового режима;
·
для
ортокоррекции изображений;
·
для
проведения проектно-изыскательных работ и мониторинга динамики рельефа;
·
для
мониторинга и прогнозирования геологических и гидрологических процессов;
·
для
создания модели возможного затопления;
·
и
для многих других.
Главным методом расчёта
цифровых моделей рельефа является метод интерполяции поверхностей, позволяющий
прогнозировать значения точек в местах отсутствия измеренных значений по
ограниченному набору опорных точек с известными значениями.
Для этого в зависимости
от вида ЦМР (регулярная, структурная, нерегулярная) производят соответствующую
выборку точек. Далее определяются со свойствами исследуемого рельефа и ставят в
соответствие пространственную корреляцию определённого типа, которая определяет
зависимость между близкими и отдалёнными пространственными объектами
(пространственную структуру данных). Автокорреляция бывает:
- положительная
(наиболее распространённая) - считается, что пространственно близкие объекты
имеют сходные характеристики;
- отрицательная
- наоборот, что пространственно близкие объекты имеют различные характеристики;
- нулевая
- характеристики объектов не зависят от их взаимного месторасположения.
При помощи интерполяции
рельеф местности представляется в одном из двух видов:
- как
функция 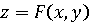 ;
;
- как
поле случайных величин.
Соответственно есть и
две основные группы методов интерполяции:
а)
детерминистские - интерполируют с примененеим математических функций без содержания
случайной компоненты:
1)
метод обратных взвешенных расстояний (ОВР);
2)
сплайн;
3)
тренд (или метод глобального полинома);
б)
геостатические - в основе лежат математические и статистические модели, учитывающие
пространственную автокорреляцию:
1)
кригинг.
Метод обратных
взвешенных расстояний основан на расчёте каждой ячейки растра путём усреднения
значения опорных точек в заданной окрестности данной ячейки. При этом вес
(вклад в интерполируемое значение) точки определяется исходя из её положения
относительно центра расчётной ячейки: чем ближе к центру, тем больше вес. Как
следует из названия вес опорной точки есть обратная функция расстояния в n-ой
степени 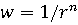 (как правило n=2).
Соответственно чем больше степень n,
тем большее влияние оказывают ближайшие точки и меньшее удалённые, что приводит
к большей детализации поверхности и её меньшей сглаженности.
(как правило n=2).
Соответственно чем больше степень n,
тем большее влияние оказывают ближайшие точки и меньшее удалённые, что приводит
к большей детализации поверхности и её меньшей сглаженности.
Лучше всего методом ОВР
интерполируются однородные поверхности с достаточным количеством равномерно
распределённых точек.
Методом
сплайн-интерполяции получается поверхность с минимальной кривизной, точно
проходящая через заданные опорные точки. Этот метод позволяет строить модель
рельефа с учётом и глобального тренда и локальных вариаций. В этом случае
минимизируется сумма квадратов величин второй производной в каждой точке
поверхности. Метод сплайн-интерполяции можно применять для плавно изменяющихся
поверхностей, для резких изменений не подходит.
Тренд-интерполяция использует
метод наименьших квадратов для подбора математической функции (полинома
заданного порядка) ко всем опорным точкам, подходящей для описания поверхности.
При этом полученная результирующая поверхность 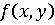 минимизирует
отклонения от входных точек: чем меньше среднеквадпатическая ошибка между
рассчитанным и входным значениями, тем точнее интерполированная поверхность представляет
входные точки). Полученная таким методом поверхность редко проходит через
изначальные опорные точки.
минимизирует
отклонения от входных точек: чем меньше среднеквадпатическая ошибка между
рассчитанным и входным значениями, тем точнее интерполированная поверхность представляет
входные точки). Полученная таким методом поверхность редко проходит через
изначальные опорные точки.
Метод
тренд-интерполяции выбирают, когда нет необходимости в точном моделировании
локальных неровностей, а необходимо определение общих тенденций моделируемого
рельефа. Ограничением применения данного метода является необходимость в медленном
изменении моделируемой характеристики.
Ключевой метод
геостатики - кригинг предназначен для анализа пространственно-распределенных
данных. Опирается данный метод на гипотезу пространственной однородности
(стационарность 2 порядка):
- пространственная
изменчивость статически однородна по всей поверхности;
- вариации
в значениях исходных опорных точек зависят от расстояния между ними, но не от
их местоположения.
При обработке
поверхности методом кригинга считаются пространственные изменения в точках как
сумма трёх компонент:
- структурной
компоненты, представляющей общий тренд рельефа в определённом направлении,
может описываться какой-либо математической функцией, либо считается. что нет
тенденции (в большинстве случаев);
- случайная,
но пространственно-коррелированная компонента - это некоторые отклонения от
тренда случайные, но связанными между собой пространственно;
- случайный
шум - по сути остаточная ошибка, случайная величина, не связанная ни с общей
тенденцией, ни друг с другом.
Одним из наиболее
распространенных методов, особенно для построения карт вручную, является способ
триангуляции. Для реализации этого способа строят систему неперекрывающихся
треугольников (проводят триангуляцию множества исходных точек на карте). В
результате этого получается представление поверхности в виде многогранника с треугольными
гранями, где проекция каждой грани на картографируемую плоскость есть соответствующий
треугольник триангуляции, а высоты равны значениям Z(i) в i-х точках.
Триангулировать множество
точек на плоскости можно разными способами, от способа зависит и получаемая
поверхность. Оптимальной для моделирования модели рельефа является триангуляция
Делоне. Её особенность в том, что для каждой исходной точки строится локальный
полином первой или второй степени и по триангуляции эти локальные полиномы складываются
в одну гладкую поверхность, что позволяет избежать изломы изолиний на ребрах
полигонов. Для создания ЦМР таким методом необходимо чтобы выполнялось условие
Делоне - внутрь окружности, описанной вокруг любого построенного треугольника,
не должна попадать ни одна из заданных точек триангуляции как показано на
рисунке 3.
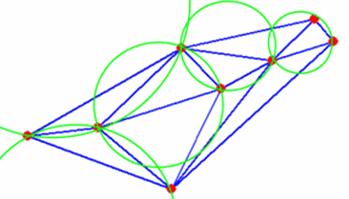
Рисунок 3 -
Условие Делоне
Следует заметить, что
обычно первичные данные цифрового моделирования рельефа имеются или с
использованием тех или иных операций приводятся к одному из двух наиболее
широко распространенных представлений поверхностей в ГИС: растровому представлению
GRID или модели TIN.
Растровая модель
рельефа относится к регулярным ЦМР. Для её реализацию всё пространство делится
на отдельные элементы - пиксели, которые являются далее не делимыми. Эти
элементы образуют регулярную сеть высотных отметок (высот). Подобные цифровые
модели рельефа создаются национальными картографическими службами многих стран.
Регулярная сеть высот представляет собой решетку с равными прямоугольниками или
квадратами, где вершины этих фигур являются узлами сетки ,что может быть
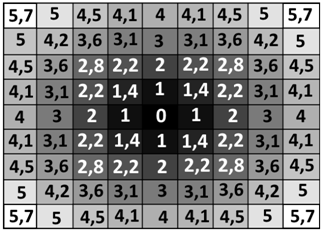
представлено в виде, показанном на рисунке 2 а), либо на плоскости регулярная
сеть высот может иметь вид, показанный на рисунке 4 а), либо в трёхмерном виде
данное представление будет иметь вид, показанный на рисунке 4б).
|
|
|
|
а)
|
б)
|
|
Рисунок 4 - Вид регулярной модели
сети высот: а) на плоскости; б) в трёхмерном изображении
|
Первым пакетом
программ, позволяющим моделировать рельеф с помощью регулярной модели высот,
который нашёл своё применение и развитие, был пакет GRID, что в переводе с
английского - решетка, сетка, сеть. Создали его в конце 1960-х гг. в
Гарвардской лаборатории машинной графики и пространственного анализа (США). В
этом пакете реализовали возможность множественного ввода различных слоёв
растровых ячеек.
В соответствии с
названием этого пакета, а также его хорошем отображении свойств регулярной
модели высот, в современных ГИС-пакетах, таких как ArcGIS и Surfer растровая
модель пространственных данных также именуется как GRID.
Основным при работе с
GRID является правильный выбор плотности сетки (пикселя), поскольку этот
параметр отвечает за пространственное разрешение будущей ЦМР. Меньший пиксель
делает ЦМР точнее, а пространственное разрешение выше. Однако, это означает
задание большего количества узлов сетки, для обработки которых требуется повышенные
компьютерные ресурсы и затрачивается большее время. Поэтому важно оптимально
подобрать размер ячейки, удовлетворив требования в достаточной точности, но не
превысив минимально необходимые для этого ресурсы.
Путем интерполяции,
аппроксимации, сглаживания и иных трансформаций к растровой модели могут быть
приведены ЦМР всех иных типов [4].
В начале 1970-х гг. был
реализован другой метод составления цифровых моделей рельефа, основанный на
нерегулярной сетке, соединяющей набор неравномерно расположенных точек, -
модель TIN (Triangulation Irregular Network - триангуляционная нерегулярная
сеть). Эта модель до сегодняшнего дня остаётся одной из самых распространённых
среди нерегулярных. В 1970-е гг. было создано несколько вариантов данной
системы, коммерческие системы на базе TIN стали появляться в 1980-е гг. как
пакеты программ для построения горизонталей. Модель TIN используется для
цифрового моделирования рельефа, при этом произвольно расположенные точи
соединяются линиями с образованием смежных непересекающихся треугольников с
разными характеристиками (длинами рёбер, углами). Однако, при всей своей
нерегулярности выбор треугольников должен подчиняться условию Делоне,
описанному выше и показанному на рисунке 3.
В пределах каждого
треугольника модели TIN поверхность обычно представляется плоскостью. Поскольку
поверхность каждого треугольника задается высотами трех его вершин, применение
треугольников обеспечивает каждому участку мозаичной поверхности точное
прилегание к смежным участкам. Это обеспечивает непрерывность поверхности при
нерегулярном расположении точек.
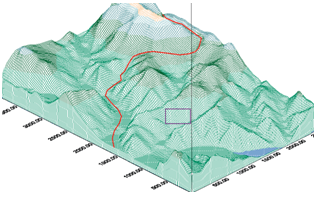
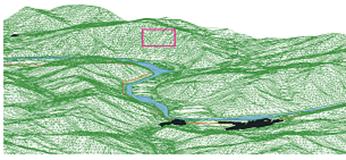
Наглядно модель TIN можно
представить в виде, приведённом на рисунке 5. При этом на рисунке 5 а) можно
наблюдать насколько точно данная модель может описывать рельеф, а на рисунке 5
б) видно, что модель действительно нерегулярная и на сколько разные
треугольники пришлось использовать для построения части рельефа.
|
|

|
|
а)
|
|
Рисунок 5 - модель TIN: а)
трёхмерное представление; б) увеличенный фрагмент рельефа
|
Для составления ЦМР
методом TIN основным методом является триангуляция Делоне, поскольку она
обладает наиболее подходящими для цифровой модели рельефа свойствами: имеет
наименьший индекс гармоничности как сумму индексов гармоничности каждого из
образующих треугольников (близость к равноугольной триангуляции), свойства
максимальности минимального угла (наибольшей невырожденности треугольников) и минимальности
площади образуемой многогранной поверхности.
Обе модели и GRID и TIN
широко распространены в настоящее время и применяются практически с равной
частотой, поэтому выбору одной из них необходимо подходить с аналитической
стороны, поскольку для решения одной задачи может идеально подходить одна и
совсем не подходить другая, для другой задачи наоборот, а для третьей могут примерно
одинаково подходить обе модели. В последнем случае необходимо исходить из рациональности
использования ресурсов и простоты использования.
Благодаря самой природе
GRID, очень сходной с природой
компьютерных устройств, также пользующихся регулярным набором пикселей, расчёт
такой модели на компьютере сравнительно прост и производится на довольно
высокой скорости. Мониторы, принтеры и прочее оборудование также работают с
набором точек, поэтому вывод изображения, просчитанного по модели GRID не
вызовет никаких затруднений и лишних затрат ресурсов.
Кроме того, растровая структура
как бы сглаживает моделируемый рельеф, нивелируя резкие грани и выступы.
Однако, это может привести к значительным отклонениям модели от реального вида
рельефа в случае, если последний имеет много остроконечных вершин, крутых
склонов и подобных резких изменений. В этом случае моделирование с использованием
метода GRID приведёт к сглаживанию и размытию структурных линий рельефа и в
общем случае к искажению полученной ЦМР. Для исправления ситуации необходимо будет
увеличить пространственное разрешение (уменьшить размер ячейки), что приведёт к
резкому возрастанию машинных ресурсов
В общем случае ЦМР по
методу GRID требуют больше машинной памяти для хранения, чем по методу TIN. Для
больших по объёму цифровых моделей, построенных по методу регулярной сетки
высот, нередко используют дополнительные средства и методы при отображении,
позволяющие экономить машинные ресурсы. Например, наиболее популярный - построение
так называемых пирамидальных слоёв, которые позволяют строить изображение с
различными уровнями детальности для различных масштабов, уменьшая тем самым
количество избыточных для данного масштаба точек и снижая сложность расчётов.
Подводя итог по модели
GRID можно сказать, что она идеально подходит для отображения географических
(геологических) объектов или явлений, характеристики которых плавно изменяются
в пространстве (рельеф равнинных территорий, температура воздуха, атмосферное
давление и тому подобное). Плохо подходит для моделирования рельефа с резкими
склонами и вершинами: для точности изображения требует слишком высоких затрат
машинных ресурсов. И абсолютно не подходит для моделирования рельефа с сочетанием
больших равнинных участков с перепадами высот, что наблюдается, например, в широких
разработанных долинах крупных равнинных рек. В таком случае при значительных
затратах ресурсы на большей части рельефа - на равнинных участках будет
наблюдаться избыточное количество точек, а при отображении склонов и уступов их
напротив может не хватить.
Модель TIN лишена таких
недостатков. Использование нерегулярной сети треугольников позволяет на плоских
участках выделить малое количество точек, построив большие треугольники, а на
участках с резкими перепадами высот, напротив, взять большое количество точек,
построив маленькие треугольники. Такой подход позволяет правильно отобразить
резкие перепады высот без излишней траты машинных ресурсов на просчёт лишних
точек плоских участков местности. Таким образом в этом случае модель TIN
позволит эффективно использовать ресурсы оперативной и постоянной памяти компьютера
для хранения и отображения цифровой модели рельефа.
Недостатком же модели
TIN, из-за её нерегулярной природы, является необходимость больших затрат
компьютерных ресурсов на обработку модели, поскольку для вывода ЦМР на экран
или на печать необходимо дополнительно проводить растеризацию (перевод изображения
из формата нерегулярных треугольников модели TIN в пиксели или точки). Данную
проблему можно решить с помощью введения некоторой гибридности: структурные
линии остаются по TIN модели, а отображается ЦМР в виде регулярного набора
точек.
Основным и довольно
существенным недостатком модели TIN является так называемый "эффект
террас": появление "псевдотреугольников" - плоских участков в
заведомо невозможной геоморфологической ситуации (например, по линии днища
V-образных долин, приведённых на рисунке 6 [2]).
Одна из основных причин
- малое расстояние между точками цифровой записи горизонталей в сравнении с
расстояниями между самими горизонталями, что характерно для большинства типов
рельефа в их картографическом отображении.
"Псевдотреугольники"
возникают там, где все три вершины треугольника лежат на одной горизонтали.
Появление таких морфологических артефактов нарушает морфографию и морфометрию
моделируемого рельефа и снижает точность и качество самой модели и ее
производных.
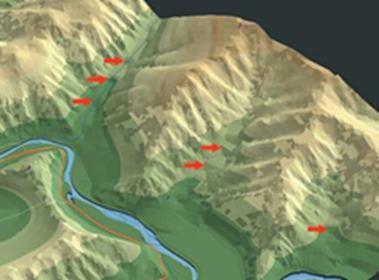
Рисунок 6 - «Эффект террас» в
долинах малых рек, возникающий при создании TIN на основе горизонталей без
учёта структурных линий рельефа (в данном случае - гидросети)
Один из способов
значительного улучшения качества и морфологического правдоподобия ЦМР состоит в
расширении модели TIN путем ее структурирования - введения в нее сети
тальвегов, водоразделов и линий перегибов и разрывов (бровок, уступов террас и
т.п.) [1,5].
Информационное
обеспечение -совокупность массивов информации, реализованные решения по видам,
объемам, размещению и формам её организации, набор методов ввода данных,
проектирование баз данных, их ведение и ак далее.
Сначала рассмотрим
возможные способы получения информации, необходимой для построения ЦМР. Для
составления цифровых моделей рельефа используются следующие источники данных:
- картографические
материалы. К ним относятся: топографические и общегеографические карты, кадастровые
планы и тому подобное. Сведения, получаемые с карт, имеют территориальную
привязку, поэтому их удобно использовать в качестве базового слоя ГИС;
- данные дистанционного
зондирования (ДДЗ). К ним относятся: материалы, получаемые с космических
носителей, аэро- и наземные съемки, и другие неконтактные методы;
- результаты полевых
обследований, это геодезические измерения природных объектов, выполняемые
нивелирами, теодолитами, электронными тахеометрами, GPS приемниками, а также
результаты обследования территорий с применением геоботанических и других
методов;
-статистические данные.
К ним относятся: гидрологические и метеорологические данные, сведения о
загрязнении окружающей среды и тому подобное;
- литературные данные: тексты,
описания, отчеты;
-прочие данные: фото,
иллюстрации, зарисовки.
Как было сказано выше
независимо от метода построения оптимальным способом хранения ЦМР является
послойное хранение. В этом случае возможно хранение гораздо большего количества
информации, отображаться и детализироваться которая будет в зависимости от
выбранного слоя, что позволяет экономить компьютерные ресурсы и не загромождать
ненужной информацией ЦМР на более общих слоях. Кроме того, широко практикуется
послойная организация цифровых моделей рельефа для разделения тематически
разной информации (географические, геологические, биологические и прочие
данные).
Начальные данные о
пространственном положении (географические данные) и связанные с ними
табличные, составляющие основу ЦМР могут быть составлены самим пользователем,
либо приобретены.
Далее эти данные могут
быть введены программу вручную с использованием дигитайзера. Растровое
изображение карты в модель можно подгрузить с использованием сканера (с
бумажных носителей), далее провести его векторизацию (оцифровку).
Составленная цифровая модель
рельефа ещё должна пройти процесс визуализации или отображения изображений
(картографических, графических) на устройствах отображения (преимущественно –
на мониторе). Этот процесс основан на преобразовании исходных цифровых данных с
помощью специальных алгоритмов. В зависимости от поставленных целей и задач
процесс визуализации ЦМР может отображаться в итоге в виде: электронной карты
(ЭК), электронного атласа, таблиц и графиков, анимации, а также трехмерного изображения
рельефа (3D-рельеф).
В настоящее время на
рынке существует огромное количество программных продуктов для создания и
анализа цифровых моделей рельефа, значительно отличающихся по функциональным
возможностям и цене. Все их можно объединить в несколько больших групп.
Мощные
полнофункциональные модули. Эта группа предлагает самые широкие возможности по
созданию цифровых моделей рельефа, но и цена таких пакетов самая большая.
Распространённость данных модулей обусловлена отсутствием необходимости в дополнительном
программном обеспечении - они представлены в виде надстройки к популярным
программным комплексам. Примерами данной группы служат модули: Autodesk Map 3D
системы AutoCAD (Autodesk Inc.), Spatial Analyst, 3D Analyst, Geostatistical
Analyst ГИСпакета ArcGIS (ESRI Inc.), Terrain пакета GeoMedia (Intergraph
Corp.) и другие.
Программы с применением
ЦМР для создания систем виртуальной реальности. Эти программы
узкоспециализированны и как правило не имеют или имеют довольно скромный набор
аналитических функций. Из подобного класса программного обеспечения наибольшую
популярность в мире приобрели: программа Virtual GIS, входящая в состав полнофункционального
комплекса ERDAS Imagine (Leica Geosystems), комплексы MultiGen Creator Terrain
Studio и MultiGen Vega Prime (MultiGen-Paradigm), программы ArcScene и ArcGlobe
ГИС-пакета ArcGIS (ESRI Inc.), а также модуль SiteBuilder 3D
(MultiGen-Paradigm) для ArcGIS.
Также
узкоспециализированными являются и программные пакеты конкретно для работы с цифровыми
моделями рельефа. Они, как правило, имеют функции создания ЦМР различными
методами, а также дальнейшего построения тематических карт на их основе.
Наиболее
известны
пакеты
программ
Surfer (Golden Software Inc.) и
MicroDEM / Terra Base (U.S. Naval Academy).
Отдельным классом можно
представить дополнительные программы, которые выполняют строго специфичные
функции необходимые при создании или обработке ЦМР. Это программы для
автоматической или полуавтоматической векторизации (оцифровке) растровых
изображений карт местности. Например, отечественнык Easy Trace (EasyTrace
Group) и MapEDIT (Резидент).
Ещё сравнительно
недавно для создания и работы с цифровыми моделями рельефа использовали дорогое
аппаратное обеспечение: графические рабочие станции на базе платформ IBM,
Silicon Graphics, Sun Microsystems или Hewlett-Packard, функционирующие под
UNIX-подобными операционными системами. В настоящий момент технический прогресс
шагнул настолько далеко, что практически обычные персональные компьютеры способны
обрабатывать ЦМР в режиме реального времени.
Для работы с цифровыми
моделями рельефа важнейшими элементами аппаратного обеспечения являются
центральный процессор, оперативная память и видеокарта. Мощность центрального
процессора обеспечивает скорость расчётов.
Жёсткий диск
(винчестер) зачастую в современных ПК является "узким бутылочным горлышком"
в передаче данных. Ведь скорость считывания информации в современных
винчестерах 70–80 Мб/с, а скорость передачи данных между процессором и
оперативной памятью ПК достигает 10 Гб/с и более. Частично решить эту проблему
можно за счёт использования RAID-массивов из быстродействующих SCSI или SATA
дисков (например, SATA-дисков WD Raptor со скоростью вращения 10 000 об./мин).
Видеокарта существенно
влияет на производительность при трёхмерном моделировании. При этом почти все
соответствующие программы используют OpenGL-драйвер. Скорость работы в
OpenGL-режиме является определяющим фактором при выборе видеокарты. Из массовых
видеокарт традиционно лучше работают с OpenGL видеокарты на базе чипов NVidia
(в отличие от ATI/AMD и других производителей). Серьёзно увеличивают
производительность видеоподсистемы ПК технологии "двойных" видеокарт
[SLI (NVidia), CrossFire (ATI/AMD)]. Профессиональные видеокарты имеют
драйвера, сертифицированные ведущими производителями программного обеспечения
ГИС, но стоят гораздо дороже.
Трёхмерное
моделирование в настоящий момент одно из самых быстроразвивающихся направлений
использования ЦМР. Отличие трёхмерной модели от двумерной вполне очевидно:
можно визуально оценить особенности рельефа местности, его изменчивость и
прочие характеристики.
Для создания трёхмерной
модели некоторой местности можно воспользоваться ортоизображением, которое
представляет собой космический снимок или аэрофотографию с устранёнными
искажениями, в результате чего масштаб всех точек выравнивается. Подготовленное
ортоизображение как бы "натягивается" на поверхность, созданную по
цифровой модели рельефа. После такой обработки можно получить достаточно
реалистичное 3D-изображение.
Однако, такое
совмещение ортоизображения и ЦМР не всегда могут точно совпадать, поскольку
некоторые части рельефа могут быть видоизменены из-за наличие растительности,
снега или других природных явлений. Кроме того, ортоизображение как правило содержит
и тени от объектов. В итоге полученное трёхмерное изображение будет зависеть от
времени года и времени суток.
Для устранения таких
эффектов и увеличить качество текстуры рельефа местности необходима
дополнительная обработка ортоизображений: дополнительная цифровая фильтрация и
ретуширование.
Интенсивное развитие трёхмерного
моделирования и анимационных технологий привело к созданию виртуальных
геоизображений. Они осчетают в себе свойства карты, перспективного снимка,
блок-диаграммы и компьютерной анимации.
С помощью виртуального
моделирования можно построить различные тематические признаковые пространства.
Виртуальные геоизображения - это многомерные пространственно-временные модели,
представляющие в элементарных ячейках информацию пространства-времени области
поверхности Земли.
Создание виртуальных
геоизображений предполагает наличие эффектов трёхмерности и анимированности
смены рельефа при изменении точки наблюдения. Эти эффекты помогают создать
иллюзию присутствия на моделируемой местности и возможности взаимодействия с
окружающим пространством.
Поскольку прочие
объекты заполнения виртуальной реальности (помимо рельефа) оптимальнее всего
моделируются в прямоугольной системе координат, то и большинство моделей для
создания виртуальной реальности также строятся в общеземных прямоугольных
системах координат (например, Гаусса– Крюгера). Однако, в этом случае основу виртуальных
геоизображений - модель рельефа необходимо адаптировать или пересчитывать
согласно этим координатам.
Таким образом создание
виртуального геоизображения предполагает наличие следующей информации: цифровой
модели рельефа, растрового изображения местности (ортоизображения), векторных
данных, дополнительных растровых изображений, аниммации, а также прочих
специальных объектов.
Несомненно основой
виртуальных геоизображений является цифровая модель рельефа, она определяет
степень соответствия виртуальной модели и реальной местности. Чем точнее и детальнее
будет ЦМР, тем реалистичнее получится виртуальное изображение. Однако, здесь
также необходимо исходить из принципа оптимальности, поскольку чем подробнее
ЦМР, тем больше компьютерных ресурсов она будет затрачивать. При этом нужно
учитывать, что местность становится возможно без труда идентифицировать только
при использовании данных масштаба 1:200 000 и крупнее. Использование более
мелкого масштаба приведёт к созданию виртуального изображения лишь в общих
чертах напоминающего моделируемую местность, а узнать её можно будет только при
значительном от неё удалении (со значительной высоты).
Наибольшее
распространение в плане обзорности получили следующие модели виртуальных
изображений: просмотр трёхмерных статических рельефов, облёт местности в реальном
времени, объезд местности в реальном времени, запись полёта по траектории с
возможностью изменения направления полёта, запись полёта по траектории без
возможности изменения. Записи полётов предполагают сохранение виртуального
полёта в видеофайл с возможностью дальнейшего просмотра.
Основное применение
виртуальных геоизображений - это их демонстрация в качестве учебных пособий и в
виде презентации на различных мероприятиях. Более серьёзного научного
применения для пространственного анализа данный вид моделирования пока не несёт,
поскольку для трёхмерного представления изображений по ЦМР, их адаптация к прямоугольным
координатам, добавление различных объектов и анимация, дополнительно связанны с
написанием сложных алгоритмов и большими затратами компьютерных ресурсов, что
не оправдывается полученными возможностями для анализа.
Виртуальные
геоизображения имеют следующее практическое применение:
-
культурно-историческое - воссоздание ландшафтов и событий определённой исторической
эпохи;
- тренировочное - моделирование
полёта авиации, поездки на автомобиле или боевой технике для тренажёров по
обучению соответствующим навыкам;
- планировочное -
визуализация стратегических планов хозяйственных и боевых операций;
-
рекламно-пропогандистская - для пропогандирования самих виртуальных моделей, а
также для эффектной рекламы некоторых видов продукции.
Геоинформационные
системы (ГИС) - это системы, которые обеспечивают сбор, хранение, обработку, доступ,
отображение и распространение пространственно-координированных данных.
ГИС-технологии - это
программно- технические комплексы, управляемые коллективом специалистов и
предназначенные для работы с цифровыми моделями пространственных объектов,
процессов и явлений.
Основные процессы при
построении цифровых моделей рельефа местности на основе ГИС-технологии остаются
примерно такими же как описано выше, но есть некоторые особенности:
- не требуется перевода
в растровые изображения, поскольку в ГИС карты уже оцифрованы;
- по ГИС-технологии
карты также обычно находятся по участкам, поэтому состыковка изображений
остаётся необходимой, но в для геоинформационных систем имеются специально
разработанные для этого модули.
- для векторизации карт
ГИС также разработаны специальные модули (например, МарЕdit), проводящие эту
операцию в автоматическом режиме.
- дальнейшее
формирование цифровых моделей рельефа и их визуализаци проходит таким же
образом как и для обычных карт с использованием тех же методов.
Характеристики
полученных ЦМР также зависят от качества данных, в частности данных ГИС, и
метода их обработки.
Однако, с помощью
ГИС-технологии возможно создание ЦМР с большим набором данных, чем на основании
обычных карт, поскольку ГИС-технологии позволяют получить не только общую
информацию о рельефе моделируемой местности, но и о некоторых конкретных её
характеристиках, например, уклонах местности, составляющих местность породах,
разнородности исследуемого рельефа и тому подобные.
В результате сбора
такой специфической информации возможно создание ЦМР, на основе которой можно
решать прикладные задачи геоизысканий или экологии, например, прогнозирование
местности затопления при наводнении, оценку степени нарушенности ландшафтов и
так далее.
В зависимости от
поставленных задач при формировании ЦМР могут быть использованы
профессиональные ГИС-технологии или специализированные. Как правило программный
продукт ГИС-технологий предлагается в базовом варианте с возможностью подбора
дополнительных надстроек согласно поставленной задачи. Базовый модуль содержит
основные операции ГИС: программную поддержку устройств ввода-вывода, возможности
экспорта и импорта данных и некоторые другие. Как правило разница между
представленными возможностями программных продуктов, реализующих ГИС-технологии,
у разных производителей не сильно отличается, поскольку технологические
разработки обычно достаточно активно заимствуются ими друг у друга.
Рынок программных
продуктов на основе ГИС-технологий в настоящее время представлен примерно 20-ю
полнофункциональными ГИС-пакетами. Наиболее популярные российские системы:
ГеоГраф, Панорама (Карта 2000), ПАРК, GeoLink; зарубежные: ArcView GIS, MapInfo
Professioal, MicroStation.
В таких
полнофункциональных пакетах обычно реализованы такие функции как работа с
базами данных, поиск по географическим объектам, математические расчёты характеристик
объектов рельефа (длины, высоты, периметра и тому подобные), создание пространственных
объектов, электронное тематическое картографирование, построение и обработка цифровых
и электронных карт, составление характеристических баз данных по особенностям
рельефа местности, приведение картографических данных к виду, пригодному для
издания и другие.
GPS (англ. Global
Positioning System - система глобального позиционирования) - спутниковая
система навигации, обеспечивающая измерение расстояния, времени и определяющая
местоположение во всемирной системе координат WGS 84.
Соответственно и основные
функции у GPS - это определение
пространственного положения (координат) заданной точки и скорости её перемещения.
При помощи специальных GPS-приёмников
эти системы используются компаниями и частными лицами для позиционирования,
навигации, проведения наблюдений и определения времени.
Инженерно-геодезические
изыскания (ИГДИ) - это комплекс работ, направленный на получение информации о
рельефе и ситуации местности; служит основой для проектирования, и для
проведения других видов изысканий и обследований.
Применяется GPS
и в инженерно-геодезических изысканиях. Однако, для определения не
относительных (длина, высота, площадь и тому подобное), а абсолютных величин (координат
заданных точек) нужно учитывать, что координаты GPS-приёмники
выдают в системе координат WGS 84, и для работы в других координатах и
нанесения на карты необходимо проводить перевод координат в соответствующую
систему.
При проведении
инженерно-геодезических изысканий GPS может применяться для уточнения координат
объектов рельефа, проведения локальных топографических съёмок линейных и
площадных объёктов, высокоточных геодезических работ, наблюдения за деформациями
земной поверхности и прочее.
Кроме того, GPS полезно
и при составлении ЦМР, поскольку позволяет получить точные координаты точек, к
примеру не отображённых на карте ,но не необходимых для построения модели. Или
провести исследование части рельефа, не имеющего картографического описания и
не доступного для прочих средств, например, ущелья.
Лазерное сканирование -
это операция определения характеристик поверхности (рельефа) и их преобразования
в цифровой вид в трёхмерной системе координат с помощью специального прибора,
называемого лазерный сканер, лазерная сканирующая система или трехмерный
лазерный сканер.
В результате лазерного сканирования по
сути получается массив данных о трёхмерной характеристике сканируемого рельефа.
Преимуществами
лазерного сканирования являются: высокая скорость и точность измерений;
возможность использования полученных данных для составления карт, топографических
планов и чертежей, в том числе различных сечений; возможность проводить относительно
дистанционно съёмку труднодоступных и опасных объектов (дальность лазерного
сканера в зависимости от особенности прибора и условий проведения съёмки оставляет
от 1 до 2 500 метров).
Кроме того технологии
лазерного сканирования позволяют автоматически сравнивать результаты измерений
одного и того же участка рельефа в разное время, что позволяет оценить
произошедшие изменения.
Принцип работы прибора
основан на выполнении измерений дальности до объекта съемки, с помощью лазерного
безотражательного дальномера и фиксации соответствующих точке горизонтального и
вертикального углов.
Для сканирования
некоторого участка рельефа при помощи технологии лазерного сканирования
необходимо задать поле исследования и плотность (разрешение) сканирования.
После запуска процесса съёмки происходит измерение относительных координат точек
исследуемой поверхности, которые формируются в общий массив данных. Полученный
массив можно визуализировать в виде поверхности, которая может расцвечиваться
по удалённости точек или в реальные цвета.
В комплект оборудования
также может входить камера высокого разрешения. Это позволяет получать массив
координат, одновременно с реальными изображениями, что является большим
преимуществом при построении ЦММ и особенно виртуальных изображений на их
основе.
Измерения по технологии
лазерного сканирования производятся автоматизированно с заданной плотностью и
точностью с автоматическим преобразованием координат лазерных отражений в
прямоугольные Декартовы. Всё это позволяет создать трехмерную математическую
модель объекта съемки. С полученным массивом координат очень удобно работать,
его можно использовать для пополнения баз ГИС и для построения или уточнения
ЦМР.
Фотограмметрическая
съёмка (от греч. photos - свет, gramma - запись и metreo - измеряю) - это
измерение объектов, записанных с помощью света (по фотографиям). С помощью
фотограмметрии по соответствующим снимкам исследуемого объекта (в нашем случае
части рельефа) можно определить форму, размеры, пространственное положение в заданной
системе координат, площадь объём, различные сечения и их изменение между
съёмками в разные моменты времени.
Для проведения
фотограмметрической обработки вначале проводится фотограмметрическая съёмка при
помощи фототеодолита (объединённые фотокамера и теодолит) или цифровой камеры.
При этом фотографирование обного объекта производится с определённых
рассчитанных точек.
Проведение
фотограмметрической съёмки заключается в том, что съёмку одного объекта
проводят с двух точек, находящихся на базисной линии. В результате этого
получаются два снимка, являющиеся стереопарой. Соответственно при дальнейшей
обработке они позволяют создать объёмную модель снимаемого объекта и рассчитать
его характеристики.
Преимущества
фотограмметрической съёмки и последующей обработки следующие: как и при
лазерном сканировании не требуется непосредственного контакта с объектом и
можно проводить съёмки труднодоступных или опасных мест; полученная информация
имеет высокую точность; возможность изучения изменений рельефа со временем.
Таким образом
полученные с помощью фотограмметрической съёмки изображения и информация после
их обработки могут также быть использованы для пополнения базы ГИС, а также для
построения ЦМР.
Для проведения работ на
объекте наряду с наземной геодезией, аэрофотосъёмкой и наземной фотограмметрии
в настоящее время всё чаще применяются GPS-технологии.
В частности GPS пользуются для
топографических съёмок местности в зоне объекта; привязки имеющихся изображений
местности к географическим координатам; планово-высотной привязки и тому
прочего.
Для получения данных
посредством GPS пользуются следующими
методами геодезических измерений: статический - в основном для создания и
развития опорных геодезических сетей; быстростатический - для создания сетей
сгущения; кинематический Stop-and-Go для топосъемки на открытой местности с
небольшим количеством контуров; непрерывный кинематический метод - для
трассирования линейных объектов; RTK (Real Time Kinematic —«кинематика
реального времени») позволяет получать координаты с высокой точностью в режиме
реального времени, этот метод является предпочтительным при наличии достаточных
возможностей.