Задача оптимізації інвестиційного портфеля та її розв’язання за допомогою нечіткої логіки
Міністерство освіти і науки України
Черкаський державний технологічний
університет
Кафедра комп’ютерних наук та
інформаційних технологій управління
Лекція
Задача оптимізації інвестиційного
портфеля та її розв’язання за допомогою нечіткої логіки
Лектор: Триус Юрій Васильович,
завідувач кафедри комп’ютерних наук та інформаційних
технологій управління, професор, доктор педагогічних наук
Черкаси - 2016
Зміст
Вступ
1. Постановка задачі оптимізації інвестиційного портфеля
2. Постановка нечіткої задачі оптимізація інвестиційного портфеля
3. Приклад розв’язування нечіткої задачі інвестиційного портфеля
Список використаних джерел
Додаток
Вступ
У практиці стратегічного управління компаніями
постійно виникає задача оптимізації інвестиційного портфеля за напрямами
діяльності.
Це задача за змістом аналогічна задачі
оптимізації фондового портфеля, але повинна вирішуватися на іншій науковій
основі. Розбіжність полягає в тому, що якщо у випадку фондового портфеля можна
допускати статистичну природу фондових індексів, то в інвестиціях на таку
статистику розраховувати не доводиться. Можливо лише говорити про певні
очікування, пов'язані з прибутковістю і ризиком відповідних інвестиційних
проектів.
Тому актуальною є проблема розробки
математичного апарату і нових методів оптимізації інвестиційного портфеля.
Одним з шляхів вирішення цієї проблеми є
застосування для розв’язування задачі оптимізації інвестиційного портфеля теорії
нечітких множин.
У наш час спостерігається підвищений інтерес до
використання теорії нечітких множин та нечіткої логіки в різних галузях науки,
техніки та економіки, зокрема в теорії прийняття рішень, теорії оптимізації,
логістиці, економічному та фінансовому аналізі, інтелектуальних інформаційних
системах.
Дана теорія знаходить широке застосування у
системах управління, системах підтримки прийняття рішень та експертних
системах, побудованих на основі нечіткої логіки. Впродовж останніх років цей
новий напрям інтенсивно розвивався, з'явилися численна кількість робіт,
присвячених теоретичним і прикладним аспектам теорії нечітких множин (див.,
наприклад, [1-7]).
Сьогодні нечітка логіка розглядається як один з
стандартних методів моделювання та проектування складних систем. Питанням
практичного застосування теорії нечітких множин та нечіткої логіки у різних
галузях діяльності людини присвячено роботи А.В. Леоненкова, Д.А. Поспєлова,
С.Д. Штовби, А.В. Матвійчука, О.О. Недосекіна, М. Сугено, Л. Ванга, Е. Мамдані,
Б. Коско, Ю.П. Зайченка та ін.
У цій лекції розглядається ефективна модель
управління інвестиційним портфелем компанії, наведена в роботі Недосєкіна О.О.
[2]. При цьому в якості вхідних даних для оптимізації виступають тільки
інтервальні значення параметрів ROI (return on investments - рентабельність
інвестіцій) для бізнесів, отримані на низових рівнях інвестиційного планування,
тобто елементи стандартної звітності. Тому метод оптимізації є дуже простим для
розуміння і легким для програмної реалізації. В основі методу лежить ідея Г.
Марковіца про оптимізацію портфеля в координатах "прибутковість-ризик",
але сам метод викладається в нечітко-множинній постановці і базується не на
статистиці бізнесу, а на очікуваннях його прибутковості в майбутньому,
виражених в інтервальній формі.
1.
Постановка задачі оптимізації інвестиційного портфеля
Нехай менеджмент компанії сформував портфель, що
складається з N інвестиціних напрямів (бізнесів), який буде існувати
певний період часу T. При цьому по кожному напряму за цей період
планується здійснити повні інвестиційні витрати, які складатимуться з стартових
інвестиційних витрат (будівлі, споруди, устаткування, ліцензії і т.д.) і
перехідних витрат чистого оборотного капіталу (незнижуваний залишок запасів
сировини, матеріалів, готової продукції, розрив між дебіторською та
кредиторською заборгованістю і т.д.). Якщо повні витрати по портфелю прийняти
за C = const, то частку витрат на i-ий бізнес позначимо як
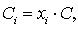
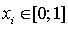 ,
,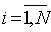 ,
,  (1)
(1)
де 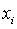 - частка, яка в портфелі належить і-му
інвестиційному напряму.
- частка, яка в портфелі належить і-му
інвестиційному напряму.
Тоді ефективність інвестиційного напряму у портфелі може
бути виміряна на основі традиційного показника ROI (return on investments -
рентабельність інвестіцій) за формулою:
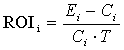 ,
, 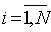 , (2)
, (2)
де Ei - інтегральний ефект від ведення бізнесу за
період існування портфеля (наприклад, всі продажі за період з вирахуванням
податку на додану вартість), T - період існування інвестиційного
портфеля, в роках. Тоді ROI вимірюється у відсотках річних.
Введемо в модель норматив прибутковості інвестиційного
портфеля 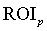 , який являє собою нижню межу
прибутковості інвестиційного портфеля (зазвичай такий норматив встановлює
власник компанії, який зацікавлений у належній віддачі на інвестований
капітал). Для умов європейських корпоративних інвестицій характерним значенням
, який являє собою нижню межу
прибутковості інвестиційного портфеля (зазвичай такий норматив встановлює
власник компанії, який зацікавлений у належній віддачі на інвестований
капітал). Для умов європейських корпоративних інвестицій характерним значенням 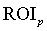 є 8%.10% річних у євро (це відповідає
прибутковості по депозитах у банках середнього рівня надійності, в
високонадійних банках відсоток по депозиту нижче).
є 8%.10% річних у євро (це відповідає
прибутковості по депозитах у банках середнього рівня надійності, в
високонадійних банках відсоток по депозиту нижче).
Нехай також визначено заздалегідь (на підставі даних
бізнес-планування), що якщо збільшувати частку витрат по i-му напряму
інвестування з 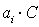 до
до 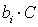 , то прибутковість бізнесу ROI буде змінюватися в інтервалі від
, то прибутковість бізнесу ROI буде змінюватися в інтервалі від  до
до 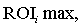 при цьому має місце обмеження:
при цьому має місце обмеження:
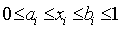 ,
, 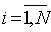 , (3)
, (3)
яке випливає з раціональних умов ведення бізнесу і
визначається менеджментом компанії з додаткових міркувань. Наприклад, виведення
чистого оборотного капіталу з бізнесу; однак у проекті залишиться постійний
інвестиційний капітал (незнижувані інвестиційні витрати бізнес-проекту), який
не буде використаний, в результаті чого прибутковість такого бізнесу буде
негативною. Навпаки, необґрунтоване надлишкове фінансування бізнес-проекту може
призвести до того, що інвестовані кошти будуть не встигати обертатися, і
зростання інтегрального ефекту бізнесу припиниться, що призведе до зниження
прибутковості проекту, у тому числі до негативних значень. Таким чином, на
підставі аналізу бізнес-планів менеджмент компанії визначає раціональні умови
господарювання, які описуються умовою (3).
З (2) випливає:
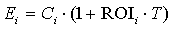 ,
, 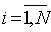 . (4)
. (4)
Тоді інтегральний ефект за всіма бізнесам портфеля
дорівнює:
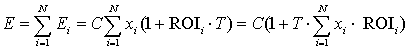 , (5)
, (5)
і тоді прибутковість інвестиційного портфеля визначається
простими співвідношеннями:
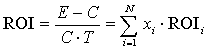 , (6)
, (6)
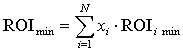 , (7)
, (7)
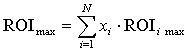 . (8)
. (8)
2.
Постановка нечіткої задачі оптимізація інвестиційного портфеля
Якщо за підсумками існування інвестиційного портфеля
виконана умова 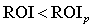 , то має місце невиконання вимог власника.
Відповідно, інвестиції в портфель слід вважати неефективними, а очікування
події зриву плану з прибутковості інвестицій портфеля можна назвати ризиком
портфеля. Показник, що характеризує очікування такого роду, позначимо як
Risk.
, то має місце невиконання вимог власника.
Відповідно, інвестиції в портфель слід вважати неефективними, а очікування
події зриву плану з прибутковості інвестицій портфеля можна назвати ризиком
портфеля. Показник, що характеризує очікування такого роду, позначимо як
Risk.
Якщо інтерпретувати інтервальне значення  як трикутно-симетричне нечітке число, то
ризик події
як трикутно-симетричне нечітке число, то
ризик події 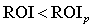 або еквівалентної події
або еквівалентної події 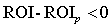 визначається за формулою:
визначається за формулою:
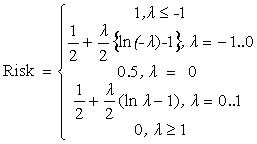 , (9)
, (9)
де
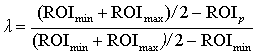 . (10)
. (10)
На рис.1 представлена залежність (9), яку доречно назвати ризик-функцією
інвестиційного портфеля, яка є функцією належності нечіткої величини "ризик
портфеля", що визначена на множині дійсних чисел R і
характеризує очікування події зриву плану з прибутковості інвестицій
портфеля: 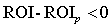 .
.
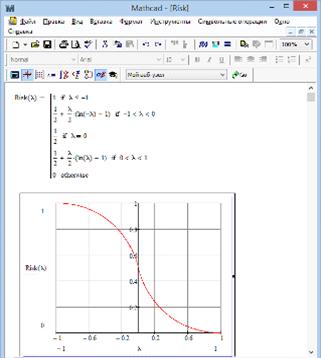
Рис. 1. Ризик-функція інвестиційного портфеля
Тоді задачу нечіткої оптимізації інвестиційного портфеля
компанії можна сформулювати у вигляді:
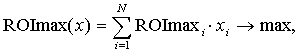 (11)
(11)
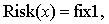 (12)p = fix2, (13)
(12)p = fix2, (13)
за наявності обмежень виду (3) на частки бізнесів у
портфелі, з урахуванням (1), тобто
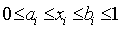 ,
, 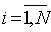 , (14)
, (14)
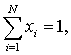 (15)
(15) 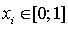 ,
,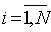 , (16)
, (16)
де, з урахування (7), (8) і (9),
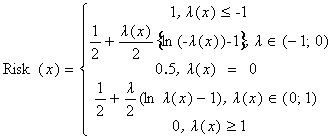 , (17)
, (17)
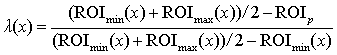 , (18)
, (18)
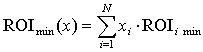 , (19)
, (19)
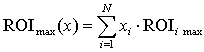 , (20)
, (20)
при цьому теоретично значення параметра 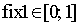 і його обирає особа, яка приймає рішення
щодо рівня ризику інвестиційного портфеля, а норматив прибутковості
інвестиційного портфеля
і його обирає особа, яка приймає рішення
щодо рівня ризику інвестиційного портфеля, а норматив прибутковості
інвестиційного портфеля 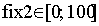 і він визначається соціально-економічними
умовами, в яких функціонує компанія та її бізнес.
і він визначається соціально-економічними
умовами, в яких функціонує компанія та її бізнес.
Задача оптимізації (11) - (20) є задачею нелінійного
програмування в силу нелінійності обмеження на ризик (12), (17), тому її розв’язування
доцільно здійснювати чисельними методами, або з використанням систем
комп’ютерної математики типу Mathcad, Matlab.
3.
Приклад розв’язування нечіткої задачі інвестиційного портфеля
Розглянемо приклад інвестиційного портфеля за N = 4
бізнесами, вхідні дані з яких представлені в табл. 1. В останній колонці табл.
1 проведений розрахунок рівня ризику бізнесу щодо планового рівня прибутковості
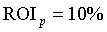 річних.
річних.
Таблиця 1
Вихідні дані за бізнесами
Номер бізнесу 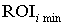 , % річних
, % річних ,
,
% річнихОбмеження на частку бізнесу знизу ai i
зверху biРизик бізнеса Riski
|
за рівнем 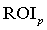
|
bi
|
|
|
1
|
9
|
14
|
0
|
0.9
|
0.047
|
|
2
|
8
|
15
|
0
|
0.8
|
0.104
|
|
3
|
6
|
16
|
0
|
0.7
|
0.239
|
|
4
|
5
|
20
|
0
|
0.6
|
0.150
|
Примітка. Величина Riski для
кожного і-го бізнесу обраховується за формулами (9), (10) при заданих 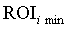 ,
,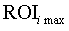 ,
, 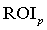 .
.
За даними табл.1 вже можна сказати, що всі чотири бізнеса
володіють ненульовою мірою ризику. Нульові нижні обмеження ai
на розміри бізнесів говорять про те, що бізнеси є високоліквідними, і постійні
інвестиційні витрати в них мінімальні. Таке становище характерно для роздрібних
торгових мереж, коли під бізнесом розуміється продаж товарів вже
"розкручених" брендів. У таких бізнесах левову частку становлять
змінні витрати, розмір яких монотонно залежить від обсягу продажів. Також
видно, що із зростанням номера бізнесу зростає невизначеність в частині його
очікуваної ефективності (розкид 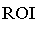 ). Це спонукає менеджмент компанії, балансуючи бізнес-портфель,
примусово обмежувати частки бізнесів, причому, чим більшу волатильність
(змінюваність у часі) має бізнес, тим жорсткіше застосовуються обмеження зверху
на його частку в портфелі.
). Це спонукає менеджмент компанії, балансуючи бізнес-портфель,
примусово обмежувати частки бізнесів, причому, чим більшу волатильність
(змінюваність у часі) має бізнес, тим жорсткіше застосовуються обмеження зверху
на його частку в портфелі.
Потрібно визначити структуру оптимального інвестиційного
портфеля 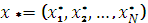
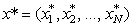 у залежності від рівня допустимого ризику
у залежності від рівня допустимого ризику 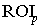 .
.
Розв’язок задачі (11) - (20) з вхідними даними, заданими в
табл.1, і різними рівнями ризику одержано за допомогою системи комп’ютерної
математики Mathcad. На рис.2 і 3 подано розв’язок задачі (11) - (20) при рівні
ризику fix1=0.174. Для всіх інших рівнів ризику розрахунки подано у Додатку.
оптимізація інвестиційний портфель нечітка множина
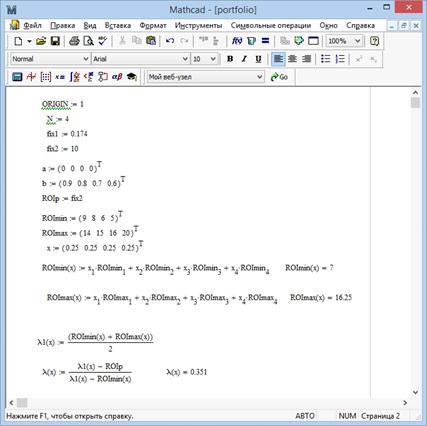
Рис. 2. Розв’язок задачі в системі Mathlab при
fix1=0.174
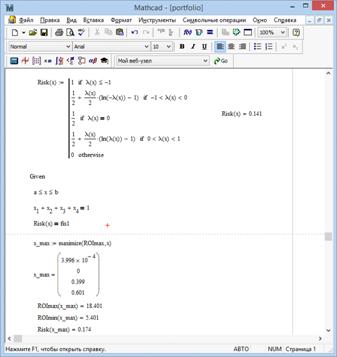
Рис. 3. Розв’язок задачі в системі Mathlab при
fix1=0.174 (продовження)
Зведені результати розв’язування задачі представлені
в табл.2.
Залежність 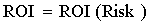 є ефективною межею портфельної множини, представленої на рис.4.
Межа є відрізком криволінійної смуги, при цьому верхня лінія межі є опуклою до
гори монотонною функцією. На цій межі розташовані портфелі, що мають
максимальну очікувану прибутковість в інвестиційному портфеля при фіксованому
рівні ризику портфеля.
є ефективною межею портфельної множини, представленої на рис.4.
Межа є відрізком криволінійної смуги, при цьому верхня лінія межі є опуклою до
гори монотонною функцією. На цій межі розташовані портфелі, що мають
максимальну очікувану прибутковість в інвестиційному портфеля при фіксованому
рівні ризику портфеля.
Таблиця 2
Зведений розв’язок задачі оптимізації
інвестиційного портфеля
|
Risk
|
Оптимальний портфель
|
|
|
1
|
2
|
3
|
4
|
 min min max max
|
|
|
0.174
|
0
|
0
|
0.399
|
0.601
|
5.401
|
18.401
|
|
0.17
|
0
|
0.046
|
0.354
|
0.6
|
5.492
|
18.354
|
|
0.15
|
0
|
0.269
|
0.131
|
0.6
|
5.938
|
18.131
|
|
0.13
|
0,257
|
0
|
0.6
|
6.457
|
17.743
|
|
0.11
|
0.57
|
0
|
0
|
0.43
|
7.279
|
16.581
|
|
0.09
|
0.741
|
0
|
0
|
0.259
|
7.965
|
15.552
|
|
0.07
|
0.875
|
0
|
0
|
0.125
|
8.499
|
14.751
|
|
0.06
|
0.9
|
0.046
|
0
|
0.054
|
8.739
|
14.368
|
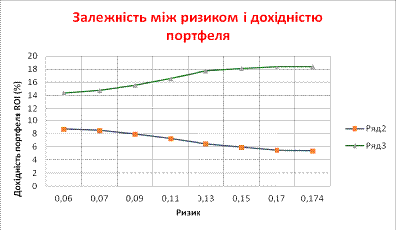
Рис. 4 Ефективна межа портфельного ризику
З табл. 2 видно, що в міру зниження рівня ризику
знижується і розкид прибутковості оптимального портфеля. Причому всю межу можна
розбити на дві частини: відрізок консервативних портфелів (ризик від
0.06 до 0.11) і відрізок агресивних портфелів (ризик від 0.13 до 0.174).
Консервативний відрізок формується бізнесами 1, 2 і 4, а агресивний - бізнесами
4, 3, 2, 1 (табл. 2). Таке розміщення портфелів на відрізках обумовлено
характером бізнесу і його розташуванням щодо планового рівня ROIp.
Оскільки всі бізнеси інвестиційного портфеля
беруть участь у формуванні ефективної межі, і бізнесів-аутсайдерів немає, то
бізнес-портфель компанії є монотонним. Відповідно, всі бізнеси в портфелі мають
право на існування в тій чи іншій пропорції.
Список
використаних джерел
1. Недосекин
А.О. Нечетко-множественный анализ риска фондовых инвестиций. Монография. -
Санкт-Петербург, 2002. - 181 с.
2. Недосекин А.О.
Оценка риска бизнеса на основе нечетких данних. [Електронний ресурс]. - Режим
доступу: http://sedok. narod.ru/sc_group.html
<http://sedok.narod.ru/sc_group.html>
. Зайченко Ю.П., Мугра
М.О. Удосконалення методу оптимізації нечіткого фондового портфелю // Вісник
НТУУ "КПІ". Інформатика, управління та обчислювальна техніка: Зб.
наук. пр. - К.: Век+, - 2011. - № 54. - 239 c.
. Зайченко Ю.П.
Нечеткие модели и методы в интеллектуальных системах. Учеб. Пособие для
студентов высших учебных заведений. - К.: Издательский дом "Слово",
2008. - 344 с.
. Зайченко Ю.П.
Исследование операций. Нечёткая оптимизация: Учеб. Пособие. - К.: Вища шк.
1991. - 191 с.
. Зайченко Ю.П.
Исследование операций: Учебник. - 6 изд., перераб. и доп. - Киев: Издательский
дом "Слово", 2003. - 688 с.
. Кофман А. Введение в
теорию нечётких множеств: Пер. с фр. - М.: Радио и связь, 1982. - 432 с.