Электромагнитные волны в проводящей среде и диэлектрики: теория и практика

Электромагнитные волны в проводящей среде и диэлектрики: теория и практика

Содержание

Введение

. Движение электромагнитных волн в веществе

.1 Плоские волны в идеальном диэлектрике

.2 Электромагнитные волны в однородной проводящей среде

. Плоские волны на поверхностях раздела двух сред

.1 Отражение и преломление плоской однородной волны на плоской поверхности раздела двух сред

.2 Формулы Френеля

.3 Отражение и преломление на границе двух идеальных диэлектриков

.4 Отражение и преломление на границе раздела с проводником

. Практическая часть

Заключение

Список использованной литературы

Введение

В вещественной среде существуют не только стационарные и ква-зистационарные поля, но и распространяются электромагнитные волны. В последней главе курса проанализированы особенности электромагнитных волн в веществе. Свет по своей макроскопической природе - электромагнитная волна. В данной работе показано, как некоторые исходные положения, оптики раскрываются на основе теории Максвелла.

Изучение явлений отражения и преломления электромагнитных волн представляет определённый практический интерес. В частности изучение плоских электромагнитных волн. Плоской электромагнитной волной называется волна, имеющая плоский фронт. Плоская волна с неменяющейся амплитудой называется плоской однородной волной. Свойства отражения и преломления электромагнитной волны используются довольно часто.

Актуальность курсовой работы заключается в том, чтосвойства отражения и преломления электромагнитных волн используются в различных областях науки и техники - медицине (например: в микроскопических методах исследования), биологии, астрономии, физике, оружейных технологиях (в оптических прицелах), защите и добычи информации (анализ возможных каналов утечки информации в волоконно-оптических линиях связи: нарушение полного внутреннего отражения) и др.

Целью работы является рассмотрение закономерностей движения полоских электромагнитных волн в проводящей и дмэлектрической среде.

Основными задачами, выделяемыми в рамках данной цели, являются:

-    характеристика движения электромагнитных волн в диэлектрике и однородной проводящей среде;

-       описание закономерностей отражения и преломления плоских волн на плоской поверхности раздела сред и на границе раздела с проводником;

-       решение практической задачи.

1. Движение электромагнитных волн в веществе

.1 Плоские волны в идеальном диэлектрике

Допустим, что пространство заполняет однородный диэлектрик с постоянными диэлектрической и магнитной проницаемостями е и fi и проводимостью, равной нулю (γ = 0).

Такая модель диэлектрика уже использовалась при изучении стационарных процессов, и она достаточно точно отображает реальные свойства сред в стационарных полях. В случае переменных полей, особенно при высоких частотах колебаний, указанные допущения оказываются слишком грубыми. Тем не менее с помощью этой простой модели удается получить многие важнейшие качественные заключения об электромагнитных, в частности световых, волнах в веществе. Воспользуемся уравнениями поля в потенциалах для однородного диэлектрика. При отсутствии свободных зарядов применяется волновая калибровка: φ = 0, divА= 0 [2].

Уравнения приобретают вид:

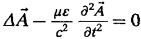
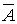  = 0

Общее решение волнового уравнения (1.1) можно представить в виде суперпозиции гармоник всевозможных частот и направлений распространения.

Отдельная гармоника есть плоская монохроматическая волна:

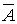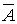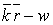= ₀cos(t)

Она отличается от таких же по форме волн в вакууме скоростью распространения. По виду уравнения (1.1) заключаем, что в среде фазовая скорость волны равна:

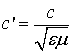
где с - фазовая скорость электромагнитных волн в вакууме.

Соответственно изменяется соотношение между волновым числом k и циклической частотой w. Если для вакуума выполнялось равенство

,

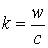то теперь для волн в веществе:

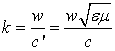
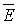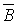К векторам поля  и  перейдем с помощью формул их связи с потенциалами:

Получим для волны в диэлектрике:

Условие (1.2) дает A0 ± k, а с учетом формул (1.6) далее следуют поперечность электромагнитных волн в веществе, правило правой тройки для последовательности векторов 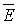, , 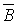, 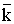связь между модулями векторов поля:

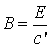
Последнее соотношение приобретает симметричную форму, если его записать для модулей векторов 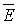 и :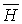

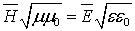
Из формул (1.7) также видно, что векторы 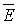 и 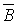 изменяются во времени синфазно. В идеальном диэлектрике ε не зависит ни от величины напряженности поля 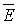, ни от его частоты w.

Поэтому фазовая скорость распространения волн в среде не зависит от частоты и равна групповой скорости. Говорят, что идеальная среда, как и вакуум, не обладает дисперсией. Однако опыт свидетельствует о зависимости распространения электромагнитных волн от частоты, что объясняется в соответствии с формулой (1.4) зависимостью диэлектри-ческой проницаемости среды от частоты колебаний поля:

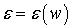
(для диэлектриков μ = 1, и эту величину можно исключить из рассмотрения).

Таким образом, реальные среды обладают дисперсией. Определяя волновое число для среды с дисперсией тем же соотношением (1.7), что и для идеального диэлектрика, получаем для произвольного волнового поля гармоники вида (1.8) [5, c.81 - 83]:

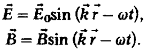
По-прежнему векторы 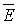, , 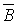 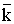образуют правую тройку, причем Е = с'В, но теперь скорость волн зависит от частоты:

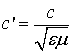
Поэтому усложняется зависимость от частоты волнового вектора (cоответственно длина волны

λ = ):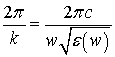

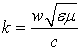
При наличии дисперсии групповая скорость (скорость волнового пакета или скорость переноса энергии) может заметно отличаться от фазовой скорости гармоник. Вычислим плотность энергии и импульса волны в среде. Согласно общей формуле имеем:

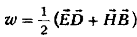
С помощью равенства (1.11) получим:

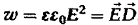
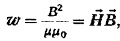
Это свидетельствует о равном вкладе электрической и магнитной составляющей поля в энергию волны.

Плотность потока энергии определяется соотношением:

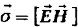
Эта формула может быть записана в нескольких видах:

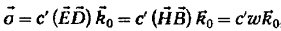
где 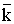₀ = .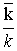

Обратимся теперь к импульсу волн в веществе. Сопоставим выражение для плотности импульса (1.17) с формулой для плотности энергии и потока энергии.

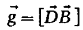
Векторы 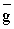и  имеют одинаковое направление. С помощью соотношений (1.4) и (1.12) заключаем, что для их модулей справедливо равенство (1.18), откуда следует [5, 9]:

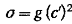
w = gc’

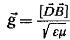
Теперь, как это нетрудно подсчитать, w = gc в соответствии с теорией относительности. Однако в таком случае теряется связь между импульсом и потоком энергии: энергия переносится со скоростью с', а импульс соответствует движению энергии со скоростью с. По этой причине считают, что нельзя однозначно определить импульс электромагнитного поля в рамках феноменологической модели вещества, отраженной в уравнениях [1, 9]:

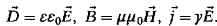
.2 Электромагнитные волны в однородной проводящей среде

Рассмотрим вопрос о распространении электромагнитных волн в проводящей среде, т. е. при условии у 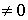. Будем, как и в других случаях, опираться на уравнения поля в потенциалах, для того чтобы использовать их готовые решения. Уравнения векторного потенциала поля совместно с материальным уравнением для зависимости плотности тока в среде от проводимости 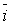 =  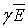приводит к следующему исходному для поставленной задачи уравнению [2]:

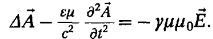
Объемные заряды в проводниках отсутствуют. Применим волновую калибровку потенциала. Если

,

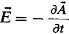то уравнение (1.22) примет вид:

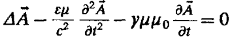
Ищем решение уравнения (1.23), совпадающее по форме с плоскими волнами, распространяющимися вдоль оси Ох:

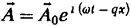
Подстановка этого выражения в уравнение (1.23) приводит к равенству

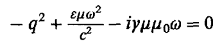
Таким образом, модуль волнового вектора q в предлагаемом решении оказался комплексным числом:

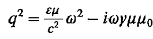
Чтобы выяснить физический смысл соответствующей волны, выделим в комплексном q действительную и мнимую части: q = а - ib.

Возведя последнее равенство в квадрат и сравнивая с уравнением (23.18), получаем систему уравнений:

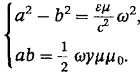
Решая систему относительно а и b, имеем:

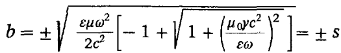
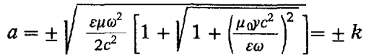
Отсюда

= ± (k - is),

а решение для потенциала поля в проводнике таково:

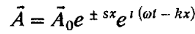
Это волна с вещественным волновым вектором k и переменной вдоль луча амплитудой. Поскольку физического смысла неограниченно растущая амплитуда не имеет, то при х > 0 используется только решение со знаком "минус" перед $. Окончательно для волны потенциала, распространяющейся в положительном направлении оси Ох, имеем [2, 4]:

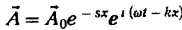
Отсюда видно, что волна в проводящей среде затухает. Затухание характеризуется параметром s, зависящим от свойств среды и частоты волны. Для всех веществ, в которых предположение о постоянстве е и имеет смысл, 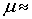1. Поэтому коэффициент затухания s определяется диэлектрической постоянной с и проводимостью среды γ.

При низких частотах

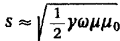
этот параметр уже получен в задаче о скин-эффекте (связь явлений распространения волн в проводящей среде и скин-эффекта как соответствующего предельного случая очевидна).

Если среда является хорошим проводником, то затухание так велико, что о распространении волн в ней говорить не приходится. Количественная оценка для металлов с помощью формулы (1.21) показывает, что для частот видимого света амплитуда волн уменьшается в е раз на отрезке

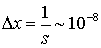м,

т. е. на расстояниях, много меньших длины волны. Это значит, что волны в проводнике не распространяются.

При падении электромагнитной волны на поверхность проводника происходит поглощение и отражение. Переменное электромагнитное поле возбуждает токи в очень тонком 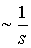 поверхностном слое проводника, а с их помощью генерируется отраженная или рассеянная волна, часть падающей энергии переходит в джоулево тепло. На этом свойстве проводников основано экранирование от электромагнитных волн с помощью металлических оболочек, футляров, кожухов.

Как показывает формула (1.24), в среде имеет место зависимость волнового вектора k от проводимости у и диэлектрической проницаемости £, носящая название дисперсии проводящей среды. Дисперсия приводит к зависимости скорости распространения волн (а значит, и показателя преломления проводящей среды) от частоты.

В соответствии с формулой (1.21) в среде (1.32) функция k(w) задана соотношением (1.29) [5, c.174 - 175].

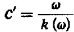
Рассмотрим сначала предельный случай идеального диэлектрика (у= 0).

Из формулы (1.30) получим:

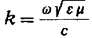
Подставляя найденное значение k в формулу (1.31), имеем:

Теперь обратимся к слабопроводящей среде с малой, но отличной от нуля проводимостью и выполним оценку для k. Считая γ малой величиной, с помощью формулы (23.20) имеем

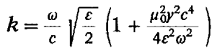
Как и ожидалось, волновой вектор и скорость волн в проводящей среде оказались зависящими от частоты колебаний и проводимости среды. Имеет место дисперсия проводящей среды. Определим также характер волн для векторов поля в слабопроводящей среде, для чего найдем векторы поля через потенциал (1.29). При волновой калибровке:

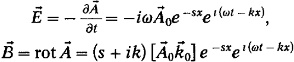
Для того чтобы придать этим выражениям удобный для анализа вид, необходимо записать комплексные множители ш и s + ik в экспоненциальной форме, т. е. выделить вещественные амплитуды волн. Поскольку

,

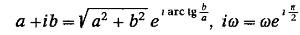то справедливо:

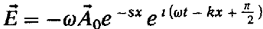
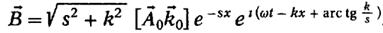
Формулы (1.37) и (1.38) показывают, что в слабопроводящем веществе имеют место затухающие плоские волны со сдвигом фаз между колебаниями векторов 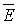,  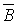и с измененным по сравнению с вакуумом соотношением между их модулями. Но по-прежнему волны поперечны, векторы 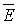, , 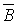, 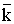составляют правую тройку [5, 8].

2. Плоские волны на поверхностях раздела двух сред

.1 Отражение и преломление плоской однородной волны на плоской поверхности раздела двух сред

При падении плоской электромагнитной волны на границу раздела двух сред возникает отраженная, а во второй - преломленная волна [1, 6].

Плоскостью падения называют плоскость, проходящую через нормаль к границе раздела сред и направления падения волны. Вектор напряженности электрического поля плоской волны 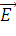 перпендикулярен направлению распространению волны, а по отношению к плоскости падения может быть ориентирован произвольно. Однако можно ограничиться рассмотрением двух ориентаций вектора .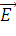

1. Вектор 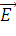 перпендикулярен плоскости падения волны. Такая волна называется параллельно поляризованная.

2. Вектор 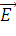 параллелен плоскости падения волны. Такая волна называется параллельно поляризованная.

Такое рассмотрение электромагнитной волны очевидно, т.к. волну с любой ориентацией вектора 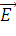 всегда можно представить в виде суперпозиции двух волн, одна из которых является нормально поляризованной, а вторая - параллельно поляризованной.

Пусть на границе двух сред с различными параметрами падает плоская однородная волна с произвольной поляризацией. Для выполнения граничных условий на поверхности раздела необходимо предположить существование отражённой и преломленной волн, распространяющихся в направлениях, параллельных плоскости падения (ZoY). Поля отраженной и преломленной волн описываются в общем случае уравнением плоской волны [6]:

, 

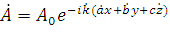где 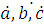 - комплексные величины;

В случаях действительных значений величин 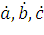, они определяются выражениями:

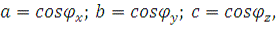
где 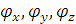 - углы между направлением распространения волны и координатными осями.

Соответствующий выбор коэффициентов 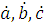 отраженной и преломленной волны, а также их амплитуда обеспечивают выполнение граничных условий на поверхности раздела сред. В результате этого поля в обеих средах удовлетворяют уравнениям Максвелла и граничным условиям. Согласно теореме единственности полученное решение является единственно возможным в данных условиях.

Найдем связь между коэффициентами 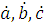 падающей, отраженной и Если падающая волна является плоской однородной волной, то отраженная волна всегда является так же плоской однородной волной. Преломленная же волна может быть плоской и однородной только в единственном случае, когда потери в первой и второй среде отсутствуют и выполняют условие

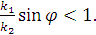
Во всех остальных случаях преломленная волна является плоской неоднородной волной.

2.2 Формулы Френеля

Определим связь между амплитудами падающей, отраженной и преломленной волн. Рассмотрим вначале падающую волну с нормальной поляризацией. Если падающая волна имеет нормальную поляризацию, то и отраженная и преломленная волны будут иметь такую же поляризацию. В справедливости этого можно убедиться, анализируя граничные условия на поверхности раздела сред [1, 4].

Если иметь составляющую с параллельной поляризацией, то граничные условия не будут выполняться ни в одной точке граничной поверхности.

Плоскость падения волны параллельна плоскости (ZoY). Направления распространения отраженной и преломленной волн также будут параллельны плоскости (ZoY) и у всех волн угол между осью X и направлением распространения волны будет равен:

а коэффициент

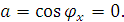
В соответствии со сказанным выше вектор 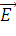 всех волн параллелен оси X, а векторы  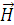параллельны плоскости падения волны (ZoY), поэтому у всех трёх волн проекция вектора 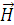 на ось X равна нулю: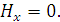

Вектор 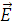 падающей волны определяется выражением:

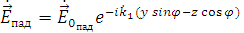
Вектор 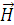 падающей волны имеет две составляющие:

,

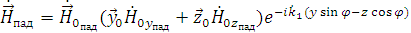где,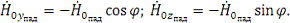

Уравнения для векторов отраженной волны имеют вид [4]:

,

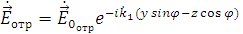
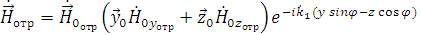где,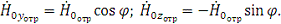

Уравнения для векторов поля преломленной волны имеют вид:

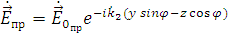
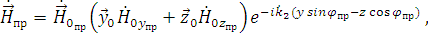
где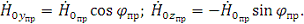

Для нахождения связи между комплексными амплитудами падающей, отраженной и преломленной волн воспользуемся граничными условиями для касательных составляющих векторов электромагнитного поля на границе раздела сред:

Поле в первой среде на границе раздела сред (2.9) будет иметь вид:

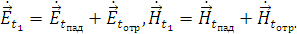
Поле во второй среде определяется полем преломленной волны:

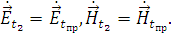
Так как вектор 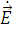 всех трёх волн параллелен границе раздела сред, а касательная составляющая вектора 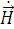 есть составляющая 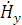, то граничные условия (1.27) можно представить в виде:

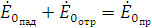
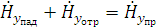
Падающая и отраженная волны являются однородными, поэтому для них справедливы равенства:

,

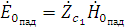
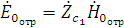где 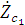 - волновое сопротивление первой среды [4, 7].

Так как поля 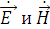 любой из рассматриваемых волн связаны между собой линейной зависимостью, то для преломления волн можно записать:

,

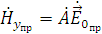где 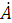 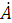- коэффициент пропорциональности.

Из выражений (1.29) получим проекции векторов :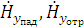

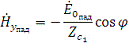
Подставив равенства (1.31) в уравнения (1.28) и учтя равенство (1.30), получим новую систему уравнений:

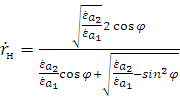
.3 Отражение и преломление на границе двух идеальных диэлектриков

У идеальных диэлектриков потери отсутствуют и 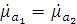. Тогда диэлектрические проницаемости сред - действительные величины и коэффициенты Френеля тоже будут действительными величинами. Определим, при каких условиях падающая волна без отражения переходит во вторую среду. Это происходит при полном прохождении волны через границу раздела сред и коэффициент отражения в этом случае должен быть равен нулю:

Рассмотрим падающую волну с нормальной поляризацией.

Коэффициент отражения будет равен нулю: 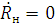 в случае, если равен нулю числитель в формуле (2.17) [8]:

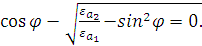
Однако, 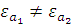, следовательно, для волны с нормальной поляризацией  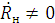при любых углах падения волны на границу раздела. Это значит, что волна с нормальной поляризацией всегда отражается от границы раздела сред.

Волны с круговой и эллиптической поляризацией, которые можно представить в виде суперпозиции двух линейно поляризованных волн с нормальной и параллельной поляризацией, будут отражаться при любых углах падения на границу раздела сред. Однако соотношение между амплитудами нормально и параллельно поляризованных составляющих в отраженной и преломленной волнах будут иным, чем в падающей волне. Отражённая волна будет линейно поляризованной, а преломленная - эллиптически поляризованной. Рассмотрим падающую волну с параллельной поляризацией.

Коэффициент отражения будет равен нулю: 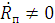 в случае, если равен нулю числитель в формуле (2.17) [4, 9]:

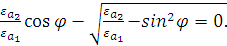
Решив уравнение (2.19), получим:

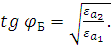
Таким образом, падающая волна с параллельной поляризацией без отражения проходит через границу раздела, если угол падения волны определяется выражением (1.38). Этот угол 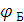 - угол Брюстера [9].

Определим, при каких условиях будет происходит полное отражение падающей волны от границы раздела двух идеальных диэлектриков. Рассмотрим случай, когда падающая волна распространяется в более плотной среде, т.е.  .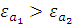

Известно, что угол преломления определяется из закона Снеллиуса:

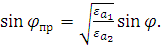
Так как: 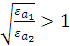, то из выражения (2.21) следует, что: .

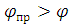При некотором значении угла падения волны на границу раздела сред получаем:

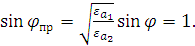
Из равенства (2.20) видно, что:

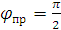
и преломленная волна скользит вдоль границы раздела сред. Угол падения волны на границу раздела сред, определяемый уравнением (2.22), называется критическим углом:

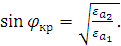
Если угол падения волны на границу раздела сред больше критическог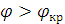о: , то 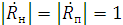. Амплитуда отражённой волны, независимо от вида поляризации, равна по амплитуде падающей волне, т.е. происходит полное отражение падающей волны.

Анализ уравнения преломленной волны показывает, что преломленная волна представляет собой плоскую неоднородную волну, распространяющуюся во второй среде вдоль границе раздела. Чем больше различие проницаемости сред, тем быстрее уменьшается поле во второй среде при удалении от границы раздела. Поле практически существует в достаточно тонком слое у границы раздела сред. Подобная волна называется поверхностной [1, 3].

.4 Отражение и преломление на границе раздела с проводником

Пусть вторая среда имеет значительную оптическую плотность по сравнению с первой средой:

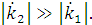
Так как:

,

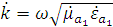то условие (1.23) имеет место в том случае, есл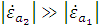и:

 и .

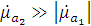Так как:

,

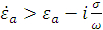то условие (1.42) выполняется, как в случае: 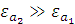, так и в случае: .

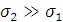Условие выполняется тогда, когда граничная поверхность разделяет реальный диэлектрик и реальный проводник.

Тангенс угла преломления определяется выражением [3, 5]:

.

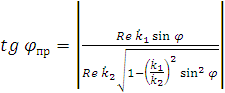В соответствии с условием (2.25) вторым слагаемым в знаменателе под корнем можно пренебречь ввиду его малости по сравнению с единицей. В результате получаем:

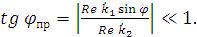
Из неравенства (1.27) следует, что угол преломления при любом значении угла падения φ мал и преломленная волна распространяется в направлении, близком к направлению нормали к граничной поверхности.

Особый интерес представляет случай, когда первая среда идеальный диэлектрик, а вторая - реальный проводник.

Волновое число в реальном проводнике определяется выражением:

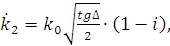
где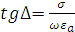  

тангенс угла диэлектрических потерь.

Тогда тангенс угла преломления будет определяться следующим выражением:

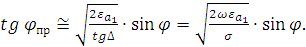
Так как удельная проводимость реальных проводников имеет порядок: 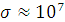См/м, то 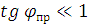, во всём диапазоне радиотехнических частотах.

Коэффициент отражения на границе раздела идеального диэлектрика и реального проводника определяется выражением:

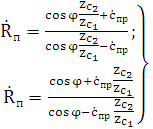
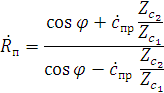
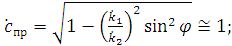
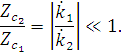
Тогда:

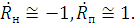
Это значит, что амплитуда отражённой волны равна амплитуде падающей волны. При этом фаза отражённой волны с нормальной поляризацией приобретает при отражении дополнительный фазовый сдвиг, равный 180 градусам [1, 7].

3. Практическая часть

1. Рассчитаем коэффициенты отражения и преломления на границах раздела сред. Найдем коэффициент отражения по формуле:

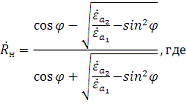
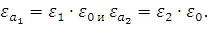
Подставим значения и рассчитаем коэффициенты отражения:

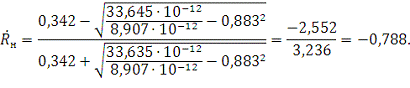
Знак минус говорит о том, что фаза электромагнитной волны изменяется на 180 градусов.

Найдем коэффициент преломления по формуле:

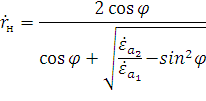
Подставим значения и рассчитаем коэффициент преломления:

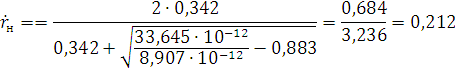
Проверка: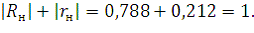

. Найдем угол падения, при котором будет отсутствовать преломленная волна:

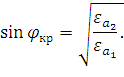
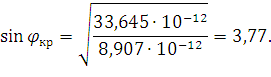
Т.к. 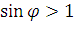, то преломленная волна будет присутствовать при любом угле падения волны на границе раздела сред.

Найдем нормальные и тангенциальные составляющие векторов 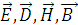 в средах при условии, что граница не заряжена.

Найдём волновое сопротивление по формуле:

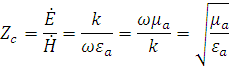
Найдём абсолютную магнитную величину:

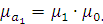
Подставим значения и получим:

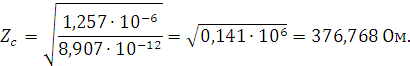
Найдём напряженность магнитного поля:

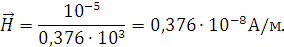
Рассчитаем нормальные составляющие векторов 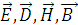 в первой среде при условии, что граница не заряжена:

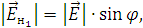
Подставим значения и произведем расчеты:

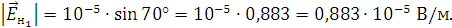
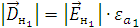
Подставим значения и произведем расчеты:

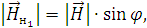
Подставим значения и произведем расчеты:

,

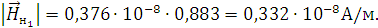
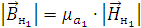Подставим значения и произведем расчеты:

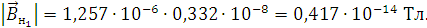
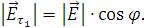
Подставим значения и произведем расчеты:

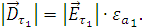
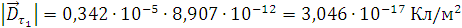
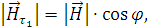
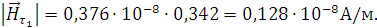
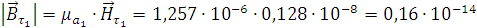
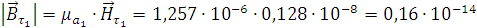 Тл.

.

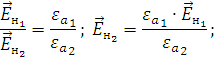
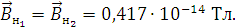
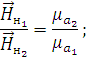
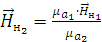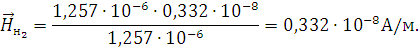
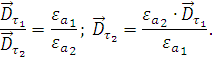
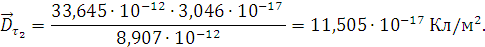
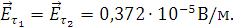
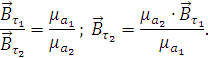
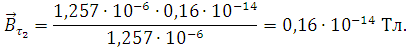
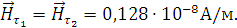
4. Найдём глубину проникновения во вторую среду по формуле:

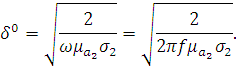
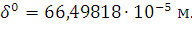
Заключение

электромагнитный отражение преломление амплитуда

В данной курсовой работе нами были рассмотрены процессы движения плоских электромагнитных волн сквозь проводящую и диэлектрическую среду, а также рассмотрен механизм их поглощения и отражения.

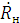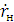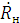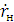В результате курсовой работы был произведен анализ процесса отражения и преломления плоских волн от плоской границы сред. Мы рассчитали коэффициенты отражения =-0,189 и преломления =0,811. Фаза отраженной волны будет изменяться на 180 градусов, поскольку <0. Фаза преломлённой волны остаётся прежней, так как >0.

При нахождении угла падения, при котором будет отсутствовать преломленная волна, мы получили, что 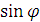=1,545, это говорит о том, что преломлённая волна будет присутствовать при любом угле падения волны на границе раздела сред.

Мы рассчитали нормальные и тангенциальные составляющие векторов в первой и второй среде при условии, что граница не заряжена

Также мы рассчитали и получили глубину проникновения волны во вторую среду: =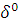

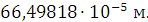
Список использованной литературы

1.   Бессонов Л.А. Теоретические основы электротехники: Электромагнитное поле: Учебник для студентов вузов.-7-е изд., перераб. и доп.- М.: Высш. школа, 2008. - 231 с.

2.       Волынский В.А. и др. Электротехника /Б.А. Волынский, Е.Н. Зейн, В.Е. Шатерников: Учеб. пособие для вузов. - М.: Энергоатомиздат, 2007.-528с.

.        Материалы в приборостроении и автоматике: Справочник / Под ред. Ю.М. Пятина. - М.: Машиностроение, 1992. - 528 с.

.        Матханов П.А. Основы анализа электрических цепей. - М.: Высш. шк., 1990. - 400 с.

.        Матханов П.А. Основы анализа электрических цепей. - М.: Высш. шк., 1990. - 400 с.

.        Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. В 2-х т.: Учебник для вузов. Том 1. - 3-е изд., перераб. и доп. - Л.: Энергоиздат, 2007. - 536 с.

.        Теоретические основы электротехники. В 3-х ч. - Ч. I. Атабеков Г.И. Линейные электрические цепи: Учебник для вузов. - 5-е изд., испр. и доп. - М.: Энергия, 2008. - 592 с.

.        Теоретические основы электротехники. В 3-х ч. - Ч. I. Атабеков Г.И. Линейные электрические цепи: Учебник для вузов. - 5-е изд., испр. и доп. - М.: Энергия, 2008. - 592 с.

.        Электротехника и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.1. Электрические и магнитные цепи. - М.: Высшая шк. - 2009. - 386 с.