Поляризация электромагнитных волн и поляризационная оптика
Курсовая
работа
Поляризация
электромагнитных волн и поляризационная оптика
Введение
Поляризация волн является одним из важнейших
свойств, характеризующих электромагнитные волны, как и поперечные волны в
целом. Изучение поведения волн с различными видами поляризации имеет ключевой
характер, как в поляризационной оптике, так и в электродинамике сплошных сред.
Рассмотрение процессов преобразования одних видов поляризации в другие при
взаимодействии электромагнитных волн с материальными средами в ряде случаев
позволяет качественно и количественно судить о структуре (форма молекул, класс
симметрии и т.д.) того или иного вещества, в виду чего поляризованное излучение
широко используется в практической деятельности.
На современном этапе развития поляризационной
оптики существует немало способов описания состояния поляризации, поэтому будет
уместным провести обзор некоторых, наиболее востребованных практически, моделей
описания поляризации электромагнитных волн. Безусловно, те методы, которые
будут приведены в данной работе, не обязательно являются «наиболее удобными»
при описании всех типов поляризации. Существует ряд альтернативных и
установившихся методов, которые при тех или иных условиях конкретной физической
задачи могут оказаться более предпочтительными. В любом случае, рассмотрения
различных видов поляризации, а также методов её описания является весьма
актуальным, именно изучению этого свойства электромагнитных волн и посвящена
настоящая работа.
1. Полностью поляризованное излучение в изотропной
среде
.1 Решение волнового уравнения
Изотропные среды, облают самыми простыми
оптическими свойствами в сравнении с иными видами материальных сред. В
соответствии с этим для иллюстрации процесса распространения электромагнитных
волн в веществе, прежде всего, следует рассмотреть именно изотропные среды.
Характерной особенностью таких сред является независимость их оптических
свойств от пространственных направлений. Связь между четырьмя основными
характеристика поля волны в таких средах дается простой пропорциональностью:
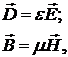
где 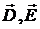 и
и 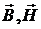 - индукции и напряжённости
электрического и магнитного полей соответственно,
- индукции и напряжённости
электрического и магнитного полей соответственно, 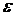 и
и 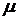 -
диэлектрическая и магнитная проницаемость рассматриваемого вещества (у
изотропных сред они являются скалярами). Для того чтобы получить вид
распространяющейся в изотропной среде волны уравнения (1.1) необходимо
дополнить системой уравнений Максвелла для материальных сред. Считая среду,
описываемую материальными уравнениями (1.1) диэлектриком запишем уравнения
Максвелла в виде:
-
диэлектрическая и магнитная проницаемость рассматриваемого вещества (у
изотропных сред они являются скалярами). Для того чтобы получить вид
распространяющейся в изотропной среде волны уравнения (1.1) необходимо
дополнить системой уравнений Максвелла для материальных сред. Считая среду,
описываемую материальными уравнениями (1.1) диэлектриком запишем уравнения
Максвелла в виде:
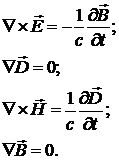
Уравнения (1.2) в совокупности с уравнениями
(1.1) составляют полную систему электродинамических соотношений описывающих
свободное электромагнитное поле в изотропной среде.
Найдём решение указанных уравнений.
Для определённости будем искать решение для вектора напряжённости
электрического поля 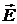 . Решение
будем искать решение в виде плоской монохроматической волны:
. Решение
будем искать решение в виде плоской монохроматической волны:
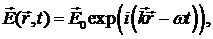
где 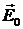 - некоторый постоянный вектор (в
общем случае комплексный),
- некоторый постоянный вектор (в
общем случае комплексный), 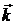 - волновой вектор,
- волновой вектор, 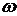 - частота
колебаний вектора
- частота
колебаний вектора 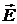 . Очевидно,
что остальные характеристики поля также будут зависеть от координат и времени
как
. Очевидно,
что остальные характеристики поля также будут зависеть от координат и времени
как 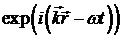 . Введём
обозначение
. Введём
обозначение 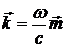 , вектор
, вектор 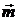 называется
вектором рефракции, его модуль равен показателю преломления данной среды.
Теперь, с учётом вышесказанного, уравнения (1.2) можно записать в более простой
форме:
называется
вектором рефракции, его модуль равен показателю преломления данной среды.
Теперь, с учётом вышесказанного, уравнения (1.2) можно записать в более простой
форме:
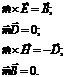
Используя систему (1.1) и первое и
третье уравнения системы (1.4) получим для вектора 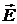 следующее
уравнение:
следующее
уравнение:
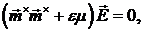
где 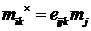 - тензор дуальный вектору
- тензор дуальный вектору 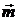 . Система
уравнений (1.5) имеет не нулевые решения лишь в том случае когда:
. Система
уравнений (1.5) имеет не нулевые решения лишь в том случае когда:
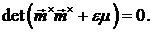
Выбирая систему координат так, чтобы
вектор 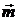 был
направлен вдоль оси
был
направлен вдоль оси 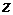 , получим:
, получим:
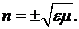
Выражение (1.6) определяет
показатели преломления среды для волны, распространяющейся в положительном
направлении выбранной оси (знак плюс) и в отрицательном (знак минус). В
дальнейшем будем использовать выражение 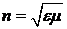 . Далее, вектор
. Далее, вектор 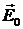 представим
в следующем виде:
представим
в следующем виде:
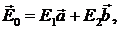
здесь 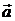 и
и 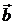 орты осей
орты осей 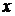 и
и 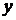 ,
, 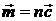 . Подставляя
выражение для вектора
. Подставляя
выражение для вектора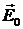 в (1.3),
убеждаемся что равенство (1.5) выполняется тождественно. Таким образом,
решением уравнения матричного уравнения (1.5) является:
в (1.3),
убеждаемся что равенство (1.5) выполняется тождественно. Таким образом,
решением уравнения матричного уравнения (1.5) является:
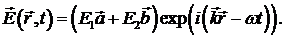
Из вида (1.7) ещё раз убеждаемся в поперечности
электромагнитных волн.
.2 Анализ решения волнового уравнения
Теперь проведём анализ соотношения
(1.7). Прежде всего, отметим, что поле внутри изотропного диэлектрика
представляет собой суперпозицию двух колебаний во взаимно перпендикулярных
направлениях. Рассмотрим некоторые важные частные случаи. Если разность фаз
между ортогональными компонентами поля равна 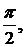 конец вектора
конец вектора 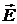 будет
описывать эллипс. Взяв действительную часть от выражения (1.7) и выделив
проекции, на соответствующие оси получим:
будет
описывать эллипс. Взяв действительную часть от выражения (1.7) и выделив
проекции, на соответствующие оси получим:
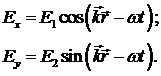
Возводя каждое из равенств (1.8) в квадрат и
затем, сложив полученные выражения, получим
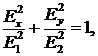
(1.9) является уравнением эллипса с
полуосями 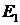 и
и 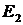 . Как и
утверждалось, конец вектора
. Как и
утверждалось, конец вектора 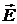 описывает эллипс, такая волна
называется эллиптически поляризованной. Далее, если амплитуды
описывает эллипс, такая волна
называется эллиптически поляризованной. Далее, если амплитуды 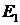 и
и 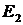 вещественны,
волна будет поляризованной линейно, вектор поля в такой волне будет совершать
колебания вдоль некоторой линии. В частности, если одна из амплитуд равна нулю,
волна будет поляризована вдоль одной из осей (
вещественны,
волна будет поляризованной линейно, вектор поля в такой волне будет совершать
колебания вдоль некоторой линии. В частности, если одна из амплитуд равна нулю,
волна будет поляризована вдоль одной из осей (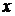 или
или 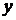 ). И, наконец, когда выполнено
условие
). И, наконец, когда выполнено
условие 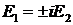 с разностью
фаз между ортогональными компонентами равной
с разностью
фаз между ортогональными компонентами равной 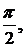 волна будет поляризована по кругу.
Причём, когда разность фаз положительна (знак плюс) конец вектора поля будет
вращаться по часовой стрелке, такая волна называется право циркулярно
поляризованной, в противном случае (знак минус) лево циркулярно поляризованной.
волна будет поляризована по кругу.
Причём, когда разность фаз положительна (знак плюс) конец вектора поля будет
вращаться по часовой стрелке, такая волна называется право циркулярно
поляризованной, в противном случае (знак минус) лево циркулярно поляризованной.
На рисунке (1.1) изображены кривые,
которые описывает конец вектора 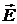 при различных видах поляризации.
при различных видах поляризации.
Рисунок 1.1. Графическое
представление поляризованного излучения
- линейная поляризация; 2 - круговая
поляризация; 3 - эллиптическая поляризация
Таким образом, полностью
поляризованное излучение в изотропных средах подразделяется на три основных
типа: линейно, эллиптически и циркулярно поляризованное.
2. Способы описания состояния
поляризации
.1 Базовая система задания состояния
поляризации
В поляризационном анализе понятие
«состояние поляризации» формализовано, т.е. введена система параметров,
полностью и однозначно определяющих значение и пространственно-временные
эволюции векторных характеристик излучения (для изотропной среды - вектора 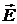 ). Иначе
говоря, указав следующие параметры:
). Иначе
говоря, указав следующие параметры:
амплитуду 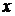 - компоненты
волны
- компоненты
волны 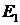 ;
;
амплитуду 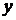 - компоненты
волны
- компоненты
волны 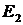 ;
;
разность фаз (а точнее её
математическое ожидание) ортогональных компонент волны 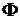 ;
;
степень когерентности ортогональных
компонент 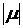 ,
,
мы можем полностью и однозначно
характеризовать состояние поляризации излучения. Для дальнейшего запишем
формулу, для определения степени когерентности:
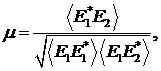
в соотношении (2.1) звёздочка
означает взятие комплексного сопряжения, а знак 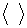 усреднение по времени
соответствующих характеристик волны. В базовой системе описания поляризации
используются следующие параметры:
усреднение по времени
соответствующих характеристик волны. В базовой системе описания поляризации
используются следующие параметры:
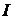 интенсивность излучения;
интенсивность излучения;
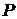 степень поляризации излучения;
степень поляризации излучения;
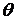 азимут поляризации;
азимут поляризации;
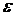 угол эллиптичности.
угол эллиптичности.
Подчеркнём, что с помощью указанных
параметров представляется возможным описывать состояние поляризации
произвольного излучения (т.к. оно может быть представлено как суперпозиция
поляризованной и неполяризованной частей). На рисунке (2.1) показаны величины 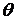 и
и 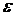 .
.
Рисунок 2.1. Поляризационный эллипс
Оси 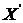 и
и 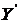 , на рисунке (2.1) называют
собственными осями эллипса поляризации.
, на рисунке (2.1) называют
собственными осями эллипса поляризации.
Теперь запишем соотношения
выражающие параметры базовой системы, через 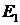 ,
, 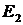 ,
, 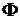 и
и 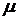 :
:
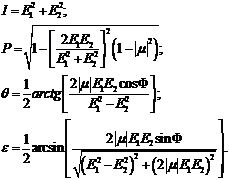
Система уравнений (1.11) однозначно описывает
состояние поляризации произвольного излучения.
.2 Вектор Джонса
Для анализа и расчёта состояний
поляризации, полностью поляризованных световых пучков наибольшее
распространение получил метод, разработанный американским физиком Р. Джонсом.
Полный вектор Джонса представляет собой столбец комплексных амплитуд двух
ортогональных компонент вектора напряжённости 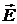 :
:
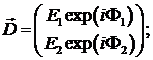
Вектор Джонса - это комплексный
вектор; его невозможно представить в виде направленного отрезка в трёхмерном
пространстве. Однако, в то время как вектор вида (2.3) однозначно определяет
состояние поляризации света, обратная связь неоднозначна. Умножение или деление
вектора на унимодулярное комплексное число (сдвиг фазы) не изменяет состояние
поляризации и интенсивность. Умножив вектор (2.3) на 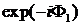 , получим
вектор вида:
, получим
вектор вида:
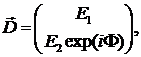
где 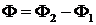 . В дальнейшем будем использовать
именно эту форму вектора Джонса. Легко видеть, что вектор вида (2.4) содержит
те же параметры, что и введённая ранее естественная система обозначения
состояния поляризации. Одним из основных свойств вектора Джонса является то,
что ортогональным поляризациям соответствуют ортогональные векторы Джонса, для
которых выполняется условие
. В дальнейшем будем использовать
именно эту форму вектора Джонса. Легко видеть, что вектор вида (2.4) содержит
те же параметры, что и введённая ранее естественная система обозначения
состояния поляризации. Одним из основных свойств вектора Джонса является то,
что ортогональным поляризациям соответствуют ортогональные векторы Джонса, для
которых выполняется условие
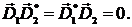
Здесь используется скалярное произведение векторов.
Если какая либо поляризация задана вектором вида (2.4), то ортогональной
поляризации соответствует вектор
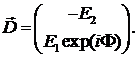
Запишем, декартовы векторы Джонса
вида (2.4) для нескольких характерных состояний поляризации. Для линейной
поляризации с горизонтальным расположением вектора 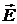 , тогда
имеем
, тогда
имеем
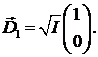
Очевидно ортогональный (вертикальная
ориентация вектора 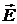 ) вектору
(2.7) вектор
) вектору
(2.7) вектор
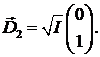
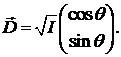
Для круговых состояний поляризации
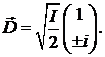
Для произвольного эллиптического состояния
поляризации декартов вектор Джонса, с помощью соотношения (2.3), может быть
представлен в виде
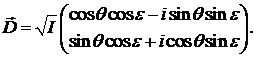
Таким образом, в рассмотренном методе для
описания состояния поляризации достаточно задать лишь один комплексный вектор
вида (2.4) (или (2.3)), в этом отношении вектор Джонса весьма удобен для
практического использования.
.3 Поляризационная переменная
В ряде поляризационных расчётов абсолютная
интенсивность излучения оказывается несущественной. К таким относятся расчёты
относительных энергетических потерь и преобразований состояний поляризации
излучения в анизотропных оптических трактах и расчёты собственных состояний
поляризации, поляризационных потерь и частотных сдвигов в оптических
резонаторах. В этих случаях нет необходимости применять полные векторы Джонса.
Основной характеристикой для
описания состояния поляризации полностью поляризованного света в анализе, где
не важна абсолютная интенсивность, может служить так называемая,
поляризационная переменная 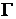 . Поляризационная переменная - это
комплексное число, представляющее собой отношение компонент вектора Джонса:
. Поляризационная переменная - это
комплексное число, представляющее собой отношение компонент вектора Джонса:
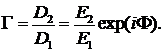
Для вычисления поляризационной переменной можно
использовать также следующие соотношения:
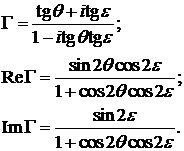
Обратные соотношения имеют вид:

Для ортогональных состояний поляризации
справедливо соотношение
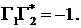
Зная поляризационную переменную, можно записать
нормированный вектор Джонса в виде, не содержащем информацию об абсолютной
интенсивности:
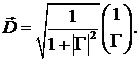
Также для полного вектора Джонса (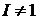 )
)
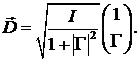
.4 Вектор Стокса
Основным и общим недостатком методов
поляризационной переменной и вектора Джонса, является то, что они не учитывают
не поляризованную часть излучения. Для решения большинства практических задач
это недопустимо. Поэтому важно рассмотреть метод позволяющий учесть
неполяризованную часть излучения. Одним из таких способов описания состояния
поляризации является система параметров Стокса (вектор Стокса), предложенная
английским физиком и математиком Дж. Стоксом в 1852 г. Вектор Стокса
записывается в виде четырёхмерного вектора следующим образом:
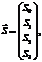
где параметры 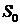 ,
, 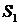 ,
, 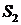 и
и 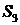 задаются
выражениями:
задаются
выражениями:
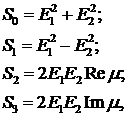
здесь, как и прежде, 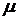 определяется
формулой (2.1).
определяется
формулой (2.1).
Вектор Стокса удобен для проведения
ряда поляризационных расчётов. Например, результирующее состояние поляризации
некогерентной суперпозиции ряда световых пучков описывается суммарным вектором
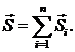
Так как в неполяризованном свете не
преобладает ни один из видов поляризации то, очевидно, в векторе Стокса (2.18)
будет отличным от нуля лишь элемент 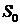 . Следовательно, соответствующий
вектор Стокса
. Следовательно, соответствующий
вектор Стокса
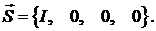
Отметим, что если параметр 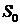 всегда
задаёт общую интенсивность, то интенсивность поляризованной части излучения
всегда
задаёт общую интенсивность, то интенсивность поляризованной части излучения

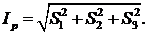
Связь параметров Стокса с
характеристиками базовой системы описания состояния поляризации

Более подробное описание всех рассмотренных в
данной главе методов описания состояния поляризации можно найти, например в
[1].
3. Сфера Пуанкаре
Наглядным геометрическим
пространственным образом для всех возможных состояний поляризации полностью
поляризованного излучения является сфера Пуанкаре, предложенная в 1892 г. Анри
Пуанкаре. Представим сферу, каждая точка которой, по аналогии с глобусом,
определяется координатами: долготой 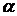 и широтой
и широтой 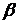 (рис. 3.1).
(рис. 3.1).
Рис. 3.1. Сфера Пуанкаре
Положим, что каждой точке сферы
соответствует состояние поляризации одинаковой интенсивности, которое задаётся
эллипсометрическими параметрами 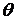 и
и 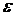 . Долгота и широта произвольной
точки связаны с азимутом и эллиптичностью поляризации следующими соотношениями:
. Долгота и широта произвольной
точки связаны с азимутом и эллиптичностью поляризации следующими соотношениями:
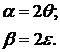
Очевидно, что всё множество состояний
поляризации совпадает с множеством точек поверхности сферы. Так, линейные
поляризации (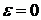 )
располагаются по экватору сферы OMSN. Точка экватора O на
пересечении с нулевым меридианом ORSL (
)
располагаются по экватору сферы OMSN. Точка экватора O на
пересечении с нулевым меридианом ORSL (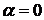 )
соответствует линейной поляризации с горизонтальной ориентацией вектора
)
соответствует линейной поляризации с горизонтальной ориентацией вектора 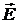 (
(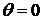 ).
Диаметрально противоположная точка сферы S (
).
Диаметрально противоположная точка сферы S ( ) отображает
линейную поляризацию с вертикальной ориентацией вектора
) отображает
линейную поляризацию с вертикальной ориентацией вектора 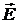 (
(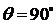 ). Линейные
поляризации с азимутом
). Линейные
поляризации с азимутом 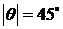 соответствуют
экваториальным точкам M и N с долготой
соответствуют
экваториальным точкам M и N с долготой 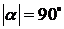 . Нулевой
меридиан ORSL заполнен
состояниями поляризации с нулевым азимутом. Полюса сферы Пуанкаре (точки R и L)
соответствуют круговым поляризациям (
. Нулевой
меридиан ORSL заполнен
состояниями поляризации с нулевым азимутом. Полюса сферы Пуанкаре (точки R и L)
соответствуют круговым поляризациям (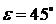 ).
).
Для теоретических расчётов более
удобно использовать связь параметров Стокса, введённых в предыдущем параграфе,
с параметрами сферы Пуанкаре [2]. Здесь в роли независимых переменных выступают
параметры 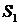 ,
, 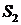 и
и 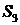 , а параметр
, а параметр
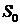 выражается
через них посредством
выражается
через них посредством
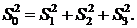
Ввиду вышесказанного
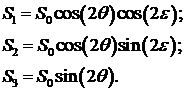
Таким образом, с помощью соотношения
(3.3) зная параметры 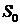 ,
, 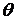 и
и 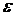 можно
геометрически (посредствам сферы Пуанкаре в координатах
можно
геометрически (посредствам сферы Пуанкаре в координатах 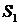 ,
, 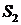 ,
, 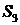 ) отобразить
произвольное состояние поляризации излучения.
) отобразить
произвольное состояние поляризации излучения.
4. Граничные условия в
электродинамике естественно гиротропных сред
Для вывода граничных условий для
естественно гиротропных сред, следует ввести материальные уравнения описывающие
связь характеристик электромагнитного поля в такой среде. Эти уравнения имеют
вид [3]
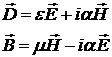
где 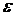 - диэлектрическая проницаемость
среды (так как параметр эллиптичности далее использоваться не будет,
недоразумений по поводу обозначений не должно возникнуть),
- диэлектрическая проницаемость
среды (так как параметр эллиптичности далее использоваться не будет,
недоразумений по поводу обозначений не должно возникнуть), 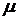 - магнитная
проницаемость,
- магнитная
проницаемость, 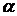 - параметр
гиротропии. Теперь сделаем ряд дополнительных замечаний о свойствах
рассматриваемой среды. Во-первых, будем рассматривать среду изотропной, в такой
среде параметры
- параметр
гиротропии. Теперь сделаем ряд дополнительных замечаний о свойствах
рассматриваемой среды. Во-первых, будем рассматривать среду изотропной, в такой
среде параметры 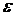 ,
, 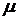 и
и 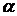 являются
скалярами. Во-вторых, предполагаем, что среда однородна, т.е.
электродинамические параметры (
являются
скалярами. Во-вторых, предполагаем, что среда однородна, т.е.
электродинамические параметры (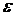 ,
,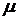 ,
, 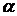 ) не зависят от координат, в
противном случае, вообще говоря, нельзя получить некоторый общий (не зная
явного вида
) не зависят от координат, в
противном случае, вообще говоря, нельзя получить некоторый общий (не зная
явного вида 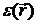 ,
, 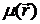 и
и 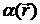 ) вид
граничных условий. С учётом сказанного граничные условия «стандартным» образом
получаются из уравнений Максвелла. Воспользуемся уравнениями Максвелла в виде
) вид
граничных условий. С учётом сказанного граничные условия «стандартным» образом
получаются из уравнений Максвелла. Воспользуемся уравнениями Максвелла в виде
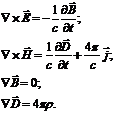
или в интегральной форме
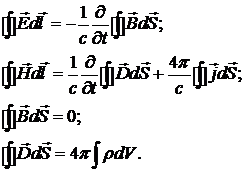
Рассмотрим гладкую границу раздела
двух естественно гиротропных сред с параметрами 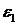 ,
, 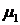 ,
, 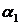 и
и  ,
, 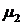 ,
, 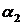 соответственно. Применим первое
уравнение системы (4.3) к бесконечно малому контуру L
изображённому на рисунке 4.1.
соответственно. Применим первое
уравнение системы (4.3) к бесконечно малому контуру L
изображённому на рисунке 4.1.
Рисунок 4.1.
Тогда имеем
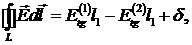
где 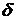 - бесконечно малая второго порядка,
- бесконечно малая второго порядка,
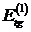 и
и 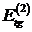 тангенциальные
составляющие вектора
тангенциальные
составляющие вектора 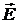 в первой и
второй средах соответственно. Далее, пренебрегая
в первой и
второй средах соответственно. Далее, пренебрегая 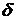 в виду его малости, пишем
в виду его малости, пишем
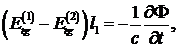
здесь 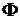 - поток магнитной индукции через
поверхность, стягиваемую контуром L. Очевидно,
- поток магнитной индукции через
поверхность, стягиваемую контуром L. Очевидно, 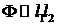 и является
величиной старшего порядка малости. Поэтому, переходя к пределу
и является
величиной старшего порядка малости. Поэтому, переходя к пределу 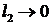 , находим
, находим
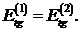
Из (4.4) явствует, что
тангенциальная составляющая вектора напряжённости электрического поля остаётся
непрерывной при переходе через границу раздела сред.
Применим аналогичный приём ко
второму уравнению системы (4.3). При этом сразу опустим член второго порядка
малости 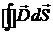 . Тогда
находим
. Тогда
находим
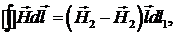
где 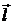 - единичный вектор контура, лежащий
в плоскости раздела. Обозначим через
- единичный вектор контура, лежащий
в плоскости раздела. Обозначим через 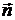 нормаль к поверхности раздела и
через
нормаль к поверхности раздела и
через 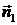 нормаль к
поверхности, охваченной контуром L. Векторы
нормаль к
поверхности, охваченной контуром L. Векторы 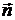 ,
, 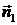 и
и 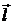 образуют
правовинтовую систему:
образуют
правовинтовую систему:
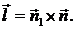
Введём, далее, понятие поверхностной
плотности тока 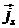 , эта
величина характеризует количество электричества, проходящее за одну секунду
через единичный отрезок на поверхности:
, эта
величина характеризует количество электричества, проходящее за одну секунду
через единичный отрезок на поверхности:
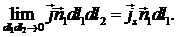
Тогда из второго уравнения (4.3) получим
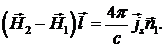
Выражая 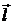 через
через 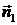 , имеем
, имеем
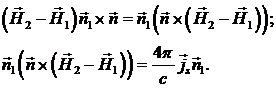
Так как ориентация вектора 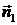 в плоскости
раздела может быть произвольной, должно выполняться равенство
в плоскости
раздела может быть произвольной, должно выполняться равенство

Из (4.5) следует, что при наличии
поверхностных токов тангенциальная составляющая вектора 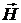 претерпевает
разрыв при переходе через границу раздела. Величина скачка
претерпевает
разрыв при переходе через границу раздела. Величина скачка 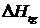 равна
равна 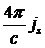 .
.
Если поверхностный ток на границе
раздела отсутствует (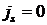 ), то
), то
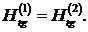
Граничные условия для нормальных
составляющих векторов 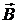 и
и 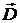 получаются
из третьего и четвёртого уравнений системы (4.3), если в качестве поверхности интегрирования,
выбрать бесконечно малую поверхность S,
изображённую на рисунке 4.2. Площадь оснований
получаются
из третьего и четвёртого уравнений системы (4.3), если в качестве поверхности интегрирования,
выбрать бесконечно малую поверхность S,
изображённую на рисунке 4.2. Площадь оснований 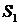 является бесконечно малой первого,
а площадь боковых граней - бесконечно малой второго порядка.
является бесконечно малой первого,
а площадь боковых граней - бесконечно малой второго порядка.
Рисунок 4.2.
Из третьего уравнения (4.3) находим
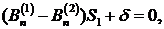
или, переходя к пределу,
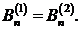
Нормальная составляющая вектора магнитной
индукции при переходе через границу раздела не претерпевает разрыва. Аналогично
из четвёртого уравнения (4.3):
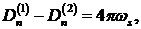
где 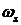 - поверхностная плотность заряда,
определяемая, как и выше,
- поверхностная плотность заряда,
определяемая, как и выше,
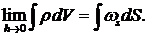
Если поверхностная плотность заряда 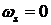 , то
, то
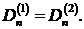
Уравнения (4.4), (4.5), (4.7) и (4.8) являются
граничными условиями, которые должны удовлетворять векторы поля на границе
раздела двух естественно гиротропных (но изотропных) сред. Данные граничные
условия совпадают с граничными условиями для случая, когда среда есть
изотропный диэлектрик [4].
5. Решение задач о нормальном и наклонном
падении электромагнитной волны на плоскую границу раздела «вакуум-гиротропная
среда»
.1 Нормальное падение линейно поляризованной
волны
Пусть, на плоскую границу раздела
вакуума (1) и гиротропной среды (2) падает (нормально) плоскополяризованная
монохроматическая волна (рисунок 5.1), в которой вектор 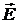 колеблется
параллельно оси
колеблется
параллельно оси 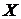 , а вектор
напряжённости магнитного поля
, а вектор
напряжённости магнитного поля 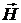 параллельно оси
параллельно оси 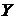 (ось
(ось 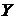 направлена
перпендикулярно плоскости рисунка). Для получения связи между векторами
направлена
перпендикулярно плоскости рисунка). Для получения связи между векторами 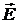 и
и 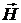 в среде (1)
воспользуемся уравнением:
в среде (1)
воспользуемся уравнением:
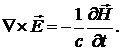
Тогда падающая волна будет иметь вид:
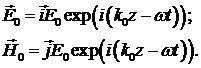
Рисунок 5.1
Отражённая волна в общем виде:
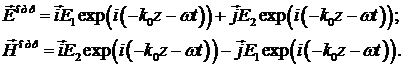
Учитывая соотношение (5.1) преломлённую волну
будем искать в виде:
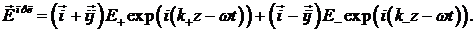
В (5.2) - (5.4) 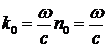 ,
, 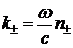 ,
, 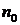 -
показатель преломления вакуума;
-
показатель преломления вакуума; 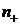 и
и 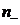 - показатели преломления
естественно гиротропной среды для право и лево циркулярно поляризованных волн;
- показатели преломления
естественно гиротропной среды для право и лево циркулярно поляризованных волн; 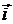 и
и 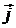 орты осей
орты осей 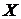 и
и 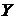 соответственно.
Теперь, для нахождения магнитной составляющей преломлённой волны воспользуемся
материальными уравнениями (4.1) и уравнением:
соответственно.
Теперь, для нахождения магнитной составляющей преломлённой волны воспользуемся
материальными уравнениями (4.1) и уравнением:
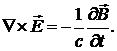
Также, будет целесообразным выписать
здесь явный вид выражений для 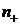 и
и 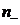 :
:
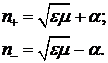
В результате не сложных вычислений и
учитывая соотношение (5.6) для поля 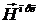 получим:
получим:
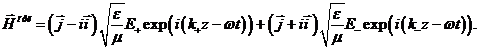
Также, будет целесообразным выписать
здесь явный вид выражений для величин 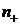 и
и 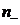 :
:
Для нахождения амплитуд падающей и
отражённой волн, воспользуемся условием непрерывности тангенциальных к границе
раздела, составляющих векторов 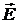 и
и 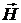 . Тогда получим следующую систему
уравнений:
. Тогда получим следующую систему
уравнений:
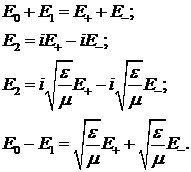
Подставив второе уравнение системы в третье,
получим из (5.8):
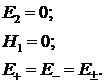
В итоге система уравнений (5.8) примет вид:
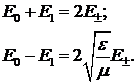
Откуда:
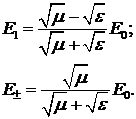
Как видно из соотношений (5.10)
коэффициенты связи между амплитудами падающей, преломлённой и отражённой волн
не зависят от параметра гиротропии 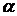 . Подчеркнём, что полученные формулы
в точности совпадают с известными формулами Френеля для случая, когда граница
раздела есть: вакуум - диэлектрик (следует помнить, что суммарная амплитуда
преломлённой волны есть
. Подчеркнём, что полученные формулы
в точности совпадают с известными формулами Френеля для случая, когда граница
раздела есть: вакуум - диэлектрик (следует помнить, что суммарная амплитуда
преломлённой волны есть 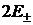 ). Теперь
для выяснения справедливости полученных соотношений, проверим выполнение закон
сохранения энергии. Именно, средняя по времени плотность потока энергии
падающей волны, должна быть равна сумме потоков уносимых преломлённой и
отражённой волной соответственно. Средняя по времени плотность потока энергии
(вектор Умова - Пойтинга) для плоских монохроматических волн [5]:
). Теперь
для выяснения справедливости полученных соотношений, проверим выполнение закон
сохранения энергии. Именно, средняя по времени плотность потока энергии
падающей волны, должна быть равна сумме потоков уносимых преломлённой и
отражённой волной соответственно. Средняя по времени плотность потока энергии
(вектор Умова - Пойтинга) для плоских монохроматических волн [5]:
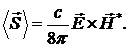
Где фигурные скобки означают, взятие среднего по
времени значения, а звёздочка означает комплексное сопряжение. В результате
закон сохранения энергии:
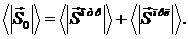
Используя выражения (5.2) - (5.4), (5.7), (5.10)
и (5.11) прямым вычислением можно убедиться, что равенство (5.12) выполняется
тождественно. Здесь же определим коэффициент отражения для рассматриваемого
случая как отношение среднего по времени отражённого потока энергии к падающему
потоку:
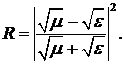
.2 Наклонное падение линейно поляризованной
волны
Теперь рассмотрим отражение, и преломление
плоской монохроматической волны при наклонном падении, на плоскую границу
раздела двух однородных (и изотропных) сред: вакуум - гиротропная среда. При
решении данной задачи будем считать, что вектор электрического поля  лежит в
плоскости падения (плоскость
лежит в
плоскости падения (плоскость 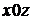 , ось
, ось 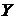 направлена в рисунок). Для удобства
определения амплитуд отражённой и преломлённой волн введём три взаимно
ортогональных вектора, которые будут характеризовать направление
распространения волны, а также направления, в которых колеблются вектора
направлена в рисунок). Для удобства
определения амплитуд отражённой и преломлённой волн введём три взаимно
ортогональных вектора, которые будут характеризовать направление
распространения волны, а также направления, в которых колеблются вектора 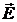 и
и 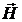 . Выберем
эти тройки векторов, так как показано на рисунке 1.2. Тогда падающая волна
будет иметь вид:
. Выберем
эти тройки векторов, так как показано на рисунке 1.2. Тогда падающая волна
будет иметь вид:
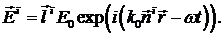
Где введено обозначение 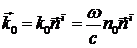 где
где 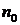 - показатель
преломления для волны в вакууме.
- показатель
преломления для волны в вакууме.
В соответствии с формулой (1.2),
преломлённые волны будем искать в виде:

Рисунок 5.2.
Отражённая волна:
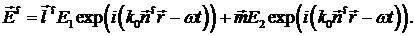
Но основе соотношений (5.1), (5.5), (5.14) -
(5.18) нетрудно записать аналогичные выражения для магнитной составляющей
рассматриваемых волн:
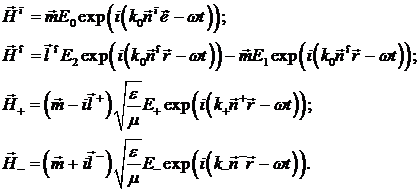
Теперь для определения амплитуд 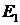 ,
, 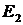 ,
, 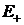 и
и 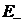 воспользуемся
условием непрерывности тангенциальных компонент векторов
воспользуемся
условием непрерывности тангенциальных компонент векторов 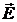 и
и 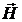 на границе
раздела
на границе
раздела 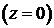 . Учитывая
выше сказанное, запишем граничные условия для электрической составляющей:
. Учитывая
выше сказанное, запишем граничные условия для электрической составляющей:
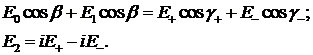
Для того чтобы решить эту систему
требуется ввести ещё два дополнительных уравнения. Эти уравнения можно получить
из граничных условий для вектора 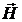 :
:
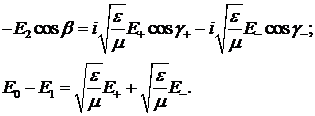
Решая совместно системы (1.19) и (1.20) получим:
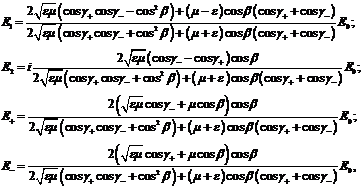
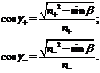
Как видно из формул (5.20) отражённая волна
является эллиптически поляризованной, этот эффект существенно отличает
естественно гиротропную среду от изотропного диэлектрика. В этом отношении,
гиротропия среды проявляется здесь как разновидность анизотропии.
При переходе к 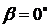 формулы
(5.20) как и следовало, переходят в соотношения (5.10). Воспользовавшись
формулами (5.11), (5.14) - (5.17) и (5.20) проверим выполнение закона
сохранения энергии. Беря проекцию на ось
формулы
(5.20) как и следовало, переходят в соотношения (5.10). Воспользовавшись
формулами (5.11), (5.14) - (5.17) и (5.20) проверим выполнение закона
сохранения энергии. Беря проекцию на ось 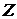 вектора Пойтинга (исходя из его
физического смысла) убеждаемся, что закон сохранения действительно выполняется
вектора Пойтинга (исходя из его
физического смысла) убеждаемся, что закон сохранения действительно выполняется
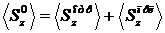
Что подтверждает справедливость полученных
соотношений.
Заключение
поляризация гиротропный излучение
Таким образом, в ходе работы были рассмотрены
основные методы, способы задания, и описания состояния поляризации излучения.
Данные методы широко используются в поляризационном анализе, при разработке и
расчёте различных поляризационных устройств. Также нами были приведены
граничные условия для естественно гиротропных сред, с помощью которых можно
решать большое число граничных задач, рассматривая те или иные оптические
эффекты.
Нами также были решены граничные задачи о
нормальном и наклонном падении электромагнитной волны на плоскую границу
раздела «вакуум - гиротропная среда». В результате были получены формулы связи,
между амплитудами падающей, отражённой и преломлённой волн. Было установлено,
что при наклонном падении волны поляризованной линейно, отражённая волна
является эллиптически поляризованной. Знание подобных эффектов, а также
соответствующих соотношений позволяет, не имея информации о веществе, качественно
и количественно судить о его структуре (свойствах симметрии молекул и т.д.).
Литература
1. Ищенко, Е.Ф. Поляризационная
оптика/ Е.Ф. Ищенко, А.Л. Соколов. - М.: Издательство МЭИ, 2005. - 336 с.
.Борн, М. Основы оптики/ М. Борн, Э.
Вольф. - М.: Наука, 1973. - 720 с.
. Фёдоров, Ф.И. Теория гиротропии/
Ф.И. Фёдоров. - Минск.: Издательство «Наука и техника», 1976. - 456 с.
. Левич, В.Г. Курс теоретической
физики. В 2-х томах. Том 1:Теория электромагнитного поля. Теория
относительности. Статистическая физика. Электромагнитные процессы в веществе/
В.Г. Левич. - М.: Наука, 1969 - 912 с.
. Ландау, Л.Д. Теоретическая физика.
В 10-ти томах. Том 8: Электродинамика сплошных сред/ Л.Д. Ландау, Е.М. Лифшиц.
- М.: Наука, 1982. - 624 с.