Разработка методологии компенсации реактивной мощности на промышленном предприятии
Введение
Производство электроэнергии
выполняется в рамках Единой энергосистемы, а также автономными
электростанциями, использующие энергии ветра, солнца, воды, химическую энергию
преобразования попутного газа, нефти и других углеводородов. Качество вырабатываемой
электроэнергии должно отвечать ГОСТ 32144-2013, где допустимое значение
отклонения не более 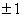 % от
номинального значения напряжения; допустимое значение отклонение частоты не
более
% от
номинального значения напряжения; допустимое значение отклонение частоты не
более 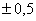 % от
номинального значения частоты.
% от
номинального значения частоты.
Отклонение параметров от нормативных
величин связано с нарушением установившихся режимов или балансов активной и
реактивной мощностей. Следствием нарушения баланса генерируемой и потребляемой
активных мощностей является изменение частоты. Следствием нарушения баланса
генерируемой и потребляемой реактивной мощностей является изменение напряжения.
Например, для асинхронных двигателей (АД) снижение напряжения на 15% от
номинального значения уменьшает электромагнитный момент на 75 %, а снижение
частоты на 5 % понижает реактивное сопротивление и увеличивает статорный ток,
что приводит к дополнительному нагреву АД.
Снижение активной составляющей тока
в линии передач связано с оптимальным выбором установочных мощностей АД при
сохранении их производительности и эффективности работы.
Снижение реактивной составляющей
связано с компенсацией реактивной мощности нагрузки.
Методология компенсации
реактивной мощности нагрузки потребителей рассматривалась как снижения потерь
мощности в сетях. При этом экономическое стимулирование установки
компенсирующих устройств в системах электроснабжения промышленных предприятий
осуществлялось с помощью скидок и надбавок к тарифам на активную электроэнергию
Компенсация реактивной мощности
- путь к уменьшению потерь в системе электроснабжения больших и малых
промышленных предприятий и ее в полной мере можно отнести к энергосберегающим
технологиям. Качество электрической энергии на предприятиях, как правило, не
соответствуют требованиям ГОСТ 32144-2013. Повышенная потребляемая из сети
реактивная мощность и снижение качества напряжения влечет за собой
дополнительные расходы на оплату электроэнергии и ремонт выходящего из строя
технологического оборудования.
Для минимизации потерь с целью
улучшения использования электрической энергии в условиях ограничений на
максимальную потребляемую мощность большая роль отводится новым техническим
средствам и системам управления, позволяющим улучшить энергетические
характеристики: повысить коэффициент мощности сети (cos(φ))
до
заданных значений и уменьшить содержание гармоник в напряжении сети. Повышение
cos(φ)
позволяет
уменьшить потребление из сети активной и реактивной энергии и увеличить срок
службы оборудования за счет разгрузки по мощности.
В последнее десятилетие возникло несоответствие
между достигнутым уровнем теории и новыми задачами развития теории источников
реактивной мощности (ИРМ).
В связи с этим в работе предлагается рассмотреть
следующие проблемы:
разработать метод и алгоритм управления ИРМ в
системе электроснабжения промышленных предприятий при наличии асимметрии по
фазам;
разработать методики проектирования регулятора
тока возбуждения синхронного компенсатора с применением современных технологий;
разработать методы и алгоритмы оптимального
управления компенсацией реактивной мощности в системах электроснабжения
предприятий.
Поставленные проблемы носят комплексный
характер. Их системное решение не получило в настоящее время развития в силу
недостаточной теоретической разработки вопросов управления. Вместе с тем,
использование микропроцессорной техники обеспечивает создание сложных и в тоже
время эффективных и надежных средств регулирования, а микропроцессорное
управление ИРМ позволяет существенно шире использовать для управления сложные
расширенные логические законы управления для снижения потерь в линии передач.
Реализация системного подхода к проектированию современных ИРМ требует развития
общей методологии проектирования ИРМ, создания новых элементов технологической
цепи производства и потребления электрической энергии недетерминированными
объектами.
С учетом вышеизложенного задача разработки и
модернизация существующих ИРМ, на основе современных технологий и элементной
базы для снижения потерь при передаче электроэнергии, является актуальной.
Глава 1. Анализ потерь и путей по их уменьшению
в системе электроснабжения промышленных предприятий
Рассматривая промышленное предприятие как
большую техническую и организационную систему, следует выделить из нее
электрическое хозяйство как подсистему.
Электрическое хозяйство является большой сложной
иерархической системой, которая включает в себя систему электроснабжения,
силовое электрооборудование и автоматизацию, электроосвещение, эксплуатацию и
ремонт электрооборудования. Во всех элементах системы электроснабжения
промышленных предприятий возникают потери электрической энергии, связанные с ее
передачей, с постоянным увеличением и усложнением электрического оборудования.
.1 Анализ потерь в системе
электроснабжения промышленного предприятия
.1.1 Классификация потерь в
системе электроснабжения промышленного предприятия
Фактические (отчетные) потери ∆Q
определяют, как разницу между электроэнергией, отпущенной с шин электрических
станций Wо.с.
и суммой электроэнергии, оплаченной потребителями Wп.о.
и израсходованной на производственные нужды энергосистемой Wп.н.:
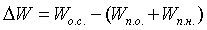 , (1.1)
, (1.1)
Величина фактических потерь включает
в себя технические потери ∆WТ и
коммерческие потери ∆WK. Технические
потери разделяются на нагрузочные потери ∆Wн, потери
холостого хода ∆Wх.х., потери на
корону ∆Wкор в линиях
электропередач и джоулевы потери ∆Wд в кабельных
линиях. Структура расхода электроэнергии показана на рис. 1.1. Классифицируют
их и по группам элементов сетей.
По электрическим сетям 0,4-20 кВ
распределяется около 40% всей вырабатываемой электроэнергии, поэтому правильное
построение системы распределения энергии, обеспечивающее высокую надежность
систем электроснабжения и уменьшение потерь в электрических сетях, имеет важное
значение [10, 11, 12].
К потерям в сетях низкого
напряжения относятся потери в понижающих трансформаторах, в кабельных линиях на
джоулево тепло, потери в измерительных трансформаторах тока и трансформаторах
напряжения, включая счетчики электроэнергии, а также расход электроэнергии на
собственные нужды подстанций [13].
Рис. 1.1 - Структура расхода
электроэнергии на ее передачу
1.1.2 Потери в понижающих
трансформаторах
Преобразование напряжения в
трансформаторных подстанциях сопровождается потерями энергии. Эти потери
покрываются за счет увеличения мощности источников питания.
Потери энергии в
трансформаторах разделяются на потери в обмотках на джоулево тепло и потери в
сердечнике. Величина потерь в трансформаторах зависит от коэффициента нагрузки
трансформатора, который равен:
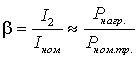 . (1.2)
. (1.2)
Потери в трансформаторе определяются
его КПД. Согласно [14] КПД трансформатора определяется по формуле:
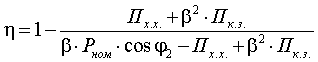 , (1.3)
, (1.3)
где Пх.х. и Пк.з.
- потери ХХ и короткого замыкания (КЗ), кВт;
Pном -
номинальная мощность трансформатора, кВА;
β - коэффициент нагрузки
трансформатора.
В [15] приведены более точные методы
расчета КПД трансформатора, но оценка результатов показывает незначительное
0,3% их отличие от значений, получаемых по формуле (1.3).
Кроме мгновенного значения потерь
используется понятие годовых и суточных относительных потерь энергии, равных
отношению потерь энергии за сутки или за год к величине энергии, потребляемой
из сети. Величина реальных суммарных потерь в понижающих трансформаторах может
достигать (5-8) % от энергии, потребляемой из сети [14].
Увеличение суммарных годовых и
суточных потерь в трансформаторах по сравнению с минимально возможными
обусловлено следующими факторами:
1) суточной и
сезонной цикличностью изменения графика нагрузки потребителей электроэнергии,
имеющей существенную величину из-за которой понижающие трансформаторы большую
часть времени работают при коэффициенте загрузки, отличающейся от оптимального
значения.
2)
сравнительно низким значением cosφ
величина, которого зависит от нагрузки и неравномерности ее распределения по
фазам.
.1.3 Потери в кабельных линиях
Силовые кабели предназначаются
для передачи и распределения электрической энергии. Сооружение и эксплуатация
кабельных линий обходятся всегда дороже воздушных.
К потерям в кабельных линиях,
которые необходимо принимать во внимание, относятся главным образом джоулевы
потери, где часть энергии, передаваемой по проводнику, переходит в тепло
расходуемое вначале на нагрев проводника до определенной температуры, а затем
на поддержание установившегося режима, т.е. теплового равновесия. Чрезмерный
перегрев проводников вызывает ускоренное старение изоляции, а контактные
соединения при этом окисляются.
Погрешности определения потерь
в кабельных линиях обусловлены неточным знанием длин линий, старением кабеля и
т.п. С целью уточнения фактических параметров линий целесообразно проводить
опыты ХХ и КЗ при выводе линий на ремонт.
Для расчета допустимой нагрузки
необходимо учитывать все источники тепла, возникающие в кабеле при его работе,
а также тепловые воздействия на кабель со стороны окружающей среды.
.1.4 Прочие потери в сетях
низкого напряжения
Известно, что потери энергии в
сетях низкого напряжения при постоянных параметрах линии, схеме питания и
передаваемой мощности меняются в зависимости от распределения нагрузки по
фазам. Несимметрия напряжения и токов приводит к дополнительным потерям мощности
и электроэнергии в сети, сокращению сроков службы электрооборудования,
проводников и трансформаторов и к перегрузке отдельных фаз.
Для оценки уровня асимметрии
напряжения введено понятие коэффициента несимметрии напряжения [18],
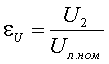 (1.4)
(1.4)
где U2 -
напряжение обратной последовательности, В;
Uл.ном -
номинальное линейное напряжение, В.
Согласно с нормативными
требованиями, приведенными в [7] коэффициент несимметрии напряжения не должен
превышать 2 %. По мере приближения к шинам трансформаторной подстанции
асимметрия резко снижается. При проектировании асимметрию учитывают путем
соответствующего увеличения нормируемых электрических нагрузок, т.е. ведут
расчет по наиболее нагруженной фазе [17].
.2 Влияние коэффициента мощности сети на потери
в системе электроснабжения промышленного предприятия
Значительная часть электроприемников потребляет
помимо активной мощности, еще и реактивную мощность. Показателем потребления
активной мощности является коэффициент мощности сети (cos(φ)).
Повышение cos(φ)
позволяет
уменьшить потребление из сети активной энергии и увеличить за счет разгрузки по
мощности срок службы оборудования [19].
На рис. 1.2 показано
относительное значение полной мощности потребляемой из сети в зависимости от cos(φ).
На рис. 1.3 представлена
диаграмма относительного значения реактивной мощности в зависимости от cos(φ).
В этих двух диаграммах за
единицу принято значение активной мощности.
На рис. 1.4 представлен график
относительного значения тока, протекающего по фазам в зависимости от
коэффициента мощности. На этом графике за единицу принято значение тока при
чисто активной нагрузке. В относительных величинах этот график численно
совпадает с графиком полной мощности. На рисунке 1.5 приведены относительные
активные потери в проводах в зависимости от cos(φ).
Рис. 1.2 - Диаграмма
относительного значения полной мощности потребляемой из сети в зависимости от cos(φ).
Рис. 1.3 - Диаграмма относительного
значения реактивной мощности в зависимости от cos(φ)
Рис. 1.4 - Диаграмма относительного
значения тока, протекающего по фазам в зависимости от cos(φ)
Рис. 1.5 - Диаграмма относительных
активных потерь в проводах в зависимости от cos(φ)
Потери в проводах и шинах
пропорциональны квадрату протекающего через них тока. Из графика (см. рис.
1.2-1.5) видно, что уже при условии cos(φ) = 0,7
происходит удвоение потерь в линиях.
При этом следует отметить, что срок
службы значительной доли силовых трансформаторов, эксплуатируемых на российских
предприятиях, перешагнул 15-летний рубеж. Для продления оставшегося срока
службы необходимо разгрузить трансформаторы по току, что уменьшит температуру
перегрева обмоток и, следовательно, уменьшит скорость старения изоляции.
Известно, что уменьшение температуры перегрева обмоток на 10 °С позволяет в
среднем удвоить оставшийся срок службы силовых трансформаторов. Учитывая
значительную стоимость силовых трансформаторов, при повышении cos(φ) наряду с
уменьшением платы за реактивную энергию возможно существенно улучшить
экономические показатели предприятия [20, 21].
1.3 Анализ путей уменьшения потерь в
системе электроснабжения промышленных предприятий за счет компенсации
реактивной мощности
Компенсирующие устройства (КУ) в
зависимости от их типа и режима работы могут генерировать или потреблять
реактивную мощность Qку,
компенсируя ее дефицит или избыток в электрической сети. Включение КУ в
какой-либо точке сети изменяет реактивную составляющую нагрузки. В итоге
изменяется полная мощность 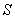 узла нагрузки в соответствии с
векторными диаграммами, показанными на рис. 1.6.
узла нагрузки в соответствии с
векторными диаграммами, показанными на рис. 1.6.
Рис. 1.6 - Компенсация дефицита (а)
и избытка (б) реактивной мощности в узле сети
Так, в результате включения КУ,
генерирующих или потребляющих реактивную мощность, изменяется передаваемая по
участкам сети реактивная мощность и, следовательно, потери напряжения 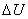 , которые
зависят от разности
, которые
зависят от разности 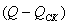 в (1.5):
в (1.5):
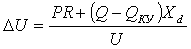 , (1.5)
, (1.5)
где 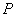 - активная мощность;
- активная мощность;
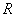 - сопротивление;
- сопротивление;
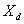 - продольное индуктивное
сопротивление.
- продольное индуктивное
сопротивление.
Создаются возможности регулирования
напряжения в узлах системы электроснабжения и на зажимах потребителей:
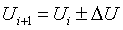 . (1.6)
. (1.6)
Реактивная мощность, передаваемая от
электростанции и других центральных источников, загружает все элементы
электрической сети, уменьшая возможность передачи активной мощности. Снижать
реактивный ток в линии передач возможно за счет установки местных источников
реактивной мощности. В этом случае уменьшается передача реактивной мощности по
участкам сетей:
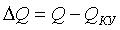 , (1.7)
, (1.7)
снижаются потери активной мощности
(более эффективно передается активная мощность при условии 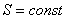 ) в них:
) в них:
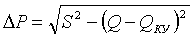 , (1.8)
, (1.8)
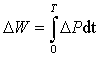 , (1.9)
, (1.9)
и создаются условия для передачи по
сети больших потоков активной мощности.
.3.1 Анализ мероприятий по уменьшению
потребления реактивной мощности приемниками электрической энергии
К мероприятиям по снижению
потребления реактивной мощности приемниками относятся [25]:
правильный выбор
электродвигателей по мощности и по типу;
замена недогруженных АД
двигателями меньшей мощности;
понижение напряжения в обмотках
асинхронных двигателей (АД), систематически работающих с малой загрузкой;
ограничение холостых ходов АД;
повышение качества ремонта
электродвигателей,
ограничение токов ХХ
трансформаторов.
Краткий анализ этих
мероприятий.
) Правильный выбор
электродвигателей по мощности и по типу. Мощность электродвигателей следует
выбирать в соответствии с режимом производственного оборудования, не допуская
излишних запасов мощности.
АД работает с наилучшими
энергетическими показателями при загрузке от 75 до 100% своей номинальной
мощности. При равных условиях в смысле мощности, частоты вращения и типа
исполнения (закрытый или открытый) АД с короткозамкнутым ротором имеют лучшие
энергетические характеристики, чем АД с фазным ротором. В связи с этим, когда
применение АД с фазным ротором не обусловлено условиями пуска и работы,
целесообразно применять АД с короткозамкнутым ротором, которые имеют худшие
энергетические показатели, чем двигатели открытого или защищенного типа той же
мощности и частоты вращения.
Для новых установок в ряде
случаев наиболее рациональным может оказаться применение синхронных двигателей,
если они допускаются условиями производства. В этом случае решение должно быть
принято на основании сравнения затрат по вариантам: при установке синхронного
двигателя и при установке АД той же мощности в совокупности с КУ.
) Замена недогруженных АД
двигателями меньшей мощности (снятие избыточной мощности).
При систематической
недозагрузке АД в первую очередь должны быть приняты меры к увеличению нагрузки
электродвигателей путем рационализации технологического процесса и увеличения
загрузки производственного оборудования. Замене подлежат АД загруженные менее
чем на 60% при условии технико-экономического обоснования и при наличии
практической возможности такой замены.
) Понижение напряжения у мало
загруженных двигателей.
В случае невозможности замены
мало загруженного АД целесообразно отказаться от снижения напряжения на его
зажимах. Снижение напряжения, подводимого к обмоткам АД, до определенного
минимального допустимого значения Umin
приводит к уменьшению потребления им реактивной мощности за счет уменьшения
тока намагничивания для создания его электромагнитного поля. Известны следующие
способы снижения напряжения у недогружённых АД:
переключение статорной обмотки
с треугольника на звезду;
секционирование статорных
обмоток;
понижение напряжения в сетях,
питающих АД путем переключения ответвлений цехового трансформатора.
Отметим, что все три
перечисленных способа понижения напряжения в обмотках мало загруженных
двигателей приводят не только к снижению реактивной мощности последних, но и к
уменьшению потерь мощности (за счет уменьшения тока ХХ) и к увеличению КПД
двигателей.
) Установка
ограничителей холостого хода станков.
Работа АД большинства станков
характеризуется тем, что в перерывах между нагрузками (в межоперационные
периоды) они вращаются на холостом ходу. При этом в ряде случаев
продолжительность работы двигателей на холостом ходу может достигать 50-60%
всего времени работы. Установка ограничителей холостого хода производится в
целях сокращения непроизводительного расхода электроэнергии и снятия реактивных
нагрузок путем отключения двигателей на межоперационный период. Установка
ограничителей холостого хода на станках является экономически целесообразной
уже в тех случаях, когда длительность межоперационного периода превышает 10 с.
Ограничитель холостого хода, применяемый в схеме управления электродвигателем с
помощью магнитного пускателя, выполняет роль отключающего и включающего
устройства, подвижная часть которого в определенный момент производственного
процесса приходит в соприкосновение с одной из деталей станка или перестает
касаться ее.
5) Повышение качества ремонта электродвигателей.
При проведении ремонта электродвигателей
недопустимо снижать их энергетические показатели. Надлежащее качество ремонта
является залогом исправной работы электродвигателей при высоких энергетических
показателях.
Совершенно недопустимы обточка ротора,
уменьшение числа проводников в пазу, расточка пазов, выжигание обмотки.
Для контроля над качеством
ремонта электродвигателей следует производить испытание их после ремонта,
уделяя особое внимание тому, чтобы ток ХХ после ремонта был не больше
номинального.
) Ограничение тока ХХ силовых
трансформаторов.
Несмотря на то, что реактивная
мощность, расходуемая на намагничивание каждого отдельного трансформатора,
сравнительно невелика, с ней приходится считаться ввиду значительного
количества трансформаторов, установленных на предприятиях, а также ввиду того,
что большинство этих трансформаторов работают круглосуточно.
К мероприятиям, направленным на
снижение реактивной мощности в трансформаторах, можно отнести:
поддержание экономичного режима
их работы;
замену и перестановку
незагруженных трансформаторов;
улучшение качества их ремонта.
Потери реактивной мощности
трансформатора зависят от его нагрузки гораздо меньше, чем у АД и в диапазоне
нагрузок примерно от 30 до 100% доля реактивных потерь в полных потерях
мощности в трансформаторе меняется не значительно. В диапазоне же нагрузок от
30% до нуля она существенно увеличивается.
.3.2 Анализ технических средств, применяемых для
компенсации реактивной мощности
Если говорить о доле
потребления реактивной электроэнергии на промышленном предприятии, то 65%
приходится на электрические двигатели, 20-25% на силовые трансформаторы, около
10% на воздушные сети и другие электроприемники.
Низкое значение коэффициента
мощности cos(φ) приводит
к увеличению загрузки по мощности электрического оборудования, начиная с
электрических генераторов, ЛЭП и других элементов электрических сетей вплоть до
самого потребителя. Увеличение загрузки по мощности происходит за счет
увеличения полного тока, протекающего через электрические сети и оборудование,
и за счет перетока реактивной мощности. Увеличение полного тока влечет за собой
увеличение потерь активной электрической энергии во всех элементах сети.
Увеличение полного тока за счет перетока реактивной мощности делает невозможным
подключение дополнительной активной нагрузки.
Основной способ нейтрализации
вышеописанных недостатков - компенсация реактивной мощности. Смысл компенсации
реактивной мощности заключается в подключении параллельно электрическому
приемнику КУ. Подключение желательно осуществлять как можно ближе к
электрическому приемнику [26].
На предприятиях для компенсации
реактивной мощности применяются синхронные компенсаторы (СК) или статических
(косинусных) конденсаторов.
Компенсация реактивной мощности
на промышленных предприятиях является задачей необходимой и должна быть
экономически оправданной.
На рис. 1.7 приведена схема
перетоков электроэнергии при отсутствии компенсации (а) с введением компенсации
(б).
Рис. 1.7 Схема перетоков
электроэнергии в линии: ККУ - комплектная конденсаторная установка;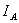 - активная
составляющая полного тока нагрузки;
- активная
составляющая полного тока нагрузки; 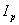 - реактивная составляющая полного
тока нагрузки
- реактивная составляющая полного
тока нагрузки
Компенсация реактивной мощности
на уже эксплуатируемом предприятии позволяет улучшить режим работы
электрического оборудования, разгрузить линии и трансформаторы от перетоков
реактивной мощности, уменьшить потери активной мощности во всех элементах
электрической сети предприятия, что снизит потребление электрической энергии
предприятием до 15% и позволит иметь резерв для подключения дополнительной
активной мощности.
К основным достоинствам
компенсации реактивной мощности относятся:
1)
снижение
тока в передающих элементах сети для уменьшения сечения кабельных и воздушных
линий;
2)
уменьшение
полной мощности для уменьшения мощности трансформаторов:
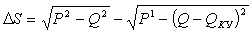 ; (1.10)
; (1.10)
1)
уменьшение
потерь активной мощности (до 10-15 %) для снижения мощности генераторов на
электростанциях:
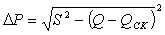 (1.11)
(1.11)
) за счет компенсации
реактивной мощности имеет место лучшее использование электрооборудования;
) с помощью компенсации
реактивной мощности можно регулировать напряжение в узле нагрузки и повысить
устойчивость электрического узла.
Говоря о компенсации реактивной
мощности с помощью устройства компенсации реактивной мощности (УКРМ) нельзя не
сказать о регулировании мощности, которое осуществляют с помощью автоматики. В
этой связи проведем анализ режимов работы УКРМ:
1)
оптимальный
режим УКРМ: КУ выдает реактивной мощности по мере необходимости;
2)
режим
недокомпенсации УКРМ: КУ выдает реактивной мощности недостаточно, значительная
часть реактивной мощности потребляется из сети. Этот режим имеет ряд
недостатков:
- через все элементы сети
протекает большой реактивный ток, что вынуждает увеличение сечений воздушных и
кабельных линий;
увеличение полной мощности, что
вынуждает завышать мощность силовых трансформаторов и их число;
увеличение потерь активной
мощности во всех элементах сети;
имеет место не эффективное
использование оборудования, которое загружено реактивным током, что ведет к
менее экономичному режиму работы, снижению срока службы оборудования;
3)режим перекомпенсации УКРМ:
КУ выдает реактивной мощности в избытке, который выдается в сеть.
Этот режим имеет ряд
недостатков:
- повышаются излишние потери
активной мощности, возникающие как следствие перекомпенсации;
в часы минимума нагрузок
чрезмерно повышается уровень напряжения, что приводит к форсированному износу и
старению изоляции обмоток электродвигателей, сокращению срока службы ламп
накаливания и нагревательных приборов, резкому сокращению срока службы силовых
конденсаторов и выходу их из строя;
ухудшается устойчивость узла
нагрузки, к которому подключено предприятие, что увеличивает риск крупной
системной аварии;
выдача реактивной мощности в
сеть при отсутствии соответствующего договора с энергосистемой жестко
контролируется и облагается крупным штрафом.
Таким образом, существует два
способа регулирования мощности КУ.
- Ручное управление.
Автоматическое управление.
Рассмотрим эти способы [27,
28,29]:
1) Ручное
управление.
Этот путь подразумевает наличие
квалифицированного обслуживающего персонала (минимум одного человека), который
будет коммутировать секции КУ, добиваясь максимального приближения к
оптимальному режиму работы КУ.
2) Автоматическое управление.
Осуществляется с помощью того
или иного блока автоматики. Главной целью любой автоматики является устранение
недостатков ручного управления мощностью КУ, вследствие чего обладает рядом
преимуществ, основные из которых: отсутствие обслуживающего персонала,
отслеживание потребления реактивной мощности предприятием и регулирование
мощности КУ и плавное регулирование.
Однако все блоки автоматики
имеют свои достоинства и недостатки.
В России выпускаются и
эксплуатируются следующие блоки автоматики: ИРФ-2М, Б 2201, АРКОН. В Белоруссии
(Минск) выпускается блок РРМ-03.
.4 Анализ влияния компенсации
реактивной мощности на параметры системы электроснабжения промышленного
предприятия
Основным потребителем
электроэнергии в нашей стране является промышленность. Если рассматривать
среднестатистическое промышленное предприятие как группу электроприемников, то
основная масса - это АД (различные станки, приводы, краны, тали и т.д.), далее
следуют силовые и сварочные трансформаторы (хотя трансформаторы преобразуют основную
часть электроэнергии, но довольно большие потери в них можно рассматривать как
потребление электрической энергии), некоторую часть составляют прочие
электрические приемники (электрических печи, котлы, тены, ЛЭП и др.) [30].
Принцип работы электрических
двигателей и силовых трансформаторов основан на создании собственного
магнитного поля, за счет которого двигатель преобразует электрическую энергию в
механическую энергию вращения ротора, а трансформаторы преобразуют и передают
электрическую энергию с помощью электромагнитного поля за счет потребления
реактивной энергии.
При компенсации реактивной мощности в цеховых
электрических сетях можно использовать низковольтные конденсаторы для снижения
потерь активной мощности в элементах сети, создаваемых реактивной составляющей
нагрузки. При этом нужно учитывать, что компенсация реактивной мощности
нагрузки приводит к повышению напряжения в цеховой электрической сети и, как
следствие, увеличению потребления активной мощности. Поэтому, решая задачу
компенсации реактивной мощности нагрузки, одновременно нужно регулировать
напряжение в цеховой электрической сети, чтобы не допустить роста
электропотребления.
Определим в общем виде фактические изменения
потерь активной мощности и потребления активной и реактивной мощности при
компенсации реактивной мощности нагрузки с учетом режима напряжения для участка
сети, приведенного на рис. 1.8.
Рис. 1.8 - Схема замещения системы внешнего
электроснабжения промышленного предприятия
В схеме нагрузка сети представлена мощностями P2
и Q2,
а источник реактивной мощности КУ Qку.
Сопротивление Rэк
и Xэк
характеризуют параметры электрической сети (линию передач), в которой имеют
место потери мощности ∆P12
и ∆Q12.
Расход электроэнергии от энергосистемы характеризуется мощностями P1
и Q1.
Баланс активной и реактивной мощности сети можно
записать:
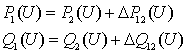 (1.12)
(1.12)
При допустимых отклонениях
напряжения зависимости потребляемой нагрузкой активной и реактивной мощностей
от напряжения можно представить [31]:
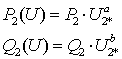 (1.13)
(1.13)
где 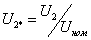 - относительное значение напряжения
в узле нагрузки;
- относительное значение напряжения
в узле нагрузки;
a и b -
коэффициенты аппроксимации;
P2 и Q2 - активная
и реактивная мощности нагрузки при условии U2 = Uном.
Статические характеристики нагрузки
позволяют представить потери активной мощности в сети:
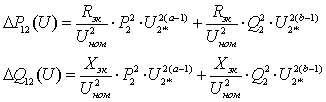 (1.14)
(1.14)
При подключении КУ к узлу нагрузки
фактическое потребление реактивной мощности из сети изменится:
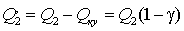 , (1.15)
, (1.15)
где γ - степень
компенсации реактивной мощности нагрузки.
При условии 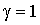 потребление
реактивной мощности из сети отсутствует.
потребление
реактивной мощности из сети отсутствует.
При этом изменяется статическая
характеристика нагрузки и коэффициент b примет
новое значение:
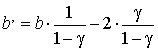 (1.16)
(1.16)
Подключение КУ в узле 2 приводит к
увеличению напряжения на
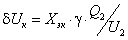 .
.
С учетом этого напряжение в узле 2
можно представить:
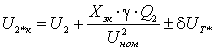 (1.17)
(1.17)
На основе приведенных преобразований
потребление активной и реактивной мощности от источника питания можно
представить в следующем виде:
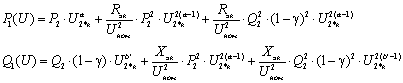 (1.18)
(1.18)
Компенсация реактивной мощности
позволяет получить экономию электрической энергии в системах электроснабжения
промышленных предприятий только на основе взаимосвязанного регулирования
реактивной мощности и напряжения в узлах комплексной нагрузки.
В реальных условиях работы систем
электроснабжения напряжение, активная и реактивная мощности нагрузки в узлах и
ветвях схемы изменяются в значительных пределах и являются реализациями
случайных функций. Поэтому компенсация реактивной мощности и регулирование
напряжения, как средство экономии энергии, могут дать значительный эффект в
виде снижения электропотребления предприятий только при реализации управления
реактивной мощностью и напряжением в реальном времени [32].
Выводы по главе
1) В системе
электроснабжения промышленных предприятий имеет место высокий уровень потерь
электрической энергии, связанный с низким коэффициентом мощности сети, которые
ведут к дополнительным экономическим затратам и отрицательно сказываются на
качестве электрической энергии. В сети низкого напряжения систем
электроснабжения промышленных предприятий большее применение нашли УКРМ с
помощью конденсаторных батарей, применение которых обусловлено их низкой
стоимостью, простотой установки и обслуживания.
) Для условий снижения
загрузки технологического оборудования цехов и производств показана
необходимость и целесообразность связного регулирования режима реактивной
мощности и напряжения в системах электроснабжения промышленных предприятий, что
позволяет достигнуть снижения электропотребления в узлах нагрузки.
) Показано неэффективное
применение конденсаторных УКРМ в системе электроснабжения промышленного
предприятия при групповой нагрузке.
Глава 2. Источники реактивной мощности
.1 Анализ систем управления конденсаторными
установками компенсации реактивной мощности в сети 0,4 кВ
В системе электроснабжения
промышленных предприятий большее применение нашли установки компенсации
реактивной мощности с помощью батарей статических конденсаторов, которые
предназначены для компенсации индуктивной компоненты и коррекции коэффициента
мощности.
В связи с тем, что количество электроэнергии,
потребляемой предприятием, изменяется в течение суток, изменяется и потребность
в реактивной мощности. В первой главе выполнен анализ существующих установок
компенсации реактивной мощности, все они работают по принципу, который основан
на измерении угла сдвига фаз между током и напряжением.
Типовая принципиальная электрическая схема
низковольтной КУ с автоматическим регулированием мощности конденсаторных
батарей представлена на рис. 2.1.
Структурная схема устройства компенсации
реактивной мощности представлена на рис. 2.2.
Рис. 2.1 - Принципиальная
электрическая схема конденсаторной установки КРМ-0,4-200 кВар
Рис. 2.2 - Структурная схема устройства
управления конденсаторной установкой
2.2 Формирование вектора напряжения на шинах
узла нагрузки
Задача формирования вектора напряжения на шинах
СК имеет ряд приближенных решений. К ним относятся:
- определение напряжения на шинах КС через
падение напряжения на активном сопротивлении нагрузки [156];
метод неполного дифференцирования, где
пренебрегают трансформаторной ЭДС и ЭДС вращения в уравнении статора СК [158].
Анализ данных методов с целью возможности их
применения при формировании вектора напряжения на шинах СК показал отсутствие
желаемой универсальности.
Для устранения данного недостатка предлагается
формировать вектор напряжения на шинах СК с помощью метода двух узлов. Под
методом двух узлов понимается метод расчета электрических цепей, в которых за
искомое принимают напряжение между двумя узлами схемы с последующим
определением токов в ветвях цепи.
Всегда можно выделить ветвь компенсации
реактивной мощности, эквивалентную пассивную и эквивалентную асинхронную
нагрузки.
Ветвь компенсации реактивной мощности,
реализуемой СК, представлена источником внутренней ЭДС Еi
с внутренним сопротивлением Z
= rS + jXsS,
где Еi
рассчитывается с помощью уравнений Парка-Горева в модификации Л.П.
Веретенникова с учетом переходных процессов в статоре СК.
Эквивалентная пассивная нагрузка 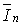 характеризует
статическую активно-индуктивную нагрузку.
характеризует
статическую активно-индуктивную нагрузку.
Эквивалентная асинхронная нагрузка 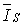 характеризуется
асинхронным двигателем, который представлен уравнениями Парка-Горева [105] и
включен на шины с напряжением U.
характеризуется
асинхронным двигателем, который представлен уравнениями Парка-Горева [105] и
включен на шины с напряжением U.
Для моделирования узла нагрузки
требуется единая система координат, в которой были бы записаны дифференциальные
уравнения СК и нагрузки в узле. Выбор скорости вращения единой системы
координат wk может быть
следующий.
Если wk = w0 и система
координат сцеплена с вращающимся магнитным полем, то ее называют синхронно
вращающейся системой координат с обозначениями осей X, Y, 0. При wk =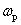 система
координат сцеплена с ротором СК, которую целесообразно применить из-за
магнитной асимметрии ротора СК. Учитывая, что ротор СК вращается синхронно с
полем, в дальнейшем систему координат будем называть системой координат ротора
или
система
координат сцеплена с ротором СК, которую целесообразно применить из-за
магнитной асимметрии ротора СК. Учитывая, что ротор СК вращается синхронно с
полем, в дальнейшем систему координат будем называть системой координат ротора
или 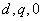 . Таким
образом, окончательно принимаем синхронно вращающуюся систему ротора
. Таким
образом, окончательно принимаем синхронно вращающуюся систему ротора 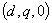
 или X, Y, 0.
или X, Y, 0.
При исследовании электромагнитных переходных
процессов СК принято [112, 113]:
1. Система координат, в которой записаны
дифференциальные уравнения СК, жестко связана с вращающейся системой координат
ротора (полем).
2. Положительное вращение осей системы
координат против часовой стрелки.
3. Ось q
определяет ось d.
4. Вектор напряжения на шинах расположен в
первом квадрате системы координат.
. Переходные процессы в машинах переменного
тока рассматриваются с помощью уравнений Парка-Горева в модификации Л.П.
Веретенникова [88].
. Пассивная нагрузка линейна.
. Активные и индуктивные сопротивления
соединительных линий равны нулю или вынесены в соответствующие параметры
элементов СК.
. Пассивная нагрузка по фазам
распределяется симметрично.
Рассмотрим схему замещения статора СК, которая
приведена на рисунке 2.3. Запишем уравнения статора СК согласно второму закону
Кирхгофа в ортогональной системе координат [109].
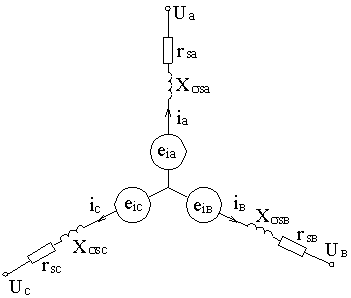
Рис. 2.3 - Схема замещения СК
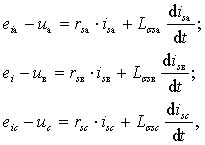
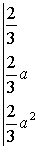 (2.1)
(2.1)
где 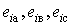 - величины мгновенных значений
внутренней ЭДС фаз a, в, c СК;
- величины мгновенных значений
внутренней ЭДС фаз a, в, c СК;
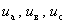 - величины мгновенных значений
напряжений фаз a, в, c СК;
- величины мгновенных значений
напряжений фаз a, в, c СК;
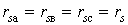 - активные сопротивления фаз
статора СК;
- активные сопротивления фаз
статора СК;
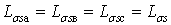 - индуктивности рассеяния фаз
статора СК;
- индуктивности рассеяния фаз
статора СК;
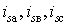 - величины мгновенных значений
токов статора фаз a, в, c. СК.
- величины мгновенных значений
токов статора фаз a, в, c. СК.
Сложив уравнения (3.61), запишем
уравнение статора в векторной форме в неподвижной системе координат
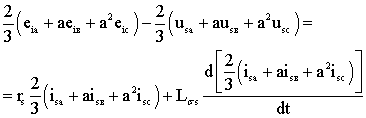 , (2.2)
, (2.2)
 .
.
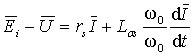
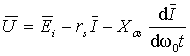 . (2.3)
. (2.3)
Из уравнения (2.3) можно записать
проекции вектора напряжения статора на оси 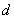 и
и 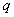 [95, 103]
[95, 103]
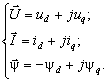 (2.4)
(2.4)
С учетом (2.4) запишем в проекциях
на оси d и q уравнения статора СК в синхронном времени:
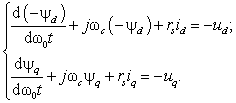 (2.5)
(2.5)
Из векторной диаграммы СК,
показанной на рисунке 2.5, выразим проекции вектора напряжения на шинах
нагрузки на оси d и q:
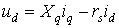 , (2.6)
, (2.6)
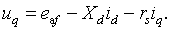 (2.7)
(2.7)
Умножив уравнение (2.7) на j и
сложив его с уравнением (2.6), получим:
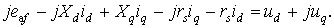 (2.8)
(2.8)
Преобразуем (2.8):
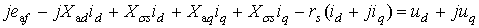
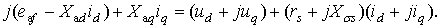 (2.9)
(2.9)
Вектор внутренней ЭДС 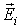 имеет свою
особенность. Учитывая математическую связь
имеет свою
особенность. Учитывая математическую связь
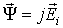 (2.10)
(2.10)
и принятое положение вектора
потокосцепления на комплексной плоскости (см. рис. 2.4) 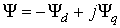 , вектор
внутренней ЭДС можно записать в виде
, вектор
внутренней ЭДС можно записать в виде
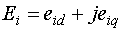 . (2.11)
. (2.11)
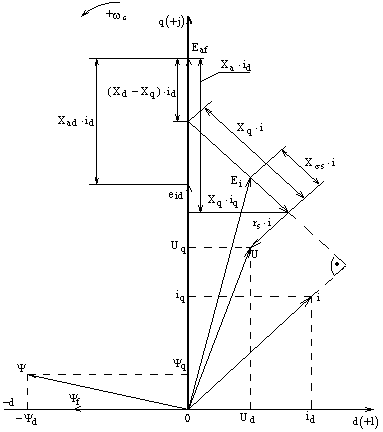
Рис. 2.4. - Векторная диаграмма СК
Численное значение проекции 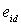 , отстающей
на 0,5
, отстающей
на 0,5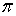 от проекции
от проекции
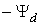 , определяем
из выражения
, определяем
из выражения
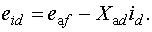 (2.12)
(2.12)
Численное значение проекции 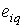 , отстающей
на 0,5
, отстающей
на 0,5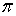 от проекции
от проекции
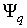 ,
определяется по формуле
,
определяется по формуле
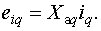 (2.13)
(2.13)
Из векторной диаграммы (рис. 2.5)
запишем численные значения проекций вектора 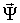 на оси d и q:
на оси d и q:
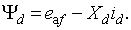 (2.14)
(2.14)
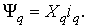 (2.15)
(2.15)
Вычтем из (2.12) выражение (2.14) и
получим проекцию вектора тока статора СК на ось d:
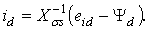 (2.16)
(2.16)
Аналогично вычтем из (2.13)
выражение (2.15) и получим проекцию вектора тока статора СК на ось q:
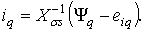 (2.17)
(2.17)
Выразим из (2.9) с учетом (2.12) и
(2.13) проекции вектора напряжения на статоре СК:
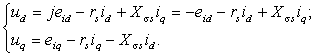 (2.18)
(2.18)
Подставив (2.17) в (2.5), получим
дифференциальные уравнения статора СК через проекцию векторов внутренней ЭДС,
потокосцеплений и токов статора в синхронном времени, которые приведены к
относительному виду с помощью системы относительных единиц статора [88]:
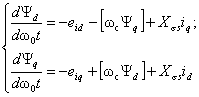 (2.19)
(2.19)
Подставив (2.16) и (2.17) в (2.19),
получим уравнения статора, исключив ток:
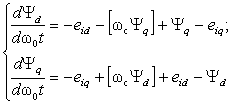 (2.20)
(2.20)
Выразим модуль напряжения статора СК

Запишем на основании второго закона
Кирхгофа дифференциальные уравнения ротора СК в проекциях на оси d и q в
синхронном времени, которые приведены к относительному виду с помощью системы
относительных единиц ротора [96]:
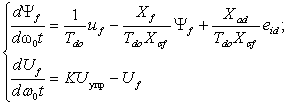 (2.21)
(2.21)
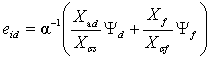 ;
;
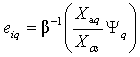 ;
;
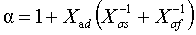 ;
;
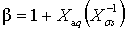 .
.
Для практического применения при
моделировании СК отметим следующие моменты:
вектор напряжения на узле нагрузки,
определенный по методу двух узлов, располагается в первом квадранте под углом 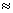 45°;
45°;
все участники нагрузки должны
приводиться к собственным базисам. Для этого необходимо физические величины
(напряжение, ток) умножить на собственный базис и разделить на базис СК.
Формирование вектора напряжения на шинах узла
нагрузки использовано при математическом описании имитационной модели СК
(Приложение Б), работающей на активно-индуктивную и асинхронную нагрузки.
.3 Нечеткое управление синхронного компенсатора
с применением алгоритма Мамдани
Рассмотрим нечеткое управление синхронного
компенсатора с применением алгоритма Мамдани.
Источники реактивной мощности (ИРМ)
предназначены для реализации баланса реактивной мощности в
электроэнергетической системе. Они обеспечивают генерирование и потребление
реактивной мощности. Основными параметрами регулирования ИРМ является
напряжение в точке его подключения и \ или реактивная мощность нагрузки, для
компенсации которой он предназначен, отдельно или вместе. ИРМ решает следующие
задачи: снижение потерь активной мощности в сети; регулирование напряжения и
ограничение напряжения в узлах нагрузки; симметрирование режима; улучшение
статической и динамической устойчивости электропередач. ИРМ подключаются к
узлам нагрузки параллельно и подразделяются на две группы. Первая группа -
синхронные генераторы станций, отдающие реактивную мощность в сеть, синхронные
(динамические) компенсаторы - для плавного регулирования как в режиме
генерирования, так и потребления, синхронные двигатели. Вторая группа -
статические ИРМ (конденсаторные батареи, насыщающиеся реакторы в зависимости
приложенного к ним напряжения в точке подключения, устройства на базе
преобразователей с искусственной коммутацией тиристоров и т.д.).
В электроэнергетике для компенсации реактивной
мощности применяют косинусные конденсаторы, работающие на частоте 50 Гц. Их
мощность, измеряемая в реактивных киловольт-амперах (квар) составляет от 10 до
100 квар. Практически они собираются в батареи и обеспечивают быстрого, но
ступенчатое регулирование с генерацией высших гармоник тока. Коммутация до 1 кВ
выполняется обычными контакторами, в сетях 6-10 кВ и выше - с помощью
тиристорных ключей переменного тока.
Синхронные компенсаторы (СК) в
отличие от косинусных конденсаторов обеспечивают плавное, но медленное регулирование
напряжения до 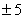 %
номинального значения из-за постоянных времени системы возбуждения, а также для
генерирования и потребления реактивной мощности. СК применяются в основном в
узлах нагрузки, изменяющейся в широких пределах. СК это электрическая машина,
работающая в режиме холостого хода (без активной нагрузки) с трех фазным
неподвижным статором и вращающимся ротором, на котором находится обмотка
возбуждения. СК, включенный в систему без возбуждения, потребляет реактивную
мощность (индуктивный режим). При включении возбуждения и увеличении тока
ротора СК переходит в режим генерирования реактивной (емкостной) режим.
Статическая характеристика СК является U-образной.
Минимальная длительная допустимая реактивная мощность СК не ниже 50%
номинальной мощности, так как возможна потеря статической устойчивости.
Достоинством СК является положительный регулирующий эффект, т.е. способность
увеличивать генерируемую реактивную мощность при снижении напряжения на его
шинах. Параметрами регулирования СК является реактивная мощность и напряжение,
ограниченные допустимыми диапазонами изменения
%
номинального значения из-за постоянных времени системы возбуждения, а также для
генерирования и потребления реактивной мощности. СК применяются в основном в
узлах нагрузки, изменяющейся в широких пределах. СК это электрическая машина,
работающая в режиме холостого хода (без активной нагрузки) с трех фазным
неподвижным статором и вращающимся ротором, на котором находится обмотка
возбуждения. СК, включенный в систему без возбуждения, потребляет реактивную
мощность (индуктивный режим). При включении возбуждения и увеличении тока
ротора СК переходит в режим генерирования реактивной (емкостной) режим.
Статическая характеристика СК является U-образной.
Минимальная длительная допустимая реактивная мощность СК не ниже 50%
номинальной мощности, так как возможна потеря статической устойчивости.
Достоинством СК является положительный регулирующий эффект, т.е. способность
увеличивать генерируемую реактивную мощность при снижении напряжения на его
шинах. Параметрами регулирования СК является реактивная мощность и напряжение,
ограниченные допустимыми диапазонами изменения 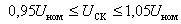 при условии выработки реактивной
мощности в пределах:
при условии выработки реактивной
мощности в пределах: 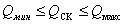 , как
показано на рисунке 2.5.
, как
показано на рисунке 2.5.
Рис. 2.5 - Зона регулирования СК
Регулирование напряжения 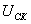 в зоне
поддерживается с заданным статизмом.
в зоне
поддерживается с заданным статизмом.
Совершенствование систем возбуждения
синхронных компенсаторов (СК) средней мощности напрямую связано с нечетким
управлением в виду отсутствия математического описания объекта. Существующие
четкие регуляторы напряжения СК реализует собой комбинированный принцип
регулирования: принцип регулирования по отклонению напряжения на шинах и
принцип регулирования по возмущению реактивного тока статора с коррекцией по
положительной производной тока ротора СК. Введение положительной производной по
току ротора уменьшает провал напряжения в случае отсутствия демпферной обмотки
СК средней мощности. Устройство формирования сигнала формирует реактивную
составляющую тока статора для уменьшения времени восстановления напряжения на
шинах статора при переменной нагрузке. Отрицательная жесткая обратная связь
парирует влияние неконтролируемых возмущений. Применение ПИД-закона регулирования
в регуляторе напряжения не всегда оправдано. Интеграл в законе регулирования
устраняет ошибку регулирования в статике, но вносит отставание по фазе.
Дифференциал в законе регулирования за счет фазового опережения, компенсирует
отставание по фазе, но не достаточно эффективно. Для устранения данного
недостатка предлагается замена классического закона управления на нечеткое
управление СК, которое является наиболее перспективным направлением современной
теории управления [1]. Контуры регулирования на основе нечеткой логики легко
реализовать и настраивать. При этом обеспечивается лучшее качество управления:
отсутствие перерегулирования и высокое быстродействие.
Рассмотрим структурную схему САР с
нечетким регулятором напряжения, которая приведена на рисунке 2.6.
Рис. 2.6 - Структурная схема САР с
нечетким регулятором напряжения
Проектирование нечеткого регулятора
напряжения СК для поддержания напряжения в заданном диапазоне предполагает
выбор лингвистических переменных, терм-множеств по каждой переменной,
формирование базы знаний (БЗ) или матрицы решений, импликации, композиции и
правила приведение к четкости [2]. БЗ может формироваться:
а) на лингвистической (качественной)
информации, поступающей от экспертов, в форме продуктивных правил;
б) на численной (количественной)
информации, полученной от измерительных устройств (датчиков).
в) с помощью оптимальной траектории,
рассчитанной по принципу максимума, и коррекции настроек ПИД-регулятора
нечеткими регуляторами [4];
Проектирование нечеткого регулятора
напряжения предполагает следующие лингвистические переменные: отклонение
напряжения на статоре СК (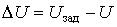 ),
производную отклонения напряжения (
),
производную отклонения напряжения (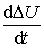 ) и ток возбуждения ротора СК.
Вектор входных переменных нечеткого регулятора
) и ток возбуждения ротора СК.
Вектор входных переменных нечеткого регулятора 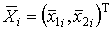 , где
, где 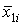 - мгновенное значение отклонения
напряжения
- мгновенное значение отклонения
напряжения 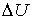 ;
; 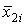 -
мгновенное значение производной отклонения напряжения
-
мгновенное значение производной отклонения напряжения 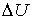 ;
; 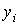 -
мгновенное значение тока возбуждения ротора СК.
-
мгновенное значение тока возбуждения ротора СК.
Зададимся описанием лингвистических
переменных:
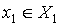 ,
, 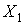 - линейное терм-множество
отклонений напряжения: очень отрицательное большое (ООБ), отрицательное большое
(ОБ), отрицательное среднее (ОС), отрицательное малое (ОМ), очень отрицательное
малое (ООМ), норма (Н), очень положительное малое (ОПМ), положительное малое
(ПМ), положительное среднее (ПС), положительное большое (ПБ), очень
положительное большое (ОПБ);
- линейное терм-множество
отклонений напряжения: очень отрицательное большое (ООБ), отрицательное большое
(ОБ), отрицательное среднее (ОС), отрицательное малое (ОМ), очень отрицательное
малое (ООМ), норма (Н), очень положительное малое (ОПМ), положительное малое
(ПМ), положительное среднее (ПС), положительное большое (ПБ), очень
положительное большое (ОПБ);
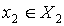 ,
, 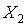 - линейное терм-множество
производных отклонения напряжения: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ,
ПОБ;
- линейное терм-множество
производных отклонения напряжения: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ,
ПОБ;
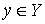 ,
, 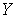 - линейное терм-множество тока
ротора СК: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ, ПОБ.
- линейное терм-множество тока
ротора СК: ООБ, ОБ, ОС, ОМ, ООМ, Н, ПОМ, ПМ, ПС, ПБ, ПОБ.
С целью компактной записи
продуктивных правил лингвистической информации составлена матрица решений,
которая приведена на рисунке 2.9.
Рассмотрим нечеткий вывод i-фрагмента
матрицы решений:
П1: если 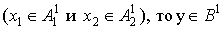 ;
;
П2: если 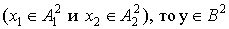 ,
,
где 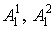 - термы Н и ООМ, соответственно,
лингвистической переменной отклонения напряжения;
- термы Н и ООМ, соответственно,
лингвистической переменной отклонения напряжения; 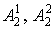 - термы Н и
ПОМ, соответственно, лингвистической переменной производной отклонения
напряжения;
- термы Н и
ПОМ, соответственно, лингвистической переменной производной отклонения
напряжения; 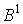 и
и 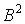 - термы i-фрагмента
дефаззификатора.
- термы i-фрагмента
дефаззификатора.
Фаззификация на синглетонной базе i-фрагмента
матрицы решений:
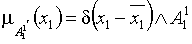 ;
;
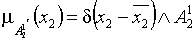 ;
;
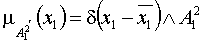 ;
;
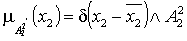 ,
,
где 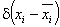 -
- 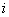 -дельта-функция (синглетон);
-дельта-функция (синглетон); 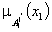 - степень
принадлежности
- степень
принадлежности 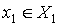 подмножеству
подмножеству
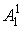 ;
; 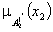 - степень
принадлежности
- степень
принадлежности 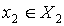 подмножеству
подмножеству
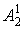 ;
; 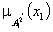 - степень
принадлежности
- степень
принадлежности 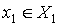 подмножеству
подмножеству
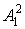 ;
; 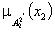 - степень
принадлежности
- степень
принадлежности 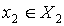 подмножеству
подмножеству
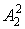 .
.
Рис. 2.7 - Линейные терм-множества:
а) по отклонению напряжения;
б) по производной отклонения напряжения; в)
функции принадлежности тока возбуждения СК
Рис. 2.8 - Матрица решений
Импликация i-фрагмента
матрицы решений:
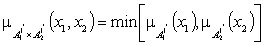 ;
;
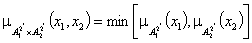 .
.
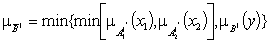 ;
;
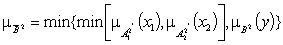 ,
,
где 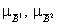 - функции принадлежности усеченных
множеств
- функции принадлежности усеченных
множеств 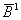 (ПМ) и
(ПМ) и 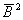 (ПОМ).
(ПОМ).
Композиция i-фрагмента
матрицы решений
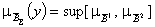 ,
,
где 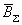 - результирующее нечеткое множество.
- результирующее нечеткое множество.
Для устранения нечеткости окончательного
результата (тока возбуждения ротора СК) существует несколько методов: метод
центра максимума (метод среднего), метод наибольшего значения (метод
максимума), метод центроида [7].
Дефаззификация (метод центроида)
Необходимо определить минимальную
координату абсцисс, соответствующей максимальной высоте нелинейного
объединенного усеченного множества.
Известны разные формулы расчета
координат ЦТ фигуры по методу центроида. Одна из них (2.22) приведена в [7].
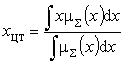 . (2.22)
. (2.22)
Формула (2.22) удобна в случае,
когда функции принадлежности дефаззификатора есть синглетоны.
Известна формула (2.23) вычисления
абсциссы ЦТ линейных объединенных усеченных множеств (фигуры), образованных из
линейных функций принадлежности дефаззификатора, с фиксацией координат
характерных точек [8].
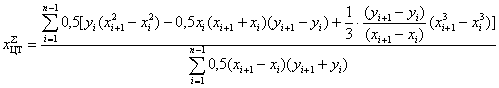 , (2.23)
, (2.23)
где 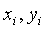 - координаты характерных точек
элементарных фигур, определяющих границы
- координаты характерных точек
элементарных фигур, определяющих границы 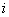 -результирующего нечеткого множества
(фигуры).
-результирующего нечеткого множества
(фигуры).
Расчет координат ЦТ фигуры по
формуле (2.23) требует знания координат характерных точек элементарных фигур и
имеет фиксированную точность, которая зависит от формы фигуры.
В [9] приводятся формулы (2.24) и
(2.25) определения координат ЦТ фигуры, которые предполагают равномерное
разбиение фигуры по оси абсцисс с построением 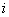 -прямоугольников разной высоты.
-прямоугольников разной высоты.
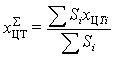 ; (2.24)
; (2.24)
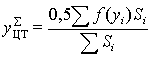 , (2.25)
, (2.25)
где 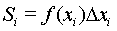 - площадь i-фигуры
(прямоугольника);
- площадь i-фигуры
(прямоугольника); 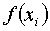 - высота i-прямоугольника;
- высота i-прямоугольника;
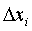 - ширина i-прямоугольника;
- ширина i-прямоугольника;
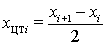 - значение
абсциссы ЦТ
- значение
абсциссы ЦТ 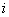 -фигуры.
-фигуры.
Недостатком применения формул (2.24)
и (2.25) является большой объем вычислений и снижение быстродействия
формирования управляющего воздействия на объект.
С целью повышения быстродействия
расчета координат ЦТ и снятия ограничений на функцию 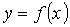 , рассмотрим
приближенный алгоритм на основе неравномерного разбиения по оси абсцисс фигуры
объединенного усеченного множества с построением
, рассмотрим
приближенный алгоритм на основе неравномерного разбиения по оси абсцисс фигуры
объединенного усеченного множества с построением 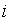 -прямоугольников равной площади и
разной высоты.
-прямоугольников равной площади и
разной высоты.
Пусть объединенное усеченное
множество описывается функцией 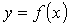 и сложная фигура расположена на
интервале [a, b] по оси
абсцисс.
и сложная фигура расположена на
интервале [a, b] по оси
абсцисс.
Предлагается следующий алгоритм
вычисления координат ЦТ фигуры:
рассчитываем площадь S сложной
фигуры;
разбиваем сложную фигуру на n простых
фигур с неравномерным разбиением по оси абсцисс, причем площади этих фигур
должны быть одинаковыми и равными 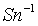 . Число разбиений n
определяется из соотношения
. Число разбиений n
определяется из соотношения 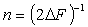 , где
, где 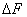 - абсолютная погрешность
воспроизведения функции
- абсолютная погрешность
воспроизведения функции 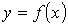 ;
;
задаемся приращением 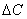 изменения
координаты абсциссы, которое должно быть хотя бы на порядок меньше, чем
изменения
координаты абсциссы, которое должно быть хотя бы на порядок меньше, чем 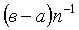 ;
;
определяем координаты точек абсцисс
в интервале разбиения 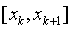 , где
, где 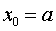 ;
; 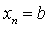 ;
; 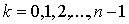 . Для
определения точек разбиения
. Для
определения точек разбиения 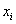 подсчитывается
значение площади
подсчитывается
значение площади 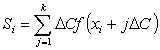 и
сравнивается со значением
и
сравнивается со значением 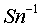 .
Увеличиваем значение
.
Увеличиваем значение 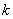 до
выполнения условия
до
выполнения условия 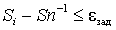 , где
, где 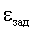 - заданная
точность. Граница
- заданная
точность. Граница 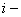 интервала
определяется по формуле
интервала
определяется по формуле
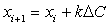 . Указанная процедура выполняется на
всем отрезке [a, b] и
определяет координаты
. Указанная процедура выполняется на
всем отрезке [a, b] и
определяет координаты 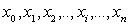 . В пределах
каждого интервала
. В пределах
каждого интервала 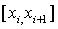 функция
функция 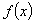 аппроксимируется
постоянными значениями
аппроксимируется
постоянными значениями 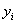 ;
;
определяем абсциссу и ординату ЦТ
объединенного усеченного множества по формулам (2.26) и (2.27), соответственно:
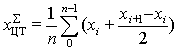 ; (2.26)
; (2.26)
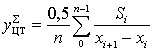 . (2.27)
. (2.27)
Приведенный алгоритм вычисления
координат ЦТ был проверен на фигуре объединенного усеченного множества,
показанного на рисунке 2.10.
 C = 0,02;
C = 0,02;
n = 8; 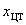 = 1,691;
= 1,691; 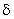 = 2,29%;
= 2,29%;
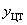 = 1,044;
= 1,044; 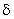 = 1,36%;
= 1,36%;
n = 8; 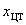 = 1,705;
= 1,705; 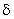 = 1,49%;
= 1,49%;
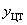 = 1,013;
= 1,013; 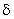 = 1,68%;
= 1,68%;
Рис. 2.9 - Пример фигуры
Таким образом, можно сделать
следующие выводы:
формула расчета координат ЦТ
объединенного линейного усеченного множества (2.23) предполагает линейные
функции принадлежности дефаззификатора с фиксацией координат характерных точек
элементарных фигур;
формулы расчета координат ЦТ (2.26)
и (2.27) объединенного усеченного множества предполагают, как линейные, так и
нелинейные функции принадлежности дефаззификатора, являются универсальными и
могут широко применяться при проектировании нечеткого регулятора.
Имитационное моделирование САР
Для проверки работоспособности
нечеткого регулятора напряжения разработана цифровая модель системы
автоматического регулирования напряжения статора СК мощностью 0,01 МВт. СК
представлен в виде уравнений Парка-Горева в модификации Л.П.Веретенникова.
Дифференциальные уравнения записаны через внутреннюю ЭДС в анормальной системе
относительных единиц. Мгновенный вектор напряжения на шинах СК определен по
методу двух узлов [10]. Нагрузкой объекта является асинхронный короткозамкнутый
двигатель мощностью 0,005 Мвт. Математическое описание установки приведено в
приложении Б.
На рисунке 2.10 приведена
осциллограмма процесса возбуждения СК и пуска асинхронного двигателя от СК.
Рис. 2.10 - Осциллограмма процесса СК и пуска
асинхронного двигателя
Результаты моделирования подтверждают
работоспособность системы автоматического регулирования напряжения статора СК с
нечетким регулятором напряжения.
Заключение:
. Замена ПИД-регулятора в системе напряжения СК
переменного тока нечетким регулятором исключает запаздывание в системе
регулирования и обеспечивает форсирующие свойства с целью уменьшения времени
восстановления напряжения при включении асинхронной нагрузки.
. Предлагаемый приближенный алгоритм позволяет
модифицировать систему нечеткого вывода применительно к нелинейным функциям принадлежности
дефаззификатора, который обеспечивает высокое быстродействие и заданную
точностью по отношению к известным алгоритмам.
. Результаты моделирования подтверждают
работоспособность нечеткого регулятора напряжения применительно к СК средней
мощности.
.4 Адаптивное нечеткое управление синхронного
компенсатора с применением нейронной технологии
Рассмотрим адаптивное нечеткое управление
синхронного компенсатора с применением нейронной технологии
Источники реактивной мощности предназначены для
реализации баланса реактивной мощности в электроэнергетической системе. Они
обеспечивают генерирование и потребление реактивной мощности. Основным
параметром регулирования источника реактивной мощности является напряжение в
точке его подключения, где реактивная мощность нагрузки является
неконтролируемым возмущением, вызывающим изменение напряжения узла нагрузки.
Источник реактивной мощности включается параллельно к узлу нагрузки.
Индуктивный ток нагрузки (ток намагничивания), необходимый для создания
номинальных магнитных потоков в асинхронных двигателях, обеспечивает у них
постоянство потокосцеплений.
Источник реактивной мощности,
выполненный на базе СК, в отличие от косинусных конденсаторов обеспечивают
плавное, но медленное регулирование напряжения до 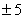 %
номинального значения. СК это электрическая машина, работающая в режиме
холостого хода с трех фазным неподвижным статором и вращающимся ротором с
беличьей клеткой, на котором находится обмотка возбуждения, подключенная к
регулируемому источнику постоянного тока. СК с обесточенной обмоткой
возбуждения потребляет реактивную мощность из сети для создания вращающего
электромагнитного поля и активную мощность для компенсации трения в
подшипниках, которой можно пренебречь. При увеличении тока возбуждения ротора
СК переходит из режима генерирования реактивной (индуктивный) мощности в режим
генерирования реактивный (емкостной) мощности. Статическая характеристика СК
является U-образной,
показанная на рисунке 2.11.
%
номинального значения. СК это электрическая машина, работающая в режиме
холостого хода с трех фазным неподвижным статором и вращающимся ротором с
беличьей клеткой, на котором находится обмотка возбуждения, подключенная к
регулируемому источнику постоянного тока. СК с обесточенной обмоткой
возбуждения потребляет реактивную мощность из сети для создания вращающего
электромагнитного поля и активную мощность для компенсации трения в
подшипниках, которой можно пренебречь. При увеличении тока возбуждения ротора
СК переходит из режима генерирования реактивной (индуктивный) мощности в режим
генерирования реактивный (емкостной) мощности. Статическая характеристика СК
является U-образной,
показанная на рисунке 2.11.
Рис. 2.11 - U-образные
характеристики СК
Переток мощности в линии при отключенном СК и
возбужденном СК приведен на рисунке 2.12.
Минимально длительно допустимая
реактивная мощность СК должна быть не ниже 50% номинальной мощности, так как
возможна потеря статической устойчивости СК. Достоинством СК является
положительный регулирующий эффект, т.е. способность увеличивать генерируемую
реактивную (емкостную) мощность при снижении напряжения и реактивную
(индуктивную) мощность при превышении напряжения на шинах узла в пределах 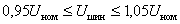 .
.
Рис. 2.12 - Процессы, протекающие в линии: а) до
компенсации и б) после компенсации реактивной мощности
Учитывая отсутствие математического описания
объекта, которое определяется количеством включенных в данный момент асинхронных
двигателей с их текущей нагрузкой и других нелинейных элементов применять
классические законы управления данным объектом не представляется возможным.
Предлагается применить нечеткое управление с применением
пропорционально-интегрального регулятора, где пропорциональную часть закона
реализовать адаптивной нечеткой компонентой регулятора.
На рисунке 2.14 приведен адаптивный
нечеткий регулятор напряжения. Регулятор включают адаптивный фаззификатор и
блоки активационных сигмоидных асимметричных функций. В адаптивных
фаззификаторах использованы сигмоидные функции принадлежности (ФП) 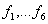 .
.
Аналитические выражения сигмоидных ФП
адаптивного нейронного фаззификатора регулятора напряжения СК представлены в
(2.28), (2.29), (2.30), (2.31) [1]:
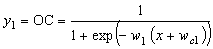 ; (2.28)
; (2.28)
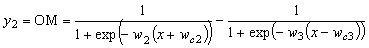 ; (2.29)
; (2.29)
Рис. 2.13 - САР регулирования
напряжения на шинах узла нагрузки: СК - синхронный компенсатор; 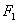 -
сигмоидные функции
-
сигмоидные функции
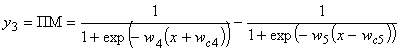 ; (2.30)
; (2.30)
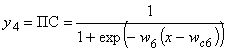 , (2.31)
, (2.31)
где 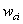 - параметры смещения сигмоидных ФП;
- параметры смещения сигмоидных ФП;
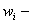 вес суммарного сигнала на входе
сигмоидных ФП.
вес суммарного сигнала на входе
сигмоидных ФП.
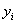 - активизированные степени
принадлежности фаззификатора синглетоном, синхронно связанным с входом
- активизированные степени
принадлежности фаззификатора синглетоном, синхронно связанным с входом 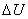 ;
;
Имена терм: ОС - отрицательное среднее,
ОМ - отрицательное малое, ПМ - положительное малое, ПС - положительное среднее.
Входной сигнал 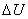 фаззификатора
нечеткого регулятора напряжения СК несет информацию об управлении и возмущениях
нагрузки (реактивная мощность нагрузки). Учитывая, что размещение терм
нейронного фаззификатора производилось только с учетом предельных значений
переменной
фаззификатора
нечеткого регулятора напряжения СК несет информацию об управлении и возмущениях
нагрузки (реактивная мощность нагрузки). Учитывая, что размещение терм
нейронного фаззификатора производилось только с учетом предельных значений
переменной 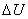 , необходимо
в дальнейшем его адаптировать с помощью нейрона с последовательным обучением
согласно рекуррентной формуле [2, 3]:
, необходимо
в дальнейшем его адаптировать с помощью нейрона с последовательным обучением
согласно рекуррентной формуле [2, 3]:
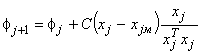 , при
, при 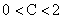 , (2.32)
, (2.32)
где 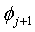 - последующий шаг j+1-итерации;
- последующий шаг j+1-итерации;
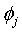 - предыдущий
шаг j-итерации;
- предыдущий
шаг j-итерации; 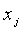 -
дискретная форма j- итерации;
-
дискретная форма j- итерации; 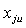 - оценка
выхода модели;
- оценка
выхода модели; 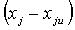 - ошибка в
оценке
- ошибка в
оценке 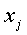 ;
; 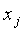 -
измеряемая функция (текущее напряжение); Т - транспонирование.
-
измеряемая функция (текущее напряжение); Т - транспонирование.
Метод последовательного обучения от
известных [1] отличается быстродействием и возможностью использования как
линейных, так и нелинейных терм.
Произведения активизированных
степеней принадлежности фаззификатора синглетоном, синхронно связанным с входом
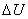 (рис.
2.14), подаются на входы функций активации
(рис.
2.14), подаются на входы функций активации 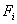 . Сигмоидные функции активации
. Сигмоидные функции активации 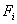 , усиливая
слабый сигнал на входе и ослабляя сильный сигнал, формируют сигнал управления
током возбуждения СК.
, усиливая
слабый сигнал на входе и ослабляя сильный сигнал, формируют сигнал управления
током возбуждения СК.
Введение адаптивного нейрона в
регулятор напряжения корректирует термы фаззификатора в нейронном исполнении к
текущим значениям отклонения 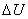 как в статике, так и динамике.
Отсутствие каких-то предварительных настроек, кроме выбора числа и размещений
сигмоидных функций принадлежности в интервале
как в статике, так и динамике.
Отсутствие каких-то предварительных настроек, кроме выбора числа и размещений
сигмоидных функций принадлежности в интервале 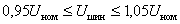 в регуляторе напряжения делает его
актуальными и способствует к широкому применению на практике. Адаптивный
нечеткий регулятор напряжения есть астатический регулятор и исключает
статическую ошибку. Введение интеграла в закон управления дополнительно
обеспечивает подавление помех на входе контура управления возбуждением СК.
в регуляторе напряжения делает его
актуальными и способствует к широкому применению на практике. Адаптивный
нечеткий регулятор напряжения есть астатический регулятор и исключает
статическую ошибку. Введение интеграла в закон управления дополнительно
обеспечивает подавление помех на входе контура управления возбуждением СК.
Результаты математического
моделирования подтвердили заложенные принципы при проектировании адаптивных
систем управления СК с применением нейронной технологии.
Выводы по главе
. Замена ПИД-регулятора в системе напряжения СК
переменного тока нечетким регулятором исключает запаздывание в системе
регулирования и обеспечивает форсирующие свойства с целью уменьшения времени
восстановления напряжения при включении асинхронной нагрузки.
. Разработано адаптивное нечеткое управление СК
с применением нейронной технологии.
3. Предлагаемый приближенный алгоритм позволяет
модифицировать систему нечеткого вывода применительно к нелинейным функциям
принадлежности дефаззификатора, который обеспечивает высокое быстродействие и
заданную точностью по отношению к известным алгоритмам.
. Результаты моделирования подтверждают
работоспособность нечеткого регулятора напряжения применительно к СК средней
мощности.
Глава 3. Разработка метода и алгоритма
управления режимом реактивной мощности при асимметрии системы электроснабжения
промышленного предприятия
Использование УКРМ позволяет существенно
повысить технико-экономические показатели электроснабжения предприятия, а
именно, повысить качество электрической энергии, уменьшить потери активной
энергии при ее передаче от источника к приемнику, уменьшить оплату за
отпущенную электроэнергию.
.1 Разработка математической модели датчика
асимметрии устройства для системы управления УКРМ
Измеритель УКРМ представляет
собой фазометр, который предназначен для измерения сдвига фаз между двумя
периодическими сигналами. Принцип работы фазометра показан на рисунке 3.1.
Рис. 3.1 - Временные диаграммы работы фазометра
Входные сигналы преобразуются в
прямоугольные импульсы, а затем выполняется их суммирование и в результате
получают величину угла сдвига фаз φ.
Предложим метод определение
угла сдвига фаз между током и напряжением электрической сети промышленного предприятия,
используя аналоговую модель измерителя.
От системы электроснабжения
через трансформатор тока, установленного в фазе, на измеритель поступают два
синусоидальных сигнала: мгновенные ток i
и напряжение u сети (см. рис.
3.2).
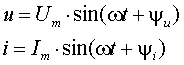 , (3.1)
, (3.1)
где Um -
максимальная амплитуда напряжения фазы сети, В;
Im -
максимальная амплитуда тока одноименной фазы сети, А;
Ψu - сдвиг
фазы по напряжению;
Ψi - сдвиг
фазы по току.
Рис. 3.2 - Синусоидальные сигналы напряжения и
тока одноименной фазы промышленной сети
Угол сдвига фаз можно определить из мгновенной
мощности сети, которая равна:
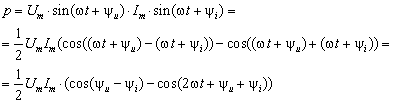 (3.2)
(3.2)
Значение сдвига фаз между током и
напряжения равно:
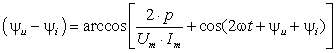 (3.3)
(3.3)
Решая задачу нахождения угла сдвига
фаз в сети однофазного тока, возникает проблема определения амплитудных
значений тока и напряжения. Ниже представлена математическая модель,
позволяющая определить амплитуду синусоидального сигнала А·sin(ωt):
. Выполним умножение исследуемого
сигнала «А·sin(ωt)» на «B·sin(ωt)» и на «В·cos(ωt)»:
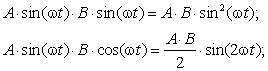 (3.4)
(3.4)
. Выполним интегрирование полученных
выражений:
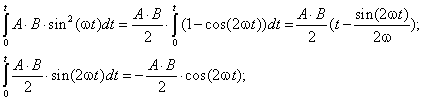 (3.5)
(3.5)
3. Выполним смещение на период T:
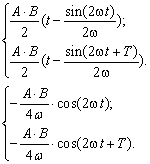 (3.6)
(3.6)
. Выполним суммирование выражений в
скобках:
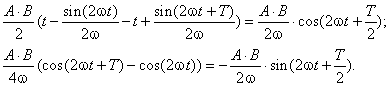 (3.7)
(3.7)
. Получившиеся выражения возведем в
квадрат:
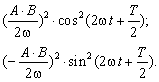 (3.8)
(3.8)
. Выполнив сложение выражений,
получим:
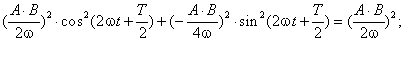 (3.9)
(3.9)
. Корень квадратный:
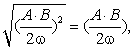 (3.10)
(3.10)
где ω = 2π∙f
-циклическая частота, рад/с,
f = 50 -
частота сети, Гц.
Если амплитуду вспомогательных
сигналов принять В = 100, то в результате получим значение искомой амплитуды
исследуемого сигнала А.
Зная амплитуды тока и напряжения
можно выразить cosφ из
мгновенной мощности сети.
.2 Выбор программы и моделирование
измерительной части конденсаторной установки компенсации реактивной мощности
Проектирование любой системы
управления в общем случае представляет собой сложную задачу, успешное решение
которой зависит от правильного выбора всех ее составляющих.
Большинство задач сводиться,
как правило, к решению систем уравнений [43, 44, 45].
При создании системы
управления, этапом предваряющим разработку технической реализации системы
является исследование работоспособности системы методом моделирования. Для
упрощения процедуры моделирования и многовариантного анализа системы
применяются проблемно-ориентированные пакеты прикладных программ.
В настоящее время наибольшее
распространение получила система инженерных и научных вычислений MatLab
с пакетом расширения визуального моделирования Simulink
[45].
Выполним моделирование
предложенной математической модели измерительной части конденсаторной УКРМ в
программе MatLab с пакетом
расширения визуального моделирования Simulink.
На рис. 3.3 представлена схема
определения амплитуды синусоидального сигнала «311∙sin
(ωt)».
Обозначения:
Sine
Wave - исследуемый
синусоидальный сигнал сети «311∙sin
(ωt)»;
100∙cos(ωt)
и 100∙sin(ωt)
- вспомогательные синусоидальные сигналы;
Product1
и Product2 - элемент
умножения сигналов;
Integ1
и Integ2 - элементы
интегрирования сигналов;
Т1 иТ2 - элементы смещения
сигналов на период Т=1/f;
Sum,
Sum1 и Sum2
- элементы суммирования сигналов;
Fcn,
Fcn1 и Fcn2
- функции математических операций;
Display
- элемент вывода информации;
Scope
- осциллограф.
На рисунке 3.4 представлена схема измерительной
части системы управления мощностью батарей статических конденсаторов.
Обозначения:
- Sine
Wave и Sine
Wave1 - синусоидальные
сигналы тока Im∙sin(ωt+ψi)
и напряжения Um∙sin(ωt+ψu);
- fs
- частота сети переменного тока, Гц;
- Ramp
- элемент времени, с;
- Subsystem(amplitude
I) - подсистема
определения амплитуды тока;
- Subsystem(amplitude
U) - подсистема
определения амплитуды напряжения;
- Subsystem1
и Subsystem - подсистема
определения сдвига по фазе тока ψi
и напряжения ψu.
Рис. 3.3 - Схема определения амплитуды
синусоидального сигнала «311.4∙sin
(ωt)»
Рис. 3.4 - Схема измерительной части системы
управления мощностью конденсаторных батарей
3.3 Разработка алгоритма управления мощностью
конденсаторной установки при несимметричной нагрузке по фазам
Зачастую от одной точки общего
присоединения получают питание как трехфазные, так и одно- или двухфазные
приемники электрической энергии. Из-за несимметричного потребления мощностей по
фазам возникают фазные токи разной величины в цепях питания этих потребителей,
что приводит к возникновению несимметрии напряжения в точке общего
присоединения, отрицательно влияющей на работу многих электроприемников.
Несимметрию напряжения характеризуют коэффициенты несимметрии по обратной 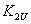 и нулевой
и нулевой 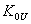 последовательности.
ГОСТ 32144-2013 установил следующие значения этих показателей: К2U = 2%, K0U = 4%.
последовательности.
ГОСТ 32144-2013 установил следующие значения этих показателей: К2U = 2%, K0U = 4%.
Наиболее чувствительная к
несимметрии напряжения электродвигательная нагрузка, обладающая малым
сопротивлением обратной последовательности. Различие напряжения по фазам
приводит к увеличению пульсаций выпрямленного напряжения.
На рисунках 3.5-3.7 приведены
графики измерений несимметрии фазных напряжений, несимметрии межфазных
напряжений и коэффициентов несимметрии прямой и обратной последовательностей
для предприятия ОАО «Армавирский электротехнический завод».
Рис. 3.5 - График фазных напряжений
Рис. 3.6 - График линейных
(междуфазных) напряжений
Рис. 3.7 - График коэффициентов
несимметрии нулевой и обратной последовательностей
Графики построены по данным
измерений качества электрической энергии, замеры выполнялись специализированной
электротехнической лабораторией Армавирского механико-технологического
института. Полученные графики показателей качества электрической энергии имеют
общий характер для ряда предприятий города Армавира.
Из анализа графиков можно сделать
вывод, что при групповой нагрузке несимметрия напряжения по обратной и нулевой
последовательности присутствует всегда, она возникает из-за несимметричного
распределения нагрузок по фазам, хоть и находится в требуемых пределах.
Несимметричная нагрузка по фазам
приводит к снижению эффекта компенсации реактивной мощности. Использование
конденсаторных установок с регулированием мощности батарей статических
конденсаторов по току одной фазы приводит к неполной компенсации или
перекомпенсации реактивной мощности в других фазах.
В таблицу 1.1 занесены данные
измерений параметров сети групповой нагрузки цеха промышленного предприятия ОАО
«Армавирский электротехнический завод». Замеры выполнялись с промежутком 30
минут.
На рисунке 3.8 и рисунке 3.9
показаны графики токов и напряжения при несимметричной нагрузке соответственно.
Несимметричный режим нагрузок возникает из-за наличия большого количества
однофазных приемников.
Таблица 1.1 - Данные измерений
параметров электрической сети цеха
|
UА, В
|
UВ, В
|
UС, В
|
IА, А
|
IВ, А
|
IС, А
|
cosφА
|
cosφВ
|
cosφС
|
|
223
|
228
|
218
|
112
|
118
|
93
|
0,61
|
0,67
|
0,71
|
|
225
|
225
|
219
|
92
|
109
|
100
|
0,63
|
0,68
|
0,7
|
|
222
|
225
|
221
|
115
|
103
|
97
|
0,62
|
0,66
|
0,68
|
|
225
|
230
|
222
|
98
|
101
|
114
|
0,63
|
0,67
|
0,69
|
|
227
|
230
|
225
|
20
|
27
|
63
|
0,7
|
0,72
|
0,74
|
|
223
|
227
|
218
|
107
|
87
|
120
|
0,61
|
0,69
|
0,68
|
|
226
|
225
|
217
|
110
|
105
|
93
|
0,6
|
0,66
|
0,7
|
|
220
|
225
|
219
|
98
|
112
|
120
|
0,63
|
0,65
|
0,69
|
|
221
|
228
|
222
|
109
|
107
|
119
|
0,61
|
0,68
|
0,71
|
Рис. 3.8 - График фазных напряжений при
несимметричном режиме нагрузок в цехе предприятия ОАО «Армавирский
электротехнический завод»
Рис. 3.9 - График токов при несимметричном
режиме нагрузок в цехе предприятия ОАО «Армавирский электротехнический завод»
Значения требуемой реактивной мощности для
поднятия cosφ в каждой
фазе для цеха до величины 0,96 занесены в таблицу 3.2.
Таблица 3.2 - Величина активной мощности и
необходимой реактивной мощности для поднятия коэффициента мощности сети до 0,96
|
PА, кВт
|
PВ, кВт
|
PС, кВт
|
QА, кВар
|
QВ, кВар
|
QС, кВар
|
|
15,2
|
18,02
|
14,39
|
15,35
|
14,78
|
10,07
|
|
13,04
|
16,67
|
15,33
|
12,26
|
13,17
|
11,19
|
|
15,82
|
15,29
|
14,58
|
15,66
|
12,99
|
11,52
|
|
13,9
|
15.56
|
17,46
|
13,07
|
12,76
|
13,27
|
|
3,2
|
4,47
|
10,49
|
2,34
|
3,00
|
6,50
|
|
14,55
|
13,62
|
17,79
|
14,7
|
10,35
|
14,05
|
|
14,9
|
15,59
|
14,65
|
15,50
|
13,25
|
10,69
|
|
13,58
|
17,13
|
18,13
|
13,7
|
15,07
|
13,78
|
|
14,69
|
16,58
|
18,76
|
14,84
|
13,10
|
13,13
|
На рисунке 3.10 приведены графики изменения
реактивной мощности, необходимой для поддержания требуемого значения
коэффициента мощности в каждой фазе.
Из графиков видно, что потребность в реактивной
мощности каждой фазы различна и зависит от индуктивной нагрузки. Для уменьшения
режимов перекомпенсации и недокомпенсации необходимо учитывать cosφ
каждой фазы, а именно регулировать мощность конденсаторных установок по
средневзвешенному значению коэффициентов мощности фаз:
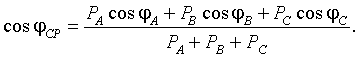 (3.11)
(3.11)
Данные скомпенсированной реактивной мощности по
значению средневзвешенного коэффициента мощности cosφ
сведены в таблицу 3.3. График, показывающий эффективность предложенного метода
регулирования мощности УКРМ, изображен на рисунке 3.11.
Блок-схема алгоритма управления мощностью
батарей статических конденсаторов при несимметричной нагрузке показана на
рисунке 3.12.
Рис. 3.10 - График, показывающий величину
реактивной мощности для поддержания требуемого значения cosφ
в каждой фазе для цеха предприятия ОАО «Армавирский электротехнический завод»
Таблица 3.3 - Расчетная реактивная мощность по
среднему коэффициенту мощности cosφ
|
cosφА
|
cosφВ
|
cosφС
|
cosφР
|
Qку, кВар
|
|
0,61
|
0,67
|
0,71
|
0,66
|
13,4
|
|
0,63
|
0,68
|
0,7
|
0,67
|
12,21
|
|
0,62
|
0,66
|
0,68
|
0,65
|
13,39
|
|
0,63
|
0,67
|
0,69
|
0,66
|
13,03
|
|
0,7
|
0,72
|
0,74
|
0,72
|
3,95
|
|
0,61
|
0,69
|
0,68
|
0,66
|
13,03
|
|
0,6
|
0,66
|
0,7
|
0,65
|
13,15
|
|
0,63
|
0,65
|
0,69
|
0,66
|
14,18
|
|
0,61
|
0,68
|
0,71
|
0,67
|
13,69
|
Рис. 3.11 - График, показывающий потребление
реактивной энергии по фазам инструментального цеха предприятия ОАО «Армавирский
электротехнический завод» и эффективность предложенного метода регулирования
мощности УКРМ
Выводы по главе
1. При групповой компенсации реактивной
мощности на промышленном предприятии необходимо учитывать, что нагрузка по
фазам распределена неравномерно. Это приводит к неравномерному потреблению
реактивной мощности по фазам, что оказывает отрицательное влияние на работу
установки компенсации реактивной мощности.
2. Разработана математическая модель устройства
для системы управления конденсаторной установкой компенсации реактивной
мощности, позволяющая определить амплитуду любого синусоидального сигнала.
3. Разработан метод управления УКРМ при
несимметричной нагрузке по фазам, применение которого позволит уменьшить потери
электрической энергии в системе электроснабжения промышленного предприятия за
счет уменьшения режимов перекомпенсации и недокомпенсации в отдельных фазах.
Глава 4. Разработка метода и алгоритма
оптимального управления режимом реактивной мощности на промышленном предприятии
.1 Разработка метода оптимальное управление
режимом реактивной мощности конденсаторных батарей на промышленном предприятии
Потери активной электроэнергии в электрических
сетях составляют 10-12 % от энергии, поступающей в сети энергосистемы, а
системах электроснабжения промышленных предприятий - 15-25 % от энергии,
получаемой на границе раздела с энергоснабжающей организацией. В этих условиях
компенсация реактивной мощности, как для энергосистемы, так и для промышленных
предприятий представляет собой значительный резерв экономии электроэнергии [46,
47, 48]. В качестве примера в табл. 4 приведены данные по потреблению активной
и реактивной энергии для подстанции 110/6 кВ. Причем данные 2008 г. отражают
потребление реактивной энергии на границе раздела с энергоснабжающей
организацией при работе компенсирующих устройств в сетях 0,4 и 6 кВ. Данные
2009 г. представляют собой естественное потребление реактивной энергии, когда
источники компенсации реактивной мощности были отключены.
Автоматическое управление мощностью
конденсаторных установок позволяет значительно снизить потери электрической
энергии.
Таблица 4.1 - Потребление электроэнергии на
подстанции 110/6 кВ
|
Год
|
Потребление
Wа, тыс.кВт*ч и Wр, тыс.кВт*ч
|
|
Май
|
июнь
|
август
|
сентябрь
|
|
Wа
|
Wр
|
Wа
|
Wр
|
Wа
|
Wр
|
Wа
|
Wр
|
Wа
|
Wр
|
|
|
2008
|
733
|
216,2
|
705
|
233
|
706
|
226
|
972
|
463
|
1003,4
|
496
|
|
|
|
-1,3
|
|
-54
|
|
-55
|
|
-4,7
|
|
0
|
|
|
2009
|
600
|
594
|
576
|
568
|
620,2
|
609
|
473,6
|
460,4
|
836,8
|
842
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим математическую модель оптимального
управления мощностью КУ в системе электроснабжения промышленного предприятия, в
i-х узлах которой
имеются не включенные секции конденсаторных батарей на протяжении расчетного
периода ∆t, а в j-х
узлах имеется не скомпенсированная реактивная мощность Q:
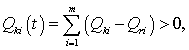 (4.1)
(4.1)
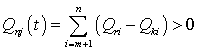 (4.2)
(4.2)
где Qki - мощность
не включенных секций конденсаторных батарей, кВар;
Qri, - не
скомпенсированная мощность реактивная мощность, кВар.
За критерий оптимальности управления
примем снижение затрат на активную и реактивную электроэнергию. Задача
оптимального управления - включение тех секций и в тех узлах, которые
обеспечивают максимальное снижение этих затрат. Поиск нужных секций представим
в виде последовательности шагов, на каждом из которых включается одна секция в
определенном узле. Тогда снижение затрат:
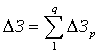 , (4.3)
, (4.3)
где ∆З - снижение затрат на
р-м шаге;
q -
количество шагов для поиска оптимального решения.
Поставленная задача решается на
основе метода динамического программирования Беллмана Р.Э [49]. В соответствии
с его положениями математическую модель управления мощностью КУ, отображающую
пошаговое включение секций, представим следующим образом:
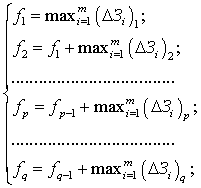 (4.4)
(4.4)
где fp -
максимальное снижение затрат на электроэнергию на р-м шаге.
Для промышленного предприятия снижение затрат
для i- го узла на р-м
шаге определяется по выражению:
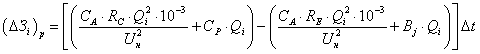 , (4.5)
, (4.5)
где Вj - удельные
потери активной мощности в j-м источнике, кВт/квар;
СА - тариф на активную
энергию, р,
СР - тариф на реактивную
энергию, р,
Uн -
номинальное напряжение распределительной сети, кВ,
RС, RЕ - активные
сопротивления линии, по которым протекают реактивная мощность от сети и от системы
электроснабжения предприятия соответственно, Ом.
В упрощенном виде формула снижения
затрат имеет вид:
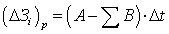 , (4.6)
, (4.6)
где А - затраты предприятия на
компенсацию реактивной мощности от энергосистемы;
В - затраты предприятия при
компенсации реактивной мощности от КУ, расположенных на территории предприятия.
При использовании мощности не
включенных секций конденсаторных батарей повышается уровень напряжения и,
следовательно, его необходимо контролировать. Условие ограничения на повышение
напряжения следующее:
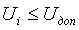 (4.7)
(4.7)
где Ui и Uдоп - текущий и
допустимый уровни напряжения.
Превышение напряжения на шинах
поверяют по условию ограничения. Если оно выполняется, то данную секцию
включают, а если не выполняется, то эту секцию не включают, и ее мощность в
дальнейших расчетах не учитывают.
Расчеты проводят до тех пор, пока
выполняются неравенства:
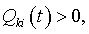
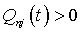 . (4.8)
. (4.8)
Расчет оптимального использования
реактивной мощности конденсаторных установок выполняется по алгоритму:
для каждой не включенной секции i-х узлов
вычисляют значение снижения затрат (∆Зi)р;
находят максимальное значение
снижения затрат по значениям, полученным в п.1;
включают мощность секции,
обеспечивающей максимальное снижение затрат;
если ограничение по напряжению
выполняется, то найденную в п.3 секцию из дальнейших расчетов исключают;
если неравенства 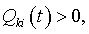
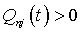 выполняются,
то продолжают расчет.
выполняются,
то продолжают расчет.
На рисунке 4.1 представлена
блок-схема алгоритма управления перетоками реактивной мощности конденсаторных
установок на промышленном предприятии.
Рис. 4.1 - Блок-схема алгоритма
управления перетоками реактивной мощности конденсаторных установок на
промышленном предприятии
4.2 Оптимизация режима реактивной
мощности в узле нагрузки
Внешнее электроснабжение предприятия
ОАО «Армавирский электротехнический завод» осуществляется по кабельной линии
напряжением 10 кВ. На территории предприятия находится центральная
распределительная подстанция (ЦРП). Предприятие относится ко второй категории
потребителей, поэтому для обеспечения требуемой надежности электроснабжения
предусмотрено резервирование по высокой стороне. Внутреннее электроснабжение
предприятия выполнено по радиальной схеме линиями 10 кВ (рис. 4.2).
Основными потребителями электрической
энергии на предприятии являются асинхронные трехфазные и однофазные двигатели,
однофазная осветительная нагрузка общего и местного назначения, трехфазные и
однофазные нагревательные элементы.
Затраты предприятия на оплату
потребления реактивной мощности можно представить как сумму трех составляющих:
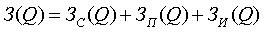 , (4.9)
, (4.9)
где ЗС(Q )-
стоимость реактивной мощности, потребленной из энергосистемы, руб.;
ЗП(Q) -
стоимость потерь активной мощности в распределительной сети предприятия от
протекания по ней реактивной мощности, руб.;
ЗИ(Q) -
стоимость потерь активной мощности в источнике реактивной мощности, руб.
Рис. 4.2 - Однолинейная схема
электроснабжения участка предприятия ОАО «Армавирский электротехнический завод»
Схема электроснабжения предприятия
ОАО «Армавирский электротехнический завод» и схема замещения представлена на
рисунке 4.3.
Стоимость потребления реактивной
энергии из энергосистемы за единицу времени (1 час) определяется величиной
реактивной мощности от энергосистемы QC и тарифом
на реактивную энергии СР:
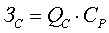 (4.10)
(4.10)
Рис. 4.3 - Схема внешнего
электроснабжения предприятия ОАО «Армавирский электротехнический завод» (а) и
схема замещения (б)
Стоимость потерь активной мощности в
системе электроснабжения предприятия можно представить в следующем виде:
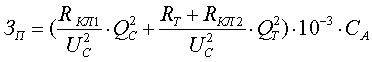 , (4.11)
, (4.11)
где RКЛ1, RКЛ2 - активное
сопротивление линии от распределительного устройства до шин распределительного
пункта, Ом;
RТ - активное
сопротивление трансформатора, Ом;
QС -
реактивная мощность, потребляемая из сети, квар;
QТ - мощность,
протекающая через трансформатор, квар;
UС -
номинальное напряжение распределительной сети, кВ;
СА - тариф на активную
энергию, руб.
Стоимость потерь активной мощности в
самом источнике реактивной мощности:
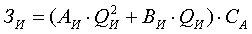 , (4.12)
, (4.12)
где QИ -
реактивная мощность источника, квар;
АИ - удельные
квадратичные потери в источнике реактивной мощности, кВ/квар2; ВИ
- удельные потери активной мощности в источнике реактивной мощности, кВ/квар;
СА - тариф на активную
энергию, руб.
Обозначим:
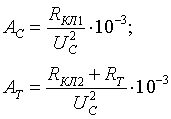 (4.13)
(4.13)
где АС, АТ -
удельные квадратичные потери в линии и трансформаторе, соответственно, кВт/квар2.
Тогда общие затраты можно переписать
в следующем виде:
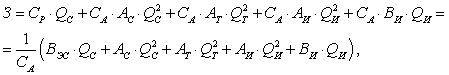 (4.14)
(4.14)
где ВЭС - удельные потери
активной мощности в системе электроснабжения, кВт/кВар.
Из условия баланса мощностей имеем:
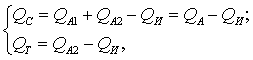 (4.15)
(4.15)
Тогда перепишем выражение для
суммарных затрат как функцию реактивной мощности источника QИ:
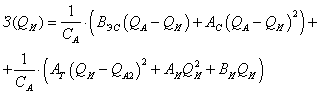 (4.16)
(4.16)
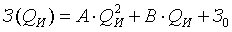 , (4.17)
, (4.17)
где А - удельные квадратичные
затраты, обусловленные потерями активной мощности в элементах системы
электроснабжения при перетекании реактивной мощности от источника, руб./кВар2:
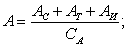 (4.18)
(4.18)
В - удельные затраты на генерацию
реактивной мощности руб./кВар:
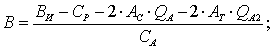 (4.19)
(4.19)
З0 - затраты, которые
будет нести предприятие при отсутствии источника реактивной мощности, руб.:
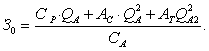 (4.20)
(4.20)
Знак коэффициента В определяет
выгоден или нет источник реактивной мощности и зависит от:
удельных потерь активной мощности в
источнике реактивной мощности и системе электроснабжения;
удельных квадратичных потерь в
элементах системы электроснабжения предприятия;
величины суммарной реактивной
нагрузки предприятия и реактивной нагрузки в его узлах, также их
потокораспределения в элементах системы электроснабжения.
На рисунке 4.4 показана графическая
зависимость затрат и их составляющих (в относительных единицах при З0 =
1) от величины реактивной мощности батарей статических конденсаторов,
построенная в результате расчетов для промышленного предприятия ОАО
«Армавирский электротехнический завод».
Анализируя полученные зависимости
можно сделать вывод, что уменьшение затрат предприятия при компенсации
реактивной мощности нагрузки по сравнению с ее отсутствием имеет место до
определенного значения QПР, при
котором стоимость скомпенсированной реактивной мощности равна стоимости потерь
активной мощности в элементах системы электроснабжения. Применение источников
реактивной энергии большей мощности, чем QПР, приводит к
убыткам от компенсации реактивной мощности для предприятия.
Функция затрат имеет минимум при значении
мощности источника питания
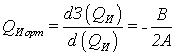 . (4.21)
. (4.21)
Рис. 4.4 - Зависимость затрат от степени
компенсации реактивной мощности
Хотя расчеты проведены для конкретного
предприятия, зависимости, представленные на рисунке 4.4, носят обобщенный
характер и отражают влияние различных факторов на эффективность компенсации
реактивной мощности в системах электроснабжения промышленных предприятий.
Учитывая, что в течение суток реактивная нагрузка предприятий и его узлов
меняется, поддержание оптимального режима реактивной мощности в системе
электроснабжения предприятия может обеспечить только автоматизированная
система, управляющая работой источников реактивной мощности.
Ниже приведен график потребления реактивной
мощности на промышленном предприятии ОАО «Армавирский электротехнический завод»
построенный по данным выборки с 16.11.2012 г. по 17.11.2012 г. показанный на
рисунке 4.5.
Рис. 4.5 - График потребления
реактивной мощности на предприятии ОАО «Армавирский электротехнический завод» с
16.11.2012 г. по 17.11.2012 г.
.3 Разработка и реализация алгоритма
управления режимом реактивной мощности на промышленном предприятии с
многоуровневой системой электроснабжения
Управление мощностью источников
реактивной энергии на промышленных предприятиях, как было описано выше,
осуществляется либо дежурным персоналом, либо устройствами автоматического
управления, контролирующими реактивный или полный ток узла нагрузки, к которому
они подключены. Такой режим работы источников реактивной мощности не является
оптимальным.
Задача оптимизации режимов реактивной
мощности для промышленных систем электроснабжения усложняется тем, что
распределительные сети предприятий имеют многоуровневую систему
электроснабжения [14] с общими участками транзита электроэнергии. Это видно из
схемы электроснабжения промышленного предприятия ОАО «Армавирский
электротехнический завод».
Это значит, что задача оптимизации
режимов работы источников реактивной мощности в системах промышленных
предприятий усложняется и требует комплексного подхода к своему решению. При
расчете оптимальных режимов нагрузок кроме факторов, указанных выше, необходимо
учитывать конфигурацию электрической сети и отличия характеристик источников
реактивной мощности.
При внедрении на предприятиях
автоматизированных систем управления источниками реактивной мощности,
охватывающих всю систему электроснабжения предприятий, встает вопрос о
разработке универсальных алгоритмов управления источниками реактивной мощности,
которые могут быть легко адаптированы для различных схем электроснабжения.
Любую систему электроснабжения
промышленного предприятия можно представить в виде многоуровневой [14],
содержащую М ветвей и N узлов. В узлах сети имеются L реактивных
нагрузок QА и К
источников реактивной мощности QИ (см. рис.
4.6). Каждый источник реактивной мощности характеризуются стоимостью
генерируемой им мощности СР. Стоимость активной энергии,
потребляемой из энергосистемы, равна СА.
Рис. 4.6 - Схема многоуровневой
системы электроснабжения промышленного предприятия
Найдем значения реактивных мощностей
источников реактивной энергии, при которых будет иметь место минимум затрат на
оплату реактивной мощности и потерь активной мощности в сети.
Суммарные затраты определяются как
сумма стоимостей потерь в линиях, потерь в источниках реактивной мощности и
стоимости потребляемой мощности от каждого источника реактивной энергии, что
математически можно записать в виде функции:
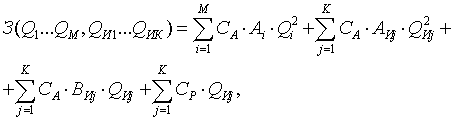 , (4.22)
, (4.22)
где Аi - удельные
квадратичные потери активной мощности в линии, кВт/квар2;
Qi -
реактивная мощность в i-ветви, квар;
QИj -
реактивная мощность j-го источника, квар;
АИj - удельные
квадратичные потери активной мощности в j-м
источнике, кВт/квар2;
ВИj - удельные
потери активной мощности в j-м источнике, кВт/квар.
Уравнения, связывающие между собой
переменные QИj и Qi,
определяются первым законом Кирхгофа и имеют вид:
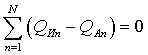 , (4.23)
, (4.23)
где QИn -
реактивная мощность источников реактивной энергии в узле нагрузки; QAn -
потребляемая реактивная мощность узла нагрузки;
Для поиска минимума функции
суммарных затрат используем метод множителей Лагранжа. Вспомогательная функция
(функция Лагранжа) имеет вид:

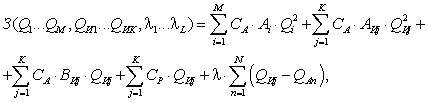 (4.24)
(4.24)
Взяв частные производные dЗ/dQi, dЗ/dQИ и граничные
условия, получим систему уравнений:
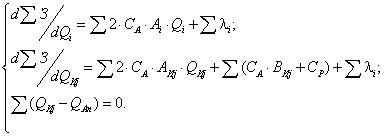 (4.25)
(4.25)
В матричном виде система уравнений
будет иметь вид:
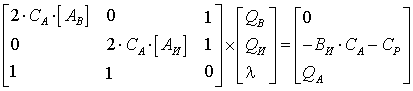 . (4.26)
. (4.26)
Столбец неизвестных системы
уравнений имеет следующую структуру:
QВ - столбец
реактивных мощностей в ветвях сети Qi;
QИ - столбец
реактивных мощностей источников реактивной энергии QИj;
λ - столбец
неопределенных множителей Лагранжа.
Столбец свободных членов системы
уравнений имеет следующую структуру:
ВИ - столбец
коэффициентов потерь в источнике реактивной мощности прямо пропорциональных
генерируемой реактивной мощности;
QА - столбец
реактивных нагрузок в узлах электрической сети.
Решение системы линейных уравнений
позволяет определить значения реактивных мощностей для каждого из источников,
включая и энергосистему, при которых издержки на компенсацию реактивной
мощности в распределительной сети и ее элементах будут минимальны.
При реализации систем управления
источниками реактивной мощности на предприятии их работа должна осуществляться
по алгоритму:
ввод массива располагаемых
источников реактивной мощности QИj;
ввод массива параметров схемы
замещения Аi$
ввод значений реактивных мощностей в
линиях электропередач Qi;
определение текущей тарифной зоны и
выбор соответствующих тарифов на активную СА и реактивную СР
мощность;
расчет вектора оптимальных значений
реактивной мощности источников по функции суммарных затрат QИ(опт);
выдача управляющих сигналов на
источники реактивной мощности.
сравнение напряжения сети с
допустимым отклонением. Если Uс<Uдоп, то
продолжать расчет. Если Uс>Uдоп, то выдать
сигналы управления напряжением в узле нагрузки.
Регулирование напряжения в системах
электроснабжения промышленных предприятий имеет свои особенности.
Распределительные сети 6-10 кВ предприятий и цеховые электрические сети 0,4 кВ
имеют небольшую протяженность и в связи с этим «сильную» связь между
напряжением на зажимах электроприемников и в отдельных точках сети с
регулированием напряжения в центре питания (центральная распределительная
подстанция, главная понизительная подстанция).
На рисунке 4.7 приведена блок-схема
алгоритма управления режимом реактивной мощности на промышленном предприятии.
Для реализации алгоритма
оптимального управления источниками реактивной мощности автоматизированная
система должна располагать следующим информационным обеспечением по системе
электроснабжения управляемого объекта:
. По системе электроснабжения
управляемого объекта:
параметры схемы замещения
электрической сети;
точки подключения источников
реактивной мощности в распределительной сети;
номинальное напряжение сети.
. По системе электропотребления:
тарифы на активную СА и
реактивную электроэнергию СР;
временные интервалы тарифных зон
суток и соответствующие им коэффициенты изменения стоимости электроэнергии.
. По источникам реактивной мощности:
технические характеристики: мощность
батарей статических конденсаторов, количество ступеней и их значение,
номинальные параметры QН и cosφН для
синхронных двигателей;
экономические показатели:
коэффициенты потерь в двигателях А и В, удельные потери активной мощности в
батареях статических конденсаторов.
Реализация предложенного алгоритма
требует достаточно высоких вычислительных ресурсов для управляющей машины.
Измерение параметров режима электрической сети и потоков мощностей может быть
осуществлено на базе систем технического учета электроэнергии при подключении
необходимых приборов учета в соответствующих точках схемы электроснабжения
(счетчиков активной и реактивной энергии, трансформаторов тока и напряжения).
Покажем работу системы управления
мощностью компенсирующих устройств на примере предприятия ОАО «Армавирский
электротехнический завод». Предприятие имеет многоуровневую систему
электроснабжения, схема замещения системы электроснабжения предприятия ОАО
«Армавирский электротехнический завод» показана на рисунке 4.8:
Рис. 4.7 - Блок-схема алгоритма
работы автоматической системы управления режимом реактивной мощности на
промышленном предприятии
Составляем уравнение функции затрат
и уравнение Кирхгофа для каждого узла схемы:
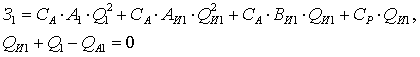
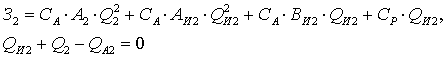
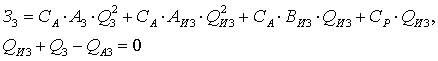
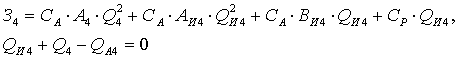
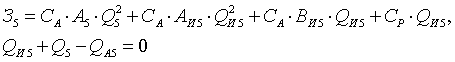
Рис. 4.8 - Схема замещения системы
электроснабжения предприятия ОАО «Армавирский электротехнический завод»
Для поиска минимума функции
суммарных затрат по методу множителей Лагранжа составим вспомогательные функции
(функции Лагранжа), которые имеют вид:
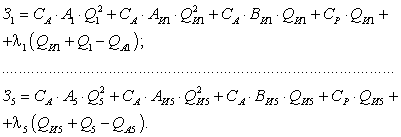
Взяв частные производные dЗ/dQi, dЗ/dQИj и граничные
условия получим систему линейных уравнений, имеющую шесть неизвестных:
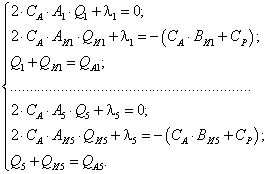
Для решения полученной системы
уравнений представим ее в матричном виде:
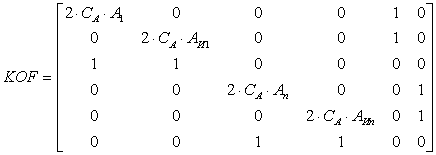
вектор неизвестных и вектор правых
частей имеют вид:
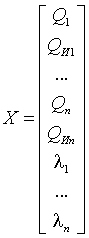
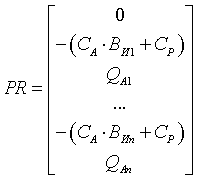
Решение системы имеет вид:
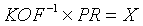
Для схемы, изображенной на рис.33:
Удельные квадратичные потери
активной мощности в линиях приходящиеся на 1 квар реактивной мощности
передаваемой по этим участкам, кВт/квар2:
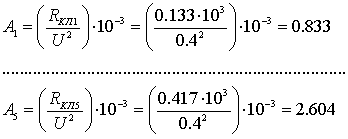
Удельные квадратичные потери
активной мощности в источниках, приходящиеся на 1 квар2 реактивной
мощности, кВт/квар2 (для конденсаторов): 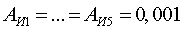 .
.
После подстановки численных значений
получим решение на примере двух узлов для системы электроснабжения предприятия
ОАО «ШАТЛ», при реактивной нагрузке в первом узле 460 квар, во втором 124 квар:
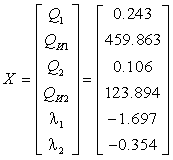
Анализируя полученные значения можно
сделать вывод, что для данного момента времени минимум затрат предприятия на
реактивную мощность будет при мощности конденсаторных установок равных в первом
узле 459,896 квар, а во втором 123,894 квар. Небольшая погрешность вычисления
является следствием применения метода Лагранжа, который сам по себе является
приближенным.
Рис. 4.9 - График зависимостей
затрат предприятия на реактивную мощность от мощности конденсаторных установок
(Qa - значения
реактивных мощностей в узле нагрузки, Qu,опт -
оптимальное значение мощности КУ)
4.4 Реализация метода оптимального
управления режимом реактивной мощности конденсаторных батарей на промышленном
предприятии
В каждом из узлов 1-3 системы
электроснабжения предприятия ОАО «Армавирский электротехнический завод»
(см.рис. 4.10) ежедневно в течении 2-х часов имеются не включенные секции
конденсаторов мощностью 25, 50 и 100 кВар, а на шинах трансформаторной
подстанции 10/0,4 кВ в это же время есть не скомпенсированная реактивная
мощность 250 кВар. Сопротивления схемы занесены в таблицу 4.1. Количество
рабочих дней в году - 240. Тариф на активную энергию 2,8 руб./(кВт·ч).
Необходимо найти секции, которые целесообразно включать на протяжении
указанного времени, и определить годовое уменьшение за счет этого платы за
электроэнергию.
Рис. 4.10 - Схема электроснабжения
цеха предприятия ОАО «Армавирский электротехнический завод»
Таблица 4.1 - Данные схемы замещения
предприятия ОАО «Армавирский электротехнический завод»
|
Элемент
схемы
|
Сопротивление
элемента, Ом
|
|
ТМ
1000/10
|
0,002
|
|
КЛ
10 кВ (4 км)
|
0,036
|
|
Линия
1 (200 м)
|
0,168
|
|
Линия
2 (160 м)
|
0,134
|
|
Линия
3 (80 м)
|
0,067
|
Расчет выполнен по алгоритму, описанному выше.
Данные расчета сведены в таблицу 4.2.
Таблица 4.2 - Результаты расчета
|
Шаг
|
Номер
узла, в котором включается секция
|
Номер
включаемой секции
|
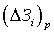 ,
руб./годМощность включаемой секции, кВарОбщая мощность не включенных КБ,
кВарНе скомпенсированная мощность по узлам системы электроснабжения
промышленного предприятия, кВар ,
руб./годМощность включаемой секции, кВарОбщая мощность не включенных КБ,
кВарНе скомпенсированная мощность по узлам системы электроснабжения
промышленного предприятия, кВар
|
|
|
|
|
1
|
3
|
3
|
1294
руб. при Ср=0 41827,2 руб. при Ср=0,34
|
100
|
425
|
150
|
|
2
|
2
|
3
|
|
100
|
325
|
50
|
|
3
|
3
|
2
|
|
50
|
275
|
0
|
Описанные выше методы компенсации реактивной
мощности могут быть использованы одновременно. Результаты расчетного
эксперимента для предприятия ОАО «Армавирский электротехнический завод»
занесены в табл. 4.3. Расчет проводился с учетом ступенчатости регулирования
мощности конденсаторных батарей и при условии, что тариф на реактивную энергию
составляет ноль рублей за кВар.
Таблица 4.3 - Результаты эксперимента на
предприятии ОАО «Армавирский электротехнический завод»
|
Сопротивление
схемы замещения, Ом
|
Мощность
секций конденсаторных батарей, QИ, кВар
|
Удельные
квадратичные потери в линиях, кВт/квар2
|
Удельные
квадратичные потери и удельные потери в источниках, кВт/квар2 ; кВт/квар
|
Потребление
реактивной мощности в узлах, кВар
|
Расчет
оптимальных значений реактивной мощности, Qопт
|
Мощность
включенных секций батарей
|
Величина
реактивной мощности от сети, кВар
|
Мощность
не включенных секций
|
Секции,
которые необходимо включить
|
Величина
реактивной мощности от сети, кВар
|
|
Rтр=0,002
|
-
|
0,0125
|
-
|
519
|
-
|
-
|
159,07
|
-
|
|
4
|
|
Rкл=0,036
|
|
0,225
|
-
|
|
-
|
-
|
|
-
|
|
|
|
Rкл1=0,168
|
5,25,50,100
|
1,05
|
0,001/
0,004
|
86
|
86,07
|
80
|
6,07
|
100
|
100
|
0
|
|
Rкл2=0,134
|
5,25,50,100
|
0,836
|
0,001/
0,004
|
128
|
127,84
|
125
|
3
|
5,50
|
2,25
|
0
|
|
Rкл3=0,067
|
5,25,50,100
|
0,69
|
0,001/
0,004
|
170
|
169,99
|
155
|
15
|
25
|
|
4
|
|
Rкл4=0,124
|
-
|
0,775
|
-
|
62
|
62,03
|
-
|
62
|
-
|
|
0
|
|
Rкл5=0,169
|
-
|
1,056
|
-
|
73
|
72,91
|
-
|
73
|
-
|
|
0
|
Выводы по главе
1. Разработан метод и алгоритм системы
управления реактивной мощностью в системе электроснабжения промышленного предприятия,
применение которого снизит затраты предприятия на оплату реактивной энергии.
2. За счет не включенных секций
конденсаторных батарей, возникающих в течение суток в узлах промышленных
предприятий, реактивную мощность целесообразно использовать для компенсации
реактивной мощности других узлов предприятия.
. Применение разработанного метода и
алгоритма существенно снижает потери электрической энергии в системе
электроснабжения промышленного предприятия и повышает эффективность
использования УКРМ, что подтверждается приведенными расчетами для предприятия
ОАО «Армавирский электротехнический завод».
Заключение
В данной работе на основе обобщения
теоретических и экспериментальных исследований разработана методология
компенсации реактивной мощности на промышленном предприятии, реализация которых
позволяет решить прикладную проблему повышения качества электрической энергии и
снижения электропотребления.
Наиболее существенные научные и практические
результаты выполненных исследований заключаются в следующем:
1) Проведен анализ потерь электрической
энергии в зависимости от передачи реактивной мощности по элементам системы
электроснабжения промышленного предприятия.
2) Для снижения загрузки технологического
электрооборудования показана необходимость и целесообразность взаимосвязного
регулирования режима реактивной мощности и напряжения в системе
электроснабжения промышленного предприятия, что позволит достигнуть снижения
электропотребления и повысить эффективность применения источников реактивной
мощности.
3) Разработан алгоритм адаптивного
нечеткого управление СК с применением нейронной технологии. Предлагаемый
алгоритм позволяет модифицировать систему нечеткого вывода применительно к
нелинейным функциям принадлежности дефаззификатора, который обеспечивает высокое
быстродействие и заданную точность по отношению к известным алгоритмам. алгоритм электроснабжение реактивный компенсатор
4) Для измерительной части системы
управления конденсаторной установкой разработана математическая модель
устройства, позволяющая определить амплитуду любого синусоидального сигнала.
Математическая модель устройства реализована в программе MATLAB
приложение Simulink.
) Разработан метод управления мощностью
батарей статических конденсаторов, позволяющий уменьшить режимы недокомпенсации
и перекомпенсации в отдельных фазах при несимметричной нагрузке
6) Разработан способ компенсации реактивной
мощности одних узлов нагрузки за счет реактивной мощности не включенных секций
конденсаторных батарей в других узлах нагрузки системы электроснабжения,
отличающийся наиболее полным использованием установок компенсации реактивной
мощности на промышленном предприятии
7) Разработан метод управления режимом
реактивной мощности узла нагрузки (предприятия), применение которого позволяет
управлять режимом реактивной мощности на промышленном предприятии, используя
значения реактивных мощностей для каждого из источников реактивной энергии, при
которых затраты на реактивную мощность в распределительной сети 0,4 кВ и ее
элементах будут минимальны.
) Внедрение разработанных способов и
методов компенсации реактивной мощности позволило получить до 15% экономии
электрической энергии на участке предприятии ОАО «Армавирский
электротехнический завод», что составляет 240 тыс. руб. в год. Достоверность
реализации разработанных способов и методов подтверждается соответствующими
документами.
1. Либерман А.С., Поляков Б.А.
Снабжение промышленных предприятий реактивной энергией. - Ростов - на Дону:
Азчерхозиздат, 1937. - 169 с.
2. Залесский А.М. Передача
электрической энергии / А.М. Залесский. Л.: Госэнергоиздат, 1948. 355 с.
. Зельцбург А.М. Экономика
электроснабжения промышленных предприятий. - М.: Высшая школа, 1973. - 272 с.
. Кудрин Б.И., Прокопчик
В.В., Елисеев Г.А. О влиянии режима напряжения в цеховых электрических сетях на
удельные расходы электроэнергии промышленных предприятий // Промышленная
энергетика. - 1987. - № 2. - С.33-35.
. Электротехнический
справочник. В 4 т. Т. 3. Производство, передача и распределение электрической
энергии. 9-е изд., стер./ Под общ. ред. проф. МЭИ В.Г. Герасимова и др.; гл.
ред. А.И. Попов. М.: Энергоатомиздат, 2004. 964 с.
. Фурсанов М.И. Методология и
практика расчетов потерь электроэнергии в электрических сетях энергосистем. /
М.И. Фурсанов. Минск: Технология, 2000. 247 с.
. ГОСТ 32144-2013.
Электрическая энергия. Совместимость технических средств электромагнитная.
Нормы качества электрической энергии в системах электроснабжения общего
назначения. - Введ. 01.07.2013 г.
. Лукас В.А. Теория
управления техническими системами: учеб. пособие для вузов - 4-е изд. испр. -
Екатеринбург: Изд-во Урал. гос. техн. ун-та, 2005. - 667 с.
. Инструкция по системному
расчету компенсации реактивной мощности в электрических сетях //Инструктивные
материалы Главгосэнергонадзора. -М.: Энергоатомиздат, 1986. - С. 276-287
. Макаров Е.Ф. Справочник по
электрическим сетям 0,4 - 35 кВ и 110 - 1150 кВ. Т. II.
/ Е.Ф. Макаров. М.: Папирус ПРО, 2003. 622 с.
. Железко Ю.С. Потери
электроэнергии в электрических сетях, зависящих от погодных условий / Ю.С. Железко,
В.А. Костюшко, С.В. Крылов // Электрические станции. 2004. № 11. С. 42 - 47.
. Справочник по
проектированию электрических сетей / И.Г. Карапетян, Д.Л. Файбисович, И.М.
Шапиров; под ред. Д.Л. Файбисовича. М.: ЭНАС, 2005. 313 с
. Железко Ю.С. Выбор мероприятий
по снижению потерь электроэнергии в электрических сетях. - М.: Энергоатомиздат,
1989. - 176 с.
. Кудрин Б.И.
Электроснабжение промышленных предприятий. - М.: Энергоатомиздат, 1995. - 416
с.
. Сергеенков Б.Н., Киселев
В.М., Акимова Н.А. Электрические машины. Трансформаторы. М.: Высшая школа,
1989. - 352 с.
. Железко Ю.С., Артемьев
А.В., Савченко О.В. Расчет, анализ и нормирование потерь электроэнергии в
электрических сетях: Руководство для практических расчетов. - М.: Изд-во НЦ
ЭНАС, 2004.
. Лосев С.Б., Чернин А.Б.
Вычисление электрических величин в несимметричных режимах электрических систем.
- М.: Энергоатомиздат, 1983. - 528 с.
. Передача и распределение
электрической энергии: Учебное пособие/ А.А. Герасименко, В.Т. Федин. - Ростов
н/Д.: Феникс; Красноярск: Издательские проекты, 2006. - 720 с. (Серия «Высшее
образование»).
. Конюхова Е.А. Режимы
напряжений и компенсация реактивной мощности цеховых электрических сетях. - М.:
НТФ «Энергопрогресс», «Энергетик», 2000. - 55 с/
. Герасименко А.А. Электроэнергетические
системы и сети. Расчеты параметров и режимы работы электрических сетей. В 2 - х
ч. Ч. 1 и 2 / А.А. Герасименко, Т.М. Чупак. Красноярск: ИПЦКГТУ, 2004. 222 с.,
172 с.
. Зельцбург А.М. Экономика
электроснабжения промышленных предприятий. - М.: Высшая школа, 1973. - 272 с/
. Федин В.Т. Принятие решений
при проектировании развития электроэнергетических системах / В.Т. Федин. Минск:
Технопринт, 2000. 165с.
. Железко Ю.С. Выбор
мероприятий по снижению потерь электроэнергии в электрических сетях / Ю.С.
Железко. М.: Энергоатомиздат, 1989. 176 с.
. Железко Ю.С. Компенсация
реактивной мощности и повышение качества электроэнергии. - М.: Энергоатомиздат,
1985. - 224 с.
. Орлов В.С. Снижение
потребления энергии при компенсации реактивной мощности в промышленных сетях
//Промышленная энергетика. - 1989. - № 4. - С. 49-50.
. Электроснабжение
промышленных предприятий: Учебник для студентов высших учебных заведений/ Б.И.
Кудрин. - М.: Интермет Инжиниринг, 2005. -- 672 с.: ил.
. Папков Б.В., Щеголькова
Т.М. Повышение эффективности электропотребления на промышленных предприятиях //
Промышленная энергетика. - 1995. - № 12. - С. 21-24
. Железко Ю.С. Компенсация
реактивной мощности в сложных электрических системах. - М.: Энергоатомиздат,
1981. 200 с.
. Компенсирующие и
регулирующие устройства в электрических системах /Г.Е. Поспелов, Н.М. Сыч, В.Т.
Федин. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1983. - 112 с.
. Арзамасцев Д.А. Снижение
технологического расхода энергии в электрических сетях /Д.А. Арзамасцев, А.В.
Липес. М.: Высшая школа, 1989. 127 с.
. Потребич А.А. Моделирование
нагрузок для расчета потерь энергии в электрических сетях энергосистем / А.А.
Потребич // Электричество. 1997. № 3. С. 7 - 12.
. Герасименко А.А. Качество
электрической энергии в электрических сетях / А.А. Герасименко, Т.И.
Поликарпов. Красноярск: КГТУ, 2002. 116 с.
. Методы робастного,
нейро-нечеткого и адаптивного управления Учебник / Под редакцией Н.Д. Егупова.
- М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. - 744 с.
34. Хижняков
Ю.Н., Южаков А.А. Нечеткая адаптивная система возбуждения БЩСГ переменного тока
средней мощности / Всероссийская научно-техническая Интернет-конференция.
Пермь, ПГТУ, 2007.
. Рутковская Д., Пилинский
М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы:
Пер. с польск. И.Д. Рудницкого. - М.: Горячая линия - Телеком, 2006. - 452 с.
. Бобко В.Д., Золотухин Ю.Н.,
Нестеров А.А. Оптимальная траектория как основа построения базы знаний
нечеткого логического контроллера. // В кн.: РОИ - 98. Распределенная обработка
информации. Труды шестого международного семинара. Новосибирск, Сибирское
отделение РАН, 1998. С. 290 - 294.
. Хижняков Ю.Н., Южаков А.А.
Нечеткий и нейронный адаптивные регуляторы возбуждения генератора средней
мощности. // Проблемы управления и моделирования в сложных системах. Труды 11
Международной конференции (22-24 июня 2009 г). Самара, Россия. С. 309-312.
. Хижняков Ю.Н., Южаков А.А.
Интеллектуальные регуляторы возбуждения генератора средней мощности. //
Информационные технологии в науке, социологии, экономике и бизнесе. Материалы
36 Международной конференции и дискуссионного научного клуба. Майская сессия.
Украина, Крым, Ялта-Гурзуф (20-30 мая) 2009. С.87.
. Круглов В.В., Борисов В.В.
Искусственные нейронные сети. Теория и практика. 2-е изд., стереотип. - М.:
Горячая линия - Телеком, 2002. - 382 с.
. Смирнов В.А., Хасанова А.А.
Особенности реализации системы управления на нечеткой логике. Изв. Челябинского
научного центра, вып. 4 (21), 2003 г.
. А. Ф. Бермант, И.Г.
Абрамович. Краткий курс математического анализа. - 8-испр. и доп. - М.: Наука,
1973. - 720 с.
. Ю.Н. Хижняков Формирование
вектора напряжения на шинах автономной электростанции. Известия ТПУ, Т.315, №
4, 2009. - С. 43-46.
. Дьяконов В.П. Simulink
4. Специальный справочник - СПБ.: Питер, 2002 г. - 528 с., ил.
. Аладьев В.З., Богдавичюс
М.А. Maple 6: Решение
математических статистических и физико-технических задач - М.: Лаборатория
базовых знаний, 2001 г. - 824 с., ил.
45. Matlab
6. Учебный курс - СПб.: Питер, 2001 г. - 592 с., ил.
. Повышение эффективности
использования энергии в промышленности Дании /под редакцией А. М. Мастепанова и
Ю. М. Когана, Минтопэнерго, М., 1999. - 242 с.
. Мелентьев Л.А. Системные
исследования в энергетике: элементы теории, направления развития «Наука», 1983г.,
Москва.
. Меламед A.M.
Современные методы анализа и прогнозирования режимов электропотребления в
электроэнергетических системах // Итоги науки и техники. Энергетические системы
и их автоматизация, 1998, т. 4. с. 4-111.
. Беллман Р.Э. Прикладные
задачи динамического программирования. Под ред. А.А. Первозванского. - М.:
Наука. Главная редакция Физико-математической литературы, 1965. - 460 с.
Статьи, опубликованные в журналах,
рекомендованных ВАК
50. Хомяков А.В. Методы компенсации
реактивной мощности в сети низкого напряжения/ Хомяков А. В. // Вестник
Воронежского государственного технического университета, том 5, №2 - Воронеж,
2009. - С. 124-128.
51. Кумаритов А.
М. Алгоритм оптимизации затрат на оплату потребления реактивной мощности при
управлении электроснабжением промышленных предприятий / Кумаритов А. М.,
Хомяков А. В.// Аудит и финансовый анализ, № 3, Москва, 2010. - С. 117-120.
52. Белозерская
Т.Ю. Разработка алгоритма управления конденсаторными установками на
промышленном предприятии /Белозерская Т.Ю., Хомяков А.В.// Естественные и
технические науки, №2 (64), г. Москва, 2013. - С. 220-224.
. Хижняков
Ю.Н., Хомяков А.В. Адаптивное нечеткое управление синхронного компенсатора с
применением нейронной технологии. Известия вузов. Электромеханика, №2, 2015. -
С. 30-35.
. Хижняков
Ю.Н., Хомяков А.В. Нечеткий регулятор напряжения синхронного компенсатора.
Интеллектуальные системы в производстве. №1, 2015. - С. 112-115.
Материалы международных конференций
55. Хомяков А. В. Автоматическое
управление установками конденсаторных батарей / Хомяков А.В.// Сборник трудов
по материалам международной научно - практической конференции, посвященной
90-летию КубГТУ и 49-летию АМТИ «Научный потенциал ВУЗа - производству и
образованию», №4. - Армавир: АМТИ (филиал) КубГТУ, 2008. - С. 203-204.
56. Хомяков А. В. Управление
мощностью источников реактивной энергии на промышленных предприятиях/ Хомяков
А.В.// Сборник материалов I
Международной научно-практической конференции «Наука и современность 2010», г.
Новосибирск, 2010. - С. 135-139.
57. Хомяков А.В. Автоматизация
управления потоками реактивной энергии в сети промышленного предприятия/
Хомяков А.В. //Материалы IV
Международной научно-практической конференции «Современное состояние
естественных и технических наук», г. Москва, 2011. - С. 110-114.
58. Хомяков А.В. Разработка
алгоритма оптимального управления потоками реактивной энергии на промышленных
предприятиях/ Хомяков А.В.// Материалы VII
международной заочной научно-практической конференции «Научная дискуссия:
инновации в современном мире» часть I,
г. Москва, 2012. - С.80-84.
. Хомяков А.В. Алгоритм
управления установками компенсации реактивной мощности в системе
электроснабжения предприятия / Белозерская Т.Ю., Хомяков А.В// Материалы II
международной научно-практической конференции «Теория и практика внедрения
новых технологий в производстве и строительстве», г. Москва, 2013. - С. 39-43.
Приложение А
Дифференциальные уравнения синхронного
компенсатора, пассивной активно-индуктивной нагрузки и асинхронной нагрузки
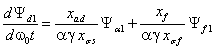
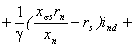
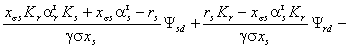
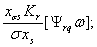
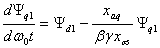
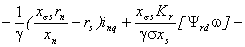
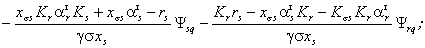
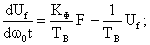
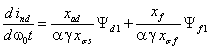
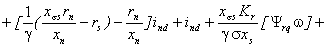
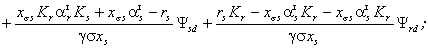
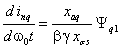
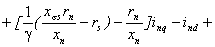
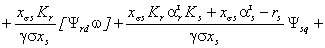
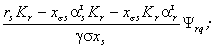
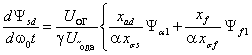
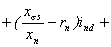
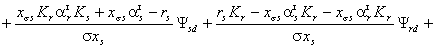
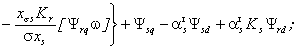

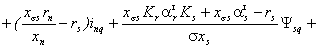
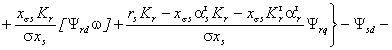
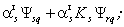
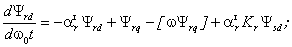
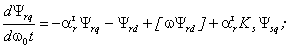
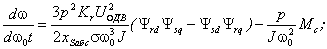
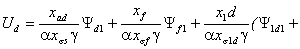
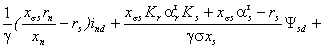
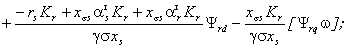
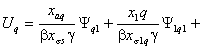
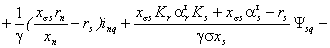
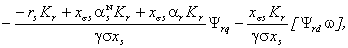
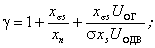
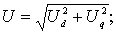
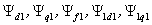 - проекции потокосцеплений статора,
обмотки возбуждения синхронного компенсатора в анормальной системе
относительных единиц по осям d и q;
- проекции потокосцеплений статора,
обмотки возбуждения синхронного компенсатора в анормальной системе
относительных единиц по осям d и q;
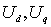 - проекции напряжения на шинах узла
нагрузки по осям d и q;
- проекции напряжения на шинах узла
нагрузки по осям d и q;
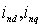 - проекции тока пассивной нагрузки
в системе относительных единиц статора по осям d и q;
- проекции тока пассивной нагрузки
в системе относительных единиц статора по осям d и q;
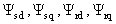 - проекции потокосцеплений статора и
ротора асинхронного двигателя (АД) в системе относительных единиц статора в
осях d и q;
- проекции потокосцеплений статора и
ротора асинхронного двигателя (АД) в системе относительных единиц статора в
осях d и q;
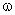 - частота вращений ротора АД;
- частота вращений ротора АД;
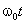 - синхронное время, рад;
- синхронное время, рад;
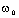 = 3,14 - круговая частота, рад/с;
= 3,14 - круговая частота, рад/с;
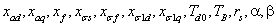 - параметры синхронного
компенсатора;
- параметры синхронного
компенсатора;
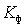 - коэффициент форсировки;
- коэффициент форсировки;
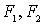 - выход нечеткого регулятора;
- выход нечеткого регулятора;
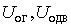 - базовое напряжение статора
синхронного компенсатора и статора АД, В;
- базовое напряжение статора
синхронного компенсатора и статора АД, В;
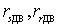 - активные сопротивления статора и
ротора АД, о.е.;
- активные сопротивления статора и
ротора АД, о.е.;
 - полные индуктивные сопротивления
статора и ротора, о.е.;
- полные индуктивные сопротивления
статора и ротора, о.е.;
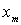 - индуктивное сопротивление
главного потока АД, о.е.;
- индуктивное сопротивление
главного потока АД, о.е.;
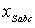 - полное индуктивное сопротивление
статора АД, Ом;
- полное индуктивное сопротивление
статора АД, Ом;
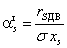 - коэффициент затухания статора АД;
- коэффициент затухания статора АД;
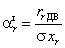 - коэффициент затухания ротора АД;
- коэффициент затухания ротора АД;
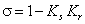 - коэффициент рассеяния по
Блонделю;
- коэффициент рассеяния по
Блонделю;
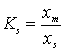 - коэффициент электромагнитной
связи статора АД;
- коэффициент электромагнитной
связи статора АД;
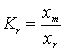 - коэффициент электромагнитной
связи ротора АД;
- коэффициент электромагнитной
связи ротора АД;
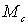 - реактивный момент сопротивления,
о.е.;
- реактивный момент сопротивления,
о.е.;
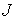 - момент инерции, кг×м2;
- момент инерции, кг×м2;
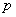 - число пар полюсов;
- число пар полюсов;
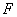 - управление током возбуждения
синхронного компенсатора.
- управление током возбуждения
синхронного компенсатора.