Основы механики грунтов
Задача 1
Дано:
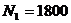 кН;
кН; 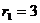 м;
м;
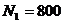 кН;
кН; 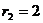 м;
м;
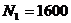 кН;
кН; 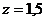 м.
м.
Определить
величины вертикальных составляющих напряжений в массиве грунта и построить
эпюры напряжений: от совместного действия сосредоточенных сил в точках на
вертикали, проходящей по оси действия силы  и на
горизонтали, расположенной в плоскости действия сил, на расстоянии
и на
горизонтали, расположенной в плоскости действия сил, на расстоянии 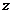 от поверхности.
от поверхности.
Решение:
Напряжение
от трех сосредоточенных сил равно:
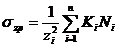 ,
,
где
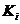 - безразмерный коэффициент, зависящий от соотношения
- безразмерный коэффициент, зависящий от соотношения 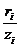 , определяется по табл. 1 приложения.
, определяется по табл. 1 приложения.
.
От совместного действия сосредоточенных сил в точках на вертикали, проходящей
по оси действия силы  .
.
Для
точки 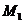 определяем коэффициенты
определяем коэффициенты 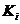 :
:
-
для силы 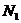 :
: 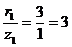 ;
; 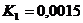 ;
;
-
для силы 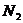 :
: 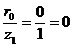 ;
; 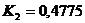 ;
;
-
для силы 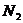 :
: 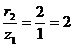 ;
; 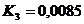 .
.
Напряжение
в точке 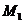 :
:
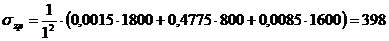 кПа
кПа
Для
точки 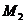 определяем коэффициенты
определяем коэффициенты 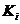 :
:
для
силы 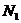 :
: 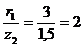 ;
; 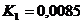 ;
;
-
для силы 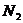 :
: 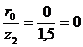 ;
; 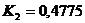 ;
;
-
для силы 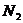 :
: 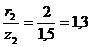 ;
; 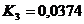 .
.
Напряжение
в точке 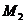 :
:
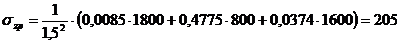 кПа
кПа
Для
точки 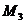 определяем коэффициенты
определяем коэффициенты 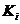 :
:
для
силы 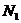 :
: 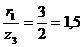 ;
; 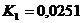 ;
;
-
для силы 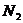 :
: 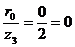 ;
; 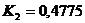 ;
;
-
для силы 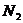 :
: 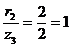 ;
; 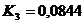 .
.
Напряжение
в точке 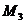 :
:
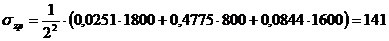 кПа
кПа
Для
точки 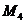 определяем коэффициенты
определяем коэффициенты 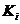 :
:
для
силы 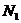 :
: 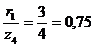 ;
; 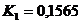 ;
;
-
для силы 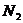 :
: 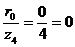 ;
; 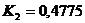 ;
;
-
для силы 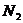 :
: 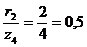 ;
; 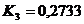 .
.
Напряжение
в точке 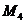 :
:
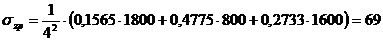 кПа
кПа
Для
точки 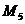 определяем коэффициенты
определяем коэффициенты 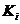 :
:
для
силы 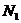 :
: 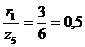 ;
; 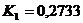 ;
;
-
для силы 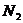 :
: 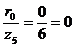 ;
; 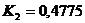 ;
;
-
для силы 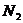 :
: 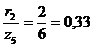 ;
; 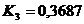 .
.
Напряжение
в точке 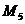 :
:
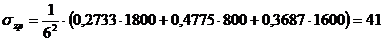 кПа
кПа
Строим
эпюру вертикальных напряжений, откладывая ординаты соответствующих напряжений в
точках на расчетной вертикали.
.
От совместного действия сосредоточенных сил в точках на горизонтали,
расположенной в плоскости действия сил, на расстоянии 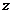 от поверхности.
от поверхности.
Для
точки 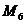 определяем коэффициенты
определяем коэффициенты 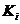 :
:
для
силы 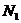 :
: 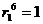 м;
м; 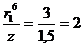 ;
; 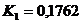 ;
;
-
для силы 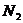 :
: 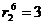 м;
м; 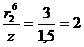 ;
; 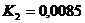 ;
;
-
для силы 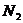 :
: 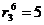 м;
м; 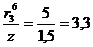 ;
; 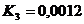 .
.
Напряжение
в точке 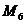 :
:
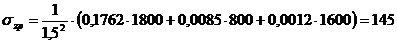 кПа
кПа
Для
точки 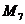 определяем коэффициенты
определяем коэффициенты 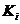 :
:
для
силы 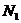 :
: 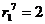 м;
м; 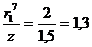 ;
; 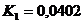 ;
;
-
для силы 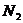 :
: 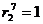 м;
м; 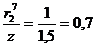 ;
; 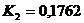 ;
;
-
для силы 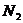 :
: 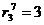 м;
м; 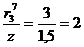 ;
; 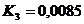 .
.
Напряжение
в точке 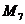 :
:
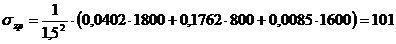 кПа
кПа
Для
точки 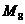 определяем коэффициенты
определяем коэффициенты 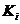 :
:
для
силы 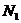 :
: 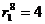 м;
м; 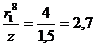 ;
; 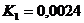 ;
;
-
для силы 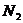 :
: 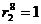 м;
м; 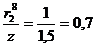 ;
; 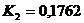 ;
;
-
для силы 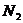 :
: 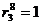 м;
м; 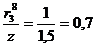 ;
; 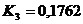 .
.
Напряжение
в точке 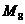 :
:
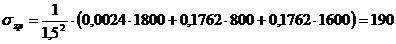 кПа
кПа
Для
точки 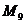 определяем коэффициенты
определяем коэффициенты 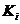 :
:
для
силы 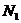 :
: 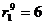 м;
м; 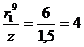 ;
; 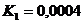 ;
;
-
для силы 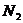 :
: 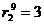 м;
м; 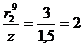 ;
; 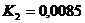 ;
;
-
для силы 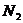 :
: 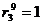 м;
м; 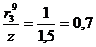 ;
; 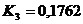 .
.
Напряжение
в точке 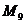 :
:
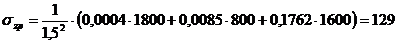 кПа
кПа
Строим
эпюру вертикальных напряжений, откладывая ординаты соответствующих напряжений в
точках на расчетной горизонтали (рисунок).
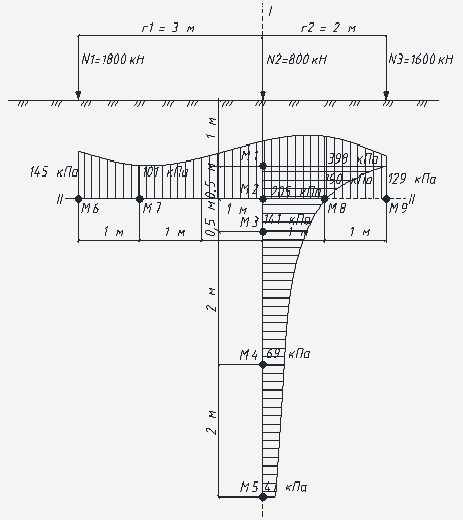
Рис.
Задача
2
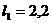 м;
м; 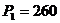 кПа;
кПа;
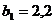 м;
м; 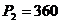 кПа;
кПа;
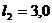 м;
м; 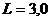 м;
м;
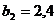 м; расчетная
вертикаль
м; расчетная
вертикаль 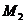 .
.
Определить
величины вертикальных составляющих напряжений в массиве грунта и построить
эпюры напряжений: от совместного действия равномерно распределенных по
площадкам нагрузок в точках на заданной вертикали.
Решение:
Заданные
плиты нагружения разбиваем на прямоугольники таким образом, чтобы они имели
общую угловую точку, через которую проходит расчетная вертикаль 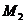 . Таким образом, имеем 8 прямоугольников:
. Таким образом, имеем 8 прямоугольников:
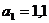 м;
м; 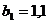 м;
м; 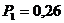 Мпа;
Мпа;
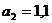 м;
м; 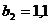 м;
м; 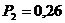 МПа;
МПа;
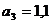 м;
м; 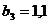 м;
м; 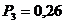 МПа;
МПа;
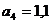 м;
м; 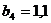 м;
м; 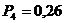 МПа;
МПа;
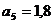 м;
м;  м;
м; 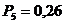 МПа;
МПа;
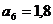 м;
м; 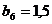 м;
м; 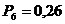 МПа;
МПа;
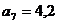 м;
м; 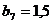 м;
м; 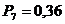 МПа;
МПа;
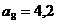 м;
м; 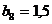 м;
м; 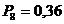 МПа
МПа
Искомые
напряжения найдем, суммируя напряжения от действия нагрузки по прямоугольникам
1, 2, 3, 4, 7, 8, взятых со знаком «плюс», и напряжения от действия нагрузки по
прямоугольникам 5, 6 со знаком «минус».
Точка
1, 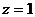 м:
м:
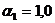 ;
; 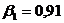 ;
; 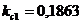 ;
;
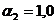 ;
; 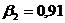 ;
; 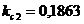 ;
;
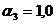 ;
;  ;
; 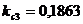 ;
;
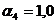 ;
; 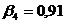 ;
; 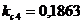 ;
;
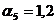 ;
; 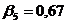 ;
; 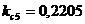 ;
;
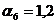 ;
; 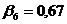 ;
; 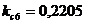 ;
;
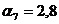 ;
; 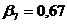 ;
; 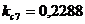 ;
;
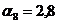 ;
; 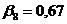 ;
; 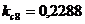
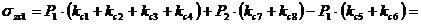
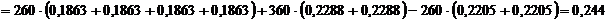 Мпа
Мпа
Точка
2, 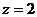 м:
м:
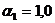 ;
; 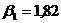 ;
; 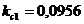 ;
;
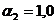 ;
; 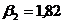 ;
; 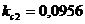 ;
;
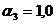 ;
; 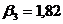 ;
; 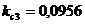 ;
;
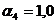 ;
; 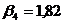 ;
; 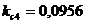 ;
;
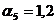 ;
; 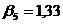 ;
; 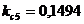 ;
;
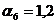 ;
;  ;
; 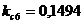 ;
;
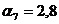 ;
; 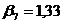 ;
; 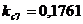 ;
;
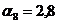 ;
; 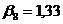 ;
; 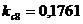

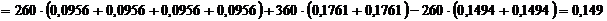 Мпа
Мпа
Точка
3,  м:
м:
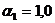 ;
; 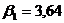 ;
; 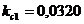 ;
;
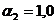 ;
; 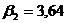 ;
; 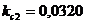 ;
;
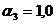 ;
; 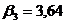 ;
; 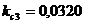 ;
;
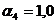 ;
; 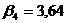 ;
; 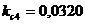 ;
;
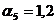 ;
; 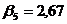 ;
; 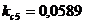 ;
;
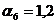 ;
; 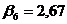 ;
; 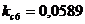 ;
;
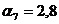 ;
; 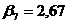 ;
; 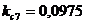 ;
;
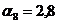 ;
; 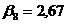 ;
; 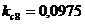
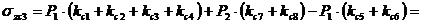
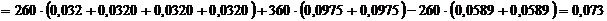 Мпа
Мпа
Точка
4, 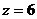 м:
м:
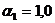 ;
; 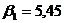 ;
; 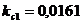 ;
;
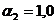 ;
; 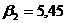 ;
; 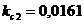 ;
;
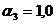 ;
; 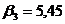 ;
; 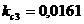 ;
;
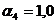 ;
; 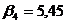 ;
; 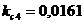 ;
;
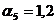 ;
; 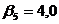 ;
; 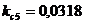 ;
;
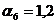 ;
; 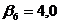 ;
; 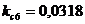 ;
;
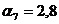 ;
; 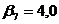 ;
;  ;
;
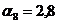 ;
; 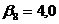 ;
; 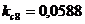
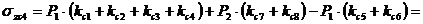
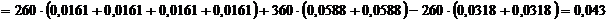 Мпа
Мпа
По
полученным значениям напряжений строим эпюру распределения напряжений sz
(рисунок).
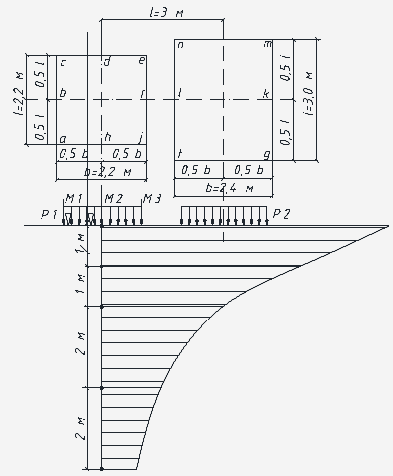
Рис.
Задача
3
Дано:
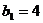 м;
м;
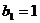 м;
м;
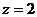 м;
м;
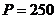 кПа;
кПа;
расчетная
вертикаль 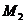 .
.
Определить
величины вертикальных составляющих напряжений в массиве грунта и построить
эпюры напряжений: от действия полосообразной нагрузки, изменяющейся по закону
прямой, в точках на расчетной и горизонтали, расположенной на расстоянии 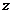 от поверхности.
от поверхности.
Решение:
Вертикальные
нормальные напряжения 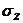 , возникающие в точках на горизонтальных площадках от
действия трапецеидальной полосовой нагрузки можно вычислить с помощью
номограммы Остербера и формуле:
, возникающие в точках на горизонтальных площадках от
действия трапецеидальной полосовой нагрузки можно вычислить с помощью
номограммы Остербера и формуле:
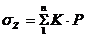
Р
- интенсивность равномерной нагрузки или же максимальная интенсивность
треугольной нагрузки.
п
- число треугольных и равномерно распределенных частей полосовой нагрузки.
точка
1:
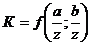
прямоугольник
треугольник
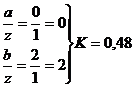
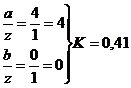
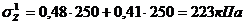
точка
2:
прямоугольник
треугольник
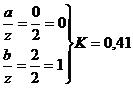

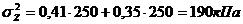
точка
3:
прямоугольник
треугольник
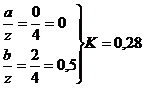
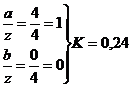
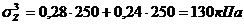
точка
4:
прямоугольник
треугольник
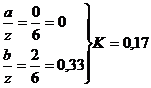
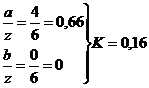
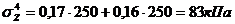
точка
5:
треугольник
прямоугольник
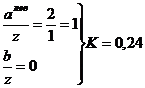
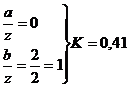
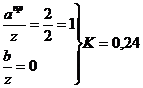
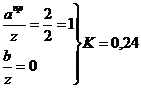
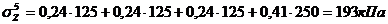
точка
6:
треугольник
прямоугольник
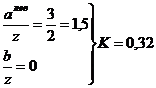
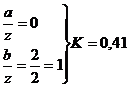


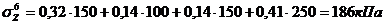
точка
7:
треугольник
прямоугольник
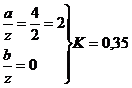
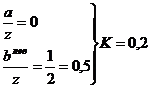
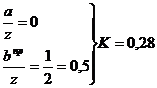
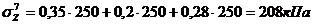
По
найденным значениям строим эпюры напряжений (рисунок).
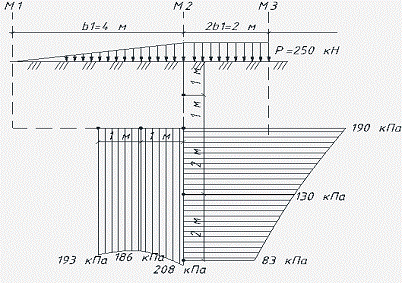
Рис.
Задача
4
Дано:
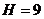 м;
м;
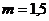 ;
;
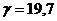 кН/м3;
кН/м3;
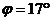 ;
;
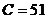 кПа.
кПа.
Определить
методом круглоцилиндрических поверхностей скольжения величину коэффициента
устойчивости откоса.
Решение:
Для
определения координат центра кривой скольжения вычисляем 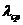 :
:
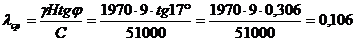
По
найденному значению 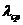 и углу
и углу 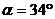 (
(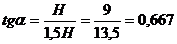 ) по графику Ямбу находим значения
) по графику Ямбу находим значения 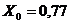 и
и 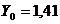 и
координаты центра вращения:
и
координаты центра вращения:
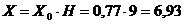 м;
м;
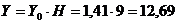 м
м
Из
найденного центра вращения через подошву откоса проводим дугу окружности
скольжения.
Разбиваем
оползневое тело на 5 блоков (рисунок), графически определяем их ширину и высоту
и производим вычисления необходимых данных, которые сводим в таблицу.
Таблица
|
Номер блока
|
Средняя высота блока, м
|
Ширина блока, м
|
Объем блока, м3
|
Вес блока 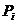 ,МнПлечо ,МнПлечо 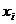 ,
мМомент ,
мМомент 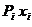 , Мн·м , Мн·м
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
2,57
|
10,74
|
0,212
|
4,18
|
-0,89
|
|
2
|
6,65
|
4,18
|
27,80
|
0,548
|
0,66
|
-0,36
|
|
3
|
9,48
|
4,18
|
39,63
|
0,781
|
3,52
|
2,75
|
|
4
|
8,55
|
4,18
|
35,74
|
0,704
|
7,71
|
5,43
|
|
5
|
4,53
|
4,18
|
18,94
|
0,362
|
11,89
|
4,3
|
Моменты
принимаются отрицательными для восходящей ветви скольжения. Для нисходящей
ветви кривой скольжения моменты положительные.
Определяем
величину коэффициента устойчивости откоса:
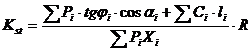 ,
,
где
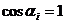 (согласно методическим указаниям);
(согласно методическим указаниям); 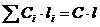 - для однородной толщи грунта.
- для однородной толщи грунта.
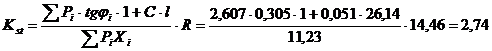
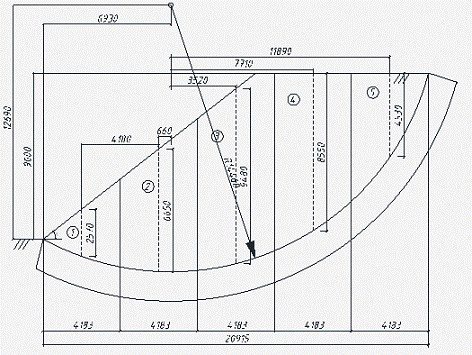
Рис.
Задача 5
Дано:
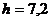 м;
м;
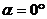 ;
;
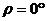 ;
;
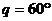 ;
;
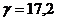 кН/м3;
кН/м3;
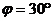 ;
;
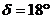 .
.
Определить горизонтальные составляющие интенсивности активного давления
грунта на подпорную стену, равнодействующую активного давления, указав ее
направление и точку приложения, построить эпюру распределения давления грунта.
Решение:
Горизонтальная
составляющая активного давления для связанного грунта на глубине 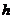 :
:
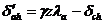 ,
,
где
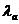 - коэффициент активного давления грунта,
- коэффициент активного давления грунта,  - давление связности.
- давление связности.
Определяем
коэффициент активного давления грунта:
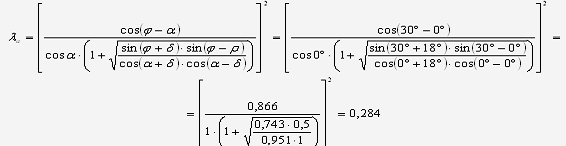
Определяем
давление связности:
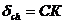 ,
,
где
коэффициент 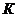 :
:
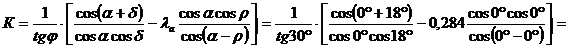
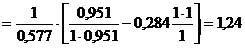
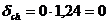 кПа
кПа
Определяем
значение горизонтальной составляющей активного давления грунта на нижней грани
подпорной стены 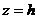 :
:
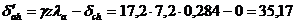 кПа
кПа
Определяем
равнодействующую горизонтального давления грунта для стены высотой 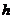 :
:
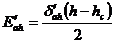 ,
,
где
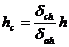 ;
;
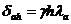 ;
;
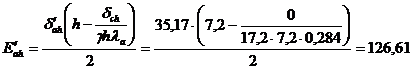 кПа
кПа
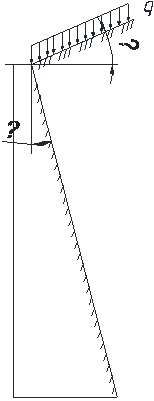
Задача
6
Дано:
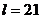 м;
м;
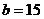 м;
м;
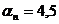 м;
м;
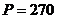 кПа;
кПа;
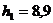 м;
м;
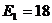 МПа;
МПа;
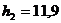 м;
м;
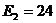 Мпа.
Мпа.
Определить
среднюю осадку основания сплошной фундаментной плиты, загруженной равномерно
распределенной нагрузкой. Плита опирается на слой песка, подстилаемый
пылевато-глинистым грунтом. Расчет осадки выполнить, применяя расчетную схему
основания в виде линейно-деформируемого слоя.
Решение:
Расчетную
толщину слоя определяем для двух случаев: основание сложено только песчаными и
только пылевато-глинистыми грунтами.
При
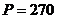 кПа
кПа 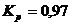 (по
интерполяции)
(по
интерполяции)
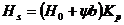 ;
;
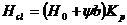 ,
,
где
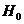 и
и 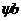 принимаются
соответственно равными для оснований, сложенных пылевато-глинистыми грунтами 9
м и 0,15; песчаными грунтами - 6 м и 0,1.
принимаются
соответственно равными для оснований, сложенных пылевато-глинистыми грунтами 9
м и 0,15; песчаными грунтами - 6 м и 0,1.
 м;
м;
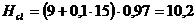 м;
м;
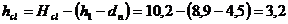 м
м
Тогда
для основания, сложенного пылевато-глинистыми и песчаными грунтами:
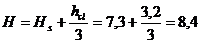 м
м
При
известном значении 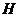 осадка основания определяется по формуле:
осадка основания определяется по формуле:
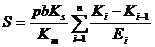 ,
,
где
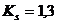 , так как
, так как 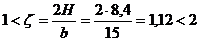 (по
табл. 7 приложения);
(по
табл. 7 приложения); 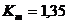 , так как
, так как 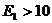 Мпа и
Мпа и 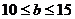 м (по табл. 8 приложения).
м (по табл. 8 приложения).
Коэффициент
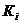 :
:
-
при 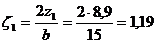 ;
; 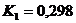 ;
;
-
при 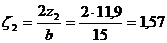 ;
; 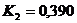
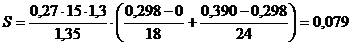 м = 7,9
см
м = 7,9
см
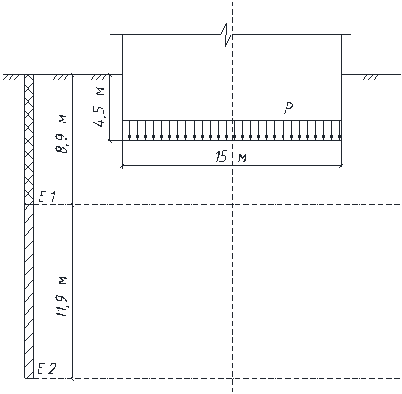
Рис.
Задача
7
Дано:
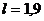 м;
м;
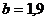 м;
м;
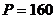 кПа;
кПа;
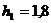 м;
м;
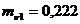 МПа;
МПа;
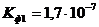 см/с;
см/с;
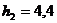 м;
м;
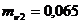 МПа;
МПа;
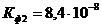 см/с.
см/с.
Определить
полную стабилизированную осадку основания абсолютно жесткого фундамента,
изменение осадки во времени. Расчет осадки выполнить, применяя метод
эквивалентного слоя грунта. Построить график изменения осадок основания во
времени.
Решение:
При
отношении сторон площади подошвы 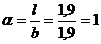 по табл.
12 приложения, при
по табл.
12 приложения, при 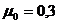 находим:
находим:
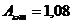
Тогда
мощность эквивалентного слоя грунта:
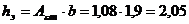 м
м
Высота
эквивалентной эпюры уплотняющих давлений:
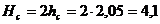 м
м
По
профилю напластований грунтов определяем расстояние 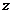 от середины каждого слоя до глубины
от середины каждого слоя до глубины 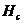 :
:
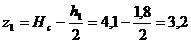 м;
м;
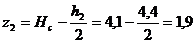 м
м
Средний
коэффициент относительной сжимаемости:
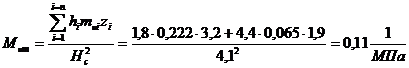
Тогда
полная стабилизированная осадка фундамента:
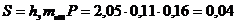 м = 4 см
м = 4 см
Определяем
средний коэффициент фильтрации:
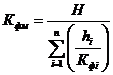 ,
,
где
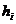 - толщина i-го слоя грунта, находящегося в
пределах
- толщина i-го слоя грунта, находящегося в
пределах 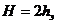
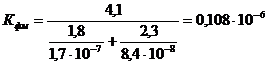 м/с
м/с
Определяем
коэффициент консолидации:
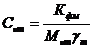 ,
,
где
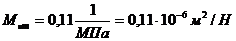 ;
; 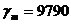 Н/м3
- удельный вес воды
Н/м3
- удельный вес воды
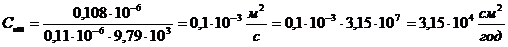
Для
вычисления осадок для любого времени ( 1, 3, 5,
10 лет) используем формулу:
1, 3, 5,
10 лет) используем формулу:
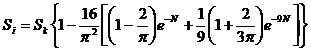 ,
,
где
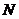 - величина в условиях односторонней фильтрации
отжимаемой воды, определяем из выражения:
- величина в условиях односторонней фильтрации
отжимаемой воды, определяем из выражения:
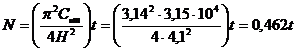
Определяем
осадки, соответствующие:
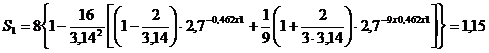 см
см
Для
последующих вычислений ограничимся первым членом ряда, стоящего в квадратных
скобках.
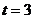 года
года
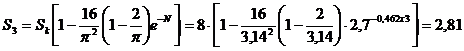 см
см
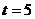 лет
лет
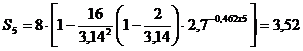 см
см
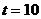 лет
лет
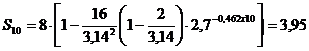 см
см
Строим
график изменения осадок во времени (рисунок).
вертикальный массив
грунт
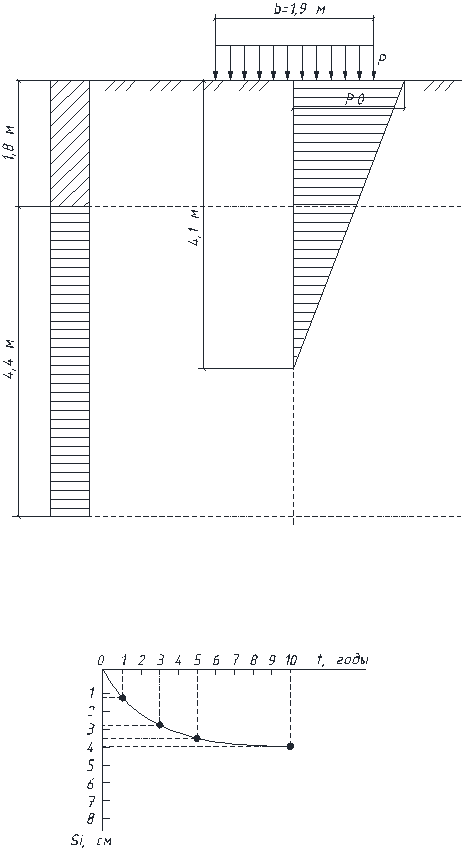
Рис.
1.