Изучение показательной и логарифмической функции в школьном курсе математики
Содержание
Введение
1. Теоретические основы изучения показательной и
логарифмической функций в школьном курсе математики
1.1
Анализ учебников
.2
Основные понятия, связанные с понятиями показательной и логарифмической функций
в школьном курсе математики
.3
Анализ результатов ЕГЭ 2012-2013 гг.
.
Решение задач с использованием логарифмической и показательной функции в
школьном курсе математики
.1
Обзор задач и упражнений на решение показательной логарифмической функций в
школьном курсе математики
.2
Методика решения типовых задач, связанных с показательной и логарифмической
функциями, в школьном курсе математики
.3
Подбор задач на нахождение и использование показательной и логарифмической
функций в школьном курсе математики
Заключение
Список
использованных источников
Введение
Изучение различных преобразований выражений и
формул занимает значительную часть учебного времени в курсе школьной
математики. Простые преобразования, опирающиеся на свойства арифметических
операций, производятся уже в начальной школе и в IV-V классах. Но основная
нагрузка по формированию умений и навыков выполнения преобразований приходится
на школьный курс алгебры. Связано это как с быстрым увеличением числа и
разнообразия совершаемых преобразований, так и с усложнением деятельности по их
доказательству и выяснению условий применимости, с выделением и изучением
понятий, преобразований. Данная исследовательская работа в области алгебры и
начала анализа на тему "Изучение показательной и логарифмической функции в
школьном курсе математики".
Большой вклад в разработку данной
темы внес математик и механик - Леонард Эйлер. Близкое к современному понимание
логарифмирования - как операции, обратной возведению в степень
<#"882814.files/image001.gif">,
где 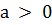 и
и
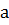
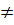 1,
называют показательной функцией.
1,
называют показательной функцией.
Основные свойства показательной функции
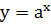 :
:
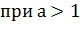 :
:
1) 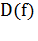 =
=
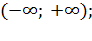
2) 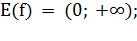
) возрастает
) непрерывна;
при 0 < 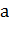 < 1:
< 1:
) 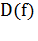 =
=
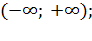
) 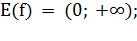
3) убывает;
) непрерывна.
График функции
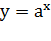 ,
,
где 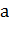 > 1 изображен
на рисунке 1.
> 1 изображен
на рисунке 1.
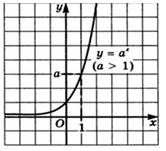
Рисунок 1 График функции
График функции 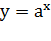 , где
, где 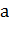 >
1
>
1
График функции 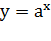 ,
где
,
где 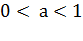 изображен
на рисунке 2.
изображен
на рисунке 2.
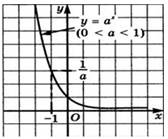
Рисунок 2 График функции
График функции 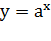 , где
, где 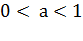
Кривую, изображенную на рисунке 1 или 2,
называют экспонентой. Впрочем, экспонентой называют и саму показательную
функцию 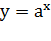 .
Так что термин "экспонента" используется в двух смыслах: и для
наименования показательной функции, и для названия графика показательной
функции. Обратите внимание на геометрическую особенность графика показательной
функции
.
Так что термин "экспонента" используется в двух смыслах: и для
наименования показательной функции, и для названия графика показательной
функции. Обратите внимание на геометрическую особенность графика показательной
функции 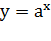 :
ось х является горизонтальной асимптотой графика функции
:
ось х является горизонтальной асимптотой графика функции 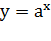 при
при
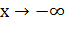 ,
если
,
если 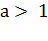 и
при
и
при 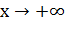 ,
если
,
если 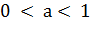 .
.
Школьники часто путают термины: "степенная
функция" и "показательная функция". Сравните:
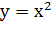 ,
,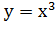 ,
,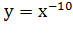 ,
,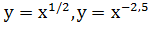 -
это примеры степенных функций.
-
это примеры степенных функций.
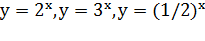 - это примеры
показательных функций.
- это примеры
показательных функций.
Вообще
математика показательный
логарифмический функция
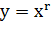 ,
,
где 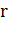 - конкретное
число, - степенная функция (аргумент х содержится в основании степени);
- конкретное
число, - степенная функция (аргумент х содержится в основании степени);
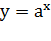 ,
,
где 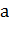 - конкретное число
(положительное и отличное от 1), называется показательной функцией (аргумент х
содержится в показателе степени).
- конкретное число
(положительное и отличное от 1), называется показательной функцией (аргумент х
содержится в показателе степени).
А такую "экзотическую" функцию, как 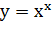 ,
не считают ни показательной, ни степенной (ее иногда называют
показательно-степенной).
,
не считают ни показательной, ни степенной (ее иногда называют
показательно-степенной).
Основные свойства показательной функции
. Если 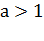 ,
то равенство
,
то равенство 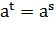 справедливо тогда
и только тогда, когда
справедливо тогда
и только тогда, когда 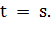
. Если 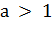 ,
то неравенство
,
то неравенство 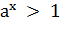 справедливо тогда
и только тогда, когда
справедливо тогда
и только тогда, когда 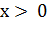 (рис. 3);
неравенство
(рис. 3);
неравенство 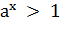 справедливо тогда
и только тогда, когда
справедливо тогда
и только тогда, когда 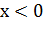 .
.
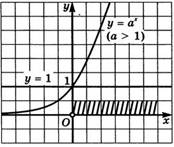
Рисунок 3 График функции
График функции 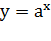
. Если 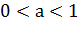 ,
то равенство
,
то равенство 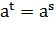 справедливо тогда
и только тогда, когда
справедливо тогда
и только тогда, когда 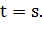
. Если 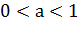 ,
то неравенство
,
то неравенство 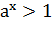 справедливо тогда
и только тогда, когда
справедливо тогда
и только тогда, когда 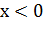 (рис. 4);
неравенство
(рис. 4);
неравенство 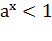 справедливо тогда
и только тогда, когда
справедливо тогда
и только тогда, когда 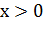 .
.
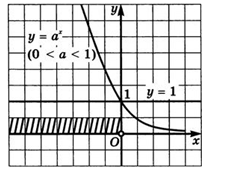
Рисунок 4 График функции
График функции 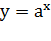
Показательными уравнениями называют уравнения
вида 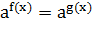 ,
где
,
где 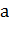 -
положительное число, отличное от 1, и уравнения сводящиеся к этому виду.
-
положительное число, отличное от 1, и уравнения сводящиеся к этому виду.
Основные свойства:
. Показательное уравнение 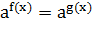 (где
(где
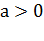 ,
,
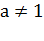 )
равносильно уравнению
)
равносильно уравнению 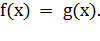
. Показательными неравенствами называют
неравенства вида 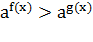 , где а -
положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.
, где а -
положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.
. Если 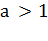 ,
то показательное неравенство
,
то показательное неравенство 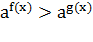 равносильно
неравенству того же смысла:
равносильно
неравенству того же смысла: 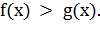 Если
Если 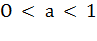 ,
то показательное неравенство
,
то показательное неравенство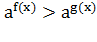 равносильно
неравенству противоположного смысла: f
равносильно
неравенству противоположного смысла: f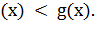
Логарифмом положительного числа 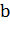 по
положительному и отличному от 1 основанию
по
положительному и отличному от 1 основанию 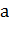 называют
показатель степени, в которую нужно возвести число а, чтобы получить число
называют
показатель степени, в которую нужно возвести число а, чтобы получить число 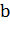 .
.
Свойства логарифма:
) 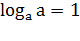
) 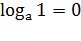
) 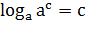
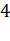 )
)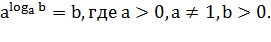
Логарифм по основанию 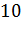 обычно
называют десятичным логарифмом и обозначают как
обычно
называют десятичным логарифмом и обозначают как 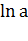 .
.
Функция 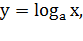 её
свойства и график.
её
свойства и график.
График функции 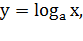 симметричен
графику функции
симметричен
графику функции 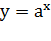 относительно
прямой
относительно
прямой 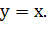
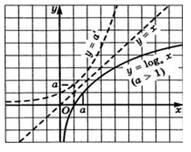
Рисунок 5 График функции
График функции 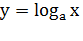
Свойства функции 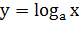 ,
,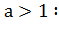
) 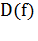 =
=
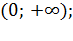
) не является ни четной, ни нечетной;
3) возрастает на (0; +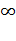 );
);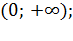
) не ограничена сверху, не
ограничена снизу;
) не имеет ни наибольшего, ни
наименьшего значений;
) непрерывна;
) 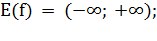
) выпукла вверх.
На рисунке 6 схематически изображены
графики функций 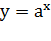 и
и 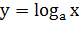 в случае,
когда
в случае,
когда 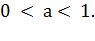
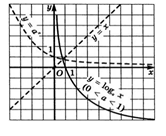
Рисунок 6 График
функции
График
функции 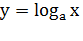
Свойства функции 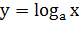 ,
,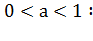
) 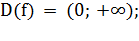
) не является ни четной, ни
нечетной;
) убывает на (0; +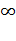 );
);
) не ограничена сверху, не
ограничена снизу;
) не имеет ни наибольшего, ни
наименьшего значений;
) непрерывна;
) 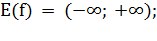
) выпукла вниз.
Отметим, что ось 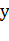 является
вертикальной асимптотой графика логарифмической функции и в случае, когда
является
вертикальной асимптотой графика логарифмической функции и в случае, когда 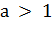 , и в
случае, когда 0 <
, и в
случае, когда 0 <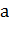 <1.
<1.
Свойства логарифмов:
1) 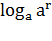
2) 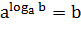
3) 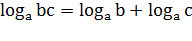
4) 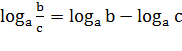 ,
,
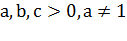
5) 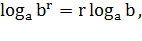
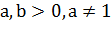
6) 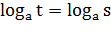 ,
,
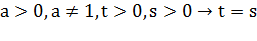
Все свойства формулируются и доказываются только
для положительных значений переменных, содержащихся под знаками логарифмов.
Логарифмическими уравнениями называются уравнения вида
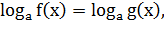
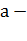 положительное
число, отличное от 1,и уравнения, сводящиеся к этому виду. Если
положительное
число, отличное от 1,и уравнения, сводящиеся к этому виду. Если 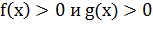 ,
то логарифмическое уравнение
,
то логарифмическое уравнение 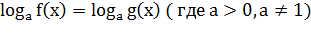 равносильно
уравнению
равносильно
уравнению 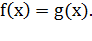
Логарифмическими неравенствами называются
неравенства вида
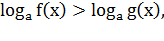
где 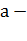 положительное
число, отличное от 1, и неравенства, сводящиеся к этому виду.
положительное
число, отличное от 1, и неравенства, сводящиеся к этому виду.
Если 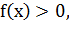 и
и
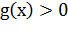 ,
то: при
,
то: при 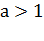 логарифмическое
неравенство
логарифмическое
неравенство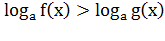 равносильно
неравенству того же смысла:
равносильно
неравенству того же смысла: 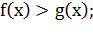 при
при 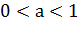 логарифмическое
неравенство
логарифмическое
неравенство
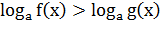 равносильно
неравенству противоположного смысла:
равносильно
неравенству противоположного смысла: 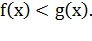
Перейдем к новому основанию логарифма. Если 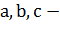 положительные
числа, причем
положительные
числа, причем 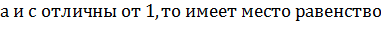 .
.
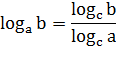
Если 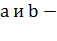 положительные
и отличные от 1 числа, то справедливо
положительные
и отличные от 1 числа, то справедливо
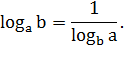
Если 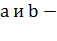 положительные
числа, причем
положительные
числа, причем 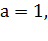 то для любого
числа
то для любого
числа 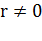 справедливо
справедливо
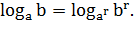
Дифференцирование показательной и
логарифмической функций.
Число 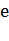 . Функция
. Функция 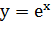 ,
её свойства, график, дифференцирование.
,
её свойства, график, дифференцирование.
Рассмотрим показательную функцию 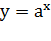 ,
где
,
где 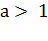 .
Для различных оснований
.
Для различных оснований 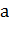 получаем различные
графики, но можно заметить, что все они проходят через точку
получаем различные
графики, но можно заметить, что все они проходят через точку 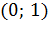 ,
все они имеют горизонтальную асимптоту
,
все они имеют горизонтальную асимптоту 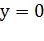 при
при
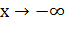 ,
все они обращены выпуклостью вниз и, наконец, все они имеют касательные во всех
своих точках.
,
все они обращены выпуклостью вниз и, наконец, все они имеют касательные во всех
своих точках.
Проведем для примера касательную к графику
функции 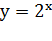 в
точке
в
точке 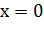 ,
рассмотренную на рисунке 7.
,
рассмотренную на рисунке 7.
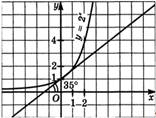
Рисунок 7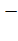 Касательная к графику функции
Касательная к графику функции 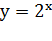
Если сделать аккуратные построения и измерения,
то можно убедиться в том, что эта касательная образует с осью 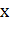 угол
35°. Теперь проведем касательную к графику функции
угол
35°. Теперь проведем касательную к графику функции 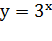 тоже
в точке
тоже
в точке 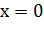 ,
которая изображена на рисунке 8.
,
которая изображена на рисунке 8.
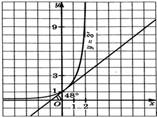
Рисунок 8  Касательная
к графику функции
Касательная
к графику функции 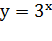
Здесь угол между касательной и осью х будет
больше 48°. А для показательной функции 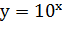 в
аналогичной ситуации получаем угол примерно 66,5°, изображенный на рисунке 9.
в
аналогичной ситуации получаем угол примерно 66,5°, изображенный на рисунке 9.
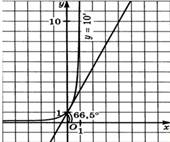
Рисунок 9 График функции
График функции 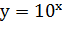
Итак, если основание а показательной функции 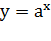 постепенно
увеличивается от 2 до 10, то угол между касательной к графику функции в точке
постепенно
увеличивается от 2 до 10, то угол между касательной к графику функции в точке 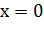 и
осью абсцисс постепенно увеличивается от 35° до 66,5°. Логично предположить,
что существует основание
и
осью абсцисс постепенно увеличивается от 35° до 66,5°. Логично предположить,
что существует основание 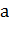 , для которого
соответствующий угол равен 45°. Это основание должно быть заключено между
числами 2 и 3, поскольку для функции
, для которого
соответствующий угол равен 45°. Это основание должно быть заключено между
числами 2 и 3, поскольку для функции 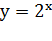 интересующий
нас угол равен 35°, что меньше, чем 45°, а для функции
интересующий
нас угол равен 35°, что меньше, чем 45°, а для функции 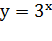 он
равен 48°, что уже немного больше, чем 45°. Доказано, что интересующее нас
основание действительно существует, его принято обозначать буквой
он
равен 48°, что уже немного больше, чем 45°. Доказано, что интересующее нас
основание действительно существует, его принято обозначать буквой 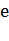 .
Установлено, что число
.
Установлено, что число 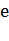 - иррациональное,
то есть представляет собой бесконечную десятичную непериодическую дробь:
- иррациональное,
то есть представляет собой бесконечную десятичную непериодическую дробь:
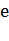 =
= 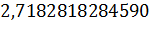 ...
;
...
;
на практике обычно полагают, что 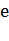
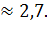
Графиком функции 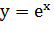 изображен
на рисунке 10. Это экспонента, отличающаяся от других экспонент (график
показательных функций с другими основаниями) тем, что угол между касательной к
графику в точке
изображен
на рисунке 10. Это экспонента, отличающаяся от других экспонент (график
показательных функций с другими основаниями) тем, что угол между касательной к
графику в точке 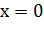 и осью абсцисс
равен 45
и осью абсцисс
равен 45 .
.
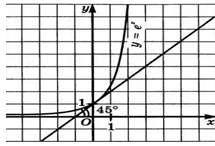
Рисунок 10 Касательная к графику функции
Касательная к графику функции 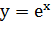
Свойства функции 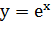 :
:
) 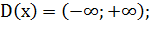
) не является ни четной, ни нечетной;
) возрастает;
) не ограничена сверху, ограничена снизу;
) не имеет ни наибольшего, ни наименьшего
значений;
) непрерывна;
) выпукла вниз.
В курсе математического анализа доказано, что
функция 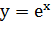 имеет
производную в любой точке
имеет
производную в любой точке 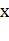 , причем
, причем
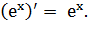
Натуральные логарифмы. Функция 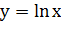 ,
её свойства, график, дифференцирование
,
её свойства, график, дифференцирование
Если основанием логарифма служит число 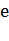 ,
то говорят, что задан натуральный логарифм.
,
то говорят, что задан натуральный логарифм.
Мы знаем, что график логарифмической функции 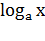 симметричен
графику показательной функции
симметричен
графику показательной функции 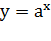 относительно прямой
относительно прямой
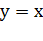 .
Значит, и график функции
.
Значит, и график функции 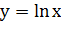 симметричен
графику функции
симметричен
графику функции 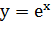 относительно
прямой
относительно
прямой 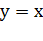 ,
изображенный на рисунке 11. Это экспонента, отличающаяся от других экспонент
(графиков логарифмических функций с другими основаниями) тем, что угол между
касательной к графику в точке
,
изображенный на рисунке 11. Это экспонента, отличающаяся от других экспонент
(графиков логарифмических функций с другими основаниями) тем, что угол между
касательной к графику в точке 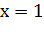 и осью абсцисс равен
45°.
и осью абсцисс равен
45°.
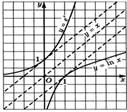
Рисунок 11  Симметрия графиков
Симметрия графиков
Свойства функции 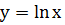 :
:
) 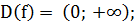
) не является ни четной, ни нечетной;
) возрастает на (
) не ограничена ни сверху, ни снизу;
) не имеет ни наибольшего, ни наименьшего
значений;
) непрерывна;
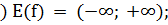
) выпукла вверх;
) дифференцируема.
В курсе математического анализа доказано, что
для любого значения 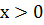 справедлива
формула дифференцирования
справедлива
формула дифференцирования
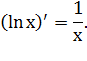
Формулы дифференцирования любой показательной и
любой логарифмической функции:
) (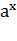 )'
=
)'
= 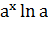 ;
;
) (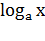 )'
)'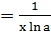 [1, с.
232-272].
[1, с.
232-272].
1.3 Анализ результатов ЕГЭ 2012-2013 гг.
В 2012 году экзамен по математике сдавали 25133
(без учета выпускников прошлых лет). Не преодолели порог успешности 1168
человек, что составляет 4,6% от общей численности выпускников, это на 0,8%
больше чем в прошлом году в нашем крае, что объясняется тем, что в 2012 году
произошло увеличение с 4 до 5 минимального числа заданий, которые необходимо
верно выполнить для достижения порога успешности. Процент учащихся,
изображенный на рисунке 1, в крае не преодолевших порог успешности в 2012 г. на
2,9% меньше чем в среднем по Росси (7,5%). В 2012 году около половины школ края
(458 из 952) сдали ЕГЭ по математике без двоек.
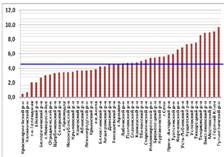
Рисунок 1 Распределение неудовлетворительных оценок на ЕГЭ-2012 по математике в
территориях края
Распределение неудовлетворительных оценок на ЕГЭ-2012 по математике в
территориях края
Самый большой прирост среднего балла в этом году
продемонстрировали выпускники Отрадненского района и заняли 4-е место, а еще в
2009 году этот район занимал последнее место в рейтинге территорий края.
Значительно вырос средний бал в Северском и
Успенском районах. И не смотря на то, что результаты этого года в данных
территориях все ещё ниже среднего по краю, для Северского и Успенского районов
налицо положительная динамика результатов работы. Это свидетельствует об
организованной системе мер по повышению качества обученности.
В тоже время, не смотря на то, что единая
технология подготовки к ЕГЭ департаментом образования и науки совместно с
ККИДППО распространялась на весь край, следует отметить территории, которые
подготовили своих учащихся к ЕГЭ не качественно.
Сигналом, что в территории есть проблемы с
подготовкой к ЕГЭ по математике были результаты краевых диагностических работ
(КДР). После детального анализа результатов КДР территориям оказывалась
методическая помощь по заказу территории. Однако результаты КДР в Выселковском,
Гулькевическом, и Кущевском районах не предвещали низких результатов на ЕГЭ,
они были средними или выше среднего по краю. Это свидетельствует либо о не
правильной организации проведения работ, либо о фальсификации их результатов.
В 2012 году на ЕГЭ по математике в нашем крае
было использовано 18 вариантов, в таблице 1 приведены средние значения процента
выполнения каждого задания по исследуемой теме.
Таблица 1 Средний
процент выполнения заданий
Средний
процент выполнения заданий
|
Номер
задания
|
В5
|
В7
|
|
Средний
процент выполнения заданий
|
84
|
58
|
|
Миним.
|
73
|
53
|
|
Максим.
|
91
|
63
|
Наилучшие результаты по выполнению заданий
первой части учащиеся нашего края показали при выполнении задания В5. Хуже
всего выпускники 2012 года справились с выполнением заданий В7, это можно
увидеть на рисунке 2. При выполнении заданий повышенного и высокого уровне
сложности выпускники 2012 года показали лучше результат по заданию С3 и хуже
справились с решением задания С5. На рисунке 3 приведен средний балл выполнения
заданий 2 ой
части.
ой
части.
Рисунок 2 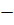 Процент
выполнения заданий 1-й части ЕГЭ-2012 по математике
Процент
выполнения заданий 1-й части ЕГЭ-2012 по математике
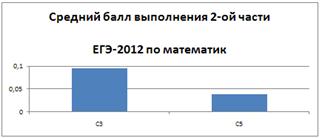
Рисунок 3 Средний балл выполнения заданий 2-й части ЕГЭ-2012 по математике
Средний балл выполнения заданий 2-й части ЕГЭ-2012 по математике
Все варианты КИМ включали задание на тождественное
преобразование выражений, содержащих степени и логарифмы (В7). В каждом
варианте ЕГЭ-2012 содержалось только одно задание непосредственно на
преобразование выражений. При выполнении этого задания учащимся необходимо было
применить основное тригонометрическое тождество с учетом знаков
тригонометрических функций по четвертям. Средний процент выполнения этого
задания оставил 58%. Следует отметить, что в 2011 году с таким же заданием в
среднем справилось 55% выпускников края.
При решении других заданий первой части
преобразований выражений не требовалось. Однако элементом решения задачи С3 и
С5 было преобразование логарифмических, показательных и степенных выражений. В
вариантах КИМ-2012 из всех видов уравнений, рассматриваемых в школьном курсе математики,
в первой части работы были представлены только логарифмические уравнения
(задания В5). Средний процент выполнения этих заданий составил 84,3%. При этом
задания "Найдите корень
уравнения 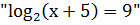 наши выпускники
выполнили на 73%, задание "Найдите
корень уравнения
наши выпускники
выполнили на 73%, задание "Найдите
корень уравнения 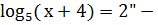 на 91%. Идея
решения этих уравнений совершенно одинакова, разница лишь в проводимых
вычислениях [7, с. 1-26].
на 91%. Идея
решения этих уравнений совершенно одинакова, разница лишь в проводимых
вычислениях [7, с. 1-26].
Теперь сравним результаты выполнения заданий В5,
В7, С3, С5, приведенные в таблицах 2 и 3.
Таблица 2  Результаты
выполнения учащимися заданий В5, В7 КИМов ЕГЭ за два года
Результаты
выполнения учащимися заданий В5, В7 КИМов ЕГЭ за два года
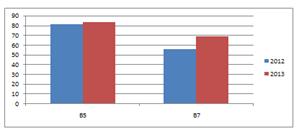
Таблица 3 Результаты выполнения учащимися заданий С3, С5 КИМов ЕГЭ за два года
Результаты выполнения учащимися заданий С3, С5 КИМов ЕГЭ за два года
|
Год
|
Количество
баллов
|
С3
|
С5
|
|
2012
|
0
|
87
|
96
|
|
2013
|
|
85,7
|
92,6
|
|
2012
|
1
|
9
|
|
2013
|
|
8,2
|
2,9
|
|
2012
|
2
|
1
|
0
|
|
2013
|
|
0,7
|
1,6
|
|
2012
|
3
|
3
|
0
|
|
2013
|
|
5,4
|
0,9
|
|
2012
|
4
|
|
1
|
|
2013
|
|
|
2
|
Задачи второй части остаются по-прежнему очень
сложными для выпускников, о чем свидетельствуют статистические данные. При
подготовке учащихся к сдаче ЕГЭ по математике целесообразно познакомить их с
опубликованными вариантами работ, критериями оценивания заданий С3 и С5, а так
же вести исчерпывающий разбор типичных ошибок, выявлять их природу и происхождение,
так как без этого нельзя обеспечить эффективные средства исправления и
предупреждения ошибок в будущем.
2. Решение задач с использованием
логарифмической и показательной функции в школьном курсе математики
.1 Обзор задач и упражнений на решение
показательной логарифмической функций в школьном курсе математики
. Решите уравнения и неравенства:
) 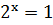 ;
;
Ответ: 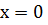 [1,
с. 239].
[1,
с. 239].
) 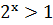 ;
;
Ответ: 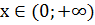 [1,
с. 240].
[1,
с. 240].
3) 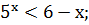
Ответ: 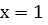 [1,
с.
243].
[1,
с.
243].
4) 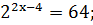
Ответ: 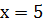 [1,
с. 244].
[1,
с. 244].
. Решите уравнение
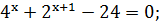
Ответ: 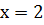 [1,
с. 245].
[1,
с. 245].
. Решите систему уравнений
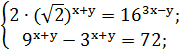
Ответ: 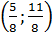 [1,
с. 246].
[1,
с. 246].
. Решите неравенство
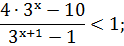
Ответ: 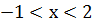 [1,
с. 248].
[1,
с. 248].
. Вычислите:
а) 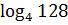 ;
;
Ответ: 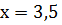 [1,
с. 250].
[1,
с. 250].
б) 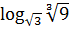 ;
;
Ответ: 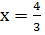 [1,
с. 251].
[1,
с. 251].
в) 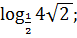
Ответ: 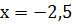 [1,
с. 251].
[1,
с. 251].
. Найдите наименьшее и наибольшее значения
функции на заданном промежутке:
а) 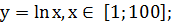
Ответ: 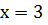 [1,
с. 254].
[1,
с. 254].
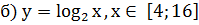 ;
;
Ответ: 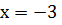 [1,
с. 254].
[1,
с. 254].
. Постройте график функции
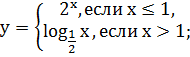
Ответ: смотрите рисунок 1 [1,
с. 256].
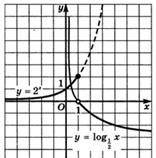
Рисунок 1- График функций
. Известно, что положительные числа 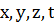 связаны
соотношением
связаны
соотношением 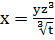 . Выразить
. Выразить 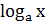 (
(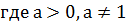 )
через логарифмы по основанию
)
через логарифмы по основанию 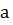 чисел
чисел 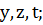
Ответ:
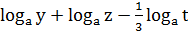 [1, с. 259].
[1, с. 259].
9. Решите уравнение
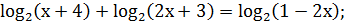
Ответ: 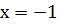 [1,
с.
264].
[1,
с.
264].
. Решите уравнение 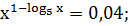
Ответ: 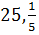 [1,
с. 265].
[1,
с. 265].
. Решите неравенство 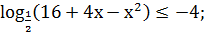
Ответ: 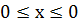 [1,
с.
269].
[1,
с.
269].
Ответ: 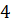 [1,
с. 272].
[1,
с. 272].
. Вычислить значение производной функции 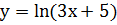 в
точке
в
точке 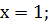
Ответ: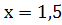 [1, с. 278].
[1, с. 278].
. Исследовать на экстремум функцию
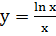 ;
;
Ответ: 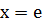 [1,
с. 279].
[1,
с. 279].
2.2 Методика решения типовых задач, связанных с
показательной и логарифмической функциями, в школьном курсе математики
1. Решите
уравнение
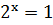 .
.
Решение. Построив в одной системе координат
графики функций 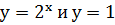 , замечаем, что они
имеют одну общую точку
, замечаем, что они
имеют одну общую точку 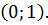 Значит, уравнение
Значит, уравнение 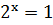 имеет
единственный корень
имеет
единственный корень 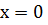 [1, с. 256].
[1, с. 256].
2. Решите
уравнение
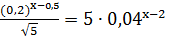 [10, с. 1].
[10, с. 1].
Решение. Здесь есть возможность и левую и правую
части уравнения представить в виде степени с основанием 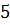 .
В самом деле:
.
В самом деле:
1) 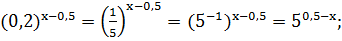
) 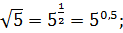
) 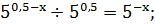
4) 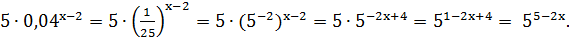
Таким образом, заданное уравнение мы
преобразовали к виду
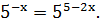
Далее получаем:
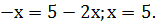
3. Решите
неравенство
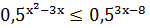 [10, с. 4].
[10, с. 4].
Решение. Заданное неравенство равносильно
неравенству противоположного смысла
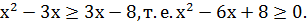
Найдем корни квадратного трехчлена
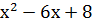 :
:
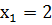 ,
, 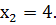
Значит, неравенство 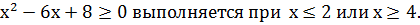
4. Вычислить
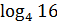 [1,
с.
260].
[1,
с.
260].
Решение. Пусть 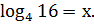 Тогда,
по определению логарифма,
Тогда,
по определению логарифма, 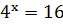 . Решая это
показательное уравнение, последовательно находим:
. Решая это
показательное уравнение, последовательно находим:
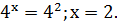
5. Найдите
наименьшее и наибольшее значения функции на заданном промежутке
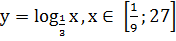 [10, с. 5].
[10, с. 5].
Решение. Функция 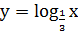 непрерывная
и убывающая, поскольку основание этой логарифмической функции, т.е. число
непрерывная
и убывающая, поскольку основание этой логарифмической функции, т.е. число  ,
меньше
,
меньше 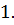 Следовательно,
своих наибольшего и наименьшего значений функция достигает на концах заданного
отрезка
Следовательно,
своих наибольшего и наименьшего значений функция достигает на концах заданного
отрезка 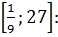
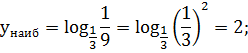
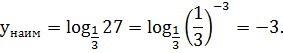
6. Вычислите
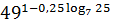 [10,
с.
6].
[10,
с.
6].
Решение. Поработаем с показателем степени:
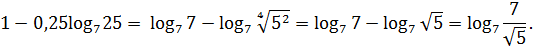
Теперь заданное числовое выражение мы можем
записать в виде 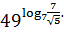 .
.
Далее находим:
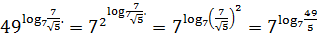 .
.
Остается вспомнить, что 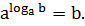 Значит,
Значит,
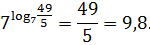
7. Решить
систему уравнений
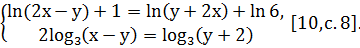
Решение. Преобразуем первое уравнение системы к
более простому виду:
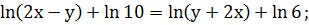
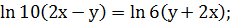
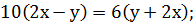
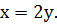
Преобразуем второе уравнение системы к более
простому виду:
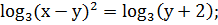
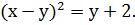
Решим полученную систему уравнений
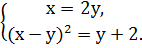
Подставив 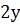 вместо
вместо
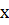 во
второе уравнение системы, получим:
во
второе уравнение системы, получим:
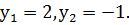
Из соотношения 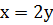 находим
соотношение:
находим
соотношение:
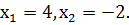
Осталось сделать проверку найденных пар 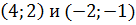 с
помощью условий, которые задают область допустимых значений переменных
с
помощью условий, которые задают область допустимых значений переменных 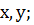 эти
условия мы находим, анализируя исходную систему уравнений. Пара (
эти
условия мы находим, анализируя исходную систему уравнений. Пара (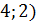 удовлетворяет условиям, а пара
удовлетворяет условиям, а пара 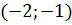 не удовлетворяет.
не удовлетворяет.
Ответ: (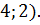
8. Решите
систему неравенств
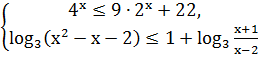 .
.
Решение.
Неравенство 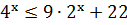 запишем
в виде
запишем
в виде
(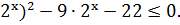
Относительно 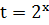 неравенство
имеет вид:
неравенство
имеет вид: 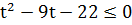 , откуда получаем:
, откуда получаем:
(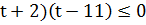 ,
,
Значит,
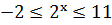 ,
, 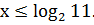
Второе неравенство системы определено при
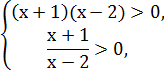
то есть при 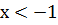 и
и
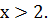 При
допустимых значениях значений переменной получаем:
При
допустимых значениях значений переменной получаем:
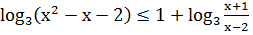 ,
, 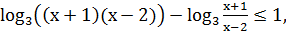
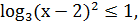
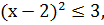
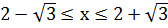 .
.
С учетом области допустимых значений переменной
получаем решение второго неравенства системы:
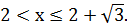
Сравним 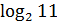 и
и
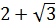 .
Так как
.
Так как 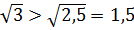 ,
то
,
то
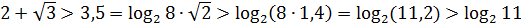 ,
,
следовательно,
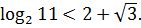
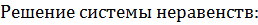
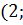
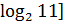 .
.
Ответ: 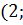
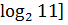 [11,
с.1].
[11,
с.1].
2.3 Подбор задач на нахождение и использование
показательной и логарифмической функций в школьном курсе математики
. Решите неравенства:
а) 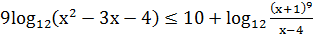 [10,
с. 6]
[10,
с. 6]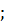
б) 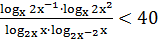 [10,
с. 3].
[10,
с. 3].
. Решите уравнения:
а) 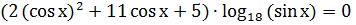 [9,
с. 5].
[9,
с. 5].
б) 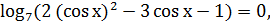
найдите все корни этого уравнения, принадлежащие
отрезку 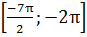 [10,
с. 2].
[10,
с. 2].
. Найдите корни уравнений:
а) 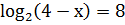 [10,
с. 8].
[10,
с. 8].
б) 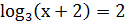 [10,
с.
7].
[10,
с.
7].
. Решите системы неравенств:
а) 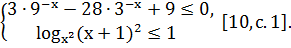
б) 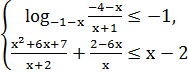
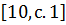 .
.
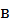 )
) 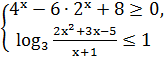 [9,
с. 1].
[9,
с. 1].
Подведем некоторые итоги. Можно выделить три
основных метода решения примеров и задач:
1) Функционально-графический
метод. Он основан на использовании графических иллюстраций или каких-либо
свойств функций.
2) Метод
уравнивания показателей. Он основан на теореме о том, что уравнение 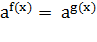 равносильно
уравнению
равносильно
уравнению 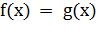 , где
, где 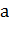 -
положительное число, отличное от 1.
-
положительное число, отличное от 1.
3) Метод
введения новой переменной.
Заключение
В данной курсовой работе по теме
"Логарифмическая и показательная функции" было рассмотрено введение
данного материала в школьный курс алгебры и начала анализа. Логарифмическая и
показательная функции часто используются для решения различных задач. В ЕГЭ на
исследуемую тему отведено четыре задания, два из которых из первой части и два
из второй. Задания бывают смешанного типа, где знание показательной и
логарифмической функции поможет решить их. Показательная функция является
математической моделью для большого класса процессов в области физики и
экономики. Поэтому изучение данной темы играет важную роль в школьном курсе
математики для школьников.
Следует отметить, что была изучена научно  методическая
литература таких авторов, как Колмогорова А.Н. и Мордковича А.Г.,
способствующая усвоению материала темы "Логарифмическая и показательная
функции". Приведены примеры смешанного типа. Подробно разобраны типовые
задачи по теме материала и выделены три основных метода решения:
методическая
литература таких авторов, как Колмогорова А.Н. и Мордковича А.Г.,
способствующая усвоению материала темы "Логарифмическая и показательная
функции". Приведены примеры смешанного типа. Подробно разобраны типовые
задачи по теме материала и выделены три основных метода решения:
) функционально-графический метод;
) метод уравнения показателей;
) метод введения новой переменной.
В процессе исследования:
- Проведен
сравнительный анализ теоретических основ изучения показательной и
логарифмической функций в школьном курсе математики;
- Проанализирован
результаты ЕГЭ 2012-2013 гг. по данной теме;
- Приведены примеры и
задачи, способствующие изучению материала темы " Логарифмическая и
показательная функции".
Подведя итоги можно сказать,
что поставленные задачи решены, цель исследования достигнута.
Список использованных источников
1.
Мордкович А.Г. Алгебра и начала математического анализа: учебник для учащихся
10 11
классов. - 10-е изд. - М., 2009.
11
классов. - 10-е изд. - М., 2009. С. 232
С. 232 273.
273.
.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. Алгебра и начала математического
анализа: учебник для 10 11 классов.
11 классов.  17-е
изд.
17-е
изд.  М.,
2008.
М.,
2008.  С.
201-261.
С.
201-261.
.
Башмаков М.И. Алгебра и начала математического анализа: учебник для учащихся 10 11
классов. - 2-е изд. - М., 1992.
11
классов. - 2-е изд. - М., 1992. С. 185
С. 185 303.
303.
.
Образовательный сайт SLOWO.ws,
2006-2013.
URL:
http://slovo.ws/urok/algebra/10/014/001.html
(16.03.2014).
.
Образовательный сайт NASHOL.COM,
2007-2014.
URL:http://nashol.com/2012061365602/algebra-i-nachala-matematicheskogo-analiza-10-11-klass-kolmogorov-a-n-abramov-u-p-2008.html
(17.03.2014).
.
Образовательный сайт NASHOL.COM,
2007-2014.
URL:http://nashol.com/20100414357/algebra-i-nachala-analiza-10-11-klassi-uchebnik-mordkovich-a-g-2001.html
(17.03.2014).
Краснодарский
краевой институт дополнительного профессионального педагогического образования,
2007-2014.
URL:
http://kkidppo.ru/metodicheskiy-analiz-ege-2012 (02.04.14).
8.
Краснодарский краевой институт дополнительного профессионального
педагогического образования, 2007-2014.
URL:http://kkidppo.ru/metodicheskiy-analiz-ege-2013
(02.04.14).
.
Образовательный сайт YOUR
TUTOR репетитор
математики и физики / статья Селиверстова Сергея Валерьевича, 2011-2013.
URL:
http://yourtutor.info/решение-систем-неравенств-репетитор
10.
Федеральный институт педагогических измерений / Открытый банк заданий ЕГЭ /
Математика, 2004-2014.
URL:
http://www.fipi.ru/os11/xmodules/qprint/afrms.php?proj= (31.03.14).
11.
Федеральный институт педагогических измерений, 2004-2014.
URL:
http://www.fipi.ru/view/sections/92/docs/
(31.03.14).
.
Столяр А.А. Методы обучения математике: пособие для учителей средней школы,
1966.
.
Стефанова Н.Л., Подходова Н.С. Методика и технология обучения математике. Курс
лекции: пособие для вузов. - М., 2005.