Формирование прочных навыков усвоения решения задач с параметрами
Содержание
I. Введение. Методика работы
с задачами, содержащими параметры..1. Знакомство с задачами, содержащими
параметрические данные через решение линейных уравнений в 7 классе..2. Введение
понятия задачи с параметрическими данными на материале линейных уравнений в 7
классе.3. Последовательность упражнений на решение уравнений и задач с
параметрами в 7 классе.4. Типы квадратных уравнений с параметрами.5. Общая
классификация задач по их типу.6. Этапы работы над задачей с параметром.. Система
упражнений для отработки навыков решения задач с параметрами.1. Классификация
задач на решение линейных уравнений с параметром
.1 Решение линейных уравнений
в зависимости от установленных значений параметра
.2. Поиск решения линейных
уравнений в зависимости от установленных значений параметра
.3. Решение линейных уравнений
с параметрами с дополнительными данными в условии задачи
.4. Тренировочные упражнения
.5. Графическая иллюстрация
решения уравнений с параметрам
.6. Линейные уравнения с
параметром, содержащие модуль
.7. Линейные уравнения с
параметром, содержащие квадратные корни.2 Классификация задач на решение
квадратных уравнений с параметром
.1 Уравнения с ограничениями для
решения
.2 Задачи на использование теоремы
Виета
.3 Задачи, в которых указан
промежуток для решения
.4 Дополнительные задания
.5 Графическая иллюстрация решения
квадратных уравнений с параметром
.6 Иррациональные квадратные
уравнения с параметром..3 Примеры решения тригонометрических уравнений с
параметрами..4 Примеры решения показательных и логарифмических уравнений с
параметрами. Приложение.1 Разработка курса по выбору для 9 класса.2
Элективный курс по решению уравнений с параметрами для 10-11 классов..
Заключение. Список литературы
I. Введение
Общеизвестно, что на ЕГЭ задания части С содержат
задачи, которым в традиционном школьном курсе в силу различных причин уделяется
мало внимания.
Одним из видов таких упражнений являются задачи,
содержащие параметры. В школьных учебниках практически нет заданий на эту тему,
потому что школьная программа охватывает узкий круг вопросов, делая основной
упор не на логику решения задач.
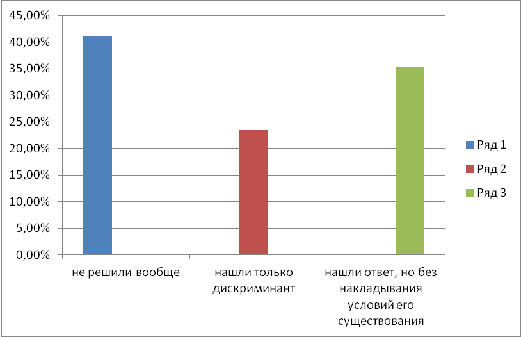
Доказательством этого служит исследование,
проведенное в 9 классе общеобразовательной средней сельской школы.
Учащимся предлагалось решить уравнение с
параметром не выше второй степени a(a+3)x2+(2a+6)x-3a-9=0
. Результаты решения представлены в диаграмме:
Овладение же методикой решения уравнений с
параметрами очень полезно: оно существенно повышает уровень математической
подготовки учащихся, позволяет чуть по-новому, как бы изнутри, взглянуть на
такие «банальные» функциональные зависимости, подробно анализируемые школьной
программой, как, к примеру, линейные и квадратные многочлены. Поэтому
знакомство с такими примерами можно организовать на факультативных занятиях,
курсах по выбору, элективных курсах, рассматривая тему «Уравнения с
параметрами». К тому же, умение решать уравнения с параметрами во многом
предопределяет успешную сдачу экзаменов.
Поэтому целью моей дипломной работы является
изучение существующих методик решения задач с параметрами в школьном курсе
математики.
Отсюда вытекают следующие задачи:
) Проанализировать содержание школьных
учебников;
) Выделить методики решения задач с
параметрами;
) Разработать систему упражнений для
отработки навыков решения задач с параметрами;
) Разработать курс по выбору для 9 класса;
) Разработать элективный курс для 10-11
классов.
Объектом являются задачи с параметрами.
Предметом - методы решения задач с параметрами.
Методы исследования: изучение литературных
источников, личный опыт работы, дедукция, индукция, анализ, синтез, обобщение,
интерпретация, конкретизация, педагогический эксперимент, математические методы
решения задач.
II. Методика работы с задачами, содержащими
параметры, в основной школе
.1 Знакомство с задачами, содержащими параметры,
через решение линейных уравнений в 7 классе
С некоторых пор основным связующим звеном всего
курса математики стала идея функциональной зависимости. Благодаря этому
устанавливается тесная связь между всеми разделами курса математики и
появляется возможность подходить к решению уравнений и задач с более общей
точки зрения в смысле полноты их решения. В связи с этим уместно привести
высказывание В. М. Брадиса: «Представляется совершенно необходимым, чтобы
учащиеся проводили исследование (то есть ставили вопрос о существовании
решения, о числе решений, об особых случаях, какие могут представляться) при
решении каждой задачи, особенно такой, какая ставится в общем виде ( содержит
параметры)».
При решении математических задач учащиеся
встречаются с различными методами исследования, применяемыми в математике, так
как решение задач « заставляет учащихся сравнивать, разъединять,
абстрагировать, соединять, индуцировать, дедуцировать, конкретизировать и
обобщать».
Математическая задача состоит из данных и
искомых величин и из условия, содержащего зависимость между данными и искомыми
величинами. Примерами задач с параметрами являются задачи такого типа:
«Определить площадь правильного треугольника со стороной а см.». данная задача
является задачей с одним параметром. Задача: «Периметры двух квадратов
составляют в сумме а см., а сумма их площадей равна b
см2. Определить стороны квадратов» является задачей с двумя параметрами.
Задача, которая не содержит в явном виде параметра, то есть в которой известная
величина не обозначена буквой, но в то же время не выражена конкретным числовым
значением, является тоже задачей с параметрическими данными. Например, задача
«Тело брошено вертикально вверх с известной начальной скоростью. Когда оно
будет на высоте 100 м.?» является задачей с одним параметром, так как начальная
скорость является известной величиной, не имеющей определённого числового
значения. При решении задач с параметрическими данными составлением уравнения
получаем уравнение с параметрическими данными, то есть уравнение, коэффициенты
которого содержат параметры или функции от параметров.
Обычно в школьной практике при решении задач и
уравнений с параметрическими данными ограничиваются выражением искомых величин
в виде функции от параметров, оставляя открытым вопрос о годности найденного
выражения как решения при тех или иных допустимых значениях параметров. Но в то
же время этот вопрос является составной частью полного и исчерпывающего решения
задачи или уравнения. В связи с широким внедрением идеи функциональной
зависимости в преподавание математики исследование решений становится посильным
уже для учащихся младших классов.
Впервые знакомство с задачами, содержащими
параметрические данные, можно организовать в 7 классе в теме « Линейные
уравнения с одним неизвестным». К этому времени учащиеся должны иметь
первоначальные навыки:
)в составлении и решении линейных уравнений с
одним неизвестным с целочисленными коэффициентами в простейших случаях.
)в решении задач с параметрическими данными
арифметическим способом.
)в установлении множества допустимых значений
букв в аналитическом выражении и величин в задаче.
Работа в этом направлении ведётся
систематически, начиная с 6 класса. Если такой работы не проводилось в 6
классе, то необходимо провести её в 7 классе.
Для ознакомления учащихся с понятием уравнения и
задачи с параметрическими данными можно использовать имеющиеся у них знания о
существовании корней линейного уравнения. На предыдущем уроке перед
рассмотрением уравнений и задач с параметрическими данными даётся в виде
домашнего задания задача: «Сумма двух натуральных чисел, из которых одно в 4
раза больше другого, равна 95. Найти эти числа».
На следующем уроке разбирается подробно
выполненное домашнее задание примерно по следующему плану. В данной задаче мы
нашли, какие будут два натуральных числа, удовлетворяющие условиям задачи.
Поставим вопрос: каким числом будет сумма двух натуральных чисел, из которых
одно в 4 раза больше другого? Знаем, что сумма будет обязательно натуральным
числом. Но может ли этой суммой быть любое натуральное число, мы пока не сумеем
ответить. Рассмотрим некоторые примеры, располагая их в таблице:
|
Первое
натуральное число
|
Второе
натуральное число
|
Сумма
этих натуральных чисел
|
|
1
|
4
|
5
|
|
2
|
8
|
10
|
|
3
|
12
|
15
|
|
4
|
16
|
20
|
|
5
|
20
|
25
|
|
6
|
24
|
30
|
|
|
|
|
|
|
На основе данных таблицы делается вывод, что
суммой искомых чисел будет натуральное число, кратное 5. Для проверки
правильности вывода решаем данную задачу в общем виде в следующей формулировке:
«Сумма двух натуральных чисел, из которых одно в 4 раза больше другого, равна
а. Найти эти числа».
Решение: одно число больше другого в 4 раза.
Если меньшее число обозначить через х, то большее число будет 4х. Их сумма
будет х+4х. По условию задачи х+4х=а, 5х=а откуда х=а/5.
Если меньшее число равно а/5, то большее число
равно 4а/5. По условию задачи искомые числа должны быть натуральными.
Следовательно, чтобы выражения а/5 и 4а/5 были натуральными, параметр а должен
быть натуральным числом, кратным 5.
Отсюда вывод: если а делится на 5, то найденные
выражения являются решениями задачи. Проверить, если а=90, 135, 242, 1022.
.2 Введение понятия задачи с параметрами на
материале линейных уравнений в 7 классе
Если мы решаем задачу с параметрическими
данными, то мы получим уравнение, которое содержит кроме буквы, обозначающей
неизвестное, ещё и параметры, то есть уравнение с параметрическими данными.
Например, в нашей задаче уравнение х+4х=а является уравнением с одним
параметром а. Решение уравнения с параметрическими данными, как мы видели,
вообще говоря, производится так же, как и решение уравнения с числовыми данными.
Дальше следует раскрыть смысл задачи и уравнения
с параметрическими данными. Задачи с параметрическими данными мы решали уже в 6
классе арифметическим способом, составляя по тексту задачи формулу решения и
исследуя полученное выражение по условиям задачи. При этом мы получили
возможность решить одновременно бесконечное множество однотипных задач с
числовыми данными. Такое свойство имеется и у уравнения с параметрическими
данными. Решая предыдущую задачу, мы получили уравнение х+4х=а и установили, что
параметр а должен иметь только натуральные значения, кратные 5, что составляет
множество допустимых значений параметра а. заменяя в полученном уравнении
параметр а его значениями из множества допустимых значений, получим следующие
уравнения с числовыми данными:
при а=5 х+4х=5
при а=10 х+4х=10
при а=15 х+4х=15
при а=20 х+4х=20
Из этого вытекает, что уравнение с
параметрическими данными представляет бесконечное число однотипных уравнений с
числовыми данными. Решая каждое из этих уравнений, мы получим решение задачи с
числовыми данными.
Для домашнего задания можно дать подобную
задачу. При этом даются дополнительно вопросы:
)Определить по полученным формулам, при каких
значениях параметра задача имеет решение.
)Вычислить по полученным формулам некоторые
величины, если значение параметра дано.
)Проверить соответствуют ли полученные значения
при некотором значении параметра тем значениям, которые мы получили, решая
задачу как задачу с числовыми данными.
В дальнейшем в течение изучения данной темы и
после этого предлагаются систематически параллельно с уравнениями и задачами с
числовыми данными и уравнения с параметрическими данными. При этом мы
ограничиваемся в основном уравнениями и задачами с одним параметром и притом
самым простейшим. Основная цель их- устранить разрыв между решением уравнений и
задач с числовыми данными и параметрическими данными и исследованием решений.
.3. Последовательность упражнений на решение
уравнений и задач с параметрами в 7 классе
Решение уравнений входит как составная часть в
решение задачи. Я присоединяюсь к мнению многих методистов, которое можно
выразить словами А. Н. Барсукова: «… мы считаем методически целесообразным и
практически необходимым, чтобы упражнения в решении и составлении уравнений как
с числовыми, так и с буквенными коэффициентами проводились параллельно для
каждого типа уравнений».
Приведём упражнения на решение уравнений и задач
с параметрическими данными, которые можно предложить в 7 классе.
Упражнение № 1.
Решить следующие уравнения относительно х:
)7с+3х=13с
)20+х-10=а
)5х2+m=5х(х+2)
)11х+а=3х
)х-3х+5х=2
)5х-k=6
)х 2+p=(х-1)2
Решение: (первого примера) Установим, какие
числовые значения могут иметь неизвестное х и параметр с на основе производимых
в уравнении действий. Подобные вопросы необходимо ставить при решении каждого
из уравнений и задач с параметрическими данными. Неизвестное х и параметр с
могут иметь любое рациональное значение, так как умножение двух рациональных
чисел всегда существует.. Решая уравнение, найдём, что х=2с.
Ответ: если с- любое рациональное число, то
х=2с.
Можно считать решение уравнения законченным. Но
в целях конкретизации необходимо, особенно на первых порах, поставить ряд
дополнительных вопросов, которые в то же время являются подготовительным
материалом для решения задач с параметрическими данными. Приведём к данному
уравнению ряд вопросов, которые могут быть предложены и при решении других
уравнений с параметрическими данными ( не обязательно всех вопросов
одновременно для каждого уравнения):
)Заполнить следующую таблицу:
|
c
|
-3
|
-2,5
|
-2
|
-1,5
|
-1
|
-0,5
|
0
|
0,5
|
1
|
|
x=2c
|
|
|
|
|
|
|
|
|
|
)Определить по таблице, при каких значениях
параметра с уравнение имеет положительные решения (отрицательные решения,
нулевое решение).
)Определить по формуле решения х=2с, при каких
значениях параметра уравнение имеет решением число 0.(положительное,
отрицательное число). Если решением уравнения является дробное выражение
(примеры 3-7), то можно поставить вопрос о целочисленности решений.
)Составить по данным таблицы график, нанеся на
горизонтальную ось значения параметра с масштабом 1 единица = 1см и на
вертикальную ось значения решения уравнения с масштабом 1 единица = 1 см.
)Определить по графику, при каких значениях
параметра решения уравнения будут положительными (отрицательными, равными
нулю); при каких значениях параметра решение уравнения будет меньше 5 (больше
2) и другое. Сравнить полученные результаты с ранее найденными по таблице и по
формуле. Записать полученные результаты, используя соответствующие
математические символы.
)Написать уравнение, если с=-1, с=3, с=0. Решить
полученные уравнения и проверить найденное решение по составленной таблице и
построенному графику.
Ответы на примеры 2-7: 2) х=а-10; 3) х=m/10;
4) х=-а/8; 5) х=2/3; 6) х=(k+6)/5;
7) x=(1-p)/2.
Упражнение № 2.
.В прямоугольном треугольнике один из углов,
прилежащих к гипотенузе, равен а градусам. Найти величину другого угла,
прилежащего к гипотенузе.
Решение. Если искомый угол равен х градусам, то
так как сумма углов, прилежащих к гипотенузе, равна 900, то 0<а<900 и
0<х<900.
По условиям задачи получается уравнение:
х+а=90,
которое имеет единственное решение
х=90-а.
Очевидно, что при 0<а<900, полученное
решение х=90-а принадлежит области допустимых значений неизвестного
(0<х<900).
Ответ: если 0<а<900 , то искомый угол при
гипотенузе равен ( 90-а) градусам.
Если при решении уравнения возникает
необходимость решить неравенство, то это можно сделать на основании свойств,
рассмотренных в примере.
Примечания. При решении задач с параметрическими
данными необходимо, особенно на первых порах, решить ту же задачу с числовыми
данными, и особенно тогда, когда решение задачи представляет для учащихся
затруднения. Также следует перед решением задачи дать ряд предварительных
заданий с целью облегчить решение задачи. Например, относитнльно данной задачи:
)Какое соотношение имеет место для углов
прямоугольного треугольника, прилежащих к гипотенузе? В каких пределах могут
измеряться величины углов прямоугольного треугольника, прилежащих к гипотенузе?
)Установить, при каких значениях параметра а
решение уравнения 2x-3(x-5)=a
будет положительным числом? Числом меньше 10?
)Написать в виде равенства предложение: сумма
углов прямоугольного треугольника, прилежащих к гипотенузе, равна 900.
После решения задачи можно предложить ещё и
дополнительные вопросы для решения:
)Заполнить таблицу
|
а
|
10°
|
20°
|
30°
|
40°
|
50°
|
60°
|
70°
|
80°
|
90°
|
|
х=90°-а
|
|
|
|
|
|
|
|
|
|
)Определить по составленной таблице, как
изменяется второй угол, прилежащий к гипотенузе, при возрастании (убывании)
первого угла, прилежащего к гипотенузе.
)Какой вид имеет треугольник при а=450?
)При каких значениях параметра а задача не имеет
решения?
)Построить график для выражения 90-а в множестве
допустимых значений параметра а.
)Определить по графику, при каких значениях
параметра а искомый угол будет больше 250? Написать ответ при помощи знака
неравенства.
)Определить по графику, при каком значении
параметра а искомый угол равняется 310. Проверить полученный результат, решая
данную задачу, как задачу с числовыми данными, то есть при а=590.
Полученную формулу решения выражать графически
является полезным в том смысле, что по графику мы можем установить свойства
искомых величин, которые в некоторых случаях учащиеся не могут установить
аналитическим путём из-за отсутствия соответствующих теоретических знаний.
Наглядное изображение поможет учащимся усматривать свойства функций, а
следовательно тех процессов, которые она выражает. Это необходимо ещё и потому,
что в учебнике для 7 класса под редакцией Теляковского отсутствуют упражнения
на решение уравнений графическим методом.
При решении задач с параметрическими данными
необходимо установить множество допустимых значений параметров и неизвестных.
После решения составленного уравнения проверяется, является ли найденное
решение уравнения решением задачи. При этом множества допустимых значений
параметров могут уточняться, после чего мы принимаем их за окончательное
множество допустимых значений параметров.
.Один из углов равнобедренного треугольника при
основании равняется m градусам.
Найти угол при вершине.
Решение. Если х- угол при вершине, то
0<х<1800 и 0<m<900.
Составленное уравнение х+2m=1800,
его решение х=1800-2m.
Ответ. Если 0<m<900,
то угол при вершине равен (1800-2m)
градусам.
.Боковая сторона равнобедренного треугольника
равна 10 см. периметр треугольника равен p
см. найти длину основания.
Решение. Так как сумма двух боковых сторон
меньше периметра, то p>20.
Если основание треугольника х, то 0<х<20, так как третья сторона
треугольника меньше суммы двух остальных сторон. Уравнение х+20= p
и его единственное решение х= p-20.
Исследование полученного решения относительно ограничений, поставленных
относительно искомого, даёт
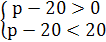
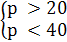 20<
p<40.
20<
p<40.
Ответ. Если 20< p<40,
то длина основания равна 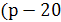 )см.
)см.
.Сумма трёх положительных чисел, из которых
каждое следующее в 10 раз больше предыдущего, составляет k.
Какие эти числа?
Ответ. Если k>0,
то искомые числа 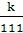 ,
, 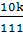 ,
и
,
и 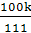 .
.
Дополнительные задания:
)Вычислить искомые числа, если их сумма k=999.
)При каких значениях k
эти числа будут натуральными? Привести примеры.
. Сумма трёх последовательных целых чисел равна p.
Найти эти числа.
Ответ. Если p-
целое число, кратное трём, то искомые числа равны 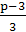 ,
,
 ,
,
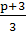 .
.
Вычислить искомые числа при p=24;
0; -12.
. Длины сторон треугольника выражаются тремя
последовательными целыми числами. Найти длину каждой стороны, если периметр
треугольника равен p см.
Решение. Пусть наименьшая сторона треугольника
равна х1 см, следующая х2 см и наибольшая х3 см. по условию задачи х2=х1+1 и
х3=х2+1=х1+2.
Так как между сторонами треугольника имеет место
соотношение х1+х2>х3, откуда
х1+х1+1>х1+2
или х1>1.
Имеем, p
и х1 натуральные числа и притом p>0
и х1>1. Уравнение
х1+х1+1+х1+2= p,
откуда х1=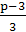 , х2=
, х2= ,
х3=
,
х3=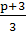 .
.
Так как х1>1, то и
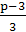 >1,
>1, 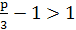 ,
,
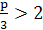 ,
p>6.
,
p>6.
Ответ. Если периметр треугольника p
выражается натуральным числом большим 6 и кратным 3, то искомые стороны
треугольника будут 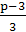 ,
,  ,
,
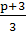 .
.
. При сложении трёх последовательных
неотрицательных целых чисел получено в сумме однозначное число p.
Какие числа сложены?
Решение. Если наименьшее из этих чисел х1, то х1≥0
и 0< p<10. х1= -1,
х2=
-1,
х2=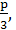 х3=
х3= +1.
+1.
Чтобы х1≥0, необходимо  -1≥0,
то есть p≥3. Чтобы
искомые числа были целыми, необходимо, чтобы p
было числом, кратным 3, то есть p=3,
6, 9, 12, 15, …
-1≥0,
то есть p≥3. Чтобы
искомые числа были целыми, необходимо, чтобы p
было числом, кратным 3, то есть p=3,
6, 9, 12, 15, …
Так как p-
однозначное число, то окончательно p=3,
6, 9.
Все возможные случаи исчерпываются тремя
возможностями:
при p=3
искомые числа 0, 1, 2.
при p=6
искомые числа 1, 2, 3.
при p=9
искомые числа 2, 3,4.
. В трёх цехах завода работает с рабочих. Во
втором цехе- в 5 раз больше, чем в первом, в третьем столько, сколько во втором
и в первом вместе. Сколько рабочих в каждом цехе?
Ответ. Если с натуральное число, делящееся на
12, то в первом цехе 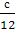 рабочих, во втором
рабочих, во втором
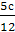 рабочих
и в третьем
рабочих
и в третьем 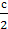 рабочих.
рабочих.
Упражнение №3.
Решить следующие уравнения относительно х:
)ах-а=3а 6) ах+х=а2+2а+1
)4-3mх=7
7) 7х+b2=bx+49
3)ax+4=-2 8) a2x+4=a(x+2)+2
)x-ax=3 9) a2x-16x=a+4
5)(k+1)x=2-x
Указание. Так как в 7 классе рассматриваются
уравнения первой степени с одним неизвестным, то и при решении уравнений с
параметрическими данными следует ограничиться случаем, когда коэффициент при
неизвестном после приведения уравнения к каноническому виду не равен нулю.
Случай, когда коэффициент при неизвестном равен нулю, в 7 классе не следует
рассматривать.
Пример решения уравнения 5.
Параметр k
и неизвестное х могут быть любыми числами. Произведя тождественные
преобразования, приведём уравнение к каноническому виду:
(k+2)х=2.
Так как мы имеем дело с уравнением первой
степени, то есть с уравнением, у которого коэффициент при неизвестном отличен
от нуля, то при k+2≠0
или k≠-2 уравнение
имеет единственное решение х=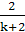 .
.
Ответы. 1) если а≠0, то х=4. 2) если m≠0,
то х=-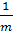 .
3) если а≠0, то х=-
.
3) если а≠0, то х=-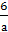 . 4) если а≠1,
то х=
. 4) если а≠1,
то х=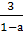 . 6) если а≠-1, то х=а+1. 7) если b≠7,
то х= b+7. 8) если а≠0
и а≠1, то х=
. 6) если а≠-1, то х=а+1. 7) если b≠7,
то х= b+7. 8) если а≠0
и а≠1, то х=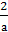 . 9) если а≠±4,
то х=
. 9) если а≠±4,
то х= 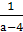 .
.
Упражнение №4.
Решить уравнения относительно х:
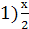 -а=2 4)
-а=2 4) 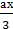 -5=10
-5=10
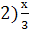 +х=а 5)
+х=а 5) 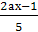 -
-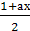 =1
=1
)х-а=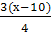
Указание. Решение примеров этого упражнения
отличается от предыдущих тем, что необходимо освободиться от дробей.
Ответы. 1) х=2(а+2) 2) х= а
3) х=4а-30 4) если а≠0, то х=
а
3) х=4а-30 4) если а≠0, то х=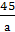 5) если а≠0, то х=-
5) если а≠0, то х=-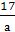 .
.
Упражнение №5.
Решить уравнения относительно х:
)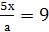 5)
5) 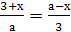 2)
2)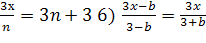
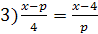 7)
7) 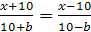
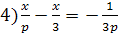 8)
8) 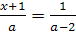
Указание. Особенность решения примеров этого
упражнения заключается в том, что при установлении множества допустимых
значений параметра необходимо исключить из этого множества значения, которые
обращают знаменатель дробей в нуль. Так, в примере 1 параметр а может иметь все
рациональные значения, кроме нуля, то есть a≠0;
в примере 6 b≠±3; в
примере 7 b≠±10.
Ответы. 1) если a≠0,
то x=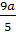 ;
2) если n≠0, то x=n(n+1);
3) если p≠0 и p≠4,
то x=p+4;
4) если p≠0 и p≠3,
то
;
2) если n≠0, то x=n(n+1);
3) если p≠0 и p≠4,
то x=p+4;
4) если p≠0 и p≠3,
то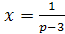 ;
5) если a≠0 и a≠-3,
то x=a-3;
6) если b≠0 и b≠±3,
то
;
5) если a≠0 и a≠-3,
то x=a-3;
6) если b≠0 и b≠±3,
то 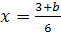 ;
7) если b≠0 и b≠±10,
то
;
7) если b≠0 и b≠±10,
то 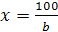 ;
8) если a≠0 и a≠2,
то
;
8) если a≠0 и a≠2,
то 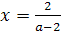 .
.
Усвоение решения уравнений и задач с
параметрическими данными в 7 классе в таком объёме вполне посильно. После
усвоения учащимися методов решения линейных уравнений с параметрами можно
провести письменную работу.
Вариант письменной работы:
)Решить уравнение относительно x:
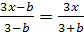
)На верхней полке книг было в 5 раз больше, чем
на нижней. Если с верхней полки переложить на нижнюю а книг, то на обеих полках
книг станет поровну. Сколько книг было сначала на каждой полке?
.4Типы квадратных уравнений с параметрами
Задачи, связанные с квадратным трёхчленом,
встречающиеся в школьной практике, чрезвычайно разнообразны. Но среди них нет
достаточного количества разнообразных квадратных уравнений, содержащих
параметр, где основное, что требуется от учащихся, это внимательное чтение
формулировки задания.
Задачи первого типа. Определить все значения
параметра а, при которых уравнение имеет один корень, два корня, не имеет
корней.
Пример 1. Определить все значения параметра а,
при которых уравнение 2ах2-4(а+1)х+4а+1=0 имеет один корень.
Решение. Здесь главное- не забыть про случай
а=0, поскольку в условии не сказано, что рассматривается квадратное уравнение.
При а=0 имеем линейное уравнение -4х+1=0 с единственным корнем х=1/4. Остальные
значения параметра а мы получим из уравнения D/4=0.
(a2+2a+1)-2a(4a+1)=0
a2-3a-2=0
a1=-1/2; a2=2.
Ответ. 0; -1/2; 2.
К азбуке квадратного трёхчлена относится и
теорема Виета.
Для того, чтобы х1 и х2 были корнями уравнения
ах2+bx+c=0,
необходимо и достаточно выполнение равенств:
х1+х2=-b/a;
х1*х2=с/а.
Из теоремы Виета следует разложение на множители
квадратного трёхчлена:
ах2+bx+c=a(x-x1)(x-x2)=0.
На теореме Виета основан целый ряд традиционных
задач и методов решения. Например:
Пусть х1 и х2 корни уравнения x2+px+q=0.
Выразить x1 4+x24
через p иq.
Решение. x1
4+x24=(x12+x22)2-2x12*x22=((
х1+х2)2-2x1*x2)2-2x12*x22=(p2-2q)2-2q2=p4-4p2*q+2q2
Ответ. x1
4+x24= p4-4p2*q+2q2.
Как мы знаем, для того, чтобы квадратное
уравнение ах2+bx+c=0
имело корни, необходимо и достаточно выполнение неравенства D≥0.
Как правило, в случае необходимости в задачах доказать, что заданное квадратное
уравнение имеет решение, начинают с вычисления его дискриминанта, с тем, чтобы
потом доказать его неотрицательность.
Однако в некоторых случаях можно указать и иные,
более простые способы доказательства существования решения квадратного
уравнения. Эти способы основываются на очевидных графических соображениях. Так,
если а>0, то для доказательства того, что уравнение ах2+bx+c=0
имеет два решения, достаточно указать одну точку х0, в которой f(x0)=ax02+bx0+c<0.
Чаще всего в качестве х0 берут 0 ( даёт достаточное условие с<0), 1 (
условие а+b+c<0)
или -1 ( условие а-b+c<0).
Пример 2. Доказать, что при любом а уравнение (a3-2a2)x2-(a3-a+2)x+a2+1=0
имеет решение.
Решение. Можно, конечно, попытаться найти
дискриминант и доказать, что он положителен, но не будем спешить. Обозначим
левую часть уравнения через f(x).
Сразу видно, что f(0)=a2+1>0
при любом а. Утверждение задачи будет доказано, если мы найдём х1, для которого
f(x1)<0.
Попробуем х1=1. (Выбор такого значения выглядит естественным, поскольку в этом
случае пропадают члены с а3). f(1)=-a2+a-1<0
при любом а. Теперь легко сделать вывод, что наше уравнение всегда имеет
решение. Более того, если a3-2a2≠0,
то есть а≠0 и а≠2, данное уравнение имеет два корня; при этом
всегда имеется корень, удовлетворяющий неравенству 0<x<1.
Полезно научить учеников в процессе поиска
решения почаще обращаться к «картинкам», искать соответствующую графическую
интерпретацию.
Задачи второго типа. Задачи на определение
знаков корней квадратного уравнения.
Теорема Виета очевидным образом используется в
задачах, в которых требуется определить знаки корней квадратного уравнения.
Пример 1. При каких значениях параметра а
уравнение x2-2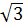 (a-3)x+a2-3a+2=0
имеет решение? Определить знаки корней в зависимости от а.
(a-3)x+a2-3a+2=0
имеет решение? Определить знаки корней в зависимости от а.
Решение. Прежде всего, если a2-3a+2<0,
1<а<2, то уравнение имеет корни разных знаков.(Дискриминант при этом
«автоматически» положителен). В остальных случаях или корней нет, или они
одного знака. Отдельно надо рассмотреть случаи, когда корни равны или один из
них равен 0. В случае положительности дискриминанта и свободного члена на
основании теоремы Виета знаки обоих корней противоположны по знаку коэффициента
при х- второму коэффициенту уравнения. Значит, для того чтобы было х1 >0 и
х2>0, необходимо и достаточно выполнения неравенств
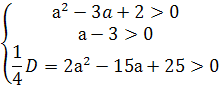
Отсюда а>5. Точно так же рассматриваются
другие случаи.
Ответ. Если а<1 или 2<а<2,5 , то
х1<0, х2<0; если а=1 или а=2,то х1<0, х2=0; если 1<а<2, то
х1<0, х2>0; если а=2,5 ,то х1=х2<0; если 2,5<а<5, то корней нет;
если а=5, то х1=х2>0; если а>5, то х1>0, х2>0.
Ответ выглядит сложнее, чем решение задачи.
Поэтому существенным этапом решения задач с параметрами является запись ответа.
Особенно это относится к тем примерам, где решение как бы «ветвится» в
зависимости от значений параметра. В подобных случаях составление ответа- это
сбор ранее полученных результатов. И здесь очень важно не забыть отразить в
ответе все этапы решения.
Задачи третьего типа. Расположение корней
квадратного трёхчлена.
Выделим прежде всего два наиболее
распространённых вида задач, связанных с расположением корней квадратного
трёхчлена.
вид. Задачи, в которых изучается расположение
корней относительно заданной точки А. Возможны 3 случая, не считая случая
отсутствия корней: оба корня меньше А; один корень меньше А, а другой больше А;
оба корня больше А. Задачи первого типа без труда сводятся к проблеме,
рассмотренной выше,- определению знаков корней квадратного трёхчлена. Это
делается при помощи замены t=
x-A,
x= t+A,в
результате которой трёхчлен относительно x
переходит в трёхчлен относительно t.
Знаки корней нового квадратного трёхчлена очевидным образом определяют
расположение корней исходного квадратного трёхчлена относительно А. можно и не
делать замены.
Пример 1. При каком значении параметра а один
корень уравнения х2-(3а+2)х+2а-1=0 больше 1, а другой меньше 1?
Решение. Решение легко получается на основании
следующего простого графического соображения. График функции у =
х2-(3а+2)х+2а-1 представляет собой параболу, ветви которой направлены вверх. По
условию эта парабола должна пересекать ось Х, причём отрезок 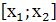 должен
содержать внутри себя точку 1.
должен
содержать внутри себя точку 1.
Следовательно, значение квадратного трёхчлена
х2-(3а+2)х+2а-1 при х=1 должно быть отрицательным. Это условие является необходимым
и достаточным для того. Чтобы выполнялись неравенства х1<1<х2.
Ответ. а>-2.
В общем случае для того, чтобы уравнение f(x)=ax2+bx+c=0
имело бы один корень меньше А, а другой больше А, необходимо и достаточно
выполнения неравенства а*f(A)<0.
Не следует последнее условие заучивать. Необходимо понять принцип его получения
и уметь провести необходимые рассуждения в конкретных задачах.
Пример 2. При каких значениях параметра а оба
корня уравнения ах2-2(2а-1)х+2-3а=0 больше 1?
Решение. Для того чтобы оба корня уравнения f(x)=
ах2-2(2а-1)х+2-3а=0 были больше 1, необходимо и достаточно выполнение следующих
условий:
)D>0;
)а*f(1)>0;
)хв=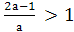
Необходимость первого условия очевидна. Второе
неравенство означает, что знак f(x)
при х=1 совпадает со знаком старшего коэффициента. Квадратные трёхчлены,
удовлетворяющие первому и второму условиям, обладают тем свойством, что все они
имеют два корня и оба эти корня либо меньше 1, либо больше 1.
Третье неравенство выделяет из них те трёхчлены,
у которых оба корня больше 1. Оно означает, что вершина параболы расположена
правее прямой х=1.
y
a>0 a>0
1 x
a<0 a<0
Система всех трёх неравенств даёт нам
необходимое и достаточное условие для того, чтобы оба корня данного уравнения
были больше 1. Второе неравенство даёт а(4-6а)>0. 0<а<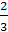 .
А из третьего неравенства следует , что а<0 или а>1. Таким образом, нам
нет необходимости решать первое неравенство, поскольку уже решённые неравенства
несовместимы.
.
А из третьего неравенства следует , что а<0 или а>1. Таким образом, нам
нет необходимости решать первое неравенство, поскольку уже решённые неравенства
несовместимы.
Ответ. Ни при каких.
вид. Задачи, в которых исследуется расположение
корней квадратного трёхчлена относительно заданного отрезка 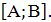 здесь
можно выделить 6 возможных случаев расположения корней (оба меньше А; один
меньше А, другой на отрезке
здесь
можно выделить 6 возможных случаев расположения корней (оба меньше А; один
меньше А, другой на отрезке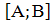 и так далее). Если
же отдельно рассматривать ситуацию, когда D=0,
то добавятся ещё 3 случая. Мы вновь не будем заниматься построением общей
теории, а рассмотрим конкретные примеры.
и так далее). Если
же отдельно рассматривать ситуацию, когда D=0,
то добавятся ещё 3 случая. Мы вновь не будем заниматься построением общей
теории, а рассмотрим конкретные примеры.
Пример 1. При каких значениях параметра а все
решения уравнения (а-1)х2-(а+1)х+а=0 удовлетворяют условию 0<х<3?
Решение. Обозначим f(x)=
(а-1)х2-(а+1)х+а. Необходимым и достаточным условием для того, чтобы f(x)
(если а≠1) имела все свои корни внутри отрезка 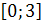 ,
будет выполнение системы неравенств:
,
будет выполнение системы неравенств:
) D≥0
) (а-1)f(0)>0
) (а-1)f(3)>0
) 0<хв<3, где хв=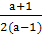 .
.
Оба неравенства 2) и3) выполняются при а>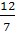 или а<0. Решим четвёртое неравенство: 0<
или а<0. Решим четвёртое неравенство: 0<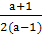 <3.
Будем иметь а>
<3.
Будем иметь а>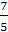 или а<-1.
или а<-1.
Значит система неравенств 2), 3), 4) имеет
решение а>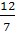 или а<-1.
Условие D≥0 даёт нам
-3а2+6а+1≥0 или 3а2-6а-1≤0, откуда
или а<-1.
Условие D≥0 даёт нам
-3а2+6а+1≥0 или 3а2-6а-1≤0, откуда 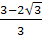 ≤а≤
≤а≤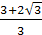 ,
а поскольку а>
,
а поскольку а>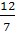 или а<-1, то
или а<-1, то 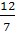 <а≤
<а≤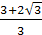 .
Отдельно рассматривается случай а=1.
.
Отдельно рассматривается случай а=1.
Ответ. 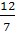 <а≤
<а≤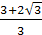 , а=1.
, а=1.
Если бы в условии требовалось, чтобы оба корня
располагались на заданном отрезке, то есть указывалось на наличие двух
различных корней, то правое нестрогое неравенство ответа следовало бы заменить
на строгое и исключить случай а=1.
Пример 2. Определить, как расположены корни
уравнения ax2-3(a+1)x+2a+7=0
относительно отрезка [-1;4].
Решение. Решим эту задачу несколько иначе,
способом, который можно назвать «обобщенным методом интервалов». Сначала
определим, где обращается в ноль дискриминант уравнения. Имеем 9(a+1)2-4a(2a+7)=0,
a2-10a+9=0,
a1=1, a2=9.
При 1<а<9 корней у данного уравнения нет.
Обозначив, как обычно, левую часть уравнения через f(x),
найдем f(-1)=6a+10,
f(4)=6a-5.
Как видно, f(-1) и f(4)
меняют знаки соответственно при а=-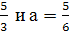 .
.
Множество значений параметра а точками -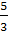 ,
0,
,
0, 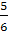 ,
1, 9 разбивается на четыре интервала и две полупрямые (к найденным ранее
значениям параметра а добавлено значение, при котором обращается в нуль старший
коэффициент, а=0).
,
1, 9 разбивается на четыре интервала и две полупрямые (к найденным ранее
значениям параметра а добавлено значение, при котором обращается в нуль старший
коэффициент, а=0).
Рассмотрим эти шесть случаев.
)а<-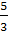 . Имеем D>0,
а<0, f(-1) =6a+10<0,
f(4)=6a-5<0,
хв=
. Имеем D>0,
а<0, f(-1) =6a+10<0,
f(4)=6a-5<0,
хв=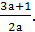 можно проверить, что при а<-
можно проверить, что при а<-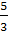 будет -1<
будет -1<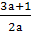 <4.
Значит уравнение имеет корни, ветви параболы направлены вниз, значения
<4.
Значит уравнение имеет корни, ветви параболы направлены вниз, значения
f(x)
при х=-1 и х=4 отрицательны, вершина параболы расположена между прямыми х=-1 и
х=4. Следовательно, в этом случае оба корня расположены между -1 и 4.
y
-1 0 4
хв x
)-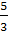 <a<0
(случай а=-
<a<0
(случай а=-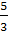 рассматривается
отдельно). Имеем f(-1)>0, f(4)<0.
А поскольку а <0, то один корень меньше -1, а другой расположен между -1 и
4.
рассматривается
отдельно). Имеем f(-1)>0, f(4)<0.
А поскольку а <0, то один корень меньше -1, а другой расположен между -1 и
4.
y
4
-1 0 x
Точно так же рассматриваются остальные четыре
случая.
Ответ: при а<-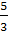 ,
,
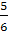 <а<1,
а>0 имеем -1 <х1<х2<4; при -
<а<1,
а>0 имеем -1 <х1<х2<4; при -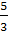 <a<0
имеем х1<-1<х2<4; при 0<а<
<a<0
имеем х1<-1<х2<4; при 0<а<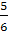 имеем -1 <
х1< 4< х2; при 1<а<9 корней нет. Если а=-
имеем -1 <
х1< 4< х2; при 1<а<9 корней нет. Если а=-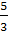 .
То х1=-1, х2=
.
То х1=-1, х2=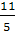 , если а=0, то один
корень х0=
, если а=0, то один
корень х0= ; если а=
; если а=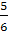 ,
то х1=
,
то х1=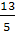 ,
х2=4; если а =1, то х1=х2=3; если а=9, то х1=х2=
,
х2=4; если а =1, то х1=х2=3; если а=9, то х1=х2=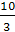 .
.
Пример 3. Определить, как расположены корни
уравнения ах2-(а3+1)х+а2=0 относительно отрезка [1;3].
Решение. В данном случае приемы, которые мы
использовали при решении предыдущего примера, не нужны; все гораздо проще,
рассматриваемое уравнение всегда (при а≠0) имеет корни: х1=а2 и х2=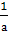 .
теперь закончить решение не составляет труда.
.
теперь закончить решение не составляет труда.
При решении задач не стоит увлекаться общими
теориями, следует попытаться сначала выявить специфику данного конкретного
примера.
.Взаимное расположение корней двух квадратных
трехчленов.
)Найти все значения параметра а, при которых
уравнения х2-(2а-1)х+а=0 и (а+1)х2-ах-1=0 имеют хотя бы один общий корень.
Решение. Решение основывается на следующей
простой идее: если два уравнения f1(x)=0
и f2(x)=0
имеют общий корень х0, то при любых k1
и k2 уравнение k1
f1(x)+
k2 f2(x)=0
имеет тот же корень х0.
Возьмем сначала k1
и k2 так, чтобы в
комбинации исчез свободный член: k1=1,
k2=а. получим после
сокращения на х, поскольку очевидно, что х0≠0, линейное уравнение
(а2+а+1)х-(а2+2а-1)=0.
Затем выберем k1
и k2 так, чтобы исчез
член с х2: k1=a+1,
k2=-1. Получим
второе линейное уравнение (2а2-1)х-(а2+а+1)=0.
Так как х должен удовлетворять обоим полученным
линейным уравнениям, для а должно выполняться соотношение
(а2+а+1)2=(а2+2а-1)(2а2-1).
Далее получаем а4+2а3-6а2-4а=0. Левая часть
разлагается на множители:
а(а3+2а2-6а-4)=а(а3-2а2+4а2-8а+2а-4)=а((а-2)а2+(а-2)4а+2(а-2))=а(а-2)(а2+4а+1).
Ответ. а1=0, а2=2, а3=-2-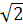 ,
а4=-2+
,
а4=-2+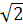 .
.
Для каждого из найденных значений а необходимо
убедиться, что соответствующие уравнения имеют решения. (достаточно проверить
существование одного из них).
Заданную пару квадратных уравнений можно
рассматривать как систему из двух уравнений с неизвестными х и а.
)Расположить корни уравнений х2+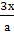 +2а=0
и х2+
+2а=0
и х2+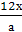 -а=0
в порядке возрастания.
-а=0
в порядке возрастания.
Решение. Обозначим f(x)=
х2+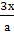 +2а,
g(x)=
х2+
+2а,
g(x)=
х2+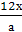 -а,
y1 и y2-
корни уравнения f(x)=0;
z1 и z2-
корни уравнения g(x)=0.
-а,
y1 и y2-
корни уравнения f(x)=0;
z1 и z2-
корни уравнения g(x)=0.
По смыслу задачи следует рассматривать лишь те
значения параметра а, для которых оба уравнения имеют решения. Условие не
отрицательности обоих дискриминантов дают нам неравенства:- 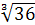 ≤а<0,
0<а≤
≤а<0,
0<а≤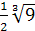 .
.
Найдем значения х, при которых f(x)=
g(x):
х=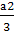 .
Уравнения имеют общий корень, если f(
.
Уравнения имеют общий корень, если f(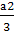 )=
g(
)=
g(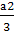 )=0,
откуда а=-3.
)=0,
откуда а=-3.
Таким образом, множество значений параметра а,
при которых оба уравнения имеют корни, разбито на два интервала.
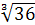 -3 0
-3 0 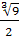 а
а
Концы интервалов удобнее рассматривать отдельно.
Возникают три случая.
)- 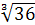 <а<-3.
Имеем f(
<а<-3.
Имеем f(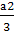 )=
g(
)=
g(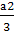 )=а(а3+27)>0.
С точностью до обозначений, какая из двух парабол соответствует f(x),
а какая g(x),
возможны два случая.
)=а(а3+27)>0.
С точностью до обозначений, какая из двух парабол соответствует f(x),
а какая g(x),
возможны два случая.
Y
- 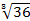 <а<-3
y
<а<-3
y
f(x)
g(x)
y1
0
z1 y2 z2 x
y1
0
y2 z1 z2 x
Посмотрим, как расположены вершины каждой из
парабол по отношению к прямой х=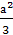 . Для f(x)
имеем хв=-
. Для f(x)
имеем хв=-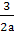 . На
рассматриваемом интервале изменения а имеем -
. На
рассматриваемом интервале изменения а имеем -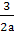 <
<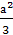 .
Вершина второй параболы также левее прямой х=
.
Вершина второй параболы также левее прямой х=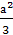 .
Следовательно, имеет место случай, когда вершины обеих парабол лежат по одну
сторону от прямой х=
.
Следовательно, имеет место случай, когда вершины обеих парабол лежат по одну
сторону от прямой х=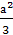 . Осталось
выяснить, какая из двух парабол на рисунке соответствует f(x),
а какая g(x).
. Осталось
выяснить, какая из двух парабол на рисунке соответствует f(x),
а какая g(x).
Если а<0 и х<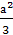 ,
то f(x)-
g(x)=
,
то f(x)-
g(x)=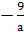 (х-
(х-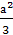 )<0,
то есть f(x)<g(x).
Значит, g(x)
при х<
)<0,
то есть f(x)<g(x).
Значит, g(x)
при х<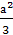 идет выше f(x)
и y1<z1<z2<y2.
Если а=-
идет выше f(x)
и y1<z1<z2<y2.
Если а=- 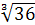 ,
то y1<z1=z2<y2.
,
то y1<z1=z2<y2.
)-3<а<0. В этом случае f(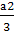 )=
g(
)=
g(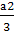 )=а(а3+27)<0.
Как и в предыдущем пункте, при х<
)=а(а3+27)<0.
Как и в предыдущем пункте, при х<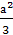 f(x)<g(x),
y1<z1<
y2< z2.
f(x)<g(x),
y1<z1<
y2< z2.
Если а=-3, то y1<z1<z2=y2.
Y
0 y1 z1 y2 z2
X
)0<а≤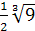 .
Имеем f(
.
Имеем f(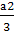 )=
g(
)=
g(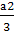 )>0.
Обе вершины слева от прямой х=
)>0.
Обе вершины слева от прямой х=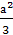 , и f(x)>g(x)
при х<
, и f(x)>g(x)
при х<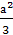 .
Следовательно, z1<y1<y2<z2.
Если а=
.
Следовательно, z1<y1<y2<z2.
Если а=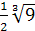 ,
то z1<y1=y2<z2.
,
то z1<y1=y2<z2.
Y
z1
y1
0 y2 z2
x
Получить правильный ответ в данном примере можно
было бы несколько проще, хотя и менее законно. Из соображений непрерывности
следует, что на каждом из трех интервалов имеет место один и тот же порядок
следования корней (граничными точками такого рода интервалов являются:
запрещенные значения параметра, в данном случае а=0; нули дискриминантов- точки
а=- 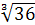 и
а=
и
а=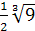 - и значения параметра, при которых уравнения имеют один и тот же корень а=-3;
в общем случае сюда надо добавить значения параметра, при которых обращается в
ноль коэффициент при х2). Для выявления этого порядка следования достаточно
рассмотреть какое-либо значение параметра а из соответствующего интервала. В
нашем случае для крайних интервалов можно взять даже их концы: а=-
- и значения параметра, при которых уравнения имеют один и тот же корень а=-3;
в общем случае сюда надо добавить значения параметра, при которых обращается в
ноль коэффициент при х2). Для выявления этого порядка следования достаточно
рассмотреть какое-либо значение параметра а из соответствующего интервала. В
нашем случае для крайних интервалов можно взять даже их концы: а=- 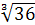 и
а=
и
а=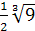 , а для среднего, например, а=-1.
, а для среднего, например, а=-1.
.5 Общая классификация задач по их типу
Так как уравнения с параметрами не выше второй
степени являются самыми распространенными в практике итоговых и конкурсных
заданий, определим их общую структуру и выделим основные их типы. Их общий вид
определяется многочленом F(a;x)=f(a)x2+g(a)x+h(a)
с параметром а или многочленом F(a;b;x)=f(a;b)x2+g(a;b)x+h(a;b)
с параметрами а и b не выше
второй степени.
Отметим, что наиболее важными в практике являются
следующие задачи:
)Решить уравнение (неравенство) с параметрами;
)Найти значение параметров, при которых общее
решение уравнения (неравенства) обладает некоторыми свойствами.
В уравнении f(a)x2+g(a)x+h(a)=0
не выше второй степени с параметром а и переменной х всякое частное уравнение
принадлежит одному из следующих типов:
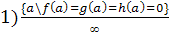 ;
;
)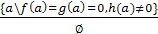 ;
;
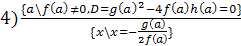 ;
;
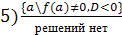 ;
;
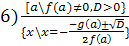 ;
;
Контрольные значения параметра определяются
уравнением f(a)=0
и уравнением D=0. На выделенных
контрольными значениями промежутках допустимых значений параметра дискриминант D
имеет определенный знак, соответствующие частные уравнения принадлежат одному
из двух последних типов.
Тогда решение всякого уравнения с параметром не
выше второй степени осуществляется по следующим этапам:
)На числовой прямой отмечаются все контрольные
значения параметра, для которых соответствующие частные уравнения не
определены.
)На области допустимых значений параметра
исходное уравнение при помощи равносильных преобразований приводится к виду f(a)x2+g(a)x+h(a)=0.
)Выделяется множество контрольных значений
параметра, для которых f(a)=0.
Если уравнение f(a)=0
имеет конечное множество решений, то для каждого найденного контрольного
значения параметра соответствующее частное уравнение решается отдельно.
Проводится классификация частных уравнений по первым трем типам.
На бесконечном множестве решений уравнения f(a)=0
проводится решение уравнения g(a)=0,
выделяются типы 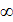 и
и 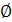 особых
частных уравнений. Множеству {a\f(a)=0,g(a)
особых
частных уравнений. Множеству {a\f(a)=0,g(a)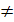 0}
соответствует тип 3) не особых частных уравнений.
0}
соответствует тип 3) не особых частных уравнений.
)Выделяются контрольные значения параметра, для
которых дискриминант D=g(a)2-4f(a)h(a)
обращается в нуль. Соответствующие не особые частные уравнения имеют двукратный
корень x=-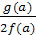 .
.
)Найденные контрольные значения параметра
разбивают область допустимых значений параметра на промежутки. На каждом из
промежутков определяется знак дискриминанта D.
Множеству {a\f(a)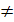 0,D<0}
соответствует тип не особых частных уравнений, не имеющих решений,, для
значений параметра {a\f(a)
0,D<0}
соответствует тип не особых частных уравнений, не имеющих решений,, для
значений параметра {a\f(a)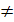 0,D>0}
частные уравнения имеют два различных действительных корня.
0,D>0}
частные уравнения имеют два различных действительных корня.
Пример 1. Решить уравнение х2-х+1=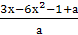 .
.
Решение. В уравнении значение а=0 является
контрольным, для него соответствующее частное уравнение не определено. На
множестве {a\a≠0}
исходное уравнение равносильно (а+6)х2-(а+3)х+1=0.
f(a)=а+6
обращается в нуль для а=-6. Соответствующее частное уравнение 3х+1=0 имеет
единственное решение х=-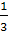 .
.
На множестве {a\a≠-6;0}
частные уравнения являются квадратными с дискриминантом D=а2+2а-15.
Дискриминант D=0 для а=-5 и а=3.
Пусть а=-5, соответствующее частное уравнение х2+2х+1=0 имеет двукратный корень
х=-1. Для а=3 соответствующее частное уравнение 9х2-6х+1=0 имеет двукратный
корень х=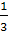 .
.
На числовой прямой отметим найденные значения
параметра и на каждом из полученных промежутков установим знак дискриминанта D.
-6 -5 0 3
а
Если ає(-5;0)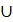 (0;3),
то соответствующие частные уравнения не имеют решений. Для значений параметров
из {a\a
(0;3),
то соответствующие частные уравнения не имеют решений. Для значений параметров
из {a\a (-
(-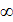 ;-6)
;-6)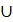 (-6;-5)
(-6;-5)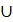 (3;
(3;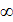 )}
частные уравнения имеют два различных корня, их общие решения х=
)}
частные уравнения имеют два различных корня, их общие решения х=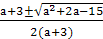 .
.
Ответ.
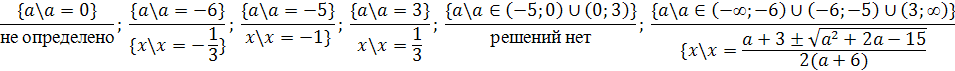
Пример 2. Решить уравнение
(Iа-2I+а-2)х2+(IIаI-3I+а-3)х+(Iа-2I-а+2)=0.
Решение. По определению модуля f(a)=
Iа-2I+а-2=
g(a)= IIаI-3I+а-3=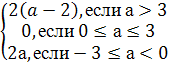
-6, если а<-3.
h(a)=
Iа-2I-а+2=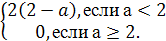
Отметим промежутки, на которых коэффициенты f(a),
g(a),
h(a)
обращаются в ноль.
f(a)=0
h(a)=0
0 2 3 а
g(a)=0
Коэффициент f(a)=
Iа-2I+а-2 обращается в нуль для а (
(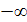 ;2].
На данном множестве значений параметра исходное уравнение равносильно уравнению
g(a)+h(a)=0.
Для а=2 частное уравнение особое, типа
;2].
На данном множестве значений параметра исходное уравнение равносильно уравнению
g(a)+h(a)=0.
Для а=2 частное уравнение особое, типа 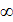 ,
так как g(2)=h(2)=0.
,
так как g(2)=h(2)=0.
Если а [0;2),
то g(a)=0,
h(a)=2(2-a)
[0;2),
то g(a)=0,
h(a)=2(2-a)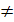 0
и частные уравнения особые, типа
0
и частные уравнения особые, типа 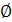 .
.
Пусть а (-
(-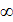 ;0),
тогда g(a)≠0
и х=-
;0),
тогда g(a)≠0
и х=-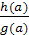 =
=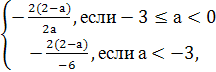 является общим решением уравнения на данном множестве значений параметра.
является общим решением уравнения на данном множестве значений параметра.
На множестве значений параметра {a|f(a)≠0}={a|a (2;
(2;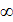 )}
соответствующие частные уравнения имеют вторую степень. Так
как
f(a)h(a)=(|a-2|+a-2)(|a-2|-(a-2))=|a-2|2-(a-2)2=0, то
дискриминант
D=g(a)2-4f(a)h(a)=g(a)2.
)}
соответствующие частные уравнения имеют вторую степень. Так
как
f(a)h(a)=(|a-2|+a-2)(|a-2|-(a-2))=|a-2|2-(a-2)2=0, то
дискриминант
D=g(a)2-4f(a)h(a)=g(a)2.
Отсюда дискриминант D=0для
значений параметра {a|a (2;3]}.
Соответствующие частные уравнения 2(а-2)х2=0 имеют двукратный корень х=0.
(2;3]}.
Соответствующие частные уравнения 2(а-2)х2=0 имеют двукратный корень х=0.
Пусть а (3;
(3;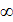 ),
тогда f(a)=2(a-2)≠0?
D=4(а-3)2>0 и
исходное уравнение имеет два различных корня х=0 и х=
),
тогда f(a)=2(a-2)≠0?
D=4(а-3)2>0 и
исходное уравнение имеет два различных корня х=0 и х=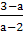 .
.
Ответ: 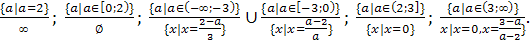
Замечание. Рассмотрим исходное уравнение как
уравнение с переменными а и х. изображение множества его решений в системе
координат Оах имеет следующий вид:
Y
x=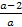
x=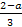

-3 0 2 3 a
x=
x=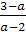
В уравнении f(a;b)x2+g(a;b)x+h(a;b)=0
не выше второй степени с параметрами а и b
и переменной х всякое частное уравнение принадлежит одному из вышеперечисленных
типов с аналогичными характеристиками. Контрольные значения параметров
определяются уравнениями f(a;b)=0
и D=g(a;b)2-4f(a;b)h(a;b)=0.
В плоскости Оаb эти уравнения
выделяют области, на которых дискриминант D
имеет определенный знак. Тогда общая схема решения уравнений с двумя
параметрами не меняется, лишь вместо числовой прямой используется координатная
плоскость Оаb. Графическое
изображение линий контрольных значений параметров и выделенных ими областей
однотипности обеспечивает наглядность в выполнении каждого из этапов решения.
Пример 3. Решить уравнение 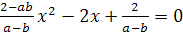 .
.
Решение. Частные уравнения не определены для
всех значений параметров a
и b, для которых a-b=0,
то есть на множестве {(a;b)|a=b}.
На области допустимых значений параметров {(a;b)|a≠b}
исходное уравнение равносильно уравнению (2-ab)x2-2(a-b)x+2=0.
Контрольными являются значения параметров, для которых 2-ab=0.
На множестве точек {(a;b)|b=a,ab=2}
гиперболы ab=2, исключая
точки (-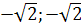 )
и (
)
и (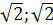 ),
соответствующие частные уравнения -2(a-b)x+2=0
имеют общее решение х=
),
соответствующие частные уравнения -2(a-b)x+2=0
имеют общее решение х=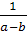 .
.
b
a
Для значений параметров {(a;b)|a≠b,ab≠2}
соответствующие частные уравнения являются квадратными. Дискриминант D=4(a-6)2-8(2-ab)=4(a2+b2-4)
обращается в нуль на множестве контрольных точек {(a;b)|a≠b,
a2+b2-4=0}
окружности a2+b2=4,
снова исключая точки(-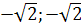 ) и (
) и (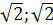 ).
).
На множестве {(a;b)|a≠b,
a2+b2=4}
точек окружности соответствующие частные уравнения (2-ab)(x-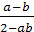 )2=0
имеют двукратный корень
)2=0
имеют двукратный корень 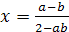 .
.
Для допустимых значений параметров, отличных от
точек гиперболы и окружности, дискриминант соответствующих квадратных уравнений
отличен от нуля. На множестве {(a;b)|a≠b,
a2+b2<4}
точек круга дискриминант D
отрицателен, и соответствующие частные не особые уравнения не имеют решений.
Для точек {(a;b)|a≠b,
ab≠2, a2+b2>4}
вне этого круга дискриминант D>0,
и общие решения уравнения х=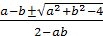 .
.
Ответ.
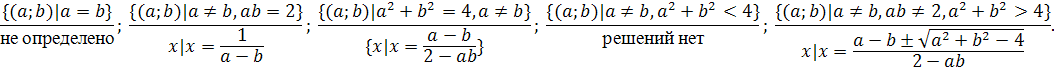
Пример 4. Решить уравнение 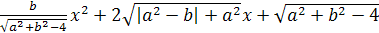 =0.
=0.
Решение. Для значений параметров {(a;b)|a2+b2-4≤0}соответствующие
частные уравнения не определены.
На области допустимых значений параметров {(a;b)|a2+b2-4>0}
выделим подмножество {(a;b)|a2+b2-4>0,b=0}
точек прямой Оа, исключая точки круга. Соответствующие частные уравнения имеют
вид 2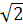 |a|х+
|a|х+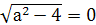 .
Их общее решение х=
.
Их общее решение х=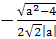 .
.
На множестве точек {(a;b)|a2+b2-4>0,b≠0}
частные уравнения имеют вторую степень. Их дискриминант D=4(|a2-b|+a2-b).
По определению модуля D=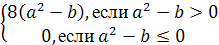 .
.
Для точек {(a;b)|a2+b2-4>0,b≠0,
b≥a2}
не ниже параболы, исключая точки круга и прямой b=0,
соответствующие не особые частные уравнения имеют вид 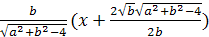 2=0.
2=0.
Тогда х=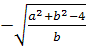 является двукратным корнем на множестве {(a;b)|a2+b2-4>0,b≠0,
b≥a2}.
является двукратным корнем на множестве {(a;b)|a2+b2-4>0,b≠0,
b≥a2}.
Все частные уравнения для значений параметров {(a;b)|a2+b2>4,
b≠0, b<a2}
вне круга и ниже параболы, исключая точки прямой b=0,
квадратные, причем дискриминант D=8(a2-b)>0.
Общие решения уравнения на данном множестве значений параметров имеют вид x=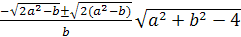 .
.
b
-2 2
a
Ответ. 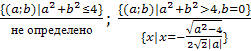 ;
;
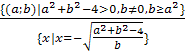 ;
;
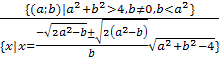 .
.
Формулировки многих заданий помимо решения уравнения
f(a)x2+g(a)x+h(a)=0
ставят задачи поиска значений параметров, для которых его общие решения f1(a)=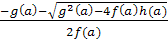 и f2(a)=
и f2(a)=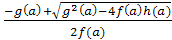 удовлетворяют одному из следующих условий:
удовлетворяют одному из следующих условий:
)оба или положительны, или отрицательны, или
имеют различные знаки;
)располагаются внутри некоторого промежутка (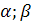 )
или вне его;
)
или вне его;
)располагаются определенным образом относительно
корней другого уравнения.
В таких формулировках присутствует некоторое
действительное число 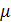 и требуется найти
значения параметра, обеспечивающие для общих решений х1=f1(a),
x2=f2(a)
одно из требований а)-в).
и требуется найти
значения параметра, обеспечивающие для общих решений х1=f1(a),
x2=f2(a)
одно из требований а)-в).
а)
б) в)
х1 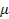 х2
х2
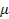 х1
х2 х1 х2
х1
х2 х1 х2
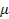
В первом случае таким числом является ноль, во
втором- числа, в третьем - один из корней другого уравнения. Простой способ
решения таких задач основан на справедливости следующих результатов о
расположении действительного числа относительно корней f1(a)
и f2(a)
многочлена F(a;x)=
f(a)x2+g(a)x+h(a)
с параметром а и переменной х.
.На множестве {a|f(a)≠0,D>0}
для общих решений f1(a)
и f2(a)
многочлена F(a;x)=
f(a)x2+g(a)x+h(a)
число удовлетворяет условию f1(a)<<f2(a)
(или f2(a)<<
f1(a))
для тех и только тех значений параметра, для которых f(a)F(a;)<0.
а)
б)
y
y
F(a;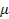 )
)
f1(a) 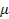 f2(a)
f2(a)
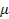 f1(a)
x
x
f1(a)
x
x
F(a;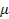 )
)
.На
множестве {a|f(a)≠0,D≥0}
для многочлена F(a;x)=
f(a)x2+g(a)x+h(a)
число 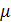 располагается
левее общих решений f1(a)
и f2(a)
для тех и только тех значений параметра, для которых f(a)F(a;
располагается
левее общих решений f1(a)
и f2(a)
для тех и только тех значений параметра, для которых f(a)F(a;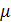 )>0
и
)>0
и 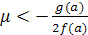 .
.
а)
б)
y
y
F(a;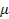 )
) 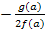
f2(a) f1(a)
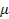 f1(a)
f2(a) x
f1(a)
f2(a) x
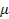
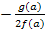 x
x
F(a;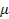 )
)
3.На
множестве {a|f(a)≠0,D≥0}
для многочлена F(a;x)=
f(a)x2+g(a)x+h(a)
число 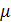 располагается
правее общих решений f1(a)
и f2(a)
для тех и только тех значений параметра, для которых f(a)F(a;
располагается
правее общих решений f1(a)
и f2(a)
для тех и только тех значений параметра, для которых f(a)F(a;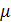 )>0
и
)>0
и 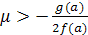 .
.
а)
y б)
y
F(a;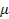 )
)
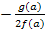
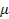
f2(a) f1(a)
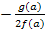
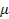 x
f1(a) f2(a) x
x
f1(a) f2(a) x
F(a;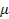 )
)
Пример 5. В уравнении (а-1)х2-2(а+1)х+а-3=0
найти все значения а, для которых его корни удовлетворяют одному из следующих
условий:
а)имеют разные знаки;
б)принадлежат промежутку (-1;5);
в)лишь меньший из корней уравнения располагается
между корнями уравнения х2-5х+6=0.
Решение. По условию для искомых значений
параметра соответствующие частные уравнения являются квадратными и имеют два
различных корня. Тогда а-1≠0 и D=8
(3а -1) >0.
а) На множестве {а /а  (
( ;1)
;1)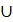 (1;
(1;
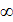 )}
корни х1 и х2 имеют разные знаки, если
)}
корни х1 и х2 имеют разные знаки, если 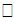 =0
располагается между ними. Это возможно только в случае, когда для F(a;x)=
(a-1)x
2-2(a+1)x+a-3
справедливо (а-1) F(а;0)<0,или
(а-1) (а-3)<0. Отсюда ,для а
=0
располагается между ними. Это возможно только в случае, когда для F(a;x)=
(a-1)x
2-2(a+1)x+a-3
справедливо (а-1) F(а;0)<0,или
(а-1) (а-3)<0. Отсюда ,для а  (1;3)
соответствующие частные уравнения имеют корни разных знаков.
(1;3)
соответствующие частные уравнения имеют корни разных знаков.
б) На множестве {а /а  (
(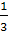 ;1)
;1)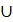 (1;
(1;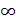 )}
корни х1 и х2 принадлежат промежутку (-1;5), если -1<х1<х2<5. Это
означает, что
)}
корни х1 и х2 принадлежат промежутку (-1;5), если -1<х1<х2<5. Это
означает, что 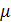 1=-1 располагается
левее х1 и х2 , а
1=-1 располагается
левее х1 и х2 , а 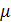 2=5- правее.
2=5- правее.
Число 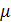 1=-1
меньше х1 и х2 лишь в случае, когда
1=-1
меньше х1 и х2 лишь в случае, когда
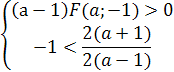
Число 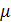 2=5
больше х1 и х2 только, если
2=5
больше х1 и х2 только, если
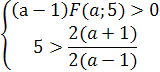
Поскольку F(a;-1)=(a-1)+2(a+1)+(a-3)=4a-2;
F(a;5)=25(a-1)-10(a+1)+(a-3)=16a-38,
то условие -1<х1<х2<5 выполняется при 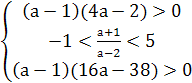 ,
то есть на множестве {a|a
,
то есть на множестве {a|a (
(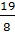 ;
;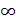 )}.
)}.
в) корни уравнения х2-5х+6=0 - числа 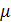 3=2
и
3=2
и 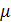 4=3.
Тогда условие 2<х1<3<х2 выполняется для тех значений параметра из
множества {а /а
4=3.
Тогда условие 2<х1<3<х2 выполняется для тех значений параметра из
множества {а /а  (
(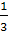 ;1)
;1)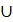 (1;
(1;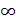 )},
которые являются решением системы
)},
которые являются решением системы 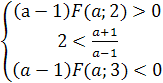 или
или
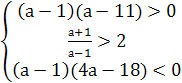 .
.
Система не имеет решений, то есть условие
2<х1<3<х2 не выполняется ни в одном из частных неравенств.
.6 Этапы работы над задачей с параметром
Как видно из рассмотренных примеров, квадратные
уравнения с параметром весьма разнообразны по своему содержанию. Техника работы
с квадратным трехчленом, основные идеи, связанные с квадратным трехчленом,
играют важную роль при решении задач с параметрами. Поэтому очень важно в таких
задачах выделять этапы решения, которые помогут прийти к какому-либо выводу.
Итак, необходимо выполнить 4 этапа:
) Знакомство с условием задачи;
) Поиск метода решения, выбор конкретного
метода и составление плана реализации;
) Реализация плана решения;
) Анализ решения и его улучшение.
Раскроем более подробно каждый из этапов.
) Знакомство с условием задачи. На данном
этапе должны быть задействованы чувства, воля, интеллект решателя. Некоторые из
действий отражены в следующей блок-схеме.
Знакомство
с условием задачи.
|
Выделение
признаков условия. Запись задания.
|
Выделение
различных объектов задания и выявление связи друг с другом, а так же с
известными объектами.
|
Определение
частей ситуации, которые знакомы, и возможные направления использования.
|
Осознание новой ситуации и переход к основному
этапу поиска метода решения задачи.
На данном этапе желательно рассмотреть объекты,
которые фигурируют в уравнении (здесь требуется рассмотреть одночлены, степень
неизвестного и тому подобное).
Выделенной на данном этапе информации бывает
недостаточно, поэтому нужна новая, поиск ее будет осуществляться на втором
этапе.
) Поиск метода решения и составление
плана. Выбор метода и возможность его применения увидеть не всегда удается, ибо
требуется видоизменить уравнение, получить новые следствия из условия,
применить известные теоретические положения, учесть индивидуальные особенности
уравнения, вспомнить аналогичные задания, проявить догадку. Действия решателя в
этом случае могут быть представлены в произвольной форме. Один из вариантов
отражен в следующей блок-схеме.
1
|
Ситуация
знакома.
|
Получение
следствий.
|
Введение
дополнительных объектов.
|
Выделение
индивидуальных особенностей ситуации.
|
Примерка
методов решения задач.
|
1 2 3 4 5 6 7 8
9 10 11 12
План решения
задач.
2
Этап поиска метода решения и составления плана
решения:
) Группировка.
) Добавление новых членов.
) Представление в виде суммы.
) Перенос из одной части в другую.
) Преобразования.
) Применение формул.
) Замена.
) Формулировка частных задач.
) Угадывание.
) Переформулировка.
) Преобразование.
) Получение следствий.
) Этап реализации плана решения. Действия
решателя могут быть представлены в следующей блок-схеме.
2
Выполнение отдельных пунктов плана
Обоснование выполнимости действий
|
Самоконтроль
и внесение необходимых корректур
|
|
1
|
2
|
3
|
4
|
5
|
Запись ответа
Этап реализации плана решения:
) Полная проверка корней.
) Решение уравнения другим методом.
) Самопроверка на основе теории.
) Выполнение обратных действий.
) Проверка выкладок.
) Анализ решения и его улучшение. К
сожалению, в большинстве случаев школьники ограничиваются тремя этапами работы
над задачей. Но если школьник действительно хочет научиться решать задачи, то
требуется уделить особое внимание завершающему этапу работы над задачей. Здесь
существенно осознать: в чем была основная трудность поиска метода решения, что
помогло найти его, как использовать опыт решения в дальнейшем и тому подобное.
Другие действия отражены в следующей блок-схеме.
3
Анализ решения.
|
Какие
трудности встретились.
|
Что
помогло найти решение.
|
Какие
были допущены ошибки.
|
Как
удалось найти и исправить.
|
|
Установление
недочетов оформления.
|
|
Упрощение
решения.
|
Более
четкое изложение.
|
Другие
методы решения задач (упущенные возможности).
|
Систематизация
опыта.
|
|
5
|
6
|
7
|
8
|
Анализ решения:
) Интересные частные случаи.
) Аналогичные задачи.
) Обобщение задачи.
) Обратные задачи.
) О решении уравнения в целом.
) О методе решения (и его поиске).
) Способ распознавания.
) Отражение в справочнике.
III. Система упражнений для отработки навыков
решения задач с параметрами
.1 Классификация задач на решение линейных
уравнений с параметром
.1 Исследование решений линейных уравнений
в зависимости от установленных значений параметра
Пример 1. Выясните, имеет ли корни уравнение при
заданном значении а: 4х-а=4х+4 при а=-2.
Решение. Преобразуя данное уравнение, получим
-а=4. Подставим значение а в уравнение -(-2)=4; 2=4. Получим ложное равенство.
Следовательно, при а=-2 уравнение корней не имеет.
Ответ. нет корней.
Пример 2. Выясните имеет ли корни уравнение при
заданном значении а: 5х+а=4х+1 при а=3.
Решение. Преобразуя данное уравнение, получим
х=1-а. подставим значение а в уравнение х=1-3; х=-2. При а =3 уравнение имеет
единственный корень х=-2.
Ответ. х=-2.
Пример 3. Найдите число а такое, чтобы уравнение
5х-4=3х+а имело корень х=1.
Решение. Преобразуя данное уравнение, получим
2х-4=а. подставим значение х в уравнение: 2*1-4=а; а=-2.
Ответ. а=-2.
.2 Поиск решения линейных уравнений с параметром
Пример 1. Решить уравнение ах=1.
Решение. На
первый взгляд представляется возможным сразу дать ответ:
х=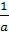 . Однако при а=0
данное уравнение решений не имеет, и верный ответ выглядит так:
. Однако при а=0
данное уравнение решений не имеет, и верный ответ выглядит так:
Ответ.
если а=0, то нет решений; если а≠0, то х=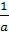 .
.
Пример 2. Решить уравнение (а-2)х=10-5х
относительно х.
Решение. (а-2)х+5х=10.
х(а+3)=10.
Если а=-3, то х*0=10- неверное равенство.
Если а≠-3, то х=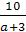 .
.
Ответ. если
а=-3, решений нет; если а≠-3, то х=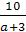 .
.
Пример 3. Решить уравнение (а2-1)х=а+1.
Решение. 1)
а=1, уравнение не имеет решений;
) а=-1, х R;
R;
) а≠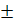 1,
х=
1,
х=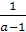 .
.
Ответ. если
а=-1,то х- любое; если а=1, то нет решений; если а≠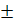 1,
то х=
1,
то х=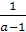 .
.
Пример 4. Решить уравнение ах+а+3=2а+5.
Решение. Решение
этого уравнения требует вначале преобразований: ах=2а+5-а-3. ах=а+2. Если а=0,
то 0=2 не верно. Следовательно, уравнение не имеет корней. Если а≠0, то
х=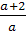 .
.
Ответ.
если а=0, то решений нет; если а≠0, то х=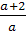 .
.
Пример 5. Решить уравнение 3х-4(х-а)=4+а.
Решение.
3х-4х+4а=4+а.
х=-4а+4+а.
х=-3а+4|*(-1).
х=3а-4.
а R.
R.
Ответ.
а R,
х=3а-4.
R,
х=3а-4.
Пример 6. При каждом значении а решите уравнение
а(х-2)=4(х+2).
Решение. ах-2а=4х+8.
х(а-4)=2а+8.
Если а=4, то х*0=16, корней нет.
Если а≠4, то х=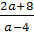 .
.
Ответ.
Если а=4, то корней нет; если а≠4, то х=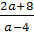 .
.
Пример 7. При каждом значении а решите уравнение
а2х-7=7а+х.
Решение.
х(а2-1)=7+7а.
Если а=1, то х*0=14, то есть корней нет.
Если а=-1, то х*0=0, то есть х R.
R.
Если а≠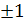 ,
то х=
,
то х=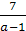 .
.
Ответ. Если
а=1, то корней нет; если а=-1, то х R;
если а≠
R;
если а≠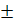 1, то х=
1, то х=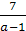 .
.
Пример 8. Решить уравнение а2х=а(х+2)-2.
Решение.
а(а-1)х=2(а-1).
Если а=1, то 0*х=2*0, то есть х R.
R.
Если а=0, то 0*х=-2, корней нет.
Если а≠0 и а≠1, то х=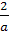 .
.
Ответ.
Если а=0, корней нет; если а=1, х R;
если а≠0 и а≠1, то х=
R;
если а≠0 и а≠1, то х=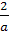 .
.
Пример 9. Решить уравнение а2(х-2)-3а=х+1.
Решение.
(а2-1)х-2а2-3а-1=0.
(а2-1)х=2а2+3а+1.
х(а-1)(а+1)=2(а+1)(а+0,5).
Если а=1, то х*0=6, то есть корней нет.
Если а=-1, то х*0=0, то есть х R.
R.
Если а≠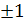 ,
то х=
,
то х=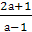 .
.
Ответ.
Если а=1, то корней нет; если а=-1, то х R;
если а≠
R;
если а≠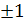 , то х=
, то х=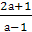 .
.
Пример 10. Решить уравнение (n2-5)x+n=n(n-4x).
Решение.
(n2-5)x+4nх=n2-n.
x(n2+4n-5)=n2-n.
Если n2+4n-5=0,
то D=16+20=36. n1=1;
n2=-5.
Если n=1,
то х*0=0, то есть х R.
R.
Если n=-5,
то х*0=30, то есть корней нет.
Если n≠1
и n≠-5, то х=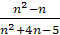 .
.
Ответ.
Если n=1, то х R;
если n=-5, то корней нет;
если n≠1 и n≠-5,
то х=
R;
если n=-5, то корней нет;
если n≠1 и n≠-5,
то х=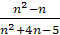 .
.
Пример 11. Решить уравнение х+ =2.
=2.
Решение.
х(1+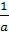 )=2.
)=2.
Если а=0, то х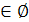 .
.
Если а≠0, то х=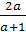 .
.
Если а=-1, то корней нет.
Ответ.
Если а≠0 и а≠-1, х=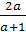 ; в остальных
случаях корней нет.
; в остальных
случаях корней нет.
Пример 12. Решить уравнение 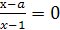 .
.
Решение.
Если х=1, то нет решений. Следовательно, х=a-
единственный корень при а≠1.
Ответ.
Если а≠1, то х=а; если а=1, то нет решений.
Пример 13. Решить уравнение 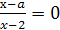 .
.
Решение.
Если а=2, то уравнение корней не имеет. Если а≠2, то х=а.
Ответ.
Если а=2, то корней нет; если а≠2, то х=а.
Пример 14. Решить уравнение 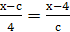 .
.
Решение.
Если с=0, то корней нет.
Если с≠0, то 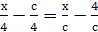 .
.
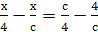 .
.
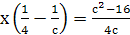 .
.
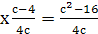 .
.
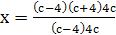 .
.
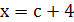 .
.
Ответ.
Если с=0, то корней нет; если с≠0, то х=с+4.
Пример 15. Решить уравнение 4=а-(bx-1).
Решение.
4=а-bx+1.
bx=a-3.
Если b=0
и а=3, то х R.
R.
Если b=0
и а≠3, то корней нет.
Если b≠0
и а≠3, то х=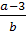 .
.
Если b≠0
и а=3, то х=0.
Ответ.
Если b=0 и а=3, то х R;
если b=0 и а≠3, то
корней нет; если b≠0 и
а=3, то х=0; если b≠0 и а≠3,
то х=
R;
если b=0 и а≠3, то
корней нет; если b≠0 и
а=3, то х=0; если b≠0 и а≠3,
то х=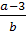 .
.
.3 Решение линейных уравнений с параметрами с
дополнительными данными в условии задачи
Пример 1. При каких значениях параметра с корень
уравнения х+с=3х-5 является неотрицательным числом?
Решение. х-3х=-с-5.
х=-с-5.
х=с+5.
х≥0 при с+5≥0.
с≥-5.
Ответ. при с≥-5.
Пример 2. Найдите все значения параметра а, при
каждом из которых число -3 является единственным корнем уравнения а2х+6а=4х-12.
Решение. х(а2-4)=-6а-12.
Если а=2, то х*0=-24, то есть корней нет.
Если а=-2, то х*0=0, то есть х R.
R.
Если а≠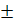 2,
то
2,
то 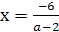 -
единственный корень.
-
единственный корень.
Х=-3.
а2+6а+24=0|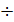 (-3).
(-3).
а2-2а-8=0.
D=4+32=36.
a1=4; a2=-2.
- не удовлетворяет условию.
Ответ. а=4.
Пример 3. Найдите все значения параметра а, при
каждом из которых уравнения ах-5=х+а и а2х-3=х+а2 имеют общий корень.
Решение. (а-1)х=а+5. Уравнение имеет корень лишь
при а≠1. 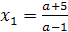 .
.
(а2-1)х=а2+3. Данное уравнение имеет корень лишь
при а≠±1. 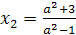 .
.
Осталось найти все значения параметра а≠±1,
при каждом из которых оба уравнения имеют общий корень, то есть х1 и х2 есть
одно и то же число.
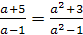 .
.
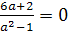 .
.
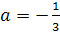 .
.
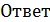 . При
. При 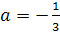 .
.
Пример 4. Найти все значения параметра а, при
каждом из которых уравнения ах+1=2х+а и а2х-1=4х+а2 имеют общий корень.
Решение. ах+1=2х+а.
х(а-2)=а-1. Уравнение имеет корень лишь при а≠2.
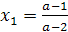 .
.
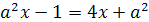 .
.
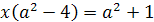 . Уравнение имеет
корень лишь при а≠±2.
. Уравнение имеет
корень лишь при а≠±2.
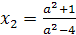 .
.
Уравнения имеют общий корень при 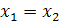 .
.
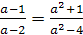 .
.
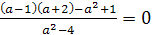 .
.
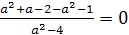 .
.
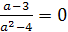 .
.
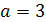 .
.
Ответ. при 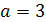 .
.
Пример 5. При каких целых значениях параметра а
корень уравнения 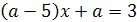 лежит в промежутке
[0;5]?
лежит в промежутке
[0;5]?
Решение. очевидно, при а≠5 уравнение имеет
корень 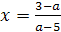 .
Найдем значения а, при которых корень уравнения лежит в промежутке [0;5]. Для
этого решим двойное неравенство 0
.
Найдем значения а, при которых корень уравнения лежит в промежутке [0;5]. Для
этого решим двойное неравенство 0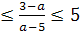 .
.
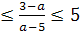
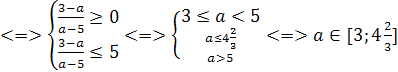
Ответ. a=3,
a=4.
.4 Тренировочные упражнения
1. 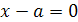
2. 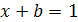
3. 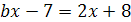
4. 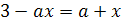
5. 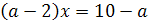
6. 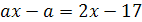
7. 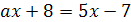
8. 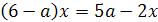
9. 3ax-4(2+x)=6
10. 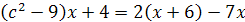
11. 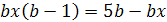
12. 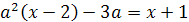
13. 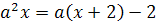
14. 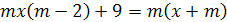
15. 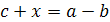
16. 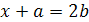
17. 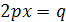
18. 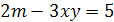
19. 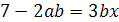
20. 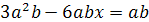
21. 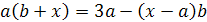
22. 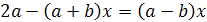
23. 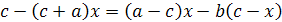
24. 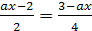
25. 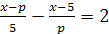
26. 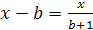
27. 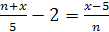
28. 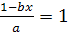
29. 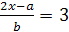
30. При каком значении а прямые 5х-3y=15
и ах+7y=-6 пересекаются в
точке, принадлежащей оси абсцисс?
. Графики функций y=(4-a)x+a
и y=ax+2
пересекаются в точке с абсциссой, равной -2. Найдите ординату точки
пересечения.
.5 Графическая иллюстрация решения уравнений с
параметрами
Как уже было отмечено, у учащихся возникают
трудности на этапе систематизации полученных результатов, в том числе и при
записи ответов. С целью её преодоления используется прием получения результата
с одновременным изображением его на координатной плоскости. Рассмотрим суть
данного приема на конкретных задачах.
Пример 1. При каждом значении а и b
решите уравнение:
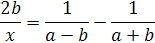
Паре чисел (а; b)
соответствует вполне определенное частное уравнение. Упорядоченную пару чисел
(а; b) мы будем
интегрировать как точку на координатной плоскости с осями а и b.
Таким образом, устанавливается взаимно однозначное соответствие между точками
плоскости и всеми частными уравнениями, определенными парой (а; b).
Следовательно, получили аналог развертки по параметру - плоскость параметров,
позволяющую наглядно представить множество значений параметров и соответствующие
им решения уравнения.
При b=±a
правая часть уравнения не имеет смысла, следовательно, уравнение не имеет
решений.
Отметим на плоскости параметров те ее точки,
координаты (а;b) которых не
являются допустимыми значениями параметров данного уравнения. То есть всем
точкам прямых b=±a
соответствуют частные уравнения, не имеющие решений.
Примечание: в скобках будем указывать решения,
соответствующие данным точкам плоскости.
b
b=-a
b=a
(решений
нет) (решений нет)
0 a
При условии x≠0
и b≠±a
исходное уравнение равносильно уравнению 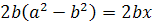 .
.
· Если b=0,
a- любое число,
отличное от нуля, то всем точкам прямой b=0
(а≠0) соответствуют частные уравнения вида 0х=0, решениями которых
являются все действительные числа, отличные от нуля.
b
b=-a
b=a
(решений
нет) (решений
нет)
b=0, a≠0
(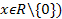
0 a
≠±b, b≠0 (x=a2-b2)
· Если b≠0
и a≠±b,
то x=a2-b2.
Таким образом, если точка с координатами (a;b)
не лежит на прямых b≠±a
и b=0, то частные
уравнения вычисляются по формуле x=a2-b2.
При записи ответа результаты исследования
считываются с плоскости параметров.
Ответ. 1. 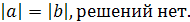
2.b=0, a≠0, 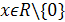
.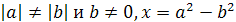 .
.
Пример 2. При каждом значении m
и n решите уравнение
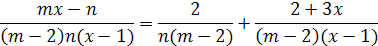
Найдем области допустимых значений переменной и
области допустимых значений параметров: 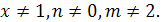 отметим
последние на плоскости параметров.
отметим
последние на плоскости параметров.
m
2 m=2 (решений
нет)
0 n=0 (решений
нет) n
При найденных ограничениях на переменную и
параметры уравнение равносильно уравнению 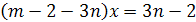 .
.
Если 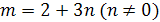 ,
то есть всем точкам прямой
,
то есть всем точкам прямой 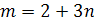 , за исключением
точки (0;2), соответствуют частные уравнения вида
, за исключением
точки (0;2), соответствуют частные уравнения вида 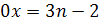 .
.
m
m=2+3n
2 m=2 (решений
нет)
n
0 n=0 (решений
нет)
Тогда:
а) при 3n-2,
то есть n=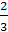 ,
m=4 имеем уравнение
0х=0, решениями которого являются все действительные числа х (х≠1) из
области определения уравнения.
,
m=4 имеем уравнение
0х=0, решениями которого являются все действительные числа х (х≠1) из
области определения уравнения.
m
4 n= , m=4
(x
, m=4
(x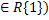
2 m=2 (решений нет)
0 n=0 (решений нет) n
б) при 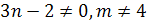 уравнение
уравнение
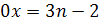 решений
не имеет.
решений
не имеет.
Если 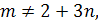 то
решения уравнения
то
решения уравнения 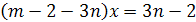 находятся по
формуле
находятся по
формуле 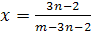 .
.
Отметим полученные результаты на плоскости параметров:
всем точкам плоскости, не лежащим на прямых m=2,
n=0, m=3n+2,
соответствуют решения уравнения, вычисленные по формуле 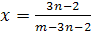 .
Но среди найденных решений уравнения при некотором наборе значений (m;n)
могут находиться х, не входящие в область определения уравнения. Исключим их:
.
Но среди найденных решений уравнения при некотором наборе значений (m;n)
могут находиться х, не входящие в область определения уравнения. Исключим их: 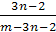 =1,
откуда m=6n.
=1,
откуда m=6n.
Следовательно, если точка плоскости лежит на
прямой m=6n
(n≠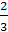 ),
то уравнение решений не имеет.
),
то уравнение решений не имеет.
m
m≠3n+2
n= , m=4
, m=4
n≠0, m≠2
(xєR\{1})
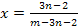 m=2
m=2
(решений нет)
2
0 n=0
n
m=2+3n
(решений нет)
(n≠ )
)
(решений нет)
Ответ. 1) n=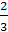 и m=4, xєR\{1}
и m=4, xєR\{1}
) n=0,
или m=6n
(n≠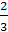 ),
или m=3n+2
(n≠
),
или m=3n+2
(n≠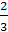 ),
или m=2,решений нет.
),
или m=2,решений нет.
) m≠3n+2
и m≠6n,
и n≠0, и m≠2
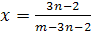 .
.
Пример 3. При каждом значении a
и b решите уравнение 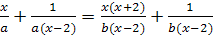 .
.
Решение. Очевидно, что при b=0
или а=0 уравнение не имеет смысла и , следовательно, не имеет решений. Кроме
того, х≠2. Пусть b≠0,
а≠0, х≠2. В этом случае уравнение равносильно уравнению 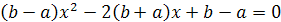 .
.
а) Воспользуемся приемом понижения степени: a=b.
Тогда уравнение примет вид 4bx=0
(b≠0), откуда
х=0. Получим, что точкам прямой b=a
(b≠0)
соответствует решение х=0.
b
b=0
(решений нет) b=a (x=0)
0 b=0
(решений нет) а
б) Пусть а≠b,
тогда 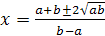 ,
где ab>0, при ab<0
решений нет.
,
где ab>0, при ab<0
решений нет.
в) Среди найденных наборов a
и b исключим
посторонние, то есть те, при которых х=2 (кроме b=0,
a=0, b=a).
Следовательно, 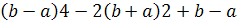 , отсюда b=9a.
Следовательно, если b=9a,
то
, отсюда b=9a.
Следовательно, если b=9a,
то 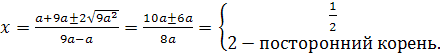
Получили, что всем точкам, лежащим на прямой b=9a,
соответствует частное решение уравнения х= , а всем остальным
точкам плоскости (не лежащим на прямых b=9a,
b=a)
, а всем остальным
точкам плоскости (не лежащим на прямых b=9a,
b=a)
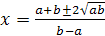 .
.
b
a=0
b=9a
(решений нет) (x= ) b=a (x=0)
) b=a (x=0)
Решений нет
b=0 (решений
нет)
0 a
Решений нет
Ответ: если ab≤0,
то решений нет; если ab>0,
то при b=a,
x=0; при b=9a,
x=0,5; при b≠9a,
b≠a,
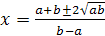 .
.
1.6 Линейные уравнения с параметром, содержащие
модуль
При решении задач с параметрами умение аккуратно
преобразовывать выражения, последовательно рассматривая «особые случаи», должно
быть дополнено способностью «чувствовать» выражения, интуитивно понимая, какие
значения может принимать выражение в целом или отдельные его части. Одним из
классов задач, способствующих развитию подобных навыков, являются задачи с
модулями. Именно такие примеры можно предложить после вводных уроков.
Пример 1. Решите уравнение 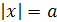 .
.
Решение. Это уравнение опирается на знание
определения модуля. Так, 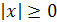 . Следовательно, a≥0.
. Следовательно, a≥0.
Ответ. а≥0.
Пример 2. Решите уравнение 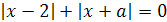 .
.
Решение. Так как каждое слагаемое
неотрицательное, то можно перейти к системе:
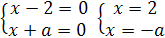
Ответ. Если а=-2, то х=2; если а≠-2, то
решений нет.
Пример 3. Решите уравнение 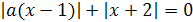 .
.
Решение. Так как каждое слагаемое
неотрицательное, то можно перейти к системе:
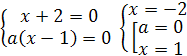
Ответ. Если а=0, то х=-2; если а≠0, то
решений нет.
Пример 4. Решите уравнение 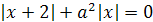 .
.
Решение. Так как каждое слагаемое
неотрицательное, то можно перейти к системе:
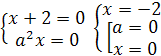
Ответ. Если а=0, то х=-2; если а≠0, то
решений нет.
Пример 5. Решите уравнение 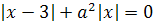 .
.
Решение. Так как каждое слагаемое
неотрицательное, то можно перейти к системе:
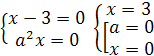
Ответ. Если а=0, то х=3; если а≠0, то
решений нет.
Пример 6. Решите уравнение 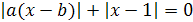 .
.
Решение. Так как 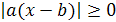 и
и
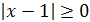 при
всех значениях х, то их сумма может оказаться равной нулю лишь при условии, что
оба слагаемых равны нулю:
при
всех значениях х, то их сумма может оказаться равной нулю лишь при условии, что
оба слагаемых равны нулю:
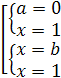
Рассмотрим два случая:
1) 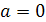 .
Тогда решением совокупности является
.
Тогда решением совокупности является 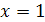 при
всех значениях b.
при
всех значениях b.
2) 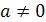 .
Тогда первая система совокупности не имеет решений, а вторая система имеет
решение
.
Тогда первая система совокупности не имеет решений, а вторая система имеет
решение 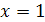 лишь
при b=1. Следовательно,
при b=1 уравнение имеет
единственное решение
лишь
при b=1. Следовательно,
при b=1 уравнение имеет
единственное решение 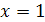 , при b≠1
не имеет решений.
, при b≠1
не имеет решений.
Ответ: при 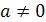 и
b≠1 нет
решений, в остальных случаях (то есть при
и
b≠1 нет
решений, в остальных случаях (то есть при 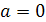 или
b=1) уравнение имеет
единственное решение
или
b=1) уравнение имеет
единственное решение 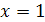 .
.
Глядя на правильный ответ, можно предложить
учащимся решение-рассуждение, не требующее никаких выкладок: сумма двух модулей
может оказаться равной нулю лишь в том случае, если оба слагаемых равны нулю.
Второе слагаемое определяет единственный возможный корень 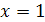 ,
а первое равно нулю лишь в том случае, если хотя бы один из множителей равен
нулю: либо
,
а первое равно нулю лишь в том случае, если хотя бы один из множителей равен
нулю: либо 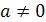 , либо b=x,
что при единственном возможном решении x=1
эквивалентно условию b=1.
Во всех остальных случаях уравнение не имеет корней.
, либо b=x,
что при единственном возможном решении x=1
эквивалентно условию b=1.
Во всех остальных случаях уравнение не имеет корней.
Пример 7. Решить уравнение 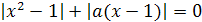 .
.
Решение. При 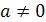 второе
уравнение системы, а значит, и сама система имеет единственное решение x=1.
Если же a=0, то из второго
уравнения получаем x - любое.
Следовательно, в этом случае система имеет два решения: x=1
или x=-1.
второе
уравнение системы, а значит, и сама система имеет единственное решение x=1.
Если же a=0, то из второго
уравнения получаем x - любое.
Следовательно, в этом случае система имеет два решения: x=1
или x=-1.
Ответ. если 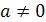 ,
то
,
то 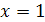 ,
если a=0, то x=±1.
,
если a=0, то x=±1.
.7 Линейные уравнения с параметром, содержащие
квадратные корни
Обратим внимание, что во всех решенных примерах
областью допустимых значений как для переменной, так и для параметра являлось
все множество действительных чисел. Разумеется, следует познакомиться с
задачами иного рода.
Пример 1. Решить уравнение  .
.
Решение. легко увидеть, что x=a
- единственный корень данного уравнения. Однако, этот результат - еще не ответ.
специфика уравнений с параметрами предполагает даже в таком тривиальном
уравнении, как x-a=0,
отмечать, что x=a
- корень при любом a.
Ответ. Если a≥0,
то x=a,
если a<0, то нет
решений.
Пример 2. Решить уравнение 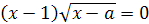 .
.
Решение. 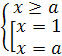 .
.
Отсюда x=a
- корень исходного уравнения при любом a,
а x=1 - корень лишь
при a≤1.
Ответ. Если a<1,
то x=0 илиx=1,
если a=1, то x=1,
если a>1, то x=a.
Пример 3. Выясните, при каких значениях
параметра a данные уравнения
имеют ровно один корень:
а) 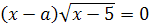 ;
;
б) 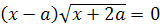 .
.
а) 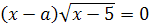 .
.
Решение. 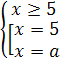
Отсюда x=5
- корень исходного уравнения при любом a≠5.
Ответ. x=5
при a≠5 -
единственный корень.
б) 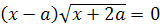 .
.
Решение. 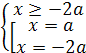
Отсюда 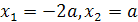 ,
если a>0. И x=-2a,
если a<0. Уравнение
имеет единственный корень лишь при а<0.
,
если a>0. И x=-2a,
если a<0. Уравнение
имеет единственный корень лишь при а<0.
Ответ. При а<0 x=-2a
- единственный корень.
Пример 4. При каких а уравнение 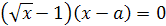 имеет
единственное решение?
имеет
единственное решение?
Решение. При любом а x=1
- корень данного уравнения, и требование единственности решения сводит задачу к
поиску условий, при которых уравнению «запрещено» иметь корни, отличные от
единицы. В то же время множитель x-a
как бы предлагает еще один корень, и, на первый взгляд, значение a=1
представляется достаточным для ответа. Но более внимательный анализ позволяет
«отмести» x=a
за счет области определения уравнения: при a<0
x=a
не является корнем.
Ответ. a=1
или a<0.
Пример 5. Решить уравнение 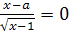 .
.
Решение. 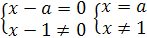
Если a=1,
то корней нет.
Ответ. Если a≠1,
то x=a,
если a=1, то корней нет.
Пример 6. Решить уравнение 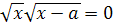 .
.
Решение. x=0
или x-a=0.
Откуда x=a.
Причем, x-a≥0.
Следовательно, x≥a.
Ответ. Если a<x,
то x=0, если a=x,
то xєR, если a>x,
то решений нет.
Пример 7. Решить уравнение 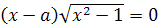 .
.
Решение. 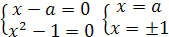 .
.
Ответ. Если 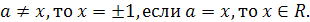
Пример 8. Решить уравнение 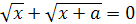 .
.
Решение. Сумма двух корней может оказаться
равной нулю лишь в том случае, если оба слагаемых равны нулю.
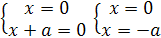 .
.
Ответ. Если a=0,
то x=0, если a≠0,
то решений нет.
Пример 9. Решить уравнение 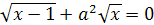 .
.
Решение. 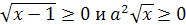 .
Следовательно,
.
Следовательно, 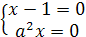 .
.
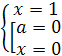 .
.
Ответ. Если a=0,
то x=1, если a≠0,
то решений нет.
.2 Классификация задач на решение квадратных
уравнений с параметром
Выделим класс задач, где за счет параметра на
переменную накладываются какие- либо искусственные ограничения. Для таких задач
характерны следующие формулировки: при каком значении параметра уравнение имеет
одно решение, два, бесконечно много, ни одного; решением уравнения является
какое-то подмножество множества действительных чисел и другие.
Прежде всего сюда относятся уравнения второй
степени. Поэтому, прежде всего, обратим внимание на распространенную ошибку: считать
такое уравнение квадратным. На самом деле это уравнение степени не выше второй.
Пользуясь этим соображением, естественно начать решение, рассмотрев случай,
когда коэффициент перед x2
равен нулю. Итак, если параметр равен нулю, то, очевидно, данное уравнение
имеет единственное решение. если же a≠0,
то имеем дело с квадратным уравнением.
.1 Уравнения с ограничениями для решения
Пример 1. Решить уравнение 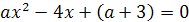 .
.
Решение. Данное уравнение имеет один параметр а.
если a=0, то пишем
линейное уравнение -4x+3=0,
которое имеет один корень 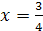 . При a≠0
уравнение является квадратным, и его корни выражаются через параметр а
формулами
. При a≠0
уравнение является квадратным, и его корни выражаются через параметр а
формулами 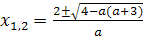 . Эти формулы имеют
числовые значения, если:
. Эти формулы имеют
числовые значения, если: 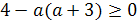 . Решая это неравенство,
находим:
. Решая это неравенство,
находим:
при 
при 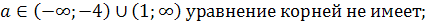
при 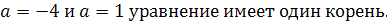
Ответ. При 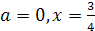 ;
при
;
при 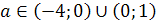 ,
,
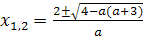 ;
при
;
при 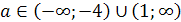 корней
нет.
корней
нет.
Пример 2. Решить уравнение 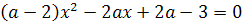 .
.
Решение. рассмотрим два случая: a=2
и a≠2. В первом
случае исходное уравнение принимает вид -4x+1=0.
Это линейное уравнение с единственным корнем 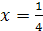 .
Во втором случае получим квадратное уравнение с дискриминантом
.
Во втором случае получим квадратное уравнение с дискриминантом 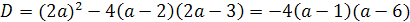 .
.
Найдем промежутки знакопостоянства
дискриминанта.
При a=1
или a=6 дискриминант
квадратного уравнения равен нулю, и оно имеет один корень 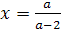 ,
то есть при a=1 получаем корень
,
то есть при a=1 получаем корень 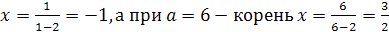 .
.
При 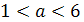 дискриминант
положительный, и квадратное уравнение имеет два корня:
дискриминант
положительный, и квадратное уравнение имеет два корня:
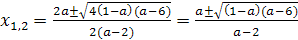 .
.
При 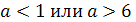 дискриминант
оказывается отрицательным. Следовательно, квадратное уравнение не имеет корней.
дискриминант
оказывается отрицательным. Следовательно, квадратное уравнение не имеет корней.
Ответ. При 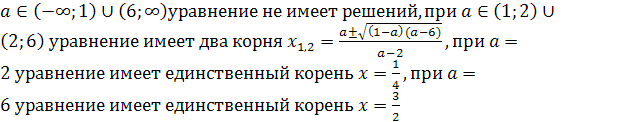 .
.
Пример 3. Решить уравнение 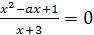 .
.
Решение. 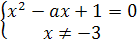 .
Наличие квадратного уравнения приведет к поиску корней дискриминанта. Вместе с
тем условие
.
Наличие квадратного уравнения приведет к поиску корней дискриминанта. Вместе с
тем условие 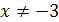 должно привлечь
внимание.
должно привлечь
внимание.
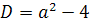 .
.
Если D>0,
то есть 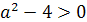 ,
,
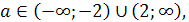 то
уравнение имеет два корня
то
уравнение имеет два корня 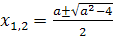 . Если
. Если 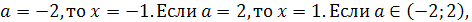 то
корней нет.
то
корней нет.
Ответ. Если 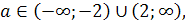 то
то
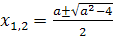 ,
если
,
если 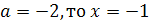 ,
если
,
если 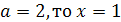 ,
если
,
если 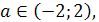 то
корней нет.
то
корней нет.
Пример 4. Решить уравнение  .
.
Решение. Если a=-6,
то решаем линейное уравнение -8x-6=0.
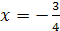 .
.
Если a≠-6,
то решаем квадратное уравнение.
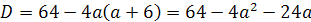 .
.
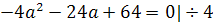 .
.
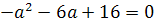 .
.
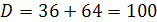 .
.
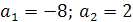 .
.
Если 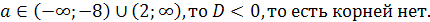
Если 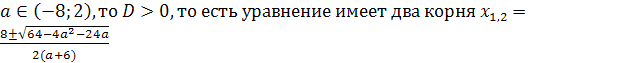 .
.
Если a=-8,
то x=-2.
Если a=2,
то x=0,5.
Ответ. Если 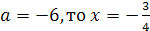 ,
если
,
если 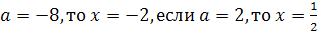 ,
если
,
если 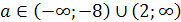 ,
то корней нет, если
,
то корней нет, если 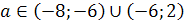 , то
, то 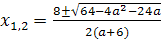 .
.
Пример 5. Найти все значения параметра b,
при каждом из которых уравнение 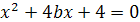 имеет два
различных корня.
имеет два
различных корня.
Решение. рассматриваемое квадратное уравнение
имеет два различных корня, если дискриминант его положительный. Запишем это
условие: 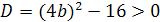 .
Из последнего неравенства получим
.
Из последнего неравенства получим 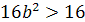 ,
откуда b>1.
,
откуда b>1.
Ответ. b>1.
Пример 6. Найти все значения параметра p,
при каждом из которых уравнение 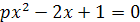 имеет два
различных корня.
имеет два
различных корня.
Решение. Выпишем условие положительности
дискриминанта данного квадратного трехчлена.
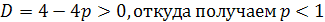 . При p=0
единственное решение.
. При p=0
единственное решение.
Ответ. 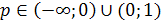 .
.
Пример 7. Найти все значения параметра p,
при каждом из которых уравнение 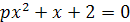 имеет ровно одно
решение.
имеет ровно одно
решение.
Решение. Пусть p=0.
Тогда исходное уравнение принимает вид x+2=0
и имеет единственное решение x=-2.
Пусть теперь p≠0.
В этом случае исходное уравнение имеет одно решение, если его дискриминант
равен нулю. Получаем D=1-8p=0,
откуда 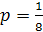 .
.
Ответ. 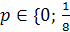 }.
}.
Пример 8. Найти все значения параметра p,
при каждом из которых уравнение 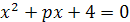 имеет одно
решение.
имеет одно
решение.
Решение. Исходное уравнение имеет одно решение
при D≥0, при этом,
если D=0, то уравнение
имеет ровно одно решение, а при D>0
- два решения (а если есть два решения, то есть и одно). Решая неравенство 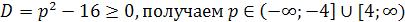 .
.
Ответ. 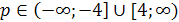 .
.
Пример 9. При каких a
уравнение имеет единственное решение 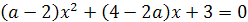 ?
?
Решение. Понятно, что нужно начинать со случая a=2.
Но при a=2 исходное
уравнение вообще не имеет решений. Если a≠2,
то данное уравнение квадратное, и казалось бы, искомые значения параметра - это
корни дискриминанта. Однако дискриминант обращается в нуль при a=2
или a=5. Поскольку мы
установили, что a=2 не подходит,
то a=5.
Ответ. a=5.
Пример 10. При каких a
уравнение 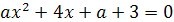 имеет более одного
корня?
имеет более одного
корня?
Решение. При a=0
уравнение имеет единственный корень, что не удовлетворяет условию. При a≠0
исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант 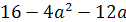 -
положителен. Отсюда получаем -4<a<1.
Однако в полученный промежуток (-4;1) входит число 0, которое, как мы уже
проверили, неприемлемо.
-
положителен. Отсюда получаем -4<a<1.
Однако в полученный промежуток (-4;1) входит число 0, которое, как мы уже
проверили, неприемлемо.
Ответ. -4<a<0
или 0<a<1.
Пример 11. При каких a
уравнение 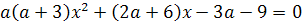 имеет более одного
корня?
имеет более одного
корня?
Решение. Стандартный шаг начать со случаев a=0
и a=-3. При a=0
уравнение имеет единственное решение. Любопытно, что при a=-3
решением уравнения служит любое действительное число. При a≠-3
и a≠0, разделив
обе части данного уравнения на a+3,
получим квадратное уравнение 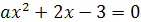 , дискриминант
которого 4(1+3a) положителен при
, дискриминант
которого 4(1+3a) положителен при 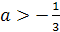 .
Опыт предыдущих промежутков показывает, что из промежутка (
.
Опыт предыдущих промежутков показывает, что из промежутка (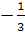 ;
;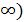 надо исключить точку a=0,
а в ответ не забыть включить a=-3.
надо исключить точку a=0,
а в ответ не забыть включить a=-3.
Ответ. a=-3
или 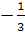 <a<0,
или a>0.
<a<0,
или a>0.
.2 Задачи на использование теоремы Виета
Пример 1. При каких значениях параметра а
уравнение 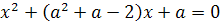 имеет корни, сумма
которых равна нулю?
имеет корни, сумма
которых равна нулю?
Решение. Это уравнение квадратное, его
дискриминант 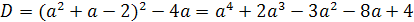 .
.
Сумма корней уравнения равна -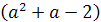 и по условию задачи она равна нулю, то есть
и по условию задачи она равна нулю, то есть 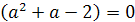 ,
что возможно при
,
что возможно при 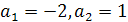 . Теперь необходимо
осуществить контроль неотрицательности дискриминанта при этих значениях а. при
а=-2 дискриминант D=0+4*2=8
положителен, тогда как при а=1 дискриминант D=0-4=-4
оказывается отрицательным.
. Теперь необходимо
осуществить контроль неотрицательности дискриминанта при этих значениях а. при
а=-2 дискриминант D=0+4*2=8
положителен, тогда как при а=1 дискриминант D=0-4=-4
оказывается отрицательным.
Ответ. а=-2.
Пример 2. При каких значениях параметра а
уравнение 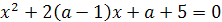 имеет хотя бы один
положительный корень?
имеет хотя бы один
положительный корень?
Решение. Данное уравнение квадратное, значит
имеет корни при неотрицательном дискриминанте. 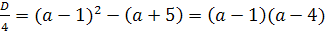
+ - +
4 a
То есть при 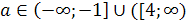 .
Значение большего (или единственного, в случае нулевого дискриминанта) корня
.
Значение большего (или единственного, в случае нулевого дискриминанта) корня 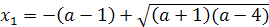 должно
быть положительным:
должно
быть положительным: 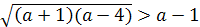 , что равносильно
(при D≥0) следующей
совокупности условий:
, что равносильно
(при D≥0) следующей
совокупности условий:
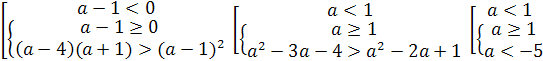
То есть а<1.
С учетом того, что 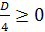 при
при
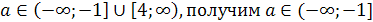 .
.
-1 1 4 а
Ответ. 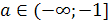 .
.
Пример 3. При каких значениях параметра а
квадратное уравнение 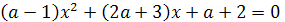 имеет корни одного
знака?
имеет корни одного
знака?
Решение. Так как по условию задачи
рассматриваемое уравнение- квадратное, то а≠1 (иначе формулировка задачи
не имеет смысла). Очевидно, условие задачи предполагает также существование
корней квадратного уравнения, что означает неотрицательность дискриминанта.
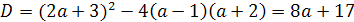 .
.
Так как по условию корни должны быть одинаковых
знаков, то 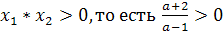 . Решением
последнего неравенства является
. Решением
последнего неравенства является 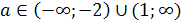 . С учетом условий D≥0
(
. С учетом условий D≥0
(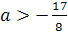 )
и а≠1 получим
)
и а≠1 получим 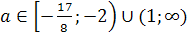 .
.
Ответ. 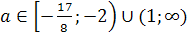 .
.
Пример 4. Сумма квадратов двух различных корней
уравнения 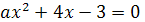 больше 10. Найти
значения параметра а, при которых выполняется данное условие.
больше 10. Найти
значения параметра а, при которых выполняется данное условие.
Решение. Уравнение имеет два различных корня,
если дискриминант положителен и а≠0.
D=16+12a.
Сумму квадратов корней данного уравнения выразим
через его коэффициенты при помощи теоремы Виета следующим образом:
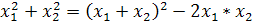
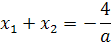
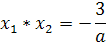
Решаем систему: 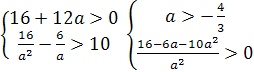
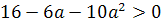
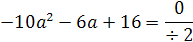
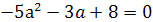
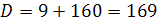
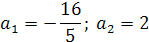
-
+ -
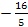 2
a
2
a
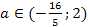 .
.
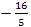 -
- 0
2 а
0
2 а
Ответ. 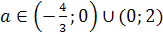 .
.
Пример 5. Найти все значения параметра p,
при каждом из которых сумма квадратов корней уравнения 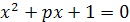 принимает
наименьшее значение.
принимает
наименьшее значение.
Решение. Выразим сумму квадратов корней данного
уравнения через его коэффициенты при помощи теоремы Виета следующим образом: 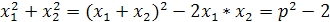 .
Выражение
.
Выражение 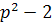 принимает
наименьшее значение при p=0.
принимает
наименьшее значение при p=0.
Ответ. p=0.
Пример 6. Найти все значения параметра p,
при каждом из которых сумма квадратов корней уравнения 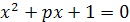 принимает
значение, равное нулю.
принимает
значение, равное нулю.
Решение. Выразим сумму квадратов корней данного
уравнения через его коэффициенты при помощи теоремы Виета следующим образом: 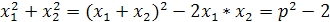 .
Поскольку сумма квадратов корней равна нулю, то решаем уравнение
.
Поскольку сумма квадратов корней равна нулю, то решаем уравнение 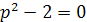 .
Находим
.
Находим 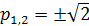 .
.
Ответ. 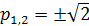 .
.
.3 Задачи, в которых указан промежуток для
решения
Пример 1. При каких значениях параметра а
уравнение 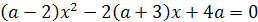 имеет два корня,
один из которых меньше 2, а другой больше 3?
имеет два корня,
один из которых меньше 2, а другой больше 3?
Решение. Так как идет речь о двух корнях, то
рассматриваемое уравнение должно быть квадратным, то есть а≠2.
Рассмотрим функцию 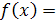
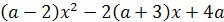 (а≠2).
Ее графиком является парабола, которая по условию задачи пересекает ось Ох один
раз на интервале (
(а≠2).
Ее графиком является парабола, которая по условию задачи пересекает ось Ох один
раз на интервале (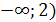 и один раз на
интервале (3;
и один раз на
интервале (3;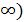 .
.
Рассмотрим два случая: а>2 и а<2.
В первом случае получим следующую систему
неравенств:
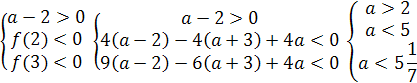
<a<5.
Во втором случае получим систему:
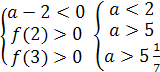 ,
,
Которая не имеет решений.
Ответ: 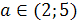 .
.
Пример 2. При каких значениях параметра а один
из корней уравнения 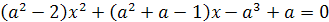 больше числа а ,а
другой меньше числа а?
больше числа а ,а
другой меньше числа а?
Решение. Задача равносильна следующей: при каких
значениях параметра а корни квадратного трехчлена 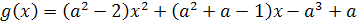 лежат
на вещественной оси по разные стороны от точки х=а?
лежат
на вещественной оси по разные стороны от точки х=а?
Для решения этой задачи воспользуемся тем общим
фактом, что для того, чтобы корни квадратного трехчлена лежали на вещественной
оси по разные стороны от числа d,
необходимо и достаточно выполнение условия 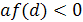 .
.
линейный уравнение задача параметр
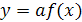
x1 d
x2 x
В нашем случае это условие принимает вид 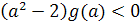 .
Следовательно, требованию задачи удовлетворяют решения неравенства
.
Следовательно, требованию задачи удовлетворяют решения неравенства 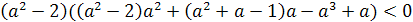 ,
где
,
где 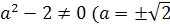 требованию
задачи не удовлетворяют).
требованию
задачи не удовлетворяют).
Решая полученное неравенство, находим, что 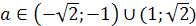 .
.
Ответ. 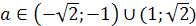 .
.
Пример 3. При каких значениях параметра а корни
х1 и х2 уравнения 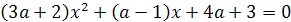 удовлетворяют
условиям х1<-1 и -1<х2<1?
удовлетворяют
условиям х1<-1 и -1<х2<1?
Решение. Задача равносильна следующей: при каких
значениях параметра а только один, а именно- больший корень квадратного
трехчлена 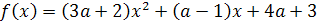 , где 3а+2≠0,
принадлежит интервалу (-1;1), а другой меньше -1?
, где 3а+2≠0,
принадлежит интервалу (-1;1), а другой меньше -1?
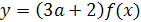
x1
-1 x2 1 x
Требования приведенной задачи выполняются только
при условиях
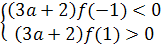 .
.
Таким образом, в нашем случае приходим к
рассмотрению системы
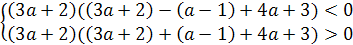 .
.
Решая эту систему, получаем, что 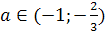 .
.
Ответ. 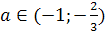 .
.
Пример 4. При каких значениях параметра а корни
уравнения 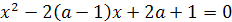 имеют разные
знаки, и оба по абсолютной величине меньше 4?
имеют разные
знаки, и оба по абсолютной величине меньше 4?
Решение. Обозначим квадратный трехчлен в левой
части исходного уравнения через f(x).
Тогда требования задачи выполняются, если совместна система:
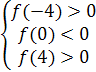 , которую подробнее
можно переписать в виде
, которую подробнее
можно переписать в виде 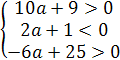 , и которой удовлетворяют
все
, и которой удовлетворяют
все 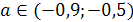 .
.
Ответ. 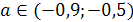 .
.
Пример 5. При каких значениях параметра а один
из корней уравнения 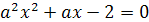 по абсолютной
величине больше 1, а другой меньше 1?
по абсолютной
величине больше 1, а другой меньше 1?
Решение. Задача равносильна следующей: при каких
значениях параметра а один из двух корней квадратного трехчлена f(x)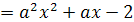 принадлежит на вещественной оси интервалу (-1;1), а второй расположен вне этого
интервала и по модулю не равен 1?
принадлежит на вещественной оси интервалу (-1;1), а второй расположен вне этого
интервала и по модулю не равен 1?
А тогда, замечая, что ровно один корень
трехчлена f(x)
принадлежит интервалу (-1;1) только в том случае, когда числа f(-1)
и f(1) имеют разные
знаки (корни по модулю не равны 1), приходим к выводу, что требование задачи
выполняется только при условии f(-1)*f(1)<0,
которое в нашем случае записывается в виде (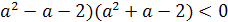 .
.
Решая это неравенство, находим, что 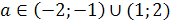 .
.
Ответ. 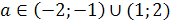 .
.
Пример 6. Найти все значения m,
при которых один из корней уравнения 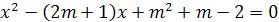 находится
между числами 0 и 2, а второй между числами 3 и5.
находится
между числами 0 и 2, а второй между числами 3 и5.
Решение. Данное квадратное уравнение имеет корни
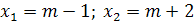 .
Очевидно,
.
Очевидно, 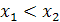 . Тогда искомые
значения параметра найдем, решив систему:
. Тогда искомые
значения параметра найдем, решив систему:
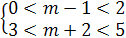
Ответ. 1<m<3.
Пример 7. Найти наибольшее и наименьшее значения
функции 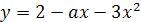 на
отрезке [-1;1].
на
отрезке [-1;1].
Решение. Данная функция возрастает на луче 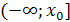 и
убывает на луче
и
убывает на луче 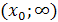 , где
, где 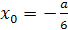 -
абсцисса вершины параболы. Этих соображений вполне достаточно для выяснения
вопроса.
-
абсцисса вершины параболы. Этих соображений вполне достаточно для выяснения
вопроса.
В данной задаче результат фактически зависит от
положения абсциссы x0
относительно отрезка [-1;1], а не от знака дискриминанта.
)
2) 3)
-1 1 х0 х -1 0 х0
1 х -1 х0 0 1 х
4)
х0 -1 1 х
Если 1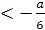 ,
то есть a<-6, то max[-1;1]y=y(1)=-a-1,
min[-1;1]y=y(-1)=a-1.
(рис.1).
,
то есть a<-6, то max[-1;1]y=y(1)=-a-1,
min[-1;1]y=y(-1)=a-1.
(рис.1).
Если -1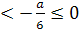 ,
то есть 0≤а<6, то max
y=y(x0)=
2+
,
то есть 0≤а<6, то max
y=y(x0)=
2+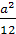 ,
min y=y(1)=-a-1.
(рис.3).
,
min y=y(1)=-a-1.
(рис.3).
Если 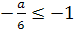 ,
то есть а≥6, то max
y=y(-1)=a-1,
min y=y(1)=-a-1.
(рис.4).
,
то есть а≥6, то max
y=y(-1)=a-1,
min y=y(1)=-a-1.
(рис.4).
2.4 Дополнительные задания
) Решите уравнение 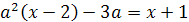 ,
если х-параметр.
,
если х-параметр.
) Решить уравнение 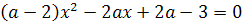 ,
а-параметр.
,
а-параметр.
) При каких а уравнение 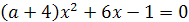 имеет
единственное решение?
имеет
единственное решение?
) При каких а уравнение 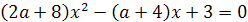 имеет
единственное решение?
имеет
единственное решение?
) При каких а уравнение а) 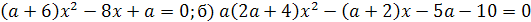 имеет
более одного решения?
имеет
более одного решения?
) Найти все значения параметра а, при которых
графики функций 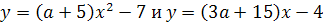 не имеют общих
точек.
не имеют общих
точек.
) Найти все значения а, при которых уравнение 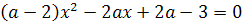 имеет
два различных корня.
имеет
два различных корня.
) Найти все значения а, при которых квадратные
уравнения: а) 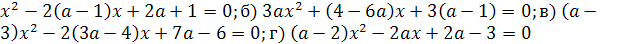 имеют корни и
определить знаки этих корней.
имеют корни и
определить знаки этих корней.
) Найти все значения а, при которых квадратный
трехчлен 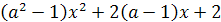 положителен
для любого х.
положителен
для любого х.
) Найти все значения а, при которых корни
уравнения 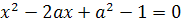 заключены между
числами 2 и 4.
заключены между
числами 2 и 4.
) Найти все значения а, при которых корни
уравнения 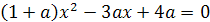 больше 1.
больше 1.
) Найти все значения а, при которых уравнение 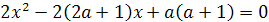 имеет
два корня, причем один из них больше а, а другой меньше а.
имеет
два корня, причем один из них больше а, а другой меньше а.
) Найти все значения а, при которых уравнение 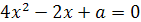 имеет
два корня, каждый из которых принадлежит интервалу (-1;1).
имеет
два корня, каждый из которых принадлежит интервалу (-1;1).
.5. Графическая иллюстрация решения квадратных
уравнений с параметром.
Также, как и с линейными уравнениями,
содержащими параметр, поступают и с квадратными уравнениями, содержащими
параметр, то есть решают их графически для упрощения систематизации знаний.
Часто такие уравнения имеют модуль или корень.
Пример 1. Найти все значения параметра а, при
которых уравнение 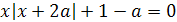 имеет единственное
решение.
имеет единственное
решение.
Решение. Данное уравнение можно переписать так: 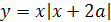 и
и
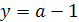 .
Посмотрим графики функций. Графики функций
.
Посмотрим графики функций. Графики функций 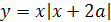 рассмотрим
в случаях, когда а<0, а=0, а>0.
рассмотрим
в случаях, когда а<0, а=0, а>0.
y
y
y
y=x|x+2a|
y=x|x|
y=x|x+2a|
0
0 -2a 0
-2a
x
x x
y=-1
y=a-1
y=a-1
Ясно, что при любом значении a<0
решение исходного уравнения единственно. При a=0
решение исходного уравнения так же единственно. Наконец, при a>0
графики выглядят так, как показано на третьем рисунке. Значит, исходное
уравнение имеет единственное решение при a-1>0
(то есть, при a>1); или при -a2>a-1
(и при a>0). В последнем
случае решим квадратное неравенство: -a2>a-1;
a2+1-1<0.
Соответствующее квадратное уравнение имеет корни: 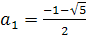 и
и
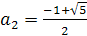 ,
значит решение неравенства таково:
,
значит решение неравенства таково: 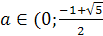 ).
Отсюда получаем ответ:
).
Отсюда получаем ответ: 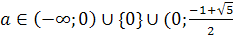 )
)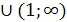 .
.
Ответ. 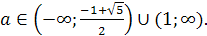
Пример 2. Найти все значения параметра a,
при которых уравнение |x2-6x|=m
имеет ровно три решения.
Решение. Построим графики функций y=|x2-6x|
и y=m
на одном чертеже.
y
9 y=m
0 6 x
Очевидно, что исходное уравнение имеет ровно три
решения тогда и только тогда, когда графики двух вышеуказанных функций
пересекаются ровно в трех точках, то есть при m=9.
Ответ. m=9.
Пример 3. Найти все значения параметра a,
при которых уравнение 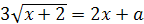 имеет решение.
имеет решение.
Решение. Возведем обе части уравнения в квадрат
и перенесем все слагаемые в правую часть, получим квадратное уравнение 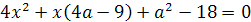 .
Найдем дискриминант
.
Найдем дискриминант 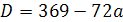 . Так как D≥0
при все значениях
. Так как D≥0
при все значениях 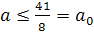 , то при каждом
таком значении a имеется
хотя бы одно решение у уравнения
, то при каждом
таком значении a имеется
хотя бы одно решение у уравнения 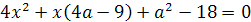 ,
а значит, и у уравнения
,
а значит, и у уравнения 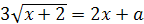 .
.
y
y=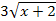
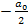
-2 0 x
y=2x+a y=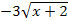
y=2x+a y=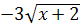
Ответ. 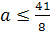
Пример 4. Найти все значения параметра, при
которых уравнение 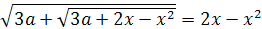 имеет решение.
имеет решение.
Решение. Сделаем замену 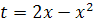 .
Тогда
.
Тогда 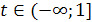 ,
и для решения задачи надо найти, при каких значениях параметра a
имеет решение уравнение
,
и для решения задачи надо найти, при каких значениях параметра a
имеет решение уравнение 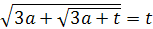 , причем
, причем 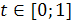 .
Возведем обе части последнего уравнения в квадрат, получим уравнение
.
Возведем обе части последнего уравнения в квадрат, получим уравнение 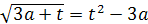 .
График функции y=
.
График функции y=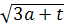 - верхняя часть параболы (I) с вершиной (-3a;0)
и ветвями, направленными вправо (рис.1), а график функции y=
- верхняя часть параболы (I) с вершиной (-3a;0)
и ветвями, направленными вправо (рис.1), а график функции y=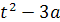 -
парабола (II) с вершиной (0;-3a)
и ветвями, направленными вверх (рис.2).
-
парабола (II) с вершиной (0;-3a)
и ветвями, направленными вверх (рис.2).
I y
II y
a>0
a>0 a=0
a<0 a=0
a<0
0 t
0 t
рис.1
рис.2
Очевидно, что части парабол (I) и (II)
(соответственно верхняя и правая половина) симметричны относительно прямой y=t,
и точки пересечения парабол лежат на этой прямой. Построим графики (I) и (II)
при a=0 (рис.3).
Очевидно, что уравнение 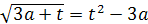 имеет два корня t1=0
и t2=1.
имеет два корня t1=0
и t2=1.
y y
y
y=t2
y=t
y=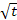 y=t2-3a
y=
y=t2-3a
y=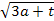
t1 t2
t t1
t t
рис.3
рис.4
рис.5
Если теперь увеличить значение a,
то часть параболы (I) сдвинется влево, а часть параболы (II)- вниз (рис.4).
Уравнение 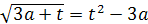 по-прежнему имеет
положительное решение, но оно, очевидно, больше единицы. Если же сделать
значение a немного меньше
нуля, то часть параболы (I) сдвинется вправо, а часть параболы (II) сдвинется
вверх, и точки их пересечения начнут сближаться, причем 0<t1<t2<1.
При некотором значении a=a0
достигается крайнее положение, при котором кривые еще имеют общую точку,
лежащую на прямой y=t
(рис.5).
по-прежнему имеет
положительное решение, но оно, очевидно, больше единицы. Если же сделать
значение a немного меньше
нуля, то часть параболы (I) сдвинется вправо, а часть параболы (II) сдвинется
вверх, и точки их пересечения начнут сближаться, причем 0<t1<t2<1.
При некотором значении a=a0
достигается крайнее положение, при котором кривые еще имеют общую точку,
лежащую на прямой y=t
(рис.5).
Решим уравнение t2-3a=t,
то есть t2-t-3a=0.
Найдем дискриминант D=1+12a,
он не отрицателен при 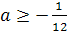 . При
. При 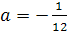 уравнение
имеет единственный корень, а при
уравнение
имеет единственный корень, а при 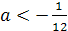 все
точки на параболе y=
все
точки на параболе y=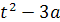 лежат выше прямой y=t.
лежат выше прямой y=t.
Ответ. 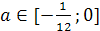 .
.
Пример 5. Найти наименьшее значение выражения a2+(b-1)2
среди тех a и b,
для которых уравнение ||x-4|-2|-ax+4a-b=0
имеет ровно три различных решения. Указать, при каких a
и b достигается
наименьшее значение.
Решение. Сделаем замену z=x-4
и преобразуем уравнение к виду ||z|-2|=az+b.
Построим график функции y=||z|-2|
и y= az+b.
y
y
y= az+b
y=||z|-2|
2b
b
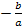
z
-2 0 2 z
Очевидно, эти графики могут пересекаться ровно в
трех точках только в следующих случаях:
1) y
2) y
3) y
2b
z 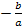 z
z
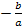 z
z
В случае 1) будет b=2,
-1<a<1, в случае 2)
будет 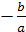 =-2,
0<a<1, в случае 3)
будет
=-2,
0<a<1, в случае 3)
будет 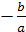 =2,
-1<a<0. В случае 1)
подстановка значения b=2
в выражение a2+(b-1)2
дает выражение a2+1, минимум
которого равен 1 при значении a=0.
В случае 2) будет b=2a;
подставляя это значение в выражение a2+(b-1)2
имеем a2+(2a-1)2=5a2-4a+1;
минимум достигается при
=2,
-1<a<0. В случае 1)
подстановка значения b=2
в выражение a2+(b-1)2
дает выражение a2+1, минимум
которого равен 1 при значении a=0.
В случае 2) будет b=2a;
подставляя это значение в выражение a2+(b-1)2
имеем a2+(2a-1)2=5a2-4a+1;
минимум достигается при 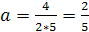 и равен
и равен 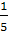 (
(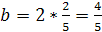 ).
В случае 3) будет b=-2a,
и подставляя это значение в выражение a2+(b-1)2,
получаем a2+(-2a-1)2=5a2+4a+1;
минимум достигается при
).
В случае 3) будет b=-2a,
и подставляя это значение в выражение a2+(b-1)2,
получаем a2+(-2a-1)2=5a2+4a+1;
минимум достигается при 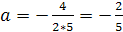 и равен
и равен 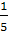 (
(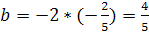 ).
).
Ответ. 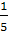
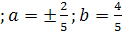 .
.
.6 Иррациональные квадратные уравнения с
параметром
Пример 1. Для каждого значения а решить
уравнение 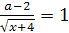 .
.
Решение. 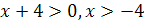 .
.
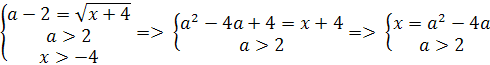
Ответ. 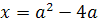 при
при
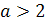 ;
при
;
при 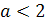 решений
нет.
решений
нет.
Пример 2. Выясните при каких значениях параметра
а уравнение 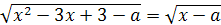 не имеет решений.
не имеет решений.
Решение. Уравнение не имеет решения при 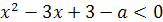 или
или
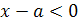 .
.
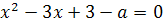 .
.
D=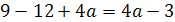
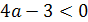 .
.
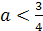 .
.
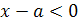 .
.
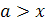 .
.
Ответ. Уравнение не имеет решения при 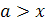 и
и
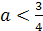 .
.
Пример 3. Для каждого значения а решить
уравнение 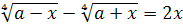 .
.
Решение. 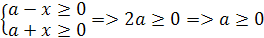 .
.
Пусть х=0.
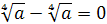
Пусть х>0.
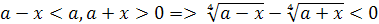 ,
,
но 2х>0, следовательно, х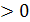 не может быть.
не может быть.
Пусть х<0.
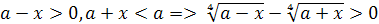 , 2x<0,
, 2x<0,
следовательно, х<0 не может быть.
Ответ. х=0 при 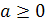 ,
при а<0 решений нет.
,
при а<0 решений нет.
Пример 4. Для каждого значения а определить
число решений уравнения 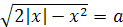 .
.
Решение. 1) 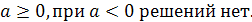
) 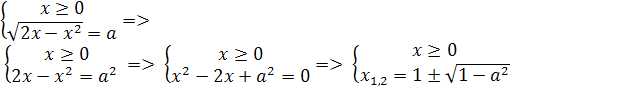
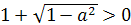 при всех а.
при всех а.
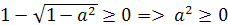 при всех а.
при всех а.
При а=1 одно решение; при а>1 нет решений,
так как 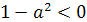 ;
при а<1 два решения.
;
при а<1 два решения.
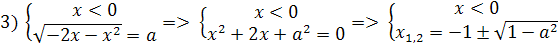 .
.
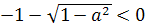 при всех а.
при всех а.
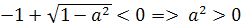 при всех а, кроме
а=0.
при всех а, кроме
а=0.
При а=0 и а=1 одно решение; при а а>1 нет
решений; при 0< а<1 два решения.
Ответ. 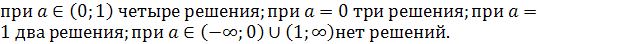
Пример 5. Найти все значения а, удовлетворяющие
условию -1<а<1, при которых выражение 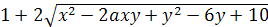 принимает
минимальное значение точно для одной пары (x;y).
принимает
минимальное значение точно для одной пары (x;y).
Решение. Выражение минимально, когда 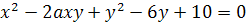 .
Решим это уравнение относительно х.
.
Решим это уравнение относительно х.
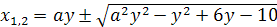 ,
,
но х должен быть единственным. Следовательно, 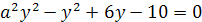 .
.
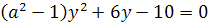 .
.
Из условия 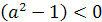 .
.
Чтобы y
был единственным, соответствующая парабола должна снизу касаться оси Ох.
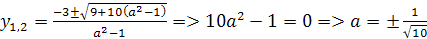 .
.
Ответ. 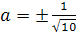 .
.
Пример 6. Число а подобрано так, что уравнение 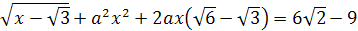 имеет
решение. Найти это решение и значение а.
имеет
решение. Найти это решение и значение а.
Решение. 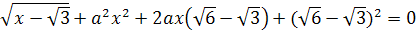
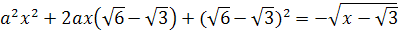 .
.
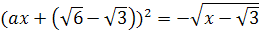 .
.
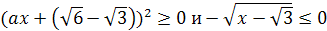 .
.
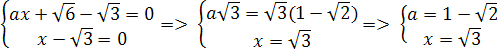 .
.
Ответ. 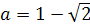 ,
,
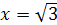 .
.
.3 Примеры решения тригонометрических уравнений
с параметрами
Пример 1. При каких значениях параметра a
значение выражения 1+cos x· (5 cos x+a sin x) будет равно нулю хотя бы при
одном значении x?
Решение. Уравнение 1+cos x · (5 cos x+a sin x) =
0 после преобразований приводится к однородному sin2 x + a sin x cos x + 6 cos2
x = 0, которое после деления на cos 2 x и замены t = tg x превращается в
квадратное: t2 +at+6 = 0. Так как t = tg x может принимать любые значения, это
уравнение будет иметь решения при условии
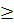 0 или D = a2 −
24
0 или D = a2 −
24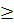 0.
0.
Ответ: a ∈
(−∞;−2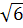 ] ∪
[ 2
] ∪
[ 2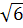 ;+∞).
;+∞).
Пример 2. При каких значениях параметра a сумма
loga (cos2 x+1) и loga(cos2 x+5) будет равна единице хотя бы при одном значении
x?
Решение. Допустимыми значениями параметра являются
все a > 0, a 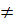 1.
1.
Из уравнения loga(cos2 x+1)+loga(cos2 x+5) = 1
получим, что (cos2 x
+ 1)(cos2 x
+ 5) = a.
Обозначим cos2 x = t, 0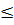 t
t 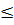 1,
тогда уравнение примет вид(t) = t2 + 6t + (5 − a) = 0.
1,
тогда уравнение примет вид(t) = t2 + 6t + (5 − a) = 0.
Условия задачи будут выполнены, если последнее
уравнение будет иметь хотя бы один корень из отрезка [0; 1] (в отличие от задачи
6.1,где корень мог быть любым числом). В данном случае исследование только
дискриминанта недостаточно. Ветви параболы направлены вверх, вершина находится
в точке tв = −3, следовательно, на отрезке [0; 1] функция f(t) монотонно
возрастает. Для того, чтобы на [0; 1] существовал корень, в силу непрерывности
необходимо и достаточно, чтобы на концах отрезка f(t) имела разные знаки f(0) ·
f(1)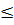 0
или (5−a)(1+6+5−a)
0
или (5−a)(1+6+5−a)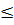 0. Решая последнее
неравенство, получаем
0. Решая последнее
неравенство, получаем
Ответ: a ∈
[5; 12].
Пример 3. Решить уравнение 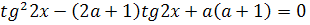 относительно
a.
относительно
a.
Решение. Уравнение квадратное относительно 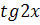 ,
следовательно, оно равносильно совокупности двух уравнений:
,
следовательно, оно равносильно совокупности двух уравнений: 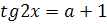 и
и
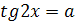 .
Отсюда получим два множества корней:
.
Отсюда получим два множества корней: 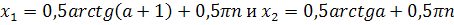 .
.
Ответ: 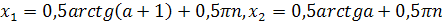 .
.
Пример 4. Решить уравнение 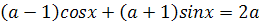 относительно
a.
относительно
a.
Решение. Приведем уравнение к виду 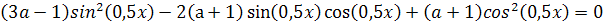 .
.
При 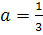 получим:
получим:
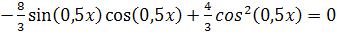 или
или
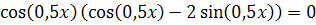 .
.
Это уравнение равносильно совокупности двух
уравнений: 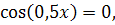 имеющему множество
решений
имеющему множество
решений 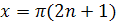 ,
и
,
и 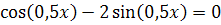 ,
равносильному уравнению
,
равносильному уравнению 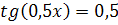 , имеющему
множество корней
, имеющему
множество корней 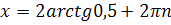 .
.
При 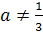 получим
уравнение равносильное исходному:
получим
уравнение равносильное исходному: 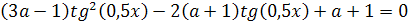 ,
имеющее два решения относительно tg(0,5x):
,
имеющее два решения относительно tg(0,5x):
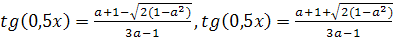 ,
при
,
при 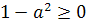 ,
то есть при |a|≤1.
,
то есть при |a|≤1.
Итак, при 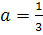 уравнение
имеет два множества корней:
уравнение
имеет два множества корней: 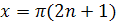 и
и 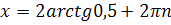 ;
при -1≤a≤1 (
;
при -1≤a≤1 (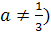
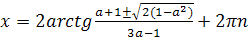 ;
при |a|>1 решений нет.
;
при |a|>1 решений нет.
Ответ: при 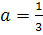
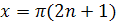 и
и
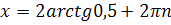 ;
при -1≤a≤1 (
;
при -1≤a≤1 (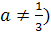
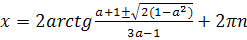 ;
при |a|>1 решений нет.
;
при |a|>1 решений нет.
Пример 5. Найти все значения параметра a, при
которых уравнение−a (2 − cos x + sin )= 2 имеет решение.
)= 2 имеет решение.
Решение. Область допустимых значений параметра
определяется системой
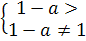 , откуда a ∈
(−∞; 0) ∪ (0; 1).
, откуда a ∈
(−∞; 0) ∪ (0; 1).
По свойствам логарифмической функции перепишем
уравнение в виде 2 − cos
x + sin
 =
(1 − a)2.
=
(1 − a)2.
Заменяя cos x = 1 − 2 sin2  и
полагая t = sin
и
полагая t = sin  , получаем
квадратное уравнение: 2t2 + t + 2a − a2 = 0.
, получаем
квадратное уравнение: 2t2 + t + 2a − a2 = 0.
Это уравнение имеет решения, если D = 8a2−16a+1
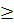 0,
откуда с учетом ОДЗ получаем∈ (−∞;
0) ∪
(0; 1 −
0,
откуда с учетом ОДЗ получаем∈ (−∞;
0) ∪
(0; 1 −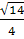 ].
].
Найдем теперь, при каких значениях параметра a
хотя бы один из корней этого уравнения будет принадлежать отрезку [−1;
1]. Так как ветви параболы f(t) = 2t2 + t + 2a − a2 направлены вверх,
вершина находится в точке tв =− , то корни
располагаются симметрично относительно точки t=−
, то корни
располагаются симметрично относительно точки t=− .
Поэтому, если меньший корень лежит в промежутке [−1; 1], то больший - тем
более. Таким образом, достаточно выяснить, при каких значениях параметра a
больший корень параболы окажется в промежутке [
.
Поэтому, если меньший корень лежит в промежутке [−1; 1], то больший - тем
более. Таким образом, достаточно выяснить, при каких значениях параметра a
больший корень параболы окажется в промежутке [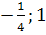 ].
Это будет в том и только в том случае, если f(1)
].
Это будет в том и только в том случае, если f(1)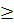 0.
Вычисляя f(1),
0.
Вычисляя f(1),
получаем неравенство 3+2a−a2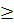 0, которое справедливо при a ∈ [−1;
3]. Пересекая этот промежуток с предыдущим, получаем
0, которое справедливо при a ∈ [−1;
3]. Пересекая этот промежуток с предыдущим, получаем
Ответ: a ∈
[−1; 0 ) ∪(0; 1 −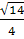 ]
]
Пример 6. В зависимости от значений параметра a
решите уравнение
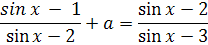
Решение. Полагая t = sin x, приведем уравнение к
виду
− 5at + 6a − 1 = 0.
Если a = 0, то решений нет.
При a 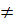 0
и при условии a ∈ (−∞;−4]
∪
(0;+∞) получаем корни уравнения t1,2 =
0
и при условии a ∈ (−∞;−4]
∪
(0;+∞) получаем корни уравнения t1,2 = 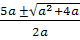 .
Так как вершина параболы f(t) = at2 − 5at + 6a − 1 находится в
точке tв =
.
Так как вершина параболы f(t) = at2 − 5at + 6a − 1 находится в
точке tв = 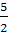 ,
,
условие |t| 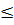 1
для меньшего из корней будет выполняться, если на концах отрезка [−1; 1]
функция будет иметь разные знаки: f(−1)·f(1)
1
для меньшего из корней будет выполняться, если на концах отрезка [−1; 1]
функция будет иметь разные знаки: f(−1)·f(1) 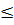 0
или (2a−1)(12a−1)
0
или (2a−1)(12a−1) 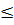 0. Решением
последнего неравенства является интервал a ∈
0. Решением
последнего неравенства является интервал a ∈
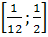 .
.
Ответ: Если a∈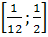 :
x=(−1)n
arcsin
:
x=(−1)n
arcsin 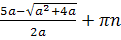 ,
n∈Z,
при других a решений нет.
,
n∈Z,
при других a решений нет.
Пример 7. Решите уравнение
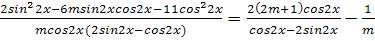 относительно m.
относительно m.
Решение. уравнение имеет смысл при m≠0.
Значение х должно удовлетворять условию cos2x≠0,
tg2x≠ .
Разделив числитель и знаменатель дроби, стоящей в левой части уравнения, на
.
Разделив числитель и знаменатель дроби, стоящей в левой части уравнения, на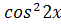 ,
а первой дроби правой части на
,
а первой дроби правой части на 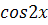 , получим уравнение
, получим уравнение
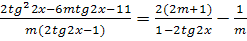 .
.
Пусть 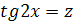 .
Несложные преобразования приводят к уравнению
.
Несложные преобразования приводят к уравнению 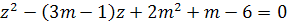 ,
имеющему два корня:
,
имеющему два корня: 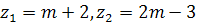 .
.
Выше было отмечено, что значения х должны
удовлетворять условию tg2x≠ .
Значит, необходимо исключить те значения m,
при которых
.
Значит, необходимо исключить те значения m,
при которых 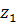 и
и 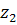 равны
0,5.
равны
0,5.
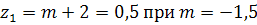 . При этом
. При этом 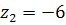 .
.
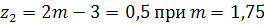 . При этом
. При этом 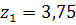 .
.
Ответ: при 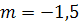
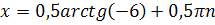 ;
при
;
при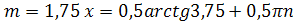 ;
при
;
при 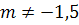 ,
,
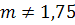 ,
,
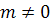 уравнение
имеет два множества корней:
уравнение
имеет два множества корней: 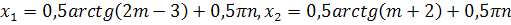 .
.
Задачи для самостоятельного решения
. В зависимости от значений параметра a решите
уравнение cos4 x
−
(a + 2) cos2x
−
a −
3 = 0.
. В зависимости от значений параметра a решите
уравнение sin4 x+cos4x+sin2x
+a= 0.
. При каких значениях параметра a уравнение(a2+8a+16)(2−2cos
x−sin2
x)+(32+2a2+16a)(cos
x−1)+3a+10=0
не имеет решений?
. При каких значениях параметра a уравнение loga−2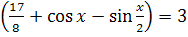 имеет решение?
имеет решение?
. При каких значениях параметра a уравнение
loga+1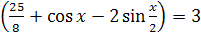 имеет решение?
имеет решение?
. При каких значениях параметра a значение
выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x?
. При каких значениях параметра a значение
выражения 3+sin x · (2 sin x+a cos x) будет равно −1 хотя бы при одном
значении x?
. При каких значениях параметра a сумма loga(sin
x + 2) и loga(sin x + 3) будет равна единице хотя бы при одном значении x?
. При каких значениях параметра a уравнение(a +
1) tg2 x - 2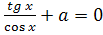 не имеет решений?
не имеет решений?
.4 Примеры решения показательных и
логарифмических уравнений с параметрами
Пример 1. При каких значениях параметра a
сумма квадратов корней уравнения
2 log4(2x2−x+2a−4a2)+log0,5(x2+ax−2a2)
= 0 больше
1?
Решение. На основании свойств логарифмов
исходное уравнение равносильно уравнению
2(2x2
− x + 2a
−
4a2) = log2(x2
+ ax −
2a2),
которое, в свою очередь, равносильно системе
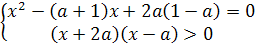
Уравнение записанной системы имеет корни x1=
1−a и x2=
2a.
Подставляя поочередно полученные значения x
в неравенство системы, получим систему 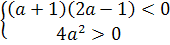 ,
из которой находим, что a
∈
(−1; 0) ∪ (0;
,
из которой находим, что a
∈
(−1; 0) ∪ (0;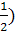
Учитывая теперь, что 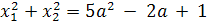 ,
из неравенства 5a2 − 2a
+ 1 > 1 получаем значения a
∈
(−∞; 0) ∪
,
из неравенства 5a2 − 2a
+ 1 > 1 получаем значения a
∈
(−∞; 0) ∪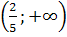 ..
..
Ответ: a
∈
(−1; 0) ∪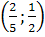 .
.
Пример 2. При каких значениях параметра a
уравнение
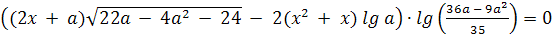
имеет по крайней мере два корня, один из которых
неотрицателен, а другой не больше −1?
Решение. Допустимые значения параметра a
определяются системой
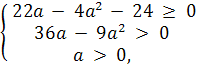 решением которой
являются все a ∈ [
решением которой
являются все a ∈ [ ;
4).
;
4).
Рассмотрим сначала случай, когда 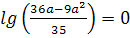 ,
откуда a1 =
,
откуда a1 = 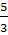 ;
a2 =
;
a2 =  .
При этих значениях параметра a любое значение x удовлетворяет исходному
уравнению, и, значит, последнее всегда имеет корни, о которых идет речь в
задаче.
.
При этих значениях параметра a любое значение x удовлетворяет исходному
уравнению, и, значит, последнее всегда имеет корни, о которых идет речь в
задаче.
Пусть теперь первая скобка исходного уравнения
равна нулю, что равносильно равенству
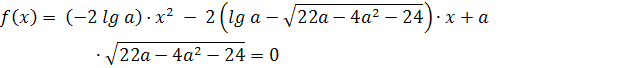
Из ОДЗ a
∈
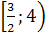 следует,
что ветви квадратного трехчлена направлены вниз, поэтому требования задачи
будут выполнены только при условии
следует,
что ветви квадратного трехчлена направлены вниз, поэтому требования задачи
будут выполнены только при условии
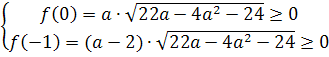 ,
,
откуда получаем с учетом ОДЗ a ∈
[ 2; 4 ) ∪ 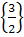 .
.
Объединяя полученные результаты, запишем
Ответ: a =  , a =
, a = 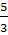 ;
a ∈
[ 2; 4 ).
;
a ∈
[ 2; 4 ).
Пример 3. При каких значениях параметра a
уравнение 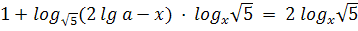 имеет решения?
имеет решения?
Решение. Допустимые значения переменной
определяются системой
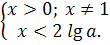
Перейдем в уравнении к логарифмам по основанию 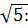
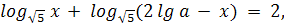
откуда получим квадратное уравнение x2 − 2
lg a · x + 5 = 0.
Если его дискриминант D = 4 lg2a − 20 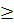 0
или | lg a|
0
или | lg a| 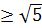 , то исходное
уравнение будет иметь решения.
, то исходное
уравнение будет иметь решения.
С учетом ОДЗ 0<x<2 lg a получаем, что lg
a>0, и, следовательно, условиям задачи удовлетворяют все 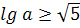 или
или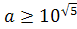 .
.
Ответ: 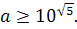
Пример 4. При каких значениях параметра a
уравнение 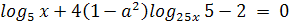 имеет два корня,
расстояние между которыми больше
имеет два корня,
расстояние между которыми больше 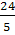 ?
?
Решение. Допустимыми значениями переменной являются
все x>0; x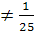 .
.
На основании свойств логарифмов преобразуем
уравнение к виду
(log5 x − 2)(log5 x + 2) + 4(1
− a2) = 0, откуда log5 x = ±2a. Таким образом,
исходное уравнение имеет два корня вида x1=
52a и x2=
5−2a. Оба эти корня
удовлетворяют первому условию ОДЗ x
> 0, а второе условие x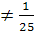 будет
выполняться при
будет
выполняться при 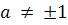 .
.
Перейдем теперь к решению задачи. Очевидно, что
при a = 0 условие задачи
не выполняется. Рассмотрим два случая:
) a
> 0, тогда 52a > 5−2a
и условие задачи равносильно неравенству 52a
−
5−2a > 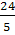 .
Выполняя замену 52a = t
> 0; 5−2a =
.
Выполняя замену 52a = t
> 0; 5−2a =  ,
получим, что t > 5 или a
>
,
получим, что t > 5 или a
>  .
.
) a
< 0, тогда наоборот, 5−2a
>52a и неравенство
имеет вид
−2a−52a
> 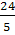 ,
откуда после аналогичной замены имеем a<−
,
откуда после аналогичной замены имеем a<−
 .
.
Ответ: a
∈
(−∞;−1) ∪ (−1;−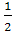 ) ∪
(
) ∪
( ;
1) ∪
(1;+∞).
;
1) ∪
(1;+∞).
Пример 5. При каких значениях параметра a
сумма 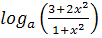 и
и
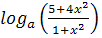 больше
единицы при всех x?
больше
единицы при всех x?
Решение. Рассмотрим
сумму логарифмов:
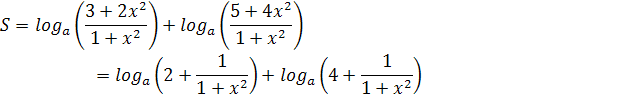
эта сумма имеет смысл при любых x.
Заменим t = 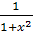 ,
тогда
,
тогда
очевидно, что 0 < t
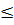 1.
1.
Составим неравенство и найдем значения параметра a,
при которых неравенство выполняется при всех t
∈
(0; 1].
и найдем значения параметра a,
при которых неравенство выполняется при всех t
∈
(0; 1].
) Если a
> 1, то логарифмическая функция возрастает. Запишем равносильное неравенство
(2 + t)(4
+ t) > a
или t2 + 6t
+ 8 − a > 0.
Абсцисса вершины параболы f(t)=t2+6t+8−a
равна tв=−3, ветви
направлены вверх, следовательно, на интервале (0; 1] функция f(t)
монотонно возрастает. Неравенство f(t)
> 0 выполняется тогда и только тогда, когда f(0)
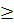 0,
откуда 1 < a
0,
откуда 1 < a
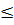 8.
8.
) При 0 < a
< 1 исходное неравенство равносильно следующему:
(t)
= t2 + 6t
+ 8 − a < 0.
Аналогично первому случаю, функция f(t)
монотонно возрастает на (0; 1], поэтому необходимо и достаточно выполнения
условия f(1) < 0, т.е.
1+6+8−a < 0, a
> 15. Полученный ответ не имеет пересечений с условием 0 < a
< 1.
Ответ: a
∈
( 1; 8 ].
Пример 6. При каких значениях параметра a
сумма 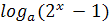 и
и
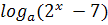 равна
единице ровно при одном x?
равна
единице ровно при одном x?
Решение. Допустимыми значениями параметра
являются все a > 0, a
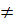 1.
1.
Составим уравнение 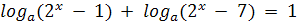 .
.
Обозначая t
= 2x > 0, запишем
систему, равносильную данному уравнению:
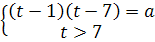 или
или 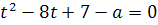
Парабола f(t)
= t2−8t+7−a
имеет вершину в точке tв
= 4, ветви направлены вверх, корни расположены симметрично относительно
вершины, поэтому условию t
> 7 может удовлетворять только больший корень, которому и будет
соответствовать единственное решение уравнения. Необходимым и достаточным
условием того, чтобы больший корень был больше 7 является неравенство f(7)
< 0
или 49 − 56 + 7 − a
< 0, откуда a > 0.
Ответ: a
∈
(0; 1) ∪
(1;+∞).
Задачи для самостоятельного решения
. В зависимости от значений параметра a
решите уравнения.
а) 4x − (2a +
1) 2x + a2 + a = 0.
б) 9lg(x−a)−lg
2 = 3lg(x−1)
в) 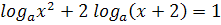
г) 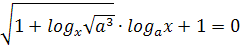
. При каких допустимых значениях параметра a
уравнение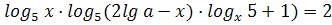 имеет решение?
имеет решение?
. При каких значениях параметра a
уравнение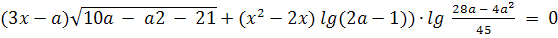 имеет
по крайней мере два корня, один из которых неположителен, а другой не меньше
двух.
имеет
по крайней мере два корня, один из которых неположителен, а другой не меньше
двух.
. При каких значениях параметра a
уравнение log3 x+(a2−4)·log3x
 −3
= 0 имеет два корня, расстояние между которыми больше 8?
−3
= 0 имеет два корня, расстояние между которыми больше 8?
. При каких значениях параметра a
уравнение 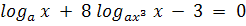 имеет два корня,
расстояние между которыми меньше
имеет два корня,
расстояние между которыми меньше  ?
?
. При каких значениях параметра a
сумма 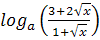 и
и
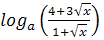 равна
единице ни при каких значениях x?
равна
единице ни при каких значениях x?
. При каких значениях параметра a
сумма 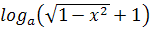 и
и
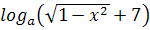 будет
меньше единицы при всех допустимых значениях x?
будет
меньше единицы при всех допустимых значениях x?
IV. Приложение
.1 Разработка курса по выбору для 9 класса
Пояснительная записка.
Изучение многих физических процессов и
геометрических закономерностей часто приводит к решению задач с параметрами. В
школе же это один из наиболее трудных разделов школьного курса математики.
Задачи с параметром являются наиболее сложными задачами ЕГЭ, поэтому
познакомиться с некоторыми идеями их решения, освоить способы решения задач с
параметром желательно как можно раньше.
Очень важно подготовить учащихся к преодолению
трудностей, связанных с решением задач с параметрами. К сожалению, в школьном
курсе не уделяется достаточно времени и внимания на изучение данного раздела.
Поэтому возникает необходимость создания курса для ознакомления с основными
видами уравнений, содержащих параметры.
Материал рассчитан на 9 класс с дальнейшим
продолжением в 10 и 11 классах. В ходе учебно-познавательной деятельности
учащимся будут предложены контрольные работы и тренировочные упражнения в конце
каждого раздела, что позволит определить качество усвоения материала и уровень
подготовки к экзаменам.
Курс рассчитан на 20 часов для 9 класса. Он
включает в себя знакомство с самим понятием параметра и с системой упражнений,
предназначенных для отработки навыков решения задач с параметрами, для
самостоятельного решения типовых задач, для подготовки учащихся к итоговой
аттестации. По инициативе учителя курс может быть продолжен решением неравенств
с параметрами, а также решением систем уравнений и неравенств с параметром.
Цель курса: развить представления о параметре,
выделять параметр из текста задачи; научить решать задачи в общем виде,
выделять частные случаи решения задач из общего решения; научить оформлять
решение задачи с параметром; изучить различные виды задач и способы их решения;
развить пространственные представления, логическое мышление и речь;
сформировать представления об изучаемых понятиях и методах как важнейших
средствах математического моделирования реальных процессов и явлений.
Задачи курса: овладение системой знаний и
умений, необходимых для решения задач с параметрами, для дальнейшего их
применения в практической деятельности, продолжения образования;
интеллектуальное развитие, формирование таких качеств личности, как ясность и
точность мысли, критичность мышления, логического мышления, способности к
преодолению трудностей; формирование представлений об методах решения задач с
параметрами; воспитание отношения к математике как к части общечеловеческой
культуры.
Обучающиеся по окончании курса должны знать: существо
понятия параметра, задачи с параметром; приводить примеры задач с параметром;
как уравнения с параметрами могут описывать реальные зависимости; каким образом
уравнения с параметрами применяются на практике.
Обучающиеся по окончании курса должны уметь:
находить параметр в задаче с параметрическими данными; отличать переменную от
параметра; определять вид задачи с параметром; находить решение задачи с
параметром; записывать развернутый ответ к задаче; строить график, описывающий
решение задачи с параметром.
Обучающиеся по окончании курса должны уметь
использовать приобретенные знания и умения в практической деятельности и
повседневной жизни для: решения несложных практических задач; устной прикидки и
оценки результата решения; интерпретации результатов решения задач с учетом
ограничений, связанных с реальными свойствами рассматриваемых процессов и
явлений.
Учебный план.
|
№
п/п
|
Темы
занятий
|
Количество
часов
|
|
|
всего
|
теория
|
практика
|
|
1
|
Линейные
уравнения с параметром.
|
5
|
2
|
3
|
|
2
|
Классификация
задач по их содержанию на материале квадратных уравнений.
|
9
|
4
|
5
|
|
3
|
Графическая
иллюстрация решения уравнений с параметрами.
|
3
|
1
|
2
|
|
4
|
Иррациональные
уравнения с параметром.
|
3
|
1
|
2
|
|
5
|
Уравнения
с параметром, содержащие знак модуля.
|
3
|
1
|
2
|
|
Итого.
|
23
|
9
|
14
|
Содержание курса.
Тема 1. Линейные уравнения с параметром. (4 ч).
Введение понятия параметра. Исследование
количества корней линейного уравнения. Знакомство с видами линейных уравнений с
параметрами и их характеристиками. Определение области допустимых значений
уравнения с параметром.
Практическая работа. Решение линейных уравнений,
в которых указано некоторое значение параметра. Поиск решения линейных
уравнений в зависимости от установленных значений параметра. Решение линейных
уравнений с параметрами с дополнительными данными в условии задачи. Проведение
контрольной работы.
Тема 2. Классификация задач по их содержанию на
материале квадратных уравнений. (8 ч).
Исследование условия существования корней
квадратного уравнения и их количества. Знакомство с классификацией квадратных
уравнений по их содержанию и алгоритмом их решений. Обобщение классификаций
задач с параметрами по их типу.
Практическая работа. Решение квадратных
уравнений с «ограничениями» для решения. Решение задач на использование теоремы
Виета. Решение задач, в которых указан промежуток для решения. Решение задач на
расположение корней квадратного уравнения. Проведение контрольной работы.
Тема 3. Графическая иллюстрация решения
уравнений с параметрами. (3 ч).
Знакомство с уравнениями, содержащими два
параметра. Исследование существования корней таких уравнений. Графическая
интерпретация решения уравнений с параметрами. Чтение графической модели
решения уравнения.
Практическая работа. Решение уравнений с
параметром графическим методом. Исследование каждого этапа решения уравнения на
графике. Выявление взаимосвязи между параметрами и переменной.
Тема 4. Иррациональные уравнения с параметром.
(3 ч).
Обобщение знаний об иррациональных уравнениях.
Исследование существования корней иррационального уравнения.
Практическая работа. Решение иррациональных
уравнений с параметром. Нахождение области допустимых значений решения и его
зависимость на параметр.
Тема 5. Уравнения с параметром, содержащие знак
модуля. (2 ч).
Обобщение знаний по теме «Модуль». Использование
определения модуля для решения уравнений, содержащих знак модуля.
Практическая работа. Способы решения уравнений с
параметром, содержащих знак модуля. Итоговый контроль полученных знаний.
Тезаурус.
Параметр- фиксированная, заданная величина,
обозначенная буквой.
Задача с параметром- задача, в которой
какая-нибудь данная или несколько из данных величин обозначены буквами
(параметрами).
Литература
Амелькин
В.В., Рабцевич В.Л. Задачи с параметрами: справочное пособие по математике.- 2
изд.- Минск: Асар,2002.
Вавилов
В.В. и др. Задачи по математике. Алгебра: справочное пособие.- М.: Наука, 1987.
Горнштейн
П.И., Полонский В.Б., Якир М.С. Задачи с параметрами.
Журнал
«Математика в школе» № 2, 2000г.
Газета
«Математика» № 13, 2007г.
Приложение 1
Контрольная работа.
Вариант 1.
. Решите уравнение: а) 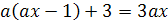 ;
б)
;
б) 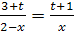 ;
в)
;
в) 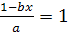 .
.
. При каком значении а прямые 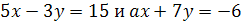 пересекаются
в точке, принадлежащей оси абсцисс?
пересекаются
в точке, принадлежащей оси абсцисс?
Вариант 2.
. Решите уравнение: а) 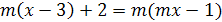 ;
б)
;
б) 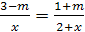 ;
в)
;
в) 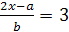 .
.
. Графики функций 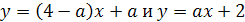 пересекаются
в точке с абсциссой, равной -2. Найдите ординату точки пересечения.
пересекаются
в точке с абсциссой, равной -2. Найдите ординату точки пересечения.
Ответы.
В-2. 1. а) Если m≠0,
m≠1, то 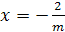 ;
если m=1, то х - любое
число; если m=0, то решений нет;
б) если m≠1, m≠2,
m≠3, то
;
если m=1, то х - любое
число; если m=0, то решений нет;
б) если m≠1, m≠2,
m≠3, то 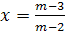 ;
если m=1, или m=2,
или m=3, то решений нет;
в) если b≠0, то
;
если m=1, или m=2,
или m=3, то решений нет;
в) если b≠0, то 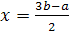 ;
если b=0, то решений нет.
2. y=-2.
;
если b=0, то решений нет.
2. y=-2.
Приложение 2
Контрольная работа.
Вариант 1.
. Решите уравнение 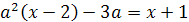 ,
если x- параметр.
,
если x- параметр.
. При каких а уравнение 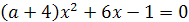 имеет
единственное решение?
имеет
единственное решение?
. Найти все значения а, при которых корни
уравнения 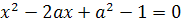 заключены между
числами 2 и 4.
заключены между
числами 2 и 4.
. При каких а уравнение 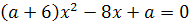 имеет
более одного решения?
имеет
более одного решения?
Вариант 2.
. Решите уравнение 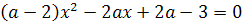 ,
если а - параметр.
,
если а - параметр.
. При каких а уравнение 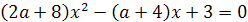 имеет
единственное решение?
имеет
единственное решение?
. Найти все значения а, при которых
уравнение 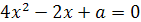 имеет два корня,
каждый из которых принадлежит интервалу (-1;1).
имеет два корня,
каждый из которых принадлежит интервалу (-1;1).
. При каких а уравнение 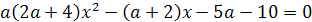 имеет
более одного решения?
имеет
более одного решения?
Ответы.
В-1. 1. При х=2,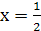 ,
то а=-1; 2. При а=-13 и а=-4; 3. При а=3; 4. При ає(-8;-6)u(-6;2).
,
то а=-1; 2. При а=-13 и а=-4; 3. При а=3; 4. При ає(-8;-6)u(-6;2).
В-2. 1. При а=2, х=1/4; при а=1, х=-1; при а=6,
х=3 и х=1; 2. При а=20 и а=-4; 3. При а<1/4; 4. При а=-2 и ає(-1/20; ).
).
Приложение 3
Контрольная работа. (итоговая)
Вариант 1.
. Решить уравнение 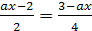 .
.
. Найти все значения параметра p,
при каждом из которых квадратное уравнение 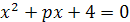 имеет
одно решение.
имеет
одно решение.
. Решите уравнение 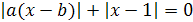 .
.
. Выясните, при каких значениях параметра
а уравнение 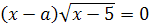 имеет ровно один
корень.
имеет ровно один
корень.
Вариант 2.
. Решить уравнение 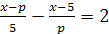 .
.
. Найти все значения параметра p,
при каждом из которых квадратное уравнение 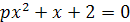 имеет
ровно одно решение.
имеет
ровно одно решение.
. Решить уравнение 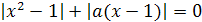 .
.
. Выясните, при каких значениях параметра
а уравнение 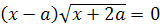 имеет ровно один
корень.
имеет ровно один
корень.
Ответы.
В-1. 1. При а≠0, 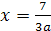 ;
2.
;
2. 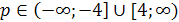 ;
3. При а≠0 и b≠1
решений нет; в остальных случаях уравнение имеет единственное решение х=1; 4.
х=5 при а≠5 - единственный корень.
;
3. При а≠0 и b≠1
решений нет; в остальных случаях уравнение имеет единственное решение х=1; 4.
х=5 при а≠5 - единственный корень.
В-2. 1. При p≠0,
p≠5 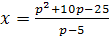 .
2.
.
2. 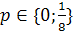 ;
3. Если а≠0, то х=1; если а=0, то х=1, х=-1. 4. При а<0 х=-2а -
единственный корень.
;
3. Если а≠0, то х=1; если а=0, то х=1, х=-1. 4. При а<0 х=-2а -
единственный корень.
.2 Элективный курс по решению уравнений с
параметрами для 10-11 классов
Пояснительная записка.
Практика экзаменов по математике показывает, что
задачи с параметрами представляют для учащихся наибольшую сложность. Именно
поэтому необходимо введение элективного курса для 10 и 11 классов. Основная
цель такого курса - повысить математическую подготовку учащихся к ЕГЭ.
Спецификой задач с параметрами является то, что
наряду с неизвестными величинами в них фигурируют параметры, численные значения
которых не указаны конкретно, но считаются конкретными и заданными на некотором
числовом множестве. При этом значения параметров существенно влияют на
логический и технический ход решения задачи и форму ответа. Ответ в задачах с
параметрами, как правило, имеет развернутый вид: при конкретных значениях
параметра ответы могут значительно различаться.
Трудности решения задач такого рода вызваны
прежде всего тем, что в любом случае, даже при решении простейших уравнений или
неравенств, содержащих параметры, приходится производить ветвление всех
значений параметров на отдельные классы, при каждом из которых задача имеет
решение. При этом следует четко и последовательно следить за сохранением
равносильности решаемых уравнений или неравенств с учетом области определения
выражений, входящих в уравнение или неравенство, а также учитывать выполнимость
производимых операций.
Некоторое представление о решении уравнений и
неравенств с параметрами и о разветвленной записи ответа учащиеся получают уже
в курсе алгебры 6-7 классов при рассмотрении в общем виде линейных, а затем
квадратных уравнений.
На таком же уровне в школьном курсе
рассматриваются линейные и квадратные неравенства. Этих знаний вместе с
элементарными представлениями о равносильности уравнений ил неравенств вполне
достаточно, чтобы на их основе положить начало выработке навыков решения
стандартных линейных или квадратных уравнений и неравенств или приводимых к ним
уравнений и неравенств. Однако школьная программа не предусматривает выработки
прочных навыков решения таких задач всеми учащимися, и углубленное изучение
соответствующих методов может быть достигнуто только на курсах по выбору в 9
классе и элективных курсах в 10 и 11 классах.
Овладение же методикой решения уравнений с
параметрами очень полезно: оно существенно повышает уровень математической
подготовки учащихся, позволяет чуть по-новому, как бы изнутри взглянуть на
такие «банальные» функциональные зависимости, подробно анализируемые школьной
программой, как, к примеру, различные виды уравнений.
В данном курсе рассматриваются основные методы и
идеи решения задач с параметрами. Разбираемые и предлагаемые для
самостоятельного решения задачи подобранны в соответствии с действующими
программами экзаменов по математике.
Актуальность элективного курса заключается в
том, что он способствует расширению знаний для успешной сдачи экзаменов и
дальнейшего обучения в высших учебных заведениях.
Данный курс предполагает рассмотрение
встречающихся в 10 и 11 классах уравнений глубже и шире. Для 10 класса курс
рассчитывает 35 часов, для 11 - 35 часов. Занятия на элективных курсах
проводятся в виде лекций и практических занятий. Освоение учащимися материала
проверяется с помощью выполнения ими задач для самостоятельного решения. В
конце курса предусмотрено проведение тестовой работы.
Цели курса:
· познакомить с алгоритмом решения
уравнений, систем уравнений, неравенств с параметром;
· научить выделять параметр из текста
задачи;
· научить решать задачи в общем виде,
выделять частные случаи решения задач из общего решения;
· научить оформлять решение задачи с
параметром;
· изучить различные виды задач и
способы их решения;
· развить пространственные
представления, логическое мышление и речь;
· сформировать представления об
изучаемых понятиях и методах как важнейших средствах математического
моделирования реальных процессов и явлений.
Задачи курса:
Образовательные:
· овладение системой знаний и умений,
необходимых для решения задач с параметрами, для дальнейшего их применения в
практической деятельности, продолжения образования;
· формирование представлений о методах
решения задач с параметрами;
Развивающие:
· интеллектуальное развитие,
формирование таких качеств личности, как ясность и точность мысли, критичность
мышления, логического мышления, способности к преодолению трудностей;
· формирование грамотной
математической речи учащихся с применением математических терминов;
Воспитательные:
· воспитание отношения к математике
как к части общечеловеческой культуры.
Методы работы.
Для достижения поставленных целей и задач особое
место в программе занимают следующие формы работы:
ü Лекции.
ü Практические занятия.
ü Самостоятельные работы.
Методы обучения:
Ø Частично-поисковый.
Ø Репродуктивный.
Ø Лекция.
Формы обучения:
v Индивидуальная.
v Групповая.
Планируемый результат.
Обучающиеся по окончании курса должны знать:
существо понятия параметра, задачи с параметром, алгоритма решения задачи с
параметром; приводить примеры задач с параметром; как уравнения с параметрами
могут описывать реальные зависимости; каким образом уравнения с параметрами
применяются на практике.
Обучающиеся по окончании курса должны уметь:
находить параметр в задаче с параметрическими данными; отличать переменную от
параметра; определять вид задачи с параметром; находить решение задачи с
параметром; записывать развернутый ответ к задаче.
Обучающиеся по окончании курса должны уметь
использовать приобретенные знания и умения в практической деятельности и
повседневной жизни для: решения несложных практических задач; устной прикидки и
оценки результата решения; интерпретации результатов решения задач с учетом
ограничений, связанных с реальными свойствами рассматриваемых процессов и
явлений.
Оценка качества знаний.
При оценке качества знаний будут использованы
задания для самостоятельного решения, итоговый тест. Причем будет учитываться
не только правильность ответа, но и сам ход решения, выбор метода решения,
умение объяснить свой ход мыслей, полнота решения.
Тезаурус.
Переменные a,b,c,…,k,
которые при решении уравнения или неравенства считаются постоянными, называются
параметрами, а само уравнение - уравнением, содержащим параметры.
Решить уравнение с параметром - значит указать,
при каких значениях параметров существуют решения и каковы они.
Два уравнения, содержащие одни и те же
параметры, называются равносильными, если:
) Они имеют смысл при одних и тех же
значениях параметров;
) Каждое решение первого уравнения
является решением второго и наоборот.
Неравенство 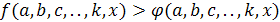 ,
где
,
где 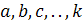 -
параметры, а x - действительная
переменная величина, называется неравенством с одним неизвестным, содержащим
параметры.
-
параметры, а x - действительная
переменная величина, называется неравенством с одним неизвестным, содержащим
параметры.
Действительное число x0
называется частным решением неравенства, если это неравенство верно при любой
системе допустимых значений параметров.
Множество всех частных решений неравенства
называется общим решением этого неравенства.
Два неравенства называются равносильными, если
они имеют одинаковые общие решения при одном и том же множестве систем
допустимых значений параметров.
Учебный план (10 класс)
|
№
п/п
|
Темы
занятий
|
Количество
часов
|
|
|
всего
|
теория
|
практика
|
|
1
|
Основные
понятия. Алгоритм решения.
|
3
|
2
|
1
|
|
2
|
Тригонометрические
уравнения с параметрами, сводящиеся к однородным.
|
5
|
1
|
4
|
|
3
|
Тригонометрические
уравнения с параметрами, решаемые введением новой переменной.
|
5
|
1
|
4
|
|
4
|
Тригонометрические
уравнения с параметрами, решаемые заменой переменной.
|
6
|
1
|
5
|
|
5
|
Решение
систем тригонометрических уравнений с параметром.
|
7
|
2
|
5
|
|
6
|
Решение
тригонометрических неравенств с параметром.
|
7
|
2
|
5
|
|
7
|
Итоговая
проверка знаний.
|
1
|
-
|
1
|
|
8
|
Итоговый
урок.
|
1
|
|
1
|
|
Итого.
|
35
|
9
|
26
|
Содержание курса.
Тема 1. Основные понятия. Алгоритм решения (3
ч).
Знакомство с основными понятиями, встречающимися
в ходе изучения элективного курса. Знакомство с алгоритмом решения уравнений и
неравенств с параметрами. Исследование области допустимых значений функций.
Тема 2. Тригонометрические уравнения с
параметрами, сводящиеся к однородным (5 ч).
Обобщение методов решения однородных
тригонометрических уравнений и их применение при решении похожих задач с
параметрами. Исследование области допустимых значений параметра и переменной.
Тема 3. Тригонометрические уравнения с
параметрами, решаемые введением новой переменной (5 ч).
Обобщение методов решения тригонометрических
уравнений введением новой переменной и применение этих методов при решении
подобных задач с параметрами. Нахождение области допустимых значений параметра.
Тема 4. Тригонометрические уравнения с
параметрами, решаемые заменой переменной (6 ч).
Обобщение методов решение тригонометрических
уравнений заменой переменной и применение этих методов при решении задач с
параметрами. Выявление различия между методом введения переменной и метода
замены переменной. Исследование области допустимых значений параметра и
переменной. Выполнение задач для самостоятельного решения.
Тема 5. Решение систем тригонометрических
уравнений с параметром (7 ч).
Разбор методов решения систем уравнений. Выбор
подходящего метода решения конкретной системы уравнений с параметрами.
Выявление влияния параметра на ход решения системы уравнений. Исследование условий
существования решения системы. Проверка решения системы с областью допустимых
значений.
Тема 6. Решение тригонометрических неравенств с
параметром (7 ч).
Рассмотрение методов решения тригонометрических
неравенств. Решение с помощью этих методов неравенств с параметрами. Связь
решения неравенства с областью допустимых значений параметра и переменной.
Зависимость свойств функций на значение параметра. Выполнение задач для
самостоятельного решения.
Тема 7. Итоговая проверка знаний (1 ч).
Проведение тестового контроля.
Тема 8. Итоговый урок (1 ч).
Подведение итогов. Анализ результатов.
Учебный план (11 класс)
|
№
п/п
|
Темы
занятий
|
Количество
часов
|
|
|
всего
|
теория
|
практика
|
|
1
|
Показательные
уравнения с параметрами.
|
5
|
2
|
4
|
|
2
|
Показательные
неравенства с параметрами.
|
6
|
1
|
5
|
|
3
|
Логарифмические
уравнения с параметрами.
|
5
|
2
|
4
|
|
4
|
Логарифмические
неравенства с параметрами.
|
6
|
1
|
5
|
|
5
|
Другие
уравнения с параметрами.
|
9
|
2
|
7
|
|
6
|
Итоговая
проверка знаний.
|
1
|
-
|
1
|
|
7
|
Итоговый
урок.
|
1
|
|
1
|
|
Итого.
|
35
|
8
|
27
|
Содержание курса.
Тема 1. Показательные уравнения с параметрами (5
ч).
Обобщение методов решения показательных
уравнений и их применение при решении показательных уравнений с параметрами.
Исследование области допустимых значений параметра и переменной. Определение
количества корней в зависимости от параметра. Влияние свойств функции на
решение уравнения.
Тема 2. Показательные неравенства с параметрами
(6 ч).
Обобщение методов решения показательных
неравенств и их применение при решении показательных неравенств с параметрами.
Исследование области допустимых значений параметра и переменной. Влияние
свойств функции на решение неравенства. Выполнение задач для самостоятельного
решения.
Тема 3. Логарифмические уравнения с параметрами
(5 ч).
Обобщение методов решения логарифмических уравнений
и их применение при решении логарифмических уравнений с параметрами.
Исследование области допустимых значений параметра и переменной. Определение
количества корней в зависимости от параметра. Влияние свойств функции на
решение уравнения.
Тема 4. Логарифмические неравенства с
параметрами (6 ч).
Обобщение методов решения логарифмических
неравенств и их применение при решении логарифмических неравенств с
параметрами. Исследование области допустимых значений параметра и переменной.
Влияние свойств функции на решение неравенств. Выполнение задач для
самостоятельного решения.
Тема 5. Другие уравнения с параметрами (9 ч).
Решение уравнений с параметрами, в которых
встречается несколько различных функций: тригонометрическая и логарифмическая;
логарифмическая и показательная. Методы перехода к функции одного вида.
Выполнение задач для самостоятельного решения.
Тема 6. Итоговая проверка знаний (1 ч).
Проведение тестового контроля.
Тема 7. Итоговый урок (1 ч).
Подведение итогов. Анализ результатов.
Литература для учителя.
1. Е.Ю. Никонов. Параметр. Самара - 1998.
. Еженедельная учебно-методическая газета
"Математика" №36/2001; №4/2002; №22/2002; №23/2002; №33/2002.
3. Ефимов Е.А., Коломиец Л.В. Задачи с
параметрами. Учебное пособие. Самара - 2002.
4. Амелькин В. В. и Рабцевич В. Л. “Задачи
с параметрами” . Издательство “Асар”. Минск 1996 г.
. Вавилов В.В. и др. Задачи по
математике. Алгебра: справочное пособие.- М.: Наука, 1987.
6. Горнштейн П.И., Полонский В.Б., Якир
М.С. Задачи с параметрами.
Литература для учащихся.
. Л. Солуковцева « Уравнения и
неравенства с параметрами», Москва, Чистые пруды,2007.
. Сборники заданий для подготовки к ЕГЭ.
. Г.А. Ястребинецкий, «Задачи с
параметрами», М. Просвещение,1986
Приложение 1
Задачи для самостоятельного решения.
Вариант 1.
. В зависимости от значений параметра а
решите уравнение 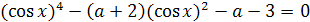 .
.
. При каких значениях параметра а
уравнение 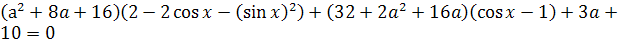 не имеет решений?
не имеет решений?
. При каких значениях параметра а
значение выражения 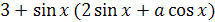 будет равно -1
хотя бы при одном значении х?
будет равно -1
хотя бы при одном значении х?
4. Решить уравнение: cos 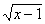 =2а.
=2а.
. Решить уравнение: tg ax2 =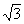
Ответы.
В-1. 1. Если 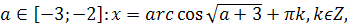 в остальных
случаях решений нет; 2.
в остальных
случаях решений нет; 2. 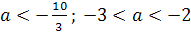 ; 3.
; 3. 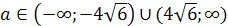 ; 4. если
|a| > 0,5, решений нет; если |a| ≤0,5 , х = 1+(2πn+аrссоs2а)2при n = 0, 1,
2,... и х=1+(2πn-arccos2a)2
при n
; 4. если
|a| > 0,5, решений нет; если |a| ≤0,5 , х = 1+(2πn+аrссоs2а)2при n = 0, 1,
2,... и х=1+(2πn-arccos2a)2
при n N; 5. при а
= 0 решений нет; при а > 0 и n = 1,2,3,… или а < 0 и n
N; 5. при а
= 0 решений нет; при а > 0 и n = 1,2,3,… или а < 0 и n Z х = ±
Z х = ± 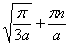 .
.
Вариант 2.
. В зависимости от значений параметра а
решите уравнение 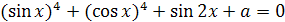 .
.
. При каких значениях параметра а
значение выражения 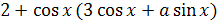 не равно нулю ни
при каких значениях х?
не равно нулю ни
при каких значениях х?
. При каких значениях параметра а
уравнение 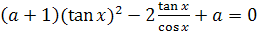 не имеет решений.
не имеет решений.
. Решите уравнение: а sin
bx = 1
5. Решить уравнение: tg ax2 =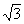
Ответы.
В-2. 1. Если 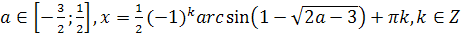 , в
остальных случаях корней нет; 2.
, в
остальных случаях корней нет; 2. 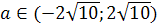 ; 3.
; 3. 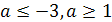 ; 4. при а = 0 или
; 4. при а = 0 или 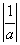 > 1 и а
> 1 и а 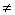 0 или а
0 или а 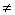 0 b = 0 решений
нет, при а
0 b = 0 решений
нет, при а 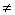 0 и
0 и  ≤ 1 и
b
≤ 1 и
b 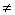 0 х =
0 х = 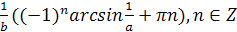 ; 5. при а =
0 решений нет; при а > 0 и n = 1,2,3,… или а < 0 и n
; 5. при а =
0 решений нет; при а > 0 и n = 1,2,3,… или а < 0 и n Z х = ±
Z х = ± 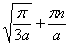 .
.
Приложение 2.
Задачи для самостоятельного решения.
Вариант 1.
. При каких значениях параметра а система
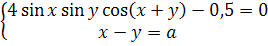 имеет
решения? Найти эти решения в зависимости от значений параметра а.
имеет
решения? Найти эти решения в зависимости от значений параметра а.
2. Решить неравенство 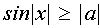 на
на 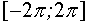 в
зависимости от значений параметра а.
в
зависимости от значений параметра а.
. При каких значениях
параметра а решением данного неравенства служит любое действительное число: 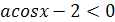 ?
?
. При каких значениях
параметра а система уравнений 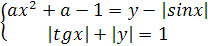 , имеет единственное решение?
, имеет единственное решение?
Ответы.
В-1. 1. Если 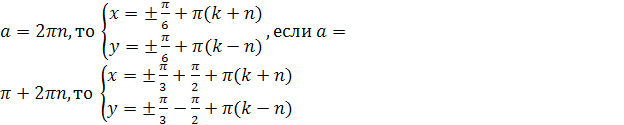 2.
2.
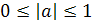 ;
3.
;
3. 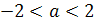 ;
4. а=2.
;
4. а=2.
Вариант 2.
. При каких значениях параметра а система
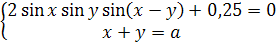 имеет
решения? Найти эти решения в зависимости от значений параметра а.
имеет
решения? Найти эти решения в зависимости от значений параметра а.
. В зависимости от значений параметра а
решите неравенство 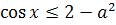 .
.
. При каких значениях параметра а
решением данного неравенства служит любое действительное число: 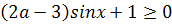 .
.
. При каких значениях параметра а система
уравнений 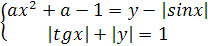 , имеет
единственное решение?
, имеет
единственное решение?
Ответы.
В-1. 1. Если 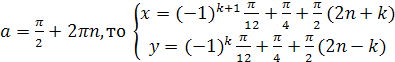 ,
если
,
если 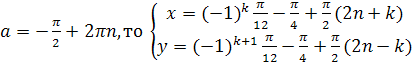 ;
2.
;
2.  3.
3.
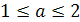 ;
4. а=2.
;
4. а=2.
Приложение 3.
Тест.
Вариант 1.
. Решите уравнение 3 cos
x = 4b
+ 1 для всех значений параметра.
а) при b ( -1; 0,5 )
х = ± arcos
( -1; 0,5 )
х = ± arcos 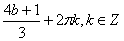 ; при b
; при b (-∞;-1]U[0,5;+∞)
реш.нет;
(-∞;-1]U[0,5;+∞)
реш.нет;
б) при b [ -1; 0,5 ]
х = ± arcos
[ -1; 0,5 ]
х = ± arcos 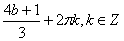 ; при b
; при b (-∞;-1)U(0,5;+∞)
реш.нет;
(-∞;-1)U(0,5;+∞)
реш.нет;
в) b (-∞;-1]U[0,5;+∞)
х = ± arcos
(-∞;-1]U[0,5;+∞)
х = ± arcos 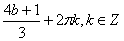 ; b
; b ( -1; 0,5 )
при реш.нет;
( -1; 0,5 )
при реш.нет;
. Найдите все действительные
значения параметра а, при которых уравнение sin2 x - 3sin x + a =0.
а) a  [ -4; 2 ] ;
б) а
[ -4; 2 ] ;
б) а  ( -4 ; 2) ;
в) а
( -4 ; 2) ;
в) а [ - 4; 2 ).
[ - 4; 2 ).
. При каких значениях а уравнение cos4 x + sin4 x = a имеет
корни?
а) a  [ 0,5; 1 ]
; б) а
[ 0,5; 1 ]
; б) а  [ -1 ; 0,5
] ; в) а
[ -1 ; 0,5
] ; в) а [ - 0,5; 1
).
[ - 0,5; 1
).
Вариант 2.
. Решите уравнение cos (3x +1 ) = b для всех
значений параметра.
а) при |b| ≤ 1
х = 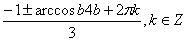 ; при |b| > 1
реш.нет;
; при |b| > 1
реш.нет;
б) при |b| ≤ 1
и b=0 х = 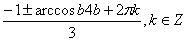 ; при |b| > 1
реш.нет;
; при |b| > 1
реш.нет;
в) при |b| > 1 х =
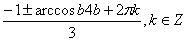 ; при |b| < 1
реш.нет;
; при |b| < 1
реш.нет;
. Найдите все действительные
значения параметра а, при которых уравнение cos2 x + asin x =2 a -7.
а) a  ( 2 ; 6 ) ;
б) а
( 2 ; 6 ) ;
б) а  ( 2 ; 4 ] ;
в) а
( 2 ; 4 ] ;
в) а [ 2 ; 6 ].
[ 2 ; 6 ].
. При каких значениях а уравнение cos6 x + sin6 x = a имеет
корни?
а) a  [ 0,25; 0,5
] ; б) а
[ 0,25; 0,5
] ; б) а  [ 0,25 ; 1
] ; в) а
[ 0,25 ; 1
] ; в) а [ - 0,25; 1
].
[ - 0,25; 1
].
Приложение 4.
Задачи для самостоятельного решения.
Вариант 1.
В зависимости от значений параметра
а решите уравнение или неравенство:
1. 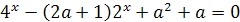
2. 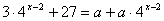
3. 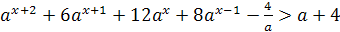
4. 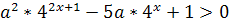
5. 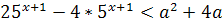
Ответы.
В-1. 1. Если а≤-1, то решений нет; если -1≤а<0,
то 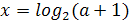 ,
если а>0, то
,
если а>0, то 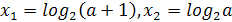 ; 2. 3. Если
0<а<1, то
; 2. 3. Если
0<а<1, то 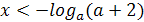 , если а=1, то
, если а=1, то 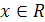 ,
если а>1, то
,
если а>1, то 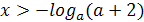 ; 4. Если а≤0,
то
; 4. Если а≤0,
то 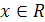 ,
если а>0, то
,
если а>0, то 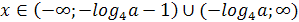 ; 5. Если а
; 5. Если а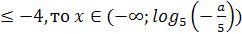 ,
если -4<а<-2, то
,
если -4<а<-2, то 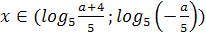 , если а=-2, то
решений нет, если -2<а<0, то
, если а=-2, то
решений нет, если -2<а<0, то 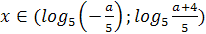 ,
если а≥0, то
,
если а≥0, то 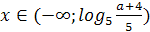 .
.
Вариант 2.
В зависимости от значений параметра а решите
уравнение или неравенство:
1. 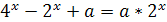
2. 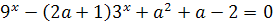
3. 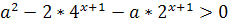
4. 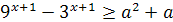
5. 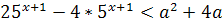
Ответы.
В-2. 1. 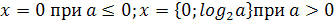 ;
2.
;
2. 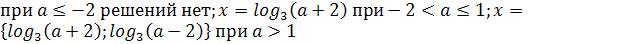 ;
3. Если а<0, то
;
3. Если а<0, то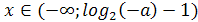 , если а=0, то
решений нет, если а>0, то
, если а=0, то
решений нет, если а>0, то 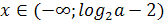 ; 4. Если а≤-1,
то
; 4. Если а≤-1,
то 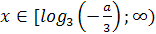 ,
если -1<а<-1/2, то
,
если -1<а<-1/2, то 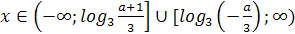 , если а=-1/2, то
, если а=-1/2, то 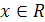 ,
если -1/2<а<0, то
,
если -1/2<а<0, то 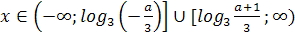 , если а≥0,
то
, если а≥0,
то 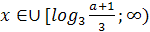 ;
5. Если а
;
5. Если а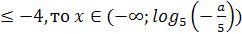 ,
если -4<а<-2, то
,
если -4<а<-2, то 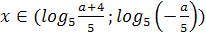 , если а=-2, то
решений нет, если -2<а<0, то
, если а=-2, то
решений нет, если -2<а<0, то 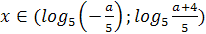 ,
если а≥0, то
,
если а≥0, то 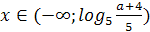 .
.
Приложение 5.
Задачи для самостоятельного решения.
Вариант 1.
. В зависимости от значений параметра а
решите уравнение 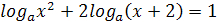 .
.
. При каких значениях параметра а уравнение
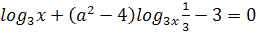 имеет
два корня, расстояние между которыми больше 8?
имеет
два корня, расстояние между которыми больше 8?
. В зависимости от значений параметра а
решите неравенство 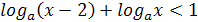 .
.
. При каких значениях параметра а для
любого х<0 выполняется неравенство 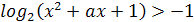 ?
?
. При каких допустимых значениях
параметра а неравенство 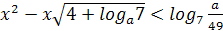 не выполняется ни
при каких х?
не выполняется ни
при каких х?
Ответы.
В-1. 1. Если 
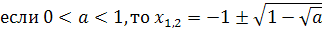 ,
,
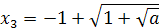 ;
если
;
если 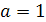 ,
то решений нет; если
,
то решений нет; если 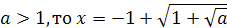 ; 2.
; 2. 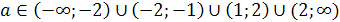 ;
3. Если
;
3. Если 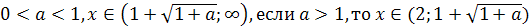 ;
4.
;
4. 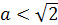 ;
5.
;
5. 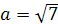 ;
;
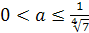 .
.
Вариант 2.
. В зависимости от значений параметра а
решите уравнение 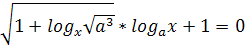 .
.
. При каких значениях параметра а
уравнение 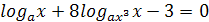 имеет два корня,
расстояние между которыми меньше
имеет два корня,
расстояние между которыми меньше  ?
?
. В зависимости от значений параметра а
решите неравенство 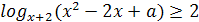 .
.
. При каких допустимых значениях
параметра а неравенство 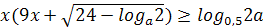 выполняется при
любых х?
выполняется при
любых х?
. При каких значениях параметра а
неравенство 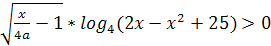 имеет 2 целых
решения?
имеет 2 целых
решения?
Ответы.
В-2. 1. Если 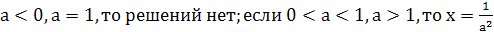 ;
2.
;
2. 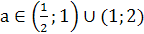 ;
3. Если
;
3. Если 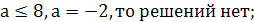 если
если
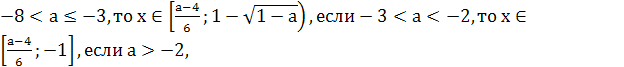 то
то
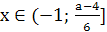 ;
4.
;
4. 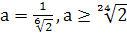 ;
5.
;
5. 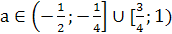 .
.
Приложение 6.
Задания для самостоятельного решения.
Вариант 1.
. При каких значениях параметра а значение
выражения 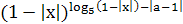 больше значения
выражения
больше значения
выражения 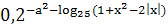 при всех
допустимых значениях х?
при всех
допустимых значениях х?
. При каких значениях параметра а сумма 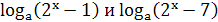 равна
единице ровно при одном х?
равна
единице ровно при одном х?
3. Найти все значения
параметра a, при каждом
из которых уравнение 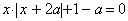 имеет
единственное решение.
имеет
единственное решение.
. Найдите все значения
параметра a, при каждом
из которых уравнение имеет три различных корня; найдите эти корни: 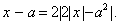
Ответы.
В-1. 1. 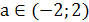 ; 2.
; 2. 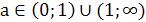 ; 3.
; 3. 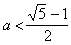 ,
, 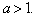 ; 4. При
; 4. При 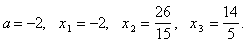 ; при
; при 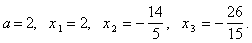
Вариант 2.
1. При каких значениях параметра а
значение выражения 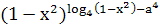 больше значения
выражения
больше значения
выражения 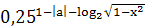 при всех
допустимых значениях х?
при всех
допустимых значениях х?
. При каких значениях параметра а сумма 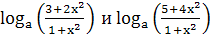 ,
больше единицы при всех х?
,
больше единицы при всех х?
3. Найдите все значения
параметра a из
промежутка 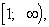 при каждом
из которых больший из корней уравнения
при каждом
из которых больший из корней уравнения 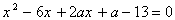 принимает наибольшее значение.
принимает наибольшее значение.
. Для каждого значения
параметра a определите
число решений уравнения 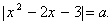
Ответы.
В-2. 1. 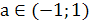 ; 2.
; 2. 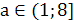 ; 3. при a = 1; 4.
Если
; 3. при a = 1; 4.
Если 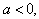 тогда
уравнение не имеет корней, если
тогда
уравнение не имеет корней, если 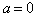 и
и 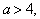 тогда уравнение имеет два корня,
если
тогда уравнение имеет два корня,
если 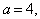 тогда
уравнение имеет три корня, если
тогда
уравнение имеет три корня, если 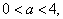 тогда уравнение имеет четыре корня.
тогда уравнение имеет четыре корня.
Приложение 7.
Тест.
Вариант 1.
. Решите уравнение 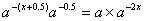
а) при а ≤ 0 х  R ; при а
> 0, а
R ; при а
> 0, а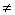 1 х = 2; при
а = 1 не имеет смысла.
1 х = 2; при
а = 1 не имеет смысла.
б) при а > 0 х  R ; при а = 1
х = 2; при а ≤ 0 не имеет смысла.
R ; при а = 1
х = 2; при а ≤ 0 не имеет смысла.
в) при а = 1 х  R ; при а
> 0, а
R ; при а
> 0, а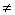 1 х = 2; при
а ≤ 0 не имеет смысла.
1 х = 2; при
а ≤ 0 не имеет смысла.
2. При каких значениях параметра уравнение
4х - а2 х+1 - 3а2 + 4а = 0 имеет единственное решение?
а) 2; б) 1 ; в) -1.
. Решите уравнение log
a x
2 + 2 log
a ( x
+ 2) = 1.
а) при а ≤ 1 х = 0,5( 2+ 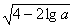 ) ; при а
=100 х = 1.
) ; при а
=100 х = 1.
б) при а > 100 реш. нет; при
1<a<100 х =
0,5( 2+ 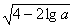 ); при а
=100 х = 1;
); при а
=100 х = 1;
при а ≤ 1 не имеет смысла .
в) при а > 100 реш.нет ; при
1<a<100 х =
0,5( 2+ 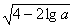 ) ;
) ;
при а ≤ 1 не имеет смысла .
4. Найдите все значения параметра, для
которых данное уравнение имеет только один корень 1+ log
2 (ax) = 2 log
2 (1 - x)
а) а > 0, а = 2 ; б) а > 0, а = - 2 ; в) а
< 0, а = - 2 .
а) а ; 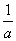 ; б) а2 ; -
; б) а2 ; -
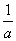 ; в ) а2 ;
; в ) а2 ; 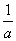
Вариант 2.
. Решите уравнение 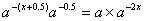
а) при а ≤ 0 х  R ; при а
> 0, х = 1; при а = 1 не имеет смысла.
R ; при а
> 0, х = 1; при а = 1 не имеет смысла.
б) при а = 1 х  R ; при а
> 0, а
R ; при а
> 0, а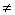 1 х = 1; при
а ≤ 0 не имеет смысла.
1 х = 1; при
а ≤ 0 не имеет смысла.
в) при а > 0х  R ; при а = 1
, х = 1; при а ≤ 0 не имеет смысла.
R ; при а = 1
, х = 1; при а ≤ 0 не имеет смысла.
2. При каких значениях параметра уравнение
а( 2 х + 2-х ) = 5 имеет единственное решение?
а) -2,5; 2,5 ; б) 2; 2,5 ; в) -2,5.
. Решите уравнение 3 lg
(x - а) - 10 lg
( x - а)+1 = 0.
а) х = а + 1000, х = а + 3√10 ;
б) х = а - 3√10 , х = а -1000 ;
в) х = а - 3√10 , х = а + 1000 .
4. Найдите все значения
параметра, для которых данное уравнение имеет только один корень 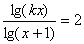
а) 4 ; б) -4 ; в) - 2
5. Решите уравнение 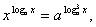 а > 0, а
а > 0, а 1
1
а) -1 ; а ; б) 1 ; - а; в ) 1 ; а
V. Заключение
Данная работа показывает, прежде всего, что так
называемая элементарная математика даже в ограниченном контексте - задачи с
параметрами - представляет собой весьма широкое поле для полноценной
математической деятельности - во всяком случае более широкое, чем
многочисленные зачастую вполне алгоритмические задачи на вычисление пределов,
производных и интегралов, которыми наполнены практические занятия студентов по
«высшей математике».
Решение задач, а точнее, уравнений с
параметрами, открывает перед учащимися значительное число эвристических приемов
общего характера, ценных для математического развития личности, применимых в
исследованиях и на любом другом математическом материале.
Исследование показало, насколько далеко практика
выпускных экзаменов оторвалась от школы, насколько велики «ножницы» между
требованиями, которые предъявляет к своему выпускнику школа, и требованиями,
которые предъявляет к своему поступающему вуз.
Поэтому я высказала в своей работе необходимость
издания массовой литературы, посвященной трудным вопросам школьной математики,
важным для подготовки к ЕГЭ, но не рассматривающимся, по разным причинам, в
школьном курсе. Также большую роль играет сам учитель, которому необходимо
создавать различные программы для курсов по выбору, элективных курсов,
факультативных занятий. Учитель, все в твоих руках.