Элементы векторной алгебры и аналитической геометрии
Министерство
высшего и среднего специального образования Республики Узбекистан
Ташкентский
институт текстильной и легкой промышленности
Удк
516.517
ЭЛЕМЕНТЫ
ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Методические
указания
Ташкент-2010
Аннотация
Методическое указание написано в виде
справочника, приведены план работы, каждый раздел содержит краткие
теоретические введения, решения типовых примеров и задачи для самостоятельного
решения. Цель
методического указания помочь студентам самостоятельно решать задачи, может
оказаться полезной и лицам, желающим повторить элементы векторной алгебры и
аналитической геометрии.
СОСТАВИТЕЛЬ
Доцент кандидат физ .- матем. наук
М.М.Сайдаматов
РЕЦЕНЗЕНТЫ
ТИТЛП проф. А.З. Маматов, НУУз проф. Б. Атажанов
Утверждено научно-
методическим
советом института
«_12__»___03____ 2010 г.
Протокол № _4___
Размножено в «_25__»
экземплярах
в типографии ТИТЛП
РАЗДЕЛ 1. ПРЯМАЯ НА ПЛОСКОСТИ
Основные формулы
. Расстояние d
между двумя точками М1(Х1 У1) и М2 (Х1 У2) определяются по формуле
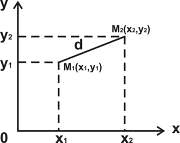
d=М1М2=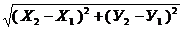 /1.1/
/1.1/
.Деление отрезка М1М2 в данном
отношении.
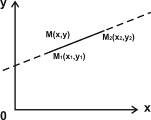
Точка М делит отрезок М1М2 в
отношении 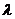 , если
, если
М лежит на отрезке или на его
продолжении и
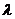 =
=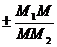 , /1.2/
, /1.2/
причем перед дробью берется знак
«плюс», если точка М лежит между М1 и М2, и знак «минус» - в противном случае.
Если дано отношение 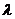 , то
координаты точек М (х, у) определяются по формулам
, то
координаты точек М (х, у) определяются по формулам
 /1.3/
/1.3/
Если точка М(х,у) является серединой
отрезка М1М2, то ее координаты определяются по формулам
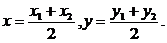 /1.4/
/1.4/
. Общее уравнение прямой
Ах+Ву+С=0 /1.5/
При В 0 из /1.5/ получается
уравнение
у=кх+в,
где угловой коэффициент 
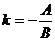 , свободный член
, свободный член 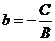 .
.
. Уравнение прямой по точке
М0(х0,у0) и угловому коэффициенту К:
у-у0=к(х-х0) /1.6/
 к=tg
к=tg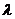
. Уравнение прямой, проходящие через
две точки: М1(х1,у1) и М2(х2,у2):
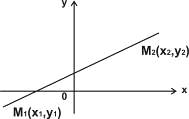
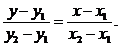 /1.7/
/1.7/
Угловой коэффициент прямой равен
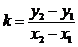 /1.8/
/1.8/
. Углом между двумя прямыми
называется наименьший из углов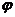 и
и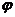 1
1
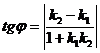 Тангенс угла между прямой с угловым
коэффициентами К1 и К2 равен
Тангенс угла между прямой с угловым
коэффициентами К1 и К2 равен
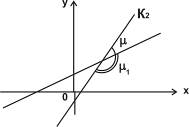
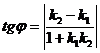 /1.9/
/1.9/
. Условие параллельности двух прямых с угловыми
коэффициентами
К1 и К2 ,
К1=К2 /1.10/

. Условие перпендикулярности двух прямых с
угловыми коэффициентами К1 и К2
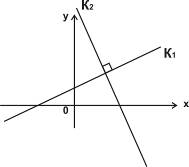
 /1.11/
/1.11/
. Расстояние от точки М1(х1,у1) до
прямой ax+by+c=0
вычисляется по формуле
 /1.12/
/1.12/
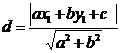
ПРИМЕРЫ
.Дана прямая 2х-3у+3=0. Составить
уравнение прямой, проходящей через точку М0(1,1):
а) параллельно данной прямой;
б) перпендикулярно данной прямой.
Решение.
а) Определим угловой коэффициент К1
из уравнения данной прямой
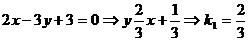
Из условия параллельности прямых -
см. формулу /1.10/ получаем угловой коэффициент искомой прямой
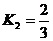
По точке М0 и угловому коэффициенту
К2 составляем уравнение - см. формулу /1.6/
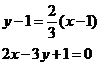
б) Из условия перпендикулярности
прямых - см. формулу /1.11/ определим угловой коэффициент искомой прямой
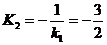
По формуле /1.6/ составляем
уравнение перпендикулярной прямой
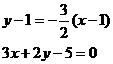
или
Ответ: а) 2х-3у+1=0;
б) 3х+2у-5=0
. Найти проекцию точки Р()2,1) на
прямой, проходящую через две точки: М1(1,-1) и М2(2,0).
Решение. Проекция Р1
является
точкой пересечения данной прямой М1М2 и перпендикулярной прямой РР1.

а) Составим уравнение прямой М1М2
см. формулу /1.7/
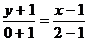
или
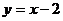
Из этого уравнения определим угловой
коэффициент: К1=1.
б) Из условия перпендикулярности
прямых см. формулу /1.11/ найдем угловой коэффициент прямой РР1:
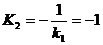
в) составим уравнение прямой РР1 по
формуле /1.6/
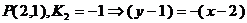
или
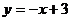
г) найдем координаты проекции Р1,
решая совместно два уравнения
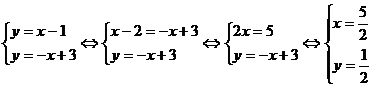
Ответ: 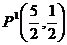
. Найти точку Q,
симметричную точке Р(5,-2) относительно прямой 5х-3у+3=0

Решение. Точка Q лежит на
продолжении перпендикуляра РР1, опущенного из точки Р на прямую, на таком же
расстоянии от прямой, что и точка Р. Поэтому точка Q делит
отрезок РР1 в отношении
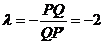 .
.
А) найдем координаты проекции Р1
(см. решение примера 2). Определим угловой коэффициент К1 данной прямой
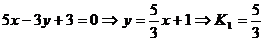 .
.
Тогда угловой коэффициент К2 прямой PQ равен - см.
формулу /1.11/
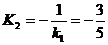 ;
;
Уравнение прямой PQ имеет вид -
см. формулу /1.6/
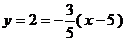
или
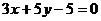 .
.
Координаты точки P1 находим
при совместном решении двух уравнений
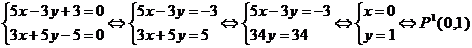
б) Находим координаты симметричной
точки по формулам /1.3/:
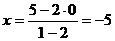 ,
, 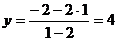 .
.
Ответ: Q(-5,4).
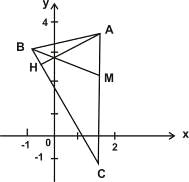
. Зная координаты вершин
треугольника А(2,4), В(-1,3) и С(2,-1) найти:
а) уравнение и длину высоты АН;
б) уравнение медианы ВМ
в) угол В.
Решение. а) составим уравнение
прямой ВС по формуле /1.7/:
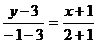
или
х+3у-5=0
Из уравнения ВС определим угловой коэффициент:
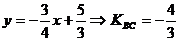
угловой коэффициент высоты АН найдем
по формуле /1.11/:
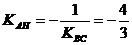
Составим уравнение прямой АН по
формуле /1.6/:
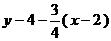
или
х-4у+10=0
Расстояние от точки А до стороны ВС
получим по формуле /1.12/:
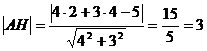
б) Найдем координаты точки М по
формулам /1.7/:
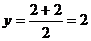 ,
, 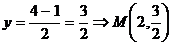 .
.
Составим уравнение медианы ВМ по
формуле /1.7/:
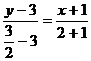
или
х+2н-5=0
в) Угловой коэффициент прямой АВ
определим по формуле /1.8/:

Угол В вычисляем по формуле /1.9/:
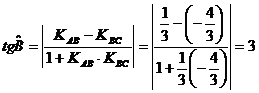
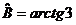
Ответ: а) АН: 3х-4у+100=0, 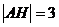
б) ВМ: х+2у-5=0
в) 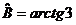
. Даны вершины треугольника А(4,6),
В(-4,0) и С(-1,-4).
Составим уравнение биссектрис его
внутреннего и внешнего углов при вершине В.

Решение. а) Из школьного курса
геометрии известно, что биссектриса ВК делит сторону АС в отношении
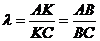
Определим длины сторон АВ и ВС по
формуле /1.1/:
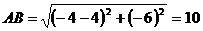 ;
; 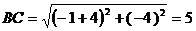 . Тогда
. Тогда 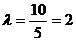
б) Координаты точки К вычислим по
формулам /1.3/:
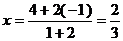 ,
, 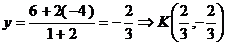 .
.
в)Составим уравнение биссектрисы ВК
по формуле /1.7/:
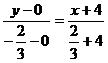
или
х+7у+4=0
г) биссектриса BL
перпендикулярна ВК, следовательно, угловой коэффициент КBL находим по
формуле /1.11/:
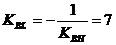 .
.
д) Составим уравнение биссектрисы BL по формуле
/1.6/:
у-0=7(х+4)
или
х-у+2В=0
Ответ: ВК: х+7у+4=0, BL: 7x-y+2B=0.
Самостоятельная
работа
. Построить прямую,
отсекающую на оси Оу отрезок  и составляющую с осью Ох угол:
и составляющую с осью Ох угол: 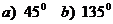 .
.
. Дан треугольник с вершинами
А(-2, 0), B(2,4), и С(4,0).
Написать
уравнения сторон треугольника, медианы AE, высоты AD и найти
длину медианы AE.
. Определить вершины и углы
треугольника, стороны которого заданы уравнениями х+3у=0, х=3, х-2у+3=0.
. Найти углы и площадь
треугольника, образованного прямыми у=2х, у=-2х и у=х+b.
РАЗДЕЛ 2. ВЕКТОРНАЯ АЛГЕБРА
№1. Векторы. Линейные
операции над векторами. Основные понятия и определения
. Вектором называется величина, которая
характеризуется числовым значением и направлением в пространстве.
Геометрически вектор изображается отрезком
определенной длины и определенного направления

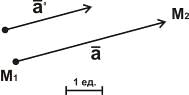
Точка 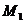 - начало вектора
- начало вектора 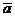 . Точка
. Точка 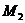 - конец
вектора
- конец
вектора 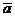 . Числовое
значение вектора
. Числовое
значение вектора 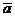 называется
модулем / длиной / вектора:
называется
модулем / длиной / вектора: 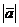 .
.
Нулевым вектором называется вектор,
у которого начало и конец совпадают.
Ортом  вектора
вектора 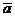 называется
вектор, имеющий единичную длину и такое же направление, как и данный вектор
называется
вектор, имеющий единичную длину и такое же направление, как и данный вектор 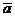 .
.
. Коллинеарным называется векторы,
лежащие на одной прямой или на параллельных прямых.
Компланарными называются векторы,
лежащие в одной плоскости или в параллельных плоскостях.
. Два вектора считаются равными, если:
а) они
имеются равные модули / длины/;
б) коллинеарные;
в) одинаково направлены.
. Линейными операциями над векторами
называются операции сложения векторов и умножения их на числа.

Суммой 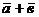 двух
векторов
двух
векторов 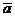 и
и 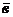 называется
третий вектор, идущий из начала вектора
называется
третий вектор, идущий из начала вектора 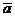 в конце вектора
в конце вектора 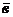 , когда
начало вектора,
, когда
начало вектора, 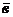 приложено к
концу вектора
приложено к
концу вектора 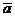 , сумму
, сумму 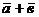 можно
представить также как диагональ параллелограмма, построенного на векторах
можно
представить также как диагональ параллелограмма, построенного на векторах 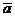 и
и 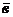 ,
приведенных к одному началу.
,
приведенных к одному началу.
Произведением 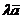 числа
числа 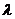 на вектор
на вектор 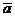 называется
такой вектор, длина которого равна
называется
такой вектор, длина которого равна 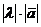 , а направление сохраняется прежним
при
, а направление сохраняется прежним
при  и
заменяется противоположным при
и
заменяется противоположным при 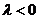 . Если
. Если 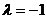 , то вектор
, то вектор 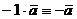 называется
противоположным вектору
называется
противоположным вектору 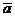 .
.
Свойства векторов
. 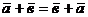 (переместительный закон)
(переместительный закон)
. 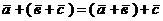 (сочетательный закон ).
(сочетательный закон ).
. 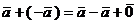
. 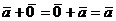
.  (распределительный закон).
(распределительный закон).
. 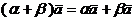 (распределительный закон).
(распределительный закон).
. 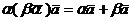
. 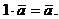
Линейной комбинацией n векторов 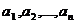 коэффициентами
коэффициентами
 называется
вектор, равный
называется
вектор, равный
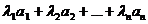 .
.
. проекцией вектора 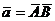 на ось
на ось 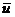 (на вектор
(на вектор 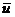 ) называется
число, равное
) называется
число, равное 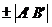 , где
, где 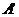 - проекцией
начала А и
- проекцией
начала А и 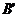 - проекцией
конца
- проекцией
конца  на ось
на ось 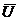 (на вектор
(на вектор 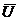 ), причем
знак “плюс” берется, когда направление
), причем
знак “плюс” берется, когда направление 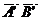 совпадает с направлением
совпадает с направлением 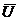 , а знак «минус”
в противном случае.
, а знак «минус”
в противном случае.

Проекция вектора вычисляется по
формуле 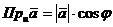 , где
, где 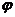 -
наименьший угол, на который надо повернуть вектор
-
наименьший угол, на который надо повернуть вектор 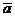 , чтобы его
направление совпало с направлением
, чтобы его
направление совпало с направлением 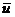 .
.
. Разложение вектора по базису.
Базисом в пространстве называются
любые три некомпланарных вектора 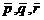 .
.
Разложить вектор 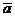 по базису
по базису 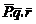 - это значит
представить вектор
- это значит
представить вектор 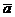 в виде
линейной комбинации
в виде
линейной комбинации
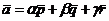 ,
,
где 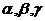 - числа, называемые координатами
вектора в данном базисе.
- числа, называемые координатами
вектора в данном базисе.
Базис в плоскости называются любые
два неколлинеарных вектора 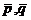 -это значит представить вектор
-это значит представить вектор 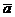 в виде
линейной комбинацией
в виде
линейной комбинацией 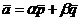 , где
, где 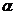 и
и 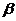 - числа,
называемые координатами вектора
- числа,
называемые координатами вектора 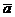 в данном базисе.
в данном базисе.
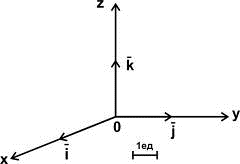
Пусть 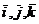 - векторы/ направленные
соответственно по осям OX, OY, OZ
прямоугольной системы координат, имеющие единичную длину.
- векторы/ направленные
соответственно по осям OX, OY, OZ
прямоугольной системы координат, имеющие единичную длину.
Базис 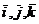 называется прямоугольным базисом.
Разложение вектора
называется прямоугольным базисом.
Разложение вектора 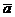 по базису
по базису 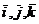 имеет вид
имеет вид 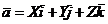 , где X,Y,Z -
прямоугольные координаты вектора
, где X,Y,Z -
прямоугольные координаты вектора 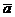 (символическое обозначение:
(символическое обозначение: 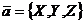 ).
).
Прямоугольные координаты вектора
равны проекциям этого вектора на оси координат.
Основные формулы в координатной
форме
1. Координаты вектора, заданного двумя
точками - началом
М1(X1,
Y1, Z1)
и концом М2(X2, Y2,
Z2): X=X2-X1,
Y=Y2-Y2,
Z=Z2-Z1
/2.1/
Cуммой и разностью
двух векторов
 ,
, 
2. Модуль
(длина)
вектора 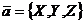 :
: 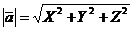 /2.2/
/2.2/
3. Направляющие косинусы
вектора 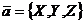 :
:
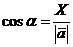 ,
, 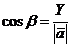 ,
, 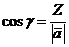 , /2.3/
, /2.3/
где 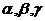 - угля между вектором
- угля между вектором 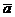 и осями
координат OX, OY, OZ соответственно.
и осями
координат OX, OY, OZ соответственно.
Направляющие косинусы связаны
формулой
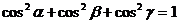 . /2.4/
. /2.4/
Орт 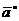 вектор
вектор 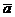 имеет
координаты
имеет
координаты 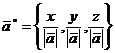 .
.
4. Координаты линейной комбинацией векторов
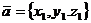 и
и 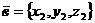
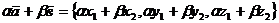 /2.5/,
/2.5/,
. Признак коллинеарности
векторов 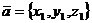 и
и 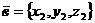 :
:
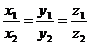 /2.6/
/2.6/
ПРИМЕРЫ
. Определить координаты и модули
векторов, заданных двумя точками
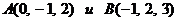
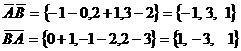
Б) Модули векторов находим по
формуле /2.2/
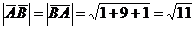
Ответ: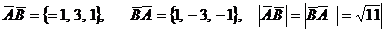
. Определить начало вектора 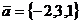 ,
направляющие конусы и орт
,
направляющие конусы и орт 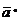 ,если конец
совпадает с точкой
,если конец
совпадает с точкой 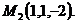
Решение. А) из формулы /2.1/
получаем координаты начала 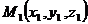 :
:
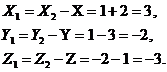
Б) Модуль вектора определим по
формуле /2.2/:
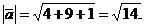
В) Направляющие конусы вычисляем по
формуле /2.3/:
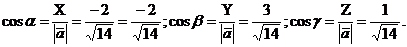
Г)Координаты орта 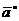 числено
равны направляющим конусам:
числено
равны направляющим конусам:
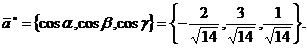
Ответ: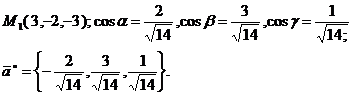
. Может ли вектор составлять с
координатами осями углы 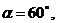
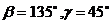
Решение. Для заданных величин 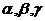 формула
/2.4/ не выполняется:
формула
/2.4/ не выполняется:
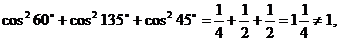 поэтому вектор не может составлять
данные углы с осями координат.
поэтому вектор не может составлять
данные углы с осями координат.
. Даны два вектора 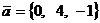 и
и 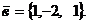
Определить 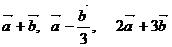 . По формуле
/2.5/ получаем:
. По формуле
/2.5/ получаем:

. Определить, при каких
значениях α
и
β
векторы
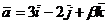 и
и 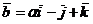 коллинеарны.
коллинеарны.
Решение. Используя признаки колинеарности
векторов - см, формулу /2.6/, составим пропорцию:
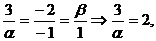
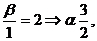

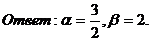
. Найти разложение вектора 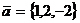 по базису
по базису 

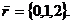
Решение. Найдем коэффициенты α, β,
γ в
разложении 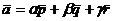 .
.
Для этого запишем данную формулу в
координатах. Координаты правой части вычислим, используя формулу /2.5/:
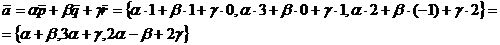
Эти координаты должны равняться
соответствующим координатам вектора 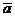 . Следовательно,
. Следовательно,
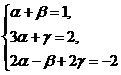
Решим полученную систему уравнений
методом исключения неизвестных /методом Гаусса/:
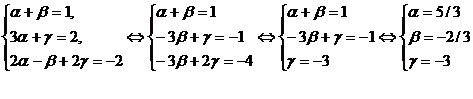
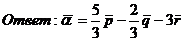
Самостоятельная
работа
. Определить координаты и
модули векторов, заданных двумя точками 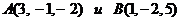 .
.
. Определить, при каких
значениях α
и
β
векторы
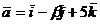 и
и
 коллинеарны.
коллинеарны.
3. Найти разложение вектора 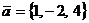 по базису
по базису 

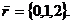
. При каких значениях m векторы 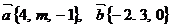 перпендикулярны
перпендикулярны
№ 2.
Скалярное произведение векторов и его применение. Основные понятия и
определения

1. Углом между векторами 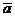 и
и  будем
называть наименьший из двух углов
будем
называть наименьший из двух углов 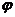 и
и 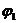 /считаем, что всегда можно сделать
параллельным переносом/.
/считаем, что всегда можно сделать
параллельным переносом/.
. Скалярным произведением 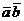 двух
векторов
двух
векторов 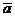 и
и  называется
число, равное произведению длин этих векторов, умноженному на косинус угла
называется
число, равное произведению длин этих векторов, умноженному на косинус угла 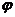 между ними:
между ними:
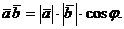
1. Скалярное произведение двух векторов равно
длине одного из них, умноженной на проекцию другого вектора на первый вектор:

2. Скалярное произведение двух векторов равно
нулю тогда и только тогда, когда либо один из векторов равен нулю, либо они
перпендикулярны.
3. Физический смысл скалярного
произведения.
Работа А равнодействующей несколько
сил 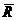 ,
приложенных к материальной точке, при прямолинейном точке, при прямолинейном
перемещении из положения М1 в положение М2, равна
,
приложенных к материальной точке, при прямолинейном точке, при прямолинейном
перемещении из положения М1 в положение М2, равна 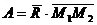 .
.
Свойства скалярного произведения.
. 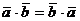 /переместительный
закон/.
/переместительный
закон/.
. 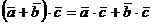 /распределительный
закон/.
/распределительный
закон/.
. 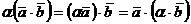 /сочетательный закон
относительно числового множителя/.
/сочетательный закон
относительно числового множителя/.
.  /скалярное произведение вектора
самого на себя равно квадрату его длины/.
/скалярное произведение вектора
самого на себя равно квадрату его длины/.
Основные формулы в координатной форме.
1. Скалярное произведение
векторов 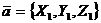 и
и 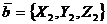 :
:
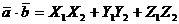 /2.7/
/2.7/
. Угол между векторами 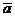 и
и  определяется
по формуле
определяется
по формуле
 /2.8/
/2.8/
3. Признак перпендикулярности
векторов 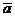 и
и  :
:
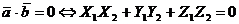 /2.9/
/2.9/
ПРИМЕРЫ

. В Параллелепипеда АBCDA`B`C`D` стороны АВ
и АD взаимно
перпендикулярны, а стороны АА` образует с ними углы в 1200.
Определить длины
диагоналей А`С и В`D если длины сторон равны АВ=2, АD=1, AA`=3.
Решение. Рассмотрим векторы 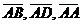 . Из рисунка
видно, что диагональ
. Из рисунка
видно, что диагональ 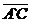 , лежащая в
плоскости АА`C`C,
удовлетворяет соотношению.
, лежащая в
плоскости АА`C`C,
удовлетворяет соотношению. 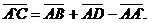
Для нахождения 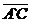 используем
4-е свойство скалярного произведения:
используем
4-е свойство скалярного произведения:
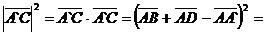
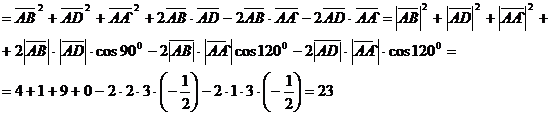
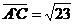
Аналогично, диагональ B`D, лежащая в
плоскости DD`B`B,
удовлетворяет соотношению

Поэтому
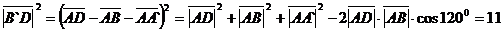
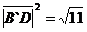
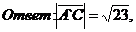
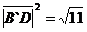 .
.

. Даны вершины треугольника
А(1,2,-1), В(-1,0,1) и С(1,1,1). Определить его внутренний и внешний углы при
вершине В.
Решение. а/ Внутренний угол при
вершине В образован векторами 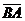 и
и 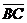 . Координаты векторов находим по
формулам /2.1/:
. Координаты векторов находим по
формулам /2.1/:
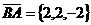
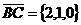
б/ Косинус угла 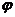 при вершине
В находим по формуле /2.8/:
при вершине
В находим по формуле /2.8/:
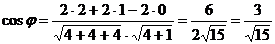 .
.
 .
.
в/ Внешний угол при вершине В равен
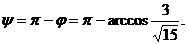
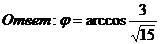 ,
, 
. Найти сектор 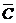 , зная, что
он перпендикулярен к векторам
, зная, что
он перпендикулярен к векторам 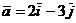 и
и 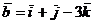 и удовлетворяет условию
и удовлетворяет условию 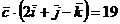
Решение. Обозначим координаты
искомого вектора 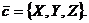
а/ Из условия перпендикулярности
векторов /2.9/ получим
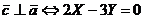
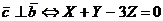
Последнее условие примера с учетом
формулы /2.7/ примет вид
Х+2Y-Z=19
б/ Полученную систему трех уравнений
с тремя неизвестными решим методом исключения:
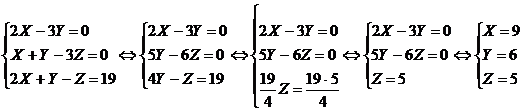
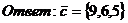 .
.
. Даны две точки М1(1,0,2) и
М2(-1,1,1). Найти проекцию вектора 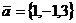 на вектор
на вектор 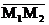 .
.
Решение. а/ Определить координаты
вектора 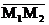 :
:
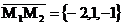 .
.
б/ Скалярное произведение 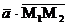 вычислим по
формуле /2.7/:
вычислим по
формуле /2.7/:
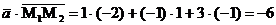
в/ Проекция вектора 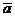 на вектор
на вектор 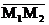 с учетом
формулы /2.8/ равна
с учетом
формулы /2.8/ равна
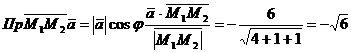
Ответ: 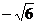 .
.
. Даны две силы 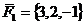 и
и  ,
приложенные к одной точке. Какую работу производит равнодействующая этих сил,
когда её точка приложения прямолинейно перемещается из положения М1(0,1,1) в
положение М2(1,-2,1)?
,
приложенные к одной точке. Какую работу производит равнодействующая этих сил,
когда её точка приложения прямолинейно перемещается из положения М1(0,1,1) в
положение М2(1,-2,1)?
Решение. а/ Равнодействующая сила 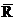 равна
равна  ;
;
б/ вектор перемещения равен 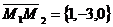
в/ Работу
вычисляем по формуле /2.9/: 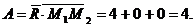
Ответ: А=4.
№ 3. Векторное произведение векторов и его применение
1. Ориентация системы векторов в пространстве.
Система трех некомпланарных векторов
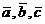 в
пространстве может иметь две ориентации: правею и левую.
в
пространстве может иметь две ориентации: правею и левую.

Поместим начала трех векторов 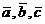 в одну
точку О и проведем через второй и третий векторы плоскость. Если смотреть из
конца третьего вектора на конец второго, то первый вектор будет расположен либо
с правой, либо с левой стороны от плоскости.
в одну
точку О и проведем через второй и третий векторы плоскость. Если смотреть из
конца третьего вектора на конец второго, то первый вектор будет расположен либо
с правой, либо с левой стороны от плоскости.
В первом случае система трех
некомпланарных векторов 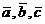 имеет правую
ориентацию, а во втором случае - левую.
имеет правую
ориентацию, а во втором случае - левую.
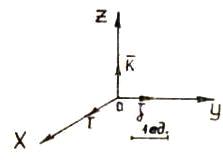

. Векторным произведением вектора 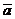 на вектор
на вектор  называется
вектор, обозначаемый символ
называется
вектор, обозначаемый символ 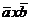 /или
/или  / к удовлетворяющий условиям:
/ к удовлетворяющий условиям:
а/ длина вектора 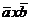 равна
произведению длин векторов
равна
произведению длин векторов 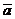 и
и  , умноженному на синус угла
, умноженному на синус угла 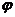 между ними:
между ними:
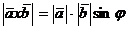 ;
;
б/ вектор 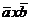 перпендикулярен
векторам
перпендикулярен
векторам 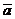 и
и  .
.
в/ система трех векторов 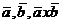 имеет
правую
имеет
правую
ориентацию. -18-
. Векторное произведение двух
векторов равно нулю тогда и только тогда, когда либо один из векторов равен
нулю, либо они коллинеарны.
. Геометрический смысл векторного
произведения.

Модуль /длина/ векторного
произведения векторов 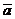 и
и  равен
площади S
параллелограмма, построенного на этих векторах, как на сторонах:
равен
площади S
параллелограмма, построенного на этих векторах, как на сторонах:
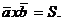 /2.10/
/2.10/
. Физический смысл векторного
произведения.
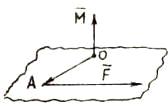
Момент 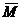 силы
силы 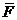 ,
приложенной к материальной точке А, относительно точки О равен
,
приложенной к материальной точке А, относительно точки О равен
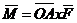 . /2.11/
. /2.11/
Свойства векторного произведения
. 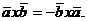 /антипереместительный
закон/
/антипереместительный
закон/
. 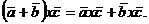 /распределительный
закон/
/распределительный
закон/
. 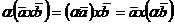 /сочетательный закон
относительно числового множителя/
/сочетательный закон
относительно числового множителя/
. 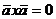 /векторное произведение вектора
на себя равно нулю/. Это свойства является следствием п.з. данного параграфа.
/векторное произведение вектора
на себя равно нулю/. Это свойства является следствием п.з. данного параграфа.
Векторное произведение вектора
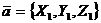 и
и 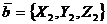
В координатной форме:
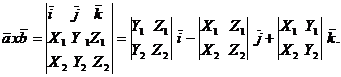 /2.12/
/2.12/
ПРИМЕРЫ
. Векторы 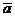 и
и  образуют
угол
образуют
угол 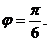 Зная, что
Зная, что 
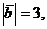 вычислить площадь параллелограмма,
построена на векторах
вычислить площадь параллелограмма,
построена на векторах 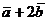 и
и 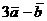
Решение. а/ Используя свойства
векторного произведения, вычислим
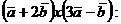
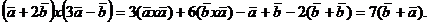
б/ Площадь параллелограмма найден, учитывая
геометрический смысл векторного произведения:
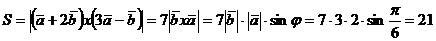 .
.
Ответ: S=21
. Даны вершины треугольника
А(1,-2,3), В(0,2,2) и С(-1,2,1). Вычислить площадь S
треугольника АВС и длину высоты h, опущенной из вершины А на сторону ВС.
Решение: а/ Рассмотрим два вектора 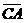 и
и 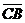 , исходящие
из общей точки С. Их координаты равны
, исходящие
из общей точки С. Их координаты равны 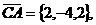
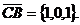
По формуле /2.12/ определим
векторное произведение этих векторов:

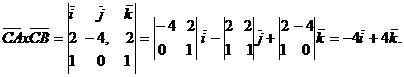
По формуле /2.10/ найдем S1 - площадь
параллелограмма, построенного на векторах 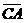 и
и 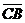 :
:
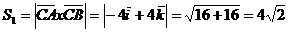 .
.
Затем вычислим площадь треугольника
АВС:
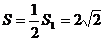 .
.
б/ По формуле /2.2/ определим длину
сторон СВ:
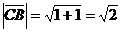 .
.
Теперь из соотношения 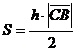 найдем
длину высоты:
найдем
длину высоты:
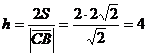
Ответ: 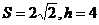
. Даны три силы 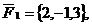
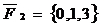 и
и 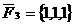 , приложенные к точке А(0,1,2).
Определить величину и направляющие косинусы момента равнодействующей этих сил
относительно начала координат О.
, приложенные к точке А(0,1,2).
Определить величину и направляющие косинусы момента равнодействующей этих сил
относительно начала координат О.
Решение. а/ найдем равнодействующую
силу R по формуле
/2.5/:
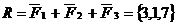
б/ Вычислим координаты вектора 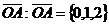
в/ По формуле /2.11/ определим
вектор момента 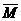 равнодействующей
силы в координатной форме:
равнодействующей
силы в координатной форме:
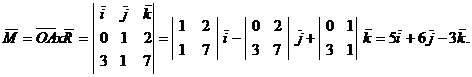
г/ Вычислим величину момента: 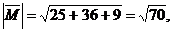 затем
направляющие косинусы момента:
затем
направляющие косинусы момента:
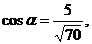
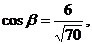
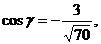
Ответ: 
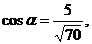
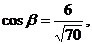
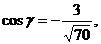
№ 4.
Смешанное произведение и его применение
. Смешанным произведением 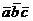 трех
векторов
трех
векторов 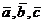 называется
число, равное скалярному произведению вектора
называется
число, равное скалярному произведению вектора 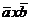 на вектор
на вектор 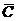 :
:
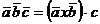
. Смешанное произведение трех
векторов равно нулю тогда и только тогда, когда либо один из векторов равен
нулю, либо они компланарны.
. Геометрический смысл смешанного
произведения.

Абсолютная величина смешанного
произведения трех векторов 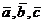 равна объему V
параллелепипеда, ребрами которого является эти векторы:
равна объему V
параллелепипеда, ребрами которого является эти векторы:
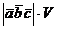 /2.13/
/2.13/
Знак смешанного произведения
определяет ориентацию системы трех векторов 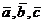 в пространстве: если
в пространстве: если  то система
имеет правую ориентацию, если
то система
имеет правую ориентацию, если 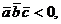 то левую.
то левую.
Свойства смешанного произведения
. 
. 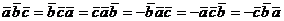 .
.
/При перестановке сомножителей
смешанное произведение не изменится, если не изменится ориентация системы
векторов. Если ориентация системы изменится, то у смешанного произведения
изменится только знак/.
Смешанного произведение векторов
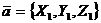 ,
, 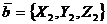 ,
, 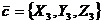
В координатной форме:
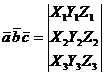 /2.14/
/2.14/
Признаки компланарности векторов 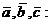
 /2.15/
/2.15/
ПРИМЕРЫ
. Вычислить объем V тетраэдра,
вершины которого находятся в точках А(-1,0,1), В(0,1,1), С(4,1,-2) и D(2,-1,0).
Решение. а/ Рассмотрим три вектора 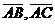 и
и 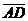 , исходящие
из общей точки А. Их координаты равны
, исходящие
из общей точки А. Их координаты равны
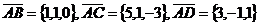 .
.
б/ Вычислим смешанное произведение
этих векторов по формуле /2.14/:
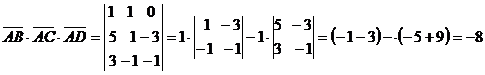
в/ Найдем объем
параллелепипеда V1, учитывая геометрический смысл
смешанного произведения, по формуле /2.13/:
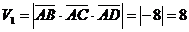
г/ Объем тетраэдра V получим из
соотношения 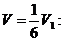
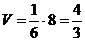
Ответ: 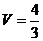
3. При
каком значении α четыре
точки А(0,1,-1), В(1,0,1), С(1,2,0) и D(1,1,α)
лежат
в одной плоскости?

Решение. а/ рассмотрим три вектора 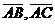 и
и 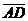 , исходящие
из общей точки А. Четыре точки А,В,С и D лежат в
одной плоскости тогда и только тогда, когда векторы
, исходящие
из общей точки А. Четыре точки А,В,С и D лежат в
одной плоскости тогда и только тогда, когда векторы 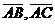 и
и 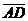 компланерны.
компланерны.
Координаты этих векторов равны 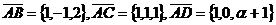 .
.
б/ Запишем условие компланетности
трех векторов 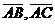 и
и 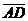 в
координатной форме - см. формула /2.15/:
в
координатной форме - см. формула /2.15/:

Вычислим полученный определитель
разложением по элементам третьей строки:
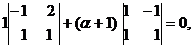 или1(-1-2)+(α+1)(1+1)=0,или-3+2(α+1)=0,
или1(-1-2)+(α+1)(1+1)=0,или-3+2(α+1)=0,
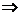
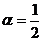
Ответ: 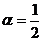
Самостоятельная работа
1. Построить пирамиду с вершинами 0(0,0,0),
А(5,2,0), В(2,5,0), С(1,2,4) и вычислить ее объем.
2. Даны векторы 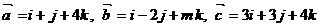 при каком
значении m векторы
компланарны.
при каком
значении m векторы
компланарны.
. Построить пирамиду с
вершинами 0(0,0,0), А(5,2,0), В(2,5,0), С(1,2,4) и вычислить площадь грани АВС
и высоту пирамиды, опущенную на эту грань.
. При каком значении α четыре точки
А(0,1,-1), В(1,0, α
), С(1,2,0)
и D(1,1,2)
лежат в одной плоскости?
РАЗДЕЛ 3. ПРИМЕНЕНИЕ ВЕКТОРОВ В АНАЛИТИЧЕСКОЙ
ГЕОМЕТРИИ
Основные формулы
. Общее уравнение плоскости

Ax+By+Cz+D=0
/3.1/
Высокий /не равный нулю/ вектор,
перпендикулярный к данной плоскости, называется её нормальным вектором. Вектор 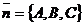 - нормальный
вектор плоскости, заданный уравнением /3.1/.
- нормальный
вектор плоскости, заданный уравнением /3.1/.
. Уравнение плоскости по точке М0(Х0,Y0,Z0) и
нормальному вектору 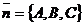 :
:
A(X-X0)+B(Y-Y0)+C(Z-Z0)=0 /3.2/

. Уравнение прямой L в
пространстве как линии пересечения двух плоскостей π1 и π2:
 /3.3/
/3.3/
Где коэффициент А1, В1, С1 не
пропорциональны коэффициентам А2, В2, С2.
. Канонические уравнения прямой L в
пространстве:
 /3.4/
/3.4/

М0(Х0,Y0,Z0) - Точка
на прямой L.
S={p, q, r} -
направляющий вектор прямой L.
. Параметрические уравнения прямой L в
пространстве:

М0(Х0,Y0,Z0) - Точка
на прямой L.
S={p, q, r} -
направляющий вектор прямой L /3.5/
λ - параметр, -∞< λ <∞.
ПРИМЕРЫ
. Составить уравнение плоскости,
проходящей через точку М(1,-1,-1) параллельно векторам 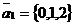 и
и 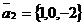 .
.

Решение. а/ По условию задачи
векторы 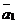 и
и 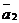 параллельны
плоскости. Следовательно, по определению векторного произведения, вектор
параллельны
плоскости. Следовательно, по определению векторного произведения, вектор 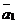 х
х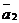 перпендикулярен плоскости и может быть взят и качестве её нормального вектора
перпендикулярен плоскости и может быть взят и качестве её нормального вектора 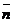 . Найдем
координаты вектора
. Найдем
координаты вектора 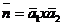 :
:
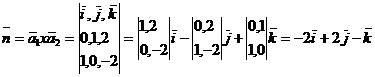
б/ По формуле /3.2/ составим
уравнение искомой плоскости:
(х-1)+2(у+1)-(z+1)=0 или
2х-2у+z-3=0
Ответ: 2х-2y-z-3=0/
. Составить уравнение плоскости,
проходящей через три точки
М1(-1,1,2), М2(0,1,-1), М3(2,-1,-1).

Решение. а/ Рассмотрим векторы М1М2
и М1М3 параллельны искомой плоскости /более того, лежат в этой плоскости/.
Следовательно, задача свелась к предыдущей задаче № 1: составить уравнение
плоскости, проходящей через точку М1 параллельно двум векторам М1М2 и М1М3.
Координаты нормального вектора ищем
по формуле
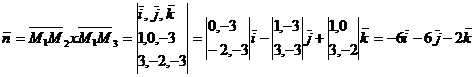
Уравнение искомой плоскости составил
по формуле /3.2/:
(x+1)-6(y01)-2(z-2)=0 или 3x+3y+z-2=0
Ответ: 3x+3y+z-2=0
. Определить, при каком значении α следующие
плоскости
х-6у+αz-4=0 и x-2y-z+1=0
а/ параллельны?
б/ перпендикулярны?

Решение. а/ Заданные плоскости
параллельны тогда и только тогда, когда их нормальные векторы  и
и 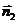 коллеарны.
Координаты нормальных векторов равны
коллеарны.
Координаты нормальных векторов равны 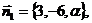
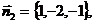
Запишем условие коллинеарности этих
векторов - см. формула /2.6/:
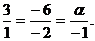
Из пропорции получим α=-3.
б/ Заданные плоскости
перпендикулярны тогда и только тогда, когда их нормальные векторы  и
и 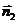 перпендикулярны.
перпендикулярны.

Запишем условие перпендикулярности
этих векторов - см. формула /2.9/:
3+12-α=0
Откуда α=15
Ответ: При α=-3. плоскости
параллельны, при α=15
плоскости
перпендикулярны.
. Составить канонические и
параметрические уравнения прямой
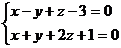

Решение. а/ Искомая прямая L является
линией пересечения двух плоскостей. Найдем какую-либо точку, принадлежащую
прямой L. Для этого
в заданных уравнениях плоскостей положим какое-либо неизвестное равным
постоянной, например, z=0.
Найдем значения двух других
неизвестных из полученной системы уравнений:
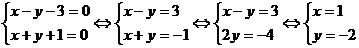
Точка М(1,-2,0) лежит на прямой L.
б/ Определим направляющий вектор
прямой S. Для этого
найдем
нормальные векторы плоскостей: 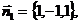
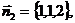 .
.
Вектор 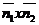 будет
параллелен обеим плоскостям и, следовательно. Линии их пересечения L. Поэтому
возьмем вектор
будет
параллелен обеим плоскостям и, следовательно. Линии их пересечения L. Поэтому
возьмем вектор 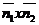 в качестве
направляющего вектора прямой L. Найдем координаты вектора
в качестве
направляющего вектора прямой L. Найдем координаты вектора 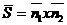 :
:
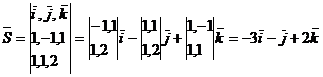
в/ По формуле /3.4/ составим
канонические уравнения прямой L:
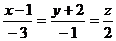
г/ По формуле /3.5/ составим
канонические уравнения прямой L:
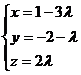 -∞<
λ <∞.
-∞<
λ <∞.
Ответ: 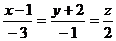 , х=1-3λ, у=2-λ, z=2λ, (-∞<
λ <∞).
, х=1-3λ, у=2-λ, z=2λ, (-∞<
λ <∞).

. Составить канонические и
параметрические уравнения прямой, проходящей через две данные точки А(0,1,-1) и
В(1,-2,0).
Решение. а/ Схематически изобразим
прямую /более того, лежит не ней/, то его можно взять в качестве направляющего:
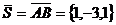
б/ По формуле /3.4/ составил
канонические уравнения прямой, проходящей через точку А(0,1,-1) в направлении
вектора 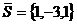
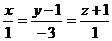 .
.
в/ По формулам /3.5/ составим
параметрические уравнения искомой прямой:
 -∞< λ <∞.
-∞< λ <∞.
Ответ: 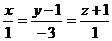 , х=λ, у=1-3λ, z=-1+λ, (-∞<
λ <∞).
, х=λ, у=1-3λ, z=-1+λ, (-∞<
λ <∞).
. Составить канонические и
параметрические уравнение прямой, проходящей через точку М(0,2,2) параллельно
прямой


Решение. Схематически
изобразим искомую прямую L и данную прямую L1. Определим
направляющий вектор 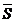 прямой L. Так как
прямые по условию параллельны, то направляющий вектор прямой L можно взять
равным направляющему вектору прямой L1. Из
заданных канонических уравнений прямой L1 получим:
прямой L. Так как
прямые по условию параллельны, то направляющий вектор прямой L можно взять
равным направляющему вектору прямой L1. Из
заданных канонических уравнений прямой L1 получим:
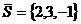
По формуле /3.4/ составим
канонические уравнения искомой прямой L:
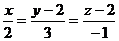
По формуле /3.4/ составим
параметрические уравнения искомой прямой L:
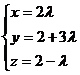 -∞< λ <∞.
-∞< λ <∞.
Ответ: 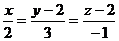 , x=2λ, y=2+3λ, z=2-λ, (-∞<
λ <∞).
, x=2λ, y=2+3λ, z=2-λ, (-∞<
λ <∞).
7. Составить канонические и
параметрические уравнения прямой, проходящей через точку М(1,-2,0)
перпендикулярно плоскости
x-3y+z-1=0.

Решение. Схематически изобразим
заданную плоскость π
и
искомую прямую L. Определим направляющий вектор
прямой L. Так как
эта прямая по условию перпендикулярна плоскости, то нормальный вектор плоскости
 параллелен
прямой L. Поэтому
возьмем вектор
параллелен
прямой L. Поэтому
возьмем вектор  в качестве
направляющего вектора
в качестве
направляющего вектора 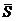 искомой
прямой L:
искомой
прямой L: 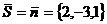
По формуле /3.4/ составим
канонические уравнения прямой:
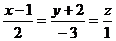
По формуле /3.5/ составим
параметрические уравнения прямой:
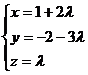 -∞< λ <∞.
-∞< λ <∞.
Ответ: 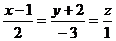 , x=1+2λ, y=-2-3λ, z=λ, (-∞<
λ <∞).
, x=1+2λ, y=-2-3λ, z=λ, (-∞<
λ <∞).
8. При каком значении α прямые
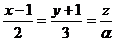 и
и 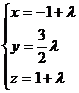
а/ параллельны? б/ перпендикулярны?
Решение. а/ Сначала из
заданных уравнений в соответствии с формулами /3.4/ и /3.5/ определим
направляющие векторы прямых
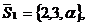
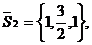
Две прямые параллельны тогда и
только тогда, когда их направляющие векторы коллинеарны. Запишем условие
коллинеарности этих векторов - см. формулу /2.6/:
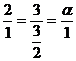 .
.
Из пропорции получим 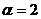
б/ Две прямые перпендикулярны тогда
и только тогда, когда их направляющие векторы перпендикулярны. Запишем условие
перпендикулярности векторов - см. формулу /2.9/:
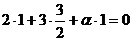
Отсюда 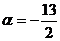 .
.
Ответ: Прямые параллельны при 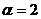 и
перпендикулярны при
и
перпендикулярны при 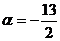 .
.
Самостоятельная
работа
1. Определить, при каком значении α следующие
плоскости
х-5у+z-4=0 и x-3y-αz+2=0
а/ параллельны? б/ перпендикулярны?
2. Составить канонические и параметрические
уравнения прямой,
проходящей через две данные точки А(2,1,-1) и
В(1,-2,0).
3. При каком значении α прямые 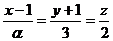 и
и 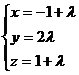
а/ параллельны? б/ перпендикулярны?
3. Составить уравнение плоскости,
проходящей через точку М(1,-1,-1)
параллельно векторам 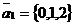 и
и 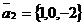 .
.
РАЗДЕЛ 4. ПОСТРОЕНИЕ ГРАФИКОВ
ФУНКЦИЯ С ПОМОЩЬЮ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
№ 1.
Простейшие геометрические преобразования
. Построение графиков функций с
помощью осевой симметрии.
А) 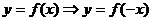 с помощью симметрии относительно
оси ОY
с помощью симметрии относительно
оси ОY
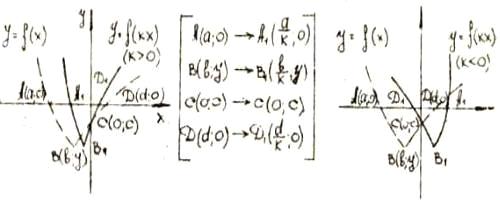
Б) 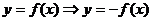 с помощью симметрии относительно
оси ОХ
с помощью симметрии относительно
оси ОХ
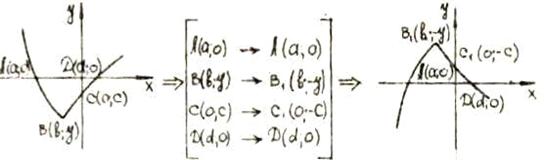
. Построение графиков функций с
помощью сжатия (или растяжения) с осями координат.
А) 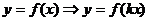 с помощью сжатия (или растяжения) к
оси ОY. Если
с помощью сжатия (или растяжения) к
оси ОY. Если 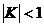 , то график
функции
, то график
функции 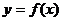 растягивают
от оси ОY в
растягивают
от оси ОY в 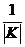 раз. Если
раз. Если 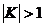 , то график
функций
, то график
функций 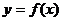 сжимают к
оси ОY в
сжимают к
оси ОY в 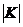 раз. При
К<0 дополнительно график функции отражают симметрично относительно оси ОY.
раз. При
К<0 дополнительно график функции отражают симметрично относительно оси ОY.

Б) 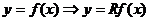 с помощью сжатия (или растяжения) к
оси ОХ. Если
с помощью сжатия (или растяжения) к
оси ОХ. Если 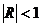 , то график
функции
, то график
функции 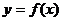 растягивают
от оси ОХ в
растягивают
от оси ОХ в 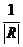 раз. Если
раз. Если 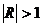 , то график
функций
, то график
функций 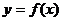 сжимают к
оси ОХ в
сжимают к
оси ОХ в 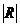 раз. При R<0
дополнительно график функции отражают симметрично относительно оси ОХ.
раз. При R<0
дополнительно график функции отражают симметрично относительно оси ОХ.

3. Построение графиков функций с
помощью переносов параллельно осям координат.
А) 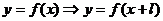 с помощью переноса параллельно оси
ОХ на вектор
с помощью переноса параллельно оси
ОХ на вектор  .
.
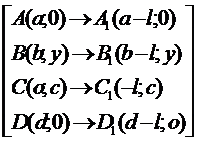

Б) 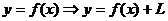 с помощью переноса параллельно оси
ОY на вектор
с помощью переноса параллельно оси
ОY на вектор 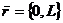 .
.
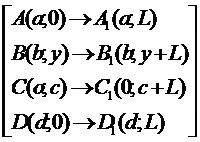
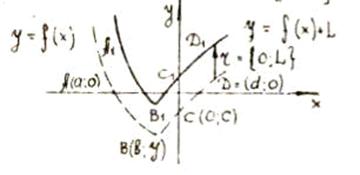
Построение графика функции 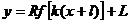 с помощью
композиции преобразований
с помощью
композиции преобразований
График функции 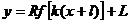 строят из
графика функции
строят из
графика функции 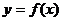 с помощью
последовательного выполнения преобразований 1 - 3:
с помощью
последовательного выполнения преобразований 1 - 3:
А) 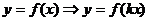

Если К<0, то дополнительно график
функции отражают симметрично относительно оси ОY.
Б) 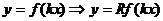

Если R<0, то
дополнительно график функции отражают симметрично относительно оси ОX
В) 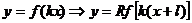

Г) 

Построение графика функции 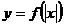
График функции 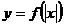 при х ≥
0 (в правой полуплоскости совпадает) получается с помощью симметрии
относительно оси ОY, уже построенной для х ≥ 0
части графика.
при х ≥
0 (в правой полуплоскости совпадает) получается с помощью симметрии
относительно оси ОY, уже построенной для х ≥ 0
части графика.

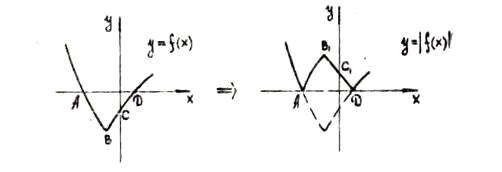
Построение графика функции 
График функции  располагается
в верхней полуплоскости и получается из графика функции
располагается
в верхней полуплоскости и получается из графика функции 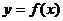 следующим
образом: все точки графика функции
следующим
образом: все точки графика функции 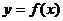 , лежащие на оси ОХ и выше её,
остаются на месте; все точки графика функции
, лежащие на оси ОХ и выше её,
остаются на месте; все точки графика функции 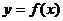 б лежащие нише оси ОХ, отражаются
симметрично относительно оси ОХ.
б лежащие нише оси ОХ, отражаются
симметрично относительно оси ОХ.
ПРИМЕРЫ
. Построить график дробно-линейной
функции 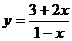
Построение. Вначале данную функцию
приводят к виду
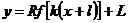 :
:
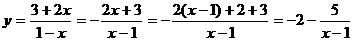
Порядок построения графика:
А) 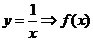 Б)
Б) 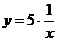 получают из
графика
получают из
графика 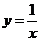 растяжением
от оси ОХ в 5 раз (ординаты всех точек увеличиваются в 5 раз).
растяжением
от оси ОХ в 5 раз (ординаты всех точек увеличиваются в 5 раз).

А) 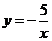 получают на график
получают на график 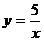 Г)
Г) 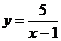 получают из
графика отраженном симметрично относи-
получают из
графика отраженном симметрично относи- 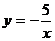 переносом параллельно тельно оси
ОХ. Оси ОХ на вектор
переносом параллельно тельно оси
ОХ. Оси ОХ на вектор 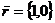 .
.

Д) 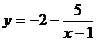 получают из графика
получают из графика 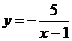 переносом
параллельно оси
ОY на
вектор
переносом
параллельно оси
ОY на
вектор 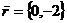 .
.

Асимптоты графика:
х=1 и у=-2
точки пересечения с осями:
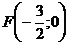 ,
, 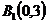
. Построить график показательной
функции 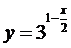 .
.
Построение. Вначале данную функцию
приводит к виду 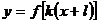 :
:
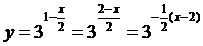
Порядок построения графика:
А) y=3x=f(x); Б)
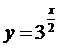 получают из
графика у=3х растяжением от оси ОY в 2 раза (абсциссы всех точек
увеличиваются в 2 раза).
получают из
графика у=3х растяжением от оси ОY в 2 раза (абсциссы всех точек
увеличиваются в 2 раза).

В) 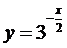 получают из графика Г)
получают из графика Г) 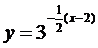 получают из
графи-
получают из
графи-
отражением симметрично ка
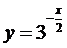 переносом
параллель-
переносом
параллель-
относительно оси ОY. но
оси ОХ на вектор 
Точка пересечения с осью ОY:
C5(0,3)

. Построить график
тригонометрической функций y=3cos(2x+1)
Построение. Вначале данную функцию
приводят к виду
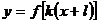
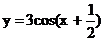
Порядок построения графика:
А) y=cosx = f(x); Б)
y=cos2x получают из
графика
y=cosx сжатием
к оси ОY в 2 раза.
-
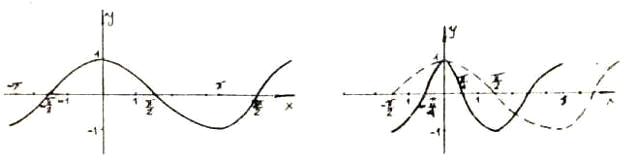
Период Т=2π Амплитуда
А=1 Период Т= π Амплитуда А=1
В) y=3cos2x получают
из графика Г) 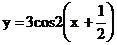 получают из
гра-
получают из
гра-
y=cos2x растяжением
от оси ОХ фика y=3cos2x
переносом пара-
в 3 раза. ллельно
оси ОХ на вектор 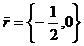 .
.

Период Т=π Амплитуда
А=3 Точки пересечения с осями:
(0;3cos1) и 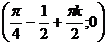 ;
; 
. Построить график логарифмической
функции
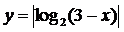
Построение. Вначале данную функцию
производят к виду:
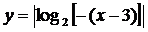
Порядок построения графика:
А) 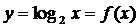
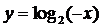 получают из
графика
получают из
графика
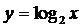 отражением части,
отражением части,
расположенной в нижней
полу-плоскости, симметрично относи-тельно оси ОХ.

В) 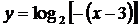 получают из Г)
получают из Г) 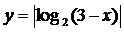 получают из
получают из
графика 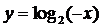 переносом графика
переносом графика
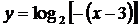 отра-
отра-
параллельно оси ОХ на вектор жжением
части, расположенной
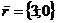 в
нижней полуплоскости, сим-
в
нижней полуплоскости, сим-
метрично относительно оси ОХ.
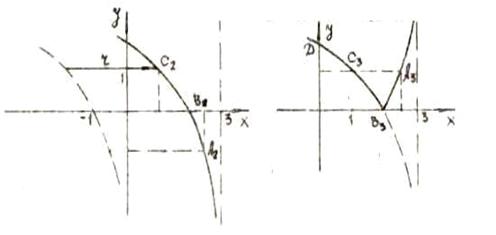
Асимптота х=3
Точки пересечения с осями:
В3(2;0) и D(0;log23)
. Построить график обратной
тригонометрической функции 
Построение.
А) 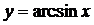 Б)
Б)  получают на
гра-
получают на
гра-
фика 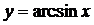 растяжением от оси ОY в 2 раза.
растяжением от оси ОY в 2 раза.

В) 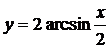 получают из гра- Г)
получают из гра- Г)  получает из
получает из
фика  растяжения от графика
растяжения от графика 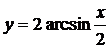 переносом
переносом
оси ОХ в 2 раза. параллельно
оси ОХ на вектор
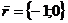

Точки пересечения с осями:
Е(-1;0) и F(0;π/3)
№ 2. Графическое решение систем неравенств
Множество решений неравенства y>f(x) (или y<f(x)) находят
следующим образом.
На плоскости строят график функции y=f(x). Множество
точек плоскости М(x,y),
расположенных выше графика y=f(x), является
множеством решений неравенства y>f(x), а
множество точек М(x,y),
расположенных ниже графика y=f(x), является
множеством решений неравенства y<f(x), причем
рассматривают только те точки, абсциссы которых принадлежит области определения
функции f(x).
Множество решений неравенства f1(x)>f2(x) определяют
следующим образом.
На плоскости строят графики функций y=f1(x) или y=f2(x).
Множество точек x оси OX, при
которых график первой функции лежит выше графика второй функции является
множеством решений неравенства f1(x)>f2(x).
Множество решений системы неравенств
получают пересечением множеств решений отдельных неравенств входящих в систему.
ПРИМЕРЫ
1.Найти множество решений
неравенства 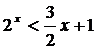 .
.
Решение: Построим графики
показательной функции
y=2x и линейной
функции 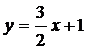 .
.
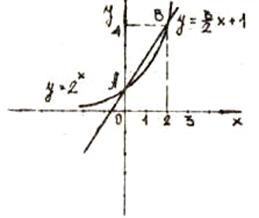
Определение точки пересечённая А(0,1) и В(2,4)
графиков.
Множество точек оси ОХ, при которых график
линейной функции лежит ниже графика показательной функции, образует интервал
(0,2).
Ответ: (0,2)
.Построить область, удовлетворяющую системе
неравенств
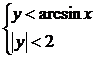
вектор произведение
неравенство геометрический
Построение:
А) Строки график функции: y=arcsin x
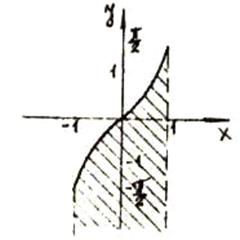
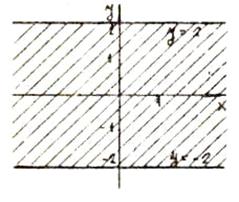
Б) Строим график функции 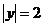 :
:
Множество решений второго
неравенства системы заштриховано на чертеже (точки, лежащие на прямых y=±2, не
принадлежат множеству решений).

В) Область, удовлетворяющая системе
неравенств получается пересечением множеств решений первого и второго
неравенств (точки, лежащие на верхней и нижней границах области, не принадлежат
множеству решений, а точки, лежащие на баковых границах, принадлежат
множеству).
.Построить область, удовлетворяющую
системе неравенств.
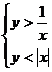

Построение:А) Строим график функции 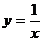
Множество решений первого
неравенства

системы заштриховано на чертеже
(точки, лежащие на оси ОY, не принадлежат множеству решений,
так как абсцисса этих точек равна нулю и не входит в область определения
функции  ).
).
Б) Строим график функции 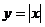 :
:
Множество решений второго
неравенства системы заштриховано
В) Области удовлетворяющие системе
неравенств, получаются пересеченными множеств решений первого и второго
неравенств (точки, держащие на границах областей, включая отрицательную полуось
и точку 0, не
принадлежат множеству решений системы).
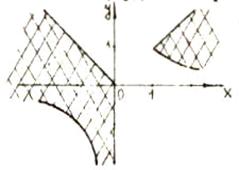
. Построить область, удовлетворенную
системе неравенств

Построение:
А) Строим графики функций y=-1 и
y=ln(2-x):

Порядок построения график:
y=ln(2-x): 1) y=lnx
) y=ln(-x)
) y=ln[-(x-2)]
Б) Строям графики прямых линий В)
Область, удовлетворяющая  . системе
неравенств, изображена на чертеже (границы области не принадлежат множеству
решений).
. системе
неравенств, изображена на чертеже (границы области не принадлежат множеству
решений).

Самостоятельная
работа
1. Построить графики функции:
а) 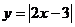 , б)
, б) 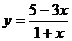 , в)
, в)  ,
,
г) 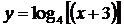 , д)
, д)  , е) y=4cos(3x-1)
, е) y=4cos(3x-1)
ЛИТЕРАТУРА
Бугров Я.С., Никольский С.М.Элементы
линейной алгебры и аналитической геометрии М: Наука 1985
Бугров Я.С. Никольский С.М.
Дифференциальное и интегральное исчисление М:. Наука 1984.
Пискунов Н.С.Дифференциальное и
интегральное исчисление М:. Наука 1985 Т.
Берман Г.М. Сборник задач по курсу
математического анализа М: Наука 1985
Клетеник Д.В. Сборник задач по
аналитической геометрии. М: Наука 1980