Векторы, пространства, гиперплоскости, гиперповерхности
Векторы, пространства, гиперплоскости, гиперповерхности
Введение
Из всех разделов алгебраической
науки одним из наиболее разработанных является раздел, называемый линейной
алгеброй. Линейная алгебра изучает матрицы (прямоугольные таблицы из чисел),
алгебраические формы (линейные, билинейные и квадратичные), линейные
пространства с линейными преобразованиями в них. Выводы линейной алгебры
особенно важны для решения многочисленных прикладных задач. Ее аппаратом, не
говоря уже о самой математике, пользуются естественные, технические,
экономические, нередко и гуманитарные науки.
Одной из характерных особенностей
линейной алгебры является то, что данная наука свободно пользуется
геометрическим языком. Здесь встречаются такие термины, как вектор, векторное
пространство, скалярное произведение, евклидово пространство, ортогональность и
другие. Вместе с тем объекты, к которым применяются данные термины, «внешне»
совсем не походят на свои геометрические прототипы (прямые, вектора, плоскости,
фигуры в 2-х и 3-х мерном пространствах). Например, роль векторов (элементов
векторного пространства) могут играть такие объекты, как многочлены, матрицы,
функции и т.д.
Несмотря на внешнее различие,
перечисленные выше совокупности объектов тесно связаны между собой: большинство
утверждений допускают равносильную формулировку для каждой из этих
совокупностей. Наиболее отчетливо эта связь выявляется как раз при изучении
произвольных векторных пространств (и линейных преобразований в них).
Таким образом, геометрические
термины, используемые в линейной алгебре, возникли вовсе не для того, чтобы
внушить «таинственные» представления о столь же «таинственных» многомерных
пространствах. Геометрическая терминология образует удобный и образный язык,
который, хотя и не может служить средством доказательств, но очень удачно
подчеркивает общность закономерностей, присущих и обычным геометрическим
образам и их многомерным аналогам.
Применение геометрического языка во
много связано и с тем, что отправной точкой для развития линейной алгебры была
аналитическая геометрия, которая изучает свойства геометрических объектов при
помощи аналитического метода (в основе которого лежит метод координат).
Для того чтобы разобраться с
геометрическими терминами, которые используются в линейной алгебре, а также
самими объектами, которые они называют, в первой части работы будем
продвигаться от простого и известного к более сложному и абстрактному. Так в §
1 Главы 1 повторим основные положения векторной алгебры, в том числе вспомним
определение свободного вектора в пространстве, операции над векторами, понятие
коллинеарности, компланарности, линейной зависимости и независимости векторов в
пространстве, рассмотрим угол между векторами и уточним определение и свойства
скалярного произведения векторов в пространстве. Далее будут изложены элементы
теории векторных пространств, а именно будет рассмотрено понятие векторного
пространства и его основные свойства, определено скалярное произведение и
введено понятие евклидова пространства. Далее будут рассмотрены базис,
размерность и подпространства линейного пространства, а также кратко затронута
тема линейных преобразований векторных пространств.
Вторая часть работы посвящена
некоторым приложениям аппарата векторных пространств, в том числе рассмотрены
системы линейных уравнений и интерпретация их решений как пересечение
гиперплоскостей в n-мерном координатном пространстве, приведен пример оптимизационной
задачи линейного программирования и изложена суть симплекс-метода (без
математических выкладок), используемого для решения таких задач. В заключение
будет представлен пример использования метода наименьших квадратов для
приближенного вычисления.
1. Теория векторов и
пространств
.1 Основные положения
векторной алгебры
уравнение линейный пространство
симплекс
Геометрическим вектором (или просто
вектором) называют направленный отрезок и обозначают AB или а, b, c и т.д. Начало вектора будем называть точкой приложения. Для
обозначения длины вектора используют символ модуля (или абсолютной величины).
Вектор называют нулевым, если начало и конец его совпадают. Нулевой вектор не
имеет определенного направления и имеет длину, равную нулю.
Векторы называются коллинеарными,
если они лежат либо на одной прямой, либо на параллельных прямых. Два вектора
называются равными, если они имеют одинаковую длину и одинаковое направление.
Все нулевые векторы считаются равными. Векторы называются компланарными, если
они лежат либо в одной плоскости, либо в параллельных плоскостях.
Векторы, изучаемые в геометрии,
называются свободными (они определены с точностью до точки приложения).
Линейными операциями принято
называть операцию сложения векторов и операцию умножения вектора на
вещественное число.
Суммой а+b двух векторов
называется вектор, идущий из начала вектора а в конец вектора b при условии, что вектор
b
приложен к концу вектора а.
Данное правило сложения векторов
называют правилом треугольника. Определенная данным образом операция сложения
векторов на множестве векторов обладает свойствами коммутативности (1),
ассоциативности (2), наличием нейтрального (3) и симметричного элементов (4).
При доказательстве свойства
коммутативности обоснуется еще одно правило сложения векторов, называемое
правилом параллелограмма: если векторы а и b приложены к общему
началу и на них построен параллелограмм, то сумма а+b (или b+а) этих векторов
представляет собой диагональ указанного параллелограмма, идущего из общего
начала векторов.
Названные выше свойства, позволяют
нам распространить правило сложения на сумму любого конечного числа векторов.
Правило следующее: если приложить вектор а2, к концу вектора а1,
вектор а3 к концу вектора а2,…, вектор аn к концу вектора аn-1, то сумма векторов будет представлять собой вектор, идущий из
начала вектора а1 в конец вектора аn. Данное правило
называется правилом замыкания ломанной до многоугольника.
Разностью а-b вектора а и
вектора b называется такой вектор с, который в сумме с вектором b дает вектор а.
Произведением λа (или аλ) вектора а на вещественное число λ называется вектор в,
коллинеарный вектору а, имеющий длину, равную │λ│×│a│… и имеющий
направление, совпадающее с направлением вектора а в случае λ>0 и противоположное
направлению вектора а в случае λ<0.
В случае, когда λ=0 или а=0,
произведение λа представляет собой нулевой вектор, направление которого не
определено. Геометрический смысл операции умножения вектора на число можно
выразить так: при умножении вектора а на число λ вектор а
«растягивается» в λ «раз».
Операция умножения вектора на число
обладает следующими свойствами:
) λ (а+b)=λа+λb - распределительное свойство числового сомножителя относительно
суммы векторов
) (λ+µ) а=λа+µа -
распределительное свойство векторного сомножителя относительно суммы чисел
) λ(µа)=(λµ) а - сочетательное свойство числовых сомножителей.
Свойства 1-7 имеют фундаментальное
значение, так как позволяют производить выкладки в векторной алгебре по тем
правилам, по которым производятся аналогичные выкладки в обычной алгебре.
Линейной комбинацией векторов будем
называть сумму произведений этих векторов на произвольные вещественные числа.
Векторы называются линейно зависимыми, если найдутся такие вещественные числа,
из которых хотя бы одно отлично от нуля, что линейная комбинация векторов с
указанными числами обращается в нуль. Векторы, не являющиеся линейно
зависимыми, называют линейно независимыми. Векторы линейно независимы, если
равенство нулю их линейной комбинации возможно лишь в случае, когда все числа
равны нулю.
Если хотя бы один из векторов
является нулевым, то эти векторы линейно зависимы. Если среди n векторов какие-либо n-1 векторов линейно зависимы, то и
все n векторов линейно зависимы.
Необходимым и достаточным условием
линейной зависимости двух векторов является их коллинеарность. Необходимым и
достаточным условием линейной зависимости трех векторов является их компланарность.
Любые четыре вектора в пространстве линейно зависимы.
Говорят, что три линейно независимых
вектора образуют в пространстве базис, если любой вектор может быть представлен
в виде некоторой линейной комбинации векторов. Аналогично определяется базис на
плоскости: два линейно независимых вектора а и b образуют на этой
плоскости базис, если любой лежащий в плоскости вектор с может быть представлен
в виде некоторой линейной комбинации векторов а и b. При этом любая тройка
некомпланарных векторов образует базис в пространстве, любая пара лежащих в
данной плоскости неколлинеарных векторов а и b образует базис на этой
плоскости.
В дальнейшем для
определенности будем рассматривать базис в пространстве. Итак, пусть а, b, с - произвольный базис в пространстве, т.е. произвольная
тройка некомпланарных векторов. Тогда (по определению базиса) для любого
вектора d найдутся такие вещественные числа, что будет справедливо
равенство: d=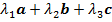
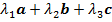
Это равенство принято
называть разложением вектора по базису, а числа λ1,
λ2, λ3 - координатами вектора относительно базиса. Разложение по базису
- единственно: это означает то, что координаты каждого вектора относительно
базиса определяются однозначно.
Основное значение базиса
состоит в том, что линейные операции над векторами при задании базиса
становятся обычными линейными операциями над числами - координатами этих
векторов. Так, при сложении двух векторов их координаты складываются. При
умножении вектора на любое число все его координаты умножаются на это число.
Аффинные координаты в
пространстве определяются заданием базиса и некоторой точки О, называемой
началом координат. Аффинными координатами любой точки М называют координаты
вектора ОМ относительно базиса а, b,
с. Декартовы прямоугольные координаты являются частным случаем аффинных
координат, соответствующим тройке взаимно ортогональных и единичных базисных
векторов.
Если обозначить буквами
А` и В` основания перпендикуляров, опущенных на произвольную ось u из концов вектора a=АВ,
то проекцией вектора а на ось u
называется величина А`В` направленного отрезка А`В`. Проекция вектора а
на ось равна длине вектора а, умноженной на косинус угла наклона вектора
а к оси u. Декартовы
прямоугольные координаты Х, Y
и Z вектора равны проекциям этого вектора на оси Оx, Oy, Oz соответственно (единичные вектора, отложенные на осях от начала
координат в положительном направлении называют также тройкой координатных ортов
i, j, k).
Скалярным произведением
двух векторов называется число, равное произведению длин этих векторов на
косинус угла между ними. В соответствии с определением проекции вектора можно
сформулировать другое эквивалентное определение скалярного произведения.
Скалярным произведением двух векторов называется число, равное произведению
длины одного из этих векторов на проекцию другого вектора на ось, определяемую
первым из указанных векторов.
Необходимым и
достаточным условием ортогональности двух векторов является равенство нулю их
скалярного произведения. Два ненулевых вектора а и b составляют острый (тупой) угол тогда и только тогда, когда их
скалярное произведение положительно (отрицательно). Скалярное произведение
векторов обладает следующими четырьмя алгебраическими свойствами:
◦
аb=bа
(переместительное свойство)
◦
(λа) b=λ(аb) (сочетательное относительно числового множителя свойство)
◦
(а+b) с=ас+bс
(распределительное относительно суммы векторов свойство)
◦
аа>0, если а ненулевой вектор, и аа=0, если а -
нулевой вектор.
Если два вектора а
и b определены своими декартовыми прямоугольными координатами а={X1, Y1, Z1} и b={X2, Y2, Z2}, то скалярное произведение этих векторов равно сумме попарных
произведений их соответствующих координат, т.е. аb=X1X2+Y1Y2+Z1Z2
На этом мы завершим
небольшой обзор курса аналитической геометрии в части операций над свободными
векторами.
1.2 Линейные
пространства: понятие, примеры, свойства
В настоящей части
рассмотрим множества объектов любой природы, для элементов которых каким-либо
способом (причем, безразлично каким) определены операция сложения элементов и
операция умножения элемента на вещественное число, причем указанные операции
обладают теми же свойствами, что и соответствующие операции над геометрическими
векторами. Такие множества называют линейными (или векторными) пространствами.
Определение. Множество V элементов x,
y, z, … любой природы
называется линейным (или векторным, или аффинным) пространством, если выполнены
следующие три требования.
1. Имеется правило,
посредством которого любым двум элементам x и y множества V ставится в соответствие третий
элемент z этого множества, называемый суммой элементов x и y и обозначаемый символом z=x+y.
. Имеется правило,
посредством которого любому элементу x множества V и любому вещественному числу λ ставится в соответствие элемент u этого множества, называемый произведением элемента x на число λ и обозначаемый символом
u=λx или u=xλ.
. Указанные два правила
подчинены следующим восьми аксиомам
1. x+y=y+x (сложение коммутативно)
. (x+y)+z=x+(y+z) (сложение ассоциативно)
. Существует нулевой элемент
0 такой, что x+0=x для любого элемента x (особая роль нулевого элемента)
. Для каждого элемента x существует противоположный (другими
словами симметричный) элемент x` такой, что x+x`=0
5. 1×x=x для любого элемента x (особая роль числового множителя 1)
6. λ(µx)= (λµ) x (сочетательное относительного числового множителя свойство)
7. (λ+µ) x= λx+µx (распределительное относительно
суммы числовых множителей свойство)
8. λ (x+y)=λx+λy (распределительное относительно суммы элементов свойство)
Следует подчеркнуть, что при
введении понятия линейного пространства абстрагируются не только от природы
изучаемых объектов, но и от конкретного вида правил образования суммы элементов
и произведения элемента на число (важно лишь, чтобы эти правила удовлетворяли восьми
аксиомам, сформулированным выше). Первые четыре аксиомы устанавливают свойства
операции сложения, и их можно было бы выразить короче, сказав, что относительно
этой операции элементы образуют абелеву группу.
Если природа изучаемых объектов и
вид правил образования суммы элементов и произведения элемента на число
указаны, то такое линейное пространство можно назвать конкретным. Далее
приведены примеры конкретных линейных пространств.
Пример 1. Множества всех свободных
векторов в трехмерном пространстве (В3), на плоскости (В2)
и на прямой (В1) с определенными в курсе аналитической геометрии
операциями сложения и умножения на число являются линейными пространствами.
Пример 2. Множество {x} всех положительных вещественных
чисел. Сумму двух элементов определим как произведение вещественных чисел x и y (понимаемое в обычном для
вещественных чисел смысле). Произведение элемента x множества {x} на вещественное число λ определим как возведение
положительного вещественного числа x в степень λ. Нулевым элементом множества {x} будет являться вещественное число
1, а противоположным (для данного элемента x) элементом будет являться
вещественное число 1/x.
Пример 3. Арифметическое n-мерное векторное пространство, где
под вектором понимается кортеж из n вещественных чисел Аn. Элемент пространства Аn обозначим x=(x1, x2,… xn), вещественные
числа xi, i=1,2,… n называют координатами вектора x. Часто множество Аn называют n-мерным координатным пространством.
Операции сложения элементов множества Аn и умножения этих
элементов на вещественные числа определяются правилами:
(x1, x2, …, xn)+(y1, y2, …, yn)= (x1+y1, x2+y2, …, xn+yn)
λ(x1, x2, …, xn) = (λx1, λx2, …, λxn)
нулевым элементом Аn является нулевой вектор
0=(0, 0, …, 0)
противоположным элементом x=(x1, x2, …, xn) является элемент
(-x1, - x2, …, - xn)
Пример 4. Множество С [a, b] всех функций x=x(t), определенных и непрерывных на
сегменте a≤t≤b. Операции сложения таких функций и умножения на вещественное
число определяются обычными правилами математического анализа.
Пример 5. Множество {Pn(t)} всех алгебраических многочленов
степени, не превышающей натурального числа n, с операциями сложения и умножения
на вещественное число определенными такими же правилами, как для функций. Можно
заметить, что на сегменте a≤t≤b множество {Pn(t)} является подмножеством С [a, b], указанного в примере 4.
Следует также отметить то, что в
сформулированном выше определении линейного пространства числа λ, µ,… брались из множества
вещественных чисел. Поэтому определенное таким образом пространство называют
вещественным линейным пространством. При более широком подходе можно брать λ, µ,… из множества комплексных
чисел. Это приведет к введению понятия комплексного линейного пространства.
Элементы произвольного линейного
пространства принято называть векторами. При этом еще раз подчеркнем то
обстоятельство, что употребление термина «вектор» в более узком смысле (так как
мы делали это в § 1) не приводит к недоразумениям. Напротив, взывая к
сложившимся геометрическим представлениям, данный образ позволяет уяснить, и
даже предвидеть ряд результатов, справедливых для линейных пространств
произвольной природы. Далее при изложении, принимая во внимание формулировку
темы курсовой работы, мы будем пользоваться как понятием «вектор» и обозначать
элементы векторных пространств как а, b, c и т.д., так и понятием элемент и обозначать их как x, y, z и т.д.
Из аксиом 1-8 в качестве логических
следствий можно получить ряд утверждений справедливых для произвольных
векторных пространств. Так, в произвольном линейном пространстве существует
единственный нулевой элемент и для каждого элемента х существует единственный
противоположный элемент. При этом нулевой вектор 0 равен произведению
произвольного элемента x на вещественное число 0. Для каждого элемента x противоположный элемент равен
произведению этого элемента x на вещественное число -1.
По аналогии с положениями аналитической
геометрии введем понятия линейной зависимости элементов произвольного линейного
пространства. Выражение вида
αx+βy+ … +γz, где α, β, …, γ - произвольные
вещественные числа, называют линейной комбинацией элементов x, y, …z пространства V.
Элементы x, y, …, z пространства V называют линейно зависимыми, если
найдутся такие вещественные числа α,
β, …, γ, из которых хотя бы одно
отлично от нуля, что линейная комбинация элементов x, y, …, z с указанными числами является
нулевым элементом пространства V, т.е. имеет место равенство: αx+βy+ … +γz=0
Элементы x, y, …, z пространства V называют линейно независимыми, если
указанная выше линейная комбинация является нулевым элементом пространства V лишь при условии α=β= …=γ=0.
Для того чтобы элементы x, y, …, z пространства V были линейно зависимы, необходимо и
достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных
элементов. При этом если среди элементов имеется нулевой, то эти элементы
линейно зависимы. А также, если часть элементов x, y, …, z линейно зависима, то и все эти
элементы являются линейно зависимыми.
Понятие линейной зависимости
является, таким образом, естественным обобщением понятий коллинеарности и
компланарности геометрических векторов. Мы знаем, что в пространстве В3
таких векторов особая роль принадлежит тройке координатных ортов i, j, k. Естественно возникает
вопрос отыскания в произвольном векторном пространстве V систем векторов, обладающих
подобными свойствами.
Совокупность линейно независимых
элементов e1, e2, … en пространства V называется базисом этого пространства, если для каждого элемента x пространства V найдутся вещественные числа x1, x2, …, xn такие, что
справедливо равенство:
x=x1e1+x2e2+ … +xnen
Данное равенство называется
разложением вектора x по базису e1, e2, …, en, а числа x1, x2, …, xn называются координатами вектора x (относительно базиса e1, e2, …, en). Разложение по
базису для каждого элемента x является единственным.
Отметим, что для арифметического
линейного векторного пространства Аn, которое было рассмотрено
в Примере 3, одним из базисов являются следующие n элементов: e1 = (1, 0, …, 0), e2 = (0, 1, …, 0), …, en = (0, 0, …, 1).
При сложении двух любых элементов
линейного пространства их координаты (относительно любого базиса) складываются;
при умножении произвольного элемента на любое число все координаты этого
элемента умножаются на это число.
Линейное пространство называется n-мерным, если в нем существует n линейно независимых элементов, а
любые n+1 элементов уже являются линейно зависимыми. В этом случае число n называют размерностью пространства,
например V, и обозначают dimV. Если линейное пространство имеет размерность n, то любые n линейно независимых элементов
образуют его базис. И, наоборот, если базис линейного пространства содержит n векторов, то размерность данного
пространства равна n. Так, размерность арифметического линейного векторного
пространства An равна n, размерность пространства {x} (рассмотренного в примере 2) равна
единице.
Следует отметить, что различные
линейные пространства одной и той же размерности n в смысле свойств, связанных с
введенными в этих пространствах операциями, по существу не отличаются друг от
друга. В этой связи вводится определение изоморфных линейных пространств. Так,
два произвольных вещественных линейных пространства V и V` называются изоморфными, если между
элементами этих пространств можно установить взаимно однозначное соответствие.
А именно, если элементам x и y пространства V отвечают элементы x` и y` пространства V`, то элементу x+y отвечает элемент x`+y`, а элементу λx - элемент λx` при любом вещественном λ. В этом случае нулевому элементу пространства R отвечает нулевой элемент
пространства R`. Можно доказать, что любые два n-мерных вещественных линейных
пространства изоморфны. Таким образом, единственной существенной
характеристикой конечномерного линейного пространства является его размерность.
Можно сказать также, что всякое n-мерное линейное пространство изоморфно n-мерному координатному пространству
Аn.
1.3 Евклидовы линейные
пространства
Следующий шаг связан с введением в
пространствах любой размерности скалярного произведения. Оно позволит говорить
в общей ситуации о таких (присущих евклидовой геометрии) понятиях, как длина,
угол, ортогональность.
В вещественном линейном пространстве
V задано
скалярное произведение, если каждой паре его векторов a, b из V соответствует действительное число,
обозначаемое (a, b), и при любом выборе векторов выполнены следующие свойства:
. (а, b)=(b, a);
2. (a`+a``,
b)=(a`, b)+(a``, b)
. (λa, b)=λ (a, b) для любого числа λ
. (a, a)≥0, причем (a, a) = 0 тогда и только тогда, когда а
=0
В этом определении выделены
важнейшие свойства обычного скалярного произведения геометрических векторов, из
которых в качестве следствия можно получить и все другие его свойства.
Линейное пространство, в котором
задано скалярное произведение, называют обычно евклидовым пространством и
обозначают Е.
Подчеркнем, что при введении понятия
евклидова пространства абстрагируются не только от природы изучаемых объектов,
но и от конкретного вида правил образования суммы элементов, произведения
элемента на число и скалярного произведения векторов (важно лишь, чтобы эти
правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам
скалярного произведения).
Если же природа изучаемых объектов и
вид перечисленных правил указаны, то евклидово пространство называется
конкретным.
Примеры евклидовых пространств
следующие.
Пример 1. Линейное пространство В3
всех свободных векторов
Пример 2. Арифметическое векторное
линейное пространство Аn, если положить то, что для любой пары векторов а=(а1, а2, … аn), b=(b1, b2, …, bn) из An
(a, b)=a1b1+a2b2+
… +anbn
Пример 3. Бесконечномерное
линейное пространство С [α, β] всех функций x(t), определенных и непрерывных на сегменте α≤t≤β. Скалярное произведение двух функций x(t) и y(t) определим как интеграл (в пределах
от α до β) от произведения этих
функций.
Для любых двух векторов a и b произвольного евклидова
пространства справедливо неравенство (a, b) 2≤(a, a), (b, b), называемое неравенством Коши-Буняковского.
В любом евклидовом пространстве
естественным образом определяется длина │a│= √(a, a). Таким образом, можно говорить,
что скалярное произведение определяет «метрику» в линейном пространстве, т.е.
способ измерения длин. В евклидовом координатном пространстве An с определенным
выше скалярным произведением действует знакомое правило для вычисления длины │a│=√a12+a22+ … +an2 - длина вектора есть корень квадратный из суммы квадратов его
координат.
В любом вещественном евклидовом
пространстве можно ввести понятие угла между двумя произвольными элементами а и
b этого
пространства. В полной аналогии с векторной алгеброй назовем углом φ между векторами а и b тот (изменяющийся в пределах от 0
до π) угол, косинус которого
определяется соотношением
cos φ = 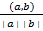
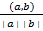
Далее, два вектора a, b евклидова пространства
назовем ортогональными, если их скалярное произведение равно нулю. Снова
апеллируя к векторной алгебре, назовем сумму а+b
двух ортогональных векторов а и b
гипотенузой прямоугольного треугольника, построенного на элементах а и b. Заметим, что во всяком евклидовом пространстве справедлива
теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Введенные понятия
позволяют выделить в евклидовом пространстве базисы особого вида - так
называемые ортонормированные базисы.
Базис e1, e2,
… en назовем ортонормированным, если он
составлен из попарно ортогональных векторов единичной длины. Это значит, что
векторы удовлетворяют соотношениям
, i = j
(ei, ej)
=
, i ≠ j
Во всяком n-мерном евклидовом пространстве Е существует ортонормированный
базис. Доказательство данного факта проводят методом математической индукции. В
ходе доказательства определяется алгоритм построения по заданной системе n линейно независимых векторов попарно ортогональных векторов
единичной длины e1,
e2, … en.
Данный алгоритм называют процессом ортогонализации.
В каждом n-мерном евклидовом пространстве Е существует много
ортонормированных базисов. Одним из них может служить декартов прямоугольный
базис координатного пространства Аn e1=(1,0, …, 0), e2=(0,
1, …, 0), … en=(0, 0, …, 1). В Примере 2 данного
параграфа мы определили скалярное произведение двух векторов пространства Аn как сумму произведений соответствующих координат этих векторов.
Оказывается та же
формула будет действовать и в любом n-мерном
евклидовом пространстве Е, если только в нем зафиксирован ортонормированный
базис, а координаты всех элементов вычисляются именно в этом базисе (т.е.
найдено разложение элементов по этому базису). В самом деле, пусть любые два
вектора а=(а1, а2, …, аn)
и b=(b1,
b2, …, bn)
разложены по ортонормированному базису e1,
e2, … en.
Тогда a=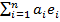
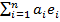 , b=
, b=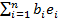
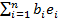 , скалярное произведение
, скалярное произведение
(a,
b)=(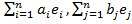
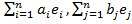 )=
)=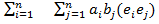
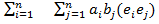 = =a1b1+a2b2+
… +anbn
= =a1b1+a2b2+
… +anbn
1.4 Подпространства.
Расстояние от вектора до подпространства
Для обычного трехмерного
пространства хорошо известен следующий факт: длина перпендикуляра, опущенного
из точки на прямую или плоскость, меньше длины любой наклонной. В известном
смысле данный факт сохраняется и в многомерных евклидовых пространствах. Чтобы
это понять, введем еще одно важное понятие, обобщающее понятия прямой и
плоскости в трехмерном пространстве.
Подмножество L линейного пространства V
называется линейным подпространством (или просто подпространством) пространства
V в том случае, если L
удовлетворяет следующим двум требованиям:
◦
Если элементы a и b принадлежат L, то и сумма a+b принадлежит L.
◦
Если элемент a принадлежит L,
то и элемент λa принадлежит L, где λ - любое вещественное число.
Простейшими примерами
подпространств служат, так называемые необоснованные подпространства - само
пространство V и нулевое подпространство.
Для всех векторов на
плоскости (пространство В2) указанные свойства выполнены, например,
для множества всех векторов, принадлежащих некоторой фиксированной прямой. В
обычном пространстве указанные свойства выполнены для плоскости.
Заметим также, что
всякое подпространство L
само образует линейное пространство относительно операций, определенных в V.
Другим примером
линейного подпространства является множество, содержащее все линейные
комбинации некой совокупности элементов a,
b, …c пространства V.
L={λ1a+λ2b+ … +λkc},
где λ1,
λ2, … λk
- произвольные скаляры.
Такое множество называют
линейной оболочкой элементов a,
b, …c. Линейная оболочка -
наименьшее подпространство, содержащее векторы a,
b, …c.
В случае, если L - подпространство евклидова пространства Е, можно говорить о
величине расстояния от любого вектора y
до этого подпространства. Будем для этого рассматривать произвольные векторы х
из L, каждый раз измеряя расстояние между y
и x длиной разности y-x.
Это условно показано на
рисунке.
За расстояние d от вектора до подпространства примем минимальную из указанных
длин, т.е. d= min│y-x│, где x
принадлежит L.
Каким же должен быть
вектор из L, для которого достигается минимум? В качестве ближайшего к y нужно взять такой вектор x0,
чтобы разность y-x0
была ортогональна (в смысле данного в § 3 Главы 1 определения) любому вектору
из подпространства L. Можно доказать, что
такой вектор x0
всегда существует и определен однозначно. Его называют ортогональной проекцией
вектора y. Следующая выкладка показывает, что длина перпендикуляра y-x0
действительно наименьшая:
│y-x│2= (y-x, y-x)=((y-x0)+(x0-x), (y-x0)+(x0-x))=(y-x0, y-x0)+2 (x - x0, y-x0)+(x - x0, x
- x0)
Согласно выбору вектора x0 мы имеем, что (x
- x0, y-x0)=0. Кроме того
(x - x0, x - x0)≥0.
Отсюда │y-x│2 ≥(y-x0, y-x0)=│y-x0│2
1.5 Линейные
преобразования векторного пространства
Остановимся еще на одном
из центральных понятий линейной алгебры, а именно, на линейных преобразованиях
векторного пространства. Линейным называется такое преобразование А векторного
пространства V, для которого выполнены следующие свойства:
А (a+b) = A(a) +A(b), для
любых a, b из V,(λa) = λA(a), для любого а из V
и любого скаляра λ
Поворот плоскости вокруг
начала координат, проектирование трехмерного пространства на координатную
плоскость дают нам простейшие примеры линейных преобразований.
Линейные преобразования
имеют самую тесную связь с матрицами. Чтобы это понять, выберем в n-мерном пространстве некоторый базис e1,
e2, … en
и рассмотрим образы базисных векторов А(e1),
A(e2), …, A(en). Каждый из них, как и всякий
вектор пространства V, является линейной комбинацией
векторов базиса, поэтому мы можем написать
Сопоставим теперь
преобразованию А матрицу A
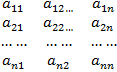
Поместив в каждый ее столбец
координаты образов А(e1),
A(e2), …, A(en) базисных векторов в самом этом
базисе. Так, для упомянутых выше примеров линейных преобразований (поворота на
угол α и проектирования на плоскость xOy)
матрицы преобразований имеют вид соответственно
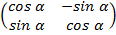
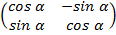 и
и 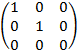
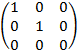
Матрицей А линейное
преобразование определено однозначно: зная ее, можно найти образ любого
вектора. Действительно, если b=b1e1+b2e2+
… +bnen, то, используя свойства
линейного преобразования и разложение (*) образа вектора по векторам базиса,
находим:
A(b)=A(b1e1+b2e2+
… +bnen) = b1A(e1)+b2
A(e2)+ … +bnA(en) = = b1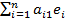
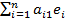 +b2
+b2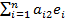
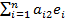 + … +bn
+ … +bn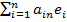
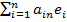 = (
= (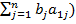
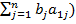 e1+(
e1+(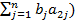
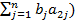 e2+ … +(
e2+ … +(
 en
en
В матричной форме это
можно выразить так: чтобы получить координаты образа, нужно матрицу преобразования
умножить на столбец вектора b:
А×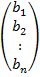
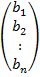 =
= 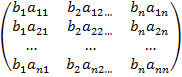
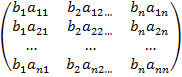
Кроме умножения
преобразований, определяемого обычным образом как композиция, имеют смысл
операции их сложения и умножения преобразования на число. Суммой преобразований
А и В называется такое преобразование А+В, что (А+В) (а) = А(а) + В(а) для
любого элемента а из множества V.
Соответственным образом определяется и умножение на скаляр (λА)
(а) = λА(а) для любого элемента а из множества V.
Можно убедиться, что
имеется полная параллель между указанными операциями над линейными
преобразованиями и соответствующими операциями над их матрицами. Так,
произведение матриц служит матрицей произведения соответствующих
преобразований, аналогично и для операций сложения и умножения на скаляр.
При рассмотрении
линейных преобразований обычно выделяют различные их классы, обладающие
некоторыми дополнительными свойствами. Так, один из важнейших классов
составляют, так называемые, ортогональные преобразования евклидова
пространства. При таком преобразовании сохраняется неизменной длина любого
вектора из V: │А(а)│ = │а│.
В случае плоскости и
трехмерного пространства преобразования этого типа исчерпываются поворотами и
зеркальными симметриями. Эти и другие типы линейных преобразований широко
используются во многих математических и прикладных вопросах.
2. Некоторые приложения
аппарата векторных пространств
.1 Системы линейных
уравнений. Гиперплоскости, гиперповерхности
Исторически первым
вопросом линейной алгебры был вопрос о линейных уравнениях. Построение теории
систем линейных уравнений потребовало таких инструментов, как теория матриц и
определителей, и оказало существенное влияние на разработку теории векторных
пространств.
В данной работе мы не
будем останавливаться на конкретных методах решения систем линейных уравнений,
так как это предполагает проведения отдельного масштабного исследования. Вместе
с тем небольшой обзор систем линейных уравнений позволит еще раз подчеркнуть
общность геометрических фигур и их многомерных аналогов, в том числе ввести
такие понятия как гиперплоскости и гиперповерхности.
При решении
геометрических задач методом координат, как правило, возникают системы линейных
уравнений с двумя или тремя неизвестными. Например, для отыскания точки
пересечения двух прямых на плоскости приходится решать систему двух линейных
уравнений с двумя неизвестными:
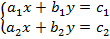
где каждое из уравнений
определяет прямую на плоскости, а решение (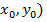
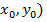 дает координаты точки
пересечения прямых, или радиуса-вектора этой точки. Аналогично и в системе
линейных уравнений с тремя неизвестными каждое уравнение можно интерпретировать
как уравнение плоскости в пространстве, а всякое решение (
дает координаты точки
пересечения прямых, или радиуса-вектора этой точки. Аналогично и в системе
линейных уравнений с тремя неизвестными каждое уравнение можно интерпретировать
как уравнение плоскости в пространстве, а всякое решение (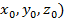
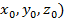 такой системы как точку
или вектор в пространстве с указанными координатами.
такой системы как точку
или вектор в пространстве с указанными координатами.
В общем случае система m линейных уравнений с n
неизвестными (или, кратко, линейная система) имеет следующий вид:
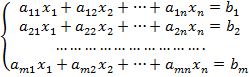
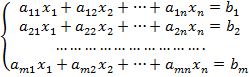
Указанная выше система
называется однородной, если все ее свободные члены 
 , i=1,2, … m.
Если хотя бы один из свободных членов отличен от нуля, то система называется
неоднородной. Система называется квадратной, если число уравнений равно числу
неизвестных (m=n). Решением системы называется такая совокупность n чисел
, i=1,2, … m.
Если хотя бы один из свободных членов отличен от нуля, то система называется
неоднородной. Система называется квадратной, если число уравнений равно числу
неизвестных (m=n). Решением системы называется такая совокупность n чисел
(c1, c2,
…, cn,) которая при подстановке в систему
на место неизвестных обращает все уравнения в верные равенства. Если система
имеет хотя бы одно решение, то она является совместной, и несовместной, если у
нее не существует ни одного решения.
Хотя непосредственное
геометрическое истолкование системы, содержащей более трех неизвестных, уже
невозможно, однако прежний геометрический язык сохраняется, если рассмотреть
данную систему в n-мерном координатном
векторном пространстве Аn
(см. Пример 3 § 2 Главы 1).
По аналогии с обычной
плоскостью множество всех n-мерных
векторов, удовлетворяющих одному линейному уравнению с n
неизвестными, называют гиперплоскостью в n-мерном
пространстве. При таком определении множество всех решений системы есть не что
иное, как пересечение нескольких гиперплоскостей.
Также гиперплоскость
определяют как подпространство с размерностью, на единицу меньшей, чем
объемлющее пространство. В общем случае уравнение гиперплоскости, проходящей
через точку Х с координатами (Х1, Х2, …Хn),
в n-мерном евклидовом векторном пространстве можно записать как
равенство: (N, x) = (N, X), где N (η1, η2, …
ηn) - вектор, ортогональный (нормальный) к гиперплоскости.
Гиперплоскость делит пространство на два полупространства, все точки каждого из
них определяются неравенствами.
В сходном смысле можно
говорить и о произвольных поверхностях или областях в n-мерном
пространстве, понимая под ними множество векторов, задаваемых одним или
несколькими уравнениями, или неравенствами, не обязательно линейными. Так,
гиперповерхностью называется множество точек, координаты которых удовлетворяют
одному равнению F(x1, x2,
…, xn) = 0 с n
неизвестными. Простейшим после плоскости примером гиперповерхности является
сфера радиуса R в n-мерном пространстве -
множество точек, координаты которых удовлетворяют уравнению 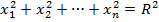
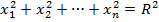 .
.
2.2 Линейное
программирование: задачи на оптимизацию и симплекс-метод
Линейное
программирование (кратко ЛП) - сравнительно недавно возникший раздел прикладной
математики, теоретической базой которого является как раз линейная алгебра.
Линейное программирование применимо к решению многих задач оптимизации, часто
возникающих на практике, прежде всего в экономической деятельности субъектов.
Так, с помощью методов ЛП можно решать задачи составления оптимального плана
производства с точки зрения максимизации прибыли или минимизации издержек,
задачи по организации транспортных перевозок (транспортные задачи), задачи
выбора инвестиционных проектов или формирования инвестиционных портфелей и
многие другие.
Во всех указанных выше
примерах существует величина, количественно характеризующая цель и называемая
целевой функцией (прибыль, издержки, транспортные расходы, доходность портфеля
ценных бумаг и т.д.). По условиям задачи требуется, чтобы целевая функция
достигла своего минимума или максимума. Целевая функция зависит от неких
величин, которые называют переменными решения или неизвестными. Поиск
оптимальных решений осуществляется при наличии вполне определенных ограничений
на изменения переменных решения.
Например, рассмотрим
задачу о рациональном снабжении завода железной рудой. Руда может доставляться
на завод из n пунктов добычи. При этом, ci
- стоимость добычи одной тонны руды на i-й
шахте и ее доставки на завод, bi
- объем добычи на i-й шахте, b - потребность завода в руде. Потребитель стремится уменьшить
расход на приобретение сырья. Если xi
- количество руды (в тоннах), которое будет доставляться с i-й шихты, то этот расход в сумме составит L=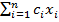
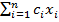 - целевая функция.
- целевая функция.
Нужно учесть при этом,
что неизвестные xi
обязаны удовлетворять ряду ограничений. Прежде всего, необходимо полностью
удовлетворить потребность завода в сырье: 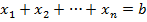
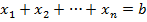 . Кроме того, очевидно,
что
. Кроме того, очевидно,
что 
 , i=1,2, … n.
Наконец, по смыслу задачи величины xi≥0,
i=1,2, … n.
, i=1,2, … n.
Наконец, по смыслу задачи величины xi≥0,
i=1,2, … n.
Таким образом, требуется
найти наименьшее значение целевой функции (минимизировать целевую функцию) при
соблюдении вышеуказанных условий.
При небольшом числе
переменных задача ЛП имеет простой геометрический смысл. Например, возьмем для
нашей задачи n=3 и конкретизируем значения исходных данных:
L=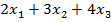
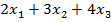
=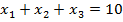
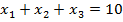
≤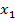
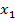 ≤3, 0≤
≤3, 0≤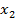
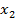 ≤8, 0≤
≤8, 0≤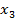
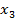 ≤5
≤5
Учитывая первое условие,
выразим x3 через x1
и x2 и подставим в целевую функцию: L=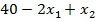
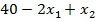 (*) при ограничениях 0≤
(*) при ограничениях 0≤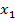
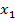 ≤3, 0≤
≤3, 0≤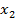
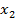 ≤8, 5≤
≤8, 5≤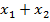
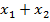 ≤10
≤10
Ограничения задают на
плоскости некую многоугольную область S.
Очевидно, что при каждом значении L,
равенство (*) для целевой функции представляет собой прямую на плоскости. При
этом изменению L соответствует
параллельный перенос прямой. Через одну из вершин многоугольника S пройдет как раз та прямая, на которой достигается интересующий
нас минимум. В нашем случае это точка с координатами x1=3,
x2=7. При этом x3=0,
L=27.
Произвольная задача ЛП
может быть сформулирована подобно рассмотренной в следующем виде: например,
минимизировать целевую функцию
L=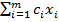
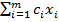
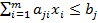
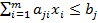 , j=1,2, … n
, j=1,2, … n
xi≥0
При m=2 ограничения, как и в примере, определяют выпуклую многоугольную
область на плоскости (или пустое множество, если ограничения несовместны), при m=3 - выпуклую многогранную область в пространстве. При этом
решение задачи, если оно существует, достигается на границе этой области, более
точно - в некоторой ее вершине. В случае произвольного m
также говорят, что ограничения определяют выпуклую многогранную область в m-мерном координатном пространстве. Такие понятия, как
«выпуклость», «граница области», «вершина», могут быть определены и в этом
случае. Если задача ЛП имеет решение, то оно достигается в вершине многогранной
области, определенной ограничениями, указанными выше.
На этом общем
утверждении основываются различные методы минимизации, в частности, и наиболее
известный из них - симплекс-метод. В упомянутом методе производится
направленный перебор вершин, такой, что при переходе от одной вершины к
следующей значение целевой функции в нашем случае уменьшается. Перебор
заканчивается, когда будет достигнут минимум целевой функции.
.3 Приближенные
вычисления с помощью метода наименьших квадратов
Высказанные в § 4 Главы
1 соображения о наименьшем расстоянии от вектора до подпространства лежат в
основе многих разновидностей известного в математике «метода наименьших
квадратов».
Данный метод можно
проиллюстрировать на примере, относящемся к серии популярных задач на смеси и
сплавы.
Плавильщик располагает
тремя сплавами: латунью, бронзой и мельхиором. Процентное содержание меди,
цинка, олова и никеля в этих сплавах указано в следующей таблице:
|
Металл
|
Латунь
|
Бронза
|
Мельхиор
|
Новый сплав
|
|
Медь
|
60
|
80
|
80
|
70
|
|
Цинк
|
40
|
0
|
0
|
10
|
|
Олово
|
0
|
20
|
0
|
10
|
|
Никель
|
0
|
20
|
10
|
Цель плавильщика - получить новый
сплав, в котором перечисленные четыре металла составляют соответственно 70, 10,
10, 10 процентов. Осуществима ли такая цель, а если нет, то насколько близко
можно подойти к желаемому составу нового сплава?
Пусть x1, x2, x3 - доли, которые должны составить
латунь, бронза и мельхиор в предполагаемом сплаве. Баланс по каждому из четырех
металлов дается уравнениями
|
Медь
|
0,6x1
|
+0,8x2
|
+0,8x3
|
=0,7
|
|
Цинк
|
0,4x1
|
|
|
=0,1
|
|
Олово
|
|
0,2x2
|
|
=0,1
|
|
Никель
|
|
|
0,2x3
|
=0,1
|
или иначе,
|
6x1
|
+8x2
|
+8x3
|
=7
|
|
4x1
|
|
|
=1
|
|
|
2x2
|
|
=1
|
|
|
|
2x3
|
=1
|
Ясно, что получившаяся систем
несовместна, и потому ответ на первый вопрос задачи отрицательный. Результат
можно выразить и иначе, если рассмотреть векторы-столбцы а1=(6, 4,
0, 0), а2=(8, 0, 2, 0), а3=(8, 0, 0, 2), b=(7, 1, 1, 1), составленные из
коэффициентов при неизвестных и свободных членов. Несовместность системы
означает, что вектор b нельзя записать в виде линейной комбинации векторов трех других
векторов а1, а2, а3. Или (что то же самое)
вектор b не содержится в линейной оболочке векторов а1, а2,
а3:
L=‹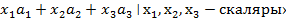
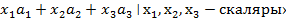
В то же время векторы из
подпространства L с точностью до
пропорциональности соответствуют тем сплавам, которые могут быть получены при
смешивании в той или иной пропорции латуни, бронзы и мельхиора. Будем
рассматривать наши векторы как элементы четырехмерного координатного евклидова
пространства со скалярным произведением, определенным по формуле из Примера 2 §
3 Главы 1. Теперь второй вопрос можно уточнить так: в подпространстве L найти вектор, ближайший к вектору b,
иными словами ортогональную проекцию вектора b
на подпространство L - вектор:
x0=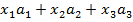
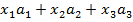 (*)
(*)
Соответствующий этому
вектору сплав и будем считать наилучшим приближением к требуемому в задаче. Для
отыскания ортогональной проекции заметим, что для всех j=1,2,3
(b, aj)=(x0+(b-x0), aj)=(x0, aj)+(b-x0, aj)=
(x0, aj)
так, как b-x0 ортогонален любому вектору из L.
Подставляя в полученные равенства (b,
aj)=(x0,
aj), выражение вектора x0 как линейного разложения по векторам а1, а2,
а3 (выражение (*)), приходим к системе линейных уравнений для
определения коэффициентов x1,
x2, x3,
решая которую находим x1≈0,22,
x2=x3≈0,39. Вектор x0=(7,56;
0,88; 0,78; 0; 78). Соответствующий ему сплав, которым может удовлетвориться
плавильщик, содержит 75,6% меди, 8,8% цинка и по 7,8% олова и никеля.
Заключение
Данная работа посвящена
таким ключевым понятиям линейной алгебры как векторы, пространства,
гиперплоскости, гиперповерхности, евклидово пространство, ортогональность и
другие. Данные понятия введены в линейную алгебру из аналитической геометрии. В
то же время объекты, к которым данные понятия применяются совсем не походят на
свои геометрические прототипы. Так в § 2 Главы 1 отмечалось, что роль векторов
(элементов линейного пространства) могут играть такие объекты, как многочлены,
матрицы, функции и т.д.
Само векторное (или
линейное) пространство определяется как множество объектов любой природы, для
элементов которых каким-либо способом (причем, безразлично каким) определены
операция сложения элементов и операция умножения элемента на скаляр. Основная
связь с аналитической геометрией состоит в том, что указанные операции обязаны
обладать теми же свойствами, что и соответствующие операции над геометрическими
векторами.
Таким образом, при
введении понятия линейного и далее евклидова пространства абстрагируются не
только от природы изучаемых объектов, но и от конкретного вида правил
образования суммы элементов, произведения элемента на число и скалярного
произведения векторов (важно лишь, чтобы эти правила удовлетворяли восьми
аксиомам линейного пространства и четырем аксиомам скалярного произведения)
При этом употребление
термина «вектор» не приводит к недоразумениям. Напротив, взывая к сложившимся
геометрическим представлениям, данный образ позволяет уяснить, и даже
предвидеть ряд результатов, справедливых для линейных пространств произвольной
природы.
Теоретическая база
линейной алгебры используется для решения многочисленных прикладных задач. В
Главе 2 мы коснулись только некоторых приложений. В § 1 Главы 2 были введены
понятия гиперплоскости и гиперповерхности в n-мерном
координатном пространстве. А решение системы линейных уравнение было
интерпретировано как пересечение нескольких гиперплоскостей.
В § 2 была затронута
тема повсеместно возникающих на практике оптимизационных задач. Методы решения
таких задач рассматриваются в одном из разделов прикладной математики,
называемом линейным программированием. Теоретической базой линейного
программирования является линейная алгебра, а пониманию сути методов решения
способствуют такие геометрические понятия как «выпуклая многогранная область»,
«граница области», «вершина» и т.п.
Многие методы теории
приближений основываются на факте, который для обычных пространств нам хорошо
известен: длина перпендикуляра, опущенного из точки на прямую или плоскость,
меньше длины любой наклонной. В § 3 Главы 2 было рассмотрено решение простейшей
задачи на смеси и сплавы, использующее метод наименьших квадратов. В этом
случае нам помог перевод задачи на язык линейной алгебры и отыскание
ортогональной проекции вектора в соответствующем подпространстве линейного
евклидова пространства.
Таким образом, введенные
в линейной алгебре понятия и выводы, полученные с их введением, применяются во
многих разделах математики, таких как математический анализ, теория
дифференциальных уравнений, функциональный анализ, теория вероятностей, теория
приближений и пр. В этих разных областях очень часто возникают ситуации, укладывающиеся
в одну и ту же общую схему, которая отражена в понятиях линейного и евклидова
пространства и других, связанных с ними.
Такие понятия как
линейная зависимость и независимость векторов, базис, размерность,
подпространство и т.д. переносятся без изменений в различные векторные
пространства над теми или иными полями (и даже не обязательно полями
вещественных (R) и комплексных (C)
чисел). Дело, конечно, не только в логической возможности подобных обобщений.
Важнее то, что во многих теоретических и практических задачах векторные
пространства оказываются полезной математической моделью изучаемого круга
вопросов, а аппарат линейной алгебры - ценным орудием для его изучения.
Список литературы
уравнение линейный
пространство симплекс
1. Аршинов М.Н., Садовский Л.Е. Грани алгебры. - М.: Факториал
Пресс, 2008
2. Барыбина И.А., Хармац А.Г. Математика 1.
Учебно-методическое пособие для студентов - М.: МГОУ, 2010
. Жаров В.К., Матвеев О.А., Панкратов А.С., Роганов А.А.
Математика. Лекции по аналитической геометрии на плоскости и в пространстве.
Выпуск 1. - М.:Янус-К, 2008
. Ильин В.А., Позняк Э.Г. Аналитическая геометрия - М.:
ФИЗМАТЛИТ, 2009
. Ильин В.А., Позняк Э.Г. Линейная алгебра - М.: ФИЗМАТЛИТ,
2010
. Зайцев М.Г. Методы оптимизации управления для менеджеров.
- М.: «ДЕЛО», 2002
. Куликов Л.Я. Алгебра и теория чисел: Учеб. пособие для
педагогических институтов: Высш школа. 1979.
. Курош А.Г. Курс высшей алгебры. − М.: Наука,
Главная редакция физико - математической литературы, 1957 и др. г.