Расчет показателей функций
Задача 1
Вычислить 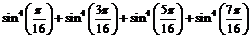 .
.
Решение
Заметим, что 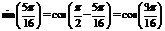 и
и
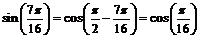 .
Тогда
.
Тогда
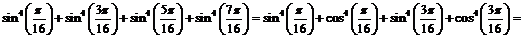
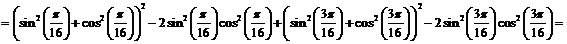
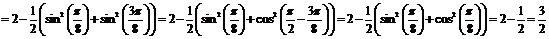 .
.
Ответ:
3/2.
Задача 2
Пусть матрицы 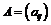 и
и
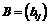 такие
что:
такие
что:  ,
,
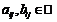 и
выполнено условие:
и
выполнено условие:
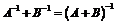 .
.
Требуется:
) Предложить матрицы 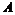 и
и
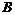 ,
удовлетворяющие этому уравнению;
,
удовлетворяющие этому уравнению;
) Доказать, что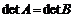 .
.
Решение
Так как, по условию
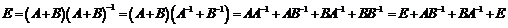 ,
,
Откуда 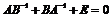 .
Обозначим
.
Обозначим 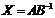 .
Тогда
.
Тогда 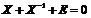 .
Умножим последнее уравнение на
.
Умножим последнее уравнение на 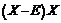 слева, получим:
слева, получим:
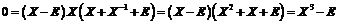 , откуда
, откуда 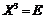 .
.
Следовательно, 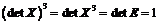 ,
то есть
,
то есть  .
Так как
.
Так как  ,
то
,
то 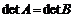 .
.
Задача 3
Доказать, что 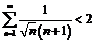 .
.
Решение
Докажем, что 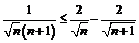 .
Умножим обе части на
.
Умножим обе части на 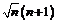 ,
получим
,
получим 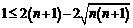 .
.
То есть, 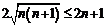 или
или
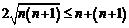 .
Что очевидно:
.
Что очевидно: 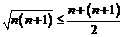 .
.
Тогда: 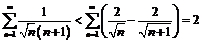 .
.
Задача 4
Разложить функцию 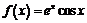 по
формуле Тейлора в окрестности точки
по
формуле Тейлора в окрестности точки 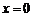 . Рассчитать коэффициент
. Рассчитать коэффициент
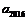 при
при
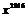 .
.
Решение
1 способ.
Непосредственно проводя вычисления производных, получим, до пятого члена:
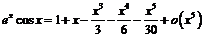 .
.
способ.
Перемножим 2 ряда, используя метод неопределенных коэффициентов:
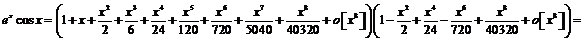
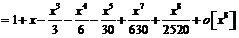 .
.
способ.
По формуле Эйлера:
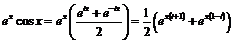 , с учётом
, с учётом 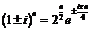 ,
получим
,
получим
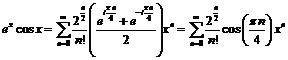 .
.
Данное разложение позволяет легко
определить любой коэффициент.
Задача 5
Найти пределы: а) 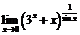 ,
б)
,
б) 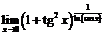 ,
в)
,
в) 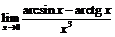 .
.
Решение. а)
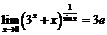 ;
б)
;
б) 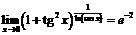 ,
в)
,
в) 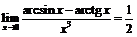 .
.
Задача 6
Дан эллипс 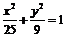 .
.
Требуется:
1) Предложить уравнение
гиперболы, имеющее такие же координаты фокусов;
) Показать, что таких
гипербол бесконечно много;
) Показать, что эти
гиперболы ортогональны данному эллипсу.
Решение
Из уравнения эллипса
получаем координаты фокусов 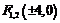 и эксцентриситет
и эксцентриситет 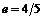 .
.
Пусть искомая гипербола
имеет вид 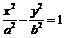 .
С учетом условий:
.
С учетом условий: 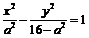 ,
где
,
где 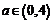 .
.
Пусть 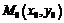 -
точка пересечения параболы и гиперболы. Уравнения касательных для этих кривых в
-
точка пересечения параболы и гиперболы. Уравнения касательных для этих кривых в
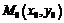 имеют
вид:
имеют
вид: 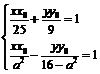 с
угловыми коэффициентами
с
угловыми коэффициентами 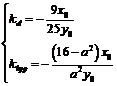 .
.
Далее, из системы
уравнений 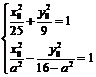 получаем
получаем
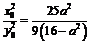 .
.
Окончательно, 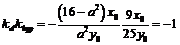 .
.
Задача 7
Найти все корни
уравнения 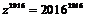 .
.
Решение
Очевидно, что данное
уравнение имеет ровно 2016 корней с учетом кратных и комплексных корней: 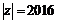 ,
,
 ,
,
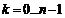 .
.
уравнение тейлор
гипербола координата
Задача 8
Накануне Летних
Олимпийских Игр 2016 года в Рио-де-Жанейро Всемирное Антидопинговое Агентство
решило проверить всех спортсменов на употребление запрещенного вещества -
мельдония. Современные методы позволяют обнаружить мельдоний, даже если
анализируется смесь проб у нескольких спортсменов. Поэтому, чтобы уменьшить
количество проб и расходы на них, было предложено смешивать пробы 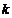 спортсменов,
и если проба дала отрицательный результат, то все спортсмены допущены к
соревнованиям. Если же результат допинг-пробы положительный, берется еще
спортсменов,
и если проба дала отрицательный результат, то все спортсмены допущены к
соревнованиям. Если же результат допинг-пробы положительный, берется еще 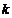 проб
у каждого спортсмена в отдельности. Найти оптимальную численность группы
проб
у каждого спортсмена в отдельности. Найти оптимальную численность группы 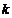 ,
если вероятность того, что спортсмен принимал мельдоний
,
если вероятность того, что спортсмен принимал мельдоний 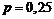 .
Считать, что число спортсменов достаточно велико.
.
Считать, что число спортсменов достаточно велико.
Решение
Вероятность того, в
группе из 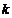 спортсменов
получится отрицательная проба равна
спортсменов
получится отрицательная проба равна 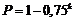 . Тогда «функция
экономии» будет
. Тогда «функция
экономии» будет  она
имеет максимум при
она
имеет максимум при 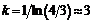 .
.
Задача 9
При каких значениях
параметра 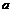 предел
предел
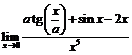 будет
конечным и ненулевым? Найти этот предел.
будет
конечным и ненулевым? Найти этот предел.
Замечание.
Разложение функции 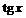 в
ряд Тейлора:
в
ряд Тейлора: 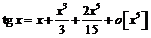
Решение
Воспользуемся
разложением в ряд Тейлора функций 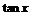 и
и 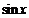 до
до
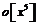 :
:
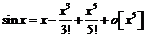 ,
,
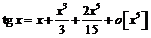 .
.
Тогда 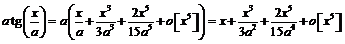 .
Для того, чтобы предел был конечным и ненулевым, необходимо, чтобы коэффициент
в числителе при
.
Для того, чтобы предел был конечным и ненулевым, необходимо, чтобы коэффициент
в числителе при 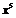 был
отличен от 0, а коэффициенты при меньших степенях были равны 0. Отсюда получим:
был
отличен от 0, а коэффициенты при меньших степенях были равны 0. Отсюда получим:
Тогда 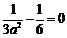 ,
откуда получаем
,
откуда получаем 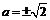 .
Для данных значений параметра
.
Для данных значений параметра 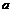
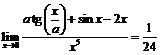 .
.
Ответ: 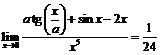 при
при
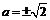 .
.
Задача 10
Найти производные 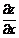 ,
,
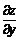 ,
если
,
если 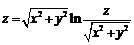
Решение
Перепишем функцию в виде
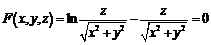 .
Тогда
.
Тогда 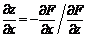 и
и
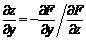 .
.
Так как 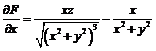 ,
,
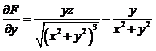 ,
,
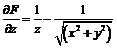 ,
то
,
то 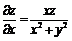 ,
,
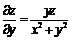 .
.
Задача 11
Вычислить площадь
фигуры, заданной условиями: 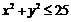 и
и 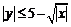 .
.
Решение
Очевидно, что фигура
симметрична относительно осей координат, поэтому 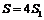 , где
, где 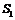 -
площадь фигуры в первой четверти. Точка пересечения линий
-
площадь фигуры в первой четверти. Точка пересечения линий 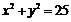 и
и
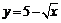 -
точка (4,3). Получим:
-
точка (4,3). Получим:
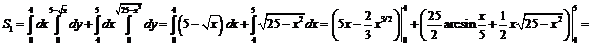
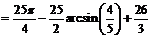 .
. 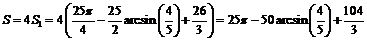
Ответ:
 .
.
Задача 12
Вычислить интегралы:
а) 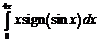 ;
б)
;
б) 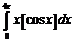 ;
в)
;
в) 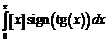 .
.
Примечание.
 -
целая часть числа
-
целая часть числа 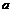 ,
,
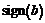 -
знак числа
-
знак числа 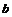 .
.
Решение
а) 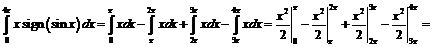
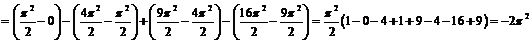 .
.
б) 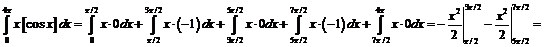
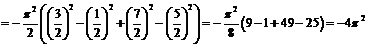 .
.
в) 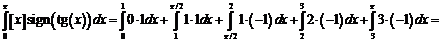
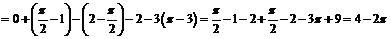 .
.
Ответ: а) 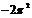 ;
б)
;
б) 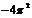 ;
в)
;
в) 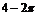 .
.
Задача 13
1. Показать, что
функция 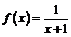 удовлетворяет
функциональному уравнению
удовлетворяет
функциональному уравнению 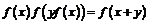 для
любых
для
любых 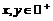 ,
где
,
где 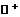 -
множество положительных вещественных чисел.
-
множество положительных вещественных чисел.
. Найти все
дифференцируемые функции 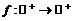 удовлетворяющие
данному функциональному уравнению для любых
удовлетворяющие
данному функциональному уравнению для любых 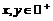 .
.
Решение
Перепишем условие в виде
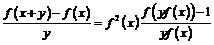 .
.
Переходя к пределу, получим
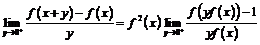 ,
,
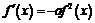 , т.е.
, т.е. 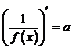 .
.
Таким образом, 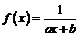 ,
где из начальных условий следует
,
где из начальных условий следует 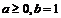 .
.
Задача 14
Решить дифференциальное
уравнение 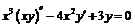 .
.
Указание.
Использовать замену 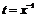 .
.
Решение
Замена 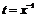 ,
получим
,
получим
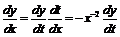 ;
; 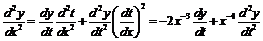 .
.
Тогда 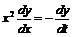 ,
,
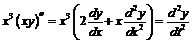 .
.
В итоге исходное
уравнение имеет вид 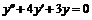 ,
с решением
,
с решением 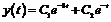 или
или
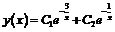 .
.
Задача 15
Сборная России по
футболу насчитывает 28 человек, каждый из которых является рыцарем (всегда
говорит правду) или лжецом (всегда лжет). Во время пресс-конференции у каждого
футболиста спросили, сколько в сборной рыцарей. Первый сказал: «Число рыцарей в
сборной - делитель 1». Второй сказал: «Количество рыцарей в сборной - делитель
2» и т.д. до 28-го, который сказал: «Количество рыцарей в сборной - делитель
28». Определите, сколько в сборной России рыцарей.
Решение
Может ли в сборной не
быть рыцарей вообще? Да. В этом случае все 28 членов сборной солгали бы, так
как 0 не является делителем никакого из названных чисел.
Может ли в сборной быть
ровно 1 рыцарь? Нет. В этом случае все 28 членов сборной оказались бы рыцарями.
1≠28.
Может ли в сборной быть
ровно 2 рыцаря? Нет. В этом случае каждый второй член сборной был бы прав, и 14
человек были бы рыцарями. 2≠14.
Может ли в команде быть
ровно 3 рыцаря? Нет. В этом случае каждый третий член сборной был бы прав, и 9
человек были бы рыцарями. 3≠9.
Может ли в сборной быть
ровно 4 рыцаря? Нет. В этом случае каждый четвёртый член сборной был бы прав, и
7 человек были бы рыцарями. 4≠7.
Может ли в сборной быть
ровно 5 рыцарей? Да. В этом случае каждый пятый член сборной был бы прав. Были
бы правы игроки под номерами 5, 10, 15, 20 и 25.
Может ли в сборной быть
ровно 6 рыцарей? Нет. В этом случае каждый шестой член сборной был бы прав. 4
человека были бы рыцарями. 6≠4.
Может ли в команде быть
больше шести рыцарей? Нет. В этом случае правду сказали бы меньше четырёх
человек.
Ответ:
В сборной России по футболу ноль или пять рыцарей.