Методы решения дифференциальных уравнений
КУРСОВАЯ
РАБОТА
Методы
решения дифференциальных уравнений
Введение
Дифференциа́льное
уравне́ние
-уравнение, связывающее значение некоторой неизвестной функции в некоторой
точке и значение её производных различных порядков в той же точке. Дифференциальное
уравнение содержит в своей записи неизвестную функцию, ее производные и
независимые переменные. Решить дифференциальное уравнение не просто. Есть
большое число способов их решения.
1.Теоретическая часть
.1 Модифицированный метод Эйлера
Суть этого метода состоит в
следующем. Сначала вычисляются вспомогательные значения искомой функции y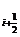
в точках t 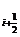= ti + 
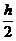с помощью
формулы:
y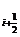 = yi + 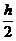fi = yi +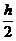f(ti, yi).
Затем находится значение правой
части уравнения в средней точке
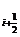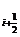= f(t, y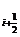) и затем полагается yi+1 = yi + h f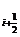, i = 0, 1,
…, n - 1.
.2 Формула Ньютона
Интерполяционный многочлен легко
определяется если его построить в виде:
(x) = С0 + С1(x - x0) + C2(x - x0)
(x - x1) + ...+ Cn(x - x0)(x - x1) ... (x - xn-1)
Исходя из условия интерполяции
<#"878209.files/image003.gif">
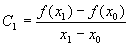
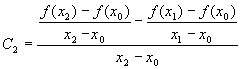и так далее.
.3 Дихотомия
Пусть задана функция 
.
Разобьём мысленно заданный отрезок
пополам и возьмём две симметричные относительно центра точки 
и 
так, что:
,
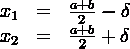Отбросим тот из концов изначального
интервала, к которому ближе оказалась одна из двух вновь поставленных точек с
максимальным значением (напомним, мы ищем минимум
<#"878209.files/image012.gif">, то берётся отрезок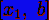 
, а отрезок 
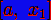отбрасывается.
Иначе берётся зеркальный
относительно середины отрезок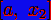 
, а отбрасывается 
.
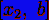Процедура повторяется, пока не будет
достигнута заданная точность, к примеру, пока длина отрезка не достигнет удвоенного
значения заданной погрешности.
На каждой итерации приходится
вычислять новые точки. Можно добиться того, чтобы на очередной итерации было
необходимо высчитывать лишь одну новую точку, что заметно способствовало бы
оптимизации процедуры. Это достигается путём зеркального деления отрезка в
золотом сечении, в этом смысле метод золотого сечения
<#"878209.files/image017.gif">, где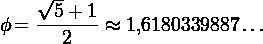 
- золотое
сечение
<#"878209.files/image019.gif">
Рис. 1.1
Тогда площадь криволинейной трапеции
приближенно можно считать равной площади фигуры, составленной из трапеций. Так
как площадь трапеции, построенной на отрезке [xi, xi+1] длины h =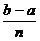 
, равна h 
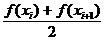, то,
пользуясь этой формулой для i = 0, 2, … , n - 1, получим квадратурную формулу
трапеций:
=
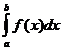»Iтр
=h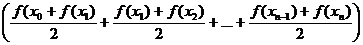
=
2. Расчетная часть
kursovaya;q:real;zagacha1(q:real);x,
y, yp, h, b: real;: integer;f (xn, yn: real): real;:= 2 * (xn * xn + yn);;:=
0;:= 0;:= 1;:= 0.1;:= 1;('Модифицированный метод Эйлера');('');('dy/dx =
2*(x^2+y), y(0) = 1');('');
writeln('| i
| x | yp | y |');
writeln('-----------------------------');('|',
i:2, ' |', x:4:1, ' |', yp:7:4, ' |', y:7:4, ' |');:= y + h/2 * f(x, y);:= y +
h * (f(x+h/2, yp));:= i + 1;:= x + h;x > b;;;zagacha2(q:real);i, k0, k1, k2:
real;h = 0.1;:array[0..2] of real = (1.2205, 1.4937, 1.8356);:=
0.2;('Интерполированный полином Ньютона');('');('dy/dx = 2*(x^2+y), y(0) = 1, n
= 2');:= main[0];:= (main[1] - k0)/h;:= ((main[2] - main[1])/h -
k1)/(2*h);('f(x)=',k0:0:3,'+(x-',i:0:1,')*',k1:0:3,'+(x-',i:0:1,')(x-',i+h:0:1,')*',k2:0:3);;;zagacha3(q:real);:real;f(x:
real): real;:= (2*sqr(x))+2*y;, E, a, b,t,d, c,g,m: real;,k:
Integer;:=0.1;:=0;:=1;:= 0;:=0;:=1;:=0;:=1;:= (a + b) / 2;(f(a) * f(c)) < 0
Then b := ca := c;(n)(b - a) <= E;:= (a + b) / 2;('koren max raven x=',
x:10:5);:= (t + d) / 2;(f(t) * f(g)) < 0 Then d := gd := g;(k)(d - t) <=
E;:= (t +d) ;
WriteLn('koren min raven x=',
x:10:4);
Readln;;zagacha4(q:real);a,
b, h, i, sum: real;: integer;f (x: real): real;:=
1.220+(x-0.2)*2.732+(x-0.2)*(x-0.3)*3.635;;('Метод трапеций');('');('Левая
граница: ');(a);('Правая граница: ');(b);('Кол-во разбиений: ');(n);:= 0;:=
0;:= (b - a)/n;:= sum + f(a+i*h) + f(a+(i+1)*h);:= i + 1;i = n - 1;(' Result:
', h/2*sum:0:4);;;.
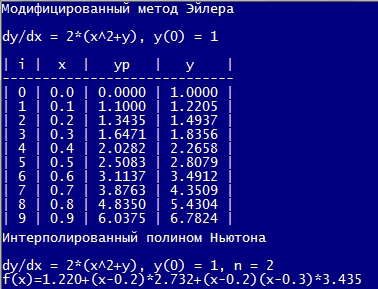
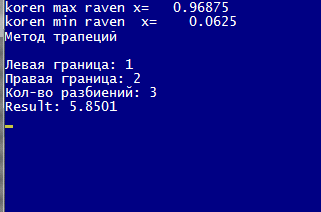
Рисунок
1-полученные значения
.Составим
Блок-схему алгоритма
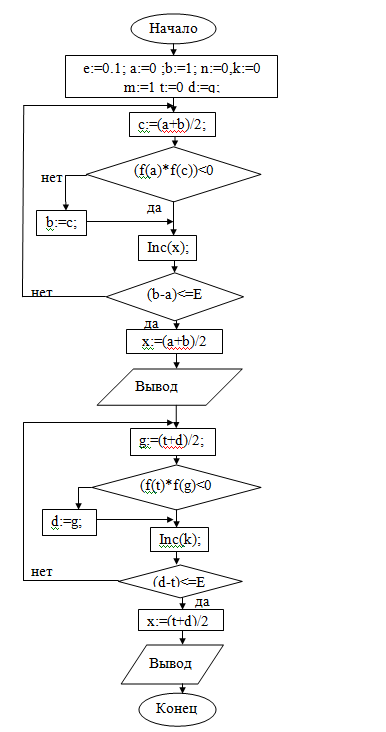
Блок-схема
3. Метод дихотомии
Освоение методов решения дифференциальных
уравнений, в ходе выполнения курсовой работы, позволяет проводить различные
вычислительные операции, которые упрощают вычисления.
Модифицированный метод Эйлера с пересчетом имеет
второй порядок точности, однако для его реализации необходимо дважды вычислять
правую часть функции. дифференциальный уравнение
эйлер полином
Интерполяционные полиномы в форме Ньютона удобно
использовать, если точка интерполирования находится вблизи начала (прямая
формула Ньютона) или конца таблицы (обратная формула Ньютона)
Дихотомическое деление привлекательно своей
простотой
Метод трапеций быстро сходится к точному
значению интеграла для периодических функций, поскольку погрешность за период
анулируется.