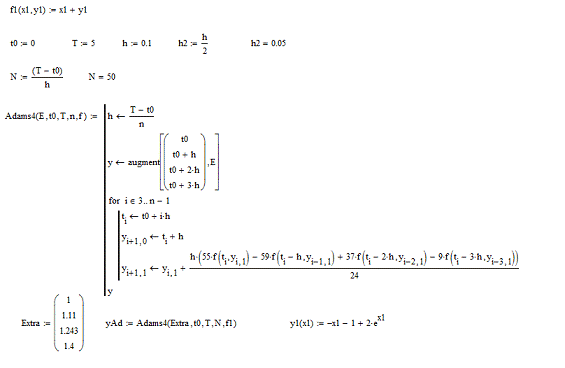Многошаговые методы решения дифференциальных уравнений
Содержание
Введение
. Теоретическая часть
.1 Постановка задачи Коши для обыкновенных дифференциальных
уравнений. Классификация методов решения
.2 Определение многошаговых методов
.3 Метод Адамса
.4 Методы прогноза и коррекции
.5 Проверка устойчивости решения
. Практическое задание
Заключение
Список литературы
Приложение 1
Приложение 2
Введение
Создание быстродействующих
электронных вычислительных машин привело к бурному развитию математики, а также
отдельных ее разделов, которые посвящены методам решения дискретных задач.
Большое значение приобрели разностные методы решения обыкновенных
дифференциальных уравнений.
Среди всевозможных методов решения
дифференциальных уравнений важную роль играют разностные методы решения задачи
Коши. Их существенным достоинством является простая алгоритмизация и реализация
на ЭВМ. Решение дифференциальных уравнений на ЭВМ играет большую и важную роль
при проведении исследований во многих областях знаний как теоретического, так и
прикладного характера.
Наибольшее распространение имеют
задачи Коши, в которых заданы начальные условия. На основе начальных условий
легко начинать процесс решения. Задачи другого типа - краевые задачи (например,
с конечными условиями или с условиями в промежуточной точке) - решаются
специальными приемами, в том числе нередко сведением к другим эквивалентным
задачам с начальными условиями.
Выделяют два класса методов решения:
одношаговые и многошаговые. Первый класс методов для нахождения следующего
значения функции требует значения только одной текущей точки, а второй -
нескольких. Поэтому методы второго класса не обладают свойством
"самостартования", т.е. ими нельзя начать решение задачи Коши, это
всегда делается одношаговыми методами.
Целью данной курсовой работы
является анализ многошаговых методов решения дифференциальных уравнений. Для
достижения поставленной цели необходимо дать определение многошаговых методов,
рассмотреть основы их построения, устойчивость и сходимость методов.
1. Теоретическая часть
.1 Постановка задачи Коши для обыкновенных
дифференциальных уравнений. Классификация методов решения
Рассмотрим обыкновенное
дифференциальное уравнение первого порядка
, 
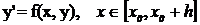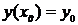(1)
где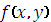 
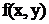- достаточно гладкая, в
общем случае, нелинейная функция двух переменных. Будем считать, что для данной
задачи (1.1), называемой задачей Коши или начальной задачей, выполняются
требования, обеспечивающие существование и единственность на отрезке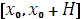 
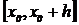её решения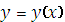 
.
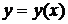Методы решения начальных
задач для ОДУ можно разделить на три группы: точные аналитические методы,
приближенные аналитические методы и численные методы.
К методам первой группы
относят такие, которые позволяют находить решения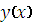 
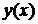в виде формулы, однако
круг их применимости достаточно узок.
В приближенных
аналитических методах строятся последовательности функций, сходящиеся к точному
решению задачи. Основная сложность при их реализации - вычисление большого
числа производных и интегралов, среди которых могут быть «неберущиеся»
интегралы.
Наиболее значимыми в
настоящее время являются численные методы решения дифференциальных уравнений,
предполагающие получение числовой таблицы приближенных значений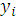 
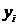искомого решения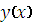 
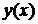на некоторой сетке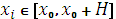 
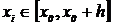значений аргумента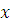 
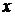. Решение получается в
виде массива чисел, являющих приближенным значение решения 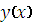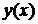на системе точек.
Численное решение задачи
(1.1) ищется в узлах сетки:
, 
.
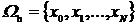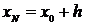Обозначим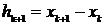 
,
,
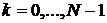расстояние между соседними узлами сетки. Если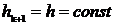 
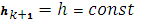, сетка называется
равномерной (регулярной); в противном случае - неравномерной (нерегулярной).
На выходе из численного
метода мы получаем последовательность значений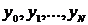 
, являющихся
приближениями к значениям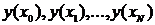 
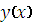
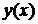точного решения в узлах сетки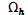 
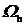. Набор чисел 
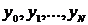называется каркасом
приближенного решения задачи Коши. Набор чисел называется проекцией точного решения
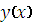
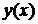задачи Коши на сетку .
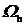Значение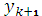
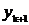, определяемое в узле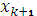 
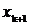, может вычисляться явно
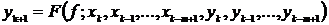
или неявно
.
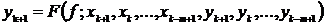Здесь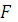 
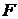- функция,
характеризующая тот или иной численный метод. В соответствии с нахождением 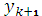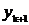методы делятся на явные
и неявные.
Также численные методы
делятся на одношаговые (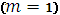
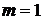) и многошаговые m -
шаговые. В одношаговых методах для получения точки 
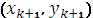
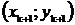требуется лишь
информация о последней рассчитанной точке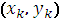 
. В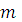 
m
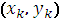
- шаговых методах для получения точки требуется информация о
предыдущих m рассчитанных точках.
.2 Определение
многошаговых методов
Рассмотрим численные
методы решения задачи Коши, которые могут быть заданы формулой:
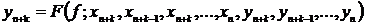(2)
Здесь значение решения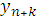 
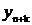в точке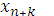 
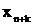определяется через
значения решения в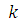
k точках, предшествующих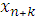 
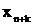. Такой метод называется
k-шаговым.
Из класса (2) выделим
многошаговые методы вида
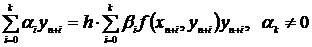, (3)
применяемые на сетке с постоянным
шагом:
, 
,
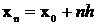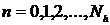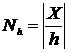, (4)
Разность между
наибольшим и наименьшим значениями индекса неизвестной функции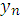 
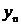, входящей в уравнение
(4), равна k. Поэтому соотношение (3) является разностным уравнением k-го
порядка, общее решение которого зависит от k параметров. Чтобы выделить
единственное решение этого уравнения, необходимо задать k дополнительных
условий на функцию 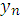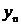. Этими дополнительными
условиями являются значения функции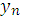 
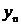при 
.
, 
,
… 
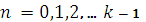
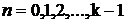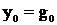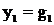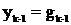, (5)
которые предполагаются известными,
их можно найти с помощью одношаговых методов.
Используя значения (4),
из уравнения (3) при n = 0 можно найти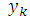 
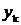, затем, используя
значения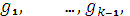 
, …, 
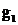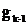и
полагая в (3) n = 1, найти. Таким образом, данный метод численного решения
дифференциального уравнения (2), (3) состоит в решении разностной задачи Коши
для разностного уравнения (3) и начальных условий (5).
Если искомое решение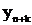 
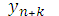входит в правую часть
этого уравнения, что бывает, когда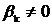 
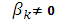, то формула (3)
определяет неявный метод. Если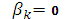
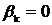, то искомое решение в
правую часть не входит и уравнение (3) может быть разрешено относительно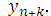
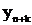. В этом случае формула
(5) определяет явный метод.
.3 Метод Адамса
Точность вычислений
одношаговых методов можно увеличить, если использовать при нахождении решения в
некотором узле xi информацию о значениях функции, полученных в нескольких (k)
предыдущих узлах сетки интегрирования (xi-1, xi-2 … xi-k).
Если используются
значения в k предыдущих узлах, то говорят о k-шаговом методе интегрирования
уравнения. Одним из способов построения многошаговых методов заключается в
следующем. По значениям функции, вычисленным в k предшествующих узлах, строится
интерполяционный полином степени (k-1) -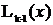 
, который используется
при интегрировании дифференциального уравнения:
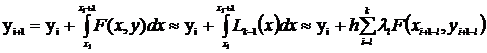(6)
где λl - квадратурные коэффициенты.
При k = 1 в качестве частного случая
получается формула Эйлера. Значения квадратурных коэффициентов для k от 2 до 4
приведены в таблице:
Таблица 1 - Значения квадратурных
коэффициентов
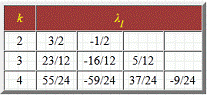
Полученное таким образом семейство
формул называется явной k-шаговой схемой Адамса (методы Адамса-Башфорта).
Например, четырехшаговая явная
формула Адамса может быть записана так:
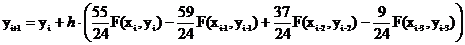(7)
Если для построения
интерполяционного полинома использовать k узлов, начиная с xi+1, то можно
получить формулы интегрирования ОДУ, известные как неявные схемы Адамса (или
методы Адамса-Моултона). Неявными эти формулы называются потому, что значение
искомой функции в (i+1)-м узле - yi+1 - оказывается одновременно и в левой и
правой частях равенства.
Квадратурные коэффициенты для
неявных методов Адамса приведены в таблице ниже.
многошаговый метод дифференциальный
уравнение
Таблица 2 - Значения квадратурных
коэффициентов для неявных методов Адамса
Например, четырехшаговая неявная
формула Адамса-Моултона имеет вид:
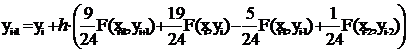(8)
Видно, что это выражение является
уравнением относительно yi+1, так как yi+1 встречается и в левой и правой его
части. Однако обычно это уравнение не решается, а значение в правой части
заменяется на рассчитанное по какой-либо явной формуле - например, формуле
Адамса-Башфорта. Такой подход лежит в основе методов
"прогноза-коррекции".
.4 Методы прогноза и коррекции
Несколько иной подход используется в
многошаговых методах прогноза и коррекции. В качестве иллюстрирующего примера
рассмотрим 2-х шаговый метод прогноза и коррекции.
Пусть дано ДУ для которого известно
значение функции в двух соседних узлах сетки:
, 
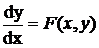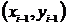и
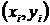(9)
Сначала строится прогноз значения в
(i+1)-ом узле интегрирования по какой-либо грубой формуле (при k=2 это метод
Эйлера) по предудущему узлу.
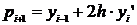, где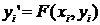 
Затем это значение корректируется по
более точной формуле, в данном случае - по формуле трапеций (неявная формула
Адамса второго порядка):
,
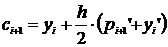где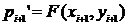 
.
В качестве решения в узле xi+1,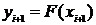 
берется
,
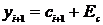где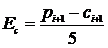 
- ошибка коррекции.
Для того чтобы начать расчет методом
прогноза и коррекции, необходимо знать значения функции в двух первых узлах
сетки - x0 и x1 -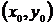 
и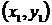 
. Обычно значение в узле x1 определяется каким-либо одношаговым
методом (методом Рунге-Кутты или Гюна).
На каждом шаге построения решения
методом прогноза и коррекции требуется вычислить всего одно значение функции, а
одно берется из предыдущего узла сетки. Поэтому он весьма экономичен по
затратам времени вычислений при достаточной точности.
Погрешность описываемого метода
пропорциональна h3 (d ~ h3).
Аналогичные схемы прогноза-коррекции
могут быть получены сочетанием явных (прогноз) и неявных (коррекция) формул
Адамса для различных k. Так, например, широко применяется четырехшаговый метод
прогноза-коррекции, в котором в качестве прогноза используется 4-х шаговая
формула Адамса-Башфорта, а для коррекции - 4-х шаговая формула Адамса-Моултона.
Погрешность такого метода пропорциональна ~ h5.
.5 Проверка устойчивости решения
Решение ОДУ в некоторой точке xi
называется устойчивым, если найденное в этой точке значение функции yi мало
изменяется при уменьшении шага интегрирования. Для проверки устойчивости, таким
образом, надо провести два расчета значения (yi) - с шагом интегрирования h и
при уменьшенной (например, двое) величине шага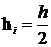 
.
В качестве критерия устойчивости
можно использовать малость относительного изменения полученного решения при
уменьшении шага интегрирования (ε - наперед заданная малая величина).
Такая проверка может осуществляться
и для всех решений на всем интервале значений x. Если условие не выполняется,
то шаг снова делится пополам и находится новое решение и т.д. до получения
устойчивого решения.
2. Практическое задание
Методом Адамса четвертого порядка
точности на отрезке [0;1] с шагом h = 0,1 решить задачу Коши для обыкновенного
дифференциального уравнения первого порядка y' = x+y, y(0)=1.
Решение:
. Найдем точное решение
дифференциального уравнения для проверки решения методом Адамса. Сделаем замену
переменной:
,
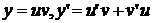тогда
(*).
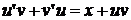
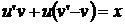Приравняем к нулю выражение в
скобках:
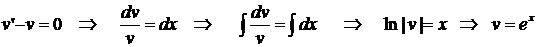
(постоянную интегрирования здесь
можно опустить).
Подставляем полученное решение в
уравнение (*):
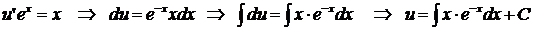
Для нахождения интеграла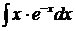 
применяем формулу интегрирования по частям:
.
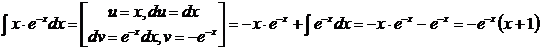В результате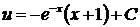 
и
.
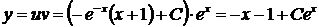Для определения постоянной
интегрирования используем начальное условие:
,
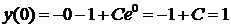откуда С = 2.
В результате частное решение
дифференциального уравнения можно записать в виде:
.
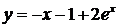. Для решения уравнения методом
Адамса 4-го порядка используем следующую интерполяционную формулу:
+1 = yi + h (55y'i - 59y'i-1 +
37y'i-2 - 9y'i-3)/24.
Так как экстраполяционный метод
Адамса 4-го порядка является многошаговым методом, то для формирования вектора
начальных значений искомой функции (это первые 4 значения), будем использовать
метод Рунге-Кутта. Для метода Рунге-Кутта интерполяционная формула имеет вид:
,
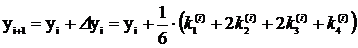где
,
,
,
.
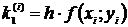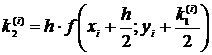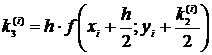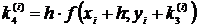Для автоматизации вычислений
используем математический пакет Mathcad 13.
Задаем начальные условия: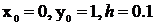 
, а далее по формулам вычисляем значения y. Листинг программы для
определения первых значений функции методом Рунге-Кутта приведен в приложении
1.
В результате получаем вектор
значений:
, 
.
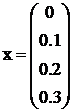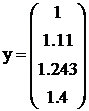После этого запрограммируем метод
Адамса в виде отдельной функции. Будем рассматривать промежуток от 0 до 1 (т.
е. 10 значений с шагом 0.1). Листинг программы для решения уравнения методом
Адамса приведен в приложении 2.
На рисунке 1 показан график решения
и точное решение уравнения на данном участке. Из графика видно, что результаты
численного решения соответствуют результату аналитического решения.
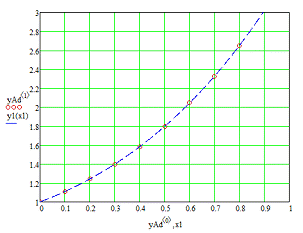
Рисунок 1 - Результаты решения
уравнения методом Адамса (символ «о») и аналитическое решение уравнения
(пунктирная линия)
Заключение
В данной курсовой работе были
рассмотрены многошаговы методы решения дифференциальных уравнений. Особое
внимание было уделено методу Адамса и методу прогноза и коррекций.
К недостаткам многошаговых методов
относится также и невозможность изменения в процессе решения величины шага (так
как они используют предыдущие точки с ранее применяемым шагом, а учет
меняющегося шага очень сложен и громоздок), это бывает необходимо для повышения
эффективности метода. Величина шага существенно влияет на точность и скорость решения,
поэтому изменение ее в процессе решения - увеличение при медленно изменяющемся
решении и уменьшение при быстро изменяющемся - очень важно для эффективности
решения. К достоинствам многошаговых методов относят в основном меньший объем
памяти компьютера, требующейся для реализации, и возможность теоретической
оценки погрешности решения.
В практической части курсовой работы
методом Адамса было решено дифференциальное уравнение с начальным условием
(задача Коши). Сравнение полученного решения с аналитическим решением
дифференциального уравнение подтвердило правильность полученного решения.
Список литературы
1. Арушанян О.Б., Залеткин С.Ф. «Численное решение
обыкновенных дифференциальных уравнений».
. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. “Численные
методы в задачах и упражнениях”. М.: Высшая школа, 2000.
. Вержбицкий В.М. «Численный методы (математический анализ
и обыкновенные дифференциальные уравнения)». Москва «Высшая школа», 2001.
. Заусаев А.Ф. Разностные методы решения обыкновенных
дифференциальных уравнений: Учеб. пособ. Самара: Самарский гос. техн. ун-т,
2010. 100 с.
. Самарский А.А., Гулин А.В. «Численные методы».М.: Наука,
1989.
Приложение 1
Листинг программы нахождения первых
четырех корней уравнения методом Рунге-Кутта
Приложение 2
Листинг программы решения
дифференциального уравнения методом Адамса 4-го порядка
