Основи математичної статистики
1. Задано вибiрку, яка
характеризує мiсячний прибуток пiдприємцiв (в тис. грн.)
· Скласти
варiацiйний ряд та статистичний розподiл вибiрки, побудувати полiгон частот.
· Скласти
iнтервальний статистичний розподiл вибiрки, розбивши промiжок (x min, x max) на
5 рiвних промiжкiв, та побудувати гiстограму частот.
· Обчислити
вибiрковi характеристики: вибiркове середне, вибiркову дисперсiю, вибiркове
середне квадратичне вiдхилення, моду та медiану, якщо вибiрка має такий вигляд:
,33,33,32,37,30,40,34,35,34,36,35,41,32,40,34,31,39,38,35
Розв'язок
Запишемо елементи
вибірки в порядку зростання, таким чином отримаємо варіаційний ряд:
37,33,33,32,37,30,40,34,35,34,36,35,41,32,40,34,31,39,38,35.
У вибірці маємо 12
різних значень, тобто варіант:
,31,32,33,34,35,36,37,38,39,40,41.
Знайдемо їх частоти:
.
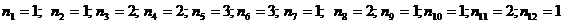Запишемо шуканий
статистичний розподіл вибірки:
|
хi
|
30
|
31
|
32
|
33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
41
|
|
ni
|
1
|
1
|
2
|
2
|
3
|
3
|
1
|
2
|
1
|
1
|
2
|
1
|
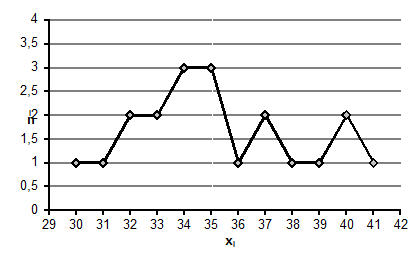
Для того щоб побудувати
полігон частот, відкладемо на осі абсцисс значення варіант xi,
а на осі ординат - значення відповідних їм частот ni і
послідовно з’єднаємо між собою точки xi, ni
відрізками.
Складемо
інтервальний статистичний розподіл вибірки. Для цього розіб’ємо інтервал [30; 41] на 5 рівних проміжків довжиною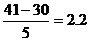 
.
|
Інтервал
|
[30; 32,2]
|
(32,2; 34,4)
|
(34,4; 36,6)
|
(36,6; 38,8)
|
(38,8; 41)
|
|
Частота
|
4
|
5
|
4
|
3
|
4
|
Для побудови гістограми
обчислимо щільності частоти:
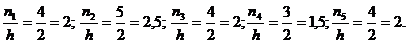
Побудуємо
гістограму частот.
Обчислимо вибіркові
середнє, дисперсію, середнє квадратичне відхилення та медіану.
Вибіркове середнє:
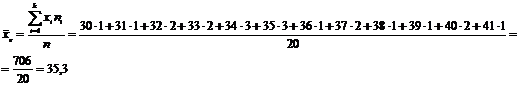
Середній квадрат
відхилення значень елементів вибірки від вибіркового середнього називається
вибірковою дисперсією. Вибіркова дисперсія дорівнює різниці середнього
квадрата елементів вибірки і квадрата вибіркового середнього:
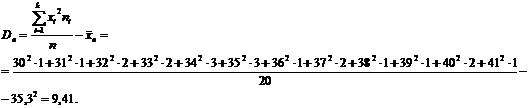
Середнє
квадратичне відхилення знаходимо як квадратний корінь з вибіркової дисперсії:
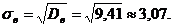
Медіаною Me
називається значення середнього елемента варіаційного ряду. Якщо обсяг вибірки n=
2m парний (як, в нашому випадку), то медіаною буде середнє значення
елементів варіаційного ряду з номерами m і m +1:
.
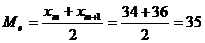Модою (Mo)
називається варіанта з найбільшою частотою:
.
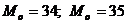статистичний
вибірка дисперсія інтервал
|
хi
|
3
|
5
|
7
|
9
|
11
|
13
|
15
|
17
|
19
|
|
ni
|
7
|
15
|
28
|
45
|
78
|
50
|
30
|
17
|
8
|
Розв'язок
Обсяг вибірки: n =
7+15+28+45+78+50+30+17+8=278.
Для побудови
довірчих інтервалів обчислимо вибіркове середнє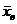 
і вибіркове середнє квадратичне відхилення 
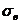за формулами:
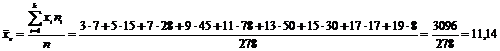
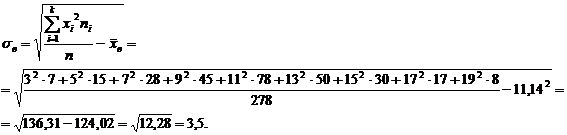
Оскільки середнє
квадратичне генеральної сукупності невідоме, то визначаємо довірчий інтервал
для математичного сподівання. Знайдемо виправлене вибіркове середнє квадратичне
відхилення:
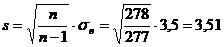
Довірчий інтервал
з надійністю γ
для математичного сподівання a нормально розподіленої генеральної сукупності
при відомому середньому квадратичному відхиленні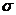 
має вигляд:
, де 
-
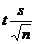точність оцінки.
Величину t
знайдемо за таблицею значень функції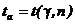 
. При значеннях γ =0,95 і n = 100 
=
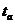1,98.
Розраховуємо довірчий
інтервал:
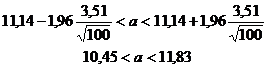
Отже, інтервал
(10,45; 11,83) покриває параметр a з надійністю γ
= 0,95.
Визначимо тепер
довірчий інтервал для середнього квадратичного відхилення σ генеральної сукупності.
Величина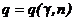 
є
табличним значенням. При γ =0,95 і n =100 
=0,14.
Оскільки <
1, то довірчий інтервал нормально розподіленої генеральної сукупності
визначається наступним чином:
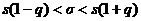
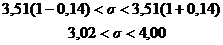
Отже, інтервал
(3,02; 4,00) покриває параметр σ
з надійністю γ = 0 95.
3.
За даними вибiрки, використовуючи критерiй Пiрсона при рiвнi значущостi α=0,05, перевiрити, чи
справджується статистична гiпотеза про нормальний розподiл генеральноi сукупностi
X:
|
хi
|
9
|
11
|
13
|
15
|
17
|
19
|
21
|
23
|
25
|
|
ni
|
5
|
9
|
11
|
14
|
18
|
15
|
12
|
10
|
6
|
Розв'язок
Визначимо обсяг вибірки:
n = 5+9+11+14+18+15+12+10+6=100.
Обчислимо вибіркове
середнє:
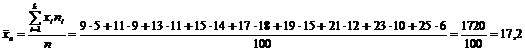
Визначимо
вибіркове середнє квадратичне відхилення:
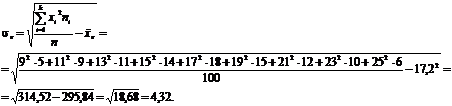
Визначимо
теоретичні частоти. З цією метою використаємо формулу:
,
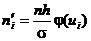де n -
обсяг вибірки; h - крок (різниця між двома сусідніми варіантами);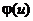 
-
диференціальна функція Лапласа:
.
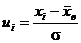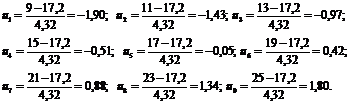
Враховуючи, що
різниця між двома сусідніми варіантами h = 2, а обсяг вибірки n =
100, визначимо теоретичні частоти. Для цього складемо розрахункову таблицю
(значення диференціальної функції Лапласа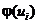 
представляють собою
табличні величини):
|
і
|
хі
|
nі
|
ui
|
|
|
|
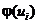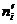
1
|
9
|
5
|
-1,90
|
0,0551
|
2,12
|
|
2
|
11
|
9
|
-1,43
|
0,1435
|
5,38
|
|
3
|
13
|
11
|
-0,97
|
0,2966
|
10,42
|
|
4
|
15
|
14
|
-0,51
|
0,3503
|
15,69
|
|
5
|
17
|
18
|
-0,05
|
0,3984
|
18,43
|
|
6
|
19
|
15
|
0,42
|
0,3653
|
16,76
|
|
7
|
21
|
12
|
0,88
|
0,2709
|
11,87
|
|
8
|
23
|
10
|
1,34
|
0,1626
|
6,55
|
|
9
|
25
|
6
|
1,80
|
0,0790
|
2,76
|
Знайдемо спостережуване
значення критерію Пірсона за формулою:
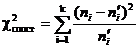
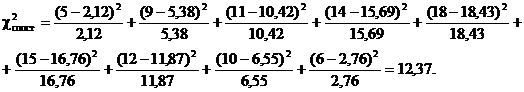
За таблицею
критичних точок розподілу χ2 при заданому рівні значущості α = 0 05, і кількості ступенів
вільності k =s - 3 = 9 - 3 = 6 (s - кількість варіант вибірки) знайдемо
критичну точку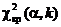
правосторонньої критичної області:
.
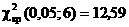Оскільки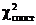 
<
,
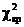то немає підстав відхиляти статистичну гіпотезу про нормальний розподіл
генеральної сукупності: емпіричні і теоретичні частоти різняться несуттєво
(випадково).