Статика. Кинематика. Динамика
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
"МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ ИМЕНИ
К.Г.
РАЗУМОВСКОГО"
(ФГБОУ
ВПО МГУТУ ИМЕНИ К.Г. РАЗУМОВСКОГО)
ИНСТИТУТ
ТЕКСТИЛЬНОЙ И ЛЕГКОЙ ПРОМЫШЛЕННОСТИ
Контрольная
работа
по
дисциплине "Теоретическая механика"
"Статика.
Кинематика. Динамика"
г.
Бобруйск 2012
ЗАДАЧА 1
Дано:
М=100 Нм , 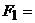 10 Н,
10 Н, 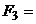 30
Н, l==0,5 м.,α1=45º,α3=60º.
30
Н, l==0,5 м.,α1=45º,α3=60º.
Найти:
Реакции связей в точках А и В, вызываемые заданными нагрузками.
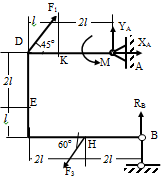
РЕШЕНИЕ:
Рассмотрим равновесие жесткой рамы. На раму
действуют силы: силы 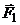 и
и 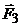 ,
пара сил с моментом М и реакции связей
,
пара сил с моментом М и реакции связей 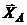 ,
,
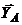 ,
,
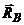 .
.
Неизвестны реакции связей 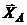 ,
,
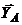 ,
,
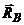 .
.
Для полученной плоской системы сил составим три
уравнения равновесия:
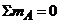 ,
,
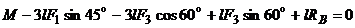 , отсюда
, отсюда
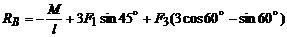 =
=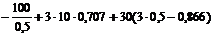 =
=
,8 (Н) - действительное направление реакции
противоположно показанному на рисунке;
уравнения проекций на оси координат
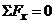 ,
, 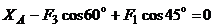 ,
отсюда
,
отсюда
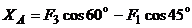 =
=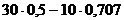 =
7,9 (Н);
=
7,9 (Н);
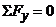 ,
, 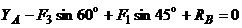 ,
отсюда
,
отсюда
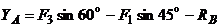 =
=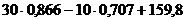 =
178,7 (Н).
=
178,7 (Н).
Ответ:XA=7,9
H,YA=178,7H.RB= ̶159,8H.
ЗАДАЧА 2
Дано:
уравнения движения точки в плоскости ху: 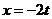 ,
,
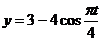 ;
;
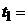 1
с.(х и у в сантиметрах,t-
в секундах)
1
с.(х и у в сантиметрах,t-
в секундах)
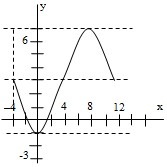
Найти:
уравнение траектории точки; скорость и ускорение, касательное и нормальное
ускорение и радиус кривизны траектории в момент 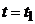 .
.
РЕШЕНИЕ:
. Уравнение траектории. Для определения
уравнения траектории точки исключим время 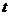 из заданных
уравнений движения.
из заданных
уравнений движения.
Тогда 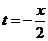 ,
,
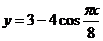 -
уравнение косинусоиды.
-
уравнение косинусоиды.
. Скорость точки. Скорость найдем по ее
проекциям на координатные оси: 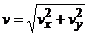 , где:
, где:
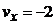 (см/с),
(см/с), 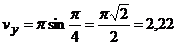 (см/с),
(см/с),
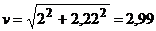 (см/с).
(см/с).
3. Ускорение точки. Находим аналогично: 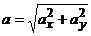 ,
,
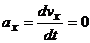 ,
,
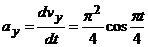 и
при
и
при 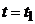 =1
с
=1
с 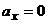 (см/с2),
(см/с2),
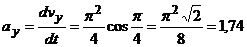 (см/с2),
(см/с2),
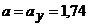 (см/с2).
(см/с2).
. Касательное ускорение. Найдем, дифференцируя
равенство 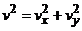 . Получим
. Получим 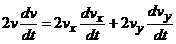 ,
откуда
,
откуда 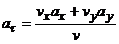 и
при
и
при 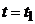 =1
с
=1
с 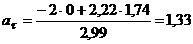 (см/с2).
(см/с2).
. Нормальное ускорение. 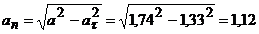 (см/с2).
(см/с2).
. Радиус кривизны траектории. 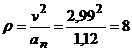 (см).
(см).
Ответ: ν=2,99
см/с ,а=1,74 см/с2,аτ=1,33
см/с2,аn=1,12
см/с2,ρ=8 см.
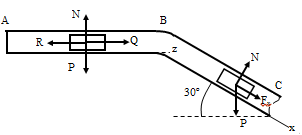
ЗАДАЧА 3
Дано:
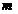 =1,6
кг,
=1,6
кг, 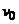 =18
м/с, Q=4 Н, R=0,4v Н,
=18
м/с, Q=4 Н, R=0,4v Н, 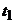 =2 с,
=2 с, 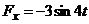 Н.
Трением груза о трубу пренебречь .
Н.
Трением груза о трубу пренебречь .
Найти:
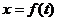 -
закон движения груза на участке ВС
-
закон движения груза на участке ВС
РЕШЕНИЕ:
1) Рассмотрим движение груза на участке АВ,
считая груз материальной точкой. На груз действуют сила тяжести 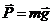 ,
реакция стенки
,
реакция стенки 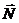 постоянная сила
постоянная сила 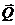 и
сила сопротивления
и
сила сопротивления 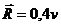 . Проведем ось
. Проведем ось 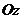 вдоль
АВ. Составим дифференциальное уравнение движение в проекции на эту ось:
вдоль
АВ. Составим дифференциальное уравнение движение в проекции на эту ось: 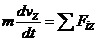 или
или
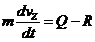 .
.
Перепишем это уравнение с учетом того, что 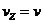 :
:
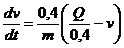 .
Обозначим
.
Обозначим 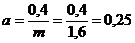 и
и 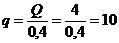 .
Тогда
.
Тогда 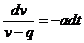 ,
интегрируем:
,
интегрируем: 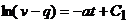 .
.
Постоянную С1 находим по начальным
условиям: при 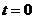
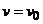 ,
что дает
,
что дает 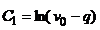 .
Следовательно
.
Следовательно 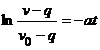 . Отсюда получаем
. Отсюда получаем
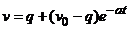 .
.
При перемещении груза в точку В 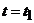 =2
с,
=2
с, 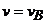 .
Тогда
.
Тогда
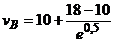 =14,85 (м/с).
=14,85 (м/с).
2). При рассмотрении движения груза на участке
ВС найденная скорость будет для движения на этом участке начальной скоростью.
Составим дифференциальные уравнения движения груза в проекции на оси 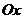 и
и
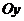 .
.
равновесие траектория ускорение
дифференциальный
Обозначим 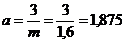 и
и
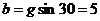 .
Разделяя переменные и интегрируя получим
.
Разделяя переменные и интегрируя получим 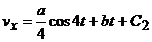 ;
при начальных условиях при
;
при начальных условиях при 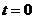
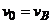 и
и
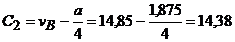 .
То есть
.
То есть 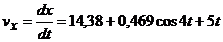 .
.
После интегрирования: 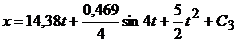 .
Т.к. при
.
Т.к. при 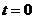
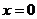 то
то
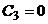 и
окончательно искомый закон движения груза на участке ВС будет:
и
окончательно искомый закон движения груза на участке ВС будет:
X=14,
38t+2, 5t2+0,117sin4t
Ответ: x=14,38t+2,5t2+0,117sin4t
, где х - в метрах, t- в
секундах.
Список литературы
Старжинский В.М.Теоретическая
механика М.Наука 1988г.
Тарг С.М. Краткий курс теоретической
механики. М.1963г. и последующие издания.
Мещерский И.В. Сборник задач по
теоретической механике. М. 1970г. И последующие издания.
Гернет М.М. Курс теоретической
механики. М. 1970г. И последующие издания.