Методы решения математических задач в Maple
Содержание
Введение
. Maple
его свойства и его возможности
.1 Новые возможности
.2 Дополнительные возможности Maple
.2.1 Графика а Maple
.2.2 Специализированные приложения
.2.3 Финансовые вычисления в Maple
.2.4 Программирование
.2.5 Справочная система
.2.6 Интернет-совместимость
.2.7 Свободные ресурсы
.2.8 Выполнение вычислений
.2.9 Возможности управления
математическим содержанием
.2.10 Создание технических
документов
.2.11 Разработка пользовательских
приложений
. Применение аналитических,
численных, графических возможностей системы Maple
для моделирования физических явлений
. Использование графики и анимации в
системе Maple в
педагогическом процессе
Заключение
Список использованных источников
Введение
В последний полтора десятка лет возникло и получило
бурное развитие новое фундаментальное научное направление - компьютерная
математика, которое зародилось на стыке математики и информатики. Первыми
серьезными средствами для автоматизированного выполнения массовых
научно-технических расчетов стали программируемые микрокалькуляторы. С
появлением персональных компьютеров их стали широко применять для численных
расчетов, программируемых на языках высокого уровня, например Фортране, Си,
Бейсике или Форте. Однако все большее распространение получают аналитические
(символьные) вычисления, обладающие гораздо большей общностью, чем численные
вычисления.
Предвестником появления систем компьютерной
математики стали специализированные программы для математических численных
расчетов, работающие в среде Microsoft
MS-DOS.
Это Eureka, Mercury,
Mathcad [MATLAB
110] под операционную систему MS-DOS.
Казалось бы это было совсем недавно - в начале 90-х годов ушедшего столетия.
Вслед за этим, на основе достижений компьютерной математики, были разработаны
новейшие программные системы символьной математики или компьютерной алгебры
(СКА). Среди них наибольшую известность получили системы Mathcad
под Windows,
Derive, Mathematica
и Maple и др.
Хотя множество (и даже большинство)
математических задач решается с помощью СКМ без программирования, это не
означает отказ от программирования вообще. Напротив, все СКМ, в частности Maple
9.5/10, имеют довольно развитый язык программирования, содержащий типовые
средства процедурного программирования, например управляющие структуры, циклы,
операторы ввода/вы- вода и т. д.
В последнее время такие языки включают в себя
средства визуально-ориентированного программировании пользовательского
интерфейса - в Maple
9.5/10 эти средства названы маплетами (maplets).
Есть одно весьма важное обстоятельство в современной реализации этих средств -
многие маплеты обеспечивают пошаговое решение математических задач с
демонстрацией промежуточных результатов вычислений. Это именно то, что давно
требовалось от СКМ в образовании и чего они не давали. Теперь подобное решение
задач стало возможным и существенно повышает значение систем Maple
9.5/10 в образовании.
СКМ широко используются для научных расчетов, в
том числе в Интернете и в мобильных вычислениях. Но особенно велика роль систем
компьютерной математики в образовании - они становятся не только удобным
инструментальным средством для выполнения огромного числа учебных расчетов, но
и средством предоставления учащимся, а нередко и педагогам, знаний в области
математики, физики и в иных науках, использующих математические методы. Трудно
переоценить и их роль в подготовке высококачественных электронных уроков,
учебных курсов и книг.
Системы класса Maple
были созданы группой ученых, занимающихся символьными вычислениями (The
Symbolic
Group), организованной
Кейтом Геддом (Keith
Geddes) и Гастоном Гонэ (Gaston
Gonnet) в 1980 году в
университете Waterloo,
Канада. Вначале система Maple
была реализована на больших компьютерах и прошла долгий путь апробации, вобрав
в свое ядро и библиотеки большую часть математических функций и правил их
преобразований, выработанных математикой за столетия развития. Есть реализации
программы на платформах ПК Macintosh,
Unix, Sun
и др.
Системам класса Maple во всем
мире посвящены многие сотни книг. Достаточно полный список книг по системам Maple можно найти
на недавно обновленном сайте разработчика этой системы - компании Waterloo Maple Software (www.maplesoft.com
<#"864628.files/image001.gif">
exp(x)
|
|
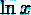
|
ln(x)
|
|
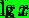
|
lg(x)
|
|

|
log[a](x)
|
|
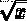
|
sqrt(x)
|
|
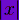
|
abs(x)
|
|
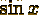
|
sin(x)
|
|

|
cos(x)
|
|

|
tan(x)
|
|
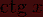
|
cot(x)
|
|
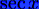
|
sec(x)
|
|

|
csc(x)
|
|
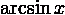
|
arcsin(x)
|
|
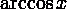
|
arccos(x)
|
|

|
arctan(x)
|
|
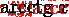
|
arccot(x)
|
|
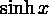
|
sinh(x)
|
|
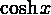
|
cosh(x)
|
|
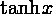
|
tanh(x)
|
|
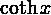
|
coth(x)
|
|
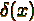 - функция
Дирака - функция
Дирака
|
Dirac(x)
|
|
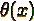 - функция
Хевисайда - функция
Хевисайда
|
Рисунок 1 Стандартные математические функции
Maple - типичная
интегрированная система, которая объединяет в себе:
) мощный язык программирования (он же язык для
интерактивного общения с системой);
) редактор для подготовки и редактирования
документов и программ;
) современный многооконный пользовательский
интерфейс с возможностью работы в диалоговом режиме;
) мощную справочную систему со многими тысячами
примеров;
) ядро алгоритмов и правил преобразования
математических выражений;
) численный и символьный процессоры;
) систему диагностики;
) библиотеки встроенных и дополнительных
функций;
) пакеты функций сторонних производителей и
поддержку некоторых других языков программирования и программ [2].

Рисунок 2
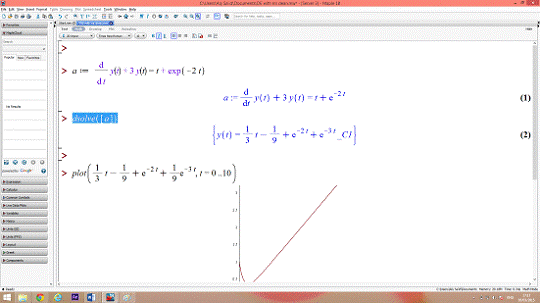
Рисунок 3
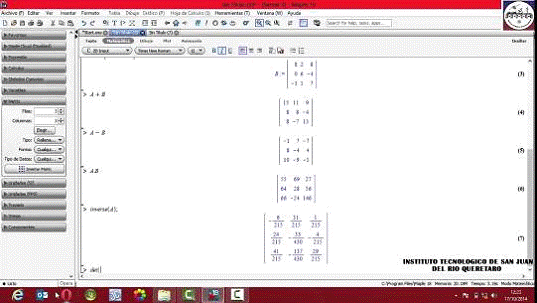
Рисунок 4
1.1 Новые возможности системы Maple
Система Maple приобрела ряд новых возможностей.
Кратко отметим их:
1) расширенная поддержка численных
алгоритмов пакета программ NAG, в том числе при решении численных задач
математического анализа и при решении дифференциальных уравнений;
2) новый обучающий курс User's Tour,
встроенный в ее справку;
3) существенно переработанные и обновленные
пакеты функций;
4) ускоренные алгоритмы целочисленных
вычислений (например, факториал числа 25000 вычисляется более чем на порядок
быстрее, чем системой Maple предыдущей версии);
5) обширный набор новых алгоритмов решения
дифференциальных уравнений, обеспечивающий дополнительную эффективность решения
задач в области моделирования физических явлений и устройств;
6) выполненное впервые 100% успешное
испытание при решении специальных тестовых задач, что является высшим
достижением на рынке средств компьютерной математики;
7) усовершенствованные и новые алгоритмы
реализации многих численных методов решения задач;
) новые встроенные пакеты
аппроксимации кривых CurveFitting,
внешних вычислений ExternalCalling,
решения линейных функциональных систем LinearFunctionalSystem,
ортогональных рядов OrthogonalSeries,
работы с полиномами PolynomialTools,
решения уравнений SolveTools
и поддержки вычислений с размерными величинами Units;
9) новый пакет для поддержки языка XML;
10) поддержка новейшего стандарта записи
математической информации - языка MathML 2.0;
11) улучшение пользовательского интерфейса, в
частности введение новой палитры ввода шаблонов векторов;
12) поддержка протокола TCP/IP,
обеспечивающего динамический удаленный доступ к данным, например, для
финансового анализа в реальном масштабе времени или данных о погоде;
13) дополнительные пакеты (Maple
PowerTools™), доступные через Интернет, поддерживающие анализ методом конечных
элементов (РЕМ), нелинейную оптимизацию и статистику, а также три новых пакета:
вычисления для новичков, теоретическая физика и программирование;
14) возможность работы с курсом
университетского математического образования, загружаемого через Интернет.
В сочетании с сохраненными возможностями
предшествующей версии системы это дает новой версии Maple обширные возможности
в эффективном решении широкого класса математических и научно-технических
задач, а также задач в области образования.
Возможности Марle:
1) вычисление сумм последовательностей;
2) вычисление произведений членов
последовательностей;
3) вычисление производных;
) вычисление интегралов;
) разложение функций в ряд;
) решение уравнений и неравенств;
) нахождение сингулярных точек функций;
) вычисление асимптотических разложений;
9) операции с полиномами;
10) аналитические операции;
11) решение
СЛАУ;
) решение дифференциальных уравнений;
) численное решение дифференциальных
уравнений;
) возможности трехмерной и двумерной
графики;
) математические пакеты.
Необходимости работы с десятичными эквивалентами
в системе Maple имеется команда, аппроксимирующая значение выражения в формате
чисел с плавающей запятой. Система Maple вычисляет конечные и бесконечные суммы
и произведения, выполняет вычислительные операции с комплексными числами, легко
приводит комплексное число к числу в полярных координатах, числовые значения
элементарных функций, а также многих специальных функций и констант.
Система Maple предлагает различные способы
представления и преобразования выражений, например, такие операции, как
упрощение и разложение на множители алгебраических выражений и приведение их к
различному виду. Систему Maple можно использовать для решения уравнений и
систем алгебраических уравнений.имеет также множество мощных инструментальных
средств для вычисления выражений с одной и несколькими переменными. Систему
Maple можно использовать для решения задач дифференциального и интегрального
исчисления, вычисления пределов, разложений в ряды, суммирования рядов,
умножения, интегральных преобразований (таких как преобразование Лапласа,
Z-преобразование, преобразование Меллина или Фурье), непрерывных или
кусочно-непрерывных функций.
Система Maple поддерживает сотни специальных
функций и чисел, встречающихся во многих областях математики, науки и техники.
Вот некоторые из них:
функция ошибок;
Эйлерова константа;
Экспоненциальный интеграл ;
Эллиптическая интегральная функция ;
Гамма-функция ;
Зета-функция ;
Ступенчатая функция Хевисайда ;
Дельта-функция Дирака ;
Бесселева и модифицированная бесселева функции.
Maple может вычислять пределы функций, как
конечные, так и стремящиеся к бесконечности, а также распознает неопределенные
пределы.
В системе Maple можно решать множество обычных
дифференциальных уравнений (ODE), а также дифференциальные уравнения в частных
производных (PDE), в том числе задачи с начальными условиями (IVP), и задачи с
граничными условиями (BVP).
Одним из наиболее часто используемых в системе
Maple пакетов программ является пакет линейной алгебры, содержащий мощный набор
команд для работы с векторами и матрицами. Maple может находить собственные
значения и собственные векторы, вычислять криволинейные координаты, находить матричные
нормы и вычислять множество различных типов разложения матриц.
Для технических применений в Maple включены
справочники физических констант и единицы физических величин с автоматическим
пересчетом формул[3].

Рисунок 5
.2
Дополнительные возможности Maple
.2.1 Графика в Maple
Графические средства Maple позволяют строить
двухмерные графики сразу нескольких функций, создавать конформные графики
функций с комплексными числами и строить графики функций в логарифмической,
двойной логарифмической, параметрической, фазовой, полярной и контурной форме.
Можно графически представлять неравенства, неявно заданные функции, решения
дифференциальных уравнений и корневые годографы. Также имеются все возможности
для выбора шрифтов для названий, надписей и другой текстовой информации на
графиках.может строить поверхности и кривые в трехмерном представлении, включая
поверхности, заданные явной и параметрической функциями, а также решениями
дифференциальных уравнений. Имеется возможность изменения качества вывода
графика на экран путем изменения таких параметров, как шрифты, яркость и
цвет.поддерживает двух- и трехмерные анимации. Эту особенность системы можно
использовать для отображения процессов, протекающих в режиме реального времени.
1.2.2 Специализированные
приложения
В Maple включены пакеты подпрограмм для решения
задач линейной и тензорной алгебры, Евклидовой и аналитической геометрии,
теории чисел, теории вероятностей и математической статистики, комбинаторики,
теории групп, интегральных преобразований, численной аппроксимации и линейной
оптимизации (симплекс метод) а также задач финансовой математики и многих,
многих других задач.
.2.3
Финансовые вычисления в Maple
Для финансовых расчетов предназначен программный
пакет finance. C его помощью можно вычислять текущую и накопленную сумму
ежегодной ренты, совокупную ежегодную ренту, сумму пожизненной ренты,
совокупную пожизненную ренту, и процентный доход на неименные облигации. Более
того, этот пакет также поможет в расчете дохода, получаемого до срока погашения
облигации. Вы можете строить таблицу амортизации, определять реальную сумму
ставки для сложных процентов и вычислять текущее и будущее фиксированное
количество для конкретной ставки сложных процентов.
.2.4 Программирование
Система Maple использует исключительно
процедурный язык 4-го поколения (4GL). Этот язык специально предназначен для
быстрой разработки математических подпрограмм и пользовательских приложений.
Синтаксис этого языка аналогичен синтаксису
языков Си, FORTRAN, BASIC и Pascal.может генерировать код, совместимый с такими
языками программирования, как FORTRAN и Cи, и с языком набора текста LaTeX.
Одним из преимуществ этого свойства является способность обеспечивать доступ к
специализированным числовым решающим программам, максимально ускоряющим решение
сложных задач. Например, с помощью системы Maple можно разработать определенную
математическую модель, и затем с помощью той же системы Maple сгенерировать
соответствующий модели Си-код.
.2.5 Справочная система
Информацию о командах и основных принципах
работы системы Maple вы можете получить различными способами. Вот лишь самые
основные из них:
контекстно-зависимая
помощь
браузер помощи -
очень удобный инструмент, позволяющий по темам и ключевым словам найти нужную
информацию.
тематический поиск
полнотекстовой поиск
история - для возвращения к странице справке, просматривавшейся
уже в текущем сеансе.
.2.6 Интернет-совместимостьявляется первым
универсальным математическим пакетом, который предлагает полную поддержку
стандарта MathML 2.0, который управляет как внешним видом, так и смыслом
математики в Интернет. Эта эксклюзивная функция делает текущую версию MathML
основным средством Интернет математики, а также устанавливает новый уровень
совместимости многопользовательской среды. TCP/IP протокол обеспечивает
динамический доступ к информации из других Интернет-сайтов, например к данным
для финансового анализа в реальном времени и данным о погоде.
.2.7 Свободные ресурсы
Обширный набор мощных инструментальных
приложений (Maple PowerTools™) и п акетов для таких областей, как анализ
методом конечных элементов (FEM), нелинейная оптимизация и нелинейной
оптимизации, университетское математическое образование.
.2.8 Выполнение вычислений
интуитивно ясный редактор уравнений, позволяющий
быстро решать сложные задачи;
расширенные возможности управления размерностью
и единицами измерения;
вычисление допустимых пределов для технических
задач;
неограниченная степень точности численных
вычислений;
высокоэффективные численные решатели, основанные
на общепринятых алгоритмах;
обновленный интерфейс графического калькулятора,
удобный для быстрого выполнения вычислений;
более 200 встроенных шаблонов для решения
основных математических задач;
более 3500 математических функций;
.2.9 Возможности управления математическим
содержанием
интерактивное представление результатов в виде
двухмерных и трёхмерных изображений и анимация;
возможность управления параметрами для проверки
гипотез;
автоматический вывод выражений и составление
моделей;
интеграция символьных и численных операций;
интерактивные помощники, ускоряющие процесс
исследования дифференциальных уравнений, оптимизации и т. д.;
интерактивный словарь содержит более 5000
терминов;
.2.10 Создание технических документов
вы можете создавать технические документы
профессионального вида, содержащие текст, интерактивные математические
вычисления, графики, рисунки и звук
вы также можете добавлять кнопки, бегунки и
другие компоненты в ваши документы
при просмотре презентаций можно скрывать
командное меню
вы можете воспользоваться расширенными
возможностями текстового редактора, включая инструменты верстки и проверку
орфографии
вы можете публиковать документы в Интернет и
развёртывать интерактивные вычисления на сайте, используя сервер MapleNet.
.2.11
Разработка пользовательских приложений
язык, специально оптимизированный для разработки
математических приложений, позволяет сократить процесс разработки на несколько
дней
вы можете настроить пользовательский интерфейс с
помощью элементов Maplets или документов Maple со встроенными графическими
компонентами
высокопроизводительные вычислений с плавающей
запятой, максимально использующие аппаратные возможности, и компиляция
пользовательских функций
отличное взаимодействие с MapleNet, другими
приложениями и веб-сайтами
автоматическая генерация кода на языках C,
Fortran, Java, MATLAB, и Visual Basic [5].- одна из самых мощных и «разумных»
интегрированных систем символьной математики, созданная фирмой Waterloo Maple,
Inc (Канада).

Рисунок 6
.
Применение аналитических, и численных и графических возможностей системы maple для
моделирования физичечских явлений
Моделирование - исследование
<https://ru.wikipedia.org/wiki/%D0%98%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5>
объектов познания
<https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%8A%D0%B5%D0%BA%D1%82_(%D1%84%D0%B8%D0%BB%D0%BE%D1%81%D0%BE%D1%84%D0%B8%D1%8F)>
на их моделях
<https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C>;
построение и изучение моделей реально существующих объектов, процессов
<https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81>
или явлений
<https://ru.wikipedia.org/wiki/%D0%AF%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_(%D1%84%D0%B8%D0%BB%D0%BE%D1%81%D0%BE%D1%84%D0%B8%D1%8F)>
с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих
исследователя.
Натурные модели. Отличительной
чертой этих моделей является их подобие реальным системам (они материальны), а
отличие состоит в размерах, числе и материале элементов и т. п. По
принадлежности к предметной области модели подразделяют на следующие:
Физические модели. Ими являются
реальные изделия, образцы, экспериментальные и натурные модели, когда между
параметрами системы и модели одинаковой физической природы существует
однозначное соответствие. Выбор размеров таких моделей ведётся с соблюдением
теории подобия. Физические модели подразделяются на объёмные (модели и макеты)
и плоские (тремплеты):
1) в данном случае под (физической) моделью
понимают изделие или устройство, являющееся упрощённым подобием исследуемого
объекта или позволяющее воссоздать исследуемый процесс или явление. Например,
предметные модели, как уменьшенные копии оригинала (глобус как модель Земли,
игрушечный самолёт с учётом его аэродинамики);
) под тремплетом понимают изделие,
являющееся плоским масштабным отображением объекта в виде упрощённой
ортогональной проекции или его контурным очертанием. Тремплетеотанарные
вырезают из плёнки, картона и т. п., и применяют при исследовании и
проектировании зданий, установок, сооружений;
) под макетом понимают изделие, собранное
из моделей и/или тремплетов.
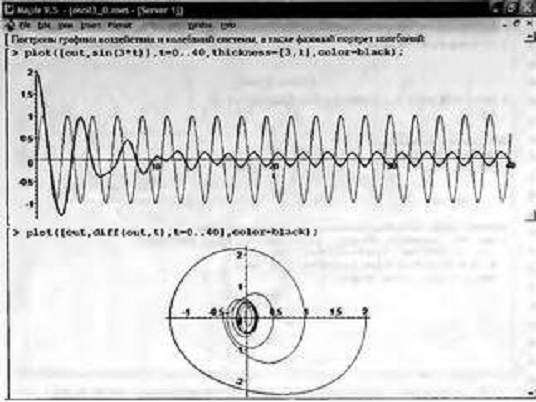
Рисунок 7
Физическое моделирование - основа наших знаний и
средство проверки наших гипотез и результатов расчётов. Физическая модель
позволяет охватить явление или процесс во всём их многообразии, наиболее
адекватна и точна, но достаточно дорога, трудоёмка и менее универсальна. В том
или ином виде с физическими моделями работают на всех этапах проектирования;
Технические модели;
Социальные модели;
Экономические модели, например, Бизнес-модель;
и т.д. [6].
Уникальные графические возможности системы
компьютерной математики (СКМ) Maple, в частности, возможности создания
трехмерных анимационных моделей, хорошо проработанные программные процедуры
численного интегрирования систем обыкновенных дифференциальных уравнений (ОДУ),
сплайновой и B - сплайновой интерполяции функций позволяют рассматривать СКМ
Maple в качестве мощного современного инструмента математического моделирования
объектов механики и родственных им. В настоящее время методы математического
моделирования в СКМ начали эффективно применяться в исследованиях
математических моделей как фундаментальных физических явлений, так и прикладных
задач. Важным преимуществом СКМ Maple является и возможность интеграции этой
системы с СКМ MatLab, которая хорошо приспособлена к моделированию электронных
систем и технологических процессов[4].
.
Использование графики и анимации в системе Maple в педагогическом процессе
Пожалуй, одно из наиболее впечатляющих свойств
программы Maple - превосходная графика. Команды построения графиков и анимации
Maple позволяют удовлетворить большинство научных и инженерных потребностей,
могут служить прекрасной иллюстрацией в учебном процессе.
Программа имеет большое количество функций и
опций настроек для построения как двух- так и трехмерных графических объектов.
Помимо команд plot и plot3d основной библиотеки имеется несколько
специализированных пакетов для этих целей:
) это прежде всего пакет plots ,
содержащий около пятидесяти команд для построения различного рода графиков и
анимации ;
) вспомогательный пакет plottools ,
позволяющий создавать различные (около тридцати) двух и трехмерные графические
примитивы, которые могут быть применены в других графиках;
) пакет stats[statplot] содержащий
команды для построения специализированных статистических графиков; пакет
DEtools , содержащий команды построения графиков решения дифференциальных
уравнений как обыкновенных так и в частных производных, фазовых портретов,
полей направлений; и, наконец, геометрический пакет geometry, содержащий
команду draw, позволяющую отобразить различные геометрические построения на
плоскости.
Версия 4 программы Maple поддерживает 45 систем
координат (в предыдущей версии поддерживало всего 4), появились также команды
changecoords и addcoords, позволяющие пользователю переходить от одной системы
координат к другой, а также вводить свои системы координат.
Математика и информатика являются частью
общечеловеческой культуры, развивают логическое, познавательное мышление в
процессе создания математических моделей при решении различных задач.
Математические знания необходимы для понимания
вероятностного подхода к измерению информации, формирования математических
представлений о вычислительных процессах современных компьютерных технологий,
использования электронных коммуникаций в сфере образования и культуры.
При изучении математики решение достаточно
сложных задач, выполнение трудоемких вычислений снижает интерес к предмету со
стороны студентов. Поэтому возникает необходимость использования различных
математических систем, позволяющих выполнять математические расчеты с числами,
формулами, графиками.
В настоящее время разработаны различные
компьютерные математические системы, с помощью которых можно решать достаточно
сложные задачи.
Наиболее удачной системой является математическая
система MAPLE, которая
может работать на компьютерах с оперативной памятью 4 Мб и требует меньше
дискового пространства. Кроме того, она имеет наиболее дружественный интерфейс,
т. е. более простой и понятный синтаксис команд. MAPLE
выпускается под разные типы компьютеров и различные операционные системы или
оболочки.
В учебном плане педагогических колледжей для
студентов художественно-графического отделения вводится предмет «Математика и
информатика».
Применение программы позволяет сэкономить время
при выполнении большого количества математических расчетов, которые отнимают
очень много времени. Проведение интегрированных уроков активизирует творческий
потенциал студентов, повышает интерес к изучению предметов [8].
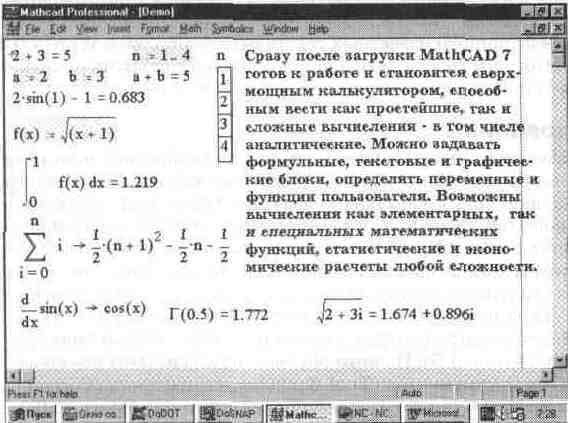
Рисунок 8
Заключение
Результаты исследования программы Maple
дают возможность создавать численно - аналитические компьютерные модели
нелинейных обобщенно - механических систем и проводить их глубокое исследование
системе компьютерной математики Maple (версии 8 - 18). При этом исследователи
получают развитый инструментарий создания оснащенных графических динамических
компьютерных моделей, позволяющий управлять их параметрами. Применение методов
сплайновой интерполяции функций позволяет значительно сократить время
промежуточных численных вычислений на компьютере при сохранении точности
передаваемых свойств математической модели. Развитые методы компьютерного
моделирования позволяют применять разработанный программный комплекс, в
частности, для разработки учебных тренажеров для изучения конкретных разделов
физики и технической физики.
математический
задача программный maple
Список используемых источников
Кафедра автоматизации научных
исследований факультета ВМК МГУ имени М. В. Ломоносова http://ani.cs.msu.su
https://ru.wikipedia.org/wiki/Maple
В. П. Дьяконов Д93 Maple
9.5/10 в математике, физике и образовании - М.: СОЛОН-Пресс, 2006. - 720 с.:
ил. - (Серия «Библиотека профессионала»).
Научная электронная библиотека
«Веда», 2003-2013.
Компания softline,
1993.
https://ru.wikipedia.org/wiki/Модель
Вестник, 2009.
ГОСУДАРСТВЕННЫЙ РУБРИКАТОР
НАУЧНО-ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ:14- - Народное образование. Педагогика