Математические модели и методы их расчета

Математические модели и методы их расчета

ВВЕДЕНИЕ

Научно-техническая революция привела к возникновению таких понятий, как большие и сложные экономические системы, обладающие специфическими для них проблемами. Необходимость решения таких проблем привела к появлению особых подходов и методов, которые постепенно накапливались и обобщались. В начале 80-х годов системность стала не только теоретической категорией, но и осознанным аспектом практической деятельности. Широко распространилось понятие того, что наши успехи связаны с тем, насколько системно мы подходим к решению возникающих проблем, а наши неудачи вызваны отсутствием системности в наших действиях. Сигналом о недостаточной системности в нашем подходе к решению какой-либо задачи является появление проблемы, разрешение же возникшей проблемы происходит, как правило, при переходе на новый, более высокий, уровень системности нашей деятельности. В различных сферах человеческой деятельности возникли различные подходы и соответствующие методы решения специфических проблем, которые получили различные названия: в военных и экономических вопросах -«исследование операций», в политическом и административном управлении -«системный подход», в философии«диалектический материализм», в прикладных научных исследованиях -«кибернетика». Позже стало ясно, что все эти теоретические и прикладные дисциплины образуют как бы единый поток, «системное движение», которое постепенно оформилось в науку, получившую название «системный анализ». В настоящее время системный анализ является самостоятельной дисциплиной, имеющей свой объект деятельности, свой достаточно мощный арсенал средств и свою прикладную область. Являясь по существу прикладной диалектикой, системный анализ использует все средства современных научных исследований - математику, моделирование, вычислительную технику и натурные эксперименты. Самая интересная и сложная часть системного анализа- это «вытаскивание» проблемы из реальной практической задачи, отделение важного от несущественного, поиск правильной формулировки для каждой из возникающих проблем, т.е. то, что называется «постановкой задачи». Многие довольно часто недооценивают работу, связанную с формулировкой задачи. Однако многие специалисты полагают, что «хорошо поставить задачу - значит на половину ее решить». Хотя в большинстве случаев заказчику кажется, что он уже сформулировал свою проблему, системный аналитик знает, что предлагаемая клиентом постановка задачи является моделью его реальной проблемной ситуации и неизбежно имеет целевой характер, оставаясь приблизительной и упрощенной. Поэтому необходимо проверить эту модель на адекватность, что приводит к развитию и уточнению первоначальной модели. Очень часто первоначальная формулировка изложена в терминах не тех языков, которые необходимы для построения модели.

Первоначально моделью называли некое вспомогательное средство, объект, который в определенных ситуациях заменял другой объект. Например, манекен в определенном смысле заменяет человека, являясь моделью человеческой фигуры. Древние философы считали, что отобразить природу можно только с помощью логики и правильных рассуждений, т.е. по современной терминологии с помощью языковых моделей. Через несколько столетий девизом английского Научного общества стал лозунг: «Ничего словами!», признавались только выводы, подкрепленные экспериментально или математическими выкладками.

В теории моделеймоделированиемназывается результат отображения одной абстрактной математической структуры на другую - тоже абстрактную, либо как результат интерпретации первой модели в терминах и образах.  Paзвитие понятия модели вышло за пределы математических моделей и стало относиться к любым знаниям и представлениям о мире. Поскольку модели играют чрезвычайно важную роль в организации любой деятельности человека их можно разделить напознавательные (когницитивные) и прагматические, что соответствует делению целей натеоретические и практические. Познавательная модельориентирована на приближении модели к реальности, которую эта модель отображает. Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися.  Прагматические моделиявляются средством управления, средством организации практических действий, способом представления образцово правильных действий или их результата, т.е. являются рабочим представлением целей. Поэтомy при обнаружении расхождения между моделью и реальностью надо направить усилия на изменение реальности так, чтобы приблизить реальность к модели. Таким образом, прагматические модели носят нормативный характер, играют роль образца, под который подгоняется действительность.Примерами прагматических моделей служат планы, кодексы законов, рабочие чертежи и т.д. Другим принципом классификации целей моделирования может служить деление моделей настатические и динамические. Для одних целей нам может понадобиться модель конкретного состояния объекта в определенный момент времени, своего рода «моментальная фотография» объекта. Такиемодели называются статическими.  В тех же случаях, когда возникает необходимостъ в отображении процесса изменения состояний, требуются динамические модели систем. В распоряжении человека имеется два типа материалов для построения моделей - средства самого сознания и средства окружающею материального мира. Соответственно этому модели делятся наабстрактные (идеальные) и материальные.  Очевидно, что кабстрактным моделямотносятся языковые конструкции и математические модели. Математические модели обладают наибольшей точностью, но чтобы дойти до их использования в данной области, необходимо получить достаточное количество знаний. По мнению Канта, любая отрасль знания может тем более именоваться наукой, чем в большей степени в ней используется математика. Упрощение является сильным средством для выявления главных эффектов в исследуемом явлении: это видно на примере таких явлений физики, как идеальный газ, абсолютно упругое тело, математический маятник и абсолютно твердый рычаг. Есть еще один, довольно загадочный, аспект упрощенности модели. Почему-то оказывается, что из двух моделей, одинаково хорошо описывающих систему, та модель, которая проще, ближе к истине. Геоцентрическая модель Птолемея позволяла рассчитать движение планет, хотя и по очень громоздким формулам, с переплетением сложных циклов. Переход к гелиоцентрической модели Коперника значительно упростил расчеты. Древние говорили, что простота - печать истины.

1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ИХ РАСЧЕТА

.1 Понятие операционного исследования

Впервые математические модели были использованы для решения практической задачи в 30-х годах в Великобритании при создании системы противовоздушной обороны. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В это время впервые был применен термин: «операционное исследование», подразумевающий исследования военной операции. В последующие годы операционные исследования или исследования операций развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами. Решения человек принимал всегда и во всех сферах своей деятельности. Раньше хотели, чтобы принимаемые решения всегда были правильными. Теперь принято говорить, что решения должны быть оптимальными. Чем сложнее объект управления, тем труднее принять решение, и, следовательно, тем легче допустить ошибку. Вопросам принятия решений на основе применения ЭВМ и математических моделей посвящена новая наука «Исследование операций», приобретающая в последние годы все более обширное поле приложений. Эта наука сравнительно молодая, ее границы и содержание нельзя считать четко определенными. Предмет под названием «Исследование операций» входит в программу элитарных вузов, но не всегда в этот термин вкладывается одно и то же содержание. Некоторые ученые под «исследованием операций» понимают, главным образом, математические методы оптимизации, такие как линейные, нелинейные, динамическое программирование. Другие к исследованию операций подходят с позиции теории игр и статистических решений. Наконец, некоторые ученые вкладывают в понятие «исследование операций» чрезмерно широкий смысл, считая ее основой системного анализа и «наукой наук».

Под термином «исследование операций» мы будем понимать применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.

Окончательно термин «исследование операций» закрепился в конце второй мировой войны, когда в вооруженных силах США были сформированы специальные группы математиков и программистов, в задачу которых входила подготовка решений для командующих боевыми действиями.

В дальнейшем исследование операций расширило область своих применений на самые разные области практики: экономика, транспорт, связь и даже чтобы человеку принять решение без ЭВМ, зачастую ничего не надо, кроме опыта и интуиции. Правда, никакой гарантии правильности, а тем более оптимальности при этом нет. Подчеркнем, что ЭВМ никаких решений не принимает. Решение принимает человек (ЛПР). А ЭВМ только помогает найти варианты решений.

Непременное присутствие человека (как окончательный инстанции принятия решений) не отменяется даже при наличии полностью автоматизированной системы управления.

Нельзя забывать о том, что само создание управляющего алгоритма, выбор одного из возможных его вариантов, есть тоже решение. По мере автоматизации управления функции человека перемещаются с одного уровня управления на другой - высший.

Основные этапы решения задачи принятия оптимальных решений с помощью ЭВМ, как показано на Рисунке 2.1

Рисунок 2.1-Основные этапы решения задачи принятия решения с помощью ЭВМ.

Выбор задачи - важнейший вопрос. Какие основные требования должна удовлетворять задача? Таких требований два: 1. должно существовать, как минимум, два варианта ее решения (ведь если вариант один, значит и выбирать не из чего); 2. надо четко знать в каком смысле искомое решение должно быть наилучшим (кто не знает, куда ему плыть - тому нет и попутного ветра). Выбор задачи завершается ее содержательной постановкой. Когда производится содержательная постановка задачи, к ней привлекаются специалисты в предметной области. Они прекрасно знают свой конкретный предмет, но не всегда представляют, что требуется для формализации задачи и представления ее в виде математической модели. Хорошую модель составить не просто. Известный математик Р.Беллман сказал так: «Если мы попытаемся включить в нашу модель слишком много черт действительности, то захлебнемся в сложных уравнениях; если слишком упростим ее, то она перестанет удовлетворять нашим требованиям». Таким образом, исследователь должен пройти между западнями Переупрощения и болотом Переусложнения. Для выполнения успеха моделирования надо выполнить три правила, которые, по мнению древних, являются признаками мудрости. Эти правила применительно к задачам математического моделирования и формулируются так: учесть главные свойства моделируемого объекта; пренебрегать его второстепенными свойствами; уметь отделить главные свойства от второстепенных. Составление модели - это искусство, творчество. Древние говорили: «Если двое смотрят на одно и то же, это не означает, что оба видят одно и то же». И слова древних греков: «Если двое делают одно и то же, это не значит, что получится одно и то же». Эти слова в полной мере относятся к составлению математических моделей. Если математическая модель - это диагноз заболевания, то алгоритм - это метод лечения.

Можно выделить следующие основные этапы операционного исследования:

наблюдение явления и сбор исходных данных;

постановка задачи;

построение математической модели;

расчет модели;

тестирование модели и анализ выходных данных. Если полученные результаты не удовлетворяют исследователя, то следует, либо вернуться на этап 3, т.e. предложить для решения задачи другую математическую модель; либо вернуться на этап 2, т.e. поставить задачу более корректно; - применение результатов исследований.

Таким образом, операционное исследование является итерационным процессом, каждый следующий шаг которого приближает исследователя к решению стоящей перед ним проблемы. В центре операционного исследования находятся построение и расчет математической модели. Математическая модель- это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему. Экономико-математическая модель- это математическая модель, предназначенная для исследования экономической проблемы. Проведение операционного исследования, построение и расчет математической модели позволяют проанализировать ситуацию и выбрать оптимальные решения по управлению ею или обосновать предложенные решения. Применение математических моделей необходимо в тех случаях, когда проблема сложна, зависит от большого числа факторов. Использование математических моделей позволяет осуществить предварительный выбор оптимальных или близких к ним вариантов решений по определенным критериям. Они научно обоснованы, и лицо, принимающее решение, может руководствоваться ими при выборе окончательного решения. Следует понимать, что не существует решений, оптимальных «вообще». Любое решение, полученное при расчете математической модели, оптимально по одному или нескольким критериям, предложенным постановщиком задачи и исследователем. В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений в различных областях экономики. Это планирование и оперативное управление производством, управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, руководство проектом, распределение инвестиций и т.п.

.2 Классификация и принципы построения математических моделей

Следующие основные этапы построения математической модели:  1. Определение цели, т.e. чего хотят добиться, решая поставленную задачу. 2. Определение пapaметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет. 3. Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели.  4. Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные. 5. Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом. 6. Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.e. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи. Введем параметры:  a-параметры модели. x-управляющие переменные или решения; X-область допустимых решений; x-случайные или неопределенные факторы; W-целевая функция или критерий эффективности (критерий оптимальности). W=W(x,a,x) В соответствии с введенными терминами, математическая модель задачи имеет следующий вид W=W(x,a,x)®max(min) (2.1) xÎX Решить задачу- это значит найти такое оптимальное решениеx^*ÎX, чтобы при данных фиксированных параметрахaи с учетом неизвестныхxфакторов значения критерия эффективностиWбыло по возможности максимальным (минимальным).

^*=W(x^*,a,x)=max(min)W(x,a,x) xÎX

Таким образом, оптимальное решение- это решение, предпочтительное перед другими по определенному критерию эффективности (одному или нескольким). Перечислим некоторые основные принципы построения математической модели: 1. Необходимо соизмерять точность и подробность модели, во-первых, с точностью тex исходных данных, которыми располагает исследователь, и, во-вторых, с теми результатами, которые требуется получить. 2. Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.

. Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи. 4. Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой (сохранять свойства и структуру при этих воздействиях). По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия. По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности. В стохастических моделях неизвестные факторы - это случайные величины, для которых известны функции распределения и различные статистические характеристики (математическое ожидание, дисперсия, среднеквадратическое отклонение и т.п.). Среди стохастических характеристик можно выделить:

-модели стохастического программирования, в которых либо в целевую функцию (2.1), либо в ограничения (2.2 )входят случайные величины;

модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной;

модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований.

Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные, значения которых не определены, используются модели с элементами неопределенности. В моделях теории игр задача представляется в виде игры, в которой участвуют несколько игроков, преследующих разные цели, например, организацию предприятия в условиях конкуренции. В имитационных моделях реальный процесс разворачивается в машинном времени, и прослеживаются результаты случайных воздействии на него, например, организация производственного процесса. В детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических задач. По виду целевой функции и ограничений детерминированные модели делятся на: линейные, нелинейные, динамические и графические. В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения. Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения. Hелинейные модели - это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений можно предложить различные способы решения. Однако может случиться и так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, либо сведя ее к известным линейным моделям, либо просто линеаризовав модель. В динамических моделях, в отличие от статических линейных и нелинейных моделей, учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.

.3 Некоторые сведения из математики

Множество точек называется выпуклыми, если оно вместе с любыми двумя точками содержит отрезок, соединяющий эти точки. Простейшими примерами выпуклых множеств могут служить: отрезок, треугольник, квадрат, некоторые геометрические тела, например, пирамида, куб и т.д. заметим, что выпуклый многоугольник обладает тем свойством, что весь расположен по одну сторону каждой из прямых, участвующих в ее образовании. выпуклой линейной комбинацией точек М₁, М₂, ... М_n называется любая точка М такая, что:

М=a₁M₁+a₂M₂+a_nM_n,

где a_i³0иa₁+a₂+ ...+a_n=1. Обобщая сказанное выше, можно сказать, что множество точек называется выпуклым, если вместе с любыми своими точками оно содержит и выпуклую произвольную комбинацию этих точек. Поскольку произвольная точка отрезка представляет собой выпуклую комбинацию его концов, то это и означает, что выпуклое множество вместе с двумя данными точками содержит весь соединяющий их отрезок. Очевидно, что всякая точка выпуклого многоугольника, лежащая внутри его или на одной из сторон, за исключением вершин, может быть представлена как выпуклая линейная комбинация других точек этого многоугольника. Напротив, вершины многоугольника не представляются в виде выпуклой комбинации двух каких-нибудь других точек. В этом смысле вершины многоугольника называют экстремальными точками. Прямая линия называется опорной, если она имеет с выпуклым многоугольником, по крайней мере, одну общую точку и весь многоугольник расположен по одну сторону от этой прямой. Через каждую из вершин многоугольника можно провести бесконечное множество опорных линий. В пространстве трех измерений, по аналогии с понятием опорной прямой вводится понятие опорной плоскости. Опорной плоскостью называется всякая плоскость, имеющая с выпуклым многогранником, по крайней мере, одну общую точку, причем такую, что весь многогранник расположен по одну сторону от нее. Опорная плоскость может иметь с выпуклым многогранником общую точку (вершину многогранника), прямую (ребро), и, наконец, общую грань.

1.4 Линейные неравенства

Рассмотрим подробнее системы линейных неравенств и покажем, что решение их тесно связано с понятиями выпуклого многоугольника и выпуклого многогранника.

Рисунок 1

Для начала рассмотрим неравенство с одной переменной величинойx₁, напримерx₁<4. Если на плоскости провести прямуюх₁=4, то она разделит всю плоскость на две части - полуплоскости: в одной из них, а именно слева от прямойх₁=4, лежат точки, абсциссы которых меньше4, а справа от прямой - точки, абсциссы которых больше4. Таким образом, неравенствоx₁<4геометрически определяет полуплоскость, как показано на рисунке 1. Рассмотрим теперь неравенство с двумя переменными типа3х₁+4х₂<12. Построим прямую линию3х₁+4х₂=12. Разделим обе части уравнения

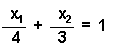
из которого видно, что прямая отсекает по осям отрезки, равные4и3. Неравенство3х₁+4х₂<12определяет собой совокупность всех точек плоскости, лежащих ниже прямой, т.е. в заштрихованной части, как показано на рисунке 2.

Рисунок 2

Чтобы легче было понять, какую именно полуплоскость определяет то или иное неравенство, мы в левую часть неравенства подставим координаты начала координат, т.е.х₁=0их₂=0. Если неравенство удовлетворяется, то оно определяет ту полуплоскость, в которой лежит начало координат, в противном случае - другую полуплоскость. Пользуясь геометрическими соображениями, найти возможные решения системы: ì3х₁+4х₂£ 12 íx₁< 2 îх₁> 0 и х₂> 0

Каждое из неравенств системы определяет полуплоскость, Полученный многоугольник является выпуклым, ибо вместе с любыми двумя точками содержит весь соединяющий их отрезок, как показано на рисунке 3 таким образом, мы видим, что выпуклый многоугольник можно задать аналитически, с помощью системы линейных неравенств. Линейное уравнение с тремя переменными: a₁₁x₁+a₁₂x₂+a₁₃x₃=b₁ определяет в пространстве некоторую плоскость, которая рассекает все пространство на два полупространства. В связи с этим неравенство a₁₁x₁+a₁₂x₂+a₁₃x₃£b₁ определяет одно из полупространств, к которому принадлежит также и сама граничная плоскость. В общем случае, когда система неравенств совместна, пространство решений образует некоторый выпуклый многогранник - многогранник решений. Частным случаем его могут быть: отдельная грань, ребро или точка. Последнее имеет место, когда система неравенств имеет одно единственное решение. Дальнейшие обобщения приводят нас к рассмотрению m линейных неравенств сn неизвестными. Каждое уравнение a_i1x₁+a_i2x₂+ ... +a_inx_n=b_i является уравнением некоторой гиперплоскости вn-мерном пространстве, которая как бы рассекает все пространство на два полупространства.

2. ПРИМЕРЫ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

математический модель линейный программирование

2.1 Транспортная задача

Уголь, добываемый в нескольких месторождениях, отправляется ряду потребителей. Нам известно, сколько угля добывается в каждом из месторождений, скажем за месяц и сколько его требуется на тот же срок каждому из потребителей. Известны расстояния между месторождениями и потребителями, а также условия сообщения между ними. Учитывая эти данные. Можно подсчитать, во что обходится перевозка каждой тонны угля из любого месторождения в любой пункт потребления. Требуется при этих условиях спланировать перевозки угля таким образом, чтобы затраты на них были минимальными. Пусть для простоты заданы всего 4 месторождения М₁, М₂, М₃, М₄, причем их ежемесячная добыча составляет a₁, а₂, а₃, а₄ тонн угля. Предположим далее, что этот уголь надо доставить в пункты потребления b₁,b₂,b₃,b₄,b₅, соответственно с ежемесячными потребностями этих пунктов. Будем считать, что общее производство угля равно суммарной потребности в нем (сбалансированность планов): a₁, а₂, а₃, а₄=b₁,b₂,b₃,b₄,b₅. Задача состоит в определении такого плана перевозок, при котором общая стоимость перевозок была бы наименьшей. Обозначим через x₁₁ количество угля (в тоннах), предназначенное к отправлению из M₁вП₁; вообще через x_ij обозначим количество угля, отправляемого из месторождения M_i в пункт потребления П_j.

Таблица 2.1

Схема перевозок примет вид, изображенный в таблице 2.1. Схема перевозки

Общее количество угля, привозимое в пунктП₁из всех месторождений, будетх₁₁₊х₁₂₊х₁₃₊х₁₄₊х_{15 =}b₁; в другие пункты -П₂, П₃и т.д. и примет вид уравнений 4.1. общее количество угля, вывозимое из М₁, будет: х₁₁₊х₁₂₊х₁₃₊х₁₄₊х_{15 =}a₁, примет вид 4.2. предполагаем, что стоимость перевозки прямо пропорциональна количеству перевозимого угля, т.е. стоимость перевозки x_ij тонн угля равна: x_ij=C_ij^.X_ij Общая стоимость S всех перевозок будет равна:

=c₁₁х₁₁+c₁₂х₁₂+c₁₃х₁₃+c₁₄х₁₄+c₁₅х₁₅+ ... +c₄₁х₄₁+c₄₂х₄₂+c₄₃х₄₃+c₄₄х₄₄+c₄₅х₄₅.

.2 Общая формулировка задачи линейного программирования

Аналогично транспортной задаче решается задача об оптимизации распределения ресурсов (трудовых, материальных, финансовых) и задача о диете. При всем разнообразии, по своему конкретному содержанию каждая из них была задачей на нахождение наиболее выгодного варианта. С точки зрения математической, в каждой задаче ищутся значения нескольких неизвестных, причем требуется, чтобы:

эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;

при этих значениях некоторая линейная функция (линейная форма) от этих неизвестных обращалась в минимум (максимум);

эти значения были неотрицательными. Задачами такого рода и занимается линейное программирование. Говоря точнее, линейное программирование - это математическая дисциплина, изучающая методы нахождения наименьшего (или наибольшего) значения линейной функции нескольких переменных, при условии, что последние удовлетворят конечному числу линейных уравнений или неравенств. Уравнения (I) называются ограничениями данной задачи, уравнение (II) называется линейной формой, а уравнение (III), строго говоря, тоже являются ограничениями, однако их не принято так называть, поскольку они являются общими для всех задач линейного программирования, а не только конкретной задачи. Любое неотрицательное решение системы уравнений называется допустимым. Допустимое решение, дающее минимум функции, оптимальное решение (если оно существует) не обязательно единственно; возможны случаи, когда имеется бесчисленное множество оптимальных решений. Наконец, саму функцию часто называют линейной формой или функцией цели. Казалось бы, т.к. задача линейного программирования ставится как задача минимизации некоторой функции, то можно применить классический прием дифференциального исчисления. Однако частные производные равны коэффициентам при неизвестных, которые в «нуль» одновременно не обращаются.

.3 Постановка задачи динамического программирования

Основные условия и область применения. В ряде реальных экономических и производственных задач необходимо учитывать изменение моделируемого процесса во времени и влияние времени на критерий оптимальности. Для решения указанных задач используется метод динамического планирования (программирования). Этот метод более сложен по сравнению с методами расчета статических оптимизационных задач.

Также непростым делом является процесс построения для реальной задачи математической модели динамическою программирования. Пусть рассматривается задача, распадающаяся на m шагов или этапов, например планирование деятельности предприятия на несколько лет, поэтапное планирование инвестиций, управление производственными мощностями в течение длительного срока. Показатель эффективности задачи в целом обозначим через W, а показатели эффективности на отдельных шагах - черезj_i,i=1,m. Если W обладает свойством аддитивности, т.е.:

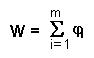 (6.3)

Можно найти оптимальное решение задачи методом динамического программирования. Таким образом, динамическое программирование- это метод оптимизации многошаговых или многоэтапных процессов, критерий эффективности которых обладает свойством(6.3). В задачах динамического программирования критерий эффективности называется выигрышем. Данные процессы управляемые, и от правильного выбора управления зависит величина выигрыша. Переменная х_i, от которой зависят выигрыш на i-м шаге и, следовательно, выигрыш в целом, называются шаговым управлениемi=1, m. Управлением процесса в целом(х)называется последовательность шаговых управлений х=(х₁, х₂, ..., х_i, ..., х_m). Оптимальное управление х^*- это значение управлениях, при котором значение W(x^*) является максимальным

^*=W(x^*)=max{W(x)} xÎX,

гдеX - область допустимых управлений. Oптимальное управление x^* определяется последовательностью оптимальных шаговых управлений: x^*= (x₁^*, x₂^*, ..., x_i^*, ..., x_m^*).

Таким образом, при выборе шагового управления необходимо учитывать: Возможные исходы предыдущего шага. Влияние управления на все оставшиеся до конца процесса шаги. В задачах динамическою программирования первый пункт учитывают, делая на каждом шаге условные предположения о возможных вариантах окончания предыдущего шага, и проводя для каждого из вариантов условную оптимизацию. Выполнение второго пункта обеспечивается тем, что в задачах динамического программирования условная оптимизация проводится от конца процесса к началу. Сперва оптимизируется последний m-й шаг, на котором не надо учитывать возможные воздействия выбранного управления х_m, на все последующие шаги, так как эти шаги просто отсутствуют. Делая предположения об условиях окончания(m-1)-го шага, для каждого из них проводят условную оптимизацию m-го шага и определяют условное оптимальное управление х_m. Аналогично поступают для(m-1)-го шага, делая предположение об исходах окончания(m-2)-го шага, и, определяя условное оптимальное управление на (m-1)-ом шаге, приносящее оптимальный выигрыш на двух последних шагах -(m-1)-ом иm-ом. Так же действуют на всех остальных шагах до первого. На первом шаге, как правило, не надо делать условных предположений, т.к. состояние системы перед первым шагом обычно известно. Для этого состояния выбирают оптимальное шаговое управление, обеспечивающее оптимальный выигрыш на первом и всех последующих шагах. Это управление является, безусловно, оптимальным управлением на первом шаге и, зная его, определяются оптимальное значение выигрыша и безусловные оптимальные управления на всех ее шагах. Многокритериальная оптимизация þ задачи, в которых оптимизацию проводят по нескольким параметрам, называют задачами многокритериальной или векторной оптимизации.

Как и при линейном программировании задачи многокритериальной оптимизации включают в себя три основные части. три основные части задачи многокритериальной оптимизации: -целевая -ограничения, -граничные

Наиболее часто целевая функция представляется обобщенными показателями эффективности, которые представляют собой взвешенную сумму частных показателей, в которую каждый из них входит с определенным весом, отражающим его важность: W=a₁^.w₁+a₂^.w₂

Для тex показателей, которые желательно увеличить, веса берутся положительные, а для тex, которые желательно уменьшить - отрицательные. Назначение коэффициентов весов проводят с помощью экспертных оценок. Методы экспертных оценок достаточно широко распространены. Математических методов определения экспертных оценок достаточно много. Рассмотрим некоторые из них.

.4 Математические методы определения экспертных оценок

Непосредственное назначение коэффициентов весов. Согласно этому методу каждый i-й эксперт для каждого k-ого параметра должен назначить коэффициент веса a_ik таким образом, чтобы сумма коэффициентов веса, назначенная одним экспертом для различных В качестве коэффициента веса k-ого параметра a_k принимают среднее значение по результатам экспертизы всех экспертов: Oценка важности параметров в баллах. В этом случае каждый эксперт назначает каждому параметру оценку по десяти бальной системе. Наиболее важный параметр оценивается более высоким баллом. В результате экспертизы заполняется таблица, и находятся коэффициенты веса.

ЗАКЛЮЧЕНИЕ

Впервые математические модели были использованы для решения практической задачи в 30-х годах в Великобритании при создании системы противовоздушной обороны. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В это время впервые был применен термин: «операционное исследование», подразумевающий исследования военной операции. В последующие годы операционные исследования или исследования операций развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами.

Решения человек принимал всегда и во всех сферах своей деятельности. Раньше хотели, чтобы принимаемые решения всегда были правильными. Теперь принято говорить, что решения должны быть оптимальными. Чем сложнее объект управления, тем труднее принять решение, и, следовательно, тем легче допустить ошибку. Вопросам принятия решений на основе применения ЭВМ и математических моделей посвящена новая наука «Исследование операций», приобретающая в последние годы все более обширное поле приложений. Эта наука сравнительно молодая, ее границы и содержание нельзя считать четко определенными.

В итоге тема моей курсовой работы раскрыта, цели разработаны, задачи поставлены.

Список используемых источников

математический модель линейный программирование

2.      Бережная, Е.В. Математические методы моделирования экономических систем [Текст] : учеб. пособие для вузов по спец. "Финансы и кредит", "Бух. учет, анализ и аудит", "Мировая экономика" / Е. В. Бережная, В.И. Бережной, 2001. - 368 с.

.        Вопросы механики и процессов управления [Текст] : [сб. ст.] / ЛГУ им. А.А. Жданова. Вып. 8: Математические методы анализа управляемых процессов, 1986. - 200 с.

.        Грицюк, С.Н. Математические методы и модели в экономике [Текст] : учеб. для студ. сред. проф. образования / С.Н. Грицюк, Е.В. Мирзоева, В. В. Лысенко, 2007. - 348 с.

.        Замков, О. О. Математические методы в экономике [Текст] : Учебник / О. О. Замков, А. В. Толстопятенко, Ю. Н. Черемных, 1998. - 368 с.

.        Карасев, А. И. Математические методы и модели в планировании [Текст] : учеб. пособие для экон. спец. вузов / А. И. Карасев, Н. Ш. Кремер, Т. И. Савельев, 1987. - 239 с.

.        Крамер, Г. Математические методы статистики [Текст] / Г. Крамер, 1975. - 648 с.

.        Кузнецов, Б. Т. Математические методы и модели исследования операций [Текст] : учеб. пособие для студ. вузов, обуч. по спец. 061800 "Математические методы в экономике" / Б. Т. Кузнецов, 2005. - 390 с.

.        Математические методы оптимизации и управления в системах [Текст] : Межвуз. темат. сб. науч. тр., 1987. - 164 с.

.        Математические методы и модели исследования операций [Текст] : учеб. для студ. вузов, обуч. по спец. 080116 "Мат. методы в экономике" и др. эконом. спец. / ред. В. А. Колемаев, 2008. - 592 с.

.        Монахов, А. В. Математические методы анализа экономики [Текст] : учеб. пособие / А. В. Монахов, 2002. - 176 с.

.        Орехов, Н. А. Математические методы и модели в экономике [Текст] : учеб. пособие для студ. вузов, обуч. по эконом. спец. / Н. А. Орехов, А. Г. Лёвин, Е. А. Горбунов, 2004. - 302 с.

.        Партыка, Т. Л. Математические методы [Текст] : учеб. для студ. сред. проф. образования / Т. Л. Партыка, И. И. Попов, 2009. - 464 с.

.        Системы и средства информатики [Текст] : ежегодник / Ин-т проблем информатики РАН ; отв. ред. И. А. Соколов. Спец. вып. : Математические методы информатики, 2001. - 160 с.

.        Шапкин, А. С. Математические методы и модели исследования операций [Текст] : учеб. для студ. вузов, обуч. по спец. 061800 "Мат. методы в экономике" / А. С. Шапкин, Н. П. Мазаева, 2007. - 400 с.

.        Шикин, Е. В. Математические методы и модели в управлении [Текст] : учеб. пособие для студентов управленческих спец. вузов / Е. В. Шикин, А. Г. Чхартишвили, 2002. - 440 с.