Принципы экономического моделирования
Задача 1
баланс модель прогноз
Регион представлен 5-ю отраслями: 1 - тяжелая
промышленность; 2 - легкая промышленность; 3 - строительный комплекс; 4 -
агропромышленный комплекс; 5 - социальная сфера. В таблице приведены
коэффициенты прямых материальных затрат, а также: f
- коэффициенты прямой фондоемкости, F
- стоимость основных фондов, t
- коэффициенты прямой трудоемкости, T
- трудовые ресурсы. Отклонения использования ресурсов F
и T допускаются в
пределах ±10% от базовых значений, указанных в таблице.
|
Матрица
А (коэффициенты прямых затрат)
|
F
|
F
|
t
|
T
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
|
1
|
0,29
|
0,11
|
0,20
|
0,16
|
0,21
|
2,1
|
3000
|
0,24
|
110
|
|
2
|
0,17
|
0,26
|
0,17
|
0,13
|
0,18
|
3,2
|
3700
|
0,55
|
210
|
|
3
|
0,11
|
0,13
|
0,06
|
0,09
|
0,03
|
3,0
|
1600
|
0,51
|
55
|
|
4
|
0,05
|
0,10
|
0,11
|
0,13
|
0,10
|
2,8
|
1500
|
0,54
|
70
|
|
5
|
0,08
|
0,11
|
0,13
|
0,17
|
0,12
|
2,3
|
1200
|
0,71
|
100
|
Разработать региональный баланс, при котором
создается максимум суммарного конечного продукта. Результаты представить в виде
таблицы. Провести анализ решения и определить, какие факторы наиболее важны для
достижения поставленной цели.
|
Межотраслевые
потоки
|
Конечный
продукт
|
Валовой
продукт
|
F
|
T
|
|
1
|
3
|
4
|
5
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
∑
|
|
|
|
|
|
|
|
|
|
Решение. Введем
переменные 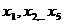 - объемы
валового производства,
- объемы
валового производства, 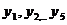 - объемы
конечного продукта. Они связаны системой уравнений Леонтьева
- объемы
конечного продукта. Они связаны системой уравнений Леонтьева 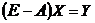 , которую в
данном случае, учитывая, что
, которую в
данном случае, учитывая, что 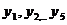 - переменные, следует записать так:
- переменные, следует записать так:
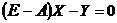 . Таким
образом, первая группа условий.
. Таким
образом, первая группа условий.
|
0,71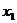 -0,11 -0,11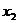 -0,20 -0,20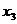 -0,16 -0,16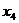 -0,21 -0,21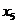 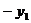 =0 =0
|
|
|
|
|
|
|
|
-0,17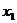 +0,74 +0,74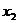 -0,17 -0,17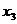 -0,13 -0,13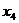 -0,18 -0,18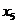 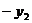 =0 =0
|
|
|
|
|
|
|
|
-0,11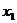 -0,13 -0,13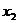 +0,94 +0,94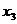 -0,09 -0,09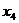 -0,03 -0,03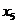 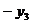 =0 =0
|
|
|
|
|
|
|
|
-0,05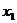 -0,10 -0,10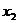 -0,11 -0,11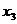 +0,87 +0,87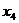 -0,10 -0,10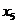 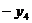 =0 =0
|
|
|
|
|
|
|
|
-0,08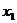 -0,11 -0,11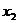 -0,13 -0,13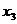 -0,17 -0,17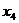 +0,88 +0,88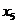 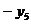 =0 =0
|
|
|
|
|
|
|
Вторая группа условий - ограничения по ресурсам.
Учитывая допустимые (в пределах ±10%) отклонения от уровней фондов,
используемых в базовом периоде, запишем следующие ограничения
|
2700,00
|
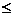 2,1 2,1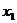 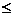 3300,00 3300,00
|
|
|
3330,00
|
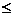 3,2 3,2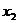 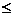 4070,00 4070,00
|
|
|
1440,00
|
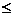 3,0 3,0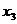
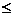 1760,00 1760,00
|
|
|
1350,00
|
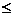 2,8 2,8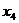
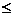 1650,00 1650,00
|
|
|
1080,00
|
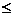 2,3 2,3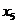 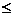 1320,00 1320,00
|
|
Аналогично для трудовых ресурсов
|
99,00
|
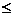 0,24 0,24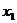 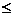 121,00 121,00
|
|
|
189,00
|
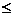 0,55 0,55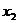 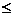 231,00 231,00
|
|
|
49,50
|
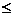 0,51 0,51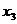
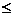 60,50 60,50
|
|
|
63,00
|
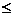 0,54 0,54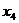
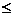 77,00 77,00
|
|
|
90,00
|
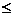 0,71 0,71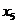 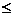 110,00 110,00
|
|
Целевая функция - максимум конечного продукта:
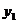 +
+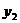 +
+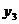 +
+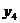 +
+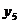
 .
.
баланс моделирование
экономический
Получили задачу линейного
программирования. Ее можно решить с помощью надстройки Solver Excel .
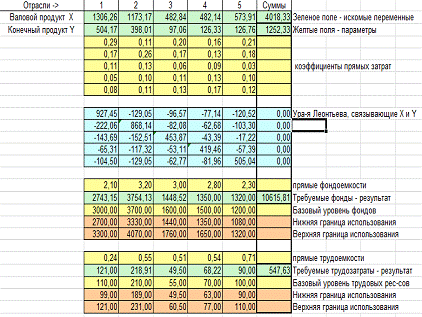
Решение задачи:
x1 = 1306,26, x2 = 1173,17, x3 = 482,84, x4 = 573,91, x5 = 4018,33,
y1 = 504,17, y2 = 398,01, y3 = 97,06, y4 = 126,76, y5 = 1252,33.
Сводная таблица результатов.
|
1
|
2
|
3
|
4
|
5
|
Y
|
X
|
F
|
T
|
|
1
|
378,82
|
129,05
|
96,57
|
77,14
|
120,52
|
504,17
|
1306,26
|
2743,15
|
121,00
|
|
2
|
222,06
|
305,02
|
82,08
|
62,68
|
398,01
|
1173,17
|
3754,13
|
218,91
|
|
3
|
143,69
|
152,51
|
28,97
|
43,39
|
17,22
|
97,06
|
482,84
|
1448,52
|
49,50
|
|
4
|
65,31
|
117,32
|
53,11
|
62,68
|
57,39
|
126,33
|
482,14
|
1350,00
|
68,22
|
|
5
|
104,50
|
129,05
|
62,77
|
81,96
|
68,87
|
126,76
|
573,91
|
1320,00
|
90,00
|
|
∑
|
914,38
|
832,95
|
323,50
|
327,86
|
367,30
|
1252,33
|
4018,33
|
10615,81
|
547,63
|
Задача 2
В таблице представлены данные, отражающие
динамику объемов производства металлургической компании по месяцам в течение
двух лет. Разработать модель и дать прогноз на глубину в один интервал.
|
T
|
Yt
|
T
|
yt
|
t
|
yt
|
T
|
yt
|
|
1
|
23,867
|
7
|
18,258
|
13
|
10,445
|
19
|
6,725
|
|
2
|
23,288
|
8
|
16,246
|
14
|
9,073
|
20
|
7,159
|
20,648
|
9
|
14,891
|
15
|
9,572
|
21
|
7,203
|
|
4
|
18,413
|
10
|
13,123
|
16
|
5,278
|
22
|
9,125
|
|
5
|
18,695
|
11
|
8,711
|
17
|
6,529
|
23
|
8,894
|
|
6
|
16,514
|
12
|
11,662
|
18
|
7,109
|
24
|
8,137
|
Решение. Используя
Excel, построим
динамический ряд по данным точкам.
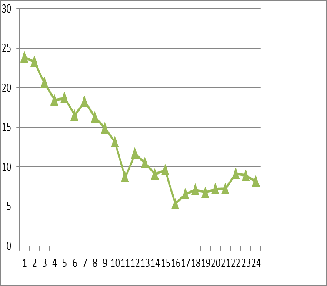
Для рассматриваемого ряда подходящим
является нелинейный тренд. Рассчитаем параметры модели 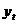 = a0 + a1t + a2t2
= a0 + a1t + a2t2
Для расчета коэффициентов регрессии
воспользуемся Excel. Занесем на лист данные задачи. Первый столбец - номера
месяцев. Второй - эти номера, возведенные в квадрат, Третий - наблюдаемая
величина.
|
t
|
t^2
|
y
|
|
1
|
1
|
23,867
|
|
2
|
4
|
23,288
|
|
3
|
9
|
20,648
|
|
4
|
16
|
18,413
|
|
5
|
25
|
18,695
|
|
6
|
36
|
16,514
|
|
7
|
49
|
18,258
|
|
8
|
64
|
16,246
|
|
9
|
81
|
14,891
|
|
10
|
100
|
13,123
|
|
11
|
121
|
|
12
|
144
|
11,662
|
|
13
|
169
|
10,445
|
|
14
|
196
|
9,073
|
|
15
|
225
|
9,572
|
|
16
|
256
|
5,278
|
|
17
|
289
|
6,529
|
|
18
|
324
|
7,109
|
|
19
|
361
|
6,725
|
|
20
|
400
|
7,159
|
|
21
|
441
|
7,203
|
|
22
|
484
|
9,125
|
|
23
|
529
|
8,894
|
|
24
|
576
|
8,137
|
Далее: Сервис > Анализ данных. В
появившемся окне выбрать строку Регрессия
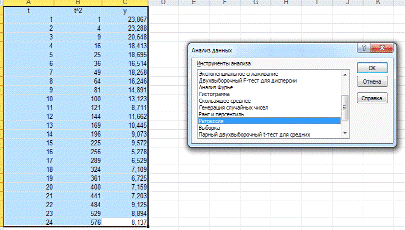
Нажимаем ОК.
В окно Входной интервал Y
ввести ссылку на диапазон значений y.
В окно Входной интервал Х ввести ссылку на
диапазон столбцов T
n T^2.
Поставить переключатель на Выходной интервал и
указать в расположенном рядом окне на ячейку выходного диапазона.
Нажать ОК.
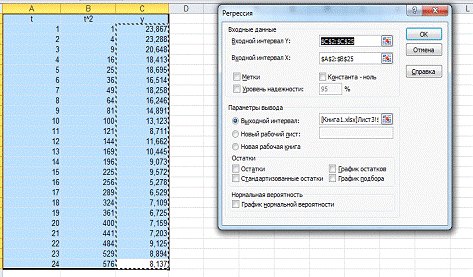
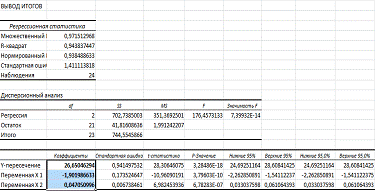
Получим (Коэффициенты регрессии выделены жирным
шрифтом).
Коэффициенты регрессии (показаны жирным шрифтом)
подставляем в модель. Получаем
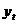 =
=
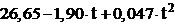 .
.
Для прогноза на один интервал
подставим в эту модель t=25, получим
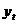 =
=
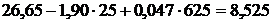 .
.