Визначення оптимальних показників діяльності структурного підрозділу Державної служби України з надзвичайних ситуацій у галузі інформаційної безпеки

Зміст

стохастичний програмування інформаційний безпека

Вступ

Розділ 1. Оцінка ефективності і ризикованості рішень провідного фахівця відділу матеріально-технічного забезпечення

.1 Постановка задачі

.2 Оцінка ризиків стратегій за показниками

.3 Оцінка ризикованості стратегій за статистичними критеріями

Розділ 2. Визначення оптимального плану випуску продукції на підприємствах засобами стохастичного програмування

.1 Постановка задачі

.2 Побудова економіко-математичної моделі стохастичного програмування для визначення оптимального плану випуску продукції на підприємствах

.3 Визначення оптимально плану випуску продукції на підприємствах

.4 Оцінка міри ризику щодо одержання максимального прибутку за загальним коефіцієнтом варіації і коефіцієнтом варіації по від’ємній семіваріації

Розділ 3. Фінансові ризики. Оцінка ступеня ризику цінних паперів. Оптимізація портфелю цінних паперів

.1 Постановка задачі

.2 Модель Шарпа. Оцінка систематичного ризику

.3 Оптимізація портфеля цінних паперів за моделями Марковіца

Розділ 4. Застосування теорії графів в інформаційній безпеці

Висновки

Використана література

Додаток А

Додаток Б

Додаток В

Додаток Г

Вступ

Розглядаючи проблеми моделювання інформаційної безпеки з точки зору організації сучасних інформаційних систем, необхідно брати до уваги багато факторів. Один з аспектів проблеми пов'язаний з тим, що поняття інформаційної безпеки не може розглядатися відокремлено від інших складових системи безпеки. Інформація є важливим ресурсом сучасного суспільства та невід'ємним елементом управління будь-якої системи, у тому числі, і системи безпеки. При цьому вона сама є об'єктом захисту. З іншого боку система безпеки взагалі, і інформаційної безпеки зокрема, є складною системою. Вона повинна забезпечувати оперативне реагування передбаченим та запобігання новим загрозам, пошук оптимальних рішень за умов багатофакторної невизначеності. Складно, а точніше неможливо запропонувати однозначні критерії, що визначають ефективність, надійність і стабільність будь-якої системи безпеки, що зумовлено багатьма причинами. Все це необхідно враховувати в процесі моделювання.

На сьогоднішній день розроблено багато моделей, що застосовуються в галузі інформаційної безпеки. Їх можна класифікувати за різними ознаками та критеріями. Наприклад, за природою реалізації розрізняють фізичні та математичні моделі; за характером параметрів опису моделі - детерміновані, стохастичні, нечіткі тощо; за видом залежностей, які описуються - дискретні, безперервні, лінійні, нелінійні, комбіновані; за метою створення моделі поділяють на створені з метою прогнозу та з метою оптимізації; за динамічними властивостями виділяють статистичні та динамічні моделі [1].

Актуальність роботи зумовлена тим, що будь-яка із запропонованих на сьогоднішній день моделей не є універсальною. Вона вирішує тільки частину проблем, визначених як пріоритетні, не враховуючи унікальність кожної системи, що знаходяться в умовах постійних змін, під впливом багатьох чинників, які часто складно не тільки описати в числах і формулах, але й визначити заздалегідь. Для вирішення цієї проблеми як методологічна основа моделювання може використовуватися теорія м'яких систем.

Метою курсової роботи стало визначення оптимальних показників діяльності структурного підрозділу ДСНС України у галузі ІБ.

Розділ 1. Оцінка ефективності і ризикованості рішень провідного фахівця відділу матеріально-технічного забезпечення

 

.1 Постановка задачі

Структурний підрозділ ДСНС планує підвищити ефективність роботи, попередньо розробивши 5 стратегій:

-           А1 - закупівля 20 одиниць АЦЛ 3-40/4-24 (43118) та 5 одиниць автомобіля першої допомоги АПП-0,4-90/300;

-           А2 - закупівля 30 одиниць АЦЛ-3.0-40 та 10 одиниць малогабаритної порошково-пінної установки (МГППУ);

-           А3- закупівля 10 одиниць пошуково-рятувального катера "Мангуст" та 4 одиниць автомобіля першої допомоги АПП-0,4-90/300;

-           А4- закупівля 2 одиниць пожежно-рятувального вертоліту Ка-32А та 15 одиниць пристроїв для дихальної реанімації "Рятувальник-10".

А5 - закупівля 3 одиниць вертоліту Мі-8МТВ-1 та 20 одиниць радіаційно-захисного комплекту одягу для пожежників, РЗК".

Діяльність пов’язана із закупівлею рятувальної техніки, відповідно до сезону та виду аварійних робіт.

Кожна з альтернативних стратегій розрахована відповідно до 6-ти станів зовнішнього середовища. (С1, С2, ….,С6).

-        С1 - проведення аварійних робіт під час виникнення пожеж у будинках;

-        С2 - проведення аварійних робіт під час виникнення пожеж у завалах;

         С3 - проведення аварійних робіт на воді;

         С4 - проведення аварійних робіт в горах;

         С5 - проведення висотних аварійних робіт;

         С5 - проведення аварійних робіт у випадку затоплення місцевості.

Кожна стратегія відповідно до стану зовнішнього середовища оцінюється прибутками, який вважається випадковою величиною.

Треба кількісно оцінити ризики кожної стратегії, застосувати статистичні критерії і вибрати найбільш ефективну стратегію закупівлі.

Табл. 1.1

Матриця стратегій і прибутків

	С1	С2	С3	С4	С5	С6
А1	5	14	18	2	17	20
А2	15	17	18	15	15	12
А3	15	14	7	17	6	12
А4	18	23	16	12	12	11
А5	4	8	14	16	17	6

 

.2 Оцінка ризиків стратегій за показниками

Математичне сподівання і середнє значення.

Для позначення середнього арифметичного всієї сукупності використовується грецька буква μ. Для випадкової величини, для якої визначено середнє значення, μ виступає ймовірнісним середнім або математичним сподіванням випадкової величини. Якщо множина X є сукупністю випадкових чисел з імовірнісним середнім μ, тоді для будь-якої вибірки хі з цієї сукупності μ = E {xi} існує математичне сподівання цієї вибірки.

На практиці різниця між μ і x, в тому, що μ є типовою змінною, яку не можна спостерігати, тому що спостерігається швидше вибірка, а не вся генеральна сукупність. Тому, якщо вибірку представляти випадковим чином (в термінах теорії ймовірностей), тоді x, (але не μ) можна трактувати як випадкову змінну, що має розподіл ймовірностей на вибірці (імовірнісний розподіл середнього). Обидві ці величини обчислюються одним і тим же способом:

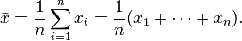
Якщо X - випадкова змінна, тоді математичне сподівання X можна розглядати як середнє арифметичне значень у вимірах величини X, що повторюються. Це є проявом закону великих чисел. Тому вибіркове середнє використовується для оцінки невідомого математичного сподівання [2].

Рис 1.1 Математичне сподівання

Математичне сподівання говорить те, що найбільною ефективною є сиратегія S2.

Загальна дисперсія, семіваріація плюс, семіваріація мінус.

Дисперсія часто застосовується в теорії ймовірностей і математичній статистиці. Означає ступінь розсіювання навколо середнього значення випадкової величини. У статистичному розумінні дисперсія є середнє арифметичне із квадратів відхилень величин від їх середнього арифметичного. На практиці часто необхідно оцінити розсіювання можливих значень випадкової величини навколо її середнього значення, а також виявити та виміряти силу зв'язку між факторними та результативною ознаками [3]. З рисунку видно, що найкращою є стратегія S5.

Dj

104,8333

180,1333

111,3667

109,5333

80,26667

Рис 1.2 Значення дисперсії для кожної стратегії

У неокласичній теорії економічного ризику виходять з того, що ризик пов’язаний лише з несприятливими для менеджера (інвестора) ефектами і для його оцінювання достатньо брати до уваги лише несприятливі відхилення від сподіваної величини. При цьому в якості міри ризику використовується семіваріація.

Показник семіваріації характеризує тільки додатні або тільки від’ємні відхилення від математичного сподівання. Додатня семіваріація розраховується за формулою:

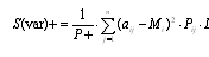
Додатня семиваріація характеризує середній квадрат відхилення тих значень прибутку, які більше від середнього. Чим менша додатня семіваріація, тим менший ризик і більший шанс отримати більше ніж запланували. Необхідно взяти ті умови стратегії, які більші за математичне сподівання, відняти від них саме математичне сподівання. Потім різницю піднести до квадрату і помножити на ймовірність взятої умови, а потім скласти різниці умов з математичним сподіванням піднесеного до квадрату і помножене на ймовірність. Для інших стратегій розраховується аналогічно. Додатня семіваріація характеризує середній квадрат відхилення тих значень прибутку, які більше від середнього. Чим менша додатня семіваріація, тим менший ризик і більший шанс отримати більше ніж запланували. У нашому випадку має найменший ризик стратегія S2.

Від’ємна семіваріація розраховується за формулою:

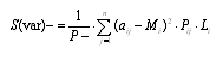
Від’ємна семіваріація характеризує середній квадрат відхилення тих значень прибутку, які менші від середнього. Чим більша від’ємна семіваріація, тим більший ризик і менший шанс отримати прибуток. S5 має найменший ризик.

Табл. 1.2

Коефіцієнти семі варіації

Показник варіації.

Середні величини мають велике теоретичне і практичне значення, оскільки вони дають змогу однією величиною охарактеризувати сукупність однотипних явищ. Проте для всебічної характеристики таких явищ їх недостатньо. Щоб установити, як відрізняються сукупності, а також які межі коливання має ознака, необхідно обчислити варіацію. Варіацією називається коливання значень правової ознаки в окремих елементах сукупності.

Для вимірювання і кількісної характеристики варіації використовується система абсолютних і відносних показників: розмах варіації, середнє лінійне відхилення, середнє квадратичне відхилення і коефіцієнт варіації.

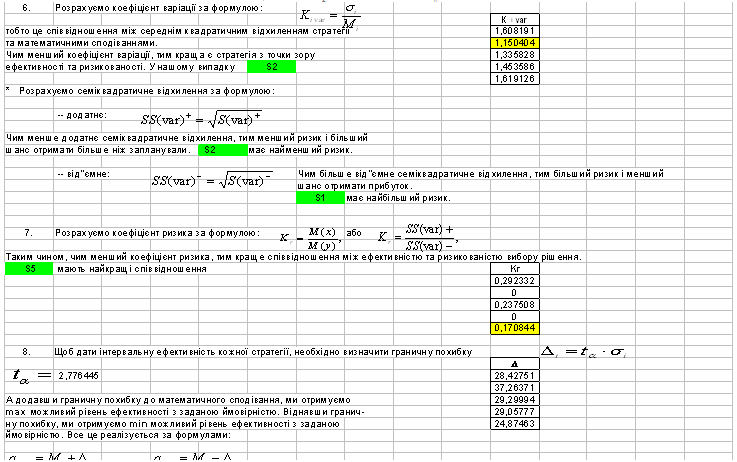
Коефіцієнт варіації це співвідношення між середнім квадратичним відхиленням стратегії та математичними сподіваннями. Чим менший коефіцієнт варіації, тим краща є стратегія з точки зору ефективності та ризикованості. Коефіцієнт варіації розраховується за формулою:

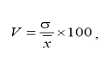
Рис 1.3 Значення коефіцієнта варіації для кожної стратегії

В нашому випадку стратегія S2 є найкращою з точки зору ефективності та ризикованості.

Середнє лінійне відхилення - це арифметична середня з абсолютних значень відхилень ознаки окремих варіантів від їх середньої арифметичної. Середнє лінійне відхилення обчислюється за формулою:

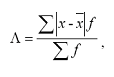
Середнє квадратичне відхилення - це корінь квадратний із середнього квадрата відхилень ознаки кожного варіанта від їх середньої арифметичної. Цей показник обчислюється за формулою:

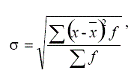
За цими показниками, стратегія S5 є найкращою.

Рис 1.4 Значення середнього квадратичного відхилення

Оцінка ризиків стратегій за розмахом і графічним зображенням.

Розмах варіації - це різниця між найбільшим і найменшим значеннями ознаки в сукупності. Залежно від того, в якому вигляді наведені первинні дані, техніка обчислення цього показника є різною: це може бути різниця між верхньою межею останнього інтервалу і нижньою межею першого інтервалу або різниця між середніми значеннями цих інтервалів.

Розмах варіації відображає тільки крайні значення ознаки, тому він є головним показником у тих випадках, коли варіанти повторюються один раз. В інших випадках розмах варіації застосовується для того, щоб одержати загальне уявлення про варіацію ознаки в усій сукупності. Розмах варіації показує ступінь оранжування (як дисперсія стандартного відхилення). Вона обчислюється за формулою:

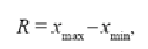
Чим більший розмах варіації, тим більшою ризикованістю володіє стратегія і навпаки, чим менший розмах варіації, тим меншою ризикованістю володіє стратегія. S5 має найменший ризик за цим показником [4].

Рис 1.5 Розмах варіації для кожної стратегії

Інтервали ефективності для кожної стратегії виглядають так:

Табл. 1.3

Інтервали ефективності

S1	-22,0608		6,366667		34,79417
S2	-25,597		11,66667		48,93038
S3	-21,3999		7,9		37,19994
S4	-21,8578		7,2		36,25777
S5	-19,3413		5,533333		30,40797

Виходячи з оцінки ризиків стратегій за різними показниками, можна зробити висновки, що стратегія S2 є найкращою з точки зору ефективності та ризикованості.

 

.3 Оцінка ризикованості стратегій за статистичними критеріями

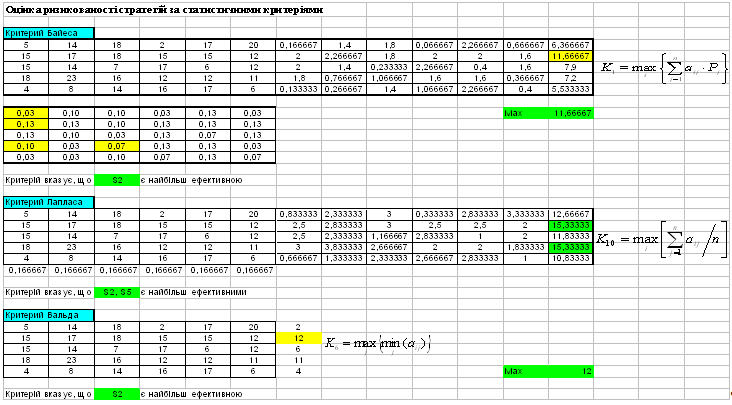
Критерій Байєса

За критерієм Байєса за оптимальні приймається та стратегія (чиста) Ai, при якій максимізується середній виграш a або мінімізується середній ризик r. Підраховуємо значення ∑(aijpj)

∑(a1,jpj) = 5*0.03+14*0.10+18*0.10+2*0.07+17*0,03+20*0,03=4.6

∑(a2,jpj) = 15*0.13+17*0.13+18*0.10+15*0.13+15*0.13+12*0.13=11.42

∑(a3,jpj) = 15*0.13+14*0.10+7*0.03+17*0.13+6*0.07+12*0.13=7.75

∑(a4,jpj) = 18*0.10+23*0.03+16*0.07+12*0.13+12*0.13+11*0.03=7.06

∑(a5,jpj) = 4*0.03+8*0.03+14*0.10+16*0.07+17*0.13+6*0.07=5.51

Табл. 1.3

Ai	П1	П2	П3	П4	П5	П6	∑(aijpj)
A1	0.16	1.4	1.8	0.06	2.26	0.6	6.36
A2	2	2.26	1.8	2	2	1.6	11.6
A3	2	1.4	0.23	2.26	0.4	1.6	7.9
A4	1.8	0.76	1.06	1.6	1.6	0.36	7.2
A5	0.13	0.26	1.4	1.06	2.26	0.4	5.53

Вибираємо з (6.36; 11.6; 7.9; 7.2; 5.53) максимальний елемент max=11.6 Висновок: вибираємо стратегію N=2.

Критерій Лапласа

Якщо ймовірності станів природи правдоподібні, для їх оцінки використовують принцип недостатнього підстави Лапласа, згідно якого всі стани природи покладаються рівноймовірними, тобто:

= q2 = ... = qn = 1/n.= 1/6

Табл. 1.4

Ai	П1	П2	П3	П4	П5	П6	∑(aij)
A1	2,66	2,83	1	0,66	1,33	2,33	10,83
A2	0,33	2,83	3,33	0,83	2,33	3	12,66
A3	2,5	2,5	2	2,5	2,83	3	15,33
A4	2	2	1,83	3	3,83	2,66	15,33
A5	2,83	1	2	2,5	2,33	1,16	11,83

Вибираємо з (10.83; 12.66; 15.33; 15.33; 11.83) максимальний елемент max=15.33. Висновок: вибираємо стратегію N=3.

Критерій Вальда

За критерієм Вальда за оптимальну приймається чиста стратегія, яка в найгірших умовах гарантує максимальний виграш, тобто:

= max(min aij)

Критерій Вальда орієнтує статистику на самі несприятливі стани природи, тобто цей критерій виражає песимістичну оцінку ситуації.

Табл. 1.5

Ai	П1	П2	П3	П4	П5	П6	max(aij)
A1	16	17	6	4	8	14	4
A2	2	17	20	5	14	18	2
A3	15	15	12	15	17	18	12
A4	12	12	11	18	23	16	11
A5	17	6	12	15	14	7	6

Вибираємо з (4; 2; 12; 11; 6) максимальний елемент max=12. Висновок: вибираємо стратегію N=3.

Критерій Севіджа

Критерій мінімального ризику Севіджа рекомендує вибирати в якості оптимальної стратегії ту, при якій величина максимального ризику мінімізується в найгірших умовах, тобто забезпечується:

= min(max rij)

Критерій Севіджа орієнтує статистику на самі несприятливі стани природи, тобто цей критерій виражає песимістичну оцінку ситуації. Знаходимо матрицю ризиків.

Ризик - міра невідповідності між різними можливими результатами прийняття певних стратегій. Максимальний виграш в j-му стовбці bj = max(aij) характеризує сприятливість стану природи.

. Розраховуємо 1-й стовбець матриці ризиків.

= 18-5 = 13; r21 = 18-15 = 3; r31 = 18-5 = 3; r41 = 18-18 = 0; r51 = 18-4 = 14;

. Розраховуємо 2-й стовбець матриці ризиків.

r12 = 23-14 = 9; r22 = 23-17 = 6; r32 = 23-14 = 9; r42 = 23-23 = 0; r52 = 23-8 = 15;

. Розраховуємо 3-й стовбець матриці ризиків.

= 18-18 = 0; r23 = 18-18 = 0; r33 = 18-7 = 11; r43 = 18-16 = 2; r53 = 18-14 = 4;

. Розраховуємо 4-й стовбець матриці ризиків.

= 17-2 = 15; r24 = 17-15 = 2; r34 = 17-17 = 0; r44 = 17-12 = 5; r54 = 17-16 = 1;

. Розраховуємо 5-й стовбець матриці ризиків.

= 17-17 = 0; r25 = 17-15 = 2; r35 = 17-6 = 11; r45 = 17-12 = 5; r55 = 17-17 = 0;

. Розраховуємо 6-й стовбець матриці ризиків.

= 20-20 = 0; r26 = 20-12 = 8; r36 = 20-12 = 8; r46 = 20-11 = 9; r56 = 20-6 = 14;

Табл. 1.6

Ai	П1	П2	П3	П4	П5	П6
A1	1	0	14	15	4
A2	15	0	0	13	9	0
A3	2	2	8	3	6	0
A4	5	5	9	0	0	2
A5	0	11	8	3	9	11

Результати обчислень оформимо у вигляді таблиці.

Табл. 1.7

Ai	П1	П2	П3	П4	П5	П6	min(aij)
A1	1	0	14	14	15	4	15
A2	15	0	0	13	9	0	15
A3	2	2	8	3	6	0	8
A4	5	5	9	0	0	2	9
A5	0	11	8	3	9	11	11

Вибираємо з (15; 8; 11; 9; 15) мінімальний елемент min=8. Висновок: вибираємо стратегію N=2.

Критерий Гурвіца

Критерій Гурвіца є критерієм песимізму - оптимізму. За оптимальну приймається та стратегія, для якої виконується співвідношення:

(si)

де si = y min(aij) + (1-y)max(aij)

При y=1 отримаємо критерій Вальди, при y=0 отримаємо - оптимістичний критерій (максимакс). Критерій Гурвіца враховує можливість як найгіршої, так і найкращої для людини поведінки природи. Чим гірші наслідки помилкових рішень, тим більше бажання застрахуватися від помилок, тим більше значення y наближається до 1.

Розраховуємо si.

= 0.5*2+(1-0.5)*20 = 11= 0.5*12+(1-0.5)*18 = 15= 0.5*6+(1-0.5)*17 = 11.5= 0.5*11+(1-0.5)*23 = 17= 0.5*4+(1-0.5)*17 = 10.5

Табл. 1.8

Ai	П1	П2	П3	П4	П5	П6	min(aij)	max(aij)	y min(aij) + (1-y)max(aij)
A1	5	14	18	2	17	20	2	20	11
A2	15	17	18	15	15	12	12	18	15
A3	15	14	7	17	6	12	6	17	11.5
A4	18	23	16	12	12	11	11	23	17
A5	4	8	14	16	17	6	4	17	10.5

Вибираємо з (11; 15; 11.5; 17; 10.5) максимальний елемент max=17. Висновок: вибираємо стратегію N=4.

Критерій Ходжа-Лемана

Для кожного рядка розраховуємо значення критерію за формулою:

= u∑aijpj + (1 - u)min(a)ij

Розраховуємо Wi.

= 0.5*3.91 + (1-0.5)*2 = 2.955= 0.5*5.51 + (1-0.5)*12 = 8.755= 0.5*4.16 + (1-0.5)*6 = 5.08= 0.5*5.97 + (1-0.5)*11 = 8.485= 0.5*3.68 + (1-0.5)*4 = 3.84

Табл. 1.9

Ai	П1	П2	П3	П4	П5	П6	∑(aijpj)	min(aj)	Wi
A1	0.16	1.4	1.8	0.06	2.26	0.66	6.36	2	4.18
A2	2	2.26	1.8	2	2	1.6	5.51	11.6	11.83
A3	2	1.4	0.23	2.26	0.4	1.6	4.16	7.9	6.95
A4	1.8	0.76	1.06	1.6	1.6	0.36	5.97	7.2	9.1
A5	0.13	0.26	1.4	1.06	2.26	0.4	3.68	5.53	4.76

Вибираємо з (4.18; 11.83; 6.95; 9.1; 4.76) максимальний елемент max=11.83. Висновок: вибираємо стратегію N=2.

Таким чином, в результаті рішення статистичної гри за різними критеріями частіше інших рекомендувалася стратегія A2.

Розв’язання задачі оцінки ефективності і ризикованості рішень фахівця з управління інформаційною безпекою у середовищі Excel подано у Додатку 1.

 

Розділ 2. Визначення оптимального плану випуску продукції на підприємствах засобами стохастичного програмування

 

.1 Постановка задачі

Задача: У структурний підрозділ ДСНС України необхідно закупити обладнання для створення КСЗІ. Було оголошено тендер на закупівлю товару, в результаті залишилось дві фірми, які надають такі послуги за доступною ціною. Кожне підприємство може запропонувати по 3 види кожної продукції А, В, С. Прибуток від реалізації одиниці продукції кожного виду є величиною випадковою, функція розподілу якого наведена в таблиці 2. Для виробництва продукції використовуються 2 види ресурсів, обсяг яких також є випадковим - функція розподілу яких наведена в таблиці 3. Норми витрат на одиницю продукції відомі і задаються в таблиці 4.

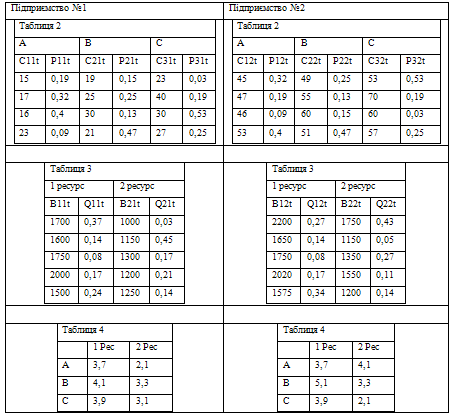
2.2 Побудова економіко-математичної моделі стохастичного програмування для визначення оптимального плану випуску продукції на підприємствах

Цільова функція залежить від випадкової величини, отже, математична модель даної задачі має вигляд:

,

.

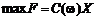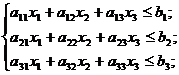
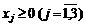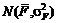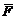Маємо одноетапну задачу стохастичного програмування з випадковими параметрами цільової функції. Очевидно, що величина F є також випадковою величиною з законом розподілу ймовірностей , де  - математичне сподівання, а  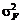- дисперсія [5].

Щоб розв’язати таку задачу, необхідно знайти математичне сподівання .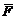

Позначимо символами 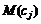,  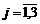- математичне сподівання прибутку від j-го виду продукції, тоді математична модель набуває вигляду:

,

.

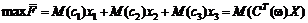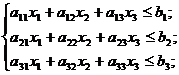
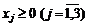У наведеній постановці маємо одноетапну задачу стохастичного програмування з М-моделлю, оскільки цільова функція є математичним сподіванням випадкової величини (прибутку).

Оскільки випадкова величина прибутку є дискретною і відомі значення відповідних ймовірностей 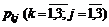, то можна безпосередньо обчислити значення 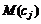 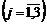. Отже, в числовому вигляді маємо:

Підприємство 1:

.

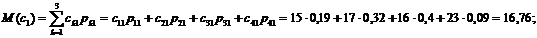
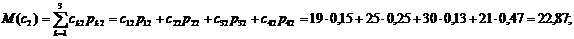
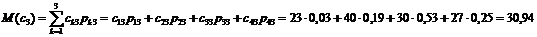Математична модель задачі набуває такого вигляду:

,

.

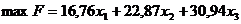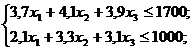
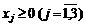Підприємство 2:

.

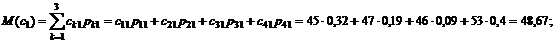
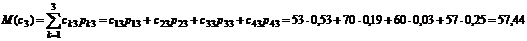Математична модель задачі набуває такого вигляду:

,

.

 

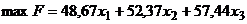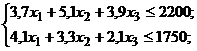
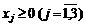.3 Визначення оптимально плану випуску продукції на підприємствах

Початкова задача зведена до задачі лінійного програмування, яку можна розв’язати симплексним методом, але оптимальний план детермінованої задачі є наближеним розв’язком початкової стохастичної.

Складемо симплекс-таблицю "Підприємство 1":

Табл. 2.1

Підприємство 1

Базис	В	x1	x2	x3	x4	x5
x4	-1700	-3.7	-4.1	-3.9	1	0
x5	-1000	-2.1	-3.3	-3.1	0	1
F(X0)	0	-16.76	-22.87	-30.94	0	0
x1	459.46	1	1.11	1.05	-0.27	0
x5	-35.14	0	-0.97	-0.89	-0.57	1
F(X0)	7700.54	0	-4.3	-13.27	-4.53	0
x1	459.46	1	1.11	1.05	-0.27	0
x5	-35.14	0	-0.97	-0.89	-0.57	1
F(X0)	7700.54	0	-4.3	-13.27	-4.53	0
x1	459.46	1	1.11	1.05	-0.27	0
x5	-35.14	0	-0.97	-0.89	-0.57	1
F(X0)	7700.54	0	-4.3	-13.27	-4.53	0
x1	459.46	1	1.11	-0.27	0
x5	-35.14	0	-0.97	-0.89	-0.57	1
F(X0)	7700.54	0	-4.3	-13.27	-4.53	0
x1	459.46	1	1.11	1.05	-0.27	0
x5	-35.14	0	-0.97	-0.89	-0.57	1
F(X0)	7700.54	0	-4.3	-13.27	-4.53	0
x1	459.46	1	1.11	1.05	-0.27	0
x5	35.14	0	-0.97	-0.89	-0.57	1
F(X0)	7700.54	0	-4.3	-13.27	-4.53	0
x1	417.68	1	-0.0488	0	-0.95	1.19
x3	39.63	0	1.1	1	0.64	-1.13
F(X1)	8226.65	0	10.27	0	3.97	-14.97
x1	417.68	1	-0.0488	0	-0.95	1.19
x3	39.63	0	1.1	1	0.64	-1.13
F(X1)	8226.65	0	10.27	0	3.97	-14.97

Оптимальним планом для підприємства 1 є 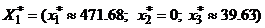, причому прибуток становить .

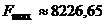Складемо симплекс-таблицю "Підприємство 2":

Табл. 2.2

Підприємство 2

Базис	В	x1	x2	x3	x4	x5
x4	2200	3.7	5.1	3.9	1	0
x5	1750	4.1	3.3	2.1	0	1
F(X0)	0	-48.67	-52.37	-57.44	0	0
x3	564.1	0.95	1.31	1	0.26	0
x5	565.38	2.11	0.55	0	-0.54	1
F(X1)	32402.05	5.82	22.74	0	14.73	0

Оптимальним планом для підприємства 2 є 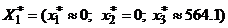, причому прибуток становить .

 

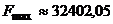.4 Оцінка міри ризику щодо одержання максимального прибутку за загальним коефіцієнтом варіації і коефіцієнтом варіації по від’ємній семіваріації

Для обрахування оцінки ризику щодо отримання максимального прибутку за загальним коефіцієнтом варіації необхідні такі дані:

Табл. 2.3

Варіанти проектів	Запроектований прибуток, тис. грн. Р	Значення ймовірності, Q	Сподіваний дохід, E (E=P*Q)
проект А	20	0,2	4
проект Б	10	0,6	6

Дисперсія - це середньозважена величина квадратів відхилень дійсних результатів від середніх очікуваних [6]. Обчислити дисперсію можна за такою формулою:

,

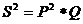де S2 - дисперсія,-запроектований прибуток,- значення ймовірності.

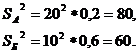
Середньоквадратичне відхилення визначають як корінь квадратний з дисперсії за формулою:

,

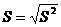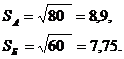
Коефіцієнт варіації - це відношення середньоквадратичного відхилення до середньої арифметичної, який показує ступінь відхилення отриманих значень:

,

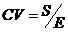де, S - середньоквадратичне значення,

Е - сподіваний дохід.

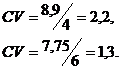
В результаті виконання математичних дій, отримаємо результат:

Табл. 2.4

Варіанти проектів	Дисперсія, S2	Середньоквадратичне відхилення, S	Коефіцієнт варіації, CV
Проект А	80	8,9	2,2
Проект Б	60	7,75	1,3

Ризик нижчий там, де коефіцієнт варіації нижчий. Тобто перевагу має той проект, де коефіцієнт варіації нижчий, а співвідношення ризику і доходу сприятливіше. Проведені вище розрахунки стверджують нижчу ризикованість проекту Б, тому капітальні вкладення доцільніше вкладати саме в цей проект.

Розділ 3. Фінансові ризики. Оцінка ступеня ризику цінних паперів. Оптимізація портфелю цінних паперів

 

.1 Постановка задачі

Нехай підрозділ ДСНС України у Львівській області вкладає свої кошти в сумі К для закупівлі відеокамер для захисту прилеглої території, сповіщувачів а також систем протипожежного захисту у 3 відділення банку (К1, К2, К3). Відома динаміка цін за місяць на банківському ринку. Розрахувати прибутковість сподіваної норми прибутку і ризик для трьох банків; дати характеристику систематичного ризику для кожного а також оптимізувати портфель цінних паперів за моделями Марковіца.

Табл. 3.1

Грошовий обіг банків за останній місяць

Дні	Ціна ак 1	Ціна ак 2	Ціна ак 3
1	66	52	77
2	61	104	81
3	83	36	42
4	56	31	60
5	49	92	61
6	75	72	42
7	62	94	95
8	71	93	90
9	53	61	47
10	26	103	86
11	54	48	100
12	57	50	83
13	50	69	82
14	64	52	29
15	41	104	50
16	74	38	88
17	88	66	65
18	75	102	65
19	59	95	94
20	55	58	37
21	52	37	43
22	28	53	45
23	37	83	83
24	65	59	83
25	79	64	94
26	41	55	39
27	91	42	100
28	102	50	56
29	95	61	73
30	53	77	103

 

.2 Модель Шарпа. Оцінка систематичного ризику

Для ефективної роботи на нестабільних банківських ринках була запропонована нова модель формування інвестиційного портфеля, яка отримала назву модель "Шарпа". Ця модель заснована на взаємозв'язку доходності кожного цінного паперу з усього безлічі N цінних паперів з прибутковістю одиничного портфеля їх цих паперів [7].

Модель "Шарпа" з'єднує прибутковість цінного паперу з прибутковістю одиничного портфеля і ризиком цього цінного паперу за допомогою функції лінійної регресії. Формула прибутковості цінного паперу наступна:

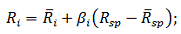
прибутковість цінного паперу;прибутковість одиничного портфеля;

βi-коефіцієнт чутливості до зміни прибутковості цінного паперу, коефіцієнт регресії в рівнянні прибутковості;

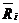- середня прибутковість цінного паперу;

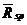- середня прибутковість одиничного портфеля.

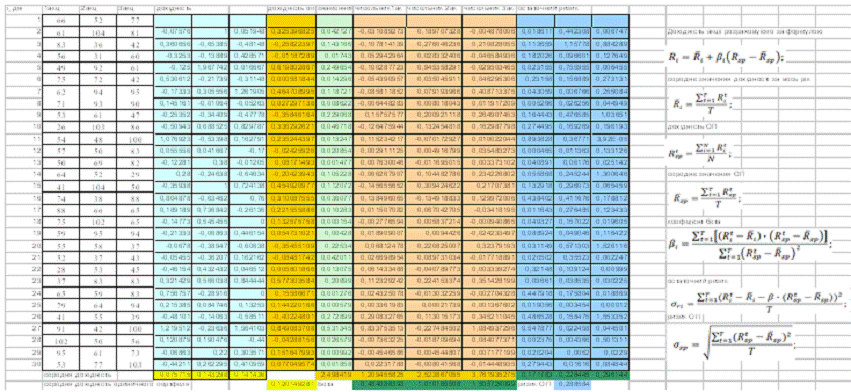
Табл. 3.2

Дохід цінних паперів

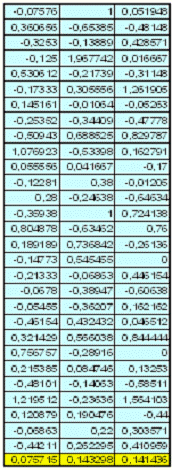
Дані, які виділені в останньому рядку - показник середньої дохідності. В моделі "Шарпа" ризик цінного паперу являє собою сукупність коефіцієнт бета і залишковоий ризик. Залишковим ризиком називають ступінь розкиду значень дохідності цінного паперу щодо лінії регресії [8].

Прибутковість в моделі "Шарпа" обчислюється так:

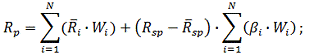
Табл. 3.3

Дохід одиничного портфеля

Ризик обчислюємо за такою формулою:

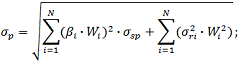
Завдання формування оптимального портфеля за моделлю "Шарпа", де ми максимізували дохідність інвестиційного портфеля і встановлюємо допустимий рівень ризику, буде виглядати наступним чином.

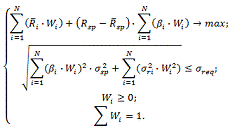
Обернена задача формування оптимального портфеля, де ми мінімізуємо загальний ризик інвестиційного портфеля з фіксованим рівнем прибутковості, має наступний вигляд:

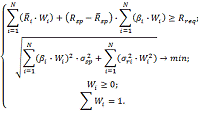
Наступним етапом розрахуємо прибутковості цих акцій за наступною формулою:

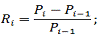
поточна прибутковість акції;поточна вартість акції;- вартість акції в попередньому періоді.

І аналогічно розраховуємо прибутковості всіх акцій.

Наступним етапом, для кожної акції розрахуємо середнє значення прибутковості за весь місяць, тобто за всі тимчасові відрізки. Формула для розрахунку наступна:

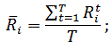
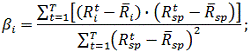
Бета

0,484088393

1,010185508

1,505726099

Рис. 3.1. Коефіцієнт бета (β)

Наступним етапом розрахуємо залишковий ризик, який являє собою ступінь розкиду прибутковості цінного паперу щодо лінії регресії [9]. Формула розрахунку залишкового ризику наступна:

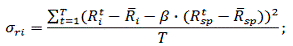
При формуванні інвестиційного портфеля з цих акцій нам ще буде потрібно розрахувати ризик одиничного портфеля:

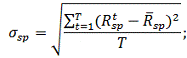
.3 Оптимізація портфеля цінних паперів за моделями Марковіца

Модель базується на тому, що показники прибутковості різних цінних паперів взаємопов'язані: із зростанням дохідності одних паперів спостерігається одночасне зростання і за іншими паперами, треті залишаються без змін, а в четвертих, навпаки, дохідність знижується. Такий вид залежності не детермінованим, тобто однозначно визначеним, а є стохастичним, і називається кореляцією.

Модель Марковіца має такі основні припущення: ,

за дохідність цінних паперів приймається математичне очікування дохідності;

за ризик цінних паперів приймається середньоквадратичне відхилення дохідності;

вважається, що дані минулих періодів, які використані при розрахунках дохідності і ризику, повністю відображають майбутні значення дохідності;

ступінь і характер взаємозв'язку між цінними паперами виражається коефіцієнтом лінійної кореляції [10].

Обрахуємо модель Марковіца покроково. У першому кроці введемо вхідні значення, згідно даного варіанту.

Табл. 3.4

Вхідні значення

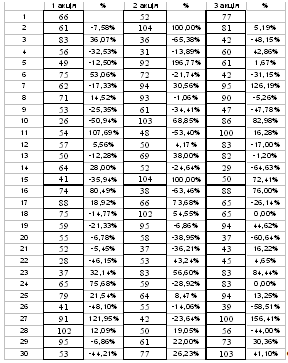
У другому кроці ми знаходимо очікуваний дохід і стандартне відхилення для кожної акції.

Табл. 3.5

Очікуваний дохід і стандартне відхилення для кожної акції

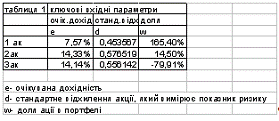
У третьому кроці будуємо дві транспоновані матриці для очікуваних доходів. В таблиці 3.5 стовпці е та w, їх і транспонуємо.

Табл. 3.6

Транспоновані матриці

wT	1,654046	0,14505	-0,799095
eT	0,075715	0,143298	0,1414356

Створюємо коваріаційну матрицю. Коваріація визначає залежність однієї акції від іншої.

В коваріаційній матриці показані залежності всіх акцій.

Табл. 3.7

Коваріаційна матриця

Обчислимо ризик (стандартне відхилення) портфеля. Формула дисперсії портфеля коштів:

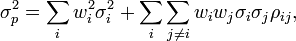
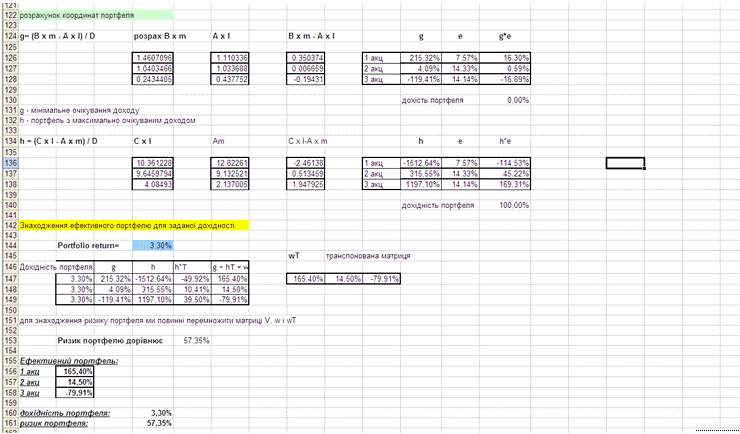
Після обрахунків за формулою, отримано значення дисперсії : 0,5735. Обчислимо координати портфеля:портфель з мінімальним сподіваним доходом; h - це портфель з максимальним сподіваним доходом [11].       

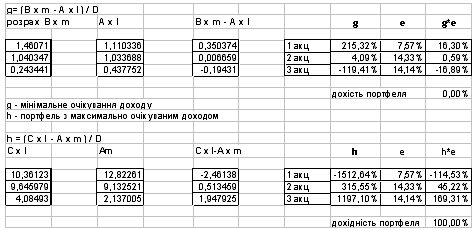
Рис. 3.2. Координати портфеля

Після чого знаходимо значення ефективного портфелю для заданої дохідності. Результат обрахунків наведено у Додатку В.

Обчислення коваріації у середовищі Excel наведено у Додатку Г.

Розділ 4. Застосування теорії графів в інформаційній безпеці

Постановка задачі: спроектувати захищену комп’ютерну мережу, яка містить 14 комп’ютерів. Відстані між комп’ютерами вказані на графі. Необхідно визначити зв`язки цієї мережі. Зокрема:

-       Виконати правильну нумерацію графу.

-       Побудувати мінімальне дерево-остов.

-       Визначити кількість шляхів від комп’ютера 1 до комп’ютера 14 та описати їх.

-       Визначити та вказати найкоротші шляхи.

Темпи виробництва, його масштаби та спеціалізація окремих галузей, багатопрофільні зв’язки обумовлюють необхідність розробки ефективних методів планування та управління, які б давали можливість оцінити змінний стан системи та передбачити її майбутнє, щоб оптимізувати відповідний процес і керувати його перебігом. Системи об’єктів дослідження разом зі зв’язками між ними називаються мережею. Графічне зображення множини досліджуваних об'єктів і зв'язків між ними називається графом.

Граф доцільно зображати у вигляді діаграми. На діаграмі об'єкти зображаються пронумерованими точками або кружками, які називаються вершинами, зв'язки між об'єктами -відрізками ліній, які з'єднують відповідні об'єкти. Якщо зв'язок між двома об'єктами А та В однобічний (від А до В є зв'язок, а зворотний зв'язок відсутній), то це зображається орієнтованим відрізком, стрілка якого відповідає напрямку зв'язку. Такий однобічний орієнтований відрізок називається дугою, а графічне зображення неорієнтованих попарних зв'язків між об'єктами -ребрами (ситуація, коли об'єкт А може бути пов'язаний з об'єктом В і навпаки). Граф, вершини якого мають лише однобічний зв'язки, називається орієнтованим, або орграфом. Маємо такий граф комп’ютерної мережі з вказаними відстанями між вершинами (комп`ютерами ). Виконаємо правильну нумерацію графа [12].

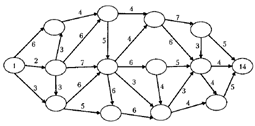
Рис. 4.1. Нумерація графа

Виконавши правильну нумерацію графа мережі, можна ефективно реалізувати алгоритм пошуку найкоротшого шляху між заданими вершинами. Реалізацію алгоритму приведено до побудови послідовності шляхів з однієї дуги, двох дуг, трьох дуг і т. д., які з’єднують вершини певного рангу з кінцевою вершиною. При цьому перегляд вершин виконується в послідовності зменшення їх номерів. На кожному етапі алгоритму відбувається перехід від вершини більш високого рангу до вершини меншого рангу за умови, що із множини всіх шляхів, які починаються в одній і тій же вершині, необхідно залишити для наступного кроку реалізації алгоритму лише найкоротший шлях від цієї вершини до завершальної. За правильної нумерації вершин такий упорядкований перехід у послідовності зменшення рангів відбувається автоматично, навіть за умови, коли нумерацію рангів вершин опущено.

Нумерацію виконаємо у довільному порядку, але від 1-ї вершини наступною по порядку буде та вершина, шлях до якої найкоротший і позначимо цю вершину 2, а всі інші нумеруємо довільно.

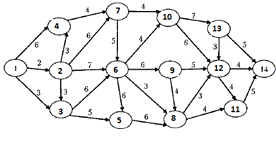
Рис. 4.2. Довільна нумерація вершин

При побудові графу планування захищеної мережі необхідно дотримуватися певних правил, щоб у подальшому можна було досліджувати його.

. Граф планування захищеної мережі не повинен мати "глухих кутів", тобто подій, з яких не виходить жодної роботи, окрім завершальної події. Поява "глухих кутів" подій свідчить про не досить ретельно виконаний аналіз взаємозв’язків.

. На графові не може бути "хвостових" подій (окрім вихідної події), тобто подій, яким не передує жодна робота. Такою "хвостовою"подією є подія яка не може відбутися, отже, не можуть відбутися і наступні події.

. Граф не може мати замкнутих контурів і петель, тобто шляхів, які з’єднують певні події з ними ж. Поява замкнутих контурів вимагає перегляду складу робіт та їх взаємозв’язків, після змістовного аналізу яких завжди з’являється можливість уникнути замкнутих контурів і петель.

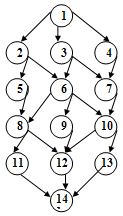
. На графові планування захищеної мережі повинна бути лише одна вихідна та лише одна завершальна подія [13].

Під час проектування залізниць,комп’ютерних мереж, ліній електропередач та інших ліній комунікації виникають проблеми побудови мережі з мінімальними витратами. Теоретично таке завдання успішно вирішується через побудову мінімального остовного дерева. Це завдання має низку методів рішення.

Інтерфейс програми має бути таким. Спочатку користувач вводить порядок графа, щоб програма могла сформувати таблицю введення даних (матриця терезів) з певним кількістю рядків і шпальт. Далі програма створює якийсь масивa [14] [14] (передбачається, що кількість вершин графа менше, або рівне 14). Цей масив ініціалізується: кожному a[i] [j] присвоюється 100 (передбачається, що максимальна довжина ребра менше 100). Потім дані з таблиці введення копіюються в масив. У осередку таблиці щось міститься у масив щось копіюється. Потім робиться цикл, який переривається тільки тоді, коли всі елементи масиву стануть знову рівні 100. Як працює цикл? Спочатку перебуває мінімальний елемент масиву (в галузі вище головною діагоналі матриці введення). Він запам'ятовується (змінна buf) і його присвоюється 100. Відповідно до алгоритму Прима, якщо ребро підходить мінімальний елемент викреслюється, а цикл починається з початку. Підходяще ребро чи ні? Складається масив з n елементів. Кожен елемент дорівнює 1 чи 0. Коли вершина входить у дерево, в елемент масиву з її номером записується 1 (спочатку всі елементи масиву, крім першого рівні 0). Щоб визначити підходяще ребро чи ні, треба подивитися, чи містяться одиниці в масиві (номери елементів рівні номерам вершин ребра). Якщо номерам вершин ребра відповідають обидві одиниця, отже, ребро не підходить. Якщо це основна умова не виконується - ребро підходить. Алгоритм перестає працювати, коли всі вершини включені у новий граф.

Окремо можна назвати процедуру малювання графа. Програма створює двомірний масив координат вершин графа (>krug [2] [14]). Вершини розташовуються на окружності на рівній відстані друг від друга. Такий спосіб дуже зручний, бо не треба тривожитися, що ребра будуть нашаровуватися одне на інше.

Визначимо кількість можливих шляхів від комп’ютера 1 до комп’ютера 14 та опишемо їх.

Розглянувши всі можливі шляхи та знайшовши їх довжини бачимо що в нашому графі захищеної мережі є лише два найкоротших шляхи 1,2,6,9,8,12,14 та 1,3,6,9,8,12,14 довжина яких складає 19 одиниць.

Пошук найкоротшого шляху між заданими вершинами (комп’ютерами) дає можливість визначити найкоротший шлях та найменшу відстань від довільної вершини графу, що в свою чергу дозволяє побудувати захищену комп’ютерну мережу з мінімальними витратами.

Висновки

В ході виконання курсової роботи мною було розглянуто та опрацьовано основні оптимальні показники діяльності структурного підрозділу ДСНС України. Під час роботи основну увагу булу приділено таким типам задач як: оцінка ефективності і ризикованості рішень фахівця ІБ, визначення оптимального плану засобами стохастичного програмування, фінансові ризики та оцінка ступеня ризику, застосування теорії графів в ІБ.

На основі розглянутого матеріалу можна зробити висновки, що при вирішенні складних завдань з багатьма факторами, для вибору оптимального рішення використовується математичне моделювання. У цьому випадку за допомогою математичної моделі відбирається серед безлічі єдиний варіант, виходячи з залежностей, закладених в алгоритмі, і прийнятого критерію оцінки ефективності. Експерт має критично оцінити практичний сенс пропонованого варіанту, врахувати вплив соціальних,психологічних та інших факторів, не врахованих в моделі.

Прийняття управлінських рішень передбачає формування певного уявлення про систему управління і процесів, що в ній відбуваються. Основним інструментальним методом такого формування є метод моделювання - спосіб теоретичних і практичних дій, спрямованих на створення і використання образу реального об’єкта (моделі), що відбиває основні властивості об’єкта.

Практичні завдання економіко-математичного моделювання містять: аналіз економічних об’єктів і процесів, прогнозування розвитку економічних процесів, прийняття управлінських рішень на всіх рівнях ієрархії управління.

Використана література

1       Основні підходи до моделювання інформаційної безпеки. [Електронний ресурс]. - Режим доступу: #"826101.files/image071.gif">

 

 

 

 

Додаток Б

Додаток В

Додаток Г