Моделирование кинетики гомогенных химических реакций
Моделирование кинетики гомогенных
химических реакций
Этапы развития химической кинетики
Химическая кинетика как наука о скоростях химических реакций начала
формироваться в 50-70 гг. XIX в.
В
1862-1867 гг. норвежские ученые Гульдберг и Вааге дали начальную формулировку
закона действующих масс [1]: при протекании химической реакции 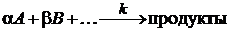 :
:
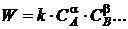 , (1.1)
, (1.1)
где
W - скорость химической реакции;
 -
концентрация i-го вещества,
-
концентрация i-го вещества, 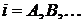 ;
;
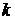 -
константа скорости;
-
константа скорости;
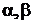 -
стехиометрические коэффициенты.
-
стехиометрические коэффициенты.
Химическая кинетика в полной мере была сформулирована в работах
Вант-Гоффа и Аррениуса в 80-х гг. XIX в.; был разъяснен смысл порядков реакций
и введено понятие энергии активации. Вант-Гофф ввел понятия моно-, би- и
полимолекулярных реакций:
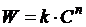 , (1.2)
, (1.2)
где
n - порядок реакции.
Вант-Гофф
и Аррениус, развивший его идеи, утверждали, что температура не есть причина
реакции, температура - причина изменения скорости реакции:
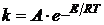 (Аррениус
в 1889 г.), (1.3)
(Аррениус
в 1889 г.), (1.3)
где
А - предэкспоненциальный множитель;
Е
- энергия активации;- газовая постоянная;
Т
- температура.
С
1890 г. величина энергии активации стала универсальной мерой реакционной
способности превращающихся веществ. Таким образом, в период 1860-1910 гг. была
создана формальная кинетика. Ясность и немногочисленность основных постулатов
отличают химическую кинетику периода Вант-Гоффа и Аррениуса.
В
последующем исходная цельность утрачивается, появляется много «кинетик»:
кинетика газофазных и жидкофазных реакций, каталитическая, ферментативная,
топохимическая и т. д.
Однако
для химика и до настоящего времени остаются наиболее важными две концепции:
1
Закон действующих
масс как закон простой реакции.
2
Сложность
механизма химической реакции.
Основные понятия химической кинетики
Кинетика гомогенных химических реакций
Скорость химической реакции есть изменение числа молей реагентов в
результате химического взаимодействия в единицу времени в единице объема (для
гомогенных реакций) или на единице поверхности (для гетерогенных процессов)
[2]:
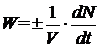 , (1.4)
, (1.4)
где
W - скорость химической реакции, 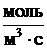 ;- объем,
м3;- число молей;- время, с.Согласно уравнению (1.4), вводя концентрацию
;- объем,
м3;- число молей;- время, с.Согласно уравнению (1.4), вводя концентрацию 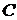 , получим
, получим
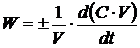 , (1.5)
, (1.5)
где
С - концентрация, моль/м3,
или
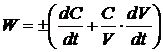 . (1.6)
. (1.6)
Для
реакций, идущих при постоянном объеме, второе слагаемое в уравнении (1.6) равно
нулю и, следовательно,
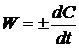 . (1.7)
. (1.7)
Одним
из основных законов химической кинетики, определяющим количественные
закономерности скоростей элементарных реакций, является закон действующих масс.
Согласно
кинетическому закону действующих масс скорость элементарной реакции при
заданной температуре пропорциональна концентрациям реагирующих веществ в
степенях, показывающих число вступающих во взаимодействие частиц [1, 2]:
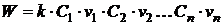 , (1.8)
, (1.8)
где
W - скорость химической реакции;
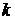 -
константа скорости;
-
константа скорости;
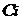 -
концентрации исходных веществ,
-
концентрации исходных веществ, 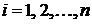 ;
;
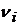 -
соответствующие стехиометрические коэффициенты в брутто-уравнении химической
реакции.
-
соответствующие стехиометрические коэффициенты в брутто-уравнении химической
реакции.
Уравнение
(1.8) справедливо для элементарных реакций. Для сложных реакций показатели
степени в уравнении (1.8) называются порядками реакции и могут принимать не только
целочисленные значения.
Константа
скорости химической реакции является функцией температуры, и зависимость от
температуры выражается законом Аррениуса:
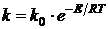 , (1.9)
, (1.9)
где
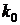 - предэкспоненциальный множитель;- энергия активации,
- предэкспоненциальный множитель;- энергия активации,
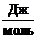 ;
;
Т
- температура, К;- газовая постоянная, 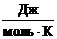 .
.
Рассмотрим
гомогенную реакцию
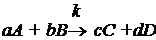 , (1.10)
, (1.10)
где
a, b, c, d - стехиометрические коэффициенты.
Согласно
закону действующих масс (1.8) скорость этой реакции запишется следующим
образом:
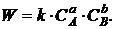 (1.11)
(1.11)
Между
скоростями реакции по отдельным компонентам (обозначим их WA, WB, WC, WD) и
общей скоростью реакции W существует зависимость
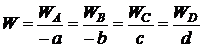 . (1.12)
. (1.12)
Отсюда
вытекают следующие выражения:
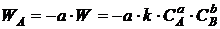 ;
;
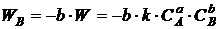 ;
;
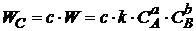 ; (1.13)
; (1.13)
 .
.
Чтобы
применить закон действующих масс к сложной химической реакции, необходимо
представить ее в виде элементарных стадий и применить этот закон к каждой
стадии отдельно.
Кинетические
уравнения
Кинетические
уравнения связывают скорость реакции с параметрами, от которых она зависит.
Наиболее важными из этих параметров являются концентрация, температура,
давление, активность катализатора.
Для
реакторов периодического действия, в которых концентрации реагирующих веществ в
каждой точке реакционного объема в ходе реакции непрерывно изменяются во
времени, скорость химической реакции есть количество молей данного вещества,
реагирующее в единицу времени в единице объема:
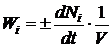 (1.14)
(1.14)
или
на единицу поверхности, для гетерогенных каталитических реакций
 , (1.15)
, (1.15)
где
Wi - скорость химической реакции, моль/м3×с;- текущее
количество i-го компонента реакционной смеси, моль;- объем реакционной смеси
или слоя катализатора (объем реактора), м3;- поверхность катализатора, м2;
d0 - удельная
поверхность катализатора, м2/м3;- время, с.
Для
реакторов непрерывного действия полного вытеснения, в которых при
установившемся режиме концентрация вещества непрерывно изменяется по длине
аппарата, скорость химической реакции есть количество молей проходящего через
реактор в единицу времени вещества, реагирующего в единице объема [3, 4]:
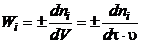 , (1.16)
, (1.16)
где
ni - мольный расход i-го компонента реакционной смеси, моль/с;
u - скорость подачи реакционной смеси, м3/с;
t - время контакта, с.
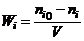 , (1.17)
, (1.17)
где
ni0 - начальное количество i-го компонента реакционной смеси, моль/с.
На
практике обычно измеряют скорость изменения мольной концентрации Сi (моль/м3;
моль/л).
Для
реактора периодического действия
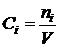 ,
, 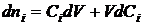 . (1.18)
. (1.18)
Для
реактора непрерывного действия
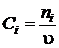 ,
, 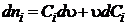 , (1.19)
, (1.19)
где
u - объемная скорость подачи реакционной смеси, м3/с.
Если
реакция не сопровождается изменением объема, то для реактора идеального
вытеснения
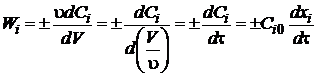 . (1.20)
. (1.20)
Для
реактора непрерывного перемешивания
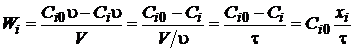 , (1.21)
, (1.21)
где
xi - степень превращения, 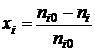 ;
;
t - среднее время
пребывания, t = V/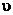 , с.
, с.
Методы
решения кинетических уравнений
Кинетические
модели - это системы обыкновенных дифференциальных уравнений, решение которых -
функции концентраций реагирующих веществ от независимого аргумента времени
[3-5].
Для
решения дифференциальных уравнений - интегрирования - применяются:
· табличный метод (с использованием таблиц интегралов) - применяется для
простейших дифференциальных уравнений;
· аналитические методы применяются для решения дифференциальных уравнений
первого порядка;
· численные методы, наиболее универсальные, позволяющие решать
системы дифференциальных уравнений любой сложности, являются основой
компьютерных методов анализа химико-технологических процессов [6, 7].
Численные методы
Простейшим численным методом решения обыкновенных дифференциальных
уравнений является метод Эйлера [5-7]. В основе этого метода лежит
аппроксимация производной при малых изменениях аргумента.
Например,
уравнение скорости химической реакции 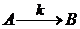 описывается
уравнением
описывается
уравнением
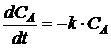 , (1.22)
, (1.22)
где СА - концентрация вещества, моль / л;
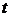 - время,
с.
- время,
с.
При
малых 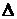 t можно приближённо принять, что
t можно приближённо принять, что
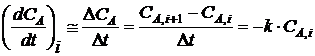 , (1.23)
, (1.23)
величину
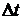 называют шагом интегрирования. Решая уравнение
(1.23), получим общую формулу Эйлера
называют шагом интегрирования. Решая уравнение
(1.23), получим общую формулу Эйлера
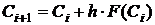 , (1.24)
, (1.24)
где
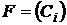 - правая часть дифференциального уравнения (например,
- правая часть дифференциального уравнения (например,
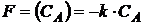 );
);
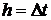 .
.
Задав начальные условия: при t = 0 С = С0, величину шага интегрирования
h, а также параметры уравнения, с помощью формулы (1.24) можно провести
пошаговый расчёт и получить решение данного уравнения (рис. 1.1).

Рис.
1.1. Графическая иллюстрация метода Эйлера
рганизуя циклические вычисления по уравнению (1.24), получим для
кинетической модели изменение концентраций реагирующих веществ от времени.
Величина шага интегрирования выбирается, исходя из достижения
минимального времени счёта и наименьшей ошибки вычислений.
Общие представления одношаговых методов решения обыкновенных
дифференциальных уравнений
Пусть имеется дифференциальное уравнение
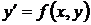 , (1.25)
, (1.25)
удовлетворяющее
начальному условию
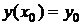 . (1.26)
. (1.26)
Требуется найти решение задачи (1.25), (1.26) на отрезке [x0, x0+X].
Выполним разбиение отрезка точками
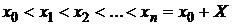 .
.
Этот
набор точек называют сеткой, а точки xi (i = i, n) -
узлами сетки.
Одношаговые
численные методы дают приближения yn к значениям точного решения y(xn) в каждом
узле сетки xn на основе известного приближения yn-1 к решению в предыдущем узле
xn-1. В общем виде их можно представить так [6, 7]:
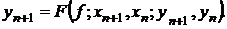 (1.27)
(1.27)
Для явных одношаговых методов функция F не зависит от yn+1.
Обозначая
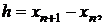
явные
одношаговые методы будем записывать также в виде
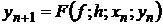 . (1.28)
. (1.28)
Явные методы типа Рунге-Кутта
Идея данного метода основана на вычислении приближённого решения y1 в
узле x0 + h в
виде линейной комбинации с постоянными коэффициентами [6, 7]:
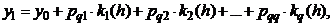 (1.29)
(1.29)
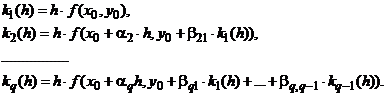
Числа
 выбираются так, чтобы разложение выражения (1.29) по
степеням h совпадало с разложением в ряд Тейлора:
выбираются так, чтобы разложение выражения (1.29) по
степеням h совпадало с разложением в ряд Тейлора:
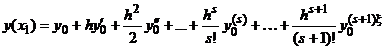 , (1.30)
, (1.30)
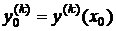 ,
, 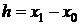 ,
, 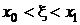 .
.
Это
эквивалентно следующему. Если ввести вспомогательную функцию
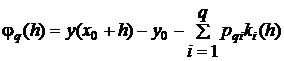 , (1.31)
, (1.31)
то ее разложение по степеням h должно начинаться с максимально возможной
степени:
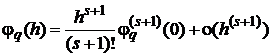 . (1.32)
. (1.32)
Если
можно определить эти постоянные так, чтобы разложение 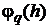 имело вид (1.32), то говорят, что формула (1.29) с
выбранными коэффициентами имеет порядок точности s.
имело вид (1.32), то говорят, что формула (1.29) с
выбранными коэффициентами имеет порядок точности s.
Величина
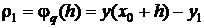 (1.33)
(1.33)
называется погрешностью метода на шаге, или локальной погрешностью
метода, а первое слагаемое в выражении (1.32)
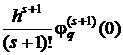 (1.34)
(1.34)
называется главным членом локальной погрешности метода.
Исследование
кинетики гомогенных химических реакций
Исследование
кинетических закономерностей протекания химической реакции методом
математического моделирования заключается в определении изменения концентраций
реагирующих веществ во времени при заданной температуре.
Пусть протекают химические реакции
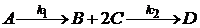 .
.
На
основании закона действующих масс запишем уравнения скоростей химических
реакций и составим кинетическую модель:
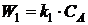 ;
;
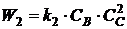 ;
;
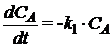 ;
;
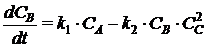 ;
;
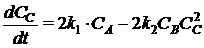 ;
;
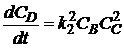 , (1.35)
, (1.35)
где СА, СВ, СС, СD -
концентрации веществ, моль/л;
ki
- константа скорости i-й химической реакции первого порядка, с-1; (для реакций
второго порядка размерность константы 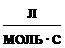 ; для
реакций третьего порядка размерность константы
; для
реакций третьего порядка размерность константы 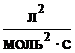 );-
скорость i-й химической реакции, моль/л×с; t - время
реакции, с.
);-
скорость i-й химической реакции, моль/л×с; t - время
реакции, с.

Рис. 1.2. Блок-схема расчета кинетики гомогенной химической реакции
методом Эйлера
Систему обыкновенных дифференциальных уравнений первого порядка (1.35)
можно решить с использованием численного метода Эйлера, алгоритм которого
записывается по уравнению (1.24).
Блок-схема расчета кинетики гомогенной химической реакции методом Эйлера
приведена на рис. 1.2.
Примеры программ расчета кинетики гомогенных химических реакций приведены
в Приложении А. Результаты исследования на математической модели (1.35) влияния
температуры на степень превращения исходного реагента и на концентрацию веществ
представлены на рис. 1.3, 1.4.

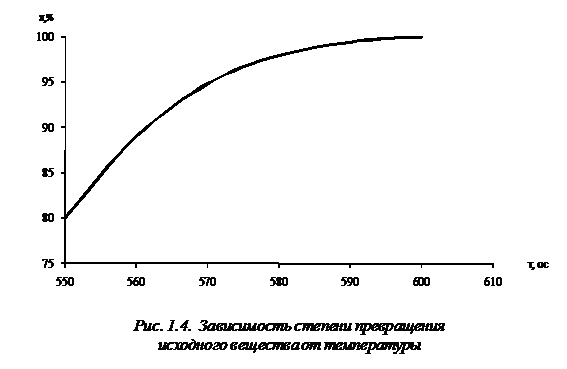
Полученные результаты позволяют сделать вывод об оптимальном времени
проведения процесса с целью получения целевого продукта. Математическая модель
(1.35) также позволяет исследовать влияние состава сырья на выход продуктов
реакции.
Необходимо учитывать, что скорость химической реакции зависит от
температуры, поэтому, чтобы использовать кинетическую модель (1.35) для
исследования процесса при различных температурах, необходимо ввести зависимость
константы скорости химической реакции от температуры по уравнению Аррениуса
(1.9).
Алгоритм метода Рунге-Кутта четвертого порядка можно записать следующим
образом:
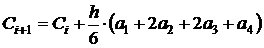 , (1.36)
, (1.36)
где ai - коэффициенты Рунге-Кутта, которые
рассчитываются по следующим формулам:
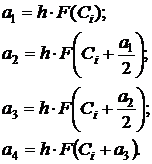 ; (1.37)
; (1.37)
Литература
кинетика химический
гомогенный
1. Панченков Г. М., Лебедев В. П. Химическая кинетика и
катализ. - М.: Химия, 1985. - 589 с.
. Яблонский Г. С., Быков В. И., Горбань А. И. Кинетические
модели каталитических реакций. - Новосибирск: Наука, 1983. - 254 с.
. Кафаров В. В. Методы кибернетики в химии и химической
технологии. - М.: Химия, 1988. - 489 с.
. Кравцов А. В., Новиков А. А., Коваль П. И. Методы анализа
химико- технологических процессов. - Томск: изд-во ТПУ, 1994. - 76 с.
. Кафаров В. В., Глебов М. В. Математическое моделирование
основных процессов химических производств. - М.: Высш. шк., 1991. - 400 с.
. Мойзес О. Е., Коваль П. И., Баженов Д. А., Кузьменко Е. А.
Информатика: учеб. пособие. В 2-х ч. - Томск, 1999. - 150 с.
. Турчак Л. И. Основы численных методов. - М.: Наука, 1987. -
320 с.
. Офицеров Д. В., Старых В. А. Программирование в
интегрированной среде Турбо-Паскаль. - Минск: Беларусь, 1992. - 240 с.
. Бесков В. С., Флор К. В. Моделирование каталитических
процессов и реакторов. - М.: Химия, 1991. - 252 с.
. Руд Р., Праустниц Дж., Шервуд Т. Свойства газов и жидкостей
/ под ред. Б. И. Соколова. - Л.: Химия, 1982. - 591 с.
. Танатаров М. А. и др. Технологические расчеты установок
переработки нефти. - М.: Химия, 1987. - 350 с.
. Жоров Ю. М. Термодинамика химических процессов. - М.:
Химия, 1985
. Расчеты основных процессов и аппаратов нефтепереработки:
справочник / под ред. Е. Н. Судакова. - М.: Химия, 1979. - 568 с.
. Кафаров В. В. Разделение многокомпонентных систем в
химической технологии. Методы расчета. - М.: Московский химико-технологический
институт, 1987. - 84 с.