Производные функций
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Национальный
исследовательский Томский политехнический Университет»
Институт
дистанционного образования
Автоматизация
технологических процессов и производств (в нефтегазовой области)
Индивидуальное
домашнее задание № 1
по
дисциплине:
Математический
анализ 2
Вариант
14
Томск
¾
2013
. Найдите частные производные первого порядка
.1 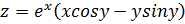 ; 1.3.
; 1.3.
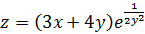 ;
;
.2 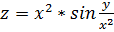 ; 1.4.
; 1.4.
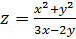 ;
;
Решение
.1 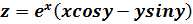 ;
;
При нахождении частной производной 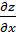 переменную
y рассматриваем как константу
переменную
y рассматриваем как константу
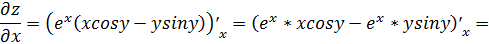
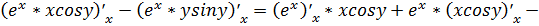
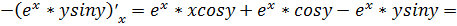
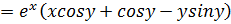 .
.
При нахождении частной производной 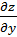 переменную
x рассматриваем как константу
переменную
x рассматриваем как константу
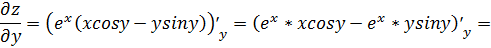
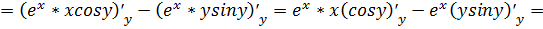
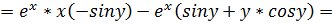
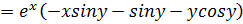 .
.
1.2 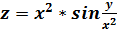
При нахождении частной производной 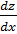 переменную
y рассматриваем как константу
переменную
y рассматриваем как константу
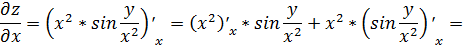
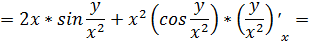
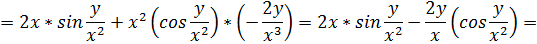
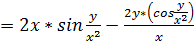 .
.
При нахождении частной производной 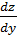 переменную
x рассматриваем как константу
переменную
x рассматриваем как константу
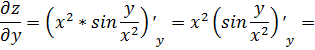
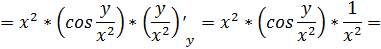
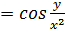 .
.
.3 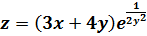
При нахождении частной производной 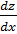 переменную
y рассматриваем как константу
переменную
y рассматриваем как константу
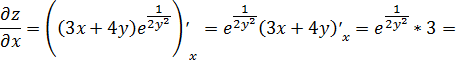
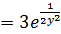 .
.
При нахождении частной производной 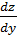 переменную
x рассматриваем как константу
переменную
x рассматриваем как константу
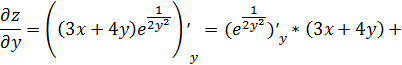
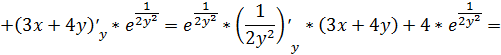
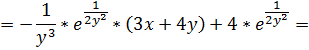
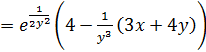 .
.
.4 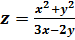
При нахождении частной производной 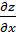 переменную
y рассматриваем как константу
переменную
y рассматриваем как константу
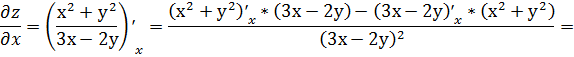
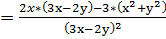 .
.
При нахождении частной производной 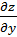 переменную
x рассматриваем как константу
переменную
x рассматриваем как константу
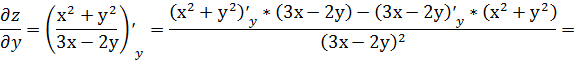
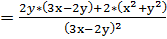 .
.
2. Найдите и постройте область определения
функции
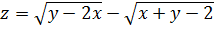 .
.
Решение
Областью определения функции 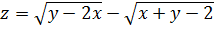 является
множество всех точек плоскости, для которых определены выражения
является
множество всех точек плоскости, для которых определены выражения 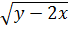 и
и
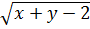 .
Выражение
.
Выражение 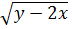 определенно тогда и
только тогда, когда подкоренное выражение неотрицательно, т.е. при
определенно тогда и
только тогда, когда подкоренное выражение неотрицательно, т.е. при 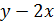 ≥0.
То же самое можно сказать и о выражении
≥0.
То же самое можно сказать и о выражении 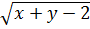 ,
т.е.
,
т.е. 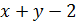 ≥0.
≥0.
Таким образом, область определения данной
функции задается системой неравенств
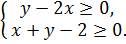
Первому неравенству 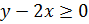 удовлетворяют
координаты всех точек плоскости, расположенных выше и на прямой
удовлетворяют
координаты всех точек плоскости, расположенных выше и на прямой 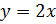 .
Второму неравенству
.
Второму неравенству 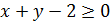 удовлетворяют
координаты всех точек плоскости, расположенных выше и на прямой
удовлетворяют
координаты всех точек плоскости, расположенных выше и на прямой 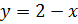 .
.
Область определения функции 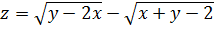 получается
в результате пересечения указанных множеств.
получается
в результате пересечения указанных множеств.
Найдем хотя бы по две точке:
|
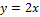
|
|
|
|
x
|
0
|
1
|
|
x
|
0
|
1
|
|
y
|
0
|
|
y
|
2
|
1
|
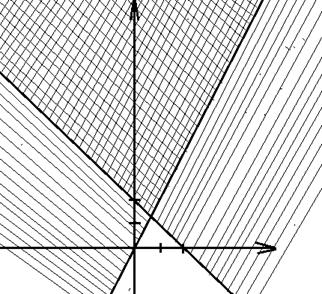
Указанной совокупности удовлетворяет множество
точек плоскости, расположенных в первой и второй координатных четвертях.
3. Найдите производную 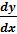 от
функции, заданной неявно
от
функции, заданной неявно
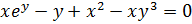 .
.
Решение
Равенство F(x,y)=0 определяет функцию одной
переменной y=y(x), заданную неявно. Для нахождения производной 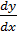 воспользуемся
формулой
воспользуемся
формулой
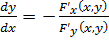 , где
, где 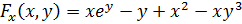 .
.
Найдем сначала 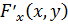 и
и
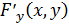
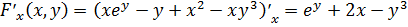 ;
;
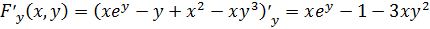 ;
;
Подставим 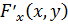 и
и
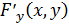 в
формулу
в
формулу 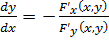 .
Получим
.
Получим
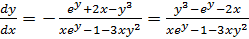 .
.
4. Найдите полный дифференциал dz функции
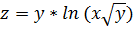 .
.
Решение
Полный дифференциал функции двух переменных 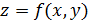 находится
по формуле
находится
по формуле
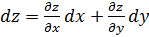 .
.
Найдем сначала частные производные первого
порядка 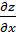 и
и
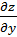 данной
функции
данной
функции 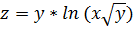 ;
;
 ;
;
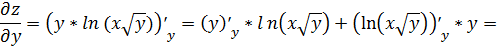
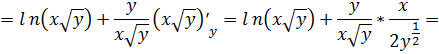
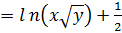 ;
;
Тогда 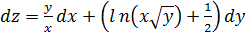 .
.
5. Докажите, что функция 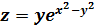 удовлетворяет
уравнению
удовлетворяет
уравнению
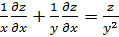 .
.
Решение
Найдем сначала частные производные первого
порядка 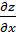 и
и
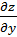 данной
функции
данной
функции 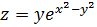 ;
;
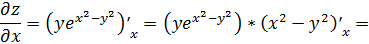
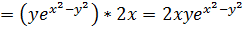 .
.
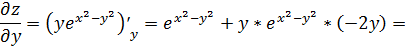
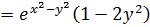 .
.
Теперь подставим частные производные. Получаем
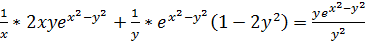 .
.
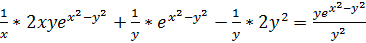 .
.
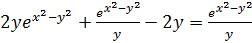 .
.
Умножаем правую и левую часть на y и делим на 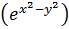 .
.
Получаем
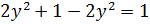 ,
,
=1.
Получили тождество, следовательно, функция 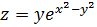 удовлетворяет
уравнению
удовлетворяет
уравнению 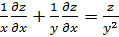
6. Исследуйте функцию 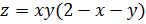 на
экстремум.
на
экстремум.
Решение
Сначала найдем стационарные точки заданной
функции
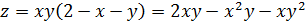 .
.
Для этого:
Находим частные производные первого порядка
 .
.
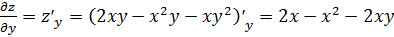 .
.
Приравниваем частные производные к нулю и решаем
систему уравнений
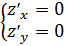 ⇒
⇒
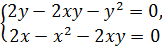
Решим систему уравнений
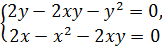 ⇒
⇒
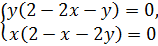 ⇒
⇒
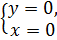
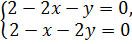 ⇒
⇒
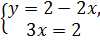 ⇒
⇒
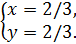
Таким образом, у нас две точки. Точка М1(0;0) и
точка М2(2/3;2/3), они являются стационарными для исследуемой функции. Проверим
достаточные условия экстремума в точке М1(0;0). Для этого найдем частные
производные второго порядка заданной функции и вычислим их значения в
стационарной точке
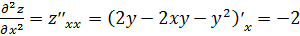 .
.
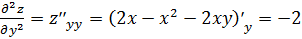 .
.
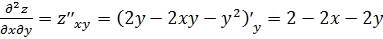 .
.
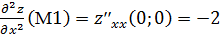 ,
,
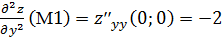 ,
,
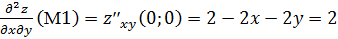 .
.
Составим ∆=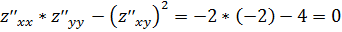 .
.
Так как ∆=0, это значит неопределенность.
Для исследования привлекают высшие производные. Мы этого делать не будем, по
крайней мере в этом семестре.
Рассмотрим точно также точку М2(2/3;2/3),
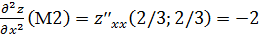 ,
,
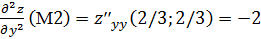 ,
,
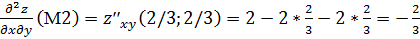 .
.
Составим ∆=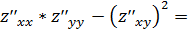
Так как ∆>0 и 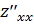 <0,
то точка М2(2/3;2/3) является для исследуемой функции точкой максимума.
<0,
то точка М2(2/3;2/3) является для исследуемой функции точкой максимума.
Чтобы найти значения максимума, координаты точки
максимума x=2/3, y=2/3 подставим в функцию
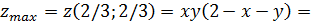
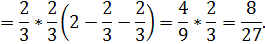
Ответ: 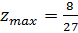 .
.
7. Найдите наименьшее и наибольшее значения
функции
производная функция
дифференциал экстремум
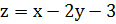 в
замкнутой области, ограниченной линиями
в
замкнутой области, ограниченной линиями
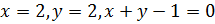 .
.
Решение
Сначала находим частные производные первого
порядка заданной функции 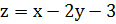
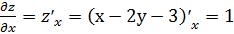 ;
;
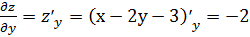 .
.
Так как частные производные не равны нулю, то
функция не имеет стационарных точек.
Исследуем функцию на границе области. Уравнения 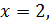
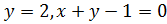 определяют на
плоскости треугольник OAB.
определяют на
плоскости треугольник OAB.
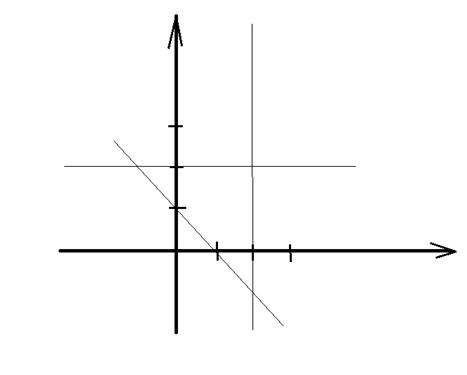
На отрезке OA , где у=2, имеем  ,
,
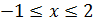 . Задача сводится к
отысканию наибольшего и наименьшего значений функции
. Задача сводится к
отысканию наибольшего и наименьшего значений функции 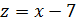 на
отрезке
на
отрезке 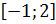 .
Так как z'=1>0, то функция всюду возрастает на отрезке
.
Так как z'=1>0, то функция всюду возрастает на отрезке 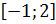 .
Следовательно, достигает своих наибольшего и наименьшего значений на концах
отрезка, т.е. в точках А
.
Следовательно, достигает своих наибольшего и наименьшего значений на концах
отрезка, т.е. в точках А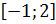 и О
и О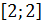 ,
соответственно. Находим
,
соответственно. Находим
z(А)=z(-1,2)=-8,(O)=z(2,2)=-5.
На отрезке ОВ где х=2, имеем 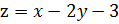 ,
,
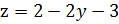 ,
,
 ,
, .
Задача сводится к отысканию наибольшего и наименьшего значений функции
.
Задача сводится к отысканию наибольшего и наименьшего значений функции  на
отрезке
на
отрезке 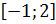 .
Так как z'=-2<0, то функция всюду убывает на отрезке
.
Так как z'=-2<0, то функция всюду убывает на отрезке 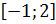 .
Следовательно, достигает своих наибольшего и наименьшего значений на концах
отрезка, т.е. в точках В
.
Следовательно, достигает своих наибольшего и наименьшего значений на концах
отрезка, т.е. в точках В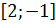 и О
и О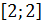 ,
соответственно. Находим
,
соответственно. Находим
z(В)=z(2,-1)=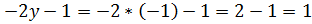 ,(O)=z(2,2)=-5
,(O)=z(2,2)=-5
На отрезке АВ где 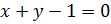 ,
т.е.
,
т.е. 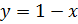 ,
имеем
,
имеем
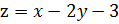 ,
, 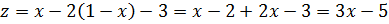 ,
,
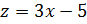 ,
, 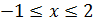 .
Задача сводится к отысканию наибольшего и наименьшего значений функции
.
Задача сводится к отысканию наибольшего и наименьшего значений функции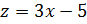 на отрезке
на отрезке 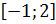 . Так как
z'=3>0, то функция всюду возрастает на отрезке
. Так как
z'=3>0, то функция всюду возрастает на отрезке 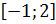 .
Следовательно, достигает своих наибольшего и наименьшего значений на концах
отрезка, т.е. в точках А
.
Следовательно, достигает своих наибольшего и наименьшего значений на концах
отрезка, т.е. в точках А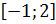 и В
и В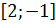 ,
соответственно. Находим
,
соответственно. Находим
z(В)=z(2,-1)=1(А)=z(-1,2)=-8
Выбирая из всех полученных значений исходной
функции наибольшее и наименьшее значения, имеем
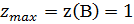 и
и 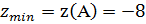 .
.
Ответ: 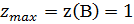 и
и
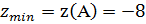 .
.
8. Найдите частные производные второго порядка
от функций
8.1 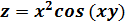 ; 8.2
; 8.2
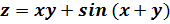 .
.
Решение
8.1 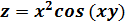
Найдем сначала частные производные первого
порядка
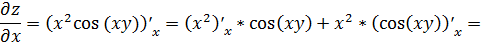
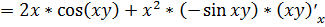 =
=
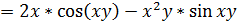 .
.
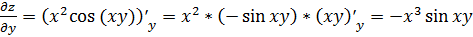 .
.
Тогда
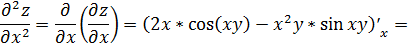
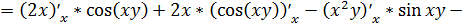
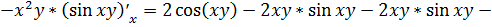
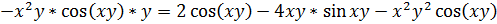 .
.
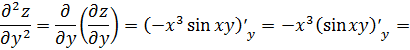
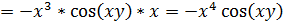 .
.
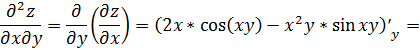
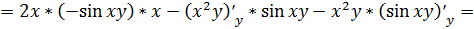
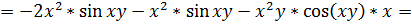
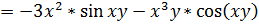 .
.
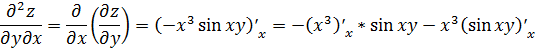
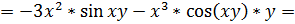
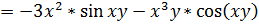 .
.
.2 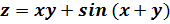
Найдем сначала частные производные первого
порядка
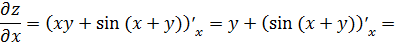
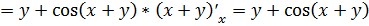 .
.
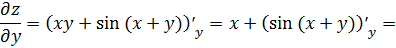
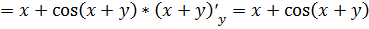 .
.
Тогда
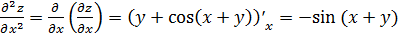 .
.
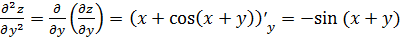 .
.
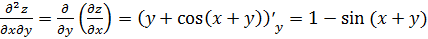 .
.
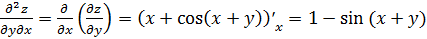 .
.
. Даны комплексные числа 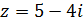 и
и
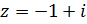 .
Найдите
.
Найдите
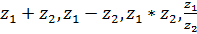 .
Ответы представьте в алгебраической форме
.
Ответы представьте в алгебраической форме
Решение
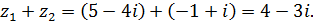
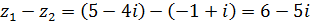 .
.
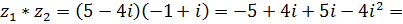
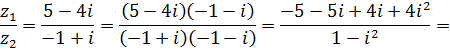
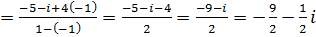 .
.
10. Постройте множество точек D комплексной
плоскости, удовлетворяющих условию 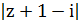 ≤2
≤2
Решение
Преобразуем выражение под знаком модуля:
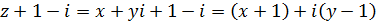 .
.
Найдем модуль этого выражения
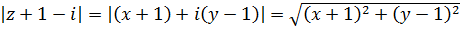 .
.
Получилось вот такое неравенство
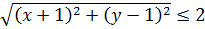
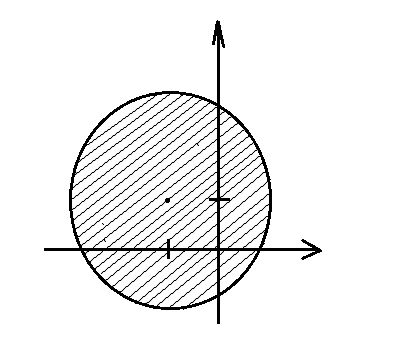
Таким образом, область D представляет собой
круговое кольцо, ограниченное окружностью 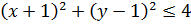 ,
с центром в точке (-1;1) радиусом r=2.
,
с центром в точке (-1;1) радиусом r=2.
Список использованной литературы
Высшая
математика. Ч. Ш: учебное пособие / А. В. Козловских; Томский политехнический
университет 2-е изд., перераб. доп. - Томск: Изд-во Томского политехнического
университета, 2007. - 91 с.