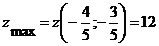Частные производные. Экстремумы функций
БЕЛОРУССКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет
непрерывного и дистанционного обучения
Специальность:
искусственный интеллект
КОНТРОЛЬНАЯ
РАБОТА ПО ВЫСШЕЙ МАТЕМАТИКЕ
Минск 2013
Задача 1.
Дана функция 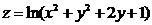 . Показать
что
. Показать
что 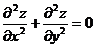
Решение:
Найдем частные производные 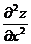 и
и 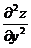 .
.
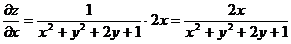
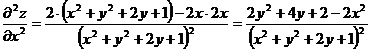
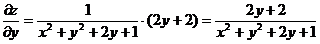
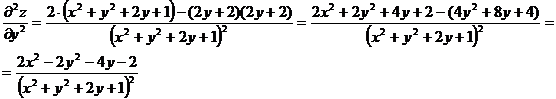
Получаем:
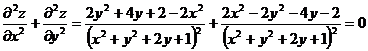
Задача 2.
Дана функция 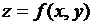 и две точки
А(х0 , y0) и В (х1,,y1).
Требуется:
и две точки
А(х0 , y0) и В (х1,,y1).
Требуется:
) вычислить значение z1 функции в
точке В;
функции в
точке В;
) вычислить приближенное значение 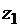 функции в
точке В исходя из значения z0 функции в
точке А, заменив приращение функции при переходе от точки А к точке В
дифференциалом;
функции в
точке В исходя из значения z0 функции в
точке А, заменив приращение функции при переходе от точки А к точке В
дифференциалом;
) составить уравнение касательной
плоскости к поверхности 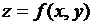 в
точке
в
точке 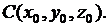
Решение:
1) 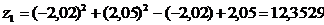
) 
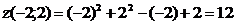
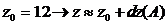
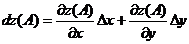
Найдем частные производные 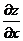 и
и 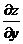 .
.
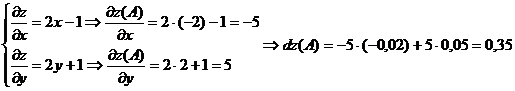
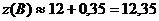
) уравнение касательной
плоскости к поверхности 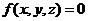 в
точке
в
точке 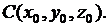
Уравнение касательной плоскости к
поверхности 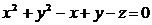 в точке
в точке 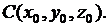 имеет вид:
имеет вид:
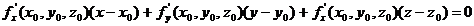
Найдем частные производные 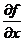 ,
, 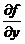 и
и 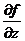 .
.
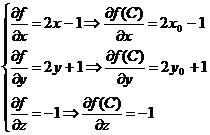
Искомое уравнение касательной плоскости имеет
вид
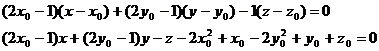
Так как в условии задачи координаты точки С не
заданы, следовательно уравнение касательной плоскости может быть найдено только
в общем виде.
Ответ:
1) 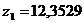
) 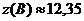
Задача 3.
Исследовать на экстремум функции двух
переменных.
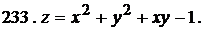
Решение:
В соответствие с достаточным условием экстремума
функции двух переменных, найдем точки, удовлетворяющие условию:
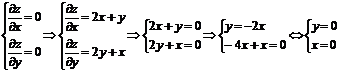
Получили одну стационарную точку
(0;0)
найдем все вторые частные
производные от функции и составим дискриминант 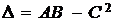 :
:
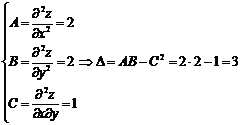
Так как дискриминант больше нуля и А>0,
то функция z имеет
минимум в точке (0;0)
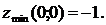
Ответ: функция z
имеет минимум в точке (0;0).
Задача 4.
Дана функция 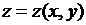 , точка
, точка 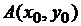 и вектор а.
Найти:
и вектор а.
Найти:
) grad z в точке 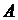 ;
;
) производную в точке 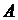 в
направлении вектора а.
в
направлении вектора а.

Решение:
1) Согласно определению
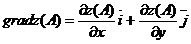
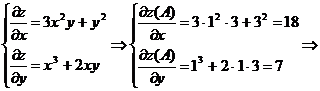
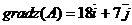
2) Производную по направлению вектора 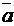 в
точке А находим по формуле
в
точке А находим по формуле
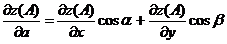
Где 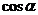 ,
, 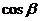 - направляющие косинусы:
- направляющие косинусы:
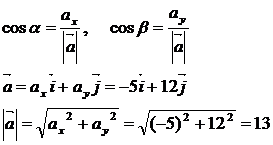
Получаем:
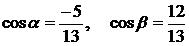
Частные производные в точке А уже
найдены. Окончательно получаем:
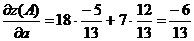
Ответ:
1) 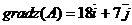
) 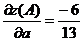
Задача 5.
Найти условный экстремум функции при
помощи функции Лагранжа. 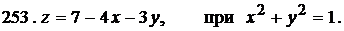
Решение:
Составляем функцию Лагранжа:
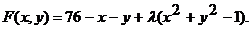
Имеем:
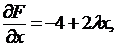
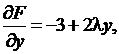
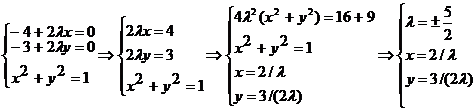
Получаем:
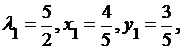
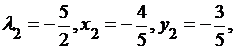
Находим:
производный функция лагранж
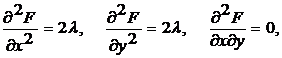
и вычисляем второй дифференциал
функции Лагранжа
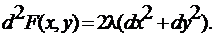
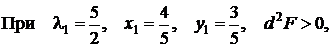
в этой точке условный минимум, 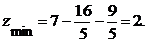
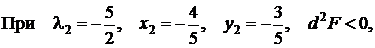
в этой точке условный максимум, 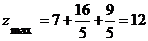
Ответ: 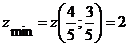 ,
,