|
Значение ПКГ изделий в начале эксперимента (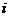 =1)[0,7500; 0,8900; 0,9500; 0,9800; 1,0100] =1)[0,7500; 0,8900; 0,9500; 0,9800; 1,0100]
|
|
|
Значение ПКГ изделий в конце эксперимента (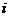 =16)[15,9000; 15,6000; 15,9500; 16,1700; 16,300] =16)[15,9000; 15,6000; 15,9500; 16,1700; 16,300]
|
|
|
Границы поля допуска
|
[0,5;18]
|
|
Метод оценки
|
МУН
|
|
Доверительная вероятность прогноза
|
0,9
|
1. Определить оценки
распределения функций плотности вероятности ПКГ в начале и конце эксперимента
(при 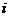 =1
и при
=1
и при 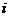 =16)
по методу уменьшения неопределенности (МУН)
=16)
по методу уменьшения неопределенности (МУН)
Метод уменьшения
неопределенностей (МУН) - это новая реализация МПВ (метода прямоугольных
вкладов), которая возникла в процессе его развития. МУН основан на
использовании нормированного равномерного распределения, заданного в интервале
[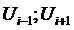 ]
вместо прямоугольного вклада шириной
]
вместо прямоугольного вклада шириной 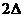 , построенного около
точки с координатой
, построенного около
точки с координатой 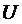 .
.
При этом для выражения
функции распределения 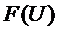 используют
кусочно-линейную интерполяцию
используют
кусочно-линейную интерполяцию
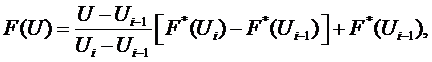 (П.1)
(П.1)
где 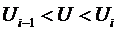 .
.
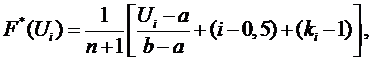 (П.2)
(П.2)
где 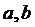 -
нижняя и верхняя границы интервала значения случайной величины
-
нижняя и верхняя границы интервала значения случайной величины 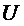 ;
;
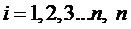 - объем выборки;
- объем выборки;
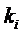 - число одинаковых
реализаций
- число одинаковых
реализаций 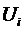 .
.
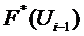 оценивается аналогично
оценивается аналогично 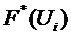 .
.
Для нахождения функции
плотности вероятности следует воспользоваться данными графика 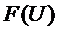 и
выражением
и
выражением
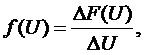 (П.3)
(П.3)
где 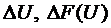 -
приращение аргумента
-
приращение аргумента 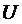 и
соответствующее приращение функции
и
соответствующее приращение функции 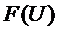 .
.
По данным таблицы П.2
для значений ПКГ в начале эксперимента составим вариационный ряд: 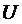
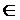 {0,7500; 0,8900; 0,9500;
0,9800; 1,0100}.
{0,7500; 0,8900; 0,9500;
0,9800; 1,0100}.
Границы поля допуска 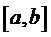 :
:
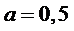 ,
, 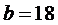 ,
,
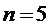 .
.
Статистические данные
значений ПКГ разбивают поле допуска значений ПКГ на интервалы:
1 участок
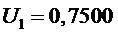 ,
,
 .
.
Определяем оценку
функции распределения (интегральный закон распределения)
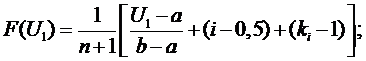
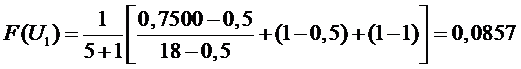 .
.
Определяем оценку
функции плотности распределения вероятности (дифференциальный закон
распределения вероятности)
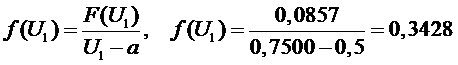
2 участок
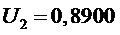 ,
,
 .
.
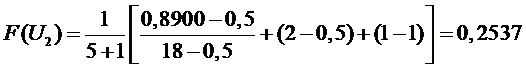
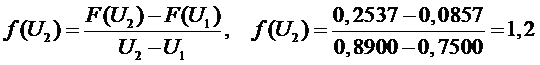
3 участок
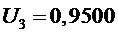 ,
,

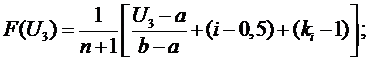
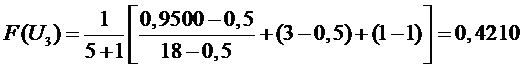 ;
;
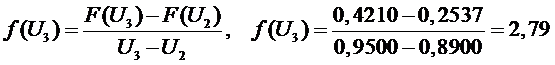
участок
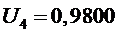 ,
,  .
.
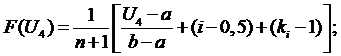

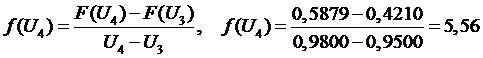
5 участок
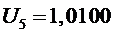 ,
,
 .
.
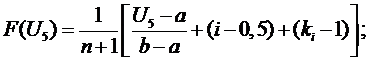
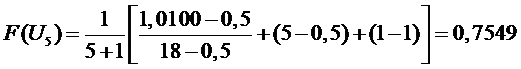 ;
;
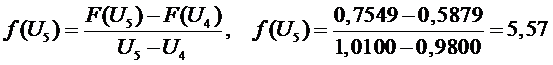
6
участок 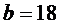 ,
,
 .
.
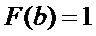
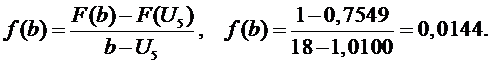
Проверка осуществляется
суммированием площадей фигур, находящихся под ломаной 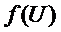 ,
т.е.
,
т.е.
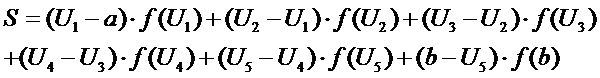
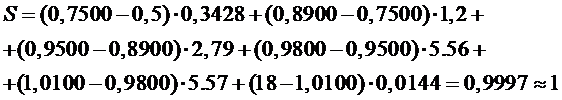
Графики 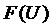 и
и
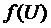 приведены
на рис.П.1 и П.2
приведены
на рис.П.1 и П.2
В начале эксперимента
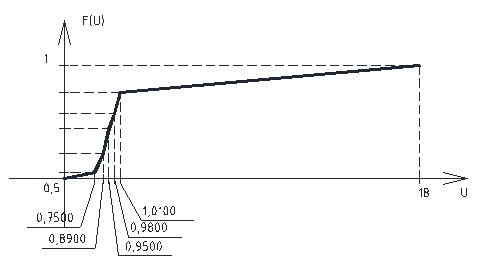
Рис. 1. График функции 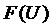

Рис. 2.График функции 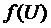
Математическое ожидание
(в начале эксперимента)
Математическое ожидание
- это значение случайной величины, относительно которого группируются все
заданные значения. Математическое ожидание(непрерывной случайной величины) есть
интеграл вида
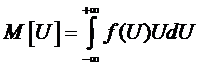 (П.4)
(П.4)
Находим математическое
ожидание
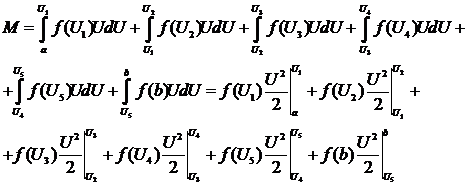
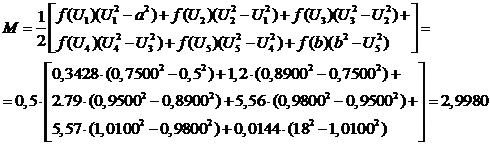
Дисперсия случайной
величины (в начале эксперимента)
Дисперсия - мера
рассеяния случайной величины около своего математического ожидания.
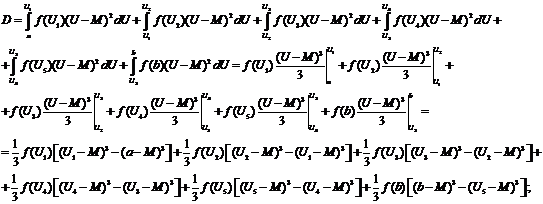
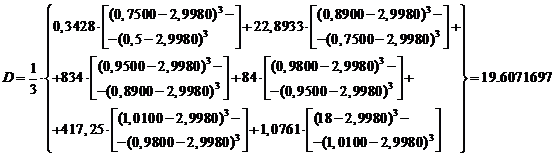
Среднее квадратическое
значение отклонения случайной величины относительно математического ожидания
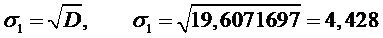 .
.
По данным табл. П.2 для
значений ПКГ в конце эксперимента составим вариационный ряд: 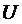
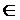 {15,6000; 15,9000;
15,9500; 16,1700; 16,3000}.
{15,6000; 15,9000;
15,9500; 16,1700; 16,3000}.
Границы поля допуска: 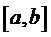
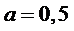 ,
, 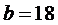 ,
,
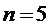 .
.
Статические данные
значений ПКГ разбивают поле допуска значений ПКГ на интервалы:
1 участок
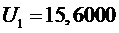 ,
,
 .
.
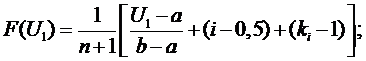
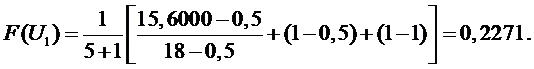
Определяем оценку
функции плотности распределения вероятности (дифференциальный закон
распределения вероятности)
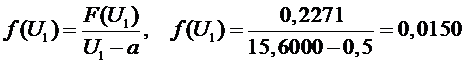
2 участок
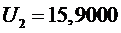 ,
,
 .
.
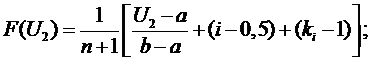
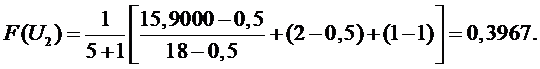
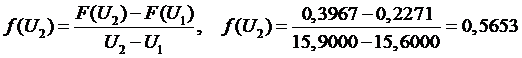
участок
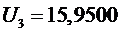 ,
,

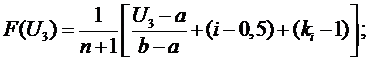
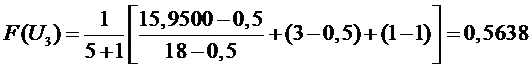 ;
;
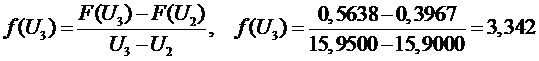
4 участок
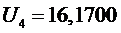
 .
.
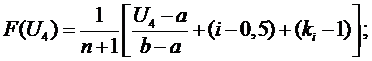
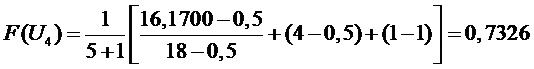
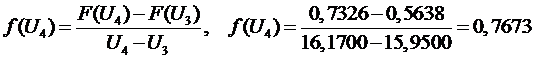
участок
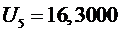 ,
,
 .
.
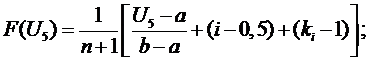
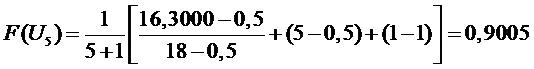 ;
;
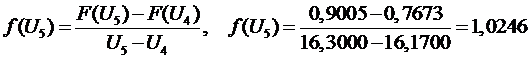
6
участок 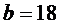 ,
,
 .
.
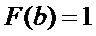
Проверка осуществляется
суммированием площадей фигур, находящихся под ломаной 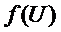 ,
т.е.
,
т.е.
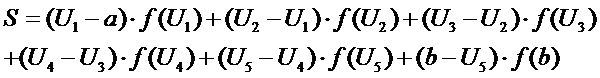
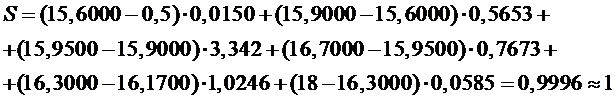
Графики 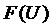 и
и
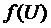 приведены
на рис.П.3 и П.4
приведены
на рис.П.3 и П.4
В конце эксперимента
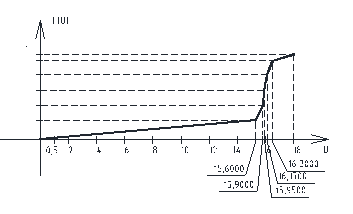
Рис. 3. График функций 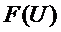
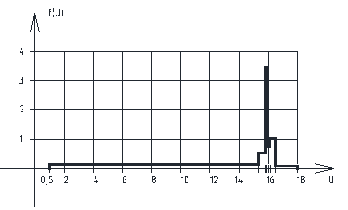
Рис. 4. График функций 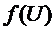
Математическое ожидание
(в конце эксперимента)
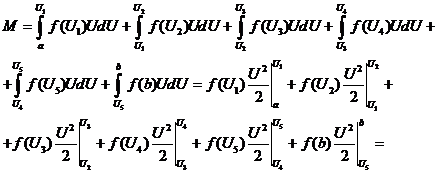
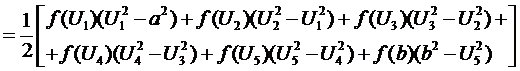
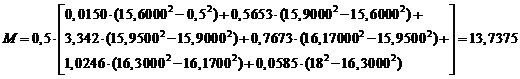
Дисперсия случайной
величины
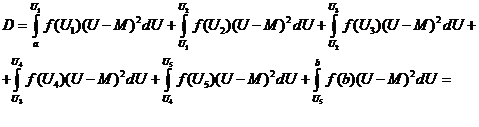
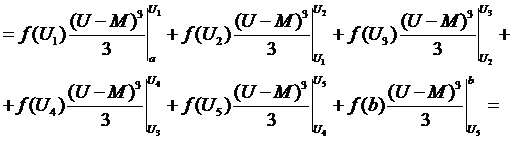
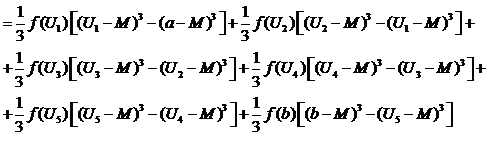
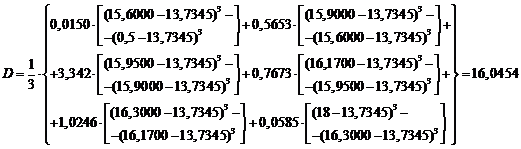
Среднее квадратическое
значение отклонения случайной величины относительно математического ожидания
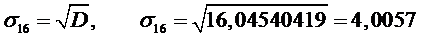 .
.
. Определение среднего
квадратического отклонения (СКО) для всех значений ПКГ
Таким образом, на
основании проведенных расчетов было установлено, что 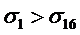
Следовательно, значение 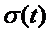 можно
записать:
можно
записать:
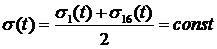
Таким образом получаем 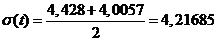
. Определение значения
критерия Стьюдента:
Значение критерия
Стьюдента 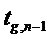 соответствующее
соответствующее
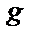 -
процентному пределу ошибки (уровню значимости ошибки) и
-
процентному пределу ошибки (уровню значимости ошибки) и  степеням
свободы определим по таблице
степеням
свободы определим по таблице
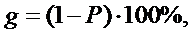
где 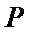 -
доверительная вероятность прогноза,
-
доверительная вероятность прогноза, 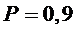 ;
;
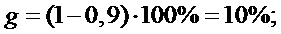
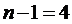 ;
;
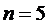 - объем выборки.
- объем выборки.
В соответствии с
полученными значениями 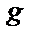 и
и
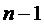
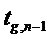 =2,132
=2,132
. Определяем значения
доверительных границ с учетом критерия Стьюдента
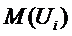 - верхняя доверительная
граница ПКГ
- верхняя доверительная
граница ПКГ
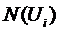 - нижняя доверительная
граница ПКГ
- нижняя доверительная
граница ПКГ
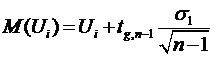 (П.5)
(П.5)
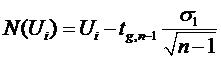 (П.6)
(П.6)
Подставляя в выражение
(П.5) и (П.6) требуемые величины определяем значение верхней и нижней
доверительных границ ПКГ соответственно. Полученные результаты сводим в табл.
П.4
|
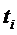 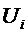 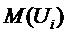 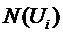
|
|
|
|
|
200
|
0,99
|
5,4852
|
-3,5052
|
|
400
|
2,212
|
6,6152
|
-2,3752
|
|
600
|
2,96
|
7,4552
|
-1,5352
|
|
800
|
3,99
|
8,4852
|
0,5052
|
|
1000
|
5,06
|
9,5552
|
0,5648
|
|
1200
|
5,76
|
10,2552
|
1,2648
|
|
1400
|
7,00
|
11,4952
|
2,5048
|
|
1600
|
8,03
|
12,5252
|
3,5348
|
8,89
|
13,3852
|
4,3948
|
|
2000
|
10,00
|
14,4952
|
5,5048
|
|
2200
|
10,87
|
15,3652
|
6,3748
|
|
2400
|
12,25
|
16,7452
|
7,7548
|
|
2600
|
12,99
|
17,4852
|
8,4948
|
|
2800
|
14,09
|
18,5852
|
9,5948
|
|
3000
|
15,11
|
19,6052
|
10,6148
|
|
3200
|
15,98
|
20,4752
|
11,4848
|
3.
Обоснование выбора математической модели прогнозирования
В ходе исследования значения ПКГ
снимаются через равные интервалы, поэтому для оценки порядка полинома
математической модели прогнозирования воспользуемся аппаратом конечных
разностей.
Имеем функцию 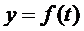 и
дискретные значения аргумента t
образуют арифметическую прогрессию с разностью h,
т.е.
и
дискретные значения аргумента t
образуют арифметическую прогрессию с разностью h,
т.е.
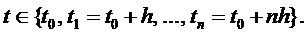
Обозначим значения  при
соответствующих значениях аргумента так:
при
соответствующих значениях аргумента так:
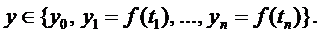
Величины
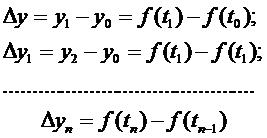
Называют разностями
первого порядка (первыми разностями).
Величины

Аналогично определяются
разности произвольного порядка m:
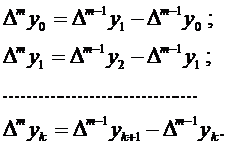
Конечные разности в
более наглядной форме представляют в форме таблицы, которая называется
диагональной. Каждый столбец таблицы составляется так, что разности
записываются между составляющими значениями уменьшаемого и вычитаемого.
|
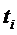 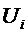 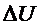 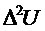 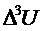
|
|
|
|
|
|
200
|
0,99
|
|
|
|
|
|
1,222
|
|
|
|
400
|
2,212
|
|
-0,474
|
|
|
|
0,748
|
|
0,756
|
|
600
|
2,96
|
|
0,282
|
|
|
|
1,03
|
|
-0,242
|
|
800
|
3,99
|
|
0,04
|
|
|
|
1,07
|
|
-0,41
|
|
1000
|
5,06
|
|
-0,37
|
|
|
|
0,7
|
|
0,91
|
|
1200
|
|
0,54
|
|
|
|
1,24
|
|
-0,75
|
|
1400
|
7,00
|
|
-0,21
|
|
|
|
1,03
|
|
0,04
|
|
1600
|
8,03
|
|
-0,17
|
|
|
|
0,86
|
|
0,42
|
|
1800
|
8,89
|
|
0,25
|
|
|
|
1,11
|
|
-0,49
|
|
2000
|
10,00
|
|
-0,24
|
|
|
|
0,87
|
|
0,75
|
|
2200
|
10,87
|
|
0,51
|
|
|
|
1,38
|
|
-1,15
|
|
2400
|
12,25
|
|
-0,64
|
|
|
|
0,74
|
|
1
|
|
2600
|
12,99
|
|
0,36
|
|
|
|
1,1
|
|
-0,44
|
|
2800
|
14,09
|
|
-0,08
|
|
|
|
1,02
|
|
-0,07
|
|
3000
|
15,11
|
|
-0,15
|
|
|
|
0,87
|
|
|
|
3200
|
15,98
|
|
|
|
Разности третьего порядка мало
отличаются от постоянных, поэтому в качестве математической модели может быть
выбран полином третьей степени.
4. Определение
параметров модели прогнозирования по методу наименьших квадратов
В основе метода наименьших квадратов
лежит условие: коэффициенты моделей должны быть таковы, чтобы значение суммы
квадратов невязок было минимальным, т.е.
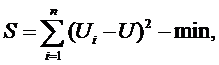
где 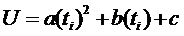 -
модель прогнозирования.
-
модель прогнозирования.
Для этого необходимо
выполнить условия минимума суммы S,
т.е.
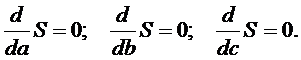
Составляем систему
уравнений для нахождения коэффициентов a,
b и с.
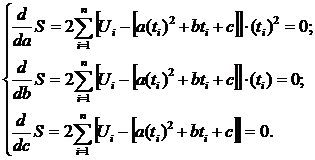
Таким образом, путем
преобразования получим:
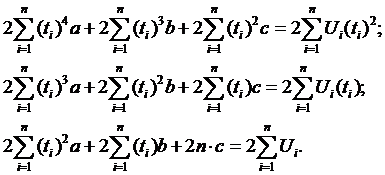
Сократив уравнения на 2,
получим:
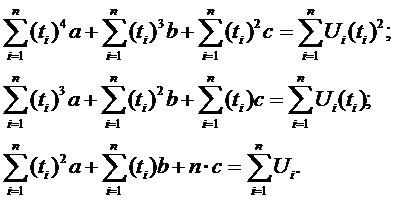
Введем обозначения:
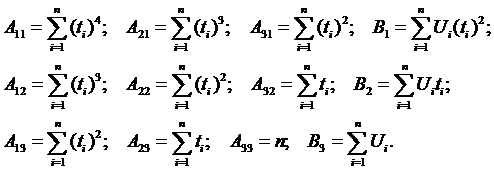
Уравнения принимают вид:
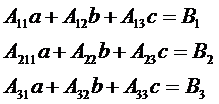
Данная система уравнений
решается по правилу Крамера: матричным способом решения систем линейных
неоднородных уравнений.
Определение параметров
модели прогнозирования для кривой 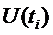 .
.
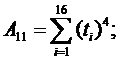
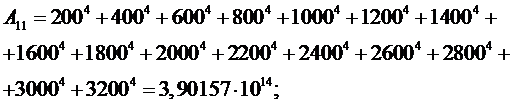
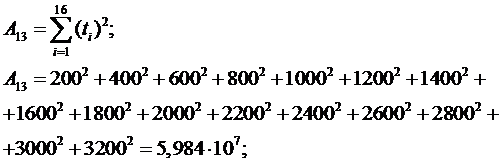
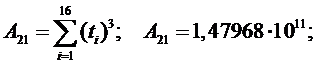
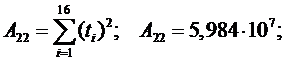
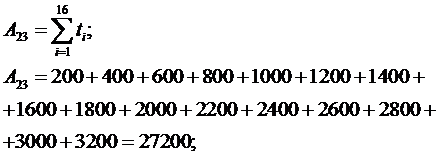
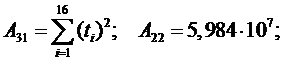
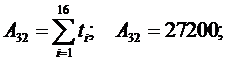
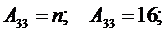
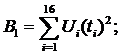
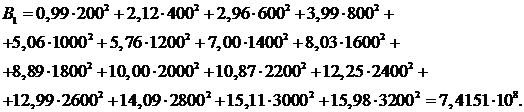
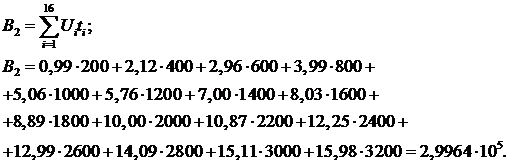
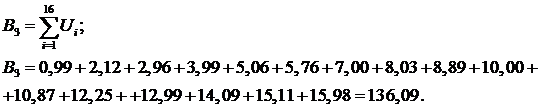
Определитель системы
находится так:
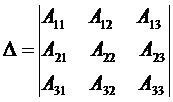
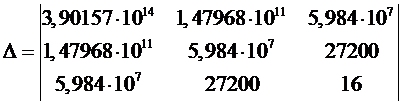
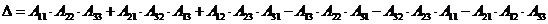
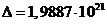
Определитель параметра a находится так:
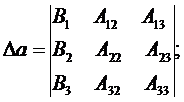
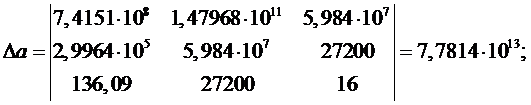
Определитель параметра b находится
так:
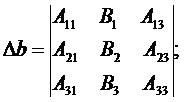
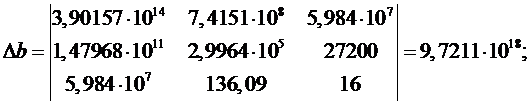
Определитель параметра с
определяется так:
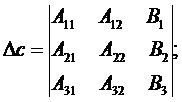
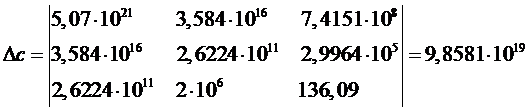
Далее
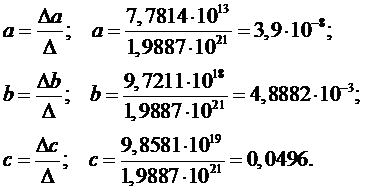
Полученная зависимость
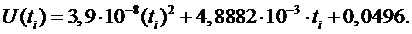
Ее график представлен на
рис. П.5.
Определение параметров
модели прогнозирования верхней границы (для кривой по данным 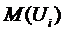 ).
).
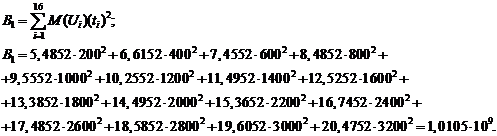
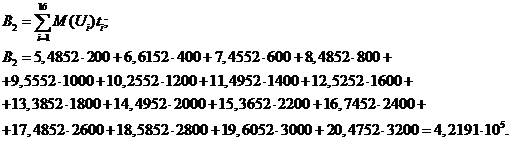
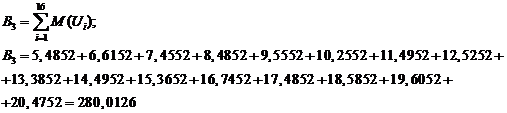
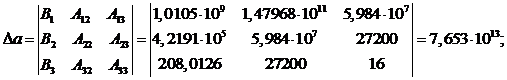
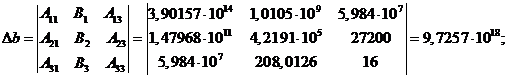
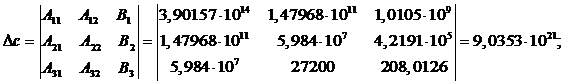
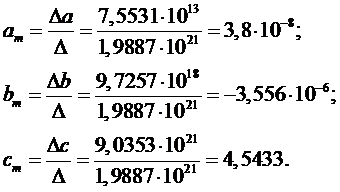
Полученная зависимость
имеет вид:
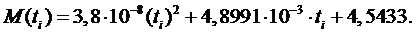
Ее график представлен на
рис. П.5.
Определение параметров
модели прогнозирования нижней границы (для кривой по данным 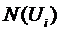 ).
).
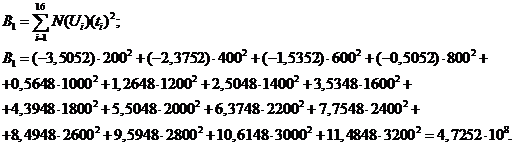
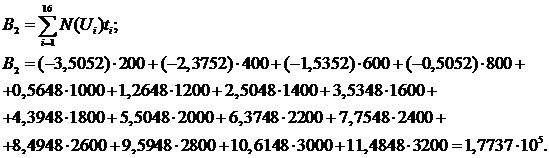
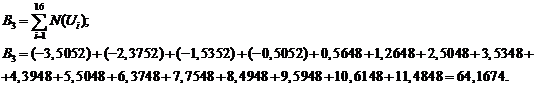
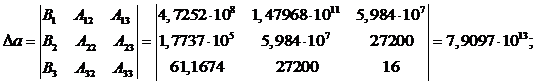
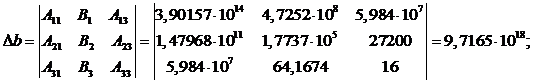
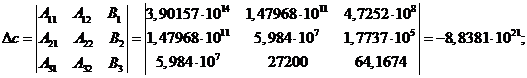
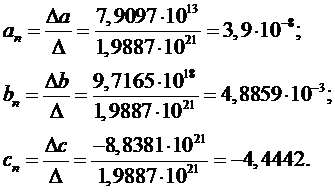
Полученная зависимость
имеет вид:
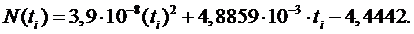
Ее график представлен на
рис. 5.

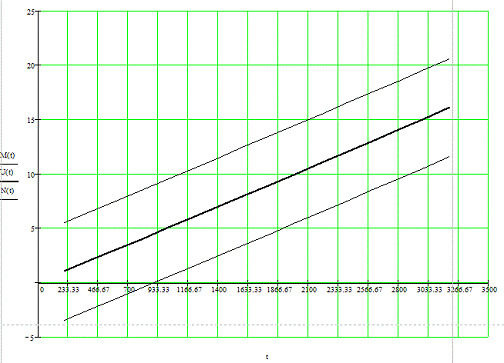
Рис. 5. Графики моделей линии
регрессии и ее доверительных границ
5. Определение наработки
до отказа
Теперь, после того, как
найдены параметры выбранной модели изменений ПКГ, производится экстраполяция ее
статистических данных до предельного состояния исследуемого параметра 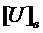 ,
и находятся оценки нижних и верхних границ доверительного интервала средней
наработки до отказа
,
и находятся оценки нижних и верхних границ доверительного интервала средней
наработки до отказа 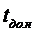 и
и
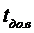 из
уравнений
из
уравнений
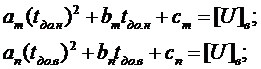
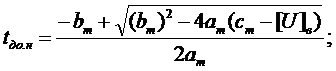
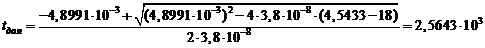
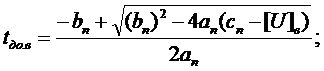
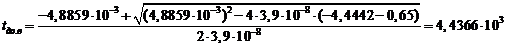
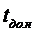 и
и 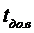 -
нижняя и верхняя границы доверительного интервала средней наработки до отказа,
следовательно средняя наработка до отказа определяется как
-
нижняя и верхняя границы доверительного интервала средней наработки до отказа,
следовательно средняя наработка до отказа определяется как
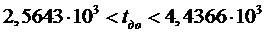
с доверительной
вероятностью прогноза P=0,9.
Список литературы
1. Надежность технических систем и ее прогнозирование / В.В.
Рыжаков. -Пенза: Изд-во Пенз. гос. технол. акад.,2011.-Ч.1.
. Надежность технических систем и ее прогнозирование / В.В.
Рыжаков. - Пенза: Изд-во Пенз. гос. технол. акад.,2011.-Ч.2.
.Надежность технических систем и ее прогнозирование. Задания и
аналитические материалы по выполнению домашних и курсовых работ./ В.В. Рыжаков.-
Пенза: Изд-во Пенз. гос. технол. акад.,2011.