Параметри інтегралів
Завдання 1. Знайти невизначені інтеграли (результати у випадках «a» i «б»
перевірити диференціюванням).
а) 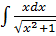
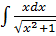 ;
;
б) 
 ;
;
в) 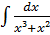
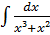 ;
;
г) 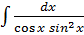
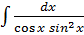
Завдання
2. Обчислити площу фігури, обмежену вказаними лініями 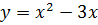
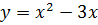 , 𝑦= 4 - 3𝑥. Виконати рисунок.
, 𝑦= 4 - 3𝑥. Виконати рисунок.
Завдання 3. Знайти загальний розв’язок диференціального рівняння першого
порядку:
𝑦ʹ+
2𝑥𝑦 = 2𝑥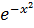
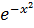
Завдання
4. Знайти частинний розв’язок диференціального рівняння
𝑦"-
2𝑦ʹ + 5𝑦 = 5
 - 4𝑥 +2
- 4𝑥 +2
який задовольняє
початкові умови:
𝑦(0)
= 0, 𝑦ʹ(0) = 2.
Завдання
5. Дослідити на збіжність числові ряди
а)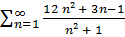
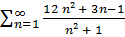
б)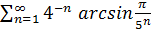
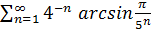
в)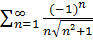
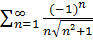
інтеграл диференційний рівняння числовий
Завдання 6. Знайти інтервал збіжності степеневого ряду й дослідити його
збіжність на кінцях інтервалу.
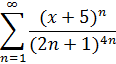
Вирішення завдання 1
а) Знайдемо 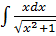
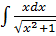 методом підстановки.
Замінюємо
методом підстановки.
Замінюємо 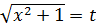
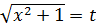 .
.
Отже, 

𝑑

𝑥𝑑𝑥=2𝑡𝑑𝑡
𝑥𝑑𝑥=𝑡𝑑𝑡
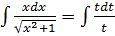
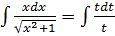 =
=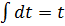
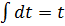 +𝑐=
+𝑐=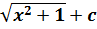
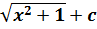
б)
Знайдемо 
 методом інтегрування
частинами:
методом інтегрування
частинами:
𝑢=𝑥
𝑑𝑢=𝑑𝑥
𝑑𝑣=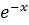
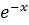 𝑑𝑥
𝑑𝑥
𝑣=- 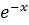
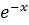
Отже,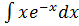
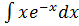 =𝑥(-
=𝑥(- 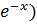
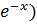 -
-
 = -𝑥
= -𝑥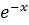
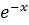 +
+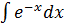
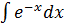 =-𝑥
=-𝑥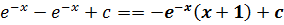
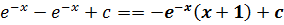
в) 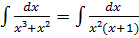
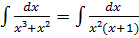
Розкладемо
підінтегральну функцію на прості дроби:
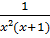
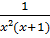 =
=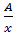
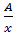 +
+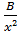
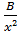 +
+ 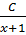
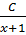
= 𝐴𝑥(𝑥+1) + 𝐵(𝑥+1)+ 𝐶𝑥²
=𝐴𝑥² + 𝐴𝑥 + 𝐵𝑥 + 𝐵 + 𝐶𝑥²
=(𝐴+𝐶)𝑥² + (𝐴+𝐵)𝑥 + 𝐵
|
𝑥²
|
0 = 𝐴+𝐶
|
⥤
𝐶 = -𝐴 = -(-1) = 1
|
|
𝑥¹
|
0 = 𝐴+𝐵
|
⥤
𝐴 = -𝐵 = -1
|
|
𝑥°
|
1 = 𝐵
|
⥤
𝐵 = 1
|
Тоді, 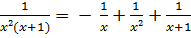

Тоді,
 +
+ 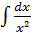
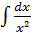 +
+ 
 = - 𝑙𝑛|𝑥|
-
= - 𝑙𝑛|𝑥|
- 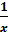
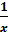 + 𝑙𝑛|𝑥+1|
+𝑐
+ 𝑙𝑛|𝑥+1|
+𝑐
г) 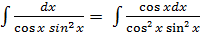
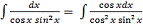 =
= 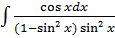
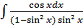 =
= 
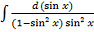
Замінюємо 
 , тоді
, тоді 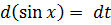
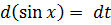
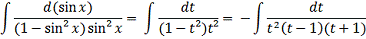
Розкладемо
підінтегральну функцію на прості дроби:
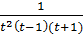
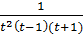 =
= 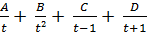
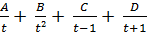 (1)
(1)
Зводимо до спільного
знаменника і прирівнюємо чисельники:
= 𝐴𝑡(𝑡²-1)+𝐵(𝑡²-1)+𝐶𝑡²(𝑡+1)+𝐷𝑡²(𝑡-1)
= 𝐴𝑡³
- 𝐴𝑡 + 𝐵𝑡²
- 𝐵 +𝐶𝑡³ + 𝐶𝑡²
+ 𝐷𝑡³ - 𝐷
= (𝐴+𝐶+𝐷)𝑡³
+ (𝐵+𝐶)𝑡² + (-𝐴)𝑡+ (-𝐵-𝐷)
Прирівнюємо коефіцієнти
при однакових степенях лівої та правої частини:
|
𝑡³𝐴+𝐶+𝐷=0⥤ -𝐶 + 𝐷=0
|
|
|
|
𝑡²
|
𝐵+𝐶=0
|
⥤
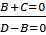 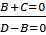 ⥤ 𝐵=𝐷 ⥤ 𝐵=𝐷
|
|
𝑡¹
|
-𝐴=0
|
⥤
𝐴 = 0
|
|
𝑡°
|
-𝐵-𝐷=0
|
⥤
-𝐵-𝐵=1 ⥤
-2𝐵=1 ⥤ 𝐵= - - 
|
𝐷
=- -

𝐴=0
Підставляємо знайдені
значення у тотожність (1):
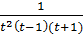
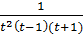 =
= 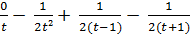
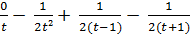
Тоді, 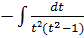
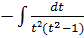 =
= 

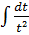
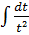 -
- 

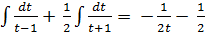
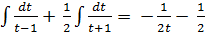 𝑙𝑛|𝑡-1| +
𝑙𝑛|𝑡-1| +
+ 
 𝑙𝑛|𝑡+1|+𝑐 = -
𝑙𝑛|𝑡+1|+𝑐 = - 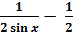
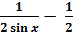 𝑙𝑛|
𝑙𝑛|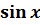
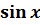 -1| +
-1| + 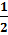
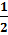 𝑙𝑛|
𝑙𝑛|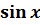
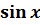 +1|+𝑐.
+1|+𝑐.
Вирішення
завдання 2
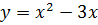
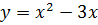 , 𝑦= 4 - 3𝑥; 𝑆 -?
, 𝑦= 4 - 3𝑥; 𝑆 -?
Знайдемо точки
перетину параболи і прямої із системи їхніх рівнянь

 ⥤
⥤ 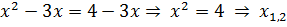
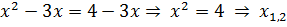 =±2 ⥤
=±2 ⥤
⥤ 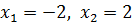
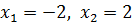
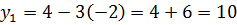
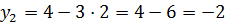
Отже, точки перетину
будуть (-2;10);(2;-2)
Зробимо малюнок.
Знайдемо вершину параболи із рівняння
𝑦'=(𝑥²-3𝑥)'=2𝑥-3=0
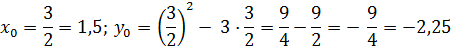
C (1,5;-2,25)
 - вершина параболи.
- вершина параболи.
Вітки параболи
направлені вгору, тому фігура знизу обмежена параболою, а зверху - прямою,
тому:
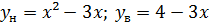
Площа такої
фігури:
𝑆=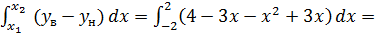
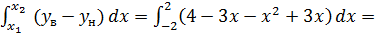
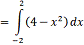
Оскільки функція
парна, тому
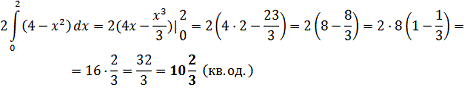
Відповідь: Площа фігури, обмежена вказаними лініями 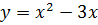
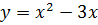 , 𝑦= 4 - 3𝑥 складає
, 𝑦= 4 - 3𝑥 складає 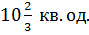
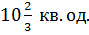
Вирішення
завдання 3
𝑦'+2𝑥𝑦=2𝑥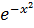
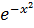
Дане рівняння є
лінійним, тому його розв’язок будемо шукати методом Бернуллі, тобто невідому функцію 𝑦 будемо шукати у вигляді добутку двох невідомих функцій 𝑢(𝑥)та 𝑣(𝑥):
𝑦=𝑢·𝑣 ⥤ 𝑦'= 𝑢'𝑣+𝑣'𝑢
Підставляємо в
рівняння:
𝑢'𝑣+𝑣'𝑢+2𝑥𝑢𝑣=2𝑥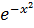
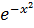
Виносимо за дужки
𝑢:
𝑢'𝑣+𝑢(𝑣'+2𝑥𝑣)=2𝑥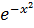
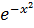
Нехай 𝑣'+2𝑥𝑣=0 (1)
Тоді 𝑢'𝑣=2𝑥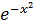
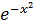 (2)
(2)
Розв’яжемо
рівняння (1):
𝑣'+2𝑥𝑣=0
⥤ 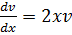
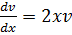 ⥤
⥤ 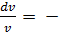
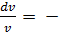 2𝑥𝑣 ⥤
2𝑥𝑣 ⥤ 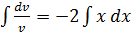
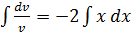 ⥤ 𝑙𝑛 𝑣 = -
⥤ 𝑙𝑛 𝑣 = - 
 ⥤
⥤
⥤ 𝑣 =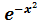
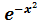
Тоді рівняння(2) ⥤ 𝑢'
 ⥤
𝑢'=2𝑥 ⥤ 𝑢=
⥤
𝑢'=2𝑥 ⥤ 𝑢=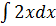
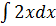 =𝑥²+𝑐 ⥤
=𝑥²+𝑐 ⥤
⥤ 𝑢=𝑥²+𝑐
Тоді, 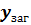
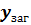 =𝑢·𝑣=
=𝑢·𝑣=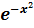
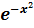 (𝑥²+𝑐) - загальний розв'язок.
(𝑥²+𝑐) - загальний розв'язок.
Відповідь: Загальний розв’язок диференціального рівняння першого порядку 𝑦ʹ+
2𝑥𝑦 = 2𝑥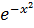
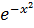 становить
становить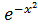
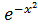 (𝑥²+𝑐).
(𝑥²+𝑐).
Вирішення
завдання 4
𝑦"- 2𝑦ʹ + 5𝑦
= 5
 - 4𝑥 +2
- 4𝑥 +2
𝑦(0)
= 0, 𝑦ʹ(0)
= 2.
Дане рівняння є
неоднорідним ІІ-го порядку із сталими коефіцієнтами.
Його загальний розв’язок:
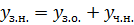
Знайдемо загальний
розв’язок відповідного однорідного рівняння:
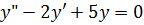
Зробимо заміну 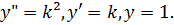
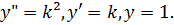
Складемо характеристичне
рівняння:
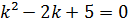
Знайдемо його корені:
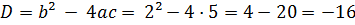
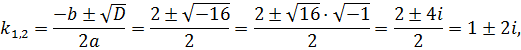
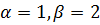
Тоді, 
 (
(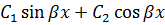
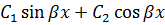 )=
)=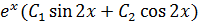
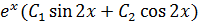 .
.
Шукаємо частинний розв’язок 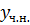
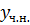 за виглядом правої
частини:
за виглядом правої
частини:
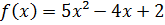
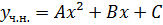
Знайдемо похідні:
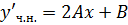
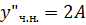
Підставимо їх в
початкове рівняння:
𝑦"- 2𝑦ʹ + 5𝑦
= 5
 - 4𝑥 +2
- 4𝑥 +2
Одержимо:
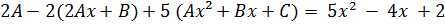
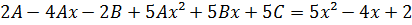
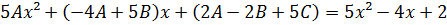
|
𝑥²
|
5𝐴=5
|
⥤
𝐴 = 1
|
|
𝑥¹
|
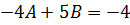
|
⥤
-4 +5𝐵 = -4 ⥤𝐵=0
|
|
𝑥°
|
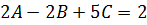
|
⥤
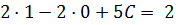 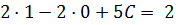 ⥤
𝐶=0 ⥤
𝐶=0
|
Тоді, 

Тоді,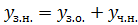
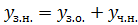 =
=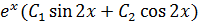
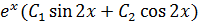 +𝑥².
+𝑥².
Знайдемо його
похідну:

 =
=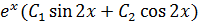
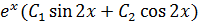 +
+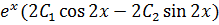
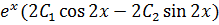 +2𝑥
+2𝑥
Підставимо в 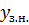
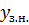 та в його похідну
та в його похідну 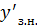
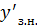 початкові умови
початкові умови
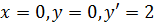
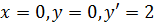
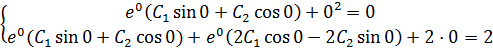
Де 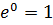
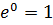 ,
,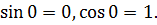
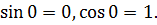
Тоді,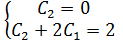
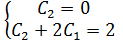 ⥤
⥤


Підставимо
значення сталих 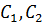
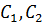 в
в 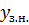
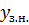 і одержимо частинний
розв’язок:
і одержимо частинний
розв’язок:
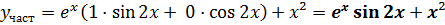
Відповідь: Частинний розв’язок диференціального рівняння
𝑦"- 2𝑦ʹ + 5𝑦
= 5
 - 4𝑥 +2, який задовольняє початкові
умови: 𝑦(0) = 0, 𝑦ʹ(0) = 2 складає
- 4𝑥 +2, який задовольняє початкові
умови: 𝑦(0) = 0, 𝑦ʹ(0) = 2 складає 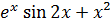
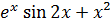 .
.
Вирішення
завдання 5
а) 
 - це числовий рід з
додатніми членами. Його збіжність перевіряється за необхідною ознакою:
- це числовий рід з
додатніми членами. Його збіжність перевіряється за необхідною ознакою:
Якщо границя
загального члена 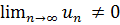
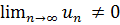 , то ряд розбіжний.
, то ряд розбіжний.
Обчислюємо 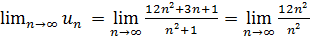
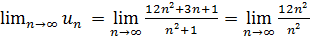 =12 ≠0, тому ряд
розбіжний.
=12 ≠0, тому ряд
розбіжний.
б) 

Збіжність
перевіримо за ознакою порівняння.
Підберемо ряд,
який обмежує даний ряд зверху або знизу.
Очевидно, що при 𝑛 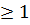
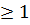 буде
буде
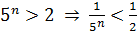
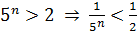 ⥤
⥤ 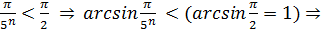
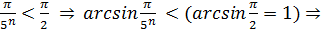
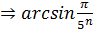
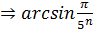
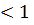
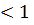 ⥤
⥤
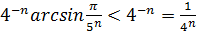
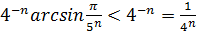
Розглянемо ряд із
загальним членом 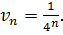
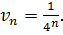 Члени цього ряду
утворюють нескінченно спадну геометричну прогресію із знаменником
Члени цього ряду
утворюють нескінченно спадну геометричну прогресію із знаменником 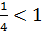
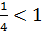 .
.
Тому за ознакою
Даламбера ряд 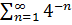
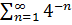 - збіжний.
- збіжний.
Оскільки, члени
досліджуваного ряду менші членів збіжного ряду, то даний ряд теж збіжний.
в)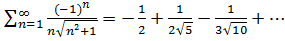
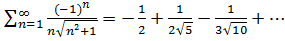 -це ряд Лейбніца.
-це ряд Лейбніца.
Його збіжність
перевіряється за ознакою Лейбніца.
1) Члени ряду
повинні спадати по модулю.
Дійсно, 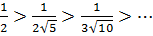
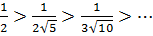
2) Загальний член
ряду має прямувати до нуля:
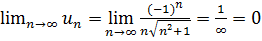
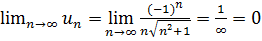 .
.
Обидві умови
виконуються, тому за ознакою Лейбніца даний ряд збігається.
Вирішення завдання 6
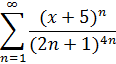
За умовою, загальний
член цього ряду 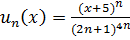
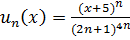
Знайдемо наступний член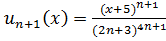
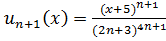
Знайдемо границю їхнього
відношення і накладемо умові, що вона 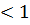
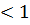 :
:
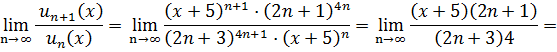
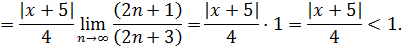
Із нерівності знайдемо
межі для 𝑥:
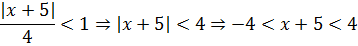
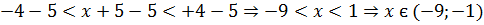
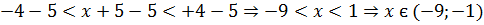
інтервал збіжності
данного ряду.
Перевіримо ряд на
збіжність на кінцях цього інтервалу:
1) 𝑥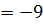
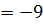 , тоді
, тоді 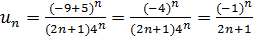
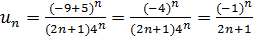 .
.
Ряд з таким загальним членом є
знакозмінним рядом Лейбніца, тому його збіжність перевіряють за ознакою
Лейбніца:
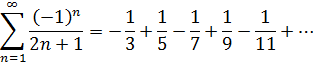
1) 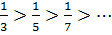
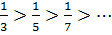 виконується
виконується
) 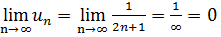
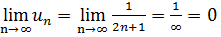 виконується
виконується
Тому ряд збіжний, і тому
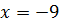
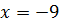 належить до області
збіжності данного ряду.
належить до області
збіжності данного ряду.
3)
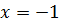
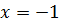 , тоді
, тоді 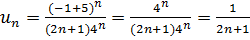
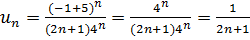
Ряд 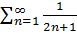
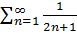 перевіряється на
збіжність за інтегральною ознакою:
перевіряється на
збіжність за інтегральною ознакою:
Оскільки, функція 𝑓(𝑥)
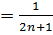
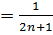 - неперервна і спадна
на інтервалі [1;
- неперервна і спадна
на інтервалі [1;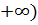
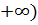 , то існує невласний
інтеграл
, то існує невласний
інтеграл 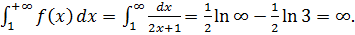
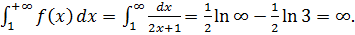
Оскільки, невласний
інтеграл розбіжний, то даний ряд теж розбіжний. Тому точка 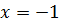
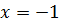 не належить до області
збіжності початкового степеневого ряду.
не належить до області
збіжності початкового степеневого ряду.
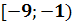
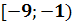 -
область збіжності.
-
область збіжності.