Метод Ньютона (метод касательных). Решение систем нелинейных алгебраических уравнений
Читинский
Государственный Университет
Энергетический
институт
Факультет
экономики и информатики
Кафедра
прикладной информатики и математики
Реферат
по
дисциплине: Численные методы
на тему:
Метод Ньютона (метод касательных). Решение систем нелинейных алгебраических
уравнений
Выполнила: ст. гр. ПИ-07-1
Злова В.В.
Чита, 2009
Содержание
Введение
1.
Метод Ньютона
1.1
Геометрическая интерпретация метода Ньютона
1.2
Алгоритм решения задач с помощью метода Ньютона
1.3
Примеры решения уравнений с помощью метода Ньютона
2.
Решение систем нелинейных алгебраических уравнений
2.1
Метод итераций
2.1.1
Пример решения системы уравнений с помощью метода итераций
2.2
Метод Ньютона
2.2.1
Пример решения системы уравнений с помощью метода Ньютона
2.3
Метод спуска
Заключение
Список
использованной литературы
Введение
Метод
Ньютона (также известный как метод касательных) - это итерационный численный
метод нахождения корня заданной нелинейной функции. Метод был впервые предложен
английским физиком, математиком и астрономом Исааком Ньютоном (1643-1727), под
именем которого и обрёл свою известность. Поиск решения осуществляется путём
построения последовательных приближений и основан на принципах простой
итерации. Метод обладает квадратичной сходимостью. Улучшением метода является
метод хорд и касательных.
Что же касается систем нелинейных алгебраических
уравнений, то итерационные методы решения данных систем приобретают особую
актуальность, в связи с тем, что к ним в отличие от систем линейных уравнений
не возможно применить прямые методы решения. Лишь в отдельных случаях систему
можно решить непосредственно.
1. Метод Ньютона
.1 Геометрическая интерпретация метода Ньютона
Этот метод применяется, если уравнение f(x)
= 0 имеет корень x
Î
[a;b],
и выполняются условия:
) функция y=f(x)
определена и непрерывна при xÎ(-
¥; + ¥)
) f(a)·f(b)<0
(функция принимает значения разных знаков на концах отрезка [a;b]);
) производные f
¢(x)
и f ²(x)
сохраняют знак на отрезке [a;b]
(т.е. функция f(x)
либо возрастает, либо убывает на отрезке [a;b],
сохраняя при этом направление выпуклости).
) f
¢(x)
¹
0 при xÎ[a;b]
Основная идея метода заключается в следующем: на
отрезке [a;b]
выбирается такое число x0,
при котором f(x0)
имеет тот же знак, что и f
²(x0),
т. е. выполняется условие f(x0)·f
²(x)>0.
Таким образом, выбирается точка с абсциссой x0,
в которой касательная к кривой y=f(x)
на отрезке [a;b]
пересекает ось Ox.
За точку x0
сначала удобно выбирать один из концов отрезка.
Пусть нам дана некоторая функция f(x)
= 0 на отрезке [a,b].
Возможно 4 случая:
- f(a)-f(b) < 0; f ¢(x)
> 0; f ²(x) > 0
f(a)-f(b) < 0; f ¢(x)
> 0; f ²(x) < 0
f(a)-f(b) > 0; f ¢(x)
< 0; f ²(x) > 0
- f(a)-f(b)
>0; f
¢(x)
< 0; f
²(x)
< 0
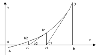
Рис. 1
Рассмотрим метод Ньютона на первом случае.
Пусть нам дана возрастающая функция y = f(x),
непрерывная на отрезке [a;b], и имеющая f ¢(x) > 0 и f ²(x)
> 0. Уравнение касательной имеет вид: y-y0= f ¢(x0)·(x-x0).
В качестве точки x0 выбираем точку B(b; f(b)). Проводим касательную к функции y
= f(x) в точке B, и обозначаем точку пересечения касательной и оси Ox точкой x1.
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к
оси Ox через точку x1, получаем точку b1. Снова проводим касательную
к функции y = f(x) в точке b1, и обозначаем точку пересечения
касательной и оси Ox точкой x2. Затем находим точку пересечения функции y=f(x)
и перпендикуляра, проведенного к оси Ox через точку x2, получаем
точку b2.
Первое приближение корня определяется по
формуле:
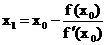 .
.
Второе приближение корня
определяется по формуле:
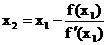 .
.
Таким образом, i-ое
приближение корны определяется по формуле:
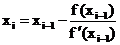
Вычисления ведутся до тех пор, пока
не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе,
или заданной точности e - до
выполнения неравенства | xi-xi-1| < e.
1.2 Алгоритм решения задач с помощью метода
Ньютона
определяем интервал (если он не задан), которому
будет принадлежать корень уравнения. Сужение интервала можно производить
методом половинного деления.
находим f
¢(x)
и f ²(x),
причем f
¢(x)
¹
0 при xÎ[a;b],
f ¢(x)
и f ²(x)
должны сохранять знак на отрезке [a;b]
выбираем один из концов отрезка [a,b] за x0,
исходя из того, что должно выполняться следующее условие f(x0)·f
²(x0)>0.
- вычисляем 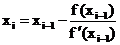 , пока не
будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или
заданной точности e - до
выполнения неравенства | xi-xi-1| < e.
, пока не
будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или
заданной точности e - до
выполнения неравенства | xi-xi-1| < e.
.3 Примеры решения уравнений с помощью метода
Ньютона
Рассмотрим применение метода Ньютона на
примерах.
) Пусть нам дана функция f(x) = sin2x-lnx,
если 1,3<x<1,5. Необходимо
найти корень уравнения с точностью до 0,0001.
Найдем первую и вторую производные исходной
функции:
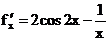
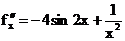
Таблица 1
|
x
|
f(x)
|
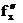
|
|
1,3
|
0,253137
|
-1,47029
|
|
1,5
|
-0,26435
|
-0,12004
|
Так как, 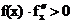 при x = 1,5, то
за x0, берем x = 1,5.
при x = 1,5, то
за x0, берем x = 1,5.
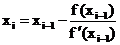
Таблица 2
|
x
|
f(x)
|
 xn-xn-1 xn-xn-1
|
|
|
1,5
|
-0,2643451
|
-2,64665166
|
|
|
1,40012093
|
-0,001798363
|
-2,59883069
|
-0,0998707
|
|
1,39942894
|
-0,0000001988
|
-2,59825545
|
-0,00059199
|
|
1,39942887
|
-0,00000000000000003
|
-2,59825539
|
-0,00000007
|
|
1,39942887
|
|
|
|
Так как 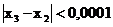 , то на
данном шаге можно остановится.
, то на
данном шаге можно остановится.
Ответ: 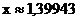
) Решить уравнение  с
с 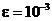 .
.
Так как нам не дан интервал,
которому принадлежит корень уравнения, то для локализации корней применим
графический способ. Преобразуем исходное уравнение к следующему эквивалентному
виду: 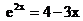
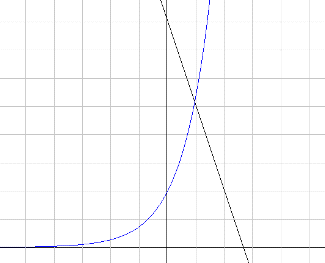
Рис. 2
Построив графики функций 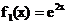 и
и  ,
определяем, что у решаемого уравнения имеется только один корень, который
находится в интервале 0.4<x<0.6. На данном интервале
действительно содержит корень уравнения, т.к.
,
определяем, что у решаемого уравнения имеется только один корень, который
находится в интервале 0.4<x<0.6. На данном интервале
действительно содержит корень уравнения, т.к. 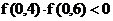
Уточним значение корня с требуемой
точностью, пользуясь методом Ньютона.
Для корректного использования
данного метода необходимо определить поведение первой и второй производной
функции на интервале уточнения корня и правильно выбрать начальное приближение
x0.
Для функции имеем:
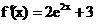 и
и 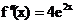 - положительные во всей области
определения функции. В качестве начального приближения необходимо выбрать
правую границу интервала x0=0.4, для которой выполняется
неравенство:
- положительные во всей области
определения функции. В качестве начального приближения необходимо выбрать
правую границу интервала x0=0.4, для которой выполняется
неравенство: 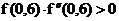
Таблица 3 Результаты вычислений
|
Номер
итерации
|
x0
|
F(x0)
|
F'(x0)
|
R
|
xn-xn-1
|
|
0
|
0,6
|
1,107982086
|
9,615964
|
0,115223192
|
|
|
1
|
0,484777
|
0,083308362
|
8,257956
|
0,010088255
|
-0,115223
|
|
2
|
0,474689
|
0,000690164
|
8,153249
|
0,000084649
|
-0,010088
|
|
3
|
0,474604
|
0,000001368
|
8,152379
|
0,000000168
|
-0,000085
|
Так как, на третьем шаге 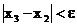 , то
дальнейшие итерации можно не производить.
, то
дальнейшие итерации можно не производить.
Ответ: 
2. Решение систем нелинейных алгебраических
уравнений
В отличие от систем линейных уравнений для
систем нелинейных уравнений не известны прямые методы решения. Лишь в отдельных
случаях систему можно решить непосредственно. Например, для системы из двух
уравнений иногда удается выразить одно неизвестное через другое и таким образом
свести задачу к решению одного нелинейного уравнения относительно одного
неизвестного. Поэтому итерационные методы для нелинейных систем приобретают
особую актуальность.
Запишем систему n нелинейных уравнений с n
неизвестными в общем виде:
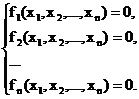
Эту систему можно записать в
компактной, операторной форме:
F(X)
= 0,
где 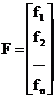 - вектор-функция
- вектор-функция
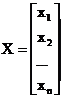 - вектор неизвестных
- вектор неизвестных
Решением системы называется набор
значений 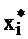 ,
, 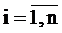 (вектор X*), при
которых все функции fi равны 0.
(вектор X*), при
которых все функции fi равны 0.
Системы нелинейных уравнений могут иметь
единственное решение, множество решений или вообще не иметь его. Поэтому
численное решение СНУ проводят в два этапа:
1 этап
- отделение решений.
2 этап
- уточнение всех или только нужных решений.
Отделить решения - значит установить количество
решений, определить приближенные значения каждого из них или указать область, в
которой решение существует и является единственным.
Для реализации данного этапа используются
графические или аналитические способы.
При аналитическом способе отделения корней
используется следующая теорема: непрерывная строго монотонная функция имеет и
притом единственный нуль на отрезке [a;b]
тогда и только тогда, когда на его концах она принимает значения разных знаков.
Достаточным признаком монотонности функции f(x)
на отрезке [a;b] является
сохранение знака производной функции.
Графический способ отделения корней
целесообразно использовать в том случае, когда имеется возможность построения
графика функции у = f(x).
Наличие графика исходной функции дает
непосредственное представление о количестве и расположении нулей функции, что
позволяет определить промежутки, внутри которых содержится только один корень.
Если построение графика функции у = f(x) вызывает затруднение, часто
оказывается удобным преобразовать данное уравнение к эквивалентному виду f1(x)=f2(x)
и построить графики функций у = f1(x) и у = f2(x)
Абсциссы точек пересечения этих графиков будут соответствовать значениям корней
решаемого уравнения.
Чаще всего задача отделения решений графическим
способом достаточно просто решается только для системы двух уравнений с двумя
неизвестными.
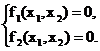
Для систем с большим числом неизвестных (n ³
3) удовлетворительных общих методов определения области существования решения
нет. Поэтому при решении СНУ эта область обычно определяется при анализе
решаемой задачи, например, исходя из физического смысла неизвестных.
Так или иначе, при завершении первого этапа,
должны быть определены промежутки, на каждом из которых содержится только один
корень уравнения.
Отделение решений позволяет:
1) Выявить число решений и область существования
каждого из них.
) Проанализировать возможность применения
выбранного метода решения СНУ в каждой области.
) Выбрать начальное приближение решения x0
из области его существования, так что x0ÎD.
При отсутствии информации об области
существования решения СНУ выбор начального приближения x0
проводиться методом проб и ошибок.
Методы уточнения решений СНУ.
Уточнение интересующего решения до требуемой
точности ε производится
итерационными методами.
Основные методы уточнения решений СНУ получены
путем обобщения итерационных процессов, используемых при решении одного
нелинейного уравнения.
.1 Метод итераций
Как и в случае одного уравнения, метод простых
итераций заключается в замене исходной системы уравнений эквивалентной системой
X=Φ(X),
где
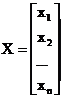
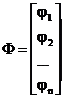
и построении итерационной
последовательности X(k+1) = Φ(X(k)), где k=1,2,3,… - номер итерации,
которая при k→∞ сходится к точному решению.
В развернутом виде формула итерационного
процесса (выражение для вычисления очередного k-го приближения решения) имеет
вид:
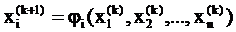 ,
,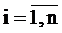
Условие окончания расчета
δ≤ε,
где ε - заданная точность решения;
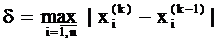
или
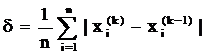
Итерационный процесс сходиться к
точному решению, если в окрестности решения соблюдаются условия сходимости:
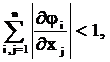
Таким образом, для уточнения решения СНУ методом
простых итераций нужно найти такое эквивалентное преобразование в X=Φ(X),
чтобы в области существования решения выполнялись условия сходимости.
.1.1 Пример решения системы уравнений с помощью
метода итераций
Решить систему нелинейных уравнений с точностью
до 0,003
Дана система нелинейных уравнений:
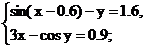
Перепишем данную систему в виде:
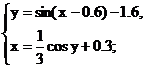
Построив графики данных функций,
определим начальные приближения.
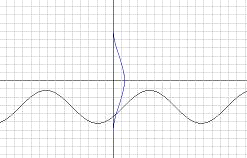
Рис. 3
Из графика видим, что система имеет
одно решение, заключенное в области D: 0<x<0.3;
-2.2<y<-1.8.
Убедимся в том, что метод итераций
применим для уточнения решения системы, для чего запишем ее в следующем виде:
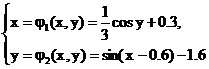
Так как
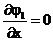
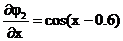
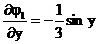
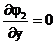
то в области D имеем
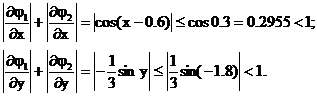
Таким образом, условия сходимости
выполняются.
Вычисления производим по формулам
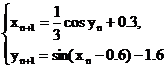
За начальные приближения принимаем x0=0.15 и y0=-2
Таблица 4
|
n
|
xn
|
yn
|
xn-0,6
|
sin(xn-0,6)
|
cosyn
|
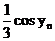
|
|
0
|
0,15
|
-2
|
-0,45
|
-0,435
|
-0,4161
|
-0,1387
|
|
1
|
0,16128
|
-2,035
|
-0,4387
|
-0,4248
|
-0,4477
|
-0,1492
|
|
2
|
0,15077
|
-2,0248
|
-0,4492
|
-0,4343
|
-0,4385
|
-0,1462
|
|
3
|
0,15382
|
-2,0343
|
-0,4462
|
-0,4315
|
-0,4471
|
-0,149
|
|
4
|
0,15098
|
-2,0315
|
-0,449
|
-0,4341
|
-0,4446
|
-0,1482
|
|
5
|
0,1518
|
-2,0341
|
-0,4482
|
-0,4333
|
-0,4469
|
-0,149
|
|
6
|
0,15104
|
-2,0333
|
-0,449
|
-0,434
|
-0,4462
|
-0,1487
|
|
7
|
0,15126
|
-2,034
|
-0,4487
|
-0,4338
|
-0,4468
|
-0,1489
|
|
8
|
0,15105
|
-2,0338
|
-0,4489
|
-0,434
|
-0,4467
|
-0,1489
|
Так как δ≤ε,
где
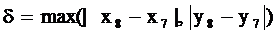 , то
, то
Ответ: 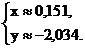
.2 Метод Ньютона
Идея метода заключается в
линеаризации уравнений системы 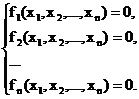 , что позволяет свести исходную
задачу решения СНУ к многократному решению системы линейных уравнений.
, что позволяет свести исходную
задачу решения СНУ к многократному решению системы линейных уравнений.
Пусть известно приближение xi(k) решения
системы нелинейных уравнений xi*. Введем в
рассмотрение поправку Dxi как разницу
между решением и его приближением:
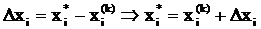 ,
, 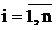
Подставим полученное выражение для xi* в исходную
систему.
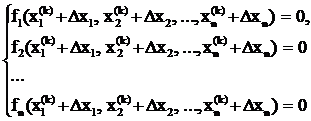
Неизвестными в этой системе
нелинейных уравнений являются поправки Dxi. Для
определения Dxi нужно
решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако
эту систему можно линеаризовать, и, решив ее, получить приближенные
значения поправок Dxi для данного
приближения, т.е. Dxi(k). Эти
поправки не позволяют сразу получить точное решение 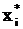 , но дают
возможность приблизиться к решению, - получить новое приближение решения
, но дают
возможность приблизиться к решению, - получить новое приближение решения
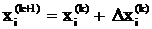 ,
, 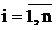
Для линеаризации системы следует разложить
функцию fi
в ряды Тейлора в окрестности xi(k),
ограничиваясь первыми дифференциалами.
Полученная система имеет вид:
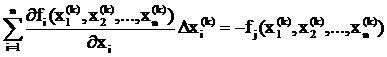 ,
, 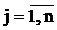
Все коэффициенты этого уравнения можно
вычислить, используя последнее приближение решения xi(k).
Для решения системы линейных уравнений при n=2,3
можно использовать формулы Крамера, при большей размерности системы n
- метод исключения Гаусса.
Значения поправок используются для оценки
достигнутой точности решения. Если максимальная по абсолютной величине поправка
меньше заданной точности e, расчет завершается. Таким образом,
условие окончания расчета:
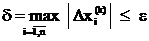
Можно использовать и среднее
значение модулей поправок:
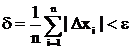
В матричной форме систему можно
записать как:
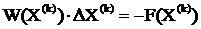
где: 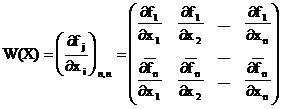 , - матрица Якоби (производных),
, - матрица Якоби (производных),
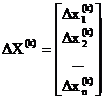 - вектор поправок
- вектор поправок
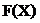 - вектор-функция
- вектор-функция
W(X(k)) - матрица
Якоби, вычисленная для очередного приближения.
F(X(k)) -
вектор-функция, вычисленная для очередного приближения.
Выразим вектор поправок ∆X(k) из 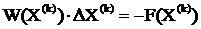 :
:
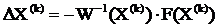
где W-1 - матрица,
обратная матрице Якоби.
Окончательно формула
последовательных приближений метода Ньютона решения СНУ в матричной форме имеет
вид:
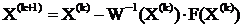
Достаточные условия сходимости для общего случая
имеют очень сложный вид, и на практике проверяются редко. Нужно отметить, что
метод сходится очень быстро (за 3 - 5 итераций), если det|W|
¹
0 и начальное приближение X(0)
выбрано близким к решению (отличаются не более чем на 10%).
Алгоритм решения СНУ методом Ньютона состоит в
следующем:
1) Задается размерность системы n, требуемая
точность ε,
начальное
приближенное решение 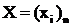 .
.
) Вычисляются элементы матрицы Якоби
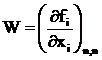
) Вычисляется обратная матрица 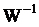 .
.
) Вычисляется вектор функция 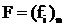 ,
, 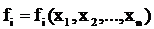 ,
, 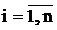 .
.
) Вычисляются вектор поправок 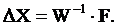
) Уточняется решение 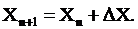
) Оценивается достигнутая точность 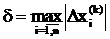
) Проверяется условие завершения
итерационного процесса δ≤ε
Если оно не соблюдается, алгоритм
выполняется снова с пункта 2.
Для уменьшения количества
арифметических действий Рафсон предложил не вычислять обратную матрицу W-1, а
вычислять поправки как решение СЛУ: 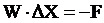 , данный метод получил название
метод Ньютона-Рафсона.
, данный метод получил название
метод Ньютона-Рафсона.
Достоинством методов Ньютона является быстрая
сходимость, недостатками - сложность расчетов (вычисление производных, многократное
решение системы линейных уравнений), сильная зависимость от начального
приближения.
.2.1 Пример решения системы уравнений с помощью
метода Ньютона
Используя метод Ньютона, решить систему
нелинейных уравнений с точностью до 0,002.
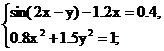
Отделение корней производим
графически.
Для построения графиков функций,
составим таблицу значений функций, входящих в первое и второе уравнение.
Таблица 5
|
x
|
-1,1
|
-1
|
-0,8
|
-0,6
|
-0,4
|
-0,2
|
0,2
|
0,4
|
0,5
|
|
x2
|
1,21
|
1
|
0,64
|
0,36
|
0,16
|
0,04
|
0,04
|
0,16
|
0,25
|
|
0.8x2
|
0,97
|
0,80
|
0,51
|
0,29
|
0,13
|
0,03
|
0,13
|
0,20
|
|
1-0.8x2
|
0,03
|
0,20
|
0,49
|
0,71
|
0,87
|
0,97
|
0,97
|
0,87
|
0,80
|
|
 0,020,130,330,470,580,650,650,580,53 0,020,130,330,470,580,650,650,580,53
|
|
|
|
|
|
|
|
|
|
|
y2
|
0,15
|
0,37
|
0,57
|
0,69
|
0,76
|
0,80
|
0,80
|
0,76
|
0,73
|
|
1.2x
|
-1,32
|
-1,2
|
-0,96
|
-0,72
|
-0,48
|
-0,24
|
0,24
|
0,48
|
0,6
|
|
0.4+1.2x
|
-0,92
|
-0,8
|
-0,56
|
-0,32
|
-0,08
|
0,16
|
0,64
|
0,88
|
1
|
|
2x-y
|
-1,17
|
-0,93
|
-0,59
|
-0,33
|
-0,08
|
0,16
|
0,69
|
1,08
|
1,57
|
|
y1
|
-1,03
|
-1,07
|
-1,01
|
-0,87
|
-0,72
|
-0,56
|
-0,29
|
-0,28
|
-0,57
|
Значения для x
можно брать исходя из следующих условий:
из первого уравнения -1<1.2x+4<1,
т.е. -1.16<x<0.5;
из второго уравнения -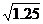 <x<
<x<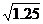 , т.е.
-1.12<x<1.12.
, т.е.
-1.12<x<1.12.
Таким образом, -1.12<x<0.5.
Система имеет два решения. Уточним одно из них,
принадлежащее области D: 0.4<x<0.5;
-0.76<y<-0.73 .
За начальное приближение примем x0=0.4; y0=-0.75.
Имеем следующие системы:
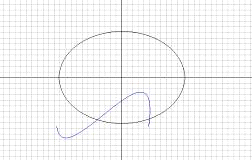
Рис. 4
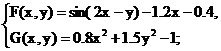
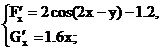
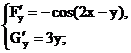
Найдем элементы матрицы Якоби 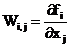 , где
, где 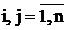 , и значения
функций в x0=0.4; y0=-0.75:
, и значения
функций в x0=0.4; y0=-0.75:
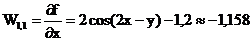
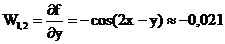
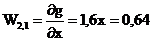
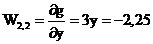
F(0,4;-0,75)=0,11978(0,4;-0,75)=-0,02825

где 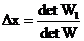 ;
; 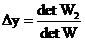 ;
;
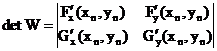

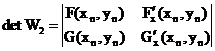
Итерационные формулы:
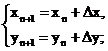 ,
,
Все вычисления производим в таблице.
|
n
|
xn
|
0.8xn2
|
2xn-yn
|
sin(2xn-yn)
|
F(xn,yn)
|
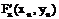 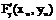 detW detW
|
detW1
|
∆x
|
|
|
|
yn
|
1.5yn2
|
|
cos(2xn-yn)
|
G(xn,yn)
|
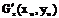 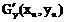
|
detW2
|
∆y
|
|
|
|
0
|
0,400
|
0,1280
|
1,55
|
0,99978
|
0,11978
|
-1,15841
|
-0,02079
|
2,6197
|
0,2701
|
0,1031
|
|
-0,750
|
0,84375
|
|
0,02079
|
-0,02825
|
0,64000
|
-2,25000
|
|
0,04394
|
0,01677
|
|
1
|
0,5031
|
0,20249
|
1,73943
|
0,98581
|
-0,01791
|
-1,53568
|
0,16784
|
3,2429
|
-0,0379
|
-0,0117
|
|
-0,7332
|
0,80644
|
|
-0,1678
|
0,00893
|
0,80496
|
-2,19969
|
|
-0,0007
|
-0,0002
|
|
2
|
0,4914
|
0,19319
|
1,71628
|
0,98944
|
-0,00026
|
-1,48994
|
0,14497
|
3,164
|
-0,0006
|
-0,0002
|
|
-0,7334
|
0,80692
|
|
-0,1449
|
0,00011
|
0,78627
|
-2,20034
|
|
-0,00005
|
-0,00001
|
Так как δ<ε, 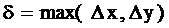 то можно
прекратить производить вычисления. Таким образом, ответ:
то можно
прекратить производить вычисления. Таким образом, ответ: 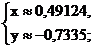
2.3 Метод спуска
Общий недостаток всех рассмотренных ранее
методов решения систем нелинейных уравнений состоит в локальном характере
сходимости, затрудняющем их применение в случаях (достаточно типичных), когда
существуют проблемы с выбором начального приближения, обеспечивающего
сходимость итерационной вычислительной процедуры. B этих случаях можно
использовать численные методы оптимизации. Для использования наглядной
геометрической интерпретации приводимых ниже рассуждений и их результатов
ограничимся рассмотрением системы, состоящей из двух уравнений с двумя
неизвестными
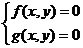
Из функций f(x,y), g(x,y) системы
образуем новую функцию
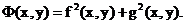
Так как эта функция не
отрицательная, то найдется точка (вообще говоря, не единственная) 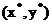 такая, что
такая, что 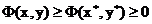
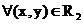
Пространственная интерпретация
метода наискорейшего спуска для функции:
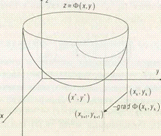
Рис. 5
Траектория наискорейшего спуска для
функции в плоскости ХОУ
Рис. 6
Следовательно, если тем или иным
способом удается получить точку 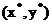 , минимизирующую функцию Ф(x,y), и
если при этом окажется, что
, минимизирующую функцию Ф(x,y), и
если при этом окажется, что 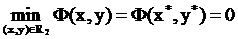 , то точка
, то точка 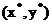 - истинное
решение системы, поскольку
- истинное
решение системы, поскольку
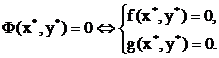
Последовательность точек 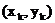 -
приближений к точке
-
приближений к точке 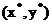 минимума
функции Ф(х,у) - обычно получают по рекуррентной формуле
минимума
функции Ф(х,у) - обычно получают по рекуррентной формуле
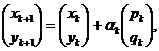
где 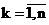 ,
, 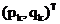 - вектор, определяющий направление
минимизации, а
- вектор, определяющий направление
минимизации, а 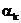 - скалярная
величина, характеризующая величину шага минимизации (шаговый множитель).
Учитывая геометрический смысл задачи минимизации функций двух переменных Ф(x,y)
- "спуск на дно" поверхности z = Ф(x,y), итерационный метод можно
назвать методом спуска, если вектор
- скалярная
величина, характеризующая величину шага минимизации (шаговый множитель).
Учитывая геометрический смысл задачи минимизации функций двух переменных Ф(x,y)
- "спуск на дно" поверхности z = Ф(x,y), итерационный метод можно
назвать методом спуска, если вектор 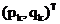 при каждом k является направлением
спуска (т. e. существует такое
при каждом k является направлением
спуска (т. e. существует такое 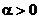 , что
, что 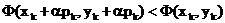 , и если множитель
, и если множитель 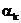 подбирается
так, чтобы выполнялось условие релаксации
подбирается
так, чтобы выполнялось условие релаксации 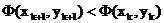 , означающее переход на каждой
итерации в точку с меньшим значением минимизируемой функции.
, означающее переход на каждой
итерации в точку с меньшим значением минимизируемой функции.
Таким образом, при построении
численного метода вида 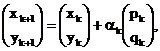 минимизации
функции Ф(x,y) следует ответить на два главных вопроса: как выбирать
направление спуска
минимизации
функции Ф(x,y) следует ответить на два главных вопроса: как выбирать
направление спуска 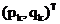 и как
регулировать длину шага в выбранном направлении с помощью скалярного параметра
- шагового множителя
и как
регулировать длину шага в выбранном направлении с помощью скалярного параметра
- шагового множителя 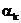 .
.
При выборе направления спуска
естественным является выбор такого направления, в котором минимизируемая функция
убывает наиболее быстро.
Как известно из математического
анализа функций нескольких переменных, направление наибольшего возрастания
функции в данной точке показывает ее градиент в этой точке. Поэтому примем за
направление спуска вектор

антиградиент функции Ф(х,у). Таким
образом, из семейства методов выделяем градиентный метод
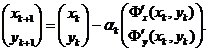
Оптимальный шаг в направлении
антиградиента - это такой шаг, при котором значение 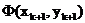 наименьшее
среди всех других значений Ф(х,у) в этом фиксированном направлении, т.е. когда
точка
наименьшее
среди всех других значений Ф(х,у) в этом фиксированном направлении, т.е. когда
точка 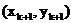 является
точкой условного минимума. Следовательно, можно рассчитывать на наиболее
быструю сходимость метода, если полагать в нем
является
точкой условного минимума. Следовательно, можно рассчитывать на наиболее
быструю сходимость метода, если полагать в нем
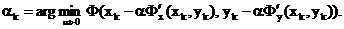
Такой выбор шагового множителя,
называемый исчерпывающим спуском, вместе с формулой 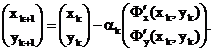 определяет
метод наискорейшего спуска.
определяет
метод наискорейшего спуска.
Геометрическая интерпретация этого метода
хорошо видна на рисунках, представленных выше. Характерны девяностоградусные
изломы траектории наискорейшего спуска, что объясняется исчерпываемостью спуска
и свойством градиента (а значит, и антиградиента) быть перпендикулярным к линии
уровня в соответствующей точке.
Заключение
В данном реферате были рассмотрены методы
решения систем нелинейных алгебраических уравнений: метод итераций, метод
Ньютона, метод спуска, а также метод Ньютона для решения нелинейных уравнений.
На примерах было показано, что с помощью данных методов можно достаточно быстро
решить нелинейное уравнение или систему нелинейных алгебраических уравнений с
указанной степенью точности. При этом использование таких программ, как Excel,
MathCad, MathLab
также существенно облегчает проводимые вычисления для нахождения корней
уравнения или системы уравнений.
ньютон уравнение итерация сходимость
Список использованной литературы
1) Краткий курс вычислительной
математики, Чита 1998.
2) Быков А.Ю.
Вычислительная математика - учебное пособие по дисциплине «Вычислительная
математика» для подготовки бакалавров технических наук по направлению 552800
«Информатика и вычислительная техника», Москва 2005.
) Калиткин Н.Н.
Численные методы - учебник для студентов математических, физических и технических
специальностей: Москва, 2000.