Конформное отображение

Конформное отображение

Введение

Одним из основных свойств таких простейших геометрических преобразований, как параллельный перенос, поворот, центральная и осевая симметрии, преобразование подобия и гомотетия, является сохранение формы тел и фигур и как следствие - сохранение углов между гладкими кривыми. Подобным свойством обладают также многие другие преобразования, но с той разницей, что свойство сохранения формы выполняется применительно не ко всему телу или фигуре, а лишь к их достаточно малым частям. Более того, при этих преобразованиях, как и при указанных выше простейших преобразованиях, имеет место свойство сохранения углов между кривыми. Такие преобразования, называемые конформными, нашли широкое применение во многих разделах математики и других наук.

КОНФОРМНОЕ ОТОБРАЖЕНИЕ - взаимно однозначное отображение областей n-мерного евклидова пространства, сохраняющее углы между кривыми.

1. Комплексная форма записи простейших преобразований плоскости

Известно, что любое комплексное число

z = x +  i*y (x, y 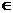 R, i² = -1)

можно единственным образом изобразить как точку M(x; y) или вектор z =(x;y)на плоскости, в результате чего между множеством С комплексных чисел и координатной плоскостью Oxy, а также множеством векторов на плоскости устанавливается взаимно однозначное соответствие. В связи с этим число z часто называют еще точкой z или вектором z. При этом сумме комплексных чисел

= x + i*y и a = α+ i*β

соответствует сумма векторов z и a, что равносильно параллельному переносу (сдвигу) точки M(x; y) на вектор a (α;β).Таким образом, на плоскости параллельный перенос на вектор a осуществляется комплекснозначной функцией

= z + a.

Пусть точка w получается из точки z поворотом вокруг начала координат на угол α. Запишем число z в тригонометрической форме

= r (cos φ+ i sin φ),

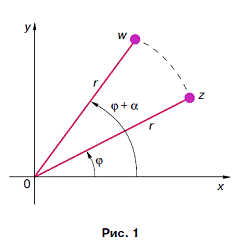
где r = | z | - его модуль (расстояние от точки z до начала координат), а φ = arg z - аргумент (угол между действительной осью Ox и вектором z). Так как число w имеет тот же модуль r, а его аргумент равен φ+α (рис. 1), то

w = r (cos (φ+ α) + i sin (φ + α)) = r (cos φ + i sin φ)(cos a + i sin α),

то есть на плоскости поворот вокруг начала координат на угол a осуществляется функцией w = (cos α + + i sin α)z. В частности, отсюда следует, что симметрия относительно начала координат, представляющая собой поворот вокруг него на угол π, осуществляется функцией w = (cos π + i sin π)z = - z.

Аналогично показывается, что гомотетия с коэффициентом k (k=0), в частности преобразование подобия с коэффициентом k (k > 0), и центром в начале координат осуществляется функцией w = kz.

Для описания приведенных выше преобразований плоскости относительно точки z₀ надо в соответствующих функциях заменить z на z - z₀. Например, поворот на угол α = π/2 вокруг точки z₀ = 1 + i осуществляется функцией

w= ( cos π/2 + i*sin π/2)(z-1-i)=iz+1-i

а симметрия относительно этой точки - функцией

w = - (z - 1 - i) = - z + 1 + i.

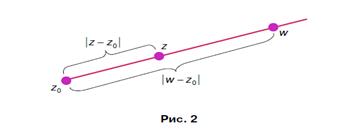
С помощью комплексной переменной описываются и более сложные преобразования плоскости, каковым, например, является инверсия с коэффициентом k (k > 0) и центром в точке z₀, которая точке z ставит в соответствие точку w, лежащую вместе с z на одном луче, выходящем из точки z₀ , и удовлетворяющую условию | z - z₀| *| w - z₀| = k (рис. 2). Данное преобразование осуществляется функцией

w = z₀ + k/(z-z₀) .

В частности, инверсия (симметрия) относительно окружности | z - z₀ | = R, определяемая как инверсия с коэффициентом k = R ² и центром в точке z₀ , осуществляется функцией w = z₀ + R ² /(z-z₀) Аналогично симметрия относительно прямой ax + by = c, называемая еще инверсией, осуществляется функцией:

W= (z(b²+a²-2abi)/(a²+b²))+((2c( a+ b*i ))/(a²+b²)= (z(b2+a2-2abi)+(a+ bi))/(a2+b2)

В частности, инверсия относительно оси абсцисс y = 0 осуществляется функцией w=z . Точки, получаемые друг из друга в результате инверсии относительно окружности (или прямой), называются симметричными относительно этой окружности (или прямой). Например, инверсия относительно окружности | z - 1 - i | = 1 с центром в точке z₀ = 1 + i и радиуса 1 осуществляется функцией w = 1 + i + 1/( z-1+i) , используя которую, в частности, найдем точку, симметричную точке z = 0 относительно данной окружности:

W=1+i+ (1/(i-1))=(1/2)*(1+i)

Записав функцию w = 1 / z в виде w=(1/z) ,видим, что она представляет собой суперпозицию w == f₂( f₁(z)) двух функций f₁ (z)=1/z , f₂(z)= z.Следовательно, отображение, осуществляемое функцией w = 1/ z, равносильно последовательному выполнению (суперпозиции) двух инверсий (симметрий): относительно окружности | z | = 1 и относительно оси абсцисс. По этой причине отображение, осуществляемое функцией w = 1/ z, называют преобразованием двойной симметрии. Аналогично можно показать, что параллельный перенос и поворот равносильны двум инверсиям относительно некоторых прямых, а преобразование подобия - двум инверсиям относительно окружностей.

Рассмотренные в данном пункте преобразования изучаются также в n-мерном евклидовом пространстве. Однако для них в пространстве измерения n ≥ 3 таких удобных форм аналитической записи, как на плоскости, нет.

. Определение и основные свойства комплексного отображения

Непрерывное отображение w = f (z) области D комплексной плоскости С в плоскость С называется конформным в точке z₀ 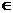 D, если в этой точке оно обладает свойствами постоянства искажения масштаба и сохранения углов.

·              Свойство постоянства искажения масштаба (или постоянства растяжений) в точке z₀ при отображении w = f (z) состоит в том, что при z z₀ отношение | f (z) - f (z₀) | / | z - z₀ | расстояния между образами f (z) и f (z₀) точек z и z₀ к расстоянию между самими точками z и z₀ стремится к определенному пределу k, не зависящему от способа стремления z к z₀ . Число k называется коэффициентом искажения масштаба в точке z₀ при отображении w = f (z).

·        Свойство сохранения (консерватизма) углов в точке z₀ при отображении w = f (z) состоит в том, что любая пара гладких кривых γ₁ , γ₂ (функция f называется гладкой на отрезке, если она имеет непрерывную производную на этом отрезке), расположенных в D и пересекающихся в точке z₀ под некоторым углом α (то есть имеющих касательные в точке z₀ , образующие между собой угол α), переходит при рассматриваемом отображении в пару гладких кривых Г₁ , Г₂ , пересекающихся в точке w₀ = f (z₀) под тем же углом α с учетом направления (рис. 3). Такое отображение называют еще конформным отображением первого рода. Если отображение сохраняет углы между кривыми по абсолютной величине, изменяя их направления на противоположные, то оно называется антиконформным или конформным отображением второго рода. Отображение области D называется конформным, если оно конформно в каждой точке области. Все рассмотренные ранее отображения, кроме инверсии, являются конформными в плоскости С, а инверсия - антиконформным отображением в С.

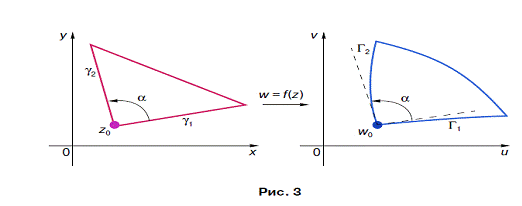
Из определения конформного отображения непосредственно следует, что если в плоскости изменения комплексной переменной z взять достаточно малый треугольник с одной из вершин в точке z₀ , то он при конформном отображении w = f (z) перейдет в малый криволинейный треугольник с вершиной в точке w₀ = f (z₀) (см. рис. 3). При этом соответственные углы у этих треугольников будут равны как по абсолютной величине, так и по направлению, а отношения их соответственных сторон будут мало отличаться от коэффициента k искажения масштаба. Таким образом, конформное отображение является отображением, сохраняющим форму достаточно малых фигур, то есть преобразованием подобия применительно к малым фигурам.

Доказано, что образ любой области при конформном отображении снова является областью. Основными проблемами теории конформных отображений являются вопрос о возможности (существовании) конформного отображения одной заданной области на другую и задача практического нахождения функций, осуществляющих это отображение. Ответ на первый вопрос в случае односвязных областей дает теорема Римана, согласно которой любые две односвязные области с границами, состоящими более чем из одной точки, можно взаимно однозначно и конформно отобразить друг на друга. Множество всех таких отображений бесконечно, и все они осуществляются аналитическими функциями, то есть функциями, имеющими производную. В частности, из этой теоремы следует, что любую односвязную область указанного типа можно бесконечным числом способов отобразить конформно на единичный круг | z | < 1 или верхнюю полуплоскость Im z > 0, чем часто пользуются в приложениях.

Сложнее обстоит дело со второй проблемой. Найти практически конформное отображение одной области на другую, особенно с помощью элементарных функций, удается не всегда. По сложности эта проблема во многом схожа с проблемой нахождения интегралов функций, существование которых если даже доказано (например, в случае непрерывных функций), но найти их практически не всегда удается. Как и в случае интегралов, данная проблема решена лишь для некоторых определенных типов областей, поэтому она до сих пор остается предметом исследований.

Наряду с конформным отображением плоских областей изучаются также конформные отображения областей в евклидовом пространстве Eⁿ измерения n > 2, которые определяются так же, как и в случае плоскости. Однако конформные отображения в Eⁿ при n > 2 образуют весьма узкий класс. Каждое такое отображение является либо преобразованием подобия, либо суперпозицией преобразования подобия и инверсии. Поэтому они в отличие от плоских конформных отображений не нашли особых приложений. Широкое применение плоских конформных отображений в различных областях науки объясняется, например, следующим. Многие дифференциальные уравнения в частных производных и их системы при замене одних переменных на другие, связанные между собой посредством функций, осуществляющих конформное отображение, либо вовсе не изменяются, либо упрощаются. Таковым является, например, уравнение Лапласа

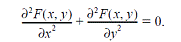
Если в этом уравнении переменные x, y заменить на новые переменные u,υ, являющиеся действительной и мнимой частью некоторой аналитической функции f (z), то уравнение не изменится. На основании этого многие задачи для уравнения Лапласа в областях сложной структуры сводятся с помощью конформного отображения w = f (z) = u + i υ к аналогичным задачам в более простых областях (круге, полуплоскости и т.д.), в которых решение задачи либо известно, либо находится проще. После этого решение задачи в исходной области получается путем обратной замены переменных.

Примеры конформного отображения.

·        Простейший пример - преобразования подобия <#"815244.files/image006.gif">, 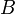 и их образов 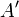,  имеет место соотношение

,

где  - положительное число, называемое коэффициентом подобия.(каждая гометия является подобием)

Рис. 4

Подобные фигуры на рисунке имеют одинаковые цвета.

·              Инверсия <#"815244.files/image013.gif">

Рис. 5

·        Любая голоморфная функция <#"815244.files/image014.gif"> и комплексно дифференцируемая в каждой точке.

Рис. 6

·        Стереографическая проекция <#"815244.files/image016.gif">

Рис. 7

 <#"815244.files/image017.gif">

Рис. 8 Карта поверхности Земли в стереографической проекции

История.

Исследованием конформных отображений занимались Л. Эйлер <#"815244.files/image018.gif">

Черт. 1

В силы этой же причины без искажения пропорций, а следовательно, и без нарушения формы, невозможно изобразить часть земной поверхности (последнюю можно принять за шаровую) на плоскости, т.е. построить карту. Оказывается, однако, что возможно строить карту, не изменяя величины углов между различными линиями земной поверхности.

Пусть нужно построить карту северного полушария, на которой все углы между различными направлениями на земной поверхности изобразятся в натуральную величину. Чтобы наглядно представить себе, как это можно сделать, вообразим большой земной глобус из какого-либо прозрачного материала, например, стекла, закрашенный непрозрачными красками так, что лишь контуры материков, стран и морей в северном полушарии, а также сетка меридианов и параллелей остаются непокрытые краской, и следовательно, прозрачными. Кроме того, можно оставить незакрашенными стороны (криволинейные) какого-либо угла PQR с вершиной в любой точке северного полушария. Если в юном полюсе глобуса впаяна маленькая, но яркая электрическая лампочка, а перед глобусом перпендикулярно к его оси помещён экран, то в тёмной комнате мы увидим на экране контурную карту северного полушария (черт.1).

Можно доказать геометрически, что на такой карте (она называется картой стереографической проекции) все углы между любыми линиями на глобусе в северном полушарии изобразятся в натуральную величину. В частности, в натуральную величину отобразится угол PQR.

Если источник света (лампочку), откуда исходят проектирующие лучи, поместить в северном полюсе глобуса, то этим же путём можно получить карту южного полушария также с сохранением натуральной величины углов. Каждая из полученных указанным путём карт представляет некоторую плоскую фигуру: если её подвергнуть конформному отображению, она перейдёт в новую фигуру, которую также можно рассматривать как географическую карту. Так как при конформном отображении углы не изменяются, то на новой карте будут сохраняться натуральные величины углов между направлениями на земной поверхности. На черт.2 слева изображена карта Гренландии в стереографической проекции, а справа - карта, которая получается из предыдущей ,если ко всем её точкам применить преобразование по формуле:

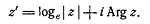
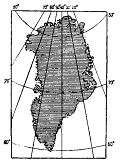
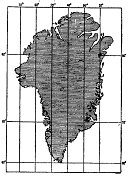
Черт.2

Здесь в качестве основания логарифмов берётся так называемое неперово число e=2,71828.,а Arg z измеряется не в градусах, а в радианах.

Без сомнения, формула эта выглядит сложной и искусственной. Карта, получившаяся в результате такого преобразования, была построена около 400 лет назад голландским учёным Меркатором. Она получила с тех пор большое распространение в навигации. Её преимущества перед картой, выполненной в стенографической проекции, состоят в том, что здесь не только меридианы, но и параллели изображаются прямыми линиями ;более того, прямыми линиями здесь изображаются также любые пути на поверхности Земли ,вдоль которых стрелка компаса сохраняет неизменное направление.

Наиболее важные применения конформных отображений относятся к вопросам физики и механики. Во многих вопросах, где речь идёт, например, об электрическом потенциале в точках пространства, окружающих заряженный конденсатор, или о температуре вокруг нагретого тела, о скоростях частиц в жидкости или газе, в потоке, движущемся в некотором канале и обтекающем при этом какие-либо препятствия и т.п. Такие задачи могут быть разрешены без больших трудностей в случае, когда встречающиеся в них тела имеют особенно простую форму(например ,в виде плоских пластин или круговых цилиндров).Однако расчёт нужно производить и во многих других случаях. Например, чтобы рассчитать самолёт при его конструировании, нужно уметь подсчитывать скорости частиц воздуха в потоке, обтекающем крыло самолёта.

Для того, чтобы свести задачу о скоростях частиц потока воздуха, обтекающего крыло самолёта, к более простой задаче обтекания круглого цилиндра, достаточно конформно отобразить фигуру, заштрихованную на черт.3,а (внешность профиля крыла) на заштрихованную фигуру черт.3,б(внешность окружности).Такое отображение осуществляется посредством некоторой функции комплексного переменного.

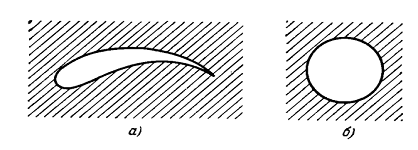
Черт. 3

Подобным же образом конформное отображение позволяет сводить решение задач о расчёте электрического потенциала и температур от случая тел произвольной формы (любого профиля сечения) к простейшим случая, где задача уже является решённой.

Всё сказанное выше о применении конформного отображения к вопросам картографии, механики и физики не сопровождалось никакими доказательствами. Рассмотрим простейшие рациональные функции, с помощью которых можно выполнить некоторые конформные отображения. Вот функции, о которых пойдёт речь:

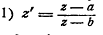 дробно-линейная функция

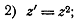
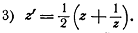
Последняя из них носит имя знаменитого русского учёного Николая Егоровича Жуковского(1847-1921).Такое название дано, потому что Н.Е. Жуковский успешно применял её к решению некоторых вопросов теории самолёта. В частности, он показал, как с помощью этой функции можно получать некоторые профили крыла самолёта, имеющие и теоретическое и практическое значение.

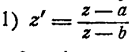дробно-линейная функция.

a, b - неравные между собой комплексные числа. Покажем, что посредством этой функции каждая дуга PLQ окружности, соединяющая точки a и b,преобразуется в некоторый прямолинейный луч P’L’,выходящий из начала координат, причём угол между положительным направлением действительной оси и этим лучём равен углу между направлением baN и касательной к дуге окружности в точке a.(черт.4)

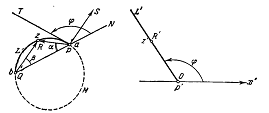
Черт.4

Пусть точка z лежит на дуге PLQ (черт.4 слева); докажем ,что её образ, т.е.соответствующая ей точка 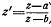, должен лежать на луче P’L’(черт. 4 справа).Чтобы построить вектор z’,нужно знать длину этого вектора и угол наклона к положительной части действительной оси(Arg z).Но z’ есть частное комплексных чисел z-a и z-b, изображаемых векторами PR и QR.Поэтому, 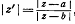, а Arg z равен углу SPR(вектор PS имеет такую же длину и направление, как и QR),отсчитываемому в направление от PS к PR. Очевидно, что 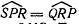) и, следовательно, измеряется половиной дуги QMP. Половиной этой же дуги измеряется и угол NPT. Поэтому, 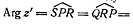 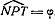. Итак, при любом положении точек z на дуге PLQ соответствующие точки 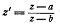 имеют один и тот же аргумент 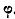.. А это означает, что все эти точки лежат на одном и том же луче P’L’, наклонённом к положительной части действительной оси под углом 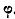.. Этот вывод справедлив и в том случае, когда PLQ-не дуга окружности, а прямолинейный отрезок PQ. Тогда нужно считать угол 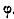=180 градусов и луч P’L’ совпадающим с отрицательной частью действительной оси.(черт.5)

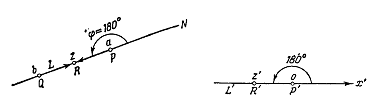
черт.5

В самом деле, если z лежит на отрезке PQ, то векторы, изображающие z-a и z-b,направлены в прямо противоположные стороны. Отсюда следует, что частное 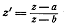 есть действительное отрицательное число, т.е. z’ лежит на отрицательной части действительной оси. Образы точки заполняют весь луч.

2)

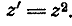
Известно, что углы с вершинами в некоторых исключительных точках могут изменяться в несколько раз. В данном случае имеется такая исключительная точка: это-начало координат А.Все углы с вершиной в точке А увеличиваются вдвое при преобразовании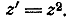

Возьмём луч АМ, выходящий из точки А и составляющий угол 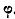с положительной частью действительной оси. (черт.6)

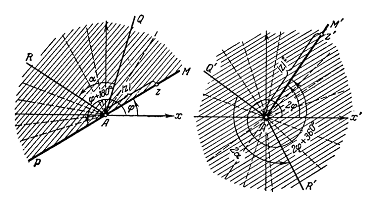
Черт.6

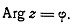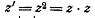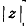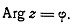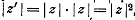Для каждой точке z ,лежащей на этом луче, . Так как вектор  получается из вектора z путём растяжения в  Раз и поворота на угол ,то ,а 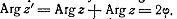 Поэтому точка z’ должна лежать на луче А’М’, выходящем из точки A’ и составляющим с положительной частью действительной оси угол 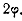если точка z будет перемещаться по АМ, начиная от точка А и далее, неограниченно отодвигаясь от неё, то соответствующая точка z’ будет перемещаться по A’M’,начиная от точки A’ и далее ,неограниченно отодвигаясь от неё; при этом расстояние от z’ до A’ всегда будет равняться квадрату расстояния от z до А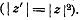 

Отсюда следует, что функция 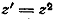 преобразует луч АМ в луч A’M’, наклонённый к оси A’x’ под углом, вдвое большим по сравнению с первоначальным углом наклона.

Легко понять, что луч АР, составляющий с Ax угол (АМ и АР лежат на одной прямой), преобразуются посредством функции 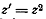в тот же луч A’M’.В самом деле, если угол , удвоить, то получится 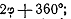луч, наклонённый к A’x’ под этим углом совпадает с A’M’.

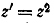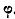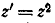Посмотрим, во что преобразуется посредством функции  фигура, заштрихованная на черт.6 слева; она называется полуплоскостью. Полуплоскость можно рассматривать как заполненную бесчисленным множеством лучей, выходящих из А и наклонённых к Ax под углами, большими ,но меньшими .лучи АМ и АР составляют границу полуплоскости (одну прямую). Функция преобразует лучи, принадлежащие полуплоскости, во всевозможные лучи ,выходящие из A’ и наклонённые к A’x под углами, большими 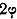,но меньшими .

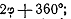Отсюда следует, что полуплоскость, ограниченная лучами АМ и АР, преобразуется в фигуру A’M’(черт.6 справа). Последнюю фигуру можно охарактеризовать как плоскость с выброшенным или исключённым) лучём A’M’.Эта фигура образована всеми точками плоскости, кроме точек, лежащих на A’M’.если в полуплоскости взять какие -либо два луча AQ и AR,наклонённые к Ax под углам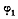и  и 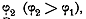Они составят между собой 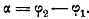.В результате преобразования 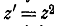 эти лучи перейдут в A’Q’ и A’R’,наклонённые к A’x’ под углами 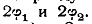.Очевидно, что угол Q’A’R’ равен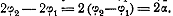

Итак, углы с вершиной в точке А удваиваются при преобразовании 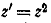, иными словами, конформность отображения нарушается в точке А.

Углы с вершиной в любой точке 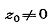не изменяются при преобразовании .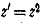

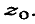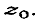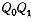Пусть L - какая-либо кривая, выходящая из точки .Если на L взять точку ,отличную от ,то направление секущей, соединяющей эти точки ,будет совпадать с направлением вектора ,изображающего разность 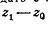 (черт. 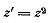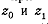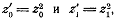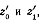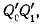7 слева)посредством функции кривая L преобразуется в некоторую кривую L’,а точки -в новые точки лежащие на кривой L’.Очевидно, что направление секущей, соединяющей  совпадает с направлением вектора изображающего разность (черт .7 справа).

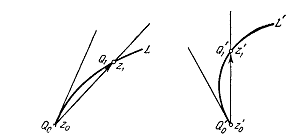
Черт. 7

Сравним между собой направления двух секущих; для этого достаточно сравнить между собой направления векторов 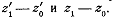.Так как угол между ними, отсчитываемый от вектора 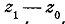к вектору 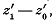,совпадает с аргументом частного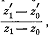,то всё сравнение сводится к подсчёту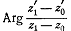.Частное 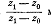можно преобразовать, заменив 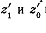их выражениями: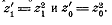

Получим:

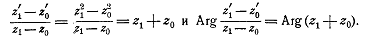
Следовательно, угол между направлениями секущих к кривым L’ и L ,проведённых через пары соответствующих точек 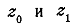 (на L) и 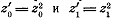 (на L’), равен 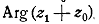. Переходя от секущих к касательным, будем неограниченно приближать точку 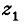по кривой L к точке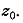

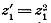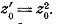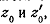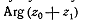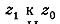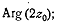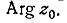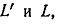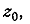Тогда и точка  будет неограниченно приближаться по кривой L’ к точку . Поэтому секущие будут неограниченно приближаться к касательным, проведённым в точках  а угол между секущими- к углу между касательными. 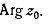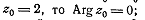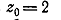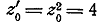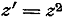Но угол между секущими равен  и при стремлении  стремится к  последний же совпадает с Итак, угол между касательными к кривым  проведённым в соответствующих точках  и  равен .Если, например,  отсюда следует, что направление касательной в точке  к любой кривой L,проведенной через эту точку, будет совпадать с направление касательной в точке  в кривой L’, в которую функция   преобразует L.Если 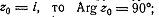следовательно ,касательная в точке 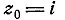к любой кривой L,проведённой через эту точку , и касательная в точке 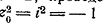  к образу кривой L’взаимно перпендикулярны.

Возвращаясь к общему случаю, можно сказать, что касательные поворачиваются на угол, равный 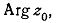когда кривые, проходящие через точку 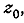 преобразуются посредством функции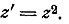

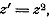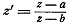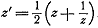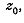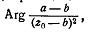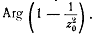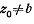Способ, которым доказана конформность отображения  применим и к другим функциям, например, к дробно-линейной  или функции Жуковского . Только здесь получаются другие выражения для угла поворота касательной. Так, для дробно-линейной функции получится, что касательные к кривым, проходящим через точку  поворачиваются на угол  а в случае функции Жуковского - на угол, равный  (в первом случае ,во втором-)

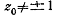Рассмотрим, во что преобразуется посредством функции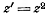 окружность, проходящая через точку А в полуокружности всевозможные лучи и отметим на каждом из них точку пересечения с окружностью. На данном чертеже для определённости изображены 7 лучей; все углы 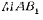, 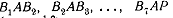взяты равными между собой 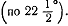.Функция 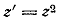преобразует их в лучи, составляющие между собой вдвое большие углы; каждый из углов 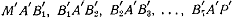 равен 45 градусов.

Подсчитаем, куда перейдут точки 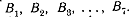Расстояние их образов 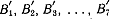от точки 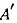будут равны квадратам расстояний 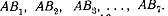 Но из черт.7 видно 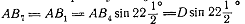 (D-диаметр окружности), далее 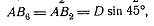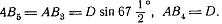. Остаётся заметить, что 

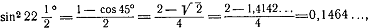
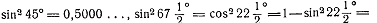0,8535…

Следовательно,

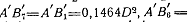
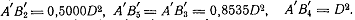
Через точки 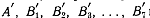 проходит кривая, являющаяся образом окружности при преобразовании 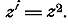 Чтобы получить о ней более точное представление, можно было бы брать большее количество лучей. Кривая эта называется кардиоидой (пер.сердцеобразная).Легко понять, что фигура, заштрихованная на черт.7 слева(она получается из полуплоскости путём выбрасывания круга),преобразуется посредством функции 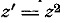в фигуру, заштрихованную на том же чертеже справа. Последняя ограничена кардиоидой и лучом A’M’, составляющим угол 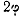с положительным направлением действительной оси. Луч A’M’ направлен по касательной к каждой из двух дуг кардиоиды, выходящих из точки А.

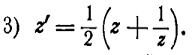Функция Жуковского.

Применим функцию к преобразованию фигуры, ограниченной двумя окружностями: одной, проходящей через точки -1 и +1, и другой, касающейся первой изнутри в точке 1; на черт.8 эта фигура заштрихована.

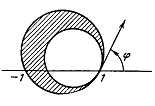
черт.8

Убедимся сначала, что преобразование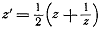можно свети к нескольким выполняемым друг за другом функциям более простым преобразованиям. Рассмотрим отношение, 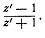заменяя в нём 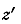выражение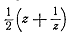м , найдём:

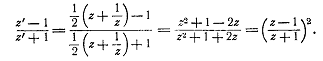
Справедливо и обратное:

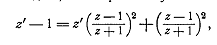
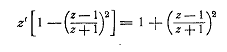
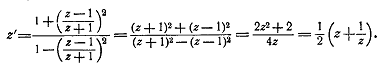
Итак, соотношения 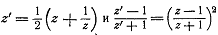 эквивалентны (одно следует из другого).

Поэтому преобразование Жуковского 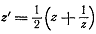 можно представить в виде . Результат должен получится тот же самый. Переход от 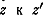можно осуществить в 3 этапа. Сначала перейти от 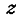к вспомогательному переменному 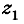по формуле

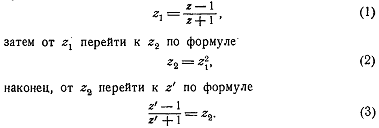
Смысл в замене одного преобразования Жуковского тремя преобразованиями в том, что каждое из них проще.

Итак, применим к фигуре, изображённый на черт.8 преобразование(1),к тому, что получится - преобразование(2), к тому, что получится после этого, прибавим преобразование (3).(черт .9)

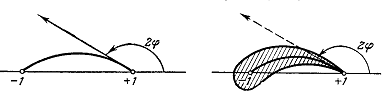
Черт.9

Меняя угол наклона касательной к окружности в точке 1 (черт.8)и радиус меньшей окружности, можно получать разные профили. Такого рода профили были предложены впервые русскими учёными С.А. Чаплыгиным и Н.Е Жуковским, почему они и называются профилями Жуковского-Чаплыгина.

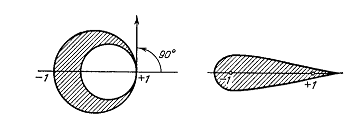
черт.10

Если угол 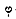 - прямой, т.е. большая окружность построена на отрезке от -1 до +1, как на диаметре, то соответствующий профиль симметричен относительно действительной оси. Такой профиль называется иногда рулём Жуковского. (черт.10)

Профили Жуковского-Чаплыгина являются основными профилями во всех исследованиях по теории крыла самолёта.

конформный отображение плоскость функция

Список литературы

1.  Конформное отображение (Сильвестров В.В. 1999), Математика