Статистическое изучение динамики социально-экономических явлений
Содержание
1.
Теоретическая часть
1.1 Оценка
адекватности тренда и прогнозирование (критерий Фишера)
2.
Практическая часть
2.1 Задача 1.
Статистическое исследование, сводка и группировка данных
.2 Задача 2.
Статистическое изучение динамики социально-экономических явлений
.3 Задача 3.
Выборочный метод в статистических исследованиях. Показатели вариаций
.4 Задача 4.
Статистика заработанной платы
.5 Задача 5.
Выявление основной тенденции развития ряда динамики
Список
литературы
1. Теоретическая часть
.1 Оценка адекватности тренда и прогнозирование (критерий Фишера)
Для практического использования моделей регрессии
большое значение имеет их адекватность, т.е. соответствие фактическим
статистическим данным.
Анализ качества эмпирического уравнения парной и множественной
линейной регрессии начинают с построения эмпирического уравнения регрессии,
которое является начальным этапом эконометрического анализа. Первое же,
построенное по выборке, уравнение регрессии очень редко является
удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей
оценкой является проверка качества уравнения регрессии. В эконометрике принята
устоявшаяся схема такой проверки, которая проводится по следующим направлениям:
· проверка статистической значимости
коэффициентов уравнения регрессии
· проверка общего качества уравнения
регрессии
· проверка свойств данных, выполнимость
которых предполагалась при оценивании уравнения (проверка выполнимости
предпосылок МНК).
Прежде, чем проводить анализ качества уравнения
регрессии, необходимо определить дисперсии и стандартные ошибки коэффициентов,
а также интервальные оценки коэффициентов. Корреляционный и регрессионный
анализ, как правило, проводится для ограниченной по объёму совокупности.
Поэтому параметры уравнения регрессии (показатели
регрессии и корреляции), коэффициент корреляции и коэффициент детерминации
могут быть искажены действием случайных факторов. Чтобы проверить, насколько
эти показатели характерны для всей генеральной совокупности, не являются ли они
результатом стечения случайных обстоятельств, необходимо проверить адекватность
построенных статистических моделей.
При анализе адекватности уравнения регрессии (модели)
исследуемому процессу, возможны следующие варианты:
. Построенная модель на основе F-критерия Фишера в
целом адекватна и все коэффициенты регрессии значимы. Такая модель может быть
использована для принятия решений и осуществления прогнозов.
. Модель по F-критерию Фишера адекватна, но часть
коэффициентов не значима. Модель пригодна для принятия некоторых решений, но не
для прогнозов.
. Модель по F-критерию адекватна, но все коэффициенты
регрессии не значимы. Модель полностью считается неадекватной. На ее основе не
принимаются решения и не осуществляются прогнозы.
Проверить значимость (качество) уравнения
регрессии-значит установить, соответствует ли математическая модель, выражающая
зависимость между переменными, экспериментальным данным, достаточно ли
включенных в уравнение объясняющих переменных для описания зависимой
переменной. Чтобы иметь общее суждение о качестве модели, по каждому наблюдению
из относительных отклонений определяют среднюю ошибку аппроксимации. Проверка
адекватности уравнения регрессии (модели) осуществляется с помощью средней
ошибки аппроксимации, величина которой не должна превышать 12-15% (максимально
допустимое значение).
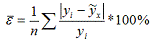
Оценка значимости уравнения регрессии в целом
производится на основе F-критерия Фишера, которому предшествует дисперсионный
анализ. В математической статистике дисперсионный анализ рассматривается как
самостоятельный инструмент статистического анализа. В эконометрике он
применяется как вспомогательное средство для изучения качества регрессионной
модели. Согласно основной идее дисперсионного анализа, общая сумма квадратов
отклонений переменной (y) от среднего значения (yср.) раскладывается на две
части: "объясненную" и "необъясненную":
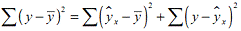
Схема дисперсионного анализа имеет следующий вид:

(n -число наблюдений, m-число параметров при
переменной x)
Определение дисперсии на одну степень свободы приводит
дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в
расчете на одну степень свободы, получим величину F-критерия Фишера.
Фактическое значение F -критерия Фишера сравнивается с табличным значением
Fтабл. (α,
k1, k2) при заданном
уровне значимости α и степенях свободы k1= m и k2=n-m-1. При этом, если
фактическое значение F-критерия больше табличного Fфакт > Fтеор, то
признается статистическая значимость уравнения в целом. Для парной линейной
регрессии m=1 , поэтому:
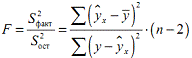
Эта формула в общем виде может выглядеть так:
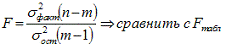
Отношение объясненной части дисперсии переменной (у) к
общей дисперсии называют коэффициентом детерминации и используют для
характеристики качества уравнения регрессии или соответствующей модели связи.
Соотношение между объясненной и необъясненной частями общей дисперсии можно
представить в альтернативном варианте:
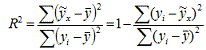
Коэффициент детерминации R2 принимает значения в
диапазоне от нуля до единицы 0≤ R2 ≤1. Коэффициент детерминации R2
показывает, какая часть дисперсии результативного признака (y) объяснена
уравнением регрессии. Чем больше R2, тем большая часть дисперсии
результативного признака (y) объясняется уравнением регрессии и тем лучше
уравнение регрессии описывает исходные данные. При отсутствии зависимости между
(у) и (x) коэффициент детерминации R2 будет близок к нулю. Таким образом,
коэффициент детерминации R2 может применяться для оценки качества(точности)
уравнения регрессии. Значение R-квадрата является индикатором степени подгонки
модели к данным (значение R-квадрата близкое к 1.0 показывает, что модель
объясняет почти всю изменчивость соответствующих переменных). Чтобы определить,
при каких значениях R2 уравнение регрессии следует считать статистически не
значимым, что, в свою очередь, делает необоснованным его использование в
анализе, рассчитывается F-критерий Фишера: Fфакт > Fтеор - делаем вывод о
статистической значимости уравнения регрессии. Величина F-критерия связана с
коэффициентом детерминации R2xy (r2xy) и ее можно рассчитать по следующей
формуле:
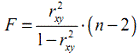
Либо при оценке значимости индекса детерминации
(аналог коэффициента детерминации):
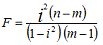
где: i2 - индекс (коэффициент) детерминации, который
рассчитывается:
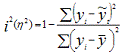
Использование коэффициента множественной детерминации
R2 для оценки качества модели, обладает тем недостатком, что включение в модель
нового фактора (даже несущественного) автоматически увеличивает величину R2.
Поэтому, при большом количестве факторов, предпочтительнее использовать, так
называемый, улучшенный, скорректированный коэффициент множественной
детерминации R2, определяемый соотношением:
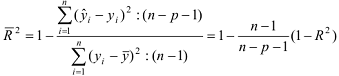
где p - число факторов в уравнении регрессии, n -
число наблюдений. Чем больше величина p, тем сильнее различия между
множественным коэффициентом детерминации R2и скорректированным R2. При
использовании скорректированного R2, для оценки целесообразности включения
фактора в уравнение регрессии, следует учитывать, что увеличение его величины
(значения), при включении нового фактора, не обязательно свидетельствует о его
значимости, так как значение увеличивается всегда, когда t-статистика больше
единицы (|t|>1). При заданном объеме наблюдений и при прочих равных
условиях, с увеличением числа независимых переменных (параметров),
скорректированный коэффициент множественной детерминации убывает. При небольшом
числе наблюдений, скорректированная величина коэффициента множественной
детерминации R2 имеет тенденцию переоценивать долю вариации результативного
признака, связанную с влиянием факторов, включенных в регрессионную модель.
Низкое значение коэффициента множественной корреляции и коэффициента
множественной детерминации R2 может быть обусловлено следующими причинами:
· в регрессионную модель не включены
существенные факторы;
· неверно выбрана форма аналитической
зависимости, которая нереально отражает соотношения между переменными,
включенными в модель.
Следует также обратить внимание на важность анализа
остатков . Остаток представляет собой отклонение фактического значения
зависимой переменной от значения, полученного расчетным путем. При построении
уравнения регрессии, мы можем разбить значение (у) в каждом наблюдении на 2
составляющие:
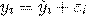
Отсюда:
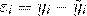
Если εi=0, то для всех наблюдений фактические
значения зависимой переменной совпадают с расчетными (теоретическими)
значениями. Графически это означает, что теоретическая линия регрессии (линия,
построенная по функции у=а0+а1х) проходит через все точки корреляционного поля,
что возможно только при строго функциональной связи. Следовательно,
результативный признак (у) полностью обусловлен влиянием фактора (х). На
практике, как правило, имеет место некоторое рассеивание точек корреляционного
поля относительно теоретической линии регрессии, т.е. отклонения эмпирических
данных от теоретических εi≠0. Величина этих отклонений и лежит в основе
расчета показателей качества (адекватности) уравнения.
Большинство предположений множественной регрессии
нельзя в точности проверить, однако можно обнаружить отклонения от этих
предположений. В частности, выбросы (экстремальные наблюдения) могут вызвать
серьезное смещение оценок, сдвигая линию регрессии в определенном направлении
и, тем самым, вызывая смещение коэффициентов регрессии. Часто исключение всего
одного экстремального наблюдения приводит к совершенно другому результату.
Выбросы оказывают существенное влияние на угол наклона регрессионной линии и
соответственно, на коэффициент корреляции. Всего один выброс может полностью
изменить наклон регрессионной линии и, следовательно, вид зависимости между
переменными. Одна точкавыброса обуславливает высокое значение коэффициента
корреляции, в то время, как в отсутствие выброса, он практически равен нулю.
При численности объектов анализа до 30 единиц
возникает необходимость проверки значимости (существенности) каждого
коэффициента регрессии. При этом выясняют насколько вычисленные параметры
характерны для отображения комплекса условий: не являются ли полученные
значения параметров результатами действия случайных причин. Значимость
коэффициентов простой линейной регрессии (применительно к совокупностям, у
которых n<30) осуществляют с помощью t-критерия Стьюдента. При этом
вычисляют расчетные (фактические) значения t-критерия для параметров a0 а1:
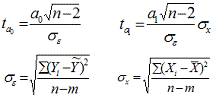
· n - число наблюдений, m-число
параметров уравнения регрессии,
· σε - (остаточное) среднее
квадратическое отклонение результативного признака от выровненных значений ŷ,
· σх - среднее квадратическое отклонение
факторного признака от общей средней.
Вычисленные, по вышеприведенным формулам, значения
сравнивают с критическими t, которые определяют по таблице значений Стьюдента с
учетом принятого уровня значимости (α) и числа степеней свободы вариации k
(ν)=n-2. В
социально-экономических исследованиях уровень значимости α обычно принимают 0,05. Параметр
признается значимым (существенным) при условии, если tрасч. > tтабл. В этом
случае, практически невероятно, что найденные значения параметров обусловлены
только случайными совпадениями.
Для оценки значимости парного коэффициента корреляции
(корень квадратный из коэффициента детерминации), при условии линейной формы
связи между факторами, можно использовать t-критерий Стьюдента:
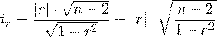
Анализ качества эмпирического уравнения множественной
линейной регрессии предусматривает оценку мультиколлинеарности факторов. При
оценке мультиколлинеарности факторов следует учитывать, что чем ближе к нулю
определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность
факторов и ненадежнее результаты множественной регрессии. Для отбора наиболее
значимых факторов Хi должны быть учтены следующие условия:
· связь между результативным признаком
и факторным должна быть выше межфакторной связи
· связь между факторами должна быть не
более 0.7
· при высокой межфакторной связи
признака отбираются факторы с меньшим коэффициентом корреляции между ними
Более объективную характеристику тесноты связи дают
частные коэффициенты корреляции, измеряющие влияние на результативный фактор Уi
фактора Хi при неизменном уровне других факторов. Коэффициент частной
корреляции отличается от простого коэффициента линейной парной корреляции тем,
что он измеряет парную корреляцию соответствующих признаков (У и Хi) при
условии, что влияние на них остальных факторов (Хj) устранено.
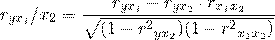
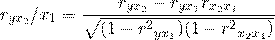
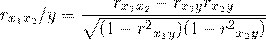
2.
Практическая часть
.1 Задача 1.
Статистическое исследование, сводка и группировка данных
С целью изучения зависимости между среднегодовой
стоимостью основных производственных фондов (ОПФ) и стоимостью выпуска
продукции (ПР) необходимо произвести группировку фирм по среднегодовой
стоимости производственных фондов. По каждой группе и совокупности фирм
рассчитать:
) число фирм;
) среднегодовую стоимость основных производственных
фондов (ОПФ);
) стоимость продукции (ПР);
) среднегодовую стоимость основных производственных
фондов на одну фирму;
) стоимость продукции на одну фирму;
) стоимость продукции на 1 руб. основных
производственных фондов (фондоотдачу).
Решение:
В качестве группировочного признака принимаем среднегодовую стоимость
основных производственных фондов.
Число групп определяем по формуле Стерджесса:
=1+3,322lgN=1+3,221lg30=6
Определяем величину интервала:
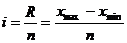 =(9-0,5)/6=1,42
=(9-0,5)/6=1,42
(
группа 0.5+1,42=1,92
группа 1,92+1,42=3,34
группа 3,34+1,42=4,76
группа 4,76+1,42=6,18
группа 6,18+1,42=7,6
группа 7,6+1,42=9,02
Таблица 1
Исходные данные
|
Фирмы
|
ОПФ
|
ПР
|
|
1
|
3,4
|
3,5
|
|
2
|
3,1
|
3,3
|
|
3
|
4,1
|
4,5
|
|
4
|
5,8
|
7,5
|
|
5
|
5,2
|
6,9
|
|
6
|
3,8
|
4,3
|
|
7
|
4,1
|
5,9
|
|
8
|
5,6
|
4,8
|
|
9
|
4,6
|
5,8
|
|
10
|
4,2
|
4,6
|
|
11
|
6,1
|
8,4
|
|
12
|
6,5
|
7,3
|
|
13
|
1,5
|
2,1
|
|
14
|
6,4
|
7,8
|
|
15
|
7,5
|
10,6
|
|
16
|
5,1
|
5,8
|
|
17
|
4,9
|
5,3
|
|
18
|
5,8
|
6
|
|
19
|
2,8
|
2,5
|
|
20
|
2,2
|
1,9
|
|
21
|
1
|
1,5
|
|
22
|
8
|
8,5
|
|
23
|
7,7
|
8
|
|
24
|
6,3
|
6,5
|
|
25
|
5
|
4,5
|
|
26
|
1,7
|
2,4
|
|
27
|
4,1
|
5,1
|
|
28
|
0,5
|
1,2
|
|
29
|
8,2
|
9,9
|
|
30
|
9
|
11,3
|
Таблица 2
Ранжированный ряд.
|
ОПФ
|
ПР
|
|
0,5 1 1,5 1,7
|
1,2 1,5 2,1 2,4
|
|
2,2 2,8 3,1
|
1,9 2,5 3,3
|
|
3,4 3,8 4,1 4,1 4,1 4,2 4,6
|
3,5 4,3 4,5 5,1 5,9 4,6 5,8
|
|
4,9 5 5,1 5,2 5,6 5,8 5,8
6,1
|
5,3 4,5 5,8 6,9 4,8 7,5 6
8,4
|
|
6,3 6,4 6,5 7,5
|
8,5 7,8 7,3 10,6
|
|
7,7 8 8,2 9
|
8 8,5 9,9 11,3
|
. Среднегодовая стоимость основных производственных фондов:
Σ ОПФ
. Стоимость продукции:
Σ ПР
. Среднегодовая стоимость основных производственных фондов на одну фирму:
Σ ОПФ/n
. Стоимость продукции на одну фирму:
Σ ПР/n
. Фондоотдача:
Σ ПР/n: Σ ОПФ/n
группа: 1,8/1,175=1,53
группа: 2,6/2,7=0,95
группа: 4,81/4,04=1,19
группа: 6,15/5,44=1,13
группа: 8,55/6,675=1,28
группа: 9,425/8,225=1,15
Таблица 3
Результаты группировки
|
Номер группы
|
Группы фирм по
среднегодовой стоимости ОПФ
|
Число фирм
|
Среднегодовая стоимость ОПФ
|
стоимость продукции
|
Среднегодовая стоимость ОПФ
на 1 фирму
|
Стоимость продукции в
среднем на 1 фирму
|
Фондоотдача
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
0,5-1,92
|
4
|
4,7
|
7,2
|
1,175
|
1,8
|
1,53
|
|
2
|
1,92-3,34
|
3
|
8,1
|
7,7
|
2,7
|
2,6
|
0,95
|
|
3
|
3,34-4,76
|
7
|
28,3
|
33,7
|
4,04
|
4,81
|
1,19
|
|
4
|
4,76-6,18
|
8
|
43,5
|
49,2
|
5,44
|
6,15
|
1,13
|
|
5
|
6,18-7,6
|
4
|
26,7
|
34,2
|
6,675
|
8,55
|
1,28
|
|
6
|
7,6-9,02
|
4
|
32,9
|
37,7
|
8,225
|
9,425
|
1,15
|
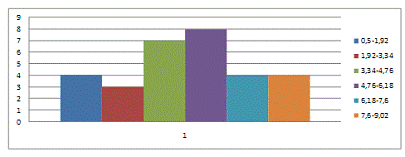
Рис. 1 Гистограмма распределения
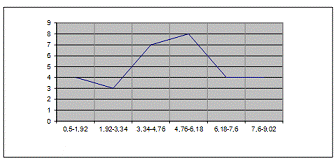
Рис. 2 Полигон распределения
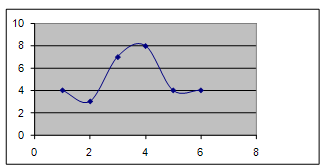
Рис. 3 Кумулята
Вывод: Разбив неоднородную совокупность из 30 фирм на 6 групп с равным
интервалом по признаку среднегодовой стоимости ОПФ. Самая многочисленная группа
4 (8 фирм) и которая примерно равна 27%, а самая малочисленная 2 (3 фирмы) и
примерно равна 10%.
2.2 Задача 2.
Статистическое изучение динамики социально-экономических явлений
По данным ряда динамики об объёмах
строительно-монтажных работ (СМР) (тыс. руб.), выполненных строительными
организациями за пятилетний период
Таблица 4
Исходные данные
|
год
|
Объем СМР
|
|
1
|
28
|
|
2
|
35
|
|
3
|
41
|
|
4
|
47
|
|
5
|
51
|
Вычислить:
) абсолютные приросты (или снижения) - цепные и
базисные
) темпы роста (или снижения) - цепные и базисные;
) темпы прироста (или снижения) - цепные и базисные;
) абсолютное содержание 1% прироста (или снижения).
Полученные данные по пунктам 1-4 представить в табл. 4.
) среднегодовой объём работ;
) средний абсолютный прирост.
) среднегодовой темп роста и прироста (или снижения).
Таблица 5
Результаты расчета
|
Год
|
Объем работ (тыс.руб.)
|
Абсолютный прирост
(тыс.руб.)
|
Темп роста (%)
|
Темп прироста (%)
|
Абсод. 1%прироста
(тыс.руб.)
|
|
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
|
|
1
|
28
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2
|
35
|
7
|
7
|
125
|
125
|
25
|
25
|
0,28
|
|
3
|
41
|
13
|
6
|
146,4
|
117,1
|
17,1
|
0,35
|
|
4
|
47
|
19
|
6
|
167,9
|
114,5
|
67,9
|
14,6
|
0,41
|
|
5
|
51
|
23
|
4
|
182,1
|
108,5
|
82,1
|
8,5
|
0,47
|
|
Итого
|
202
|
|
|
|
|
|
|
|
1. Определяем базисный и цепной абсолютные приросты по формулам:
регрессия фишер статистика вариация
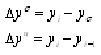
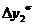 =35-28=7 (шт.)
=35-28=7 (шт.)
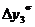 =41-28=13
=41-28=13
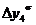 =47-28=19
=47-28=19
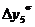 =51-28=23
=51-28=23
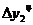 =35-28=7
=35-28=7
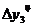 =41-35=6
=41-35=6
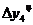 =47-41=6
=47-41=6
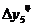 =51-47=4
=51-47=4
где yi - изучаемый уровень ряда;б - уровень ряда, принятого за базисный;-
уровень ряда, предшествующий изучаемому.
. Рассчитываем базисный и цепной темпы роста:
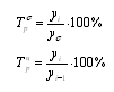
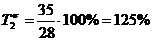
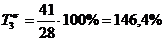

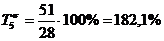
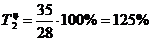
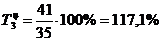
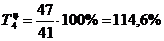
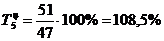
. Определяем базисный и цепной темпы прироста:
Тп=Тр-100%
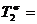 125%-100%=25%
125%-100%=25%
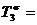 146,4%-100%=46,4%
146,4%-100%=46,4%
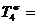 167,9%-100%=67,9%
167,9%-100%=67,9%
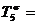 182,1%-100%=82,1%
182,1%-100%=82,1%
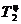 =125%-100%=25%
=125%-100%=25%
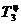 =117,1%-100%=17,1%
=117,1%-100%=17,1%
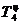 =114,6%-100%=14,6%
=114,6%-100%=14,6%
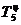 =108,5%-100%=8,5%
=108,5%-100%=8,5%
. Находим абсолютное содержание одного процента прироста:
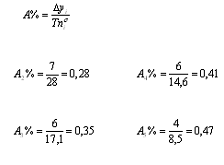
. Вычисляем среднегодовой объем работ:
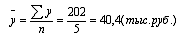
6. Рассчитываем средний абсолютный прирост:
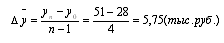
. Находим средний темп роста:
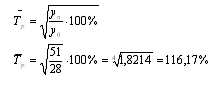
. Определяем средний прирост:
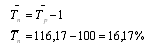
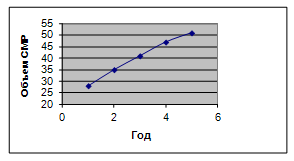
Рис. 4 Динамика объемов строительных работ
Вывод: На графике виден стабильный рост по годам объема
строительно-монтажных работ, выполненных строительными организациями за 5 лет.
2.3 Задача 3.
Выборочный метод в статистических исследованиях. Показатели вариации
Для изучения дневной выработки рабочих предприятия была проведена 10%-я
бесповторная выборка, в результате которой получены исходные данные о
распределении рабочих по производительности труда, представленные в таблице.
Таблица 6
Исходные данные
|
Группа рабочих с дневной
выработкой изделий, штук
|
Число рабочих, чел.
|
|
10-20
|
5
|
|
20-30
|
10
|
|
30-40
|
40
|
|
40-50
|
27
|
|
50-60
|
10
|
|
Итого
|
92
|
На основе приведенных данных вычислить:
) среднедневную выработку рабочего;
) дисперсию и среднеквадратическое отклонение;
) коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборки и возможные границы, в
которых ожидается среднедневная выработка всех рабочих строительного
предприятия.
Решение.
Таблица 7
|
х
|
f
|
хi
|
хi·fi
|
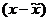
|
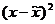
|
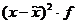
|
|
10-20
|
5
|
15
|
75
|
-23
|
529
|
2645
|
|
20-30
|
10
|
25
|
250
|
-13
|
169
|
1690
|
|
30-40
|
40
|
35
|
1400
|
-3
|
9
|
36
|
|
40-50
|
27
|
45
|
1215
|
7
|
49
|
1327
|
|
50-60
|
10
|
55
|
550
|
17
|
289
|
2890
|
|
Итого
|
92
|
175
|
3490
|
|
|
8588
|
1. Определяем среднедневную выработку рабочих:
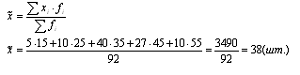
2. Вычисляем дисперсию:
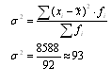
3. Рассчитываем среднеквадратическое отклонение:
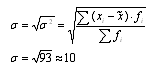
4. Находим коэффициент вариации по формуле:
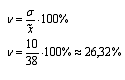
5. Определяем среднюю ошибку выборки по формуле:
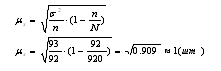
где п - число рабочих выборочной совокупности, чел.
6. Определяем предельную ошибку выборки по формуле:
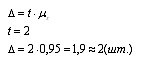
7. Находим границы среднедневной выработки генеральной совокупности:
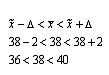
Вывод: Среднедневная выработка рабочего равна 38шт.
38шт.
Среднее значение выработки одного рабочего строительного предприятия
находится в пределах от 36,1 до 39,9, при вероятности p=0,954. Таким образом
среднедневная выработка как раз находится в пределах 36,1-39,9.
2.4 Задача 4. Статистика заработной платы
Имеются следующие данные о количестве рабочих и их заработной плате по
предприятиям в двух отраслях.
Таблица 8
|
Отрасль
|
Базисный период
|
Отчетный период
|
|
Число работающих, чел.
|
Средняя з/п. тыс. руб.
|
Число работающих, чел.
|
Средняя з/п. тыс. руб.
|
|
1
|
150
|
560
|
200
|
600
|
|
2
|
270
|
930
|
300
|
1200
|
Вычислить индексы средней заработной платы:
1) по каждой отрасли;
) по двум отраслям:
а) индекс переменного состава;
б) индекс постоянного состава;
в) индекс структурных сдвигов.
Решение.
1. Определяем индивидуальный индекс средней з/п:
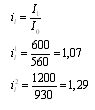
2. Рассчитываем индекс переменного состава:
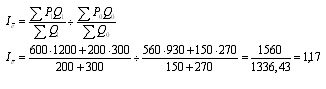
3. Вычисляем индекс постоянного состава:
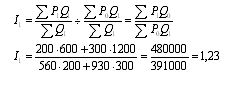
4. Находим индекс структурных сдвигов:
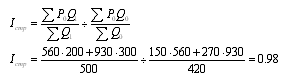
Вывод: Средняя заработная плата в первой отрасли возросла на 7%, во
второй - на 29%. Поскольку индекс среднегодовой заработной платы переменного
состава равен 1,17, значит уровень средней заработной платы по двум отраслям
вырос на 17%. Индекс среднегодовой заработной платы постоянного состава равен
1,23, значит, уровень средней заработной платы по двум отраслям возрос на 23%.
.5 Задача 5. Выявление основной тенденции развития ряда динамики
Выявить тенденцию, складывающуюся в динамике объема продаж, используя
метод аналитического выравнивания. Построить график зависимости изменения
уровней ряда от времени. Используя уравнение адекватной математической функции,
рассчитать прогнозный объем продаж на четвертый квартал. Сделать выводы.
Таблица 9
Исходные данные
|
Месяцы
|
Объем продаж, млн. руб.
|
|
1
|
2
|
|
1
|
23
|
|
2
|
25,4
|
|
3
|
24,7
|
|
4
|
26,2
|
|
5
|
27,3
|
|
6
|
28,2
|
|
7
|
33,7
|
|
8
|
36,8
|
|
9
|
40,1
|
Порядок выполнения:
1. Прямолинейная функция
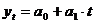
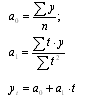
Таблица 10
Расчётные данные для прямолинейной функции
|
|
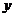
|
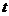
|
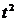
|
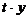
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
23
|
-4
|
16
|
-92
|
|
1
|
2
|
3
|
4
|
5
|
|
2
|
25,4
|
-3
|
9
|
-76,2
|
|
3
|
24,7
|
-2
|
4
|
-49,4
|
|
4
|
26,2
|
-1
|
1
|
-26,2
|
|
5
|
27,3
|
0
|
0
|
0
|
|
6
|
28,2
|
1
|
1
|
28,2
|
|
7
|
33,7
|
2
|
4
|
67,4
|
|
8
|
36,8
|
3
|
9
|
110,4
|
|
9
|
40,1
|
4
|
16
|
160,4
|
|
Итого
|
265,4
|
0
|
60
|
122,6
|
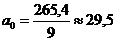
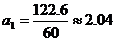
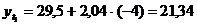
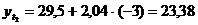
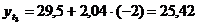
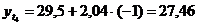
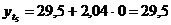
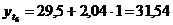
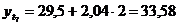
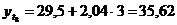
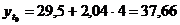
Таблица 11
Расчёт стандартной ошибки аппроксимации
|
|
|
1
|
2
|
|
1,66
|
2,7556
|
|
2,02
|
4,0804
|
|
-0,72
|
0,5184
|
|
-1,26
|
1,5876
|
|
-2,2
|
4,84
|
|
1
|
2
|
|
-3,34
|
11,1556
|
|
0,12
|
0,0144
|
|
1,18
|
1,3924
|
|
2,44
|
5,9536
|
|
Итого
|
32,298
|
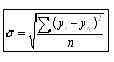
- стандартная ошибка выборки.
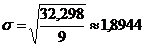
2. Парабола 2-го порядка
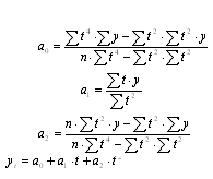
Таблица 12
Расчётные данные для параболы 2-го порядка
|
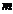
|
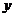
|
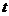
|
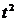
|
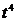
|
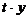
|
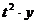
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
23
|
-4
|
16
|
-92
|
368
|
|
2
|
25,4
|
-3
|
9
|
81
|
-76,2
|
228,6
|
|
3
|
24,7
|
-2
|
4
|
16
|
-49,4
|
98,8
|
|
4
|
26,2
|
-1
|
1
|
1
|
-26,2
|
26,2
|
|
5
|
27,3
|
0
|
0
|
0
|
0
|
0
|
|
6
|
28,2
|
1
|
1
|
1
|
28,2
|
28,2
|
|
7
|
33,7
|
2
|
4
|
16
|
67,4
|
134,8
|
|
8
|
36,8
|
3
|
9
|
81
|
110,4
|
331,2
|
|
9
|
40,1
|
4
|
16
|
256
|
160,4
|
641,6
|
|
Итого
|
265,4
|
0
|
60
|
708
|
122,6
|
1857,4
|

Таблица 13
Расчёт стандартной ошибки аппроксимации
|
|
|
1
|
2
|
|
-0,836
|
0,698896
|
|
1,486
|
2,208196
|
|
0,136
|
0,018496
|
|
0,414
|
0,171396
|
|
-0,28
|
0,0784
|
|
-1,746
|
3,048516
|
|
0,816
|
0,665856
|
|
0,406
|
0,164836
|
|
-0,376
|
0,141376
|
|
Итого
|
7,195968
|

- стандартная ошибка выборки.
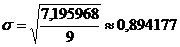
3. Парабола 3-го порядка
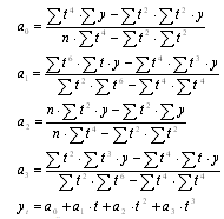
Таблица 14
Расчётные данные для параболы 3-го порядка
|
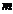
|
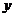
|
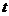
|
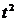
|
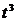
|
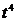
|
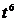
|
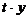
|
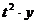
|
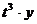
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
23
|
-4
|
16
|
-64
|
256
|
4096
|
-92
|
368
|
-1472
|
|
2
|
25,4
|
-3
|
9
|
-27
|
81
|
729
|
-76,2
|
228,6
|
-685,8
|
|
3
|
24,7
|
-2
|
4
|
-8
|
16
|
64
|
-49,4
|
98,8
|
-197,6
|
|
4
|
26,2
|
-1
|
1
|
-1
|
1
|
1
|
-26,2
|
26,2
|
-26,2
|
|
5
|
27,3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
6
|
28,2
|
1
|
1
|
1
|
1
|
1
|
28,2
|
28,2
|
28,2
|
|
7
|
33,7
|
2
|
4
|
8
|
16
|
64
|
67,4
|
134,8
|
269,6
|
|
8
|
36,8
|
3
|
9
|
27
|
81
|
729
|
110,4
|
331,2
|
993,6
|
|
9
|
40,1
|
4
|
16
|
64
|
256
|
4096
|
160,4
|
641,6
|
2566,4
|
|
Итого
|
265,4
|
0
|
60
|
0
|
708
|
9780
|
122,6
|
1857,4
|
1476,2
|

Таблица 15
Расчёт стандартной ошибки аппроксимации
|
|
|
1
|
2
|
|
-0,616
|
0,379456
|
|
1,21
|
1,4641
|
|
-0,258
|
0,066564
|
|
0,154
|
0,023716
|
|
-0,28
|
0,0784
|
|
-1,486
|
2,208196
|
|
1,21
|
1,4641
|
|
0,682
|
0,465124
|
|
-0,596
|
0,355216
|
|
Итого
|
6,504872
|

стандартная ошибка выборки.
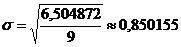
4. Показательная функция
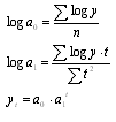
Таблица 16
Расчётные данные для показательной функции
|
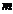
|
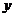
|
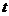
|
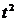
|
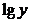
|
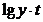
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
23
|
-4
|
16
|
1,361728
|
-5,44691
|
|
2
|
25,4
|
-3
|
9
|
1,404834
|
-4,2145
|
|
3
|
24,7
|
-2
|
4
|
1,392697
|
-2,78539
|
|
4
|
26,2
|
-1
|
1
|
1,418301
|
-1,4183
|
|
5
|
27,3
|
0
|
0
|
1,436163
|
0
|
|
6
|
28,2
|
1
|
1
|
1,450249
|
1,450249
|
|
7
|
33,7
|
2
|
4
|
1,52763
|
3,05526
|
|
8
|
36,8
|
3
|
9
|
1,565848
|
4,697543
|
|
9
|
40,1
|
4
|
16
|
1,603144
|
6,412577
|
|
Итого
|
265,4
|
0
|
60
|
13,16059
|
1,750522
|
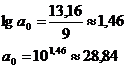
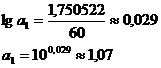
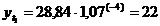
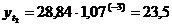
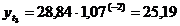
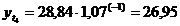
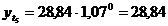
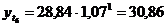
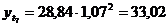
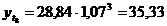
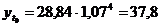
Таблица 17
Расчёт стандартной ошибки аппроксимации
|
|
|
1
|
2
|
|
0,998102
|
0,996208
|
|
1,857969
|
3,45205
|
|
-0,48997
|
0,240073
|
|
-0,75327
|
0,567417
|
|
-1,54
|
2,3716
|
|
-2,6588
|
7,069217
|
|
0,681084
|
0,463875
|
2,160194
|
|
2,296643
|
5,274569
|
|
Итого
|
22,5952
|

- стандартная ошибка выборки.
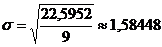
Парабола 3-го порядка - адекватная математическая функция, т.к.
стандартная ошибка аппроксимации имеет наименьшее значение равное 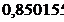 . Используя уравнение адекватной
математической функции, необходимо рассчитать прогнозируемый объем продаж на
четвертый квартал: октябрь (
. Используя уравнение адекватной
математической функции, необходимо рассчитать прогнозируемый объем продаж на
четвертый квартал: октябрь (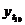 ), ноябрь (
), ноябрь (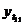 ), декабрь (
), декабрь ( ).
).
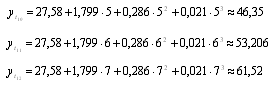
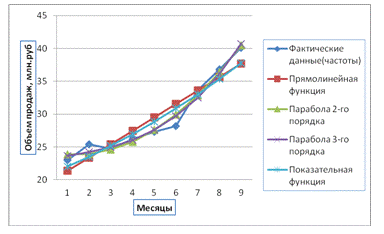
Рис. 5. Динамика изменения уровней ряда от времени для теоритических и
эмпирических уровней.
Вывод. Адекватной математической функцией признается парабола 3-го
порядка, т.к. стандартная ошибка аппроксимации имеет наименьшее значение,
равное 0,850155.
Список литературы
1.
Методические указания к выполнению курсовой работы / В.В. Бызеев. Л.А. Раевский,
К.А. Малышева. - Пенза: ПГУАС, 2008. - 20 с.
. Теория
статистики: Учебник / Р.А. Шмойлова, В.Г. Минашкин, Н.А. Садовникова, Е.Б.
Шувалова; под ред. Р.А. Шмойловой. - 4-е изд., перераб. и доп. - М.: Финансы и
статистика, 2003. - 656 с.
. HELPSTAT.ru