Статистические модели в геологии
Введение
В данной контрольной работе
рассматриваются методы построения статистических моделей при обработке
гидрогеологической, инженерно-геологической и геоэкологической информации. Эти
методы в настоящее время являются наиболее широко применяемыми при гидрогеологических,
инженерно-геологических и геоэкологических исследованиях. С их помощью можно
получить качественно новые выводы и обобщения, которые имеют как практическую,
так и научную ценность.
Целью работы является
приобретение навыков статистического анализа. Для этого необходимо освоить
теоретический материал, методики анализа и осуществить его практическую
реализацию с помощью использования специальных программ, наиболее широко
распространённой из которых в настоящее время является STATISTICA
(StatSoft).
1.Задание, исходные данные
В данном задании даны механические и физические
свойства рыхлых несвязных горных пород (модуль деформации Е1, кГ/см2,
коэффициент пористости ε1
моренных суглинков - Московская морена и коэффициент пористости ε2
моренных суглинков - Днепровская морена) Подмосковья
Для решения контрольной работы необходимо:
) Построить гистограммы распределения
показателей, выявить законы распределения, при необходимости нормализовать
исходные данные. Вычислить обобщенные статистические характеристики, оценить
точность их вычисления.
) Проверить гипотезы:
§ о законе распределения выборок;
§ об однородности выборок;
§ об изменчивости показателей;
§ сравнить выборки между собой.
4)Рассчитать нормативные (эффективные) и
расчетные показатели.
5)Определить необходимое количество наблюдений.
Исходные данные Е1, кГ/см2,
ε1 и ε2
сведены
в таблицу 1.
Таблица 1. Исходные данные
|
Номер
пробы
|
Е1,
кГ/см2
|
ε1
|
ε2
|
|
1
|
500
|
0,49
|
0,61
|
|
2
|
460
|
0,5
|
0,47
|
|
3
|
360
|
0,54
|
0,52
|
|
4
|
530
|
0,46
|
0,51
|
|
5
|
380
|
0,5
|
0,57
|
|
6
|
570
|
0,44
|
0,49
|
|
7
|
420
|
0,54
|
0,49
|
|
8
|
380
|
0,6
|
0,55
|
|
9
|
500
|
0,48
|
0,55
|
|
10
|
440
|
0,52
|
0,52
|
|
11
|
300
|
0,57
|
0,53
|
|
12
|
530
|
0,46
|
0,6
|
|
13
|
490
|
0,49
|
|
14
|
870
|
0,46
|
0,62
|
|
15
|
460
|
0,49
|
0,51
|
|
16
|
500
|
0,47
|
0,54
|
|
17
|
430
|
0,54
|
0,47
|
|
18
|
310
|
0,58
|
0,62
|
|
19
|
1200
|
0,48
|
0,42
|
|
20
|
520
|
0,44
|
0,54
|
|
21
|
570
|
0,48
|
0,51
|
|
22
|
490
|
0,5
|
0,50
|
|
23
|
430
|
0,52
|
0,46
|
|
24
|
370
|
0,58
|
0,55
|
|
25
|
420
|
0,49
|
0,67
|
. Группировка данных, построение гистограмм и их
анализ
Результаты наблюдений и экспериментальных
исследований, отраженные в количественных показателях, обычно заносят в
таблицу, где каждое значение отвечает точке наблюдения, номеру образца или
пробы.
Большую наглядность обеспечивает расположение
исходных данных в таблице в определенной последовательности. Такую
последовательность называют вариационным рядом. Далее разбивают вариационный
ряд на определенные интервалы, количество которых можно вычислить по формуле
К≈a*lgn+1
Где n
- количество исходных данных (объем выборки);
а - коэффициент, который следует принимать от 3
до 5 при n<30, а=3, при n=30-70,
а=4, при n >70, а=5.
Количество интервалов всегда является целым числом, поэтому необходимо
применить правило округления.
После определения количества интервалов
вычисляется шаг
Δh=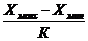
Где Хмакс и Хмин
- максимальное и минимальное значения в исходных данных.
Затем определяют границы интервалов
группировки:
интервал - от Хмин до Хмин
+ Δh;
интервал - от Хмин + Δh до Хмин
+ 2Δh;
………………………………………
Кй интервал - от Хмин
+(К-1) Δh до Хмакс
Далее подсчитывается количество
исходных данных, попавших в каждый интервал группировки, которое обычно
обозначается ni и называется частотой. Относительная частота
рассчитывается по формуле:
ωi =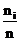
Гистограммы
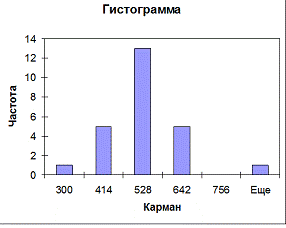
Данные распределены по нормальному закону.
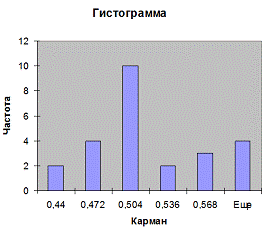
Данные распределены по нормальному закону.
Данные распределены по нормальному закону.
3.Вычисление обобщенных
статистических характеристик
Центральные значения
Выборочным аналогом математического ожидания,
характеризующим положение центра, является среднее арифметическое
Хср=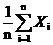
Выборочная медиана представляет
собой срединное значение вариационного ряда. Если вариационный ряд имеет
нечетное число членов 2к+1, медиане отвечает средний, к+1, член ряда, если
четное - 2к, медиана равна среднему арифметическому из значений центральных
членов ряда:
me=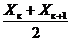
Модой называется абсцисса точки,
имеющая максимальную ординату кривой распределения.
|
Е1,
кГ/см2
|
ε1
|
ε2
|
|
Среднее
арифметическое, 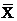 497,20,50520,5324 497,20,50520,5324
|
|
|
|
|
Медиана,
me
|
460
|
0,5
|
0,52
|
|
Мода
|
500
|
0,5
|
0,51
|
Характеристики рассеяния
Основной мерой рассеяния является дисперсия.
Выборочная дисперсия вычисляется по формуле
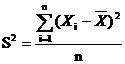 при n>30
при n>30
или
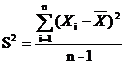 при n<30
при n<30
Квадратный корень из дисперсии
называется среднеквадратичным отклонением или стандартом:
S=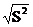
Относительной характеристикой
изменчивости является коэффициент вариации, выборочное значение которого
вычисляется по формуле
V=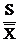
|
Е1,
кГ/см2
|
ε1
|
ε2
|
|
Дисперсия,
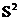 33737,670,0019590,003386 33737,670,0019590,003386
|
|
|
|
|
Среднеквадратич.
отклонение, S
|
183,6782
|
0,044264
|
0,058186
|
|
Коэффициент
вариации, V
|
0,369425
|
0,087617
|
0,109291
|
Характеристики симметрии и степени сжатости
кривых распределения
Степень симметричности кривой по оси абсцисс
характеризует коэффициент асимметрии, выборочное значение которого вычисляется
по формуле
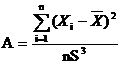
Коэффициент асимметрии может быть -
или +. Положительные значения коэффициента асимметрии свидетельствуют о том,
что распределение вытянуто в сторону больших значений(правостороння
асимметрия), отрицательное значение - о его вытянутости в сторону малых
значений. При строго симметричных распределениях коэффициент асимметрии равен
нулю. Если 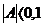 ,
распределение практически симметрично, при
,
распределение практически симметрично, при 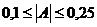 - слабо симметрично, при
- слабо симметрично, при 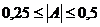 -
ассиметрично и при
-
ассиметрично и при 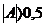 - резко
симметрично.
- резко
симметрично.
|
Коэффициент
асимметрии, 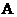 Е1,
кГ/см2ε1ε2 Е1,
кГ/см2ε1ε2
|
|
|
|
|
2,747201
|
0,605707
|
0,508214
|
|
распределение
|
резко
симметрично
|
резко
симметрично
|
резко
симметрично
|
Для характеристики степени сжатости или
растяжения кривой распределения по оси ординат служит эксцесс, выборочное
значение которого вычисляется по формуле
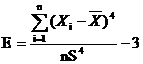
Коэффициент эксцесса может быть
положительным и отрицательным. Положительный эксцесс свидетельствует о
скоплении исходных данных в середине вариационного ряда и о сжатой форме кривой
распределения, отрицательный - о более равномерном распределении вариант и
распластанной кривой. Нулевое значение коэффициента эксцесса отвечает
нормальному распределению.
|
Коэффициент
эксцесса, 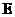 Е1,
кГ/см2ε1ε2 Е1,
кГ/см2ε1ε2
|
|
|
|
|
9,149804
|
-0,38847
|
0,15573
|
Оценка точности вычисления обобщенных
статистических характеристик
Величину стандартной ошибки среднего
арифметического вычисляют по формуле
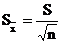
Показатель точности вычисляется по
формуле
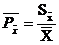
Стандартная ошибка медианы
вычисляется по формуле
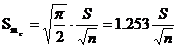
Стандартная ошибка стандартного
отклонения вычисляется по формуле
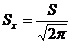
Стандартная ошибка коэффициента
вариации вычисляется по формуле
Стандартная ошибка асимметрии
вычисляется по формуле
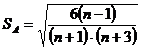
Стандартная ошибка эксцесса
вычисляется по формуле
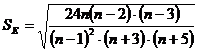
|
Е1,
кГ/см2
|
ε1
|
ε2
|
|
Величина
стандартной ошибки, 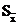 36,735630,0088530,011637 36,735630,0088530,011637
|
|
|
|
|
Показатель
точности, 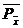 0,0738850,0175230,021858 0,0738850,0175230,021858
|
|
|
|
|
Стандартная
ошибка медианы, 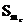 46,029750,0110930,014582 46,029750,0110930,014582
|
|
|
|
|
Стандартная
ошибка стандартного отклонения, 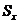 73,471260,0177060,023275 73,471260,0177060,023275
|
|
|
|
|
Стандартная
ошибка коэффициента вариации, 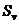 0,0522450,0123910,015456 0,0522450,0123910,015456
|
|
|
|
|
Стандартная
ошибка ассимметрии, 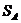 0,4636840,4636840,463684 0,4636840,4636840,463684
|
|
|
|
|
Стандартная
ошибка эксцесса, 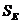 0,9017210,9017210,901721 0,9017210,9017210,901721
|
|
|
|
. Проверка статистических гипотез
Проверка гипотезы о нормальности распределения
Нормальное распределение симметрично
и характеризуется определенной степенью сжатости. Коэффициент асимметрии и
эксцесс нормального распределения равны нулю. Принято считать, что если
выборочные значения коэффициента асимметрии и эксцесса удовлетворяют
неравенствам: 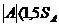 и
и 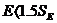 , то
гипотеза о нормальном распределении может быть принята. Если же не выполняется
хотя бы одно из приведенных неравенств, то гипотеза о нормальности
распределения должна быть отвергнута.
, то
гипотеза о нормальном распределении может быть принята. Если же не выполняется
хотя бы одно из приведенных неравенств, то гипотеза о нормальности
распределения должна быть отвергнута.
Проверка гипотезы о нормальности распределения.
|
Е1,
кГ/см2
|
|A|> 1.5 Sa |E| > 1.5 Se
|
Гипотеза
о нормальности распределения может быть отвергнута
|
|
ε1
|
|A| <1.5 Sa |E| <1.5Se
|
Гипотеза
о нормальности распределения может быть принята
|
|
ε2
|
|A|< 1.5Sa |E| <1.5Se
|
Гипотеза
о нормальности распределения может быть принята
|
Проверка принадлежности вариант к статистической
совокупности
Наиболее употребимым критерием является
«правило трех сигм». Критические точки при применении этого критерия
вычисляются по формуле 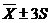 . Далее все
варианты проверяются исходя из следующего неравенства
. Далее все
варианты проверяются исходя из следующего неравенства
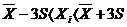
Если все значения в выборке входят в
этот интервал, то выборка считается однородной. Те варианты, которые не
попадают в установленный интервал из выборки, должны быть удалены.
Проверка принадлежности варианта к
статистической совокупности
|
Пределы
|
Аномальные
значения
|
|
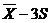 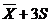
|
|
|
|
Е1,
кГ/см2
|
-53,8345
|
1048,234
|
Выборка
неоднородна
|
|
ε1
|
0,372407
|
0,637993
|
Выборка
однородна
|
|
ε2
|
0,357841
|
0,706959
|
Выборка
однородна
|
Проверка независимости определений
Определения независимы друг от друга -
стационарная изменчивость (нулевая гипотеза), или имеет место пространственная
зависимость - тренд (альтернативная гипотеза). Для проверки используется
величина
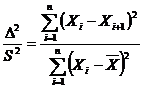
Проанализируем выборку Е1,
кГ/см2:
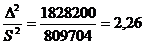
Проанализируем выборку ε1:
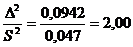
Проанализируем выборку ε2:
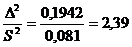
Нулевая гипотеза отвергается в
пользу альтернативной, если эта величина будет меньше или равна критическому
значению (см. табл. 1.1. в методичке). Критическое значение критерия 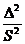 для
установления тренда из таблицы с объемом выборки n=25 равно
1,367. Критическое значение выборки по всем 3 показателям больше табличного
значения, значит имеет место стационарная изменчивость (нулевая гипотеза).
для
установления тренда из таблицы с объемом выборки n=25 равно
1,367. Критическое значение выборки по всем 3 показателям больше табличного
значения, значит имеет место стационарная изменчивость (нулевая гипотеза).
Проверка различия между выборочными
совокупностями
Для сравнения двух выборочных
совокупностей используют средние и дисперсии. Для проверки по среднему
применяется критерий Стьюдента
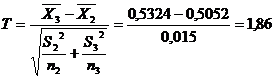
Величина Т при выполнении нулевой
гипотезы распределена по закону Стьюдента с 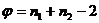 . Критические точки распределения
Стьюдента можно найти в табл. 1.2. (см. методичку). Из данной таблицы Ткр=
2,00. Расчетные значения меньше критических, то подходит нулевая гипотеза.
. Критические точки распределения
Стьюдента можно найти в табл. 1.2. (см. методичку). Из данной таблицы Ткр=
2,00. Расчетные значения меньше критических, то подходит нулевая гипотеза.
Для проверки по дисперсии
используется критерий Фишера
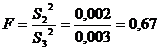
Критические точки распределения
Фишера представлены в табл. 1.3. (см. методичку). По таблице Fкр=1,7.
Расчетное значение меньше критического, то подходит нулевая гипотеза.
5. Определение нормативных и
расчетных параметров
Согласно ГОСТ 20522-96 при
инженерно-геологических изысканиях в качестве нормативного показателя Хн всех
характеристик грунтов за исключением удельного сцепления С и угла внутреннего
трения φ
принимают
среднее арифметическое значение Х и вычисляют по формуле
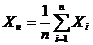
Однако при распределениях
значительно отличающихся от нормального среднее является неэффективным
параметром. Поэтому для его нахождения, например при логнормальном законе
распределения, применяется зависимость
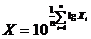
Во избежание ошибок при расчетах,
требующих повышенной точности и надежности, применяются не обобщенные,
нормативные или эффективные, а расчетные значения показателей. Для вычисления
расчетных показателей наиболее часто применяют метод доверительных пределов,
основанный на вычислении такого значения показателя, которое с заданной
надежностью не будет меньше (больше) истинного среднего.
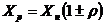
где ρ - показатель
точности оценки среднего значения характеристики вычисляемый по формуле
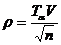
где Тα -
коэффициент, применяемый в зависимости от заданной односторонней доверительной
вероятности α
и
числа степеней свободы f = n-1 (Тα=1,71)
|
Показатель
точности, 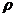 Е1,
кГ/см2ε1ε2 Е1,
кГ/см2ε1ε2
|
|
|
|
|
0,13
|
0,03
|
0,04
|
|
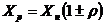 497,2±0,130,5±0,030,53±0,04 497,2±0,130,5±0,030,53±0,04
|
|
|
|
6.Установка
числа определений
Одним из методов установления числа определений
для вычисления обобщенных показателей является метод, основанный на
стабилизации выборочной дисперсии или коэффициента вариации при увеличении
объема выборки. Для удобства строят графики в координатах S2 от n
или V от n.
Число определений можно считать достаточным,
когда изменения характеристик рассеяния становится меньше 5-10 % от их
значения.
Количество частных определений для установления
нормативного и расчетного значения инженерно-геологических характеристик
вычисляют по формуле
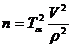
Значения Тα=1,70
принимают по табл. 1.2. из методички при односторонней доверительной
вероятности α = 0,05 и числе степеней
свободы φ
= n-1.
Графики для установления числа определений n
по величине выборочной дисперсии
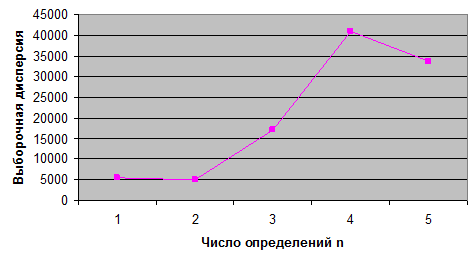
Рис.1
Для Е1, кГ/см2 количество
частных определений равно:
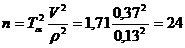
Из рисунка 1 и полученного значения n=24, можно
сказать, что количество частных определений достаточно для данной выборки.
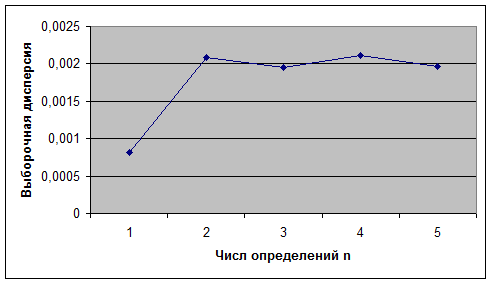
Рис.2
Для ε1
количество
частных определений равно:
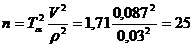 ,
,
Из рисунка 2 и полученного значения n=25, можно
сказать, что количество частных определений достаточно для данной выборки.
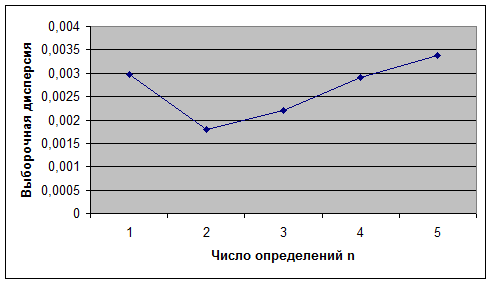
Рис.3
Для ε2
количество
частных определений равно:
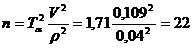 .
.
Из рисунка 3 и полученного значения n=22, можно
сказать, что количество частных определений достаточно для данной выборки.
Заключение
статистический геологический
информация
В процессе выполнения данной работы сформировался
методический подход к построению статистических моделей при обработке
гидрогеологической, инженерно-геологической и геоэкологической информации.
Такой подход является наиболее универсальным, так как содержит множество
методов, использование которых позволяет сделать новые научные и практические
выводы. Реализация данного подхода может быть применима для любых природных
условий и любых типов объектов при обработке гидрогеологических,
инженерно-геологических и геоэкологических показателей.
Список литературы
1. Семячков А.И., Почечун
Статистические методы в гидрогеологии, инженерной геологии и геоэкологии:
Екатеринбург, 2005, с.86.
2. ГОСТ 20522-96 Грунты. Методы
статистической обработки.