Типовые звенья и их соединения. Характеристики автоматических систем. Анализ устойчивости
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Самарский
государственный аэрокосмический университет имени академика С.П. Королёва
(национальный исследовательский университет)» (СГАУ)
Факультет
заочного обучения
Кафедра
космического машиностроения
Расчетно-графическая
работа по курсу
«Теория
Автоматического Управления»
Выполнил
студент группы 9617
Мельник
Дмитрий Витальевич
Проверил
Давыдов Игорь Евгеньевич
Самара 2014
г.
Тема: Типовые звенья и их соединения.
Характеристики автоматических систем. Анализ устойчивости
Цель работы:
.Изучить динамические характеристики типовых
звеньев и их соединений;
.Провести оценку устойчивости системы по
критерию Гурвица, Михайлова, Вишнеградова.
Система задана структурной схемой,
представленной на рисунке(1). На структурной схеме обозначено:
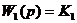
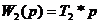
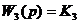
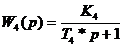
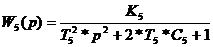
Структурная схема системы
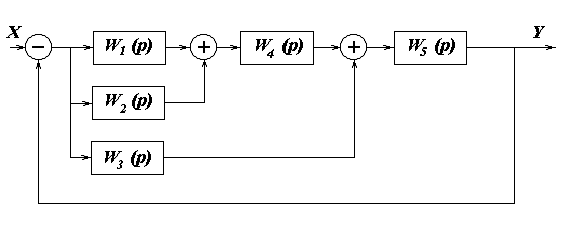
Рис.1
Используя правила соединения
динамических звеньев, сводим структурную схему к одноконтурной и определяем
передаточную функцию разомкнутой системы:
динамический соединение
устойчивость критерий
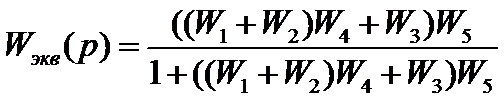
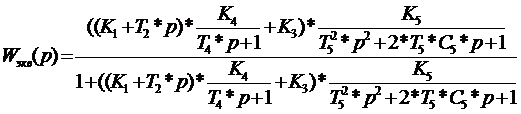
|
№
варианта
|
|
Коэффициенты
|
|
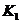 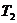 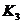 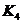 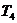 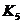 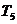 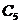
|
|
|
|
|
|
|
|
|
2
|
1,5
|
0,237
|
1
|
3,5
|
0,08
|
1,12
|
0,5
|
0,3
|
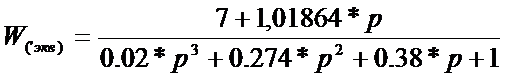
Нахождение характеристического
полинома замкнутой системы:
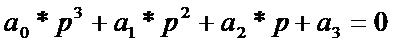
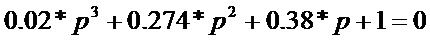
Определение устойчивости системы:
Метод:
Критерий Гурвица;
Критерий Михайлова;
Критерий Вышнеградского;
Устойчивость - свойство системы (шар
- поверхность) приходить в исходное состояние после прекращения действия
возмущения.
Математическая устойчивость по
характеру возмущенного движения относительно невозмущенного движения после
прекращения действия возмущения.
Физическая трактовка понятия
«устойчивости»: если выведенная из состояния равновесия, а далее
предоставленная самой себе система вновь приходит в исходное положение - это
устойчивая система.
Определение устойчивости системы по
алгебраическому критерию Гурвица
Для того чтобы корни
характеристического уравнения
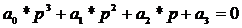 имели отрицательную вещественную
часть, а система была устойчивой, необходимо и достаточно, чтобы
имели отрицательную вещественную
часть, а система была устойчивой, необходимо и достаточно, чтобы 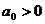 диагональные
определители таблиц, составленных из коэффициентов уравнения
диагональные
определители таблиц, составленных из коэффициентов уравнения 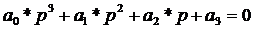 , были
больше нуля.
, были
больше нуля.
Правило составления таблицы:
. По главной диагонали
записываются коэффициенты с нарастающими индексами, начиная с 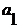 .
.
. Каждый из столбцов
заполняется вверх коэффициентами с нарастающими индексами, вниз - с убывающими
индексами.
. На место отсутствующих
коэффициентов проставляются нули.
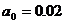
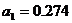
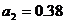
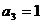
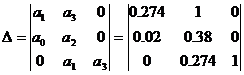
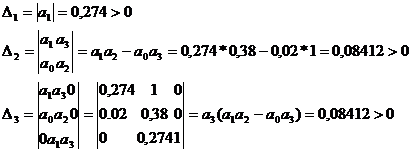
Т.К. все определители больше 0,
значит система устойчива. Данная система является устойчивой по критерию
Гурвица. т.к. все определитель больше нуля.
Определение устойчивости системы по
критерию Михайлова
Необходимо определить условия, при
которых корни характеристического уравнения имеют отрицательную вещественную
часть.
Рассмотрим полином 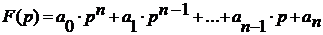 , который
соответствует характеристическому уравнению
, который
соответствует характеристическому уравнению 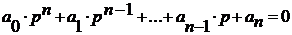
Выразим полином через корни
уравнения:
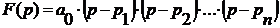 ,
,
где 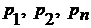 - корни характеристического
уравнения.
- корни характеристического
уравнения.
Каждый из корней 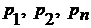 можно
представить на комплексной плоскости в виде точки, вещественная часть которой
определяется по оси абсцисс, а мнимая - по оси ординат. Кроме того, каждая
точка может быть определена в виде вектора, модуль которого равен произведению
модулей отдельных сомножителей, а аргумент - сумме аргументов отдельных
сомножителей.
можно
представить на комплексной плоскости в виде точки, вещественная часть которой
определяется по оси абсцисс, а мнимая - по оси ординат. Кроме того, каждая
точка может быть определена в виде вектора, модуль которого равен произведению
модулей отдельных сомножителей, а аргумент - сумме аргументов отдельных
сомножителей.
Так как корни 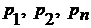 - вектора,
- вектора, 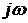 - вектор,
следовательно,
- вектор,
следовательно, 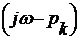 - тоже
вектор.
- тоже
вектор.
Предположим, что в левой
полуплоскости, соответствующей устойчивости, располагается 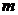 корней.
Тогда в правой полуплоскости будет
корней.
Тогда в правой полуплоскости будет 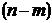 корней, где
корней, где 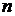 - порядок
характеристического уравнения. Предположим, что
- порядок
характеристического уравнения. Предположим, что 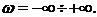 каждый из разностных векторов
сходится в одной точке.
каждый из разностных векторов
сходится в одной точке.
При изменении 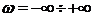
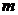 разностных
векторов, соответствующих устойчивой системе и расположенных в левой
полуплоскости, повернутся против часовой стрелки (положительное направление) на
угол
разностных
векторов, соответствующих устойчивой системе и расположенных в левой
полуплоскости, повернутся против часовой стрелки (положительное направление) на
угол 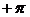 , а
, а 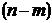 разностных
векторов, расположенных в правой полуплоскости, повернутся по часовой стрелке
(отрицательное направление) на угол
разностных
векторов, расположенных в правой полуплоскости, повернутся по часовой стрелке
(отрицательное направление) на угол 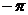 .
.
Так как аргумент сомножителя равен
сумме аргументов отдельных сомножителей. Тогда суммарный угол поворота
определяется таким образом:
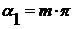 - в левой полуплоскости;
- в левой полуплоскости; 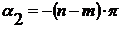 - в правой
полуплоскости.
- в правой
полуплоскости.
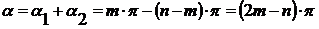 .
.
Если бы все корни уравнения (2)
располагались в левой полуплоскости, что соответствовало бы устойчивой системе,
тогда суммарный угол поворота был бы 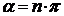 (устойчивая САУ). Следовательно, об
устойчивости можно судить по углу поворота вектора.
(устойчивая САУ). Следовательно, об
устойчивости можно судить по углу поворота вектора.
При изменении 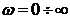 конец
вектора
конец
вектора 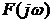 описывает
кривую, которая называется кривой Михайлова (характеристическая кривая). Она
симметрична относительно оси
описывает
кривую, которая называется кривой Михайлова (характеристическая кривая). Она
симметрична относительно оси 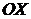 .
.
Критерий Михайлова: если при
изменении 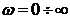 характеристическая
кривая проходит последовательно
характеристическая
кривая проходит последовательно 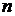 квадрантов в положительном
направлении, то такая система устойчива (
квадрантов в положительном
направлении, то такая система устойчива (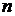 - степень характеристического
уравнения).
- степень характеристического
уравнения).
Для построения характеристической
кривой:
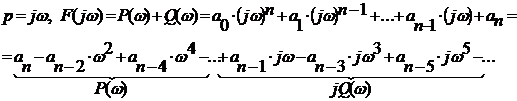
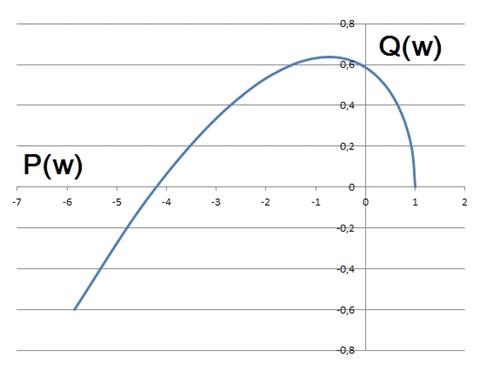
Построив кривую Михайлова мы видим
что система пересекает последовательно 3 квадранта для полинома третьего
порядка, то по критерию Михайлова система устойчива.
Критерий устойчивости Вышнеградского
Условие устойчивости:
) Положительность всех коэффициентов
характеристического уравнения;
2) 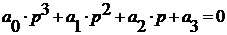 .
.
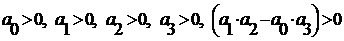 .
.

Проверим на устойчивость при помощи
критерия устойчивости Вышнеградского
,02>0;0.274>0;0.38>0;1>0;(0.274*0.38-0.02*1)>0;
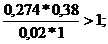
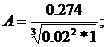
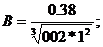 A*B>1;
A*B>1;
По критерию Вышнеградского система
устойчива.
Заключение:
Определение устойчивости по корням
характеристического уравнения: для устойчивости системы необходимо и
достаточно, чтобы корни характеристического уравнения имели отрицательную
вещественную часть, или же вещественная часть комплексно-сопряженного корня 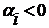 .
Определение устойчивости по корням характеристического уравнения для 3-го и
4-го порядка затруднительно, а для 5-го и более высокого порядка уравнений
аналитически не решается, для определения устойчивости есть так называемые
критерии устойчивости, которые позволяют, не решая ДУ, определить устойчивость.
Эти критерии определяют знак корней характеристического уравнения, не вычисляя
их численного значения. Положительные корни указывают на неустойчивость
системы, а отрицательные - на устойчивость.
.
Определение устойчивости по корням характеристического уравнения для 3-го и
4-го порядка затруднительно, а для 5-го и более высокого порядка уравнений
аналитически не решается, для определения устойчивости есть так называемые
критерии устойчивости, которые позволяют, не решая ДУ, определить устойчивость.
Эти критерии определяют знак корней характеристического уравнения, не вычисляя
их численного значения. Положительные корни указывают на неустойчивость
системы, а отрицательные - на устойчивость.
Все критерии устойчивости делятся на
алгебраические и частотные. К алгебраическим критериям относятся критерии
Гурвица. К частотным критериям относятся критерии Михайлова.
Проведя проверку по критериям
Гурвица, Вышнеградского и Михайлова выяснили что система устойчива.
Программа для расчета критериев
устойчивости
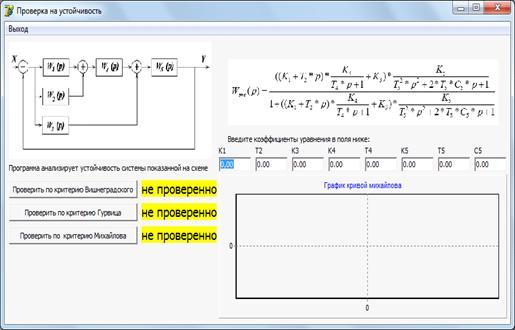
Вводим коэффиценты системы:
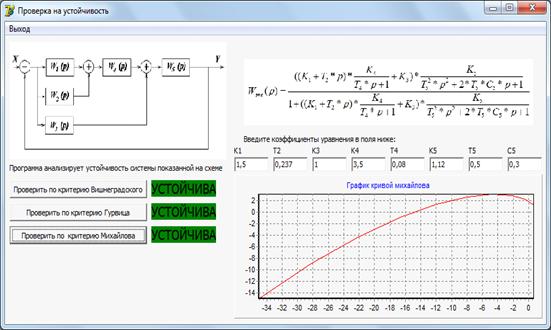
Листинг Программы:
Unit1;, Messages, SysUtils,
Variants, Classes, Graphics, Controls, Forms,, StdCtrls, ExtCtrls, jpeg, Menus,
Buttons, TeEngine, Series,, Chart, TeeFunci;= class(TForm): TMainMenu; N1:
TMeuItem; img1: TImage;: TLabel; img2: TImage; lbl2: TLabel;: TLabeledEdit;
lbledt2: TLabeledEdit;: TLabeledEdit; lbledt4: TLabeledEdit;: TLabeledEdit;
lbledt6: TLabeledEdit;: TLabeledEdit; lbledt8: TLabeledEdit;: TBitBtn; btn2:
TBitBtn; btn3: TBitBtn;: TLabel; lbl4: TLabel; lbl5: TLabel;: TChart; Series1:
TLineSeries;: TAddTeeFunction;N1Click(Sender: TObject); procedure
btn1Click(Sender: TObject);btn2Click(Sender: TObject); procedure
btn3Click(Sender: TObject);{ Private declarations }{ Public declarations };:
TForm1; k1,k3,k4,k5,t4,t2,t5,a0,a1,a2,a3,c5:Real;chit();//считывание
коэффициентов;vish();//Проверка по Вишнеградову;gyrv();//Проверка по
Гурвицу;mich();//Проверка по Михайлову;{$R *.dfm}TForm1.N1Click(Sender:
TObject);Close(); end;chit();:=StrToFloat(Form1.lbledt1.text);
t2:=StrToFloat(Form1.lbledt1.text);:=StrToFloat(Form1.lbledt1.text);
k4:=StrToFloat(Form1.lbledt1.text);:=StrToFloat(Form1.lbledt1.text);
k5:=StrToFloat(Form1.lbledt1.text);:=StrToFloat(Form1.lbledt1.text);
c5:=StrToFloat(Form1.lbledt1.text);;vish();:=Sqr(t5)*t4;a1:=2*t5*c5*t4+sqr(t5);a2:=t4+2*t5*c5;a3:=1(a0>0)and(a1>0)and(a2>0)and(a3>0)and((a1*a2-a0*a3)>0)
then.lbl3.Caption:=('УСТОЙЧИВА');Form1.lbl3.Color:=clGreen;.lbl3.Caption:=('НЕ
УСТОЙЧИВА');Form1.lbl3.Color:=clRed;;end;gyrv();:=Sqr(t5)*t4;a1:=2*t5*c5*t4+sqr(t5);a2:=t4+2*t5*c5;a3:=1;(a1>0)and((a1*a2-a0*a3)>0)and((a3*(a1*a2-a0*a3))>0)
then.lbl4.Caption:=('УСТОЙЧИВА');Form1.lbl4.Color:=clGreen;.lbl4.Caption:=('НЕ
УСТОЙЧИВА');Form1.lbl4.Color:=clRed;;end;mich();q:Integer;,e,r:Real;:Boolean;Form1.Series1.Clear;Form1.lbl5.Caption:=('Проверяется');Form1.lbl5.Color:=clBlue;:=0;q:=0
to 9
do:=w+0.2;:=-a0*(w*w*w)+a2*w;:=-a1*(w*w)+a3;.Series1.AddXY(r,e);(r<-3)and(e>0)
then t:=True;;t=true
then.lbl5.Caption:=('УСТОЙЧИВА');Form1.lbl5.Color:=clGreen;.lbl5.Caption:=('НЕ
УСТОЙЧИВА');Form1.lbl5.Color:=clRed;;end;TForm1.btn1Click(Sender:
TObject);chit(); vish();end;TForm1.btn2Click(Sender: TObject);chit();
gyrv();end;TForm1.btn3Click(Sender: TObject);chit();mich();end;.