Методы получения и применения квантовых точек
Оглавление
Введение
. Использование и применение
квантовых точек
. Обзор теоретических
исследований по вертикально связанным квантовым точкам в полупроводниках
.1 Кулоновские корреляции и
электронно-дырочная жидкость в двойных квантовых ямах
.2 Модель
.3 Корреляционная энергия
. Теория функционала
плотности. Уравнение Кона-Шэма
3.1 Метод расчета
.2 Результаты и их обсуждение
. Стационарное уравнение
Шрёдингера
.1 Общий случай
.2 Случай трёхмерного
пространства
Заключение
Список использованных
источников
Введение
Несмотря на применение полупроводниковых материальных квантовых точек, в
физике и технике, теоретическое исследование электронных свойств вертикально
связанных квантовых точек, изучены недостаточно, в связи с чем, в настоящей
курсовой работе, формируется многоэлектронная задача, для вертикально связных
квантовых точек, разделенных небольшим расстоянием.
В настоящее время, квантовые точки (КТ), являются перспективными
объектами для реализации устройств с квантовой логикой [1].
Большинство операций по обработке информации в таких устройствах основано
на эффекте резонанса в квантовой среде. Резонанс (резонансное туннелирование)
предполагает наличие идентичных соседних состояний. Известно, что, например, в
случае идентичных квантовых ям резонансное туннелирование между ними является
основным типом транспорта носителей заряда в сверхрешетках [2]. Однако в
однослойном массиве КТ такую ситуацию трудно реализовать из-за дисперсии КТ по
размерам и относительно больших расстояний между ними в плоскости. В многослойном
массиве распределение размеров КТ по вертикали становится гораздо более
предсказуемыми управляемым[3]. При образовании одного слоя, КТ являющиеся
упругими включениями, создают дальнодействующие поля упругих напряжений. Таким
образом, нижние слои КТ создают модуляцию упругой энергии на поверхности
спейсера (области растяжения над точками). При осаждении следующего слоя, атомы
мигрируют в места с меньшим расхождением , по постоянной решетки. В итоге, за
счет такой вертикальной корреляции образуются колонки КТ. Как правило, размеры
КТ в колонке немного увеличиваются (при одном и том же спейсере), что приводит
к “красному” сдвигу в фотолюминесценции (ФЛ). Кроме того, необходимо учитывать
большую вероятность туннелирования при маленьких прослойках, в КТ с более
глубокими уровнями размерного квантования. Увеличение толщины барьера,
наоборот, уменьшает вероятность туннелирования (экспоненциально) и
соответственно приводит к “синему” сдвигу полосы ФЛ. Таким образом, в
многослойных структурах возможно исследовать новые квантово-механические
объекты - вертикально связанные (посредством туннелирования) квантовые точки
(ВСКТ). Массивы ВСКТ проявили себя как качественно новый объект. Их рост в
вертикальном направлении скоррелирован и является более управляемым. В таких
структурах можно наблюдать резонансные явления, поскольку разделяющий барьер
очень мал и высока вероятность туннелирования. Однако из-за наличия некоторого
расхождения по размерам в направлении оси роста, идентичных состояний между
соседними КТ не получается. Необходимо внешнее воздействие, чтобы привести
уровни в резонанс. В данной работе внешнее электрическое поле, ориентированное
вдоль колонок, рассматривается как инструмент управления резонансами между
неидентичными вертикально-связанными КТ.
В последнее время в опто и наноэлектронике находят применение
вертикальные нанопроволоки или нитевидные нанокристаллы (ННК) - нанообъекты,
имеющие длину в десятки раз превышающую их диаметр. Рост таких нитевидных
кристаллов возможен на основе широкого круга материалов: металлов, керамик,
полупроводников [4]. Полупроводниковые ННК обладают уникальными электронными и
оптическими свойствами [5]. На основе ННК можно создавать светоизлучающие
устройства со сверхнизким энергопотреблением, зонды для атомно-силовых микроскопов,
автоэмиссионные катоды, туннельные диоды, одноэлектронные транзисторы,
однофотонные излучатели [6]. На основе вертикальных ННК , созданы полевые
транзисторы [7].
1.
Использование и применение квантовых точек
Обычно используемые в дисплеях, также могут передавать изменения
температуры в клетке.
Квантовые точки, используемые на сегодняшнем рынке - это наноразмерные
полупроводники, которые изменяют цвет в зависимости от изменений температуры.
Точки имеют два слоя - внутреннее ядро селенида кадмия и внешняя оболочка
сульфида цинка. Так как квантовые точки биосовместимы, учёные используют их в
качестве альтернативы флоуресцентным красителям, чтобы метить и отслеживать
клеточные компоненты, чаще всего в пробирках.
 <#"805299.files/image002.gif"> <#"805299.files/image003.gif">
<#"805299.files/image002.gif"> <#"805299.files/image003.gif">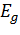 .
Нанокристалл из полупроводника (справа) характеризуется дискретными уровнями
энергии, подобными уровням энергии одиночного атома. В нанокристалле
.
Нанокристалл из полупроводника (справа) характеризуется дискретными уровнями
энергии, подобными уровням энергии одиночного атома. В нанокристалле 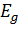
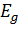 является
функцией размера: увеличение размера нанокристалла ведет к уменьшению
является
функцией размера: увеличение размера нанокристалла ведет к уменьшению 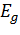
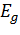 .
.
Квантовой точкой (КТ) может считаться любой кусочек проводника ,
ограниченный по всем трем пространственным координатам , размеры которого
достаточно маленькие для того, чтобы проявление квантовых эффектов были
существенными. В большинстве случаев решающим фактором для создания квантовой
точки является наличие трехмерной потенциальной ямы, в которой носители заряда
оказываются, заперты по всем трем пространственным координатам.
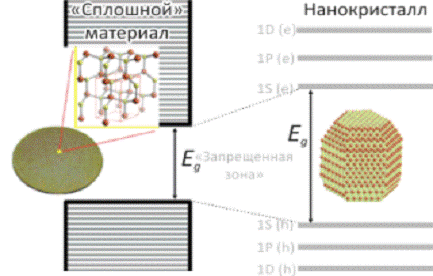
Рисунок 3-Дискретные уровни энергии в нанокристаллах
2. Обзор
теоретических исследований по вертикально связанным квантовым точкам в
полупроводниках
В данном пункте проведем обзор статьи А.А. Васильченко, Е.Н. Тумаева,
Д.А. Ермохина "Расчеты основного состояния квазидвумерной
электронно-дырочной плазмы"
Теорию функционала плотности можно легко обобщить на многокомпонентные
системы. Так для двухкомпонентной системы (электроны и дырки) полная энергия
запишется как
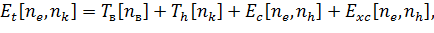
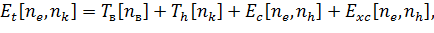 (1)
(1)
где
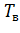
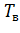 ,
, 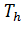
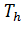 -
кинетическая энергия носителей,
-
кинетическая энергия носителей, 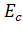
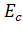 -
электростатическая энергия,
-
электростатическая энергия, 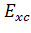
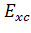 -
обменно-корреляционная энергия. Варьируя выражение (1) по плотностям
-
обменно-корреляционная энергия. Варьируя выражение (1) по плотностям 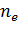
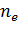 и
и 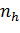
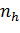 , получим
два уравнения Шредингера:
, получим
два уравнения Шредингера:
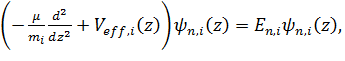
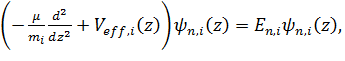 (2)
(2)
где
i=e,h
Здесь
и далее используется экситонная система единиц: энергия измеряется в единицах 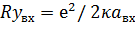
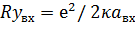 , а длина
в единицах,
, а длина
в единицах, 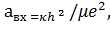
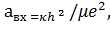 где -
оптическая масса.
где -
оптическая масса.
Таким
образом, проблема сводится к решению двух одномерных нелинейных уравнений
Шредингера для частиц в первой и во второй ямах, которые описываются
потенциалами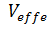
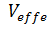 (z)=
(z)=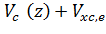
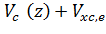 (z) и
(z) и 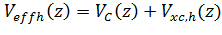
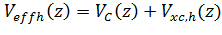 , где
, где 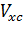
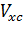 -
обменно-корреляционный потенциал, а электростатический потенциал
-
обменно-корреляционный потенциал, а электростатический потенциал 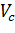
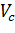 находится
из уравнения Пуасcона :
находится
из уравнения Пуасcона :
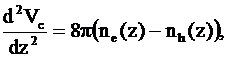 (3)
(3)
с граничными условиями:
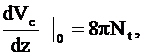
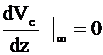 , (4)
, (4)
где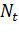
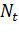 =
=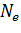
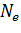 -
-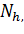
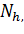
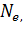
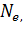
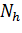
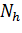 ,
-двумерные плотности электронов и дырок, соответственно.
,
-двумерные плотности электронов и дырок, соответственно.
Чтобы
упростить вычисления, далее будем считать, что заполнен только один уровень
размерного квантования. Когда заполнен только нижний уровень размерного
квантования, плотности носителей задаются выражениями:
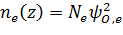
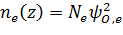 (z),
(z), 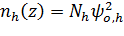
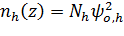 (z) ,
(5)
(z) ,
(5)
Для обменно-корреляционной энергии используем приближение локальной
плотности:
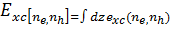
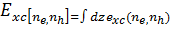 (6)
(6)
где
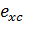
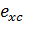 (
(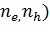
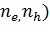 -
обменно-корреляционная энергия электронов и дырок на единицу объема.
-
обменно-корреляционная энергия электронов и дырок на единицу объема.
Тогда
обменно-корреляционные потенциалы имеют вид:
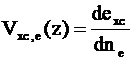 ,
, 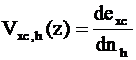 . (7)
. (7)
В
общем случае вид выражения для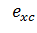
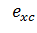 неизвестен. В случае нейтральной электронно-дырочной плазмы для
обменно-корреляционной энергии имеется аппроксимационная формула:
неизвестен. В случае нейтральной электронно-дырочной плазмы для
обменно-корреляционной энергии имеется аппроксимационная формула:
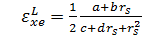
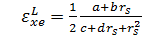 , (8)
, (8)
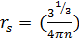
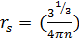 , a=-4,8316
, b=-5,0879, c=0,0152, d=3,0426.
, a=-4,8316
, b=-5,0879, c=0,0152, d=3,0426.
Для
однокомпонентной системы ( ne nh =0 ) будем использовать следующее выражение:
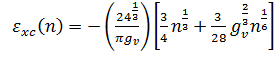
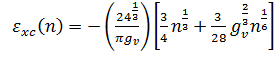 , (9)
, (9)
где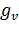
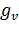 - число
эквивалентных долин.
- число
эквивалентных долин.
В
общем случае возьмем следующую аппроксимацию для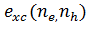
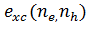 :
:
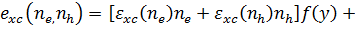
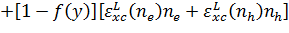
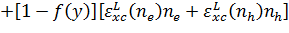 , (10)
, (10)
где
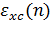
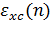 и
и 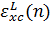
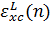 -
обменно-корреляционные энергии на частицу задаются формулами (9) и (8),
соответственно,
-
обменно-корреляционные энергии на частицу задаются формулами (9) и (8),
соответственно, 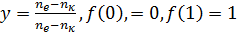
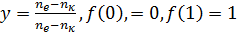
Для
f (y) используется такое же выражения, как в работе :
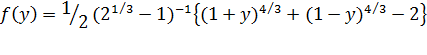
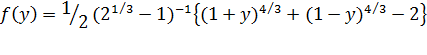 (11)
(11)
Предполагаем,
что существует равновесие между поверхностью и объемом, тогда должны
выполняться условия:
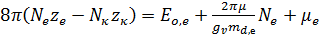
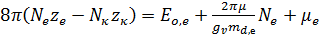 , (12)
, (12)
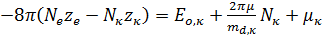
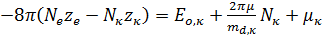 , (13)
, (13)
где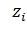
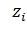 -
среднее удаление электронов (дырок) от поверхности полупроводника,
-
среднее удаление электронов (дырок) от поверхности полупроводника, 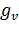
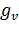 - число
эквивалентных долин, e и h- квазиуровни Ферми для электронов и дырок,
- число
эквивалентных долин, e и h- квазиуровни Ферми для электронов и дырок,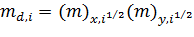
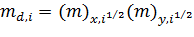 .
.
Таким
образом , задавая e и h мы можем найти концентрации 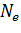
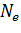 и
и 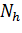
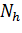 для
заданных значений
для
заданных значений 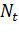
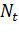 .
.
Физическая
причина образования второго слоя очень проста. Предположим, что первый слой является
электронным, а второй дырочным. Тогда при освещении светом, когда e и 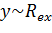
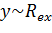 , падение
потенциала в электронном слое происходит на расстоянии порядка нескольких
экситонных радиусов
, падение
потенциала в электронном слое происходит на расстоянии порядка нескольких
экситонных радиусов 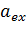
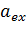 и дырки
смогут находиться вблизи электронного слоя. Переэкранировка внешнего
электрического поля электронами будет гаситься дырками, причем дырки совместно
с электронами будут сами создавать себе потенциальную яму.
и дырки
смогут находиться вблизи электронного слоя. Переэкранировка внешнего
электрического поля электронами будет гаситься дырками, причем дырки совместно
с электронами будут сами создавать себе потенциальную яму.
Оценим
изменение полной энергии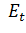
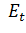 при
добавлении к двумерному слою электронов двумерного слоя дырок плотности
при
добавлении к двумерному слою электронов двумерного слоя дырок плотности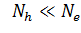
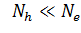 . Пусть
слои находятся на расстоянии
. Пусть
слои находятся на расстоянии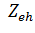
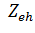 , тогда,
считая, что носители образуют - слои, получаем для изменения электростатической
энергии:
, тогда,
считая, что носители образуют - слои, получаем для изменения электростатической
энергии: 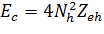
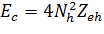 . В
кинетической энергии учитываем только энергию движения вдоль поверхности. Тогда
получим для вклада кинетической энергии в
. В
кинетической энергии учитываем только энергию движения вдоль поверхности. Тогда
получим для вклада кинетической энергии в 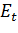
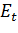 : ∆T
: ∆T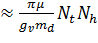
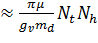 . Для
изменения обменно-корреляционной энергии запишем приближенное выражение:
. Для
изменения обменно-корреляционной энергии запишем приближенное выражение: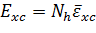
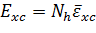 , где
, где 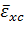
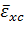 -средняя
обменно-корреляционная энергия.
-средняя
обменно-корреляционная энергия.
Таким
образом, изменение полной энергии Et запишется в следующем виде:
Et=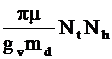 +4Nh2zeh+ Nh
+4Nh2zeh+ Nh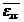 , (14)
, (14)
Используя
простую аппроксимацию, для 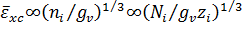
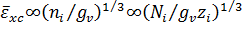 и
пренебрегая электростатической энергией , получаем необходимое условие для
образования 2МЭДП:
и
пренебрегая электростатической энергией , получаем необходимое условие для
образования 2МЭДП:
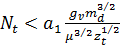
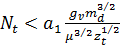 , (15)
, (15)
где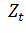
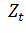 -
характерный размер волновой функции электронов,
-
характерный размер волновой функции электронов, 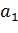
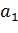 -
константа, численное значение которой порядка единицы.
-
константа, численное значение которой порядка единицы.
Из
выражения (15) следует, что наиболее стабильное состояние 2МЭДП будет
наблюдаться для поверхностей с большими 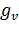
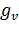 и
и 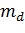
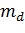 .
.
Для
того чтобы показать возможность образования второго слоя (например,
электронного) необходимо вычислить среднюю энергию связи электрона и дырки:
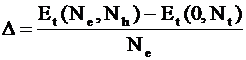
и волновые функции электронов и дырок для поверхности кремния (100):
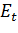
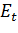 =1012см-2,
Ne=4*1011см-2.
=1012см-2,
Ne=4*1011см-2.
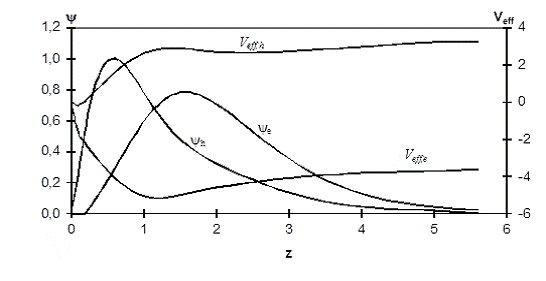
Рисунок 4- Самосогласованные потенциалы
На
рис. 5 показана зависимость средней энергии от электронной плотности для e-h
слоя при различных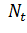
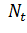 . Область
существования 2МЭДП находится из условия
. Область
существования 2МЭДП находится из условия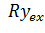
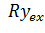 . Видно,
что существует область плотностей
. Видно,
что существует область плотностей 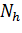
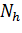 (а значит
и область для квазиуровней Ферми e и h), в которой возможно образование 2МЭДП. Убывание
средней энергии связи с возрастанием плотности Ne (или
(а значит
и область для квазиуровней Ферми e и h), в которой возможно образование 2МЭДП. Убывание
средней энергии связи с возрастанием плотности Ne (или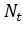
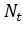 )
происходит в основном из-за возрастания кинетической энергии носителей вдоль
поверхности полупроводника. Поэтому для поверхностей с большими эффективными продольными
массами и (или) большим числом эквивалентных долин 2МЭДП может образовываться
для более широкой области плотностей во втором слое. Отметим, что для
поверхности (100) существует критическая концентрация
)
происходит в основном из-за возрастания кинетической энергии носителей вдоль
поверхности полупроводника. Поэтому для поверхностей с большими эффективными продольными
массами и (или) большим числом эквивалентных долин 2МЭДП может образовываться
для более широкой области плотностей во втором слое. Отметим, что для
поверхности (100) существует критическая концентрация 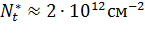
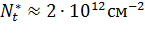 , выше
которой образование 2МЭДП невозможно.
, выше
которой образование 2МЭДП невозможно.
На
рисунке 5 приведены результаты для (111) поверхности кремния. Именно для этой
поверхности имеется наибольшее число эквивалентных долин и, следовательно,
кинетическая энергия носителей дает наименьший вклад в полную энергию.
Сравнение рисунков 4 и 5 показывает, что средняя энергия связи электрона и
дырки существенно больше для поверхности кремния (111)
Интересная особенность возникает в зависимости суммы квазиуровней Ферми
электронов и дырок от концентрации носителей во втором слое (рис.).
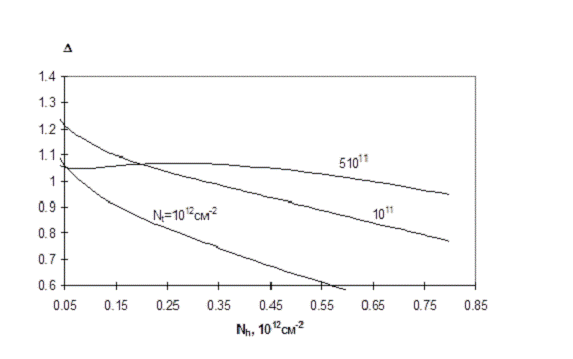
Рисунок 5- Зависимость средней энергии связи электронов и дырок от
концентрации дырок в кремнии (111)
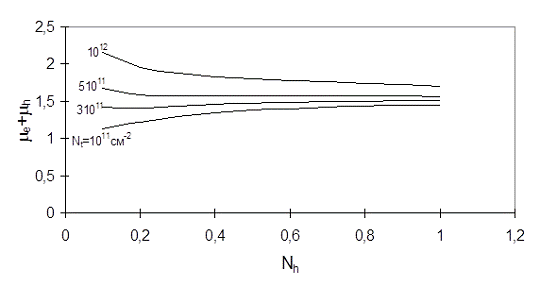
Рисунок 6- Зависимость суммы квазиуровней Ферми от концентрации дырок во
втором слое для eh-слоя на (111)
поверхности кремния.
При
концентрациях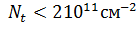
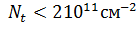 сумма e+h
увеличивается с возрастанием
сумма e+h
увеличивается с возрастанием 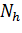
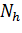 . Такая
зависимость связана с тем, что при низких концентрациях главную роль играет
обменно-корреляционное взаимодействие. Монотонное возрастание суммы
квазиуровней Ферми с увеличением концентрации во втором слое может привести к
пространственной неустойчивости во втором слое носителей.
. Такая
зависимость связана с тем, что при низких концентрациях главную роль играет
обменно-корреляционное взаимодействие. Монотонное возрастание суммы
квазиуровней Ферми с увеличением концентрации во втором слое может привести к
пространственной неустойчивости во втором слое носителей.
Условие устойчивости равновесия между поверхностью и объемом запишется в
следующем виде:
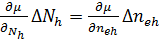
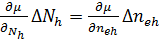 (16)
(16)
где
e+h,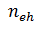
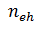 - число
электронно-дырочных пар в объеме полупроводника,
- число
электронно-дырочных пар в объеме полупроводника,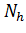
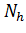 и
и 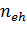
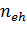 -
флуктуации плотности во втором слое и объеме полупроводника, соответственно.
-
флуктуации плотности во втором слое и объеме полупроводника, соответственно.
При
полной постоянной концентрации носителей величины 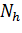
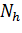 и
и 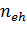
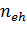 имеют
противоположные знаки, поэтому при различных знаках у производных в выражении
(16) состояние системы всегда будет устойчивым. При одинаковых знаках
производных состояние может быть неустойчивым, поэтому в этом случае второй
слой должен разбиваться на области с плотностью
имеют
противоположные знаки, поэтому при различных знаках у производных в выражении
(16) состояние системы всегда будет устойчивым. При одинаковых знаках
производных состояние может быть неустойчивым, поэтому в этом случае второй
слой должен разбиваться на области с плотностью 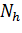
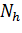 , при
которой условие (16) выполняется. Очевидно, в этом случае возможно разбиение
второго слоя на капли, которые могут не перекрываться друг с другом. При таком
разбиении второй слой будет диэлектриком, и проводимость по второму слою будет
отсутствовать, что подтверждается результатами эксперимента.
, при
которой условие (16) выполняется. Очевидно, в этом случае возможно разбиение
второго слоя на капли, которые могут не перекрываться друг с другом. При таком
разбиении второй слой будет диэлектриком, и проводимость по второму слою будет
отсутствовать, что подтверждается результатами эксперимента.
В
работе найдено, что при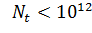
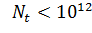 см-2
проводимость поверхностных пар не наблюдается. В этой работе исчезновение
проводимости объясняется существованием фазового перехода плазма-жидкость, т.
е. образованием объемных e-h капель, связанных со слоем поверхностного заряда.
см-2
проводимость поверхностных пар не наблюдается. В этой работе исчезновение
проводимости объясняется существованием фазового перехода плазма-жидкость, т.
е. образованием объемных e-h капель, связанных со слоем поверхностного заряда.
В
представленной здесь модели этот эффект объясняется разбиением на двумерные
капли, которое происходит при 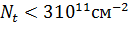
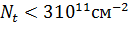 .
Расхождение экспериментального и теоретического значения, по-видимому, связано
с уменьшением роли обменно-корреляционного взаимодействия в нашей модели. В
случае, если взять в формуле (10) f(y)=1, тогда
критическое значение плотности
.
Расхождение экспериментального и теоретического значения, по-видимому, связано
с уменьшением роли обменно-корреляционного взаимодействия в нашей модели. В
случае, если взять в формуле (10) f(y)=1, тогда
критическое значение плотности 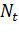
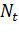 , ниже
которой отсутствует проводимость, составляет приблизительно 21012см-2.
, ниже
которой отсутствует проводимость, составляет приблизительно 21012см-2.
Из
рис. 6 также видно, что 2МЭДП может существовать только при нахождении
квазиуровней Ферми электронов и дырок в достаточно узкой полосе. Как следует из
результатов, представленных на рис. 6, величины квазиуровней Ферми практически
не имеют общих областей при различных 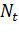
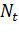 . Это
значит, что для данной интенсивности внешнего излучения 2МЭДП может существовать
только в узком диапазоне величины
. Это
значит, что для данной интенсивности внешнего излучения 2МЭДП может существовать
только в узком диапазоне величины 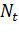
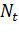 , что
противоречит результатам эксперимента. Это противоречие снимается, если в
теории увеличить роль обменно-корреляционного взаимодействия. В частности ,
расчеты, выполненные с f(y)=1 (обменно-корреляционная энергия задается формулой
(9), показали, что области существования 2МЭДП с различными
, что
противоречит результатам эксперимента. Это противоречие снимается, если в
теории увеличить роль обменно-корреляционного взаимодействия. В частности ,
расчеты, выполненные с f(y)=1 (обменно-корреляционная энергия задается формулой
(9), показали, что области существования 2МЭДП с различными 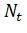
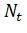 сильно
перекрываются.
сильно
перекрываются.
Кроме
полученных выше эффектов, на поверхности полупроводника возможно образование
многослойной системы, т.е. системы состоящей из чередующихся слоев электронов и
дырок. Отметим также, что 2МЭДП может образоваться на поверхности
полупроводника при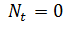
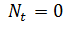 .
.
.1
Кулоновские корреляции и электронно-дырочная жидкость в двойных квантовых ямах.
В. С. Бабиченко(a), И. Я. Полищук(bc)
(a) Российский научный центр “Курчатовский институт”, г. Москва
(b) Московский физико-технический институт (государственный университет)
(c) Max Planck Institute for the Physics of Complex Systems.
Показано, что многочастичные кулоновские корреляции в двойных квантовых
ямах с пространственно разделенными электронами и дырками приводят к образованию
вырожденной электронно-дырочной жидкости со средним расстоянием между
частицами, меньшим размера изолированного экситона. Это состояние оказывается
энергетически более выгодным, чем газ экситонов. Результаты получены в
предположении, что в системе имеется много различных сортов электронов и дырок,
что характерно, в частности, для многодолинных полупроводников. Обсуждается
связь с экспериментами, в которых наблюдались люминесцирующие области в таких
системах.
В последнее время резко возрос интерес к исследованию двойных квантовых
ям (ДКЯ) в связи с возможностью экспериментальной реализации
ДКЯ, в которых электроны и дырки расположены в пространственно
разделенных областях, туннелирование между которыми является исчезающее малым.
Исследование пространственно разделенных электронов и дырок в ДКЯ было
инициировано тем, что в таких системах возможно образование связанных состояний
электрона и дырки (экситонов), с большим временем жизни . Это время на
несколько порядков больше, чем время жизни экситонов в обычных трехмерных
полупроводниках, что способствует возможности наблюдения их бозе-конденсации.
Дальнейшие исследования таких систем показали, что их фазовая диаграмма может
быть довольно сложной. В настоящей работе, вычисляется вклад кулоновских корреляций
в энергию основного состояния многокомпонентной вырожденной электронно-дырочной
плазмы в ДКЯ. В рассматриваемой модели ДКЯ предполагается, что электроны и
дырки пространственно разделены. При этом электроны движутся в одном двумерном
слое, а дырки -в другом, расположенном на расстоянии l от первого слоя.
Рассматривается случай, когда электронно-дырочная плазма является
многокомпонентной. При этом имеется ν различных сортов электронов и такое
же количество сортов дырок, причем ν ≫ 1. При достаточно малой плотности
системы, электроны и дырки образуют связанные состояния (экситоны). При
достаточно низкой температуре система может рассматриваться как вырожденный
бозе-газ. Однако с увеличением плотности электронно-дырочной плазмы n, когда
среднее расстояние между частицами n−1/2 становится меньше или порядка
радиуса изолированного экситона Rex , связанные состояния электронов и дырок
разрушаются и система трансформируется в вырожденную сильно корре-лированную
плазму. Впервые вычисление корреляционной энергии многокомпонентной вырожденной
электронно-дырочной плазмы в обычных трехмерных многодолинных полупроводниках с
числом долин ν ≫ 1, основанное на отборе диаграмм по
параметру 1/ν, было проведено в работе .
В данной работе показано, что многочастичные кулоновские корреляции
приводят к существованию отрицательного минимума энергии основного состояния
вырожденной электронно-дырочной плазмы в ДКЯ как функции плотности n. При этом
минимум имеет место при такой плотности neq, при которой среднее расстояние
между частицами −1/2 является величиной, меньшей размера экситона, neq −1/2
< Rex. Оказывается, что указанный минимум лежит ниже энергии основного
состояния экситонного газа, так что энергия системы ε
eq в расчете на одну
частицу есть отрицательная величина, причем |εeq| имеет значение, большее величины
энергии связи экситона |εex | поэтому системе энергетически не выгодно находиться в
состоянии с малой плотностью n ≪ neq, при которой она представляет собой газ
экситонов. В результате система оказывается в состоянии, которое представляет
собой электронно-дырочную жидкость. При этом если полное число частиц таково,
что плотность n > neq , то система является однородной, а если n < neq ,
то система распадается на капли жидкой фазы. Следует отметить, что образующаяся
электронно-дырочная жидкость обладает сильными электронно-дырочными
корреляциями вблизи поверхности Ферми. Характерный радиус таких корреляций
оказывается больше среднего расстояния между частицами. Следовательно, данные
корреляции не могут быть связаны с наличием бозе-частиц, каковыми являются
экситоны.
.2 Модель
Для
описания многочастичных эффектов в пространственно разделенной
электронно-дырочной плазме в ДКЯ предполагается, что электроны расположены в
одном бесконечно тонком двумерном слое, а дырки - в другом. Ниже используется
система единиц, в которой эффективный заряд электрона (дырки) e/√ κ0 = 1 (где κ0 - статическая
диэлектрическая постоянная среды), постоянная Планка = 1, а эффективная масса
электрона m = 1. При этом для простоты предполагается, что она равна
эффективной массе дырки. Мы рассматриваем случай многокомпонентной
электронно-дырочной плазмы. Число ν сортов электронов (дырок) считается большой величиной (ν ≫ 1). В этом случае импульс Ферми и энергия Ферми для
электронов и дырок одинаковы и равны 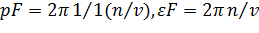
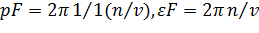 , где n -
концентрация электронов (дырок). Температура системы предполагается малой по
сравнению с энергией Ферми (T ≪ εF). Таким
образом, электронно-дырочная плазма является вырожденной. Гамильтониан системы
может быть записан в виде H = H0 + U, где H0 - кинетическая энергия, а U
-кулоновское взаимодействие.
, где n -
концентрация электронов (дырок). Температура системы предполагается малой по
сравнению с энергией Ферми (T ≪ εF). Таким
образом, электронно-дырочная плазма является вырожденной. Гамильтониан системы
может быть записан в виде H = H0 + U, где H0 - кинетическая энергия, а U
-кулоновское взаимодействие.
2.3
Корреляционная энергия
В
данной работе учет многочастичных корреляций сводится к вычислению
собственно-энергетической части 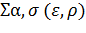
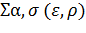 как
суммы диаграмм, главных по параметру 1/ν ≪ 1. Это означает , что при отборе диаграмм учитываются
только те из них, которые в каждом порядке теории возмущений по кулоновскому
взаимодействию максимальны по параметру 1/ν.Каждая фермионная петля вносит в диаграмму вклад, пропорциональный
большому параметру ν. Поэтому в каждом порядке теории возмущений по
взаимодействию мы оставляем только диаграммы, которые содержат максимальное
число таких петель. Такой отбор диаграмм, по существу, является 1/ν-разложением и приводит к главной последовательности
диаграмм, формально совпадающей с последовательностью RPA-диаграмм. Отбор
диаграмм по параметру 1/ν
≪1 приводит к системе самосогласованных уравнений .
как
суммы диаграмм, главных по параметру 1/ν ≪ 1. Это означает , что при отборе диаграмм учитываются
только те из них, которые в каждом порядке теории возмущений по кулоновскому
взаимодействию максимальны по параметру 1/ν.Каждая фермионная петля вносит в диаграмму вклад, пропорциональный
большому параметру ν. Поэтому в каждом порядке теории возмущений по
взаимодействию мы оставляем только диаграммы, которые содержат максимальное
число таких петель. Такой отбор диаграмм, по существу, является 1/ν-разложением и приводит к главной последовательности
диаграмм, формально совпадающей с последовательностью RPA-диаграмм. Отбор
диаграмм по параметру 1/ν
≪1 приводит к системе самосогласованных уравнений .
В
общем случае К. э. представляет собой разность энергии основного состояния
системы ферми-частиц и её значения, определённого в приближении Хартри - Фока
Согласно Паули принципу, два электрона с одинаковым направлением спина не могут
находиться в одной ячейке фазового пространства, что эквивалентно отталкиванию
между ними. Это приводит к тому, что средняя кинетическая энергия электронного
газа, даже при нулевой температуре, отлична от нуля и в случае газа большой
плотности даёт основной вклад в энергию системы. Принцип Паули приводит также к
корреляции во взаимном расположении электронов с параллельными спинами, к-рой
соответствует обменная энергия. Вклад этого типа корреляции в энергию системы
можно учесть с помощью теории возмущения в её первом приближении. Кроме того,
существует корреляция <#"805299.files/image088.gif">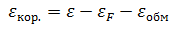 , где
, где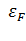
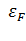 -
средняя кинетическая энергия электронного газа при Т=0К, рассчитанная на один
электрон <#"805299.files/image090.gif">
-
средняя кинетическая энергия электронного газа при Т=0К, рассчитанная на один
электрон <#"805299.files/image090.gif">
=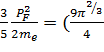
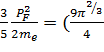 )
)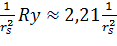
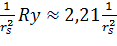 Ry
Ry
[здесь
PF- ферми-импульс электронов, 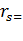
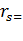 (
(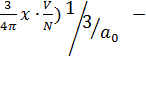
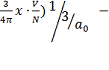 ср.
расстояние между электронами в единицах боровского радиуса
ср.
расстояние между электронами в единицах боровского радиуса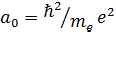
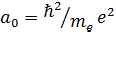 ,
, 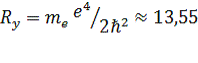
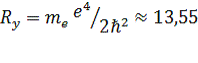 эВ
(ридберг)];
эВ
(ридберг)];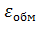
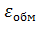 .-ср.энергия
кулоновского взаимодействия в электронном газе на один электрон:
.-ср.энергия
кулоновского взаимодействия в электронном газе на один электрон:

Положит,
заряд <#"805299.files/image101.gif">
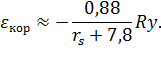
где
U1 = -0,88.
Для
электронного газа большой плотности (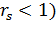
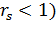 Вигнер
вычислил К. э. вариац. методом. Интерполируя между этими двумя пределами,
Вигнер нашёл
Вигнер
вычислил К. э. вариац. методом. Интерполируя между этими двумя пределами,
Вигнер нашёл
Случай
большой плотности может быть исследован более строго. Суммирование главных,
дающих наибольшую степень расходимости
<#"805299.files/image103.gif">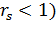 приводит
к разложению
приводит
к разложению
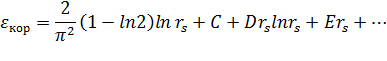
Первый
логарифмический член разложения, был определён Маке (Macke, 1950) на основе
теории возмущений, а затем получен Д. Бомом и Д. Пайнсом (D. Bohm, D. Pines,
1953) методом коллективных переменных. Пост. член С= - 0,096 был вычислен М.
Гелл-Маном и К. Бракнером (М. Gell-Mann, К. Brueckner, 1957) методом
суммирования Фейнмана диаграмм, ими же была оценена величина третьего и
четвёртого членов разложения. К. э. была также вычислена Ф. Нозьером (Ph.
Nozieres) и Д. Пайнсом в 1958 методом коллективных переменных.
Для
реальных металлов плотности электронного газа соответствуют значениям 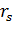
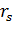 в
интервале
в
интервале 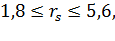
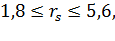 т. е.
промежуточным плотностям. Для оценки К. э. щелочных металлов можно применить
модель свободного электронного газа, без учёта кристаллической решётки.
т. е.
промежуточным плотностям. Для оценки К. э. щелочных металлов можно применить
модель свободного электронного газа, без учёта кристаллической решётки.
Пренебрежение
Н. э. приводит к неверной оценке роли корреляций электронов с параллельными
спинами (поскольку при этом совершенно не учитывается корреляция электронов с
антипараллельными спинами). Без учёта К. э. при очень малых плотностях
оказывается возможным ферромагнетизм электронного газа, учёт же К. э. делает
его невозможным.
3. Теория
функционала плотности. Уравнение Кона-Шэма.
Идея Кона и Шэма состоит в замене гамильтониана сложной систем на
систему, для которой функционал плотности может быть вычислен в явном виде.
Отметим, что этот пункт является самым слабым местом в теории, поскольку
выполнить такие вычисления не всегда возможно.
Сначала мы обсудим ситуацию, когда основной интерес вызывает основное
состояние. Это ситуация наиболее прозрачна для понимания. Затем будет показано
что, фактически, и спектр возбуждений может быть выражен через электронную
плотность, относящуюся к основному состоянию.
Подход Кона-Шэма основывается на двух предположениях:
) Точная электронная плотность основного состояния может быть
заменена на плотность свободных частиц вспомогательной системы.
) Вспомогательный гамильтониан выбирается так, что он имеет обычную
кинетическую энергию и эффективный локальный потенциал, который ответственен за
кулоновское взаимодействие, корреляцию и обмен.
Уравнение Кона-Шэма применяется для многоэлектронных задач(2-х и более),
в задачах одноэлектронных, решение связанно с уравнением Шреденгера. Если
одноэлектронная задача, то обменная и корреляционная энергия не существует, так
как по определению эти виды энергии связанны минимум с двумя электронами. Таким
образом, в данном случае подход не используется, в связи с тем, что 2-х
электронную задачу можно решить либо точн , либо приближенно. Если электрона
три и больше, то возможен подход уравнения функционала плотности, который
учитывает обменные и корреляционные эффекты.
Теория Кона-Шэма (метод функционала плотности) лежит в основе современных
расчетов электронных свойств конденсированных систем. Достигнутые в этом
направлении успехи систематизированы во многих статьях и монографиях, которые
не всегда доступны для обучающихся.
Основное положение метода функционала плотности (Density functional
theory) основываются на том факте, что важнейшие свойства системы
взаимодействующих частиц могут быть выражены с помощью функционала электронной
плотности n® . Эта скалярная функция трех переменных (точки наблюдения)
определяет, в принципе, всю информацию об основном состоянии и спектре
возбуждений. Существование такого функционала для многоэлектронной системы,
находящейся при нулевой температуре, впервые было доказано в работе Кона и
Хоэнберг . В работе Мермина доказательство теоремы типа Кона и Хоэнберга
распространено на системы при произвольной температуре. Однако в этих работах
не содержалось конкретного способа построения такого функционала. Практический способ
построения функционала плотности приведен в работе Кона и Шэма (the Kohn-Sham
ansatz). После этого появилось огромное число публикаций, в который выполнено
построение функционала плотности и на его основе выполнены расчеты конкретных
физических систем. Для более углубленного изучения метода функционала плотности
следует обратиться к монографиям и обзорным статьям.
Численно
решена система уравнений Кона-Шэма для двумерных электронов в квантовой точке с
большим числом электронов (до 140 электронов). Найдены новые серии магических
чисел для полного углового момента электронов в квантовой точке в сильном
магнитном поле. Показано, что в магнитном поле при низких средних плотностях
электронов учет обменного взаимодействия приводит к локализации на примеси двух
электронов, а электронная плотность имеет пики и впадины с периодом 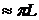 .
.
Начало
использованию DFT методов в вычислительной химии положило внедрение в расчетную
схему орбиталей, предложенное Коном и Шэмом. Основная идея теории Кона-Шэма
состоит в разделении функционала кинетической энергии на две части, первая
вычисляется точно с использованием формально построенных орбиталей, отвечающих
системе невзаимодействующих электронов TS, вторая представляет собой
поправочный член - коррекцию (correction).
В
настоящее время одним из самых мощных методов учета многочастичного
взаимодействия является теория функционала плотности (ТФП). В данной работе
исследуются электронные свойства двумерных квантовых точек в перпендикулярном
магнитном поле с помощью ТФП. Ожидается, что подобные системы в будущем найдут
ряд практических применений, таких как логические наноустройства и
переключатели.
3.1 Метод
расчета
В
дальнейшем будем использовать атомную систему единиц, в которой энергия выражается
в единицах 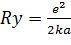
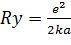 , а длина
в единицах
, а длина
в единицах 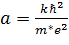
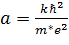 , где
, где 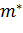
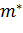 -
эффективная масса электрона, k - диэлектрическая проницаемость. Все вычисления будут
проведены для КТ на основе GaAs, для которого k=12,4 и
-
эффективная масса электрона, k - диэлектрическая проницаемость. Все вычисления будут
проведены для КТ на основе GaAs, для которого k=12,4 и 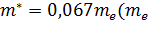
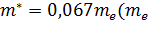 - масса
свободного электрона).
- масса
свободного электрона).
Согласно
ТФП полная энергия многоэлектронной системы во внешнем потенциале 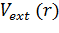
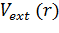 есть
однозначный функционал плотности электронов n(r)
есть
однозначный функционал плотности электронов n(r)
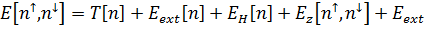
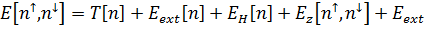 (3.1)
(3.1)
где
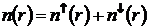 ,
, 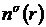 -
плотность электронов с данным направлением спина
-
плотность электронов с данным направлением спина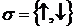 , r=(x,y),
, r=(x,y), 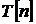 - кинетическая энергия невзаимодействующих электронов
в магнитном поле напряженности В, которое задается векторным потенциалом
- кинетическая энергия невзаимодействующих электронов
в магнитном поле напряженности В, которое задается векторным потенциалом 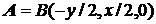 .
.
Второе
слагаемое в выражении (3.1) связано с внешним взаимодействием и в двумерном
случае задается выражением
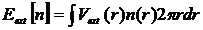 , (3.2)
где
, (3.2)
где 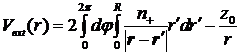 , (3.2)
, (3.2)
Внешний
потенциал 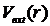 создается примесью с зарядом z0 и положительно
заряженным фоном плотности n+. Для КТ с N электронами
величина R находится из условия электронейтральности
создается примесью с зарядом z0 и положительно
заряженным фоном плотности n+. Для КТ с N электронами
величина R находится из условия электронейтральности  . Во многих работах удерживающий потенциал от
положительно заряженного фона (первое слагаемое в формуле (3.2)) заменяется
параболическим потенциалом , равным
. Во многих работах удерживающий потенциал от
положительно заряженного фона (первое слагаемое в формуле (3.2)) заменяется
параболическим потенциалом , равным  .
Действительно, при малых r первое слагаемое в выражении (3.2) имеет квадратичную
зависимость от r, при этом
.
Действительно, при малых r первое слагаемое в выражении (3.2) имеет квадратичную
зависимость от r, при этом
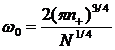 , (3.3)
, (3.3)
Кулоновская
энергия имеет следующий вид
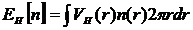 , (3.4)
, (3.4)
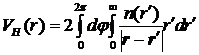 , (3.5)
, (3.5)
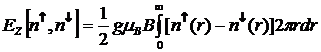 , (3.6)
, (3.6)
где
g - фактор Ланде,  -
магнетон Бора.
-
магнетон Бора.
Трудность ТФП состоит в том, что вид обменно-корреляционной энергии Exc
[n] в общем случае неизвестен. На практике используют различные приближения для
обменно-корреляционной энергии, и поэтому точность результатов обычно
составляет больше нескольких процентов. В дальнейшем нами учитывается только
обменная энергия и для нее используется приближение локальной плотности (ПЛП)
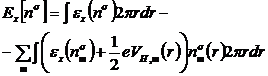 , (3.7)
, (3.7)
где
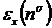 - обменная энергия на один электрон для однородного
электронного газа, которая для нижнего уровня Ландау имеет следующий вид
- обменная энергия на один электрон для однородного
электронного газа, которая для нижнего уровня Ландау имеет следующий вид
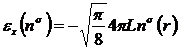 , (3.8)
, (3.8)
здесь
L - магнитная длина, 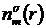 -
плотность m-го электрона со спином
-
плотность m-го электрона со спином 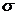 .
.
Следует
остановиться подробнее на формуле (3.7). В ПЛП компенсация самодействия
электронов обменной и кулоновской энергии оказывается неполной. Когда число
электронов конечно и мало, необходимо исключить самодействие электронов в
обменной и кулоновской энергии раздельно, что и сделано в выражении (3.7).
Для
GaAs величина g -фактора мала (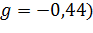
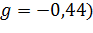 ,
поэтому вклад зеемановской энергии значительно меньше, чем кулоновской и
кинетической энергии, поэтому в выражении (3.1) величиной
,
поэтому вклад зеемановской энергии значительно меньше, чем кулоновской и
кинетической энергии, поэтому в выражении (3.1) величиной
 пренебрегаем.
пренебрегаем.
Вычисления
будут проводиться для магнитных полей, при которых занят только нижний уровень
Ландау. Варьируя энергию (3.1) и учитывая круговую симметрию, получаем
уравнения Кона-Шэма
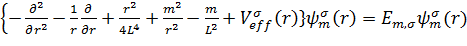
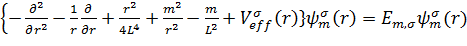 , (3.9)
, (3.9)
с эффективным одночастичным потенциалом
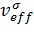
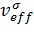 (r)=
(r)=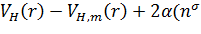
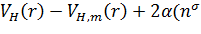 (r)-
(r)-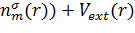
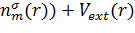 , (3.10)
, (3.10)
где m - угловой момент электрона,
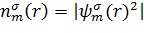
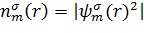 ,
, 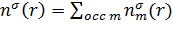
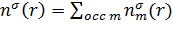 ,
,
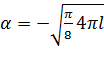
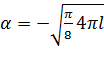 .
.
.2 Результаты
и их обсуждение
Нелинейная
система уравнений Кона-Шэма решалась численно с помощью метода итераций.
Итерационный процесс продолжался пока собственные значения для всех m
величина 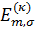
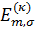 на
на 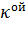
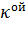 итерации
и (k+1)ой итерации не удовлетворяли условию
итерации
и (k+1)ой итерации не удовлетворяли условию 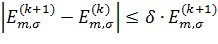
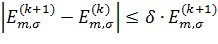 , где для
разных задач величина
, где для
разных задач величина 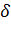
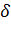 изменялось
в пределах от
изменялось
в пределах от 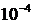 до
до 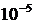 .
Проведено сравнение полученных результатов с точными результатами .Различие
между результатами, полученными с использованием ТФП, и точными результатами
составило менее 5 процентов, и были получены те же магические числа, как и в
точных вычислениях. Видно, что величина энергии, вычисленная с помощью ТФП,
приблизительно на 13% больше точной величины, а положения минимумов энергии
совпадают. Отметим, что учет корреляционной энергии уменьшает полную энергию в
ТФП.
.
Проведено сравнение полученных результатов с точными результатами .Различие
между результатами, полученными с использованием ТФП, и точными результатами
составило менее 5 процентов, и были получены те же магические числа, как и в
точных вычислениях. Видно, что величина энергии, вычисленная с помощью ТФП,
приблизительно на 13% больше точной величины, а положения минимумов энергии
совпадают. Отметим, что учет корреляционной энергии уменьшает полную энергию в
ТФП.
Как
правило, метод теории функционала плотности, используется совместно с
-формализмом Кона Шэма <#"805299.files/image149.gif">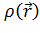 ,
включающей вклад всех электронов [3-5]. При выводе уравнений Кона-Шэма (КШ),
являющихся аналогом уравнений Хартри-Фока делается следующее допущение.
Предполагается, что для любой реальной системы с потенциалом
,
включающей вклад всех электронов [3-5]. При выводе уравнений Кона-Шэма (КШ),
являющихся аналогом уравнений Хартри-Фока делается следующее допущение.
Предполагается, что для любой реальной системы с потенциалом 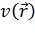
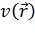 и
плотностью
и
плотностью 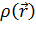
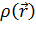 существует
такая воображаемая «невзаимодействующая» система (т.е. система, в которой
отсутствует межэлектронное взаимодействие) с некоторым одноэлектронным
потенциалом, электронная плотность которой
существует
такая воображаемая «невзаимодействующая» система (т.е. система, в которой
отсутствует межэлектронное взаимодействие) с некоторым одноэлектронным
потенциалом, электронная плотность которой 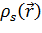
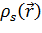 совпадает
с точной электронной плотностью реальной системы
совпадает
с точной электронной плотностью реальной системы 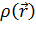
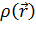 . Для
такой системы точное решение многоэлектронного уравнения Шредингера
представляется слэтеровским детерминантом Φ(
. Для
такой системы точное решение многоэлектронного уравнения Шредингера
представляется слэтеровским детерминантом Φ(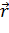
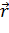 ),
состоящим из одноэлектронных орбиталей
),
состоящим из одноэлектронных орбиталей 
 ,
плотность выражается как
,
плотность выражается как

 , (3.2.1)
, (3.2.1)
а
одноэлектронные орбитали получаются как решение одночастичного уравнения
Шредингера:
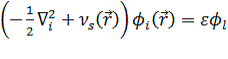
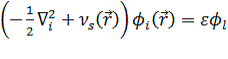 (
(
 ).
).
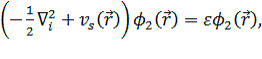
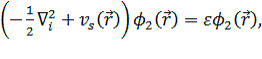 (3.2.2)
(3.2.2)
Доказывается,
что если такой потенциал существует, то он единственный.
Для
невзаимодействующей системы функционал энергии имеет следующий вид:
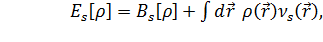
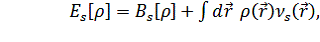 (3.2.3)
(3.2.3)
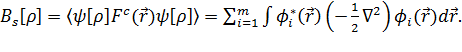
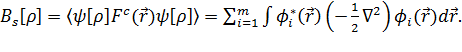 (3.2.4)
(3.2.4)
Для
реальной взаимодействующей системы имеем:
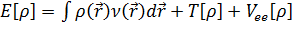
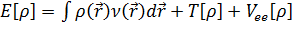 ,
,
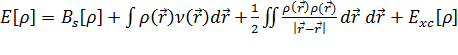
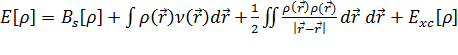 , (3.2.5)
, (3.2.5)
где
величина 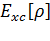
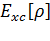 получила
название обменно-корреляционного функционала.
получила
название обменно-корреляционного функционала.
В
теории Кона-Шэма уравнение имеет следующий вид:
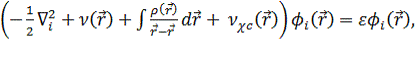
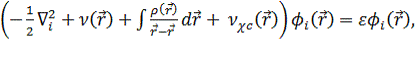 (3.2.6)
(3.2.6)
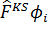
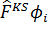 (
(
 )=
)=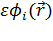
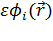 ,
,
где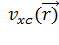
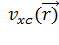 -
обменно-корреляционный потенциал.
-
обменно-корреляционный потенциал.
Точный
вид обменно-корреляционного функционала неизвестен, но из разных физических
соображений было предложено много разных вариантов. Если 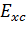
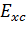 выражен в виде:
выражен в виде: 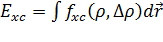
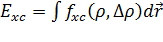 , то
можно получить для матричного элемента (
, то
можно получить для матричного элемента (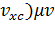
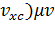 следующее выражение:
следующее выражение:

 . (3.2.7)
. (3.2.7)
Это
выражение уже может быть непосредственно использовано при формировании матрицы
КШ в представлении базисных АО.
Обменно-корреляционные
функционалы.
Различают
локальные (если есть зависимость только от r) и нелокальные (градиентные, если
зависят также и от 
 )
обменно-корреляционные функционалы.
)
обменно-корреляционные функционалы.
Наиболее
распространенные локальные функционалы: D30, VWN, хартри-фоковский.
D30
(Dirac 1930 г., другое название: Slater)
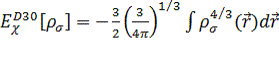
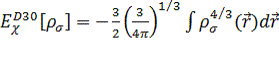 , (3.2.8)
, (3.2.8)
-
WVN (Vasko, Wilk, Nussair, 1980). Результат получен численным решением задачи в
модели электронного газа. Формула сложная, поэтому здесь не приводится.
HF
(хартри-фоковский обменный функционал.) Формула может быть легко выведена из
обычных уравнений Хартри-Фока.
Нелокальные
функционалы: B88, LYP, PW91.
B88(Becke
1988 г.)
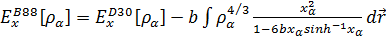
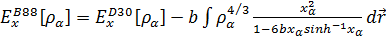 , (3.2.9)
, (3.2.9)
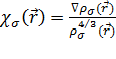
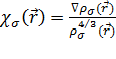 .
.
где,
b=0.0042, здесь и ниже.
- LYP (Lee, Yang, Parr, 1988 г.)
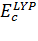
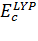 =-
=-
 ,
,
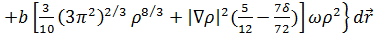
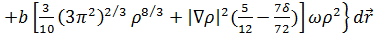 (3.2.10)
(3.2.10)
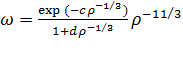
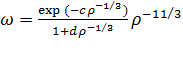 ,
,
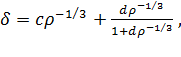
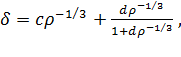
где,= 0.04918, b = 0.132, c = 0.2533, d =
0.349.
PW91 (Perdew 1991 г.)
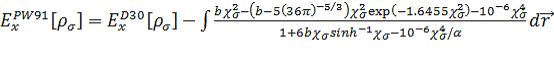
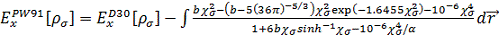 .
(3.2.11)
.
(3.2.11)
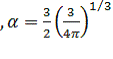
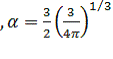 .
.
В
результате комбинирования рассмотренных выше обменных и корреляционных
функционалов получаются следующие наиболее популярные обменно-корреляционные
функционалы:
1) BLYP:
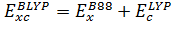
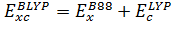 ,
(3.2.12)
,
(3.2.12)
2) BP:
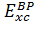
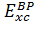 =
=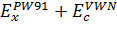
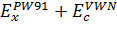 ,
(3.2.13)
,
(3.2.13)
3) LSDA:
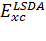
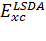 =
=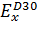
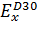 +
+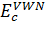
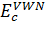 , (3.2.14)
, (3.2.14)
а
также «гибридные», т.е. те, которые содержат вклад 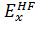
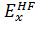 .
.
4) B3P:
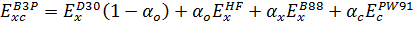
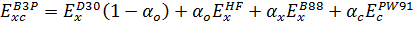 ,
(3.2.15)
,
(3.2.15)
где a0
= 0.2, ax= 0.72, ac= 0.81.
5) B3LYP:
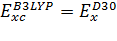
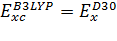 (1-
(1-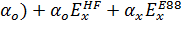
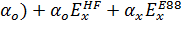 (1-
(1-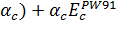
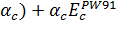 ,
(3.2.16)
,
(3.2.16)
Основные особенности реализации и применения.
Реализация очень похожа на ХФ, но требуется представление для r: либо
специальный базисный набор, либо трехмерная сетка. В последнее время склоняются
именно к трехмерной сетке. В этом случае в любой точке
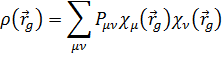
Сложность стандартного алгоритма (с негибридным функционалом) составляет
~O(N3). Если воспользоваться быстрым затуханием базисных функций, то в ряде
случаев удается получить O(N2) и даже O(NlogN). Этот вопрос ниже будет
рассмотрен подробнее. В случае гибридного функционала никаких преимуществ по
времени вычисления перед ХФ нет. Работает медленнее (иногда в разы, иногда в
десятки раз), чем ХФ из-за дополнительной работы.
Основной недостаток - невозможность систематического уточнения
результата. Метод - невариационный в буквальном смысле этого слова. Однако, он
является вариационным в рамках того функционала плотности, который
используется. В случае ХФ есть КВ, дающее хотя и трудоемкую, но все-таки
возможность улучшения результатов. В данном случае получаемый результат
рассматривается как окончательный, т.к. он включает и обмен, и корреляции. По
этой причине использовать после этого КВ или MPn абсолютно бессмысленно.
Интересно, что в некоторых программах такая возможность не заблокирована. По
тем же причинам, имеются значительные трудности применения DFT к возбужденным
состояниям .
Достоинства. Возможность получения хороших по точности результатов при
разумных затратах. Относительно слабая зависимость от базиса, возможность
получения приемлемых результатов уже с малыми базисами.
4.
Стационарное уравнение Шрёдингера
.1 Общий
случай.
В
квантовой физике
<#"805299.files/image197.gif">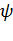 ,
описывающая чистое состояние объекта, которая называется волновой функцией
<#"805299.files/image198.gif">
,
описывающая чистое состояние объекта, которая называется волновой функцией
<#"805299.files/image198.gif">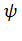 в
частных физических задачах. Таким уравнением является уравнение Шрёдингера.
в
частных физических задачах. Таким уравнением является уравнение Шрёдингера.
Пусть
волновая функция
<#"805299.files/image157.gif"> )(
)(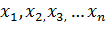
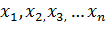 ), в
определенный момент времени t она будет иметь вид
), в
определенный момент времени t она будет иметь вид 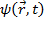
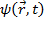 . В таком
случае уравнение Шрёдингера запишется в виде:
. В таком
случае уравнение Шрёдингера запишется в виде:
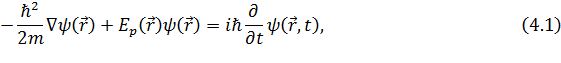
где
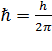
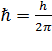 , h -
постоянная Планка
<#"805299.files/image203.gif">
, h -
постоянная Планка
<#"805299.files/image203.gif">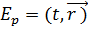
внешняя
по отношению к частице потенциальная энергия
<#"805299.files/image204.gif">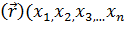 в момент
времени t,
в момент
времени t,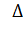
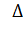 -
оператор Лапласа <#"805299.files/image206.gif">
-
оператор Лапласа <#"805299.files/image206.gif">
Форма
уравнения Шрёдингера показывает, что относительно времени его решение должно
быть простым, поскольку время входит в это уравнение лишь через первую
производную в правой части. Действительно, частное решение для специального
случая, когда 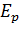
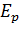 не
является функцией времени, можно записать в виде:
не
является функцией времени, можно записать в виде:
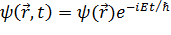
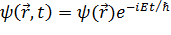 , (4.3)
, (4.3)
где
функция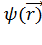
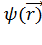 должна
удовлетворять уравнению:
должна
удовлетворять уравнению:
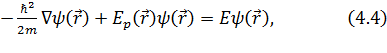
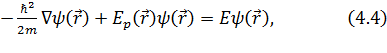
которое
получается из уравнения Шрёдингера (4.1) при подстановке в него, указанной выше
формулы для 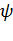
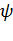 (4.3).
Заметим, что это уравнение вообще не содержит времени; в связи с этим оно
называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не
содержащее времени).
(4.3).
Заметим, что это уравнение вообще не содержит времени; в связи с этим оно
называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не
содержащее времени).
Выражение
(4.3) является лишь частным решением
<#"805299.files/image211.gif"> ) от
времени проста, но зависимость её от координаты не всегда имеет элементарный
вид, так как уравнение (4.4) при одном выборе вида потенциальной функции
) от
времени проста, но зависимость её от координаты не всегда имеет элементарный
вид, так как уравнение (4.4) при одном выборе вида потенциальной функции 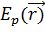
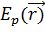 совершенно
отличается от того же уравнения при другом выборе этой функции. В действительности,
уравнение (4.4) может быть решено аналитически лишь для небольшого числа
частных типов функции
совершенно
отличается от того же уравнения при другом выборе этой функции. В действительности,
уравнение (4.4) может быть решено аналитически лишь для небольшого числа
частных типов функции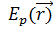
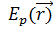 .
.
Важное
значение имеет интерпретация <#"805299.files/image211.gif">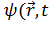 ) в
уравнении (4.3) имеет экспоненциальный
<#"805299.files/image214.gif">
) в
уравнении (4.3) имеет экспоненциальный
<#"805299.files/image214.gif">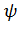 умножается <#"805299.files/image215.gif">
умножается <#"805299.files/image215.gif">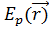 .
Следовательно, из соображений размерности <#"805299.files/image216.gif">
.
Следовательно, из соображений размерности <#"805299.files/image216.gif">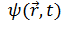 .
.
Наиболее общая форма уравнения Шрёдингера - это форма, включающая
зависимость от времени:
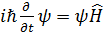
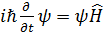 , (4.5)
, (4.5)
где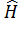
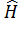 -
гамильтониан
<#"805299.files/image219.gif">
-
гамильтониан
<#"805299.files/image219.gif">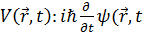 )=
)=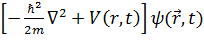
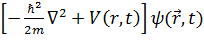 : (4.6)
: (4.6)
4.2 Случай
трёхмерного пространства
В
трёхмерном
<#"805299.files/image221.gif"> в декартовой системе координат заменяется выражением
в декартовой системе координат заменяется выражением
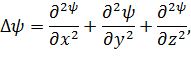
тогда уравнение Шрёдингера примет вид:
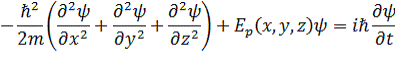
где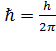
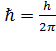 , h -
постоянная Планка
<#"805299.files/image225.gif">
, h -
постоянная Планка
<#"805299.files/image225.gif">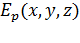 -
потенциальная энергия в точке (
-
потенциальная энергия в точке (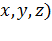
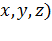 .
.
Заключение
На основании данных курсовой работы, можно сделать следующие выводы: 1)
из статьи А.А. Васильченко, Е.Н. Тумаева и Д.А. Ермохина "Расчеты
основного состояния квазидвумерной электронно-дырочной плазмы", следует,
что на поверхности полупроводника возможно образование многослойной системы,
т.е. системы состоящей из чередующихся слоев электронов и дырок. Отмечено
также, что 2МЭДП может образоваться на поверхности полупроводника при Nt=0. 2)
метод функционала плотности удобен для расчета физических свойств, как мало,
так и много-элетронных систем. 3) в статье В. С. Бабиченко, И. Я. Полищук
"Кулоновские корреляции и электронно-дырочная жидкость в двойных квантовых
ямах ", выявлены следующие выводы о том, что при достаточно малой
плотности системы, электроны и дырки образуют связанные состояния (экситоны).
При достаточно низкой температуре система может рассматриваться как вырожденный
бозе-газ. Однако с увеличением плотности электронно-дырочной плазмы n, когда
среднее расстояние между частицами n−1/2 становится меньше или порядка
радиуса изолированного экситона Rex , связанные состояния электронов и дырок
разрушаются и система трансформируется в вырожденную сильно корре-лированную плазму.
Для описания многочастичных эффектов в пространственно разделенной
электронно-дырочной плазме в ДКЯ предполагается, что электроны расположены в
одном бесконечно тонком двумерном слое , а дырки - в другом.
Представленные выводы показывают, что проблема описания электронных
свойств вертикально связанных квантовых точек, в полном объеме далека от своего
решения, и поэтому мы хотим рассмотреть эту проблему заново, для этого мы
применяем уравнение Шредингера и методы теории возмущения, что касается уравнения
Кона-Шэма, он позволяет решать важные задачи, но требует трудоемких численных
расчетов.
Список использованных источников
квантовый кулоновский
уравнение шредингер
1. Атомная структура полупроводниковых систем / отв. ред.
А.Л. Асеев.- Новосибирск: Издательство СО РАН, 2006.- 292 с.
. Васильченко, А.А. Расчеты основного состояния
квазидвумерной электронно-дырочной плазмы / А.А. Васильченко, Е.Н. Тумаев, Д.А.
Ермохин
Статья
В. С. Бабиченко, И. Я. Полищук "Кулоновские корреляции и
электронно-дырочная жидкость в двойных квантовых ямах"
4. S.Empedocles, M.Bawendi Spectroscopy of Single CdSe
Nanocrystallites. applications. Pure Appl.Chem., 2000, v.72, p. 3-9.
. Turton, R.. The quantum dot A journey into the
future of microelectronics. - New York: Freeman, 2000- 211 p.
. Jeong, H. The Kondo effect in an artificial q
quantum dot molecule / H. Jeong, A.M. Chang // Science- 2001- V.293- P.
2221-2223.
. Farmer, S.C. Photoluminescent polymer/quantum dot
composite nanoparticles / S.C.Farmer, T.E.Patten // Chem. Mater. - 2001.- V.13
- P.3920-3926.
. T.Baron, F.Martin, P.Mur et.al. Low pressure
chemical vapor deposition growth of silicon quantum dots on insulator for
nanoelectronics devices. Appl. Surf. Sci. 2000, v.164, p.29-34.
. G.Markovich, C.Patrick, S.E.Henrichs, at. al.
Architectonic quantum dot solids. Acc.Chem.Res. 1999, 32, 415-423.
. H.-M.Xiong, Xu Zhao, Jie-Sheng Chen New
polymer-Inorganic Nanocomposites: PEO-ZnO and PEO-ZnO-LiCLO4 films J.Phys.
Chem.B 2001,105, 10169-10174.
. S.Empedocles, M.Bawendi Spectroskopy of single CdSe
nanocrystallines А.Chem.Res. 1999, 32,
389-396.
. M.Nirmal, L.Brus Lumininescence Photophysics in
semiconductor nanocrystals. Acc.Chem.Res. 1999, 32, 407-414.
. S.P.Gubin Metalcontaining nano-particles within
polymeric matrices: preparation, structure and properties. Colloids and
Surfaces A: Physicochemical and Engineering Aspects. 2002, 202, 155-163.
. А.А.Алехин, С.Ю.Суздальцев, Р.К. Яфаров. Тонкая
структура углеводородных пленок, полученных в плазме микроволнового газового
разряда низкого давления. // Письма в ЖТФ. 2003. Т.29, вып. 15. С. 73-79.
. Леденцов, В.М. Устинов, В.А. Щукин, П.С. Копьев, Ж.И.
Алферов, Д. Бимберг. Гетероструктуры с квантовыми точками: получение, свойства,
лазеры. Обзор. ФТП, 1998г, 32, №4. С.385 - 410.
. J.W Cahn. Trans. Met. Soc., 242, 166 (1968).
. I.P. Ipatova, V.G. Malyshkin, V.A. Shchukin. J.
Appl. Phys., 74, 7198 (1993).
. I.P. Ipatova, V.G. Malyshkin, V.A. Shchukin. Phil.
Mag. B, 70, 557 (1994).