Метод Гаусса решения систем линейных алгебраических уравнений

Метод Гаусса решения систем линейных алгебраических уравнений

Белорусский государственный университет

Факультет прикладной математики и информатики

Кафедра вычислительной математики

Лабораторная работа №1

Тема: «Метод Гаусса решения систем линейных алгебраических уравнений»

Подготовил: студент 2 курса 2 группы

Зинькович И.А.

Преподаватель: Самусенко А.В.

Минск

Теоретический материал

Пусть есть система:

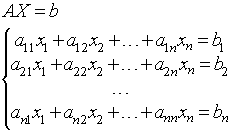
Прямой ход состоит из n - 1 шагов исключения.

-й шаг. Целью этого шага является исключение неизвестного x₁ из уравнений с номерами i = 2, 3, …, n. Предположим, что коэффициент a₁₁ ¹ 0. Будем называть его главным элементом 1-го шага.

Найдем величины q_i1 = a_i1/a₁₁ (i = 2, 3, …, n), называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, …, n-го уравнений системы первое уравнение, умноженное соответственно на q₂₁, q₃₁, …, q_n1. Это позволит обратить в нуль коэффициенты при x₁ во всех уравнениях, кроме первого. В результате получим эквивалентную систему

₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b_1,22⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + … + a_2n⁽¹⁾x_n = b₂^(1),₃₂⁽¹⁾x₂ + a₃₃⁽¹⁾x₃ + … + a_3n⁽¹⁾x_n = b₃⁽¹⁾,_n2⁽¹⁾x₂ + a_n3⁽¹⁾x₃ + … + a_nn⁽¹⁾x_n = b_n⁽¹⁾.

в которой a_ij⁽¹⁾ и b_ij⁽¹⁾ вычисляются по формулам

_ij⁽¹⁾ = a_ij − q_i1a_1j, b_i⁽¹⁾ = b_i − q_i1b₁.

2-й шаг. Целью этого шага является ислючение неизвестного x₂ из уравнений с номерами i = 3, 4, …, n. Пусть a₂₂⁽¹⁾ ≠ 0, где a₂₂⁽¹⁾ - коэффициент, называемый главным (или ведущим) элементом 2-го шага. Вычислим множители 2-го шага

_i2 = a_i2⁽¹⁾ / a₂₂⁽¹⁾ (i = 3, 4, …, n)

₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … +             a_1nx_n =         b₁          ,₂₂⁽¹⁾x₂ +      a₂₃⁽¹⁾x₃ +     … + a_2n⁽¹⁾ x_n =   b₂⁽¹⁾      ,₃₃⁽²⁾x₃ + … +    a_3n⁽²⁾x_n =       b₃⁽²⁾        ,_n3⁽²⁾x₃ +      … + a_nn⁽²⁾x_n =     b_n⁽²⁾      .

Здесь коэффициенты a_ij⁽²⁾ и b_ij⁽²⁾ вычисляются по формулам: a_ij⁽²⁾ = a_ij⁽¹⁾ - q_i2a_2j⁽¹⁾, b_i⁽²⁾ = b_i⁽¹⁾ - q_i2b₂⁽¹⁾.

Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.й шаг. В предположении, что главный (ведущий) элемент k-го шага a_kk^(k-1) отличен от нуля, вычислим множители k-го шага q_ik = a_ik^(k-1) / a_kk^(k-1) (i = k + 1, …, n) и вычтем последовательно из (k + 1)-го, …, n-го уравнений полученной на предыдущем шаге системы k-e уравнение, умноженное соответственно на q_k+1,k, q_k+2,k, …, q_nk.

После (n - 1)-го шага исключения получим систему уравнений

₁₁x₁ + a₁₂x₂ +   a₁₃x₃ + … + a_1nx_n =     b₁       ,₂₂⁽¹⁾x₂ +        a₂₃⁽¹⁾x₃ +     … +  a_2n⁽¹⁾x_n =     b₂⁽¹⁾                ,₃₃⁽²⁾x₃ +          … +    a_3n⁽²⁾x_n =         b₃⁽²⁾   ,_nn^(n-1)x_n =      b_n^(n-1)  .

матрица A^(n-1) которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.

Обратный ход. Из последнего уравнения системы находим xn. Подставляя найденное значение x_n в предпоследнее уравнение, получим x_n-1. Осуществляя обратную подстановку, далее последовательно находим x_n-1, x_n-2, …, x₁. Вычисления неизвестных здесь проводятся по формулам

_n = b_n^(n-1) / a_nn^(n-1),_k = (b_n^(k-1) - a_k,k+1^(k-1)x_k+1 - … - a_kn^(k-1)x_n) / a_kk^(k-1), (k = n - 1, …, 1).

Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы a_kk^(k-1). Поэтому если один из главных элементов оказывыется равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.

линейный алгебраический уравнение гаусс

Условие задания

Решить методом Гаусса систему линейных уравнений Ax = b, где A = D + C*k. Матрицы D, C, b взяты из №41, k = 0,2.

Код программы (main.cpp)

#include <fstream>

#include <cmath>namespace std;round(double x) {(x < 0) ? ceil(x-0.5): floor(x+0.5);

}main(){SIZE;** A;** copy;* b;* result;* delta;k = 0.2;in("in.txt");>> SIZE;= new double*[SIZE];= new double*[SIZE];(int i = 0; i < SIZE; i++){[i] = new double[SIZE];[i] = new double[SIZE];

}** D = new double*[SIZE];(int i = 0; i < SIZE; i++)[i] = new double[SIZE];(int i = 0; i < SIZE; i++)(int j = 0; j < SIZE; j++)>> D[i][j];** C = new double*[SIZE];(int i = 0; i < SIZE; i++)[i] = new double[SIZE];(int i = 0; i < SIZE; i++)(int j = 0; j < SIZE; j++)>> C[i][j];(int i = 0; i < SIZE; i++)(int j = 0; j < SIZE; j++){[i][j] = D[i][j] + C[i][j] * k;[i][j] = A[i][j];

}= new double[SIZE];= new double[SIZE];= new double[SIZE];(int i = 0; i < SIZE; i++){>> b[i];[i] = b[i];

}(int i = 0; i < SIZE; ++i) {(A[i][i]!= 0) {[i] /= A[i][i];(int j = SIZE - 1; j >= i; --j) {[i][j] /= A[i][i];

}

}(int j = i + 1; j < SIZE; ++j) {(int k = i; k < SIZE; k++) {(i == k);[j][k] -= A[j][i] * A[i][k];

}[j] -= result[i] * A[j][i];[j][i] = 0;

}

}(int j = SIZE - 1; j >= 0; j--){(int i = 0; i < j; i++){[i] -= A[i][j] * result[j];[i][j] = 0;

}

}out("out.txt");* f = fopen("out.txt", "w");(int i = 0; i < SIZE; i++){[i] = round(result[i] * 100000) / 100000;

}(int i = 0; i < SIZE; i++)(f, "%.5lf\n", result[i]);(int i = 0; i < SIZE; i++) (int j = 0; j < SIZE; j++) {sum = 0; (int k = 0; k < SIZE; k++) += copy[i][k] * result[k];[i] = abs(b[i] - sum);

}(int i = 0; i < SIZE; i++)(f, "\n%.10lf", delta[i]);(f);

}

В результате получили X:

.9169573287

.2508817999

.1237128647

.0277923094

.0872656987

.2322239583

Округляя до пяти знаков после запятой:

.91696

.25088

.12371

.08727

.23222

При вычислении AX - B, где X - округлённые данные, получим:

.0000061000

.0000061000

.0000057000

.0000022000

.0000035000

.0000031000