Решение систем линейных алгебраических уравнений методом прогонки
Федеральное
агентство по образованию
ФГОУ
СПО «Уфимский авиационный техникум»
Курсовая
работа
Решение
систем линейных алгебраических уравнений
методом
прогонки
по
дисциплине «Численные методы»
Студент Д.Р.
Мусакалимов
Руководитель работы
Э.Р. Ахматсафина
Содержание
Введение
1.
Теоретическая часть
1.1.
Метод Гаусса
1.2
Метод прогонки
2.
Постановка и решение задачи
2.1
Формулировка задачи
2.2
Решение системы методом Гаусса
2.3
Решение системы методом прогонки
3.
Программная реализация
3.1
Блок-схема
3.2
Текст программы
3.3
Тестовый пример
3.4
Решение задачи с помощью ЭВМ
Заключение
Список
использованной литератур
Введение
линейное уравнение гаусс алгоритм
Решение систем линейных алгебраических уравнений
- одна из основных задач вычислительной линейной алгебры. Хотя задача решения
системы линейных уравнений сравнительно редко представляет самостоятельный
интерес для приложений, от умения эффективно решать такие системы часто зависит
сама возможность математического моделирования самых разнообразных процессов с
применением ЭВМ. Значительная часть численных методов решения различных (в
особенности - нелинейных) задач включает в себя решение систем линейных
уравнений как элементарный шаг соответствующего алгоритма.
Одна из трудностей практического решения систем
большой размерности связанна с ограниченностью оперативной памяти ЭВМ. Хотя
объем оперативной памяти вновь создаваемых вычислительных машин растет очень
быстро, тем не менее, еще быстрее возрастают потребности практики в решении
задач все большей размерности. В значительной степени ограничения на
размерность решаемых систем можно снять, если использовать для хранения матрицы
внешние запоминающие устройства. Однако в этом случае многократно возрастают
как затраты машинного времени, так и сложность соответствующих алгоритмов.
Поэтому при создании вычислительных алгоритмов линейной алгебры большое
внимание уделяют способам компактного размещения элементов матриц в памяти
ЭВМ.
К счастью, приложения очень часто приводят к
матрицам, в которых число ненулевых элементов много меньше общего числа
элементов матрицы. Такие матрицы принято называть разреженными. Одним из
основных источников разреженных матриц являются математические модели
технических устройств, состоящих из большого числа элементов, связи между
которыми локальны. Простейшие примеры таких устройств - сложные строительные
конструкции и большие электрические цепи.
Известны примеры решенных в последние годы
задач, где число неизвестных достигало сотен тысяч. Естественно, это было бы
невозможно, если бы соответствующие матрицы не являлись разреженными (матрица
системы из 100 тыс. уравнений в формате двойной точности заняла бы около 75
Гбайт).
Цель заданной работы - освоить решение систем
линейных алгебраических уравнений методам прогонки.
Курсовой проект состоит из трех частей.
Теоретическая часть описана в первой части. Практическая (ручной расчет
поставленной задачи методом прогонки) реализована во второй части. В третьей
представлены алгоритмы решения задачи методом прогонки, программная реализация
метода.
1. Теоретическая часть
.1 Метод Гаусса
Алгоритм решения СЛАУ
<#"656787.files/image001.gif">
с трехдиагональной матрицей 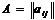 , т.е. с
матрицей, все элементы которой,не лежащие на главной и двух побочных
диагоналях, равны нулю
, т.е. с
матрицей, все элементы которой,не лежащие на главной и двух побочных
диагоналях, равны нулю 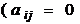 при
при 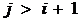 та
та 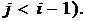
В общем случае системы линейных
алгебраических уравнений с трехдиагональной матрицей имеют вид
Для численного решения систем трехдиагональными
матрицами применяется метод прогонки, который представляет собой вариант метода
последовательного исключения неизвестных.
Т.е. матрицу А можно записать

Идея метода прогонки состоит в
следующем. Решение системы (1) ищется в виде

где 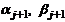 - неизвестные коэффициенты, которые
последовательно находятся от
- неизвестные коэффициенты, которые
последовательно находятся от 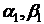 до
до 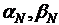 (прямая прогонка), а затем
последовательно вычисляются
(прямая прогонка), а затем
последовательно вычисляются 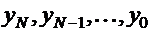 (обратная прогонка) .
(обратная прогонка) .
Выведем формулы для вычисления 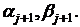 Из (3)
можно получить
Из (3)
можно получить
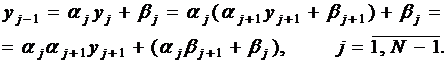
Подставляя имеющиеся выражения для 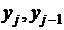 в уравнение
(1), приходим при
в уравнение
(1), приходим при 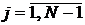 к уравнению
к уравнению
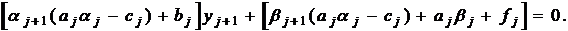 Последнее
уравнение будет выполнено если коэффициенты
Последнее
уравнение будет выполнено если коэффициенты 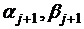 выбрать такими, чтобы выражения в
квадратных скобках обращались в нуль.
выбрать такими, чтобы выражения в
квадратных скобках обращались в нуль.
А именно, достаточно положить
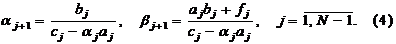
Для отыскания всех 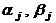 достаточно
задать
достаточно
задать 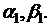
Эти начальные значения находим из
требования эквивалентности условия (3) при 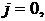 т.е. условия
т.е. условия 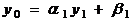 , первому
из уравнений (2).
, первому
из уравнений (2).
Таким образом, получаем
 (5)
(5)
Нахождение коэффициентов 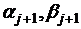 по формулам
(4), (5) называется прямой прогонкой. После того, как прогоночные коэффициенты
по формулам
(4), (5) называется прямой прогонкой. После того, как прогоночные коэффициенты 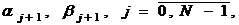 найдены,
решение системи (1), (2) находится по рекуррентной формуле (3), начиная с
найдены,
решение системи (1), (2) находится по рекуррентной формуле (3), начиная с 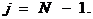 Для начала
счета по этой формуле требуется знать
Для начала
счета по этой формуле требуется знать 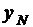 , которое определяется из уравнений
, которое определяется из уравнений
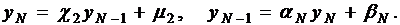
И равно
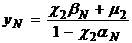 .
.
Нахождение 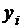 по формулам
по формулам
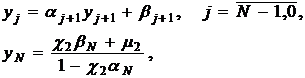 (6)
(6)
называется обратной прогонкой.
Алгоритм решения системы (1), (2)
определяемый формулами (4)-(6) называется методом прогонки.
Метод прогонки можно пременять, если
знаменатели выражений (4), (6) не обрщаются в нуль.
Покажем, что для возможности
применения метод прогонки достаточно потребовать, чтобы коэффициенты системы
(1), (2) удовлетворяли условиям
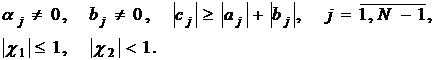
Сначала докажем по индукции, что при
условиях (7), (8) модули прогоночных коэффициентов 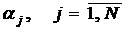 не
превосходят единицы. Согласно (5), (8) имеем
не
превосходят единицы. Согласно (5), (8) имеем 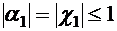 . Предположим, что
. Предположим, что 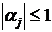 для
некоторого
для
некоторого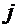 и докажем,
что
и докажем,
что 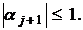
Прежде всего для любых двух
комплексных чисел 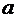 и
и 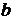 докажем
неравенство
докажем
неравенство
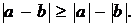
Из неравенства треугольника имеем
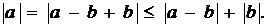
Откуда
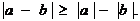
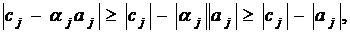
а, используя (7) , получаем
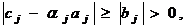


т.е. знаменатели выражений (4) не
обращаются в нуль.
Более того
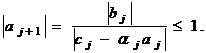
Следовательно, 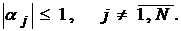
Далее, учитывая второе из условий
(8) и только что доказанное неравенство 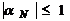 , имеем
, имеем
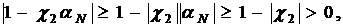
т.е. не обращается в нуль и
знаменатель в выражении для 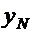 .
.
К аналогичному выводу можно прийти и
в том случае, когда условия (7), (8) заменяются условиями
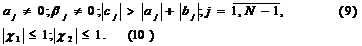
Таким образом при выполнении условий
(7), (8) (так же как и условий (9), (10)) система (1), (2) эквивалентна системе
(4)-(6). Поэтому эти условия гарантируют существование и единственность решения
системы (1), (2) и возможность нахождения этого решения методом прогонки.
Кроме того, доказанные неравенства 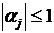 ,
, 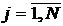 обеспечивают
устойчивость счета по рекуррентным формулам (6). Последнее означает, что
погрешность,внесенная на каком-либо шаге вычислений, не будет возрастать при
переходе к следующим шагам.
обеспечивают
устойчивость счета по рекуррентным формулам (6). Последнее означает, что
погрешность,внесенная на каком-либо шаге вычислений, не будет возрастать при
переходе к следующим шагам.
Действительно, пусть в формуле (6)
при 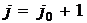 вместо
вместо 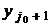 вычислена
величина
вычислена
величина 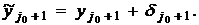
Тогда на следующем шаге вычислений,
т.е. при 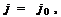
вместо
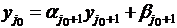
получим величину 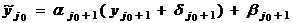 и
погрешность окажется равной
и
погрешность окажется равной
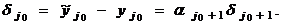
Отсюда получаем, что 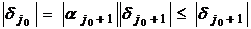 ,т.е.
погрешность не возрастает.
,т.е.
погрешность не возрастает.
Подсчитаем число арифметических
действий, выполняемых при решении задачи (1), (2) методом прогонки.
По формулам (4), что реализуемые с
помощью шести арифметических действий, вычисления производятся 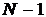 раз, по
формуле (6) выполняется 5 арифметических действий, наконец по формуле (3),
требующей всего два действия, вычисления осуществляются
раз, по
формуле (6) выполняется 5 арифметических действий, наконец по формуле (3),
требующей всего два действия, вычисления осуществляются 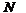 раз. Итак в
методе прогонки всего затрачивается
раз. Итак в
методе прогонки всего затрачивается
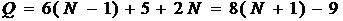
арифметических действий, т.е. число
действий растет линейно относительно числа неизвестных 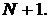
При решении же произвольной системы
линейных алгебраических уравнений методом Гаусcа число действий пропорционально
кубу числа неизвестных.
2. Постановка и решение задачи
.1 Формулировка задачи
Решение систем линейных
алгебраических уравнений методом прогонки (на примере системы 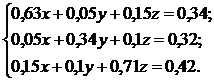 )
)
.2 Решение системы методом Гаусса
Дана система:
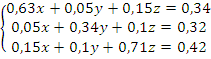
Преобразуем в матрицу:
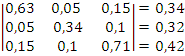
Чтобы было легче работать, умножим
каждый член матрицы на 100:
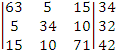
Преобразуем матрицу, умножив вторую
строку на 3 и вычтем из третью строку:
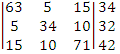
Получим:
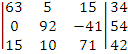
Далее, умножим первую строку на 5 и
вычтем 21 умноженную на третью строку
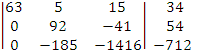
.Найдем сумму третьей строки
умноженной на 92 и второй строки умноженной на 185
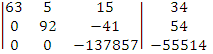
В результате преобразований данная
система приводится к треугольному виду:
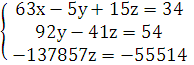
из последнего уравнения находим z:
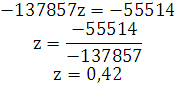
подставляя это значение во второе
уравнение, получаем:
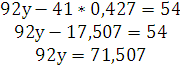
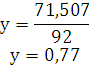
из первого уравнения, подставив
полученные значения, получим:
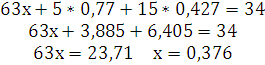
Выполним проверку
подставим полученные значения x,y,z
в первую строку данной матрицы:
,63*0,376+0,05*0,777+0,15*0,427=0,34
,05*0,376+0,34*0,777+0,1*0,427=0,32
,15*0,376+0,1*0,777+0,71*0,427=0,42
Проверка выполнена.
2.3 Решение системы методом прогонки
Приведем матрицу к виду:
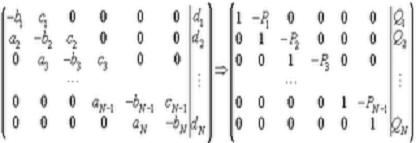 <#"656787.files/image082.gif">
<#"656787.files/image082.gif">
- умножим вторую строку на 15 и
вычтем из нее первую строку:
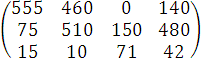
- третью строку умножим на 5 и
вычтем из нее третью строку:
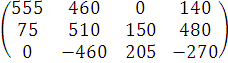
Мы преобразовали матрицу к виду:
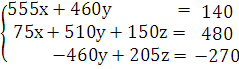
Вычислим значения прогоночных
коэффициентов 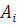
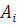 и
и 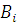
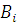 :
:
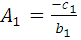
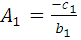 =
= 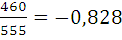
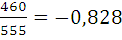
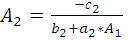
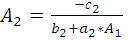 =
= 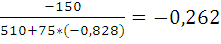
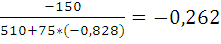
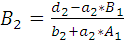
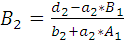 =
= 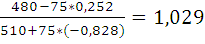
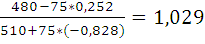
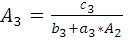
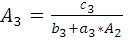 =
= 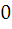 т.к
т.к 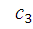
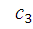 =0
=0
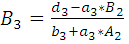
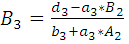 =
= 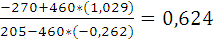
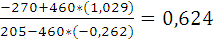
Обратный ход
Вычислим значение 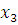
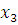 :
:
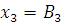
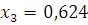
Подставив в формулу значение 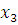
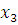 , вычислим значение
, вычислим значение 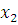
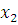 :
:
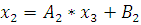
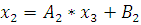
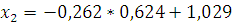
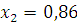
Подставив в формулу значение 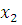
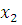 , вычислим значение
, вычислим значение 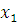
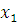 :
:
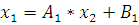
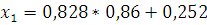
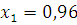
3/ Программная реализация
.1 Блок-схема


.2 Текст программы
Unit1;
interface, Messages, SysUtils,
Variants, Classes, Graphics, Controls, Forms,, StdCtrls;= class(TForm): TEdit;:
TLabel;: TEdit;: TLabel;: TEdit;: TEdit;: TLabel;: TEdit;: TLabel;: TEdit;:
TEdit;: TLabel;: TLabel;: TEdit;: TLabel;: TEdit;: TLabel;: TEdit;: TButton;:
TLabel;: TLabel;: TLabel;: TLabel;btn1Click(Sender: TObject);
{ Private declarations }
{ Public declarations };: TForm1;
{$R *.dfm}
// нажатие на
"вычислить"TForm1.Click(Sender: TObject);=3; // размерность массивов
и матриц
C, D,
E : array
of Real;
//матрица уравнений: array of Real; // чему равны уравнения (первая часть):
array of Real; // результат,k : Integer; // для циклов, перебора, BET : array
of Real; // Alpha и Beta для предв. вычислений: Real;
{установим длины массивов}
SetLength(C,n);(D,n);(E,n);(B,n);(Y,n);
(ALF,n);(BET,n);
{заполним
массивы}
//главная диагональ
(d):[0]:=strtofloat(edtD1.text);[1]:=strtofloat(edtD2.text);[2]:=strtofloat(edtD3.text);
//диагональ
c (та что пониже d)
c[0]:=0;[1]:=strtofloat(edtC2.text);
c[2]:=strtofloat(edtC3.text);
//диагональ
e (та что повыше d)
e[0]:=strtofloat(edtE1.text);[1]:=strtofloat(edtE2.text);
e[2]:=0;
//заполняем
чему равны наши выражения
b[0]:=strtofloat(edtB1.text);[1]:=strtofloat(edtB2.text);
b[2]:=strtofloat(edtB3.text);
//проверим,
можно ли считать этим способом:
k:=0;i:=0 to n-1
doAbs(d[i])>Abs(c[i])+abs(e[i]) then k:=k+1;
if
k=0 then begin('Данный способ не применим, т.к. условие диагонального
преобладания матрицы не выполняется :( ');;;
{вычисление
вспомогательных величин}
ALF[0]:= -(E[0]/D[0]);[0]:=
B[0]/D[0];
{прямой ход}I:=
1 to n - 1 do:= d[i] + c[i]*ALF[i-1];[i]:= -(e[i]/znam);[i]:=
(-c[i]*BET[i-1]+b[i])/znam;
end;
{обратный
ход, нахождение корней}
Y[n-1]:=(b[n-1]-c[n-1]*BET[n-2])/(d[n-1]+c[n-1]*ALF[n-2]);I:=
n - 2 downto 0 do[i]:=Y[i+1]*ALF[i]+BET[i];
//вывод результата.Caption:='X
= ' + floattostr(Y[0]);.Caption:='Y = ' + floattostr(Y[1]);.Caption:='Z = ' +
floattostr(Y[2]);
end;.
.3
Тестовый пример
В
качестве тестового примера возьмем :
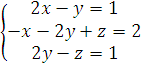
При
ручном подсчете корни равны: x=-3 y=-7 z= -15

Рисунок
1. Результат работы программы.
3.4
Решение задачи с помощью ЭВМ
При
решении системы линейных алгебраических уравнений методом прогонки с помощью
Delphi получаем:

Рисунок
2. Результат работы программы (метод прогонки)
Заключение
Решение
систем линейных алгебраических уравнений - одна из основных задач
вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений
сравнительно редко представляет самостоятельный интерес для приложений, от
умения эффективно решать такие системы часто зависит сама возможность
математического моделирования самых разнообразных процессов с применением ЭВМ.
Значительная часть численных методов решения различных (в особенности -
нелинейных) задач включает в себя решение систем линейных уравнений как
элементарный шаг соответствующего алгоритма.
Численные
методы являются одним из мощных математических средств решения задачи.
Простейшие численные методы мы используем всюду, например, извлекая квадратный
корень на листке бумаги. Есть задачи, где без достаточно сложных численных
методов не удалось бы получить ответа; классический пример - открытие Нептуна
по аномалиям движения Урана.
Одним
из самых распространенных методов решения систем линейных уравнений является
метод прогонки. Условие преобладания диагональных элементов обеспечивает также
устойчивость метода прогонки относительно погрешностей округлений. Последнее
обстоятельство позволяет использовать метод прогонки для решения больших систем
уравнений. Метод прогонки оказывается устойчивым даже при нарушении условия
преобладания диагональных элементов.
В
ходе выполнения курсовой работы мы проделали ручной расчет заданного уравнения,
выполнили расчет на языке программирования Delphi. Также мы выполнили тестовый
пример для проверки метода прогонки.
Список
использованной литературы
Карманов
В.Г. Математическое программирование. - М.: Наука 1986
Пирумов
У.Г. Численные методы. - М.: Изд-во МАИ, 1998
Бахвалов
Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. - М.:
Высшая школа, 2001.
Самарский
А.А., Гулин А.В. Численные методы. -М.:Наука,1989.-432с.