Решение систем линейных алгебраических уравнений методом простой итерации
Федеральное агентство по образованию
ФГОУ СПО «Уфимский авиационный
техникум»
Курсовая работа
по дисциплине «Численные методы»
Решение систем линейных
алгебраических уравнений методом простой итерации
Студент В.Р. Хизбуллина
Руководитель работы
Э.Р. Ахматсафина
Содержание
Введение
. Теоретическая часть
.1 Метод Гаусса
.2 Метод простой итерации
. Постановка и решение задачи
.1 Формулировка задачи
.2 Решение задачи методом Гаусса
.3 Решение задачи методом простой итерации
. Программная реализация
.1 Блок-схема
.2 Текст программы
.3 Тестовый пример
.4 Решение задачи с помощью ЭВМ
Заключение
Список литературы
Введение
Все используемые на практике методы решения систем линейных
алгебраических уравнений можно разделить на две большие группы: точные методы и
итерационные методы.
Под точным методом решения понимается метод, позволяющий теоретически
получить точное значение всех неизвестных в результате конечного числа
арифметических операций (метод Гаусса).
Итерационные методы позволяют получить решение лишь в виде предела
последовательности векторов, построение которого производится единообразным
процессом, называется процессом итерации, или последовательных приближений.
Вдобавок, итерационные методы находят широкое применение и при решении еще
одной вычислительной задачи линейной алгебры, называемой полной проблемой
собственных значений (отыскание всех собственных значений и отвечающих им
собственных векторов заданной матрицы), т.к. намного удобнее вычислить предел
некоторых числовых последовательностей без предварительного определения
коэффициентов характеристического многочлена.
Преимуществом итерационных методов является удобное применение в
современной вычислительной технике, т.к. решения, полученные с помощью прямых
методов обычно содержат погрешность. Итерационные методы же позволяют получить
решение данной системы с заранее определенной погрешностью. Явным преимуществом
является значительное превосходство над точными методами по скорости и удобнее
реализуются на практике.
Цель курсовой работы - освоить решение систем линейных алгебраических
уравнений методом простой итерации.
Курсовой проект состоит из трех частей: первая - теоретическая, в ней
описана теория по методу простой итерации. Вторая часть (практическая) содержит
решение системы методами Гаусса и простой итерации. В третьей части представлен
алгоритм решения задачи методом простой итерации, программная реализация
метода.
1. Теоретическая часть
.1 Метод Гаусса
В разделе « Численные методы линейной алгебры» рассматриваются численные
методы решения систем линейных алгебраических уравнений (СЛАУ) и численные
методы решения задач на собственные значения и собственные векторы матриц.
Среди численных методов алгебры существуют прямые методы, в которых
решение получается за конечное фиксированное число операций и итерационные
методы, в которых результат достигается в процессе последовательных
приближений.
Из прямых методов решения СЛАУ рассмотрим методы Гаусса и простых
итераций.
В методе Гаусса матрица СЛАУ с помощью равносильных преобразований
преобразуется в верхнюю треугольную матрицу, получающуюся в результате прямого
хода. В обратном ходе определяются неизвестные.
Пусть дана СЛАУ
 (1)
(1)
Запишем расширенную матрицу системы:

На первом шаге алгоритма Гаусса выберем диагональный элемент 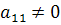 (если он равен 0, то первую строку
переставляем с какой-либо нижележащей строкой) и объявляем его ведущим, а
соответствующую строку и столбец, на пересечении которых он стоит - ведущими.
Обнулим элементы
(если он равен 0, то первую строку
переставляем с какой-либо нижележащей строкой) и объявляем его ведущим, а
соответствующую строку и столбец, на пересечении которых он стоит - ведущими.
Обнулим элементы 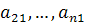 . ведущего столбца. Для этого сформируем числа
. ведущего столбца. Для этого сформируем числа 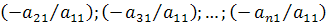 . Умножая ведущую строку на число
. Умножая ведущую строку на число 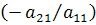 складывая со второй и ставя
результат на место второй строки, получим вместо элемента
складывая со второй и ставя
результат на место второй строки, получим вместо элемента 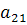 нуль, а вместо элементов
нуль, а вместо элементов 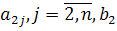 - соответственно элементы
- соответственно элементы 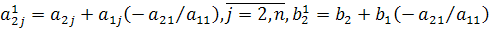 и т.д.
и т.д.
Умножая ведущую строку на число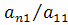 , складывая с n-ой строкой и ставя
результат на место n- ой строки, получим вместо элемента
, складывая с n-ой строкой и ставя
результат на место n- ой строки, получим вместо элемента 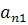 нуль, а остальные элементы этой
строки будут иметь вид:
нуль, а остальные элементы этой
строки будут иметь вид:
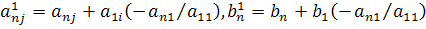
Сохраняя ведущую строку неизменной, получим в результате 1-го шага
алгоритма Гаусса следующую матрицу:
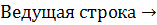
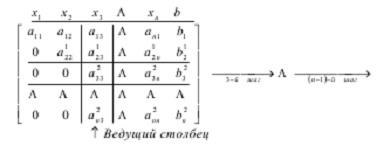
На втором шаге алгоритма Гаусса в качестве ведущего элемента выбирается
элемент (если он равен нулю, то вторую строку взаимно меняем на нижележащую
строку). Формируются числа 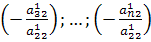 которые ставятся около ведущей строки. Умножая ведущую
строку на число
которые ставятся около ведущей строки. Умножая ведущую
строку на число 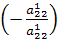 и складывая результат с третьей строкой, получим вместо
элемента
и складывая результат с третьей строкой, получим вместо
элемента 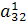 нуль, а вместо элементов
нуль, а вместо элементов 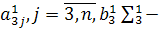 элементы
элементы 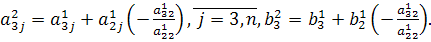 И так далее.
И так далее.
Умножая ведущую строку на число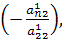 складывая результат с n-ой строкой и ставя полученную сумму
на место n-ой строки, получим вместо элемента
складывая результат с n-ой строкой и ставя полученную сумму
на место n-ой строки, получим вместо элемента 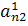 нуль, а вместо элементов,
нуль, а вместо элементов,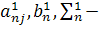 элементы
элементы 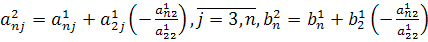 Сохраняя 1-ую и 2-ую строки матрицы
неизменными, получим в результате второго шага алгоритма Гаусса следующую
матрицу:
Сохраняя 1-ую и 2-ую строки матрицы
неизменными, получим в результате второго шага алгоритма Гаусса следующую
матрицу:

После (n-1)-го шага алгоритма Гаусса получаем
следующую расширенную матрицу содержащую верхнюю треугольную матрицу СЛАУ

Прямой ход алгоритма Гаусса завершен.
В обратном ходе алгоритма Гаусса из последнего уравнения сразу
определяется 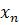 , из предпоследнего -
, из предпоследнего - 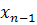 и т.д. Из первого уравнения
определяется
и т.д. Из первого уравнения
определяется 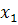
1.2 Метод
простой итерации
При большем числе неизвестных линейная система (ЛС впоследствии) схема
метода Гаусса, дающая точное приближение, становиться весьма сложной.
В этих условиях для нахождения корней системы иногда удобнее использовать
приближенные методы вычисления. Изложим здесь один из этих методов - метод
итераций.
При большом числе уравнений прямые методы решения СЛАУ (за исключением
метода прогонки) становятся труднореализуемыми на ЭВМ прежде всего из-за
сложности хранения и обработки матриц большой размерности. В то же время
характерной особенностью ряда часто встречающихся в прикладных задачах СЛАУ
является разреженность матриц. Число ненулевых элементов таких матриц мало по
сравнению с их размерностью. Для решения СЛАУ с разреженными матрицами
предпочтительнее использовать итерационные методы.
Методы последовательных приближений, в которых при вычислении
последующего приближения решения используются предыдущие, уже известные
приближенные решения, называются итерационными.
Рассмотрим СЛАУ (1) с невырожденной матрицей (det A≠0). Приведем СЛАУ к
эквивалентному виду
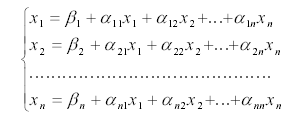 (2)
(2)
Такое приведение может быть выполнено различными способами. Одним из
наиболее распространенных является следующий:
Разрешим систему (1) относительно неизвестных при ненулевых диагональных
элементах, aii ≠0,i=1,n (если какой-либо коэффициент на главной диагонали равен
нулю, достаточно соответствующее уравнение поменять местами с любым другим
уравнением). Получим следующие выражения для компонентов: вектора 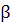 и матрицы
и матрицы 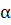 эквивалентной системы:
эквивалентной системы:
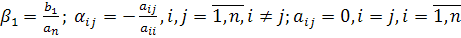 (3)
(3)
При таком способе приведения исходной СЛАУ к эквивалентному виду метод
простых итераций носит название метода Якоби. В качестве нулевого приближения
вектора неизвестных примем вектор правых частей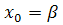 или
или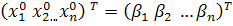
Тогда метод простых итераций примет вид:
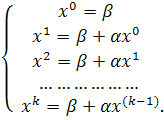 (4)
(4)
Из (4) видно преимущество итерационных методов по сравнению, например, с
рассмотренным выше методом Гаусса. В вычислительном процессе участвуют только
произведения матрицы на вектор, что позволяет работать только с ненулевыми
элементами матрицы, значительно упрощая процесс хранения и обработки матриц.
Имеет место следующее достаточное условие сходимости метода простых итераций [
1 ]. Метод простых итераций (4) сходится к единственному решению СЛАУ (2) (а
следовательно и к решению исходной СЛАУ (1)) при любом начальном приближении 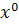 , если какая-либо норма матрицы
, если какая-либо норма матрицы 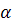 эквивалентной системы меньше
единицы.
эквивалентной системы меньше
единицы. 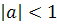 . Если используется метод Якоби
(выражения (3) для эквивалентной СЛАУ), то достаточным условием сходимости
. Если используется метод Якоби
(выражения (3) для эквивалентной СЛАУ), то достаточным условием сходимости
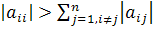
является диагональное преобладание матрицы A, т.е. (для каждой строки матрицы A модули элементов, стоящих
на главной диагонали, больше суммы модулей недиагональных элементов). Очевидно,
что в этом случае 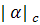 меньше единицы и, следовательно, итерационный процесс (4)
сходится. Приведем также необходимое и достаточное условие сходимости метода
простых итераций. Для сходимости итерационного процесса необходимо и
достаточно, чтобы спектр матрицы
меньше единицы и, следовательно, итерационный процесс (4)
сходится. Приведем также необходимое и достаточное условие сходимости метода
простых итераций. Для сходимости итерационного процесса необходимо и
достаточно, чтобы спектр матрицы 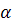 эквивалентной системы лежал внутри
круга с радиусом, равным единице.
эквивалентной системы лежал внутри
круга с радиусом, равным единице.
При выполнении достаточного условия сходимости оценка погрешности решения
на k - ой итерации дается выражением:
Где x* - точное решение СЛАУ. *
Процесс итераций останавливается при выполнении условия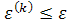 , где
, где 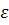 задаваемая вычислителем точность.
задаваемая вычислителем точность. Принимая во внимание, что из (5)
следует неравенство
Принимая во внимание, что из (5)
следует неравенство
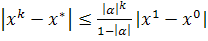
можно получить априорную оценку необходимого для достижения заданной
точности числа итераций. При использовании в качестве начального приближения
вектора 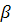 такая оценка определится неравенством:
такая оценка определится неравенством:
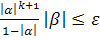 откуда получаем априорную оценку
числа итераций k при
откуда получаем априорную оценку
числа итераций k при 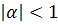

Следует подчеркнуть, что это неравенство дает завышенное число итераций 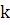 , поэтому редко используется на
практике.
, поэтому редко используется на
практике.
Замечание. Поскольку 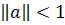 является только достаточным (не необходимым) условием
сходимости метода простых итераций, то итерационный процесс может сходиться и в
случае, если оно не выполнено. Тогда критерием окончания итераций может служить
неравенство
является только достаточным (не необходимым) условием
сходимости метода простых итераций, то итерационный процесс может сходиться и в
случае, если оно не выполнено. Тогда критерием окончания итераций может служить
неравенство
 .
.
2. Постановка и решение задачи
2.1
Формулировка задачи
Решение систем линейных алгебраических уравнений методом простой итерации
(на примере системы 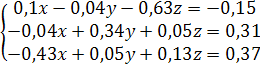 с точностью
с точностью 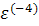 )
)
2.2
Решение задачи методом Гаусса

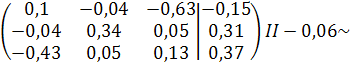
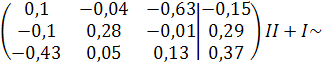
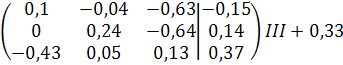
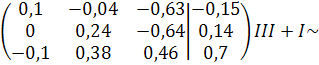
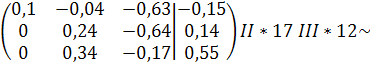
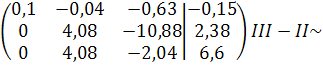
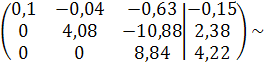
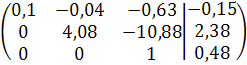
Z=0,48
4, 08y - 10, 88z = 2, 38
4,08y-5,11=2,38
,08y=7,49=1,83
,1x-0,04y-0,63z=-0,15
,1x-0,04*1,83-0,63*0,48=-0,15
0,1x-0,07-0,3=-0,15
,1x=0,22
x=2,2
Проверка:
,1*2,2 - 0, 04*1, 83 - 0, 63*0, 48 = -0, 15
, 22 - 0, 07 - 0, 3 = -0, 15
, 22 - 0, 37 = -0, 15
, 15 = -0, 15
2.3
Решение задачи методом простой итерации
алгебраический уравнение гаусс итерация
Рассмотрим систему:
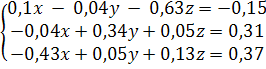
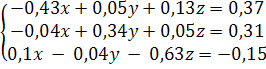
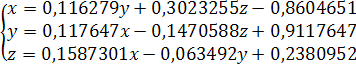
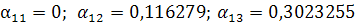 ;
;
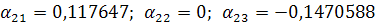 ;
;
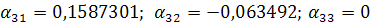 ;
;
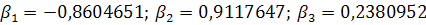 ;
;
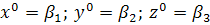 ;
;
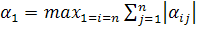
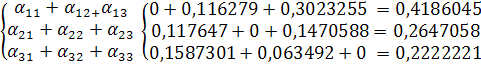
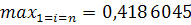
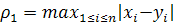
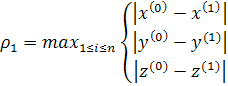
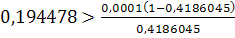
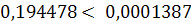 неверно
неверно
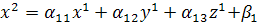
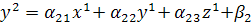
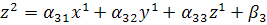
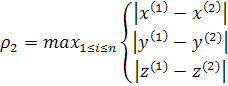
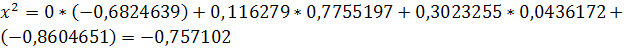
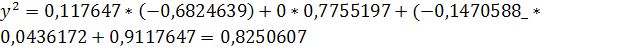
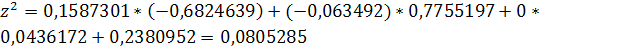
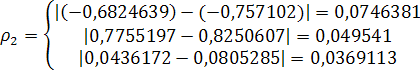
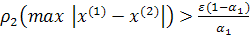
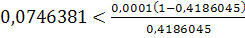
 неверно
неверно
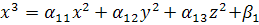
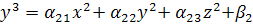
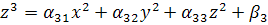
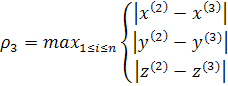
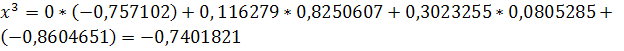
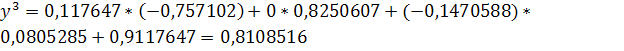
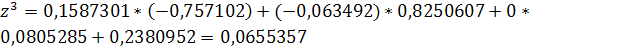
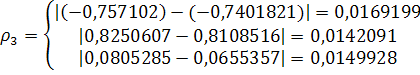
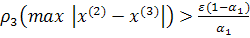
 неверно
неверно
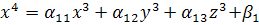
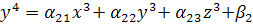
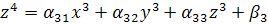
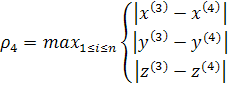
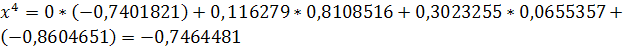

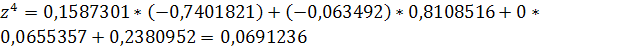
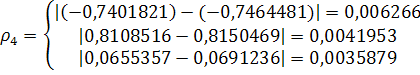
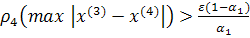
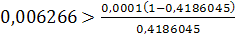
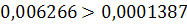
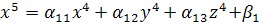
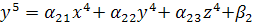
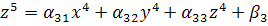
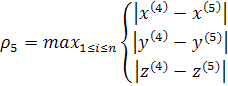
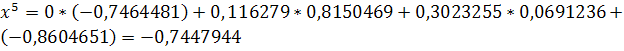
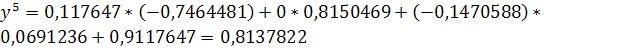
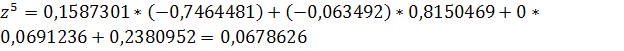
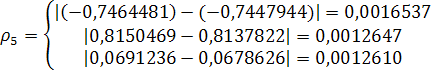
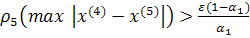
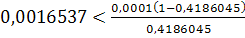
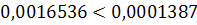 неверно
неверно
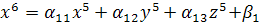
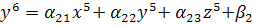
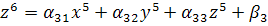
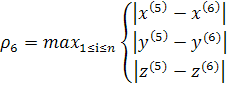

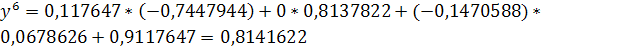
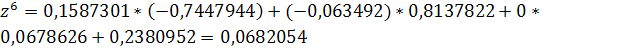
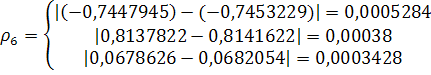
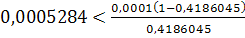
 неверно
неверно
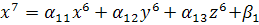
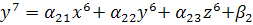
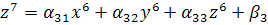

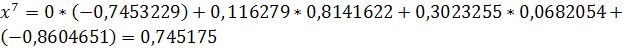
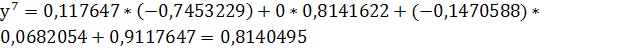
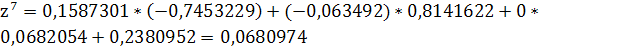
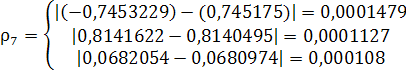
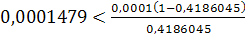
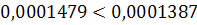 неверно
неверно
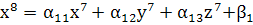
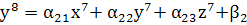
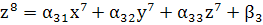
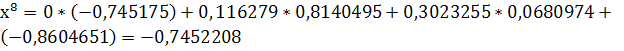
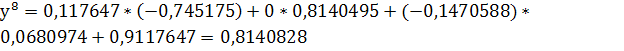
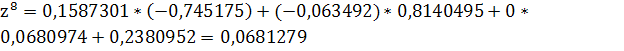
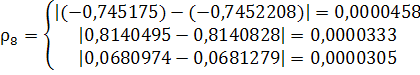
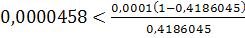
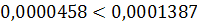 верно
верно
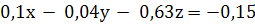
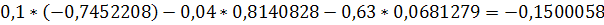
3.
Программная реализация
3.1
Блок-схема

3.2 Текст
программы
A -
массив в который записывается система
B -
массив в который записывается система приведенная к виду
С - массив В умноженный на начальное приближение
L -
массив В с обнуленной главной диагональю
S -
все суммы
H -
массив α1 α2 α3
q - α
E -
точность
X -
массив значений Х
Program p1; uses crt;n=10;A,B,C,l:array[1..n,1..n] of
real;,q,max,E,w,z:real;,F,g,h,x:array[1..n] of real;,o,i,j:
integer;,x2,x3,x11,x12,x13,max1,max2,max3:real;clrscr;('Vvedite chislo
peremennih');(m);('Vvedite chislo uravneniy');(o);:=o+1;('Vvedite
e->');(w);[1,1]:=0.1; a[1,2]:=-0.04; a[1,3]:=-0.63;
a[1,4]:=-0.15;[2,1]:=-0.04; a[2,2]:=0.34; a[2,3]:=0.05;
a[2,4]:=0.31;[3,1]:=-0.43; a[3,2]:=0.05; a[3,3]:=0.13;
a[3,4]:=0.37;('privedenie k vidu');j:=1 to o do
Begin[1,j]:=-(A[3,j]/a[3,1]);[2,j]:=-(A[2,j]/a[2,2]);[3,j]:=-(A[1,j]/a[1,3]);;;i:=1
to m do Beginj:=1 to o doj=o then B[i,j]:=-(B[i,j]);end;i:=1 to m do beginj:=1
to o do(' ',B[i,j]:3:3);;
end;;('x1=',b[1,2]:3:3,'x2+',b[1,3]:3:3,'x3+',b[1,o]:3:3);('x2=',b[2,1]:3:3,'x1+',b[2,3]:3:3,'x3+',b[2,o]:3:3);('x3=',b[3,1]:3:3,'x1+',b[3,2]:3:3,'x2+',b[3,o]:3:3);;i:=1
to n do beginj:=1 to o-1 doI<>j then[i,j]:=b[i,j];;i:=1 to m do beginj:=1
to o-1 do(' ',L[i,j]:3:3); writeln; end;('Nachalnoe priblijenie');i:=1 to m do
Begin[i]:=B[i,o]; writeln(' ',F[i]:3:3); end;:=g[1];I:=1 to m do Begin
S:=0;J:=1 to o-1 do[i]:=g[i]+abs(L[i,j]);('alpha=',g[i]:3:3);max1<g[i] then
max1:=g[i]; end;('max1=',max1:3:3);:=h[1];j:=1 to o-1 do Begin S:=0;i:=1 to m
do:=s+abs(L[i,j]);[i]:=S;('alphaS=',g[i]:3:3);max2<g[i] then max2:=g[i];
end;('max2=',max2:3:3);:=0;I:=1 to m do BeginJ:=1 to o-1 do:=S+sqr(L[i,j]);
end;:=sqrt(S);('max3=',S:3:3);[1]:=max1;[2]:=max2;[3]:=S;I:=m downto 1
doh[i]<1 then q:=h[i];('q=',q:3:3);;
z:=((w*(1-q))/q);('z=',z:3:3);[1,1]:=b[1,4];[2,2]:=b[2,4];[3,3]:=b[3,4];i:=1 to
m do beginj:=1 to o-1 do(' ',L[i,j]:3:3); writeln; end;;('iteraciya');I:=1 to m
do[i]:=0;I:=1 to m doj:=1 to o-1 doi<>j then[i,j]:=L[i,j]*f[j] else
c[i,j]:=l[i,j];i:=1 to m do beginj:=1 to o-1 do(' ',c[i,j]:3:3); writeln;
end;I:=1 to m doj:=1 to o-1 do[i]:=x[i]+(c[i,j]);i:=1 to m
do('x=',x[i]:3:3);i:=1 to m do Begin[i]:=abs(f[i]-x[i]);(D[i]:3:3);
end;;:=d[1];i:=1 to m do Beginmax<D[i] then max:=D[i]; end;i:=1 to m do
Begin[i]:=x[i]; writeln('novoe=',F[i]:3:3); end;('max=',max:3:3); until
max<z;.
3.3
Тестовый пример
В качестве тестового примера возьмем систему ее решение можно найти
аналитически, оно имеет вид
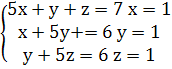
Результат работы программы на тестовом примере приведен на рисунке 1
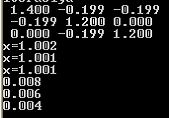
Рисунок 1. Тестовый пример
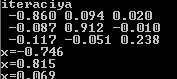
Рисунок 2 Решение системы
Заключение
В данной работе описаны и реализованы с помощью блок-схем и языка
программирования Turbo Pascal базовые задачи вычислительной
математики: решение систем линейных алгебраических уравнений, полиномиальная
интерполяция, среднеквадратичное приближение функции, численное интегрирование
функций. Представленные методы и реализованные алгоритмы достаточно просты, но
в тоже время эффективны для большого количества задач.
Список
литературы
1. Бахвалов
Н., Жидков Н., Кобельков Г. Численные методы. М.: Лаборатория базовых знаний,
2001. 632 с.
2. Вержбицкий
В.М., Численные методы. Линейная алгебра и нелинейные уравнения. М.: Высшая
школа, 2000. 266 с.
. Вержбицкий
В.М., Основы численных методов. М.: Высшая школа, 2002. 840 с.
. Пирумов
У.Г. Численные методы. М.: Дрофа, 2003. 224 с.
. Фаронов
В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. - М.: Нолидж, 1997. -
616 с.