Параметрические и непараметрические методы оценивания

Параметрические и непараметрические методы оценивания

Министерство образования и науки Красноярского края

Государственное образовательное учреждение

высшего профессионального образования

«Сибирский государственный аэрокосмический университет

имени академика М.Ф. Решетнева»

Кафедра системного анализа и исследования операций

Реферат

по теме: «Параметрические и непараметрические методы оценивания»

Выполнил студент

группы БС 11-01

Малаховский М. А.

Проверил преподаватель

Медведев А.В.

Красноярск 2013

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Параметрические методы оценки

Непараметрические методы оценки

ПРАКТИЧЕСКАЯ ЧАСТЬ

Практическая часть №1

Практическая часть №2

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

В последние годы сравнительно остро возникла проблема решения разнообразных задач кибернетики в условиях, когда объем априорной информации об исследуемом процессе или объекте оказывается довольно малым, и сведения о функции цели, ограничениях, действующих на него, не являются исчерпывающими. Это объясняется тем фактом, что быстрая замена одних технологических процессов другими, замена технологического оборудования или его модернизация приводят к необходимости развития методов и подходов построения разнообразных адаптивных систем, способных в процессе функционирования, с целью рационального ведения этих процессов, улучшать свои рабочие характеристики. Потребность в построении обучающихся систем возникает не только в технологических и производственных процессах, но и в других областях деятельности человека (экономика, медицина, социология, биология и т.п.). По существу речь идет об исследуемом объекте и достаточному для математической постановки задачи, которая имеет место в каждом конкретном случае.

Непараметрическая статистика, в частности стохастические аппроксимации различных типов, явились основой для разработки соответствующих адаптивных систем. Последние сохраняют основные свойства стохастических аппроксимаций, которые были положены в основу при их синтезе, и тесно связаны с объемом априорной информации. В данном реферате основное внимание уделяется изложению информации о параметрических и непараметрических системах адаптации.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Параметрические методы оценки

Процедура Роббинса-Монро

Пусть f(x) - некоторая неизвестная функция, значения которой могут быть измерены в любой точке x Î E₁. Функция f(x) - монотонная, непрерывная и имеет единственный корень f(x)=0 в точке x⁰. Задача состоит в том, чтобы выработать такой план эксперимента, чтобы x_s®x⁰ при s®¥. Наблюдения y_s=f(x_s) статически независимы. Тогда имеем

y_s+1(x_s,w)=f(x_s)+g(s+1,x_s,x(s+1,w)),

где x(s,w) - последовательность независимых случайных величин, определенным на некотором вероятностном пространстве (W,U,P) wÎW - элементарные случайные события, причем M{g(s,x,w)}=0 при любых xÎE₁. Для решения этой задачи Роббинса-Монро предложена следующая процедура

_s+1=x_s+c_sf_s+1(x_s,w),

где x₀ - произвольное число. Последовательность положительных чисел c_s удовлетворяет условиям Роббинса-Монро

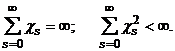
Первое из этих условий необходимо для сходимости x_s к x₀ при s®¥ даже при отсутствии случайных ошибок. Иными словами, необходимо, чтобы c_s были не слишком малыми. с другой стороны c_s должны быть не слишком большими, в противном случае случайные ошибки нарушают эту сходимость, поэтому необходимо выполнение второго условия (1.4.5).

Теорема 1.1. Пусть выполнены неравенства:

) sup f(x)(x-x₀)<0 "e>0,

e<x-x⁰<e^-1,

) f²(x)+M{g²(s,x,w)}<b(1-x²), b>0 - постоянная.

Тогда при выполнении условий Роббинса-Монро для любого xÎЕ₁, процесс x_s, определяемый (1.4.4), сходится с вероятностью 1 при s®¥ к корню уравнения f(x)=0, т.е. к x₀ и

P{lim x_s=x⁰}=1.

Можно также показать, что x_s сходится к x⁰ в среднеквадратическом.

Алгоритм Литвакова

Алгоритм Литвакова позволяет отыскать близкое к оптимальному значение вектора параметров 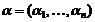 с помощью следующей процедуры

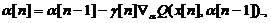
при не оптимальном .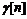

Сущность его состоит в следующем.

Пусть дана обучающая выборка объема 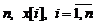. Положив  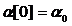и 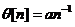, где а - некоторая постоянная, осуществляется итеративный процесс вычислений по формуле на п-ом шаге находится 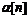, которое принимается в качестве нового начального условия и процесс вычислений продолжается по той же самой выборке .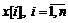

В результате получаем оценк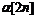у . Продолжая этот процесс к-раз, найдем оценку 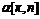. Результат Литвакова и состоит в том, что оценка 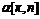 для достаточно больших к (точнее 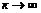) приближается к 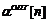. Во многих практических задачах к не превышает 5.

Алгоритм Кестена

Известно, что скорость сходимости рекуррентных вероятностных алгоритмов типа при 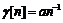 определяется степенным знаком - это следствие влияние помех. Если бы помехи отсутствовали, то следовало бы 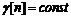 и скорость сходимости при этом возрастает и определяется показательным законом.

Сущность алгоритма Кестена состоит в том, что вдали от 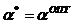 роль помех при измерениях 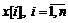 мала и разность 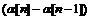 будет иметь постоянный знак, а вблизи 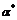 знак 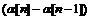 уже существенно зависит от помех и будет меняться. Поэтому в алгоритме Кестена 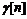 не меняется, когда разность 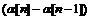 уже не меняет своего знака, и 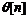 меняется, если знак 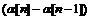 изменяется.

Чтобы определить разность 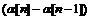 необходимо по крайней мере два наблюдения. Поэтому 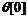 и 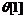 выбираются произвольно (обычно равными единице). Дальнейшее определение 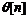 подчинено правилу

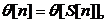
где 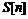 целочисленная функция, определяемая выражением

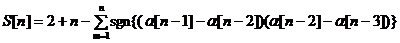
где 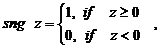z - произвольный аргумент.

Непараметрические методы оценки

Здесь мы рассмотрим стохастические аппроксимации непараметрического типа. Основным их отличительным свойством от известных является отсутствие этапа выбора конкретной формы аппроксимирующего полинома с точностью до вектора параметров.

Непараметрические аппроксимации основаны на соответствующих оценках плотности вероятности, введенных Парзеном Е. в 1962 г.

Непараметрическая оценка плотности вероятности

Пусть х_i.,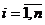 статически независимые наблюдения случайной величины х, распределенной с плотностью вероятности р(х). Естественно связать с каждой точкой 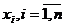 дельта функцию 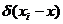, тогда статистика

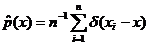
оказывается несмещенной оценкой р(х) .

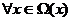Действительно, вычислим M{p(x)}:

= =…=

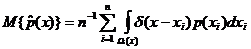
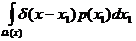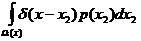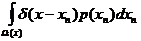
Следовательно,

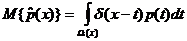
Применяя известное свойство δ-функции, получим 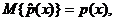 а это и означает несмещенность данной оценки, но она не может быть использована в конкретных расчетах, поэтому естественно δ-функцию "размазать" в окрестности точки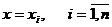

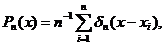
где 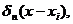 уже не дельта-функция, но обращается в последнюю при n→∞.Далее, в качестве 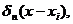 мы будем рассматривать следующий тип колоколообразных функций

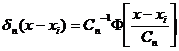
Тогда оценка p_n (x)примет вид

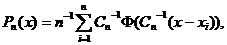
где интегрируемая с квадратом функция Ф такова, что

Φ(z)<∞,

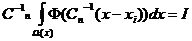
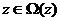
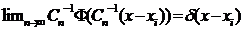
а параметр С_n (коэффициент размытости) удовлетворяет условиям:

C_n>0, n=1,2…,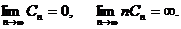

Непараметрическая оценка кривой регрессии

Пусть имеется статически независимые наблюдения двух случайных величин (х,у)=(х₁,у₁),…,(х_n,у_n), распределенных с неизвестной плотностью вероятности Р(х,у). Предполагается, что р(х)>0 "xÎW(x). При аппроксимации неизвестных стохастических зависимостей у от х часто используют регрессию у по х:

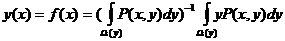
непараметрическая оценка которой, как известно, имеет вид

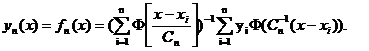
Данную оценку можно получить из 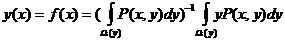подстановкой в нее непараметрической оценки двумерной плотности вероятности Р(х,у) и при условии, что

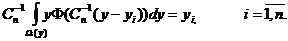
Выполнение последнего требования всюду в дальнейшем предполагается.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Практическая часть №1

Постановка цели

В первой части практической работы необходимо получить приближение зависимости, используя параметрические методы оценки.

Заранее известна функция, для которой нужно получить приближение - 1)y=0,35*cos(0.5x) - пробный эксперимент; 2)y=sin(0.5x). Исходя из зависимости, необходимо сформировать выборку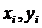, с помощью которой собственно и необходимо оценить параметры для приближения.

Практические результаты

В качестве приближения была выбрана следующая зависимость - 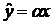. Хотелось бы отметить, что, так как зависимость заранее известна и на заданном промежутке данная кривая схожа с прямой, параметр оценки всего один. Это сделано, прежде всего, для лучшего понимания процесса.

Для приближения не случайно выбрана несовпадающая структура, это вносит некоторые помехи в выборочные значения.

В данной работе использовалось процедура Робинса-Монро, которая была оптимизирована с помощью алгоритмов Литвакова и Кестона. В результате этой оптимизации, параметр 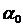 не влияет на оценку параметра 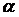. Доказательством чего является процесс сходимости 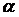 при разных .

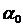)y=0,35*cos(0.5x) - пробный эксперимент

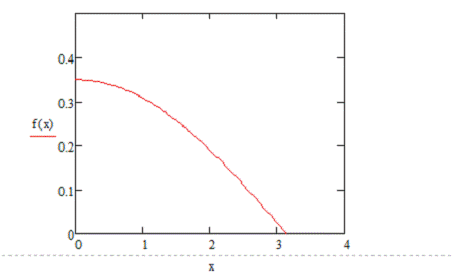
В качестве приближения была выбрана следующая зависимость -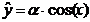

При выборке n=100

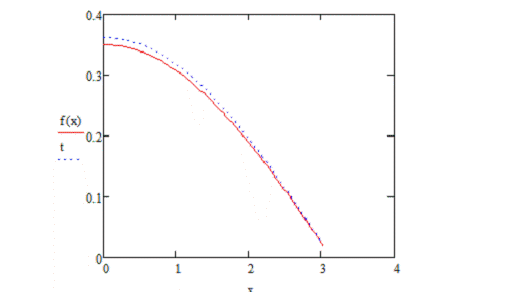
Увеличим выборку (n=400):

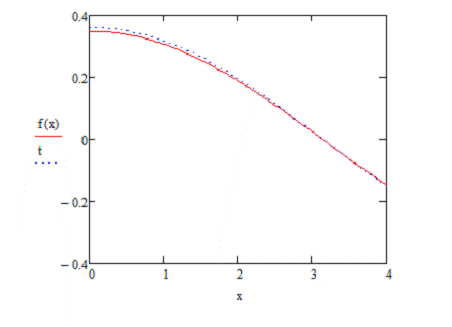
Аппроксимация становится лучше.

В качестве приближения возьмем -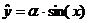

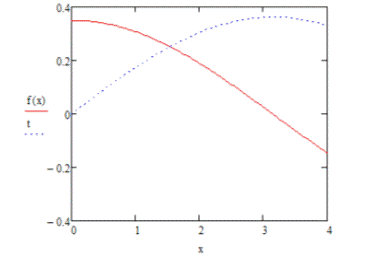
При сходимости по параметрам, но при неправильном выборе структуры, модель может быть неадекватной реальному объекту или процессу, требуют знания структуры.

)y=sin(0.5x)

В качестве приближения была выбрана следующая зависимость -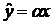

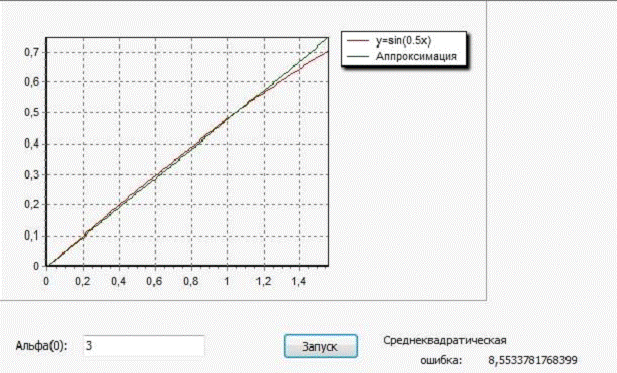
В целом, можно отметить, что полученные результаты достаточно неплохи, потому что график функции и приближения схожи, а значение среднеквадратической ошибки не так велико.

Вывод: При сходимости по параметрам, но при неправильном выборе структуры, модель может быть неадекватной реальному объекту или процессу, требуют знания структуры. Если структура выбрана верно, то с увеличением выборки аппроксимация становится лучше.

Практическая часть №2

параметрический стохастический аппроксимация регрессия

Постановка задачи

В данной части работы необходимо получить приближение зависимости с помощью непараметрических методов оценки.

Также как и в первой работе, изначально известна функция - y=7∙cos(x), для которой необходимо получить приближение. Исходя из данной зависимости, необходимо получить выборку значений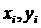. После чего, полученные выборочные значения должны быть использованы для получения зависимости. Зависимость нужно восстановить, используя методы непараметрической оценки.

Практические результаты

В данной работе получение приближения осуществлялось с помощью следующей оценки:

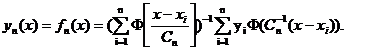
Параметр размытости (сглаживания) был определен следующим образом - 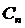=0,4. В результате получилось следующее приближение:

При выборке n=100

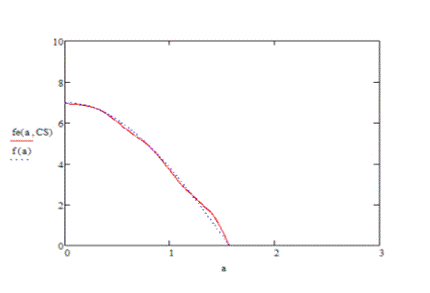
Попробуем увеличить выборку (n=400)

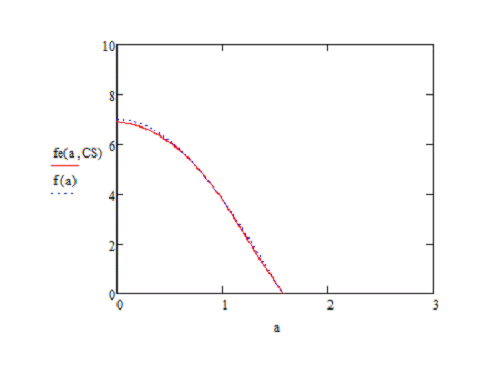
Аппроксимация становится лучше.

Для того чтобы убедиться в правильности работы процедуры, данная непараметрическая оценка была применена к другой функции: y=sin(x)

При выборке n=400

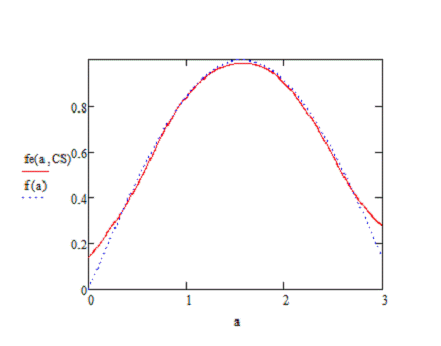
В данной работе проводились эксперименты со значением параметра размытости 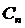. Значение сначала было увеличено, затем уменьшено. Итогом увеличения параметра стало следующее приближение:

При выборке n=100 и 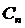=7

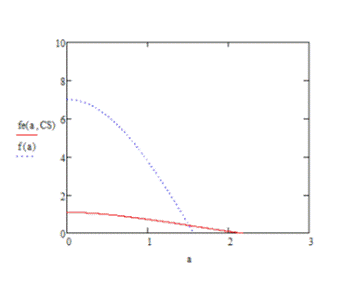
Аппроксимация хуже, что еще раз доказывает правильность работы процедуры.

Уменьшение же параметра не привило, к каким либо кардинальным изменениям, в силу того, значение параметра 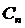=0,4 достаточно мало, чтобы получить достойное приближение.

Попробуем одновременно увеличить выборку и параметр размытости:

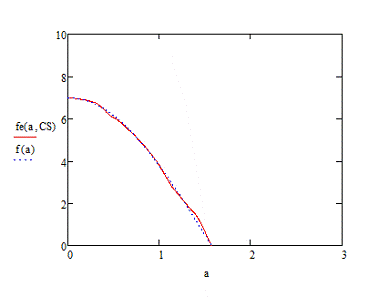
n=400 и 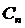=0.2

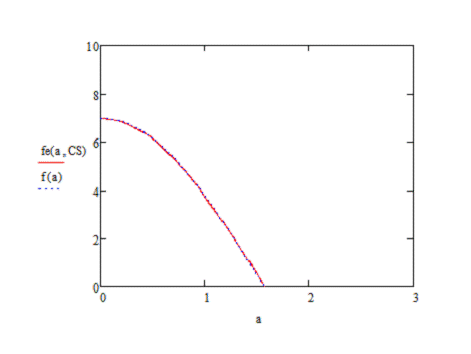
Точная аппроксимация, совпадение с истиной.

Вывод: При увеличении объема выборки и уменьшении параметра размытости аппроксимация улучшается, независимо от функции, для которой необходимо получить приближение, не требуется знание структуры.

ЗАКЛЮЧЕНИЕ

Таким образом, можно сделать следующие выводы:

«Параметрический подход» подразумевает, что мы знаем структуру исследуемого процесса или объекта, но не знаем параметры этой структуры, эти параметры необходимо определить.

От уровня априорной информации зависит то, с каким видом алгоритма (параметрическим или непараметрическим) мы будем работать. Если априорной информации достаточно для выбора структуры объекта, то можно работать с параметрическими алгоритмами. Непараметрический подход используется в случаях недостаточной априорной информации об изучаемом процессе, объекте. Непараметрический и параметрический подходы имеют свои преимущества и недостатки.

Преимущества параметрических алгоритмов:

·        Менее ресурсоемкие алгоритмы (требует меньшего количества вычислительных операций в сравнении с непараметрическими алгоритмами);

·        После определения неизвестных коэффициентов мы можем определить характер поведения объекта или процесса в любой части допустимой области.

Недостатки параметрических алгоритмов:

·        Требуют знания структуры объекта, процесса;

·        При сходимости по параметрам, но при неправильном выборе структуры, модель может быть неадекватной реальному объекту или процессу.

Преимущества непараметрических алгоритмов (непараметрическая аппроксимация):

·        Отсутствие необходимости выбора структуры объекта с точностью до вектора неизвестных параметров;

·        Универсальность алгоритмов позволяет работать с различными зависимостями;

·        При увеличении объема выборки, согласно среднеквадратичной сходимости, оценка функциональной зависимости сходится к истинной зависимости.

Недостатки непараметрических алгоритмов (непараметрическая аппроксимация):

·        Большое число вычислительных операций (в сравнении с параметрическим подходом);

·        Являются более сложными методами обработки исходной информации (выборки).

СПИСОК ЛИТЕРАТУРЫ

1.   Медведев А.В. Математические основы теории адаптивных систем. Красноярск, СибГАУ, 2007.

2.      Методы стохастической аппроксимации.