Исследование первых двух моментов состоятельной оценки спектральной плотности многомерного временного ряда
Исследование первых двух моментов состоятельной оценки
спектральной плотности многомерного временного ряда
Введение
Почти в каждой области встречаются
явления, которые интересно и важно изучать в их развитии и изменении во
времени. В повседневной жизни могут представлять интерес, например,
метеорологические условия, цены на тот или иной товар, те или иные
характеристики состояния здоровья индивидуума и т.п. Все они изменяются во
времени. Совокупность измерений какой-либо одной характеристики подобного рода
и представляет собой временной ряд.
Одной из главных задач спектрального
анализа временных рядов является построение и исследование оценок спектральных
плотностей стационарных случайных процессов, так как они дают важную информацию
о структуре процесса.
Методы анализа временных рядов
широко используются в различных областях науки и техники, их можно применять
при анализе больших объемов данных, получаемых в процессе вибрационных
испытаний или извлекаемых из сводок экономических данных.
Среди непараметрических методов
спектрального оценивания одним из наиболее распространенных является метод
Уэлча, в котором для построения оценки спектральной плотности производится
осреднение периодограмм, построенных по пересекающимся и непересекающимся интервалам
наблюдений. Цель перекрытия - увеличить число осредняемых отрезков при заданной
длине временного ряда и тем самым уменьшить дисперсию итоговой оценки.
В данной работе вычислены первые два
момента состоятельной оценки спектральной плотности, исследовано
асимптотическое поведение математического ожидания и дисперсии построенной
оценки. Проведен сравнительный анализ оценки спектральной плотности в
зависимости от окон просмотра данных и числа разбиения наблюдений для
временного ряда, представляющего собой последовательность наблюдений за
атмосферным давлением в городе Бресте с января 2006 г. по март 2010 г.
спектральный плотность временной
асимптотический
1. Понятия и
определения, используемые в работе
Временным рядом (r-мерным временным рядом) называется
совокупность функций вида
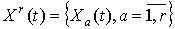 .
.
Действительным случайным
процессом 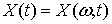 называется
семейство случайных величин, заданных на вероятностном пространстве
называется
семейство случайных величин, заданных на вероятностном пространстве 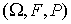 ,
где
,
где 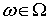 ,
,
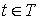 ,
,
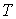 -
некоторое параметрическое множество.
-
некоторое параметрическое множество.
Если 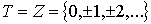 ,
или
,
или 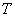 -
подмножество из
-
подмножество из 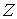 ,
то говорят, что
,
то говорят, что 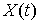 ,
,
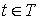 -
случайный процесс с дискретным временем.
-
случайный процесс с дискретным временем.
Если 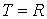 ,
или
,
или 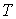 подмножество
из
подмножество
из 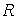 ,
то говорят, что
,
то говорят, что 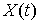 ,
,
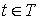 -
случайный процесс с непрерывным временем.
-
случайный процесс с непрерывным временем.
Математическим ожиданием
случайного процесса 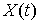 ,
,
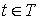 ,
называется функция вида
,
называется функция вида
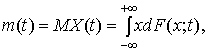
где 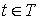 .
.
Дисперсией случайного
процесса 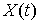 ,
,
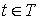 ,
называется функция вида
,
называется функция вида
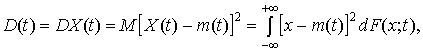
где 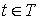 .
.
Спектральной плотностью
случайного процесса, 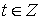 ,
называется функция вида
,
называется функция вида
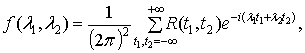
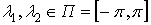 , при условии, что
, при условии, что
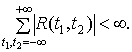
Спектральная плотность 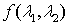 непрерывная,
периодическая функция с периодом, равным
непрерывная,
периодическая функция с периодом, равным 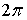 по каждому из
аргументов.
по каждому из
аргументов.
Ковариационной функцией
случайного процесса 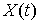 ,
,
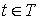 ,
называется функция вида
,
называется функция вида
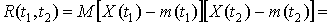
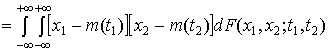
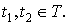
Смешанным моментом 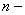 го
порядка,
го
порядка, 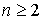 ,
случайного процесса
,
случайного процесса 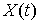 ,
,
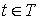 ,
называется функция вида
,
называется функция вида
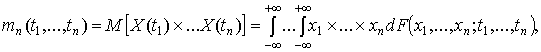
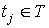 ,
, 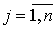 .
.
Заметим, что
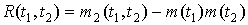 ,
,
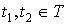 .
.
Пусть 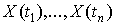 -
значения случайного процесса
-
значения случайного процесса 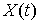 в точках
в точках 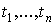 .
Функция
.
Функция
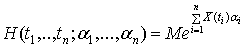
называется
характеристической функцией, где 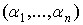 - ненулевой
действительный вектор,
- ненулевой
действительный вектор, 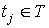 ,
,
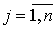 .
.
Смешанным
семиинвариантом (кумулянтом) 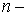 го порядка,
го порядка, 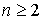 ,
случайного процесса
,
случайного процесса 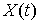 ,
,
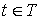 ,
называется функция вида
,
называется функция вида
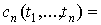
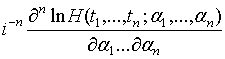 ,
,
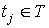 ,
, 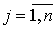 ,
которую также будем обозначать как
,
которую также будем обозначать как  .
.
Приведем соотношения,
связывающие смешанные моменты и смешанные семиинварианты для 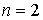 и
и
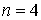 .
.
При 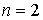
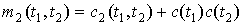 ,
,
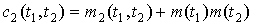 ,
,
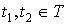 .
.
При 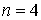
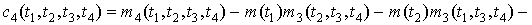
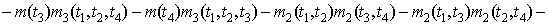
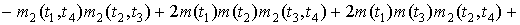
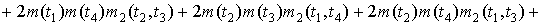
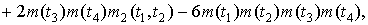
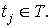
Семиинвариантной
спектральной плотностью 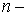 го
порядка,
го
порядка, 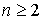 ,
случайного процесса
,
случайного процесса 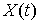 ,
,
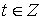 ,
называется функция вида
,
называется функция вида
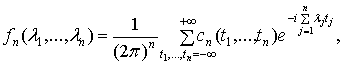
 , при условии, что
, при условии, что
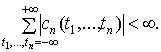
Случайный процесс 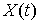 ,
,
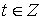 называется
стационарным в узком смысле (строго стационарным), если для любого натурального
называется
стационарным в узком смысле (строго стационарным), если для любого натурального
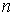 ,
любых
,
любых 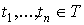 и
любого
и
любого 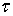 ,
такого что
,
такого что 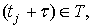
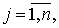 выполняется
соотношение
выполняется
соотношение
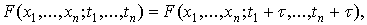
где 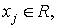
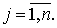
Случайный процесс 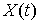 ,
,
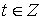 ,
называется стационарным в широком смысле, если
,
называется стационарным в широком смысле, если 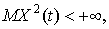
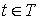 и
и
1)
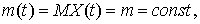
)
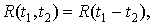
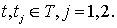
Спектральной плотностью
стационарного случайного процесса 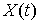 ,
, 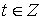 ,
называется функция вида
,
называется функция вида
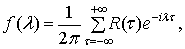
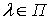 , при условии, что
, при условии, что 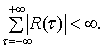
Семиинвариантной
спектральной плотностью 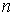 -го
порядка,
-го
порядка, 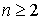 ,
стационарного СП
,
стационарного СП 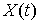 ,
,
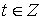 ,
называется функция вида
,
называется функция вида
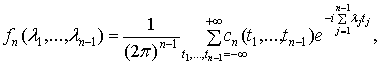
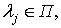
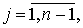 при
условии, что
при
условии, что
2. Построение оценки
спектральной плотности многомерного временного ряда и вычисление первых двух
моментов оценки
.1 Построение оценки
спектральной плотности
Рассмотрим
действительный стационарный случайный процесс 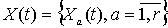 ,
, 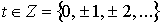 с
с
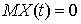 ,
(
,
(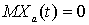 ,
,
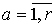 ),
),
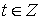 ,
неизвестной ковариационной матрицей
,
неизвестной ковариационной матрицей 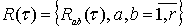 ,
, 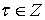 ,
где
,
где
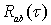 =
=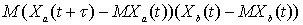 ,
,
и неизвестной матрицей
спектральных плотностей 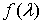
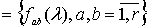 ,
, 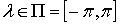 ,
где
,
где
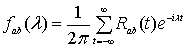 .
.
Пусть 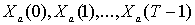 -
-
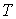 последовательных
наблюдений, полученных через равные промежутки времени, за составляющей
последовательных
наблюдений, полученных через равные промежутки времени, за составляющей 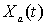 процесса
процесса
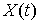 ,
,
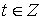 ,
,
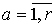 .
.
Предположим, что число
наблюдений 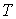 представимо
в виде
представимо
в виде 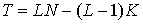 ,
где
,
где 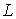 -
число пересекающихся интервалов, содержащих по
-
число пересекающихся интервалов, содержащих по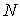 наблюдений, а
наблюдений, а 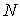 ,
, - целые числа,
- целые числа, 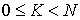 .
.
Заметим также, что если 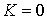 ,
то
,
то 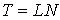 ,
где
,
где 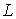 -
число непересекающихся интервалов, содержащих по
-
число непересекающихся интервалов, содержащих по 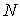 наблюдений.
наблюдений.
Модифицированное
конечное преобразование Фурье наблюдений 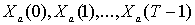 определяется выражением
определяется выражением
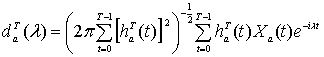 , (1.1)
, (1.1)
где 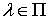 ,
,
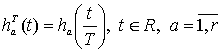 -
сглаживающие функции или окна просмотра данных, свойства которых рассмотрены в
работе [2].
-
сглаживающие функции или окна просмотра данных, свойства которых рассмотрены в
работе [2].
На каждом из интервалов
разбиения построим модифицированное конечное преобразование Фурье наблюдений,
имеющее вид
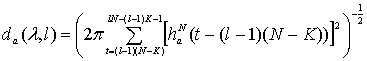
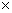
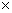
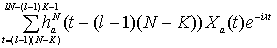 ,
(1.2)
,
(1.2)
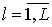 ,
, 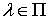 ,
где
,
где 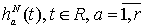 -
окна просмотра данных. Таким образом, сглаживание наблюдений на каждом из
отрезков разбиения производится одним и тем же окном просмотра данных.
-
окна просмотра данных. Таким образом, сглаживание наблюдений на каждом из
отрезков разбиения производится одним и тем же окном просмотра данных.
Сделаем в выражении
(1.2) замену переменной суммирования 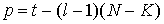 , получим
, получим
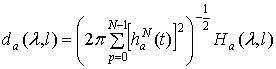 , (1.3)
, (1.3)
где
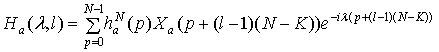 , (1.4)
, (1.4)
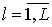 ,
, 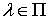 ,
,
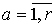 .
.
На каждом из интервалов
разбиения построим статистику 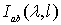 , задаваемую равенством
, задаваемую равенством
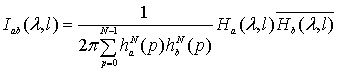 , (1.5)
, (1.5)
где 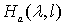 задается
выражением (2.4),
задается
выражением (2.4), 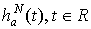 -
окна просмотра данных,
-
окна просмотра данных, 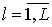 ,
,
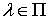 ,
,
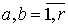 .
.
Статистику 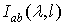 будем
называть модифицированной периодограммой на
будем
называть модифицированной периодограммой на  ом отрезке разбиения
наблюдений.
ом отрезке разбиения
наблюдений.
В качестве оценки
взаимной спектральной плотности процесса исследована статистика вида
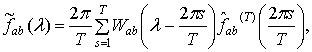 (1.6)
(1.6)
где 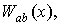
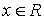 ,
,
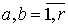 -
спектральное окно, а
-
спектральное окно, а 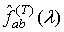 ,
,
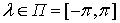 -
оценка взаимной спектральной плотности процесса
-
оценка взаимной спектральной плотности процесса 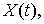
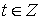 ,
построенная по методу Уэлча
,
построенная по методу Уэлча
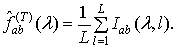 (1.7)
(1.7)
Относительно окон
просмотра данных и спектральных окон будем предполагать
Предположение 1.1
Пусть окна просмотра данных 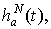
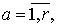
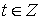 ограничены
единицей и имеют ограниченную постоянной вариацию.
ограничены
единицей и имеют ограниченную постоянной вариацию.
Предположение 1.2 Пусть
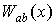 непрерывная,
периодическая функция с периодом
непрерывная,
периодическая функция с периодом 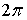 , имеет ограниченную
вариацию и является ядром.
, имеет ограниченную
вариацию и является ядром.
2.2 Вычисление
математического ожидания, дисперсии и ковариации построенной оценки
Докажем некоторые вспомогательные
результаты.
Лемма 1.1. Для любого целого р справедливо следующее соотношение
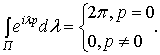 (1.8)
(1.8)
Доказательство. Если 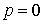 ,
то доказательство очевидно. Рассмотрим случай
,
то доказательство очевидно. Рассмотрим случай 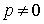 . Воспользуемся формулой
Эйлера
. Воспользуемся формулой
Эйлера
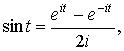
Тогда
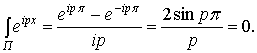
Лемма доказана.
Лемма 1.2. Если
функции 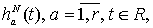 являются
окнами просмотра данных и удовлетворяют предположению 1.1, то
являются
окнами просмотра данных и удовлетворяют предположению 1.1, то
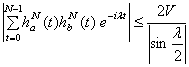 , (1.9)
, (1.9)
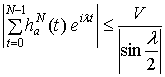 , (1.10)
, (1.10)
для любого 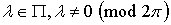 .
.
Доказательство. Докажем
соотношение (1.9). Используя преобразование Абеля, можно записать
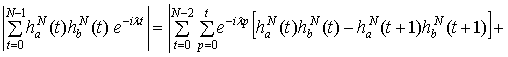
+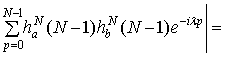
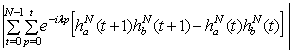 ,
,
в силу того, что 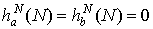 .
Используя тот факт, что для любого натурального
.
Используя тот факт, что для любого натурального 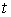 и любого
действительного
и любого
действительного 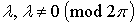 ,
,
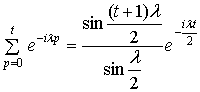 , (1.11)
, (1.11)
Получим следующее
выражение
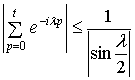 .
.
Тогда
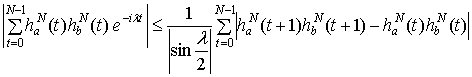 .
.
Учитывая ограниченность
функций 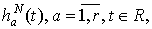 единицей,
будем иметь
единицей,
будем иметь
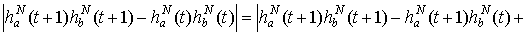
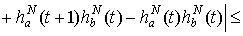
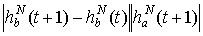 +
+
+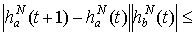
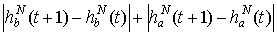 .
.
Следовательно,
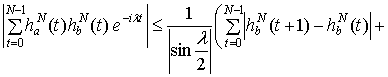
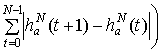 .
.
Тогда, используя
ограниченность вариации постоянной  , получим (1.9).
Соотношение (1.10) доказывается аналогично. Лемма доказана.
, получим (1.9).
Соотношение (1.10) доказывается аналогично. Лемма доказана.
Лемма 1.3. Если
функция 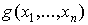 непрерывна
на
непрерывна
на 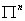 и
является периодической с периодом
и
является периодической с периодом 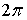 по каждому из
аргументов, то для любого
по каждому из
аргументов, то для любого 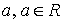 ,
справедливо соотношение
,
справедливо соотношение
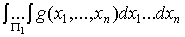 =
=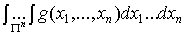 ,
(1.12)
,
(1.12)
где 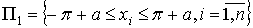 .
.
Доказательство.
Представим интеграл в правой части в виде суммы трех интегралов
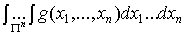 =
=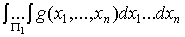 -
-
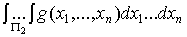 +
+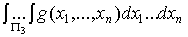 =
=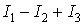 ,
,
где
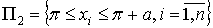 ,
,
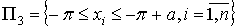 .
.
Покажем, что 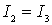 .
Сделаем в
.
Сделаем в  замену
переменных интегрирования
замену
переменных интегрирования 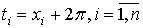 .
Учитывая, что
.
Учитывая, что 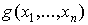 имеет
период
имеет
период 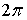 по
каждому из аргументов, имеем
по
каждому из аргументов, имеем
 =
=
где 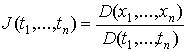 -
якобиан, равный единице. Лемма доказана.
-
якобиан, равный единице. Лемма доказана.
Теорема 1.1. Математическое
ожидание оценки взаимной спектральной плотности 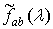 ,
,
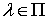 ,
,
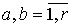 ,
задаваемой соотношением (1.6), имеет вид
,
задаваемой соотношением (1.6), имеет вид
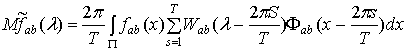 , (1.13)
, (1.13)
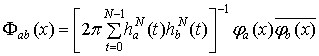 , (1.14)
, (1.14)
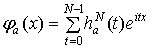 , (1.15)
, (1.15)
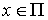 .
.
Доказательство.
Подставляя вместо 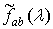 ее
выражение в явном виде, используя соотношения (1.4), (1.5) и учитывая свойства
математического ожидания, получим
ее
выражение в явном виде, используя соотношения (1.4), (1.5) и учитывая свойства
математического ожидания, получим
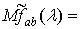
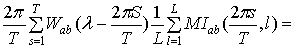
=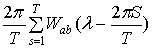
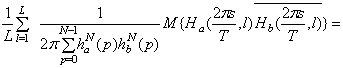
=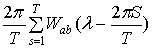
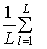
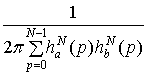
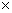
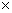

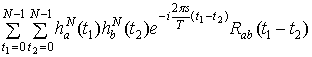 .
.
Учитывая, что
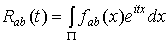 , (1.16)
, (1.16)
получим требуемый
результат. Теорема доказана.
Теорема 1.2. Ковариация
оценки взаимной спектральной плотности 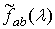 ,
, 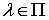 ,
,
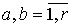 ,
задаваемой соотношением (1.6), имеет вид
,
задаваемой соотношением (1.6), имеет вид
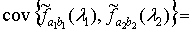
=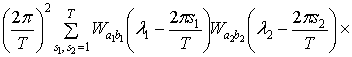
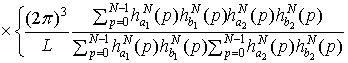
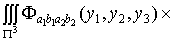
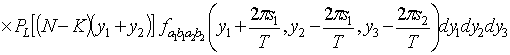 +
+
+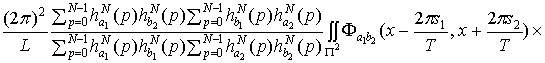
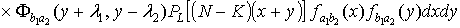 +
+
+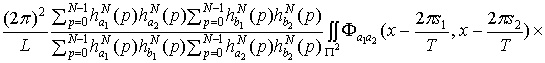
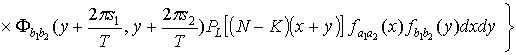 (1.17)
(1.17)
где
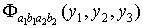 =
=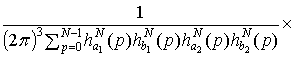
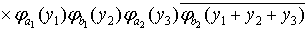 , (1.18)
, (1.18)
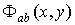 =
=
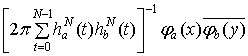 , (1.19)
, (1.19)
где 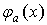 задается
выражением (1.15),
задается
выражением (1.15), 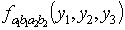 -
семиинвариантная спектральная плотность 4-го порядка, а
-
семиинвариантная спектральная плотность 4-го порядка, а
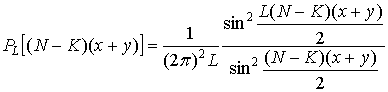 , (1.20)
, (1.20)
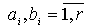
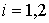 .
.
Доказательство.
Используя определение ковариации, свойства математического ожидания и
соотношение (1.7), получим
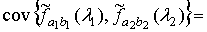
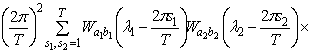
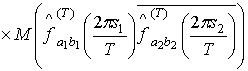
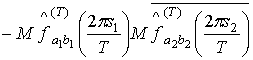 =
=
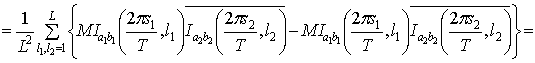
=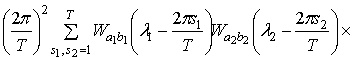
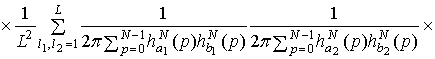
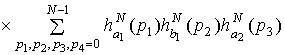
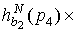
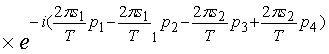
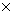
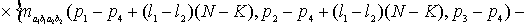
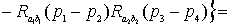
=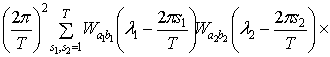
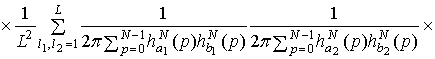
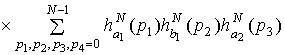
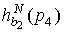
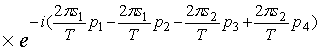
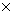
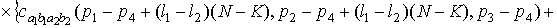
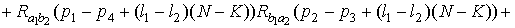
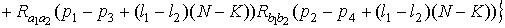 .
.
Таким образом, последнее
выражение можно представить в виде суммы трех слагаемых 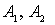 и
и
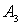 .
.
Рассмотрим 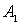 .
.
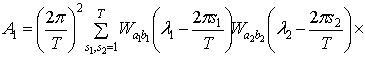
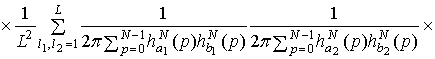
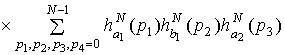
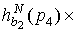
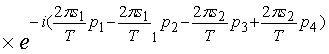
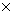
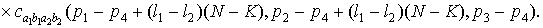
Учитывая соотношение,
связывающее смешанный семиинвариант 4-го порядка и семиинвариантную
спектральную плотность 4-го порядка, а также соотношение (1.15), получим
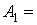
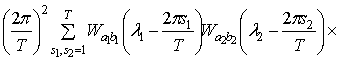
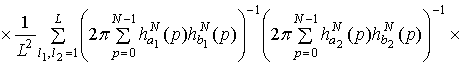
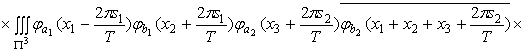
 .
.
Сделаем замену
переменных интегрирования 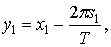
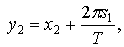
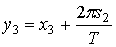 .
Учитывая (1.11), (1.18), (1.20), на основании леммы 1.3 получим
.
Учитывая (1.11), (1.18), (1.20), на основании леммы 1.3 получим
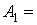
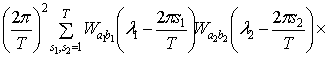
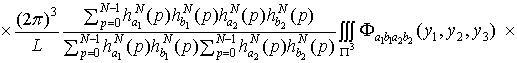
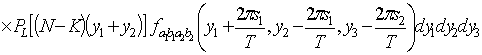 .
.
Рассмотрим 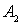 .
.
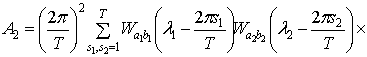
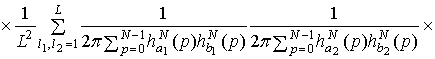
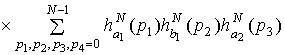
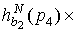
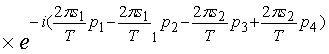
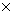
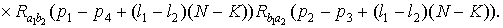
Учитывая соотношения
(1.15), (1.16), запишем
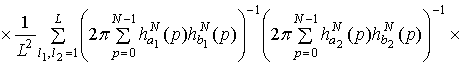
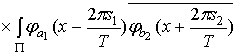
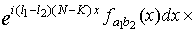
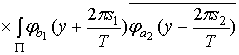
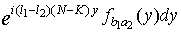 .
.
Используя соотношения
(1.19), (1.20), получим
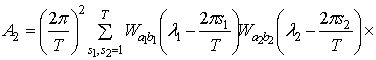
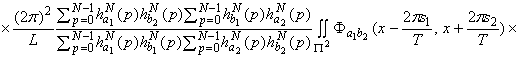
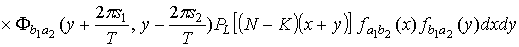 .
.
Рассмотрим 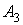 .
.
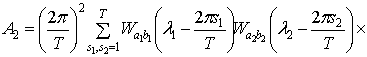
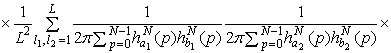
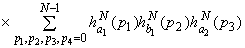
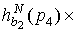
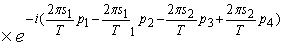
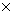
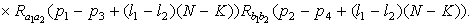
Учитывая соотношения
(1.15), (1.16), получим
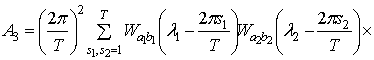
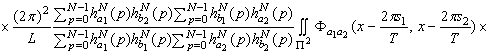
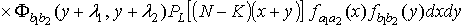 .
.
Теорема доказана.
Теорема 1.3. Дисперсия
оценки взаимной спектральной плотности 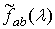 ,
, 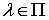 ,
,
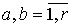 ,
задаваемой соотношением (1.6), имеет вид
,
задаваемой соотношением (1.6), имеет вид
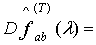
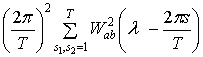
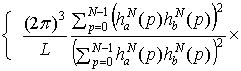
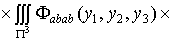
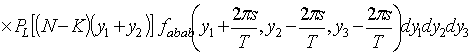 +
+
+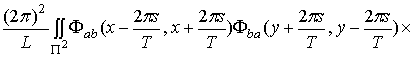
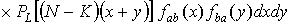 +
+
+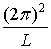
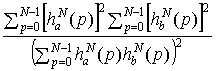
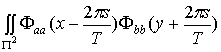
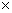
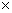
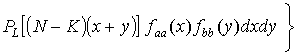 . (1.21)
. (1.21)
где 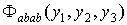 ,
,
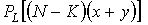 ,
,
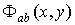 ,
, 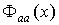 задаются
выражениями (1.18), (1.20), (1.19), (1.15) соответственно,
задаются
выражениями (1.18), (1.20), (1.19), (1.15) соответственно,  ,
,
 ,
a
,
a 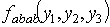 -
семиинвариантная спектральная плотность 4-го порядка.
-
семиинвариантная спектральная плотность 4-го порядка.
Доказательство следует
из теоремы 1.2, положив 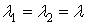 ,
,
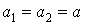 ,
,
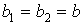 .
.
3. Исследование
асимптотического поведения моментов построенной оценки
3.1 Исследование
асимптотического поведения математического ожидания построенной оценки
Исследуем
асимптотическое поведение математического ожидания оценки взаимной спектральной
плотности 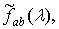
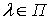 ,
,
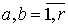 ,
заданной соотношением (1.6).
,
заданной соотношением (1.6).
Теорема 2.1.
Если взаимная спектральная плотность 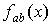 непрерывна в точке
непрерывна в точке 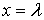 и
ограничена на
и
ограничена на 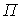 ,
окна просмотра данных
,
окна просмотра данных 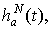
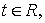
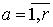 удовлетворяют
предположению 1.1, а спектральные окна предположению 1.2, то для оценки
удовлетворяют
предположению 1.1, а спектральные окна предположению 1.2, то для оценки 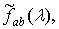
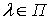 ,
заданной выражением (1.6), справедливо соотношение
,
заданной выражением (1.6), справедливо соотношение
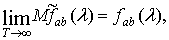 (2.1)
(2.1)
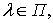
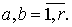
Доказательство.
Используя свойства математического ожидания и функции
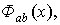
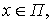
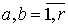 вида
вида
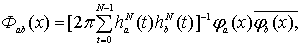 (2.2)
(2.2)
где 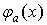 задано
выражением (1.15), запишем
задано
выражением (1.15), запишем
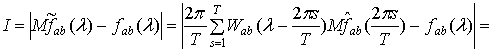
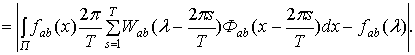
Откуда, учитывая лемму
Д5.1 работы [1], получим
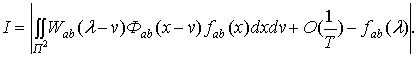
Сделаем замену переменных
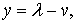
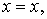 тогда,
тогда,
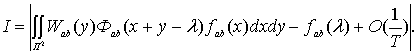
Сделаем замену
переменных 
 ,
получим
,
получим
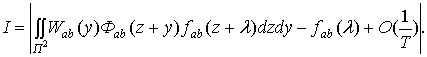
Учитывая, что свертка
двух ядер является ядром,
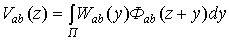 -
-
ядро. Тогда,
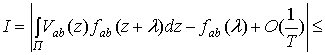
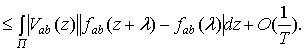
Так как взаимная
спектральная плотность 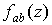 непрерывна
в точке
непрерывна
в точке 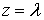 и
ограничена на
и
ограничена на 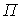 ,
а
,
а 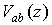 является
ядром, получим требуемый результат. Теорема доказана.
является
ядром, получим требуемый результат. Теорема доказана.
Таким образом,
статистика 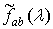 ,
заданная выражением (1.6), является асимптотически несмещенной оценкой взаимной
спектральной плотности
,
заданная выражением (1.6), является асимптотически несмещенной оценкой взаимной
спектральной плотности 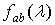 ,
,
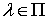 ,
,
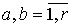 .
.
Лемма 2.1.
[1] Если на отрезке 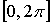 функция
функция 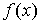 имеет
ограниченную вариацию, то
имеет
ограниченную вариацию, то
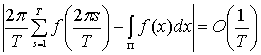 .
.
Как частный случай из
леммы 4.1 можем получить соотношение
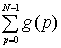 ~
~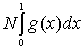 ,
(
,
(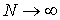 ) (2.3)
) (2.3)
где функция 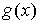 -
произвольная функция ограниченной вариации на отрезке
-
произвольная функция ограниченной вариации на отрезке 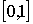 .
.
Лемма 2.2. Для
функции 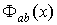 ,
заданной выражением (2.2), справедливы соотношения
,
заданной выражением (2.2), справедливы соотношения
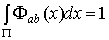 , (2.4)
, (2.4)
для любого 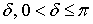 ,
,
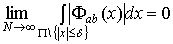 , (2.5)
, (2.5)
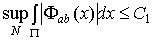 , (2.6)
, (2.6)
где
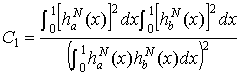 . (2.7)
. (2.7)
Доказательство.
Подставляя 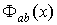 в
явном виде, получим
в
явном виде, получим
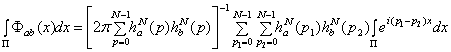 .
.
Используя соотношение
(1.8) получим (2.4).
Докажем соотношение
(2.5). Нетрудно видеть, что
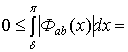
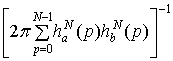
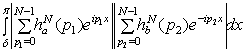 .
.
Используя (1.9), получим
Аналогично можно
показать, что
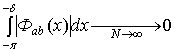 .
.
Откуда следует
справедливость соотношения (2.5).
Докажем (2.6). Используя
неравенство Гельдера, получим
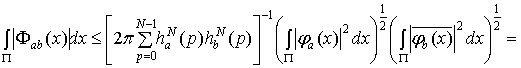
=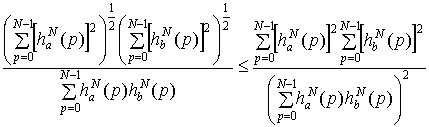 .
.
Откуда, используя (2.3),
получим требуемый результат. Лемма доказана.
Исследуем скорость
сходимости математического ожидания оценки 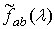 , предполагая, что
, предполагая, что 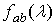 ,
,
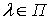 ,
удовлетворяет условию
,
удовлетворяет условию
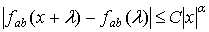 ,
, 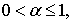 (2.8)
(2.8)
для любых 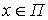 ,
,
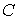 -
некоторая положительная константа,
-
некоторая положительная константа, 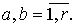
Лемма 2.3.
Для ядра 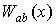 ,
,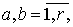
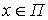 ,
при любом
,
при любом 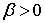
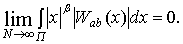 (2.9)
(2.9)
Доказательство. Запишем
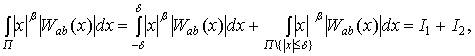
где 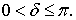
Так как функция 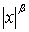 непрерывна
на
непрерывна
на 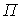 ,
следовательно, для любого
,
следовательно, для любого 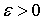 существует
существует
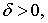 что
как только
что
как только 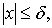 то
то
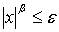 ,
поэтому
,
поэтому
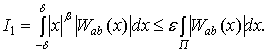
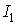 можно сделать сколь
угодно малым за счет выбора
можно сделать сколь
угодно малым за счет выбора 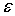 . Значит,
. Значит,
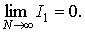
Рассмотрим 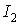 .
.
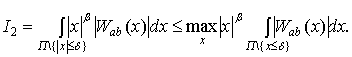
Аналогично можно
доказать, что
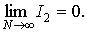
Лемма доказана.
Лемма 2.4.
Для ядра, заданного выражением (2.2), при любом 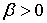 справедливо
справедливо
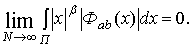 (2.10)
(2.10)
Доказательство. Запишем
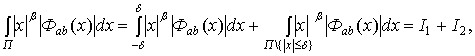
где 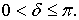
Так как функция 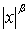 непрерывна
на
непрерывна
на 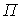 ,
следовательно, для любого
,
следовательно, для любого 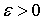 существует
существует
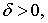 что
как только
что
как только 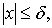 то
то
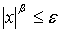 ,
поэтому
,
поэтому
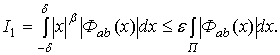
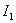 можно сделать сколь
угодно малым за счет выбора
можно сделать сколь
угодно малым за счет выбора 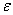 . Значит,
. Значит,
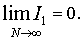
Рассмотрим 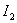 .
.
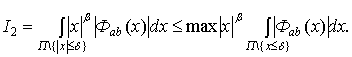
Аналогично можно
доказать, что
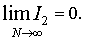
Лемма доказана.
Теорема 2.2. Если
взаимная спектральная плотность 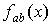 ,
, 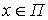 ,
,
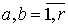 ,
удовлетворяет предположению 1.2, то для математического ожидания оценки
,
удовлетворяет предположению 1.2, то для математического ожидания оценки 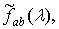
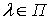 ,
,
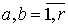 ,
задаваемой (1.6), имеет место равенство
,
задаваемой (1.6), имеет место равенство
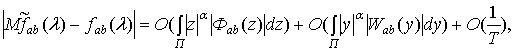 (2.11)
(2.11)
где 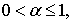 а
а
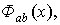
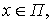
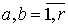 задается
выражением (2.2).
задается
выражением (2.2).
Доказательство. Учитывая,
что математическое ожидание оценки 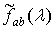 имеет вид
имеет вид
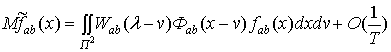 ,
,
сделав замену переменных
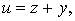
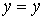 ,
получим
,
получим
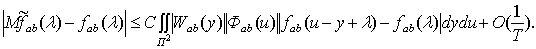
Откуда, учитывая
соотношение (2.8), можем записать
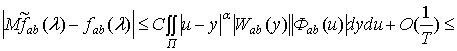
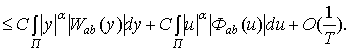
На основании лемм 2.3 и
2.4, получим требуемый результат. Теорема доказана.
3.2 Исследование
асимптотических свойств ковариации и дисперсии построенной оценки
Исследуем
асимптотическое поведение оценки взаимной спектральной плотности 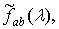
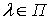 ,
,
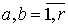 ,
заданной соотношением (1.6).
,
заданной соотношением (1.6).
Теорема
2.4. Если взаимная спектральная плотность 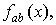
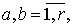 непрерывная
в точках
непрерывная
в точках 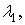
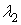 и
ограничена на
и
ограничена на 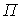 ,
семиинвариантная спектральная плотность 4-го порядка ограничена на
,
семиинвариантная спектральная плотность 4-го порядка ограничена на 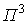 ,
окна просмотра данных
,
окна просмотра данных 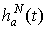 ,
,
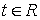 ,
,
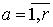 ,
удовлетворяют предположению 1.1, а спектральные окна удовлетворяют
предположению 1.2,
,
удовлетворяют предположению 1.1, а спектральные окна удовлетворяют
предположению 1.2,
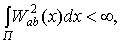 (2.12)
(2.12)
то для статистики,
задаваемой соотношением (1.6), справедливо соотношение
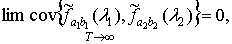 (2.13)
(2.13)
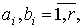
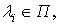
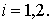
Доказательство.
Используя определение ковариационной функции и свойства математического
ожидания, ковариация статистики 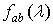 ,
, 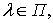
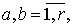 может
быть представлена в виде
может
быть представлена в виде
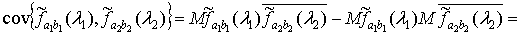
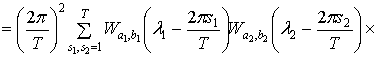
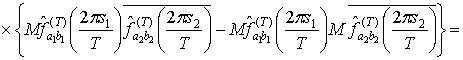
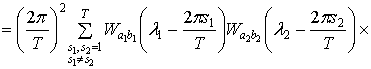
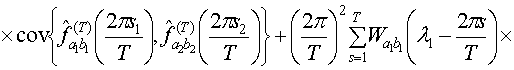
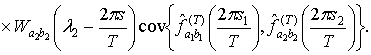
Учитывая, что в
соответствии с теоремой 3 работы [2]
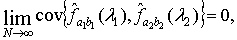
и так как спектральные
окна 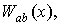
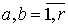 удовлетворяют
предположению 1.2, справедливо соотношение (2.13).
удовлетворяют
предположению 1.2, справедливо соотношение (2.13).
Теорема доказана.
Теорема 2.5. При
сохранении условий теоремы 2.4 для статистики, задаваемой соотношением (1.6),
справедливо соотношение
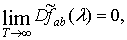 (2.14)
(2.14)
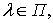
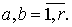
Из соотношений (2.14),
(2.1) следует, что
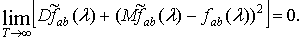 (2.15)
(2.15)
Таким образом, статистика
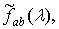
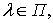
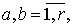 в
условиях теоремы 2.4 является состоятельной в среднеквадратическом смысле
оценкой взаимной спектральной плотности.
в
условиях теоремы 2.4 является состоятельной в среднеквадратическом смысле
оценкой взаимной спектральной плотности.
4. Сравнительный анализ
оценки спектральной плотности в зависимости от окон просмотра данных и числа
интервалов разбиения наблюдений
Проведем сравнительный анализ оценки
(1.7) для различных окон просмотра данных и числа интервалов разбиения
наблюдений. Рассмотрим следующие окна просмотра данных:
1. 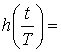 1
- окно Дирихле;
1
- окно Дирихле;
. 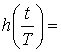 1-
1-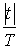 - окно Фейера;
- окно Фейера;
. 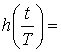
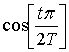 ;
;
. 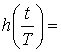
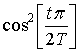 - окно Хэннинга;
- окно Хэннинга;
. 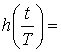
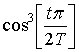 - окно Хэмминга;
- окно Хэмминга;
. 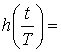
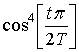 - окно Хэмминга;
- окно Хэмминга;
. 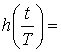
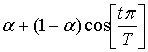 , где
, где 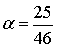 -
окно Хэмминга;
-
окно Хэмминга;
. 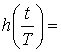 1-
1-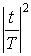 - окно Рисса;
- окно Рисса;
. 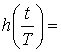
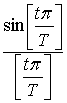 .
.
Для исследования оценки (1.7) был
исследован ряд, состоящий из 200 наблюдений показателей атмосферного давления в
городе Бресте с января 2006 года по март 2010 года.
При разбиении исходной
последовательности наблюдений на L непересекающихся интервалов по N значений в каждом были рассмотрены
случаи:
1. L=50, N=4;
2. L=20, N=10;
3. L=4, N=50;
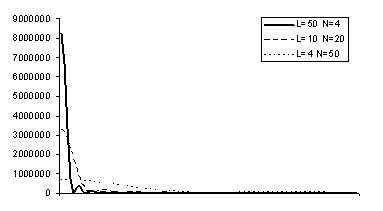
Графики оценки спектральной
плотности
Построенные по 200 наблюдениям за
показателями атмосферного давления в городе Бресте с января 2006 г. по март
2010 г. для числа разбиений L=50, L=10, L=4 для окна Дирихле.
Графики оценки спектральной
плотности
Построенные по 200 наблюдениям за
показателями атмосферного давления в городе Бресте с января 2006 г. по март
2010 г. для числа разбиений L=50, L=10, L=4 для окна Фейера.
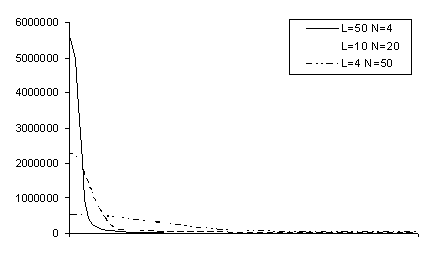
Графики оценки спектральной
плотности
Построенные по 200 наблюдениям за
показателями атмосферного давления в городе Бресте с января 2006 г. по март
2010 г. для числа разбиений L=50, L=10, L=4 для окна Хэннинга.
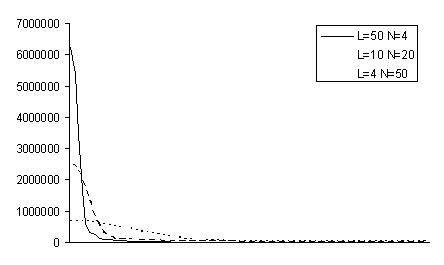
Проведем сравнительный анализ оценки
(1.7) в зависимости от выбора окна просмотра данных:
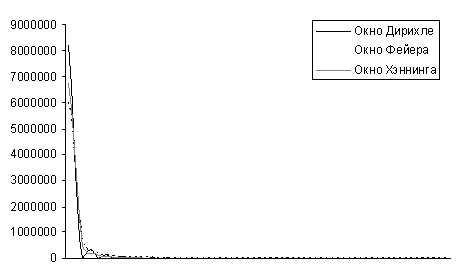
Графики оценки спектральной
плотности
Построенные по 200 наблюдениям за
показателями атмосферного давления в городе Бресте с января 2006 г. по март
2010 г. для числа разбиений L=50 для окон Дирихле, Фейера и Хэннинга.
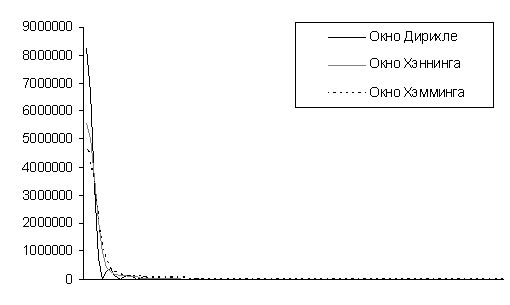
Графики оценки спектральной
плотности
Построенные по 200 наблюдениям за
показателями атмосферного давления в городе Бресте с января 2006 г. по март
2010 г. для числа разбиений L=50 для окон Дирихле, Хэннинга и Хэмминга.

Графики оценки спектральной
плотности
Построенные по 200 наблюдениям за
показателями атмосферного давления в городе Бресте с января 2006 г. по март
2010 г. для числа разбиений L=50 для окон Дирихле, Хеннинга и Рисса.
Дисперсия оценки взаимной
спектральной плотности минимальна при использовании окон Дирихле и Рисса,
следовательно, наиболее эффективным является использование этих окон просмотра
данных.
Заключение
Основные результаты исследования
можно выразить следующими положениями:
– вычислены математическое
ожидание, дисперсия и ковариация оценки взаимной спектральной плотности,
построенной путем осреднения модифицированных периодограмм по пересекающимся
интервалам наблюдений с использованием спектральных окон для многомерных
временных рядов и произвольных окон просмотра данных;
– исследовано
асимптотическое поведение первых двух моментов построенной оценки.
– исследована
скорость сходимости оценки спектральной плотности.
Результаты работы имеют
теоретическое и практическое значение. Могут быть использованы при обработке
данных в больших объемах, а также в режиме реального времени. Результаты могут
быть использованы в учебном процессе.
Список источников
1 Бриллинджер,
Д. Временные ряды. Обработка данных и теория / Д. Бриллинджер. - М.: Мир,
1980.-536 с.
2 Mirskaya, Elena I. Investigation of the Moments of Averaged
Estimates of the Second Order Spectra / Elena I. Mirskaya, Jana V. Vasilenko,
Sergei A. Marzan // Computer Algebra Systems in Teaching and Research, Siedlce
/ University of Podlasie - Siedlce, 2009. - P. 82-85.
3 Труш, Н.Н. Случайные процессы. Преобразование Фурье наблюдений /
Н.Н. Труш, Е.И. Мирская. - Мн.: БГУ, 2000. - 60 с.
Труш, Н.Н. Асимптотические методы статистического анализа
временных рядов / Н.Н. Труш. - Мн.: БГУ, 1999.-218 c.
Колмогоров, А.Н. Элементы теории
функций и функционального анализа / А.Н. Колмогоров, С.В. Фомин. - М.: Наука,
1989.-624 с.
Марчук, А.Ю. Исследование
математического ожидания состоятельной оценки взаимной спектральной плотности /
А.Ю. Марчук // Материалы VI Республиканской научной конференции молодых ученых и студентов «Современные проблемы математики и вычислительной техники», Брест,
26-28 ноября 2009 г. / Брестский гос.
технический ун-т; под общ. ред. Т.В.
Строкач. - Брест, 2009. - Ч. 2. - С. 156-158.
Марчук, А.Ю. Построение оценки спектральной плотности для чисел
солнечной активности по Вольфу / А.Ю. Марчук, Е.И. Мирская // Сборник
материалов межфакультетской научно-практической конференции, посвященной
260-летию со дня рождения П.С. Лапласа, Брест, 27 марта 2009 г. / Брестский
гос. университет им. А.С. Пушкина; под общ. ред. С.А. Марзана. - Брест, 2009. -
Ч. 2. - С. 38.
8 Мирская, Е.И. Исследование
скорости сходимости первого момента сглаженной оценки взаимной спектральной
плотности / Е.И. Мирская, А.Ю. Марчук // Материалы VI международной
научно-практической конференции «Бъдещи изследвания - 2010», София, 17-25
февраля 2010 г. - София, 2010. - Ч. 15. - С. 30-33.
Марчук, А.Ю. Исследование первого момента сглаженной оценки
взаимной спектральной плотности / А.Ю. Марчук, Е.И. Мирская // Материалы IV международной
молодежной научно-практической конференции «Научный потенциал молодежи -
будущему Беларуси», Пинск, 9 апреля 2010 г. / Полесский государственный
университет; под общ. ред. К.К. Шебеко - Пинск, 2010. - Ч. 4. - С. 183-184.