Определение плотности материала пластинки

Определение плотности материала пластинки

Определение плотности материала пластинки

Введение

Цель работы: определить плотность материала пластинки, научиться рассчитывать погрешности прямых и косвенных измерений.

Приборы и принадлежности: металлическая пластинка, штангенциркуль, микрометр.

При выполнении лабораторных работ физического практикума необходимо измерять различные величины. Под измерением понимается сравнение измеряемой величины с другой, однородной ей величиной, принятой за единицу измерения. Истинное значение физической величины обычно абсолютно точно определить нельзя из-за погрешности измерений. Поэтому расчёт погрешности является одним из наиболее важных этапов обработки экспериментальных результатов. Измерения подразделяются на прямые и косвенные. При прямых измерениях определяемая величина непосредственно сравнивается с единицей измерения при помощи измерительного прибора, проградуированного в соответствующих единицах. К этим измерениям относятся: измерение длины линейкой, штангенциркулем или микрометром; измерение массы тела на весах; промежутков времени секундомером; температуры термометром; силы электрического тока амперметром и т. д.

При косвенных измерениях искомая величина y вычисляется из результатов прямых измерений других величин, которые связаны с измеряемой величиной определённой функциональной зависимостью: y = y(x₁, x₂, x₃, …, x_k), где x₁, x₂, x₃, …, x_k - находятся по результатам прямых измерений. Пример: плотность вещества вычисляется при помощи определяемых прямыми измерениями величин: массы и объёма тела 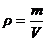; мощность тока по измеряемым непосредственно величинам силе тока и напряжению N = IU.

1. Виды погрешностей

Погрешности подразделяются на систематические, случайные, погрешности округления и промахи.

Систематической - называют такую погрешность, которая остаётся постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Систематические погрешности связаны с приборной погрешностью и со степенью точности аналитических выражений. Например, недостаточная точность градуировки приборов, недостаточная чувствительность или разрешающая способность дают вклад в систематическую погрешность. Вклад в систематическую погрешность может дать воздействие неучитываемых внешних факторов. Так, при определении на рычажных весах массы тела, как правило, не учитывается выталкивающая сила воздуха, действующая на взвешиваемое тело и разновесы, т. е. предполагается, что m_тела= m_грузов. В действительности объём тела и разновесов различны, поэтому на них действуют различные выталкивающие силы и равновесие достигается при m_тела ≠ m_грузов. Например, если, не учитывая действия выталкивающей силы, измерить массу водорода или гелия в воздушном шаре, то она получится отрицательной. Погрешность, вносимая при каждом отдельном измерении называется приборной погрешностью и связана с точностью прибора. Точность прибора задаётся классом точности прибора, либо указывается в паспорте прилагаемом к прибору. Как правило, приборная погрешность равна половине точности прибора.

Если на приборе указан класс точности Е (0,1; 0,2; 0,54 1,0; 1,5; 2,5; 4), то приборная погрешность может быть рассчитана по следующей формуле:

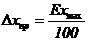
где x_max- наибольшее значение, которое может быть измерено по шкале прибора.

В случае, когда на приборе не указан класс точности, приборная погрешность принимается равной половине цены наименьшего деления.

Случайными называются погрешности, вызванные различными причинами, заранее неизвестными и действующими при каждом отдельном измерении различным образом. Причинами случайных погрешностей могут являться: несовершенство наших органов чувств, влияние внешних условий (непостоянство температуры, давления и т. д.), колебания здания, в котором проводятся измерения, колебания воздуха и т. д. Случайные погрешности могут изменять результаты измерений в обе стороны - то увеличивая, то уменьшая их. Эти погрешности полностью устранить нельзя.

При косвенных измерениях в погрешность определяемой величины даёт вклад погрешность округления, устранить которую в некоторых случаях принципиально невозможно. Например, число π является иррациональным, т. е. имеет бесконечно большое число значащих цифр, а именно: π = 3,14159265… . При расчётах необходимо ограничить число значащих цифр. Полагая π = 3,14 или π = 3,142 допускается погрешность округления, соответствующая Δπ = 0,0016 или Δπ = 0,000413. Влияние погрешности округления на погрешность измеряемой величины можно полностью устранить, если при расчётах брать число значащих цифр в округляемой величине на две больше, чем число цифр в выражении измеряемой величины. Например, если измеренный диаметр тела 4,2 см, то для нахождения площади надо брать число π = 3,142.

Промахи - это ошибочные измерения, возникающие в результате небрежности отсчёта по прибору, неправильного включения прибора или неразборчивой записи результатов измерений. Если промах допущен (результат измерения какой-либо величины при этом резко отличается от результатов других измерений этой же величины), то при определении измеряемой величины это ошибочное измерение надо отбросить и проделать повторное измерение.

2. Расчёт погрешности при прямых измерениях

Проведя серию из прямых измерений некоторой величины x, мы получаем набор значений x₁, x₂, x₃, …, x_k. Наиболее точно истинное значение величины x характеризуется средним арифметическим 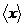 результата k измерений:

.

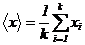Истинная погрешность измерения при этом равна:

Δx_ист.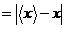

Поскольку истинное значение величины x измерить невозможно, то и определить Δx_ист тоже нельзя. На практике используют различные приближённые методы определения погрешности.

Предположим сначала, что погрешность измерения определяется полностью случайной погрешностью Δx_сл. Для оценки случайной погрешности делаются следующие предположения:

. случайные погрешности отдельных измерений могут принимать непрерывный ряд значений;

. погрешности равной величины, но противоположного знака встречаются одинаково часто;

. случайная погрешность обращается в нуль при бесконечно большом числе измерений.

Поскольку на практике число измерений ограничено, то случайная погрешность не равна нулю. Наиболее точно истинное значение погрешности измерений характеризует абсолютная погрешность Δx, которая учитывает случайную и приборную погрешности и может быть рассчитана по формуле:

.

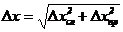Мерой точности результатов измерений является относительная погрешность измерения, определяемая по формуле:

.

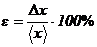Приведём алгоритм обработки результатов при прямых измерениях.

. Измерить n раз некоторую величину x, получив значения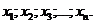

. Вычислить среднее значение результатов измерений:

.

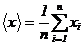. Определить отклонение от среднего каждого результата измерений:

.

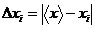. Рассчитать среднеквадратичную погрешность по формуле:

.

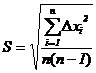. Выбрать значение надёжности измерений α.

Надёжностью результата называется вероятность того, что истинное значение измеряемой величины x_ист попадает в интервал 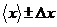, где Δx - абсолютная погрешность, которая будет вычислена после обработки результатов измерений.

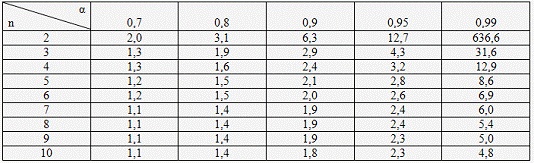
. По таблице 1 найти значение коэффициента Стьюдента t_α,N.

Таблица 1. Значения коэффициентов Стьюдента.

7. Оценить приборную погрешность :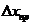

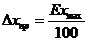, если известен класс точности E,

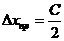, если класс точности прибора не указан (C - цена деления прибора).

. Вычислить абсолютную погрешность:

,

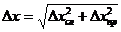где:.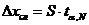

. Найти относительную погрешность измерения:

.

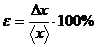. Записать результат измерений в виде:

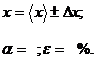
Прежде чем записать результат измерений необходимо произвести округление абсолютной и относительной погрешностей и среднего значения. При округлении погрешностей необходимо знать, что погрешности всегда округляются в сторону большего и никогда не включают в себя больше двух значащих цифр. Значащими цифрами называются все цифры кроме 0, а также 0 в двух случаях:

а) когда он стоит между значащими цифрами;

б) когда он стоит в конце числа и известно, что единица соответствующего разряда в данном числе не имеется.

Если первая значащая цифра в погрешности больше 4, то все остальные цифры округляются. Так, например, если при вычислении погрешностей получилось, что Δx = 718, ε = 5,34%, то после округления в том и другом случае должна остаться только первая значащая цифра, причём округление ведётся в сторону большего. Тогда получаем после округления: Δx = 800, ε = 6%.

Если первая значащая цифра в погрешности меньше 5, то округление ведётся до двух первых значащих цифр. Например, если при вычислении погрешностей получилось, что Δx = 353,4, ε = 14,25%, то после округления должны остаться только две первые значащие цифры с учётом округления в большую сторону: Δx = 360, ε = 15%.

После округления абсолютной погрешности необходимо округлить и среднее значение измеряемой величины. Округление ведётся до сомнительной цифры. Сомнительной в среднем значении называется цифра в том разряде, в котором начинается и абсолютная погрешность. Если погрешность содержит в себе десятки, то число десятков в среднем значении будет сомнительным. Например, в серии измерений получаем ‹x› = 5873 м, Δx = 32 м. Сомнительным является разряд десятков, поэтому после округления до сомнительного разряда получаем: ‹x› = 5870 м, Δx = 32 м и окончательный результат можно записать в виде:

x = (5870 ± 32) м.

3. Расчёт погрешностей при косвенных измерениях

При косвенных измерениях для вычисления погрешности воспользуемся методом дифференциального исчисления.

Пусть искомая величина y = f(x), где x - непосредственно измеряемая величина. Пусть при измерении величины x допущена погрешность Δx, поэтому искомая величина y вычисляется тоже не точно, а с некоторой погрешностью Δy. Для того, чтобы рассчитать Δy, запишем тождество Δy = Δy, затем умножим и разделим его правую часть на Δx_i :

.

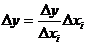Для малых значений Δx_i справедливо соотношение:

;

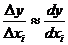следовательно:

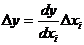.  (1)

Таким образом, абсолютная погрешность функции равна абсолютной погрешности аргумента, умноженной на производную этой функции по этому аргументу.

Если искомая величина y является функцией нескольких переменных y = f(x₁, x₂, …, x_k), где x₁, x₂, …, x_k - непосредственно измеряемые величины и их погрешности равны Δx₁, Δx₂, …, Δx_k, то при вычислении абсолютной погрешности Δy нужно учесть погрешности, вносимые всеми этими величинами x_i. Погрешность, обусловленная неточностью измерения величины x₁ будет равна, согласно формуле (1):

обусловленная неточностью измерения x₂ :

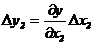 и т. д.

В выражении 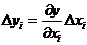 берётся частная производная, потомучто в данном случае учитывается зависимость величины y только от конкретной величины x_i , все остальные аргументы считаются постоянными величинами.

Рассчитав Δy_i, абсолютную погрешность измерения можно вычислить по формуле:

.

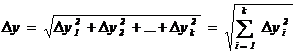Подставив в это выражение значения Δy_i, получаем:

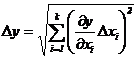. (2)

Относительная погрешность косвенных измерений вычисляется по формуле:

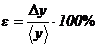
где ‹y› - значение функции, полученное после подстановки в неё средних аргументов ‹x₁›,‹x₂›, …, ‹x_k›.

Подставляя в (3) выражение (2), получаем:

.

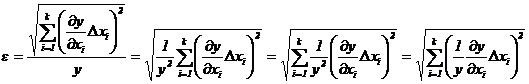Учитывая, что 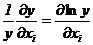, получаем:

.

Запишем алгоритм вычисления погрешностей при косвенных измерениях.

. Обработать результаты прямых измерений каждой из величин согласно предыдущему параграфу.

. Вычислить величину ‹y›, подставив в расчётную формулу среднее значение непосредственно измеряемой величины.

. Вывести формулы для расчёта Δy или ε согласно уравнениям (2), (4).

. Вычислить абсолютную и относительную погрешности результата.

. Провести округление результатов расчёта.

. Записать результат измерений в виде:

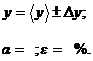
При проведении округления пользуются теми же правилами, что и при обработке результатов прямых измерений. Следует учитывать, что если в расчётную формулу входят величины, которые в процессе эксперимента не измеряются и для них не указана величина погрешности, то обычно считается, что эта погрешность составляет ± 0,5 единицы наименьшего разряда, представленного в числе. Например, дана масса m = 230,6 г, погрешность следует принять равной ± 0,05 г. Если в расчётную формулу входят числовые постоянные (π, g и т. д.), то за погрешности этих величин принимаются погрешности округления.

4. Вычисление погрешностей при косвенных измерениях, когда контролируемые условия не воспроизводимы

При невоспроизводимых измерениях невозможно найти средние значения измеряемых величин ‹x_i›, поэтому методика расчёта погрешностей, изложенная в предыдущем параграфе, неприемлема. В этом случае при обработке результатов следует придерживаться следующего порядка:

. Измерить величины x_ki n раз, где k - номер измеряемой величины, приписываемый параметрам, от которых зависит y = f(x₁, x₂, ..., x_k), i - номер измерения величины x_k.

. Рассчитать n раз значения y, получив величины y₁, y₂, …, y_n, где y_i =yf(x_1i, x_2i, ..., x_ki).

. Найти среднее значение ‹y› по формуле:

.

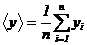. Вычислить отклонение от среднего:

.

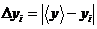. Определить среднеквадратичную погрешность измерений y:

.

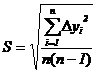. Задать значение надёжности α и по таблице 1 найти коэффициент Стьюдента t_α,N.

. Рассчитать случайную погрешность:

.

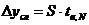. Вычислить средние значения ‹x_k›:

.

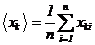. Определить приборные погрешности .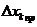

. Вывести формулу для нахождения приборной погрешности Δy_пр:

.

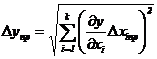. Рассчитать Δy_пр, подставив в полученное выражение средние значения ‹x_k› и величины приборных погрешностей .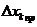

. Вычислить погрешность измерений:

.

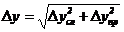. Найти относительную погрешность:

.

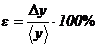. Записать полученный результат в виде:

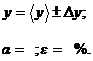
Методика работы.

Плотность материала пластинки может быть определена по известной массе и объёму пластинки, если использовать формулу:

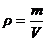
где m - масса пластинки;

V - объём пластинки.

Масса пластинки выгравирована на её грани, а объём определяется по формуле:

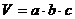
где a, b, c - длина, ширина и толщина пластинки соответственно.

Таким образом, для определения плотности материала пластинки необходимо сначала измерить a, b, c затем рассчитать объём по формуле (6) и плотность материала по формуле (5).

Порядок выполнения работы.

. Измерить не менее трёх раз длину, толщину, ширину пластинки и занести полученные результаты в таблицу 2.

. Рассчитать погрешности измеренных величин, используя методику, описанную в § 2.

. Записать в таблицу 3 массу пластинки m и погрешность измерения массы Δm.

. Рассчитать средний объём пластинки, подставив в формулу (6) средние значения ‹a›,‹b›,‹c›.

. Определить по формуле (5) плотность материала пластинки.

. Вычислить погрешность измерения плотности по методу, описанному в § 3.

Все расчёты необходимо записывать в отчёте по лабораторной работе. Окончательно результаты вычислений заносятся в таблицы 2 и 3.

Таблица 2

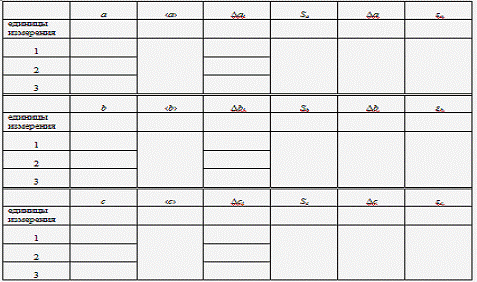
Таблица 3

Контрольные вопросы

1. Классификация измерений.

. Виды погрешностей.

3. Определение среднеквадратичной погрешности и коэффициента Стьюдента.

. Определение приборной погрешности.

. Порядок обработки результатов при прямых измерениях.

. Порядок вычисления погрешностей при косвенных измерениях.

. Вычисление погрешностей в случае невоспроизводимых условий.

. Правила округления результатов вычислений.

Литература

плотность материал пластинка

1. Касандрова О. Н. Лебедев В. В. Обработка результатов наблюдений, - 1970.

. Зайдель А. Н. Элементарные оценки ошибок измерений, - 1967.

. Каленков С. Г. Соломахо Г. И. Практикум по физике, - 1990.