Приближённое вычисление тройного интеграла
Министерство образования и науки РФ
ФГБОУ ВПО «Воронежский
государственный технический университет»
Факультет информационных технологий и
компьютерной безопасности
Кафедра систем автоматизированного
проектирования и информационных систем
КУРСОВАЯ РАБОТА
по дисциплине: «Математика»
Тема: «Приближённое вычисление
тройного интеграла»
Разраб. Cтудент
ИС-121 И.А. Мешулин
Руководитель проф. М.Л. Лапшина
2013
Содержание
Введение
. Численное интегрирование
.1 Постановка задачи
.2 Численное интегрирование по простейшим формулам
.3 Вычисление определенного интеграла методом Симпсона
.4 Интегрирование квадратурными формулами Ньютона - Котеса и
методом "три восьмых"
.5 Интегрирование с автоматическим выбором количества узлов
методом Рунге
.6 Интегрирование с автоматическим выбором количества узлов
.7 Вычисление интеграла по Ромбергу
.8 Формулы Гаусса
. Программная реализация задачи
.1 Постановка задачи на разработку программы
.2 Выбор средств реализации
.3 Системные требования
.4 Структура программы
.5 Диалог взаимодействия
.6 Контрольный пример
Заключение
Список использованной литературы
Приложение. Листинг программы
Введение
Цель работы состоит в изучении и анализе методов численного
интегрирования функций; реализация этих методов в виде машинных программ на
языке высокого уровня и практическое решение задач численного интегрирования на
ЭВМ.
Курс численных методов является важной частью математической подготовки
студентов. Его значение в настоящее время определяется не только
увеличивающимися возможностями применения методов вычислительной математики в
вузовском учебном процессе, но и проникновением численных алгоритмов
приближенного решения задач в практические сферы.
Интегрирование прослеживается еще в древнем Египте примерно в 1800 г до
н.э. Математический папирус демонстрирует знание формулы объема усеченной
пирамиды. Первым известным методом для расчета интегралов является метод
исчерпывания Евдокса (примерно 370 г до н.э.), который пытался найти площади и
объемы, разрывая их на бесконечное множество частей, для которых площадь или
объем уже известны. Следующий крупный шаг в исчислении интегралов был сделан в
Ираке в 11 веке математиком Ибн ал-Хайсамом. В своей работе «Об измерении
параболического тела» он приходит к уравнению четвертой степени. Решая эту
проблему, он проводит вычисления, равносильные вычислению определенного
интеграла. Следующий значительный прогресс в исчислении интегралов появится
лишь в 16 веке. В работах Кавальери с его методом неделимых, а также в работах
Ферма, были заложены основы современного интегрального исчисления. Дальнейшие
шаги были сделаны в начале 17 века Барроу и Торричелли, которые представили
первые намеки на связь между интегрированием и дифференцированием.
Область исследования - математический анализ.
Объект исследования - теория кратных интегралов.
Предмет исследования - тройные интегралы
Проблема исследования - применение кратных интегралов
Методы исследования - изучение литературы, сравнение, обобщение,
аналогия, анализ и классификация информации
Задачи исследования:
§ раскрыть понятие «тройной интеграл».
§ рассмотреть некоторые приложения кратных интегралов
§ показать примеры вычисления кратных интегралов
§ рассмотреть применение тройных интегралов для вычисления объема, массы,
площади, моментов инерции, статистических моментов и координат центра масс тела
на конкретных примерах.
1.
Численное интегрирование
1.1 Кратные интегралы: определение, свойства.
численное тройной интеграл формула
Пусть в области D
задана непрерывная скалярная функция n переменных:
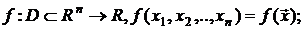
n=1 | n=2 |
n=3
)
Введем произвольное разбиение области D на «ячейки»σi
без пропусков и наложений 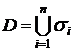 ; выберем произвольно точку AiÎσi; обозначим: Δσi
«меру ячейки» (Δxi - длина отрезка;
ΔSi
- площадь σi ; ΔVi
- объем σi);
d=max{ di } - «диаметр разбиения», di -
«диаметр ячейки» - наибольший линейный размер ячейки; m,M - наименьшее и
наибольшее значения функции в области D
; выберем произвольно точку AiÎσi; обозначим: Δσi
«меру ячейки» (Δxi - длина отрезка;
ΔSi
- площадь σi ; ΔVi
- объем σi);
d=max{ di } - «диаметр разбиения», di -
«диаметр ячейки» - наибольший линейный размер ячейки; m,M - наименьшее и
наибольшее значения функции в области D 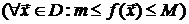 .
.
)
Назовем множество Pn={σi; Ai; i=1,..,n} разбиением с отмеченными точками и составим сумму Sn(Pn,f)=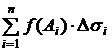 .
.
Определение
1.
.1
Сумма произведений значений функции в отмеченных точках на меру ячейки
разбиения называется «интегральной суммой» для функции f при разбиении Pn области D.
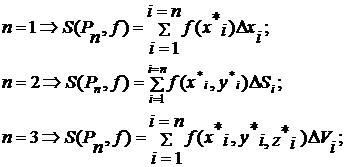
Сумма
произведений меры ячейки разбиения на наименьшее (наибольшее) значение функции
в ячейке называется нижней Ln (верхней Un) суммой Дарбу:
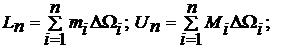
Определение
2.
Если
существует конечный предел интегральных сумм при измельчении разбиений 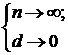 , (который не зависит ни от разбиений ни от выбора
отмеченных точек) его называют интегралом от функции f по области D и
пишут
, (который не зависит ни от разбиений ни от выбора
отмеченных точек) его называют интегралом от функции f по области D и
пишут
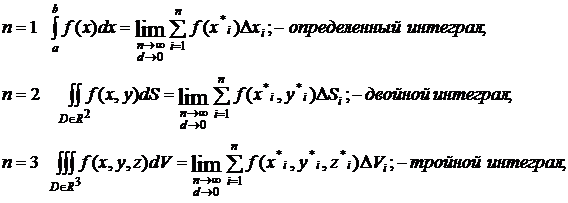
Свойства
интеграла
Аддитивность
- 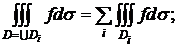 - интеграл по объединению областей равен сумме
интегралов по каждой части области.
- интеграл по объединению областей равен сумме
интегралов по каждой части области.
Линейность
- 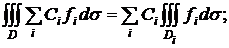 - интеграл от линейной комбинации функций равен
линейной комбинации интегралов.
- интеграл от линейной комбинации функций равен
линейной комбинации интегралов.
Геометрическая
иллюстрация 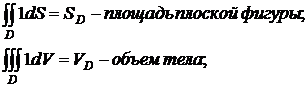
Оценки
интеграла для непрерывной функции f:
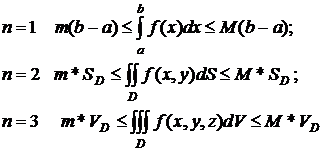
Теорема
(существования).
Функция
многих переменных, непрерывная в области D, интегрируема
в ней.
1.2 Вычисление двойного интеграла в прямоугольных
координатах
По определению:
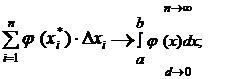
Пусть
область интегрирования D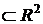 ограничена на промежутке x Î [a,b] линией у=ун(х) снизу и линией у=уВ(х)
сверху. Пользуясь «свободой» разбиения и выбора отмеченных точек области,
ограничена на промежутке x Î [a,b] линией у=ун(х) снизу и линией у=уВ(х)
сверху. Пользуясь «свободой» разбиения и выбора отмеченных точек области,
внутри
каждого вертикального «столбика» xi<x<xi+1 выберем
отмеченные точки  с одинаковыми абсциссами:
с одинаковыми абсциссами: 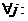 x=xi*.
x=xi*.
упорядочим
суммирование в интегральной сумме
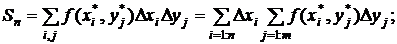
Несложно
заметить, что внутренняя сумма представляет интегральную сумму для интеграла от
функции одной переменной 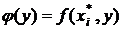 - сужения функции f на прямую x=xi*, так что
- сужения функции f на прямую x=xi*, так что
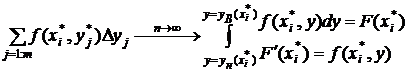
После
этого, внешняя сумма 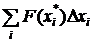 так же представляет интегральную сумму для интеграла
от функции одной переменной F(x), так что
так же представляет интегральную сумму для интеграла
от функции одной переменной F(x), так что
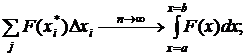
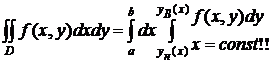
При
другом «порядке интегрирования»
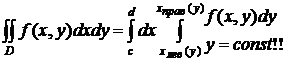
Таким
образом, вычисление двойного интеграла сводится к двукратному интегрированию
функций одной переменной, причем (1) внутреннее интегрирование функции одной
переменной (сужения функции f на координатную линию: x=const
|| OY à
g(y)=f(x,y) или y=const ||OX à g(x)=f(x,y)); выполняется вдоль отрезка 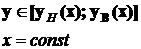 или
или 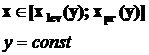 ,
переменные границы которого - уравнения линий, ограничивающих область D
СНИЗУ и СВЕРХУ или СЛЕВА и СПРАВА;
,
переменные границы которого - уравнения линий, ограничивающих область D
СНИЗУ и СВЕРХУ или СЛЕВА и СПРАВА;
(2)
повторное интегрирование (внешний интеграл) функции одной переменной
выполняется по отрезку x Î [a;b]
или y Î [c;d],
где a,b и c,d - являются наименьшее и наибольшее значения «второй»
переменной во всей области интегрирования D.
Замечание.
Если при выбранном порядке интегрирования границы области вдоль соответствующей
координатной прямой задаются различными уравнениями («сложная область»),
область интегрирования следует разбить на «простые части».
.
Из свойства аддитивности интеграла следует, что 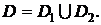
Область
D1
принадлежит полосе 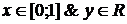 и ограничена СНИЗУ линией yH≡0
и СВЕРХУ - линией yB(x)=1-x.
и ограничена СНИЗУ линией yH≡0
и СВЕРХУ - линией yB(x)=1-x.
Область
D2
принадлежит полосе 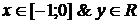 и ограничена СНИЗУ линией yH≡0
и СВЕРХУ - линией yB(x)=
и ограничена СНИЗУ линией yH≡0
и СВЕРХУ - линией yB(x)= -
(верхняя полуокружность).
-
(верхняя полуокружность).
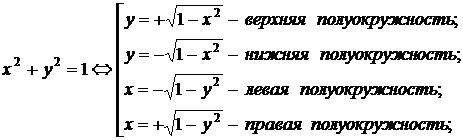
.
При другом порядке интегрирования:
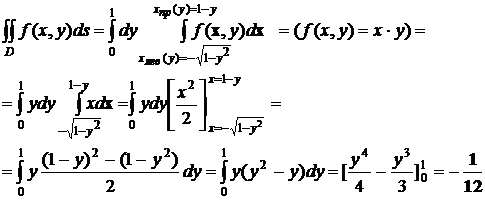
(в)
Так как вдоль линии y=const граница области D «справа»
задается двумя различными уравнениями 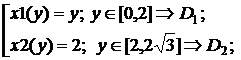 , запишем
интеграл как сумму двух интегралов
, запишем
интеграл как сумму двух интегралов
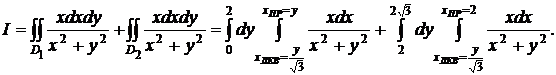
1.3 Вычисление двойного интеграла
в полярных координатах; обобщенные полярные координаты
Рассмотрим на плоскости две системы координат - прямоугольную и полярную.
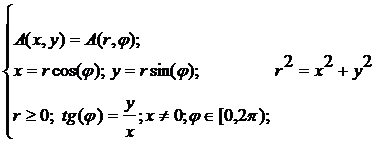
Уравнение
линий на плоскости:
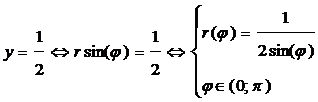
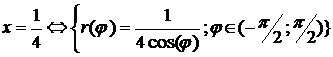
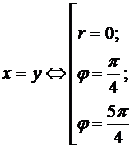 2+y2=a2
ó r=a; φ Î [0;2π); =x2 ó r(φ)=sin(φ)/cos2(φ)2+2x+y2=0 [(x+1)2 +y2=1]
ó r2+2rcos(φ)=0 ó r=0;
2+y2=a2
ó r=a; φ Î [0;2π); =x2 ó r(φ)=sin(φ)/cos2(φ)2+2x+y2=0 [(x+1)2 +y2=1]
ó r2+2rcos(φ)=0 ó r=0;
r(φ)=-2cos(φ)
Пусть
область интегрирования D Î R2 ограничена линиями r=r1(φ),r=r2(φ), φ=φ1 и φ(D) Î [φ1;φ2].
)
Введем разбиение Pn области интегрирования линиями «полярной сетки» r=const
(концентрические окружности) и φ=const (лучи) на ячейки Ωij
-«криволинейные прямоугольники». При измельчении разбиений площадь ячейки равна
ΔSij=riΔriΔφj à
dS=rdrdφ.
)
Выберем в каждой ячейке сектора φ Î [φj;φj+1] отмеченные точки
A(ri*;φj*) с одинаковыми полярными
углами φj*.
)
Упорядочим суммирование в интегральной сумме
 à
à
à 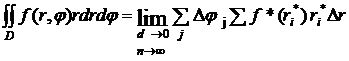
В
результате предельного перехода при измельчении разбиений придем к заключению:
«Вычисление
двойного интеграла в полярных координатах
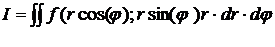
сводится
к двукратному интегрированию функций одной переменной, при этом
внешнее
интегрирование выполняется по промежутку [φmin; φmax] или [rmin;rmax], границы которого соответствуют наименьшему и
наибольшему значениям одной переменной во всей области;
внутреннее
интегрирование выполняется вдоль линии полярной сетки r=const
(окружность)или φ=const
(луч), причем пределы этого интегрирования
r1(φ),r2(φ) или φ1(r), φ2(r) -
уравнения границ области вдоль линии.»
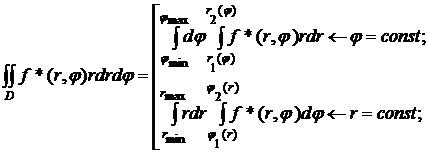
Пример 1.
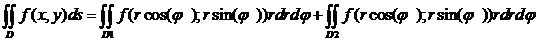
=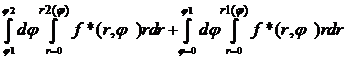
tg(φ1)=2ó
φ1=arctg(2);tg(φ2)=4 ó φ2=arctg(4);
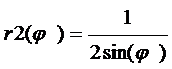 ;
;
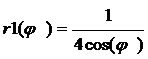
Пример
2.
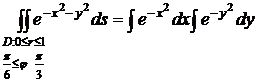 à «бесперспективно,
à «бесперспективно,
так
как первообразная функции exp(-x2)не
выражается через элементарные функции, в полярных же координатах
=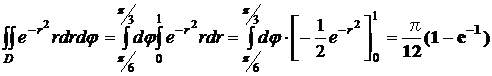
Пример 3.

=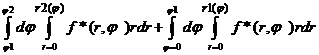
tg(φ1)=2ó
φ1=arctg(2);tg(φ2)=4 ó φ2=arctg(4);
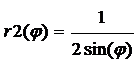 ;
;
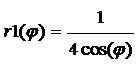
Замечание.
Если область интегрирования ограничена эллипсом или его дугой, рекомендуется
ввести «обобщенные полярные координаты», которые отображают эллипс в единичный
круг:
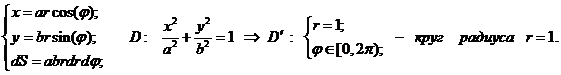
Например,
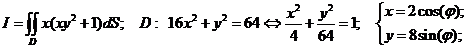
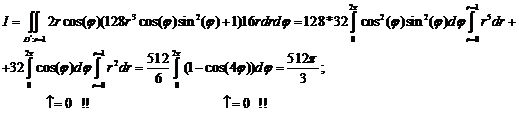
Типовая
задача экзамена: (1)Восстановить область интегрирования; (2) изменить порядок
интегрирования; (3) записать двойной интеграл в полярных координатах
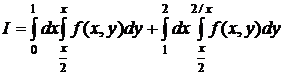
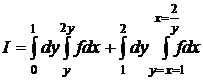
1.4 Вычисление тройных интегралов.
В R3 используются три системы координат: прямоугольная,
цилиндрическая и сферическая.
Таблица
Координатные поверхности,
Линии их пересечения
|
|
Прямоугольная M(x,y,z)
|
X=constó плоскости || YOZ Y=constó -»-»-»|| XOZ Z=constó
-»-»-»|| XOY (x,y)=constó ||OZ-линия
пересечения двух плоскостей
|
|
Цилиндрическая M(r,φ,z)
|
r=constó соосные цилиндры φ=constó плоскости через ось
OZ z=constó плоскости ||XOY (r,φ)=constó прямая ||OZ-линия пересечения цилиндра и плоскости
(направляющая цилиндра) (z,r)=const<=>окружность- линия пересечения
цилиндра и плоскости (z,
φ)=constó луч||XOY- линия пересечения двух плоскостей
|
Сферическая
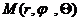 R=constó
концентрические сферы
R=constó
концентрические сферы
φ=constó плоскости через ось OZ
Θ=constó прямые круговые конусы
(R, φ)=constóокружность- линия пересечения сферы и плоскости
(R,Θ)=constóокружность- линия пересечения сферы и цилиндра
|
(φ,Θ)=constó луч-линия пересечения конуса и плоскости
|
|
По
определению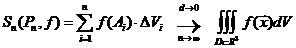 ; ΔVi-объем
ячейки при разбиении координатными поверхностями выбранной системы координат.
; ΔVi-объем
ячейки при разбиении координатными поверхностями выбранной системы координат.
В
прямоугольной системе ячейка разбиения - прямоугольный параллелепипед, его
объем ΔV=Δxi∙Δj∙Δk à
dV=dxdydz.
В
цилиндрической и сферической системах ячейка - криволинейный прямоугольный
параллелепипед со сторонами {Δri;riΔφj;Δzk}
и
{RiΔθk;ΔRi;Risin(θk)Δφj}
ΔV=Δri∙riΔφj∙Δzk à
dV=rdrdφdz
ΔV=RiΔθk∙ΔRi∙Risin(θk)Δφj==>dV=R2sin(θ)dRdθdφ
Следовательно,
тройной интеграл в этих системах имеет вид:
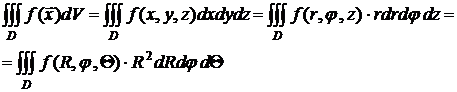
Сведение
интеграла от ФНП к кратному (последовательному) интегрированию функций одной
переменной соответствует упорядочению суммирования в интегральной сумме. В
прямоугольной и цилиндрической системах координат упорядочение суммирования
позволяет выделить сумму, соответствующую интегральной сумме двойного интеграла
по проекции области интегрирования D Î R3 на одну
из координатных плоскостей, например, на XOY:
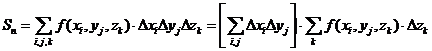
Такому
упорядочению суммирования соответствует сведение тройного интеграла к
интегрированию функции одной переменной φ(z)=f((x,y)=const;z)
вдоль прямой (x,y)=const, перпендикулярной координатной плоскости XOY,
и двойному интегралу по проекции DXY области D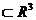 на эту плоскость.
на эту плоскость.
Алгоритм
вычисления тройного интеграла в прямоугольных и цилиндрических координатах.
)
Спроецировать область интегрирования D Ì R3 на одну из координатных плоскостей: например, на
плоскость XOY à DXY =
ПРXOY(D).
)
Записать уравнения поверхностей, ограничивающих область D
вдоль прямой, перпендикулярной выбранной координатной плоскости, выразив из
уравнения поверхности G(x,y,z)=0 соответствующую координату через две другие:
G(x, y, z) = 0 Þ [z =
z(x, y) или y = y(x, z) или x = x(y, z)]
)
Проинтегрировать функцию одной переменной, например,
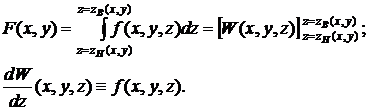
)
После этого вычислить двойной интеграл от функции F(x, y) в
прямоугольных или в полярных координатах по проекции области D Ì R3 на соответствующую координатную плоскостью.
Например,
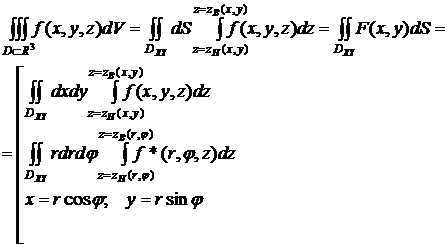
Пример.
Вычислить тройной интеграл

)Область
D ограничена: слева - плоскостью y=0;
справа - сферой радиуса 1; снизу-сверху-спереди-сзади - поверхностью цилиндра
радиуса 1;
Очевидно,
что проекция D на YOZ и XOY ПРYOZD= ПРXOZD - объединение
прямоугольника и сектора круга R=2; проекция же на плоскость XOZ ПРXOZD- круг радиуса r=1.
)
уравнения поверхностей «слева и справа» вдоль линии (x,z)=const||ZOX
YЛЕВ(x,z)≡0; x2+y2+z2=4
à YПР(x,z)=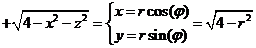 .
.
)
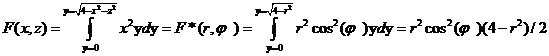
) 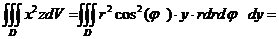
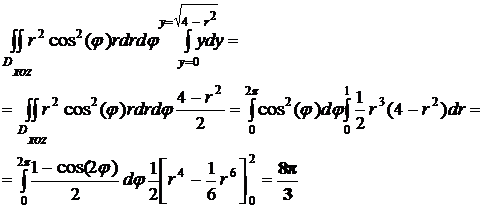
1.5 Замена переменных в двойном и в тройном интегралах
Пусть
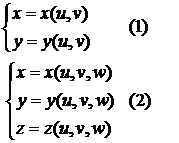
и
соответствующие ФНП имеют непрерывные частные производные. Введем матрицу Якоби
частных производных:
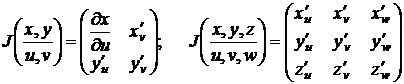
Замена
переменных в двойном (1) и тройном (2)интегралах выполняется по следующему
алгоритму:
Записывается
матрица Якоби и вычисляется ее определитель det(J).
Подынтегральная
функция преобразуется к новым переменным
f(x,y)=f*(u,v); f(x,y,z)=f*(u,v,w)
Область
интегрирования Dxy, Dxyz отображается в соответствующую область Duv, Duvw.
Вычисляется
интеграл
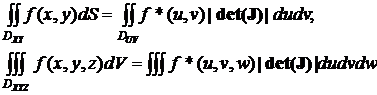
Пример
1. Вычислить
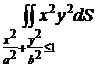
)
Введем обобщенные полярные координаты (ОПК):
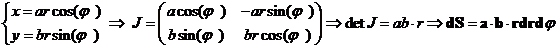
в
частности, a=b=1à
dS = rdrdφ
)
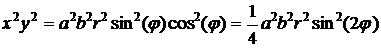
)
Эллиптическая область интегрирования 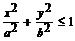 в ОПК
отображается в единичный круг r≤1; φ Î
[0;2π], поэтому
в ОПК
отображается в единичный круг r≤1; φ Î
[0;2π], поэтому
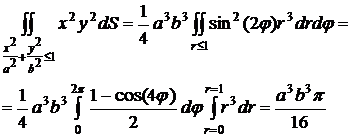
Пример2.
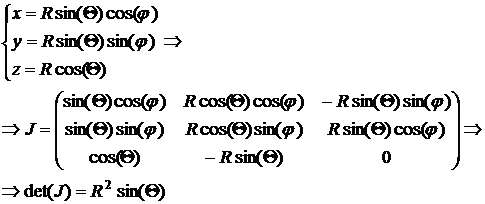
à dV=R2sin(Θ)dRdΘdφ.
1.6 Геометрические приложения тройных интегралов
Геометрическое приложение - вычисление объема любого
пространственного тела.
Объем тела U в декартовых координатах Oxyz выражается формулой
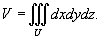
В
цилиндрических координатах объем тела равен
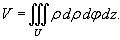
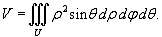
Пример
Найти
объем шара x2 + y2 + z2 ≤ R2.
Решение.
Вычислим
объем части шара, расположенной в первом октанте (x ≥ 0, y ≥ 0, z ≥
0), и затем умножим результат на 8. Получаем
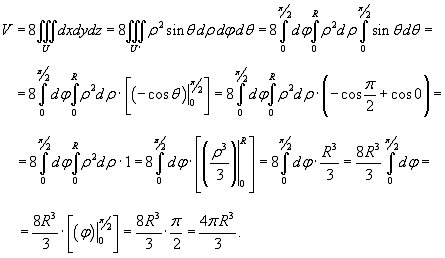
В
результате получена известная формула для объема шара радиусом R.
1.7 Физические приложения тройных интегралов
Масса и статические моменты тела
Пусть тело занимает объем U и его объемная плотность в точке M(x,y,z)
задана функцией ρ(x,y,z). Тогда масса тела m вычисляется с помощью
тройного интеграла:
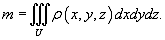
Статические
моменты тела относительно координатных плоскостей Oxy, Oxz, Oyz выражаются
формулами
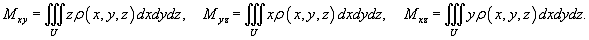
Координаты
центра тяжести тела вычисляются по формулам:
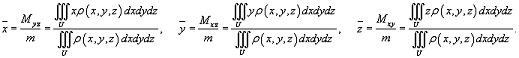
Если
тело является однородным с плотностью ρ(x,y,z) = 1 для точек M(x,y,z) в области U, то центр тяжести тела
зависит только от геометрии тела и называется центроидом.
Моменты
инерции тела
Моменты
инерции тела относительно координатных плоскостей Oxy, Oxz, Oyz определяются
выражениями
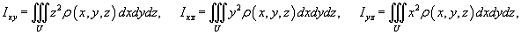
а
моменты инерции тела относительно координатных осей Ox, Oy, Oz вычисляются по
формулам
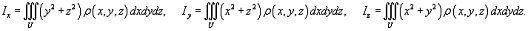
Как
видно, справедливы соотношения
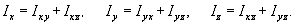
Моментом
инерции тела относительно начала координат называется интеграл
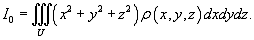
Момент
инерции относительно начала координат можно выразить через моменты инерции
относительно координатных плоскостей:
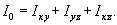
Тензор
инерции
Используя
рассмотренные выше 6 чисел Ix, Iy, Iz, Ixy,
Ixz, Iyz, можно составить так называемую матрицу инерции
или тензор инерции тела:
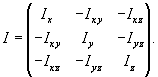
Данный
тензор является симметричным, и, следовательно, его можно привести к
диагональному виду при определенном выборе осей Ox', Oy', Oz'. Значения
диагональных элементов (после приведения тензора к диагональному виду)
называются главными моментами инерции, а указанные направления −
собственными векторами или главными осями инерции.
Если
тело вращается вокруг оси, не совпадаюшей с главной осью инерции, то оно будет
испытывать вибрации при высоких скоростях вращения. Поэтому, при
конструировании таких устройств необходимо, чтобы ось вращения совпадала с
одной из главных осей инерции. Например, при замене шин автомобиля проводится
их балансировка: небольшие грузики добавляются к колесам, чтобы обеспечить
совпадение оси вращения с главной осью инерции и исключить вибрации.
Гравитационный
потенциал и сила тяготения
Ньютоновым
потенциалом тела в точке P(x,y,z) называется интеграл
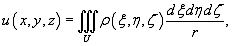
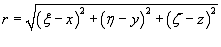
где
ρ(ξ,η,ζ) − плотность тела, и.
Интегрирование
выполняется по всему объему тела. Зная потенциал, можно вычислить силу
притяжения материальной точки массы m и заданного распределенного тела с
плотностью ρ(ξ,η,ζ) по формуле
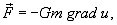
где
G − гравитационная постоянная.
Пример
Найти
массу шара радиуса R, плотность γ которого пропорциональна квадрату расстояния от центра.
Решение.
По
условию, плотность γ задана соотношением γ = ar2, где a −
некоторая постоянная, r − расстояние от центра. Массу шара удобно
вычислить в сферических координатах:

1.8
Примеры
Задача. Вычислить объем тела, ограниченного заданными поверхностями:
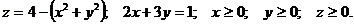
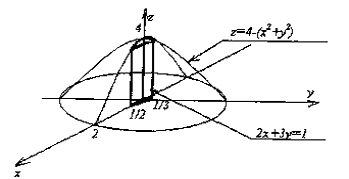
Решение.
При сведении тройного интеграла к
трехкратному и в расстановке пределов в каждом из трех определенных интегралов
действуем по аналогии со случаем двойного интеграла. Область интегрирования V в
примере считаем правильной в направлении оси OZ, т.к. любая
прямая, параллельная оси OZ, пересекает границу области не более чем в двух
точках. Учитывая, что объем области V выражается в декартовых
координатах формулой
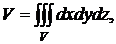
а
область V ограничена снизу плоскостью z=0, а сверху -
поверхностью параболоида вращения z=4-(x2+y2) можно
свести тройной интеграл к вычислению двойного интеграла от однократного:
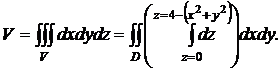
Сначала
вычисляется внутренний интеграл по переменному z с нижним
пределом z=0 и верхним пределом z=4-(x2+y2).
Областью интегрирования D во внешнем двойном интеграле является проекция тела V на
плоскость XOY, имеющая вид:

Линия
входа в эту область y=0, линия выхода 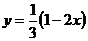 .
Проекцией области D на ось OX служит отрезок
.
Проекцией области D на ось OX служит отрезок 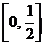 . Отсюда
следует, что во внутреннем интеграле по у нижний предел 0, верхний предел
. Отсюда
следует, что во внутреннем интеграле по у нижний предел 0, верхний предел 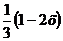 , а во внутреннем интеграле по х нижний предел 0, а
верхний предел
, а во внутреннем интеграле по х нижний предел 0, а
верхний предел 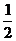 . В итоге объем V вычисляется с
помощью трехкратного интеграла следующим образом:
. В итоге объем V вычисляется с
помощью трехкратного интеграла следующим образом:
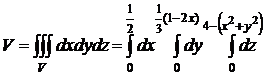
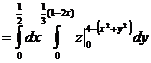
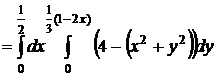 =
=

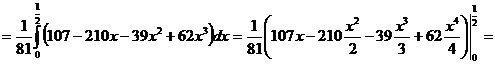
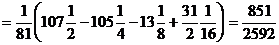 .
.
Задачи
Вычислить
объем тела, ограниченного поверхностями 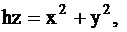
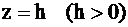 .Найти координаты центра масс тела, предполагая, что
оно однородно.
.Найти координаты центра масс тела, предполагая, что
оно однородно.
РЕШЕНИЕ.
Данное тело ограничено снизу параболоидом  , сверху
плоскостью z=h и проектируется в круг
, сверху
плоскостью z=h и проектируется в круг 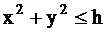 плоскости
XOY.
плоскости
XOY.
z
y
х
Рис. 1. Область интегрирования
Используем цилиндрические координаты:
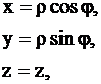
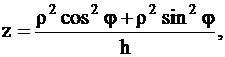 т.е.
т.е. 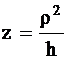 .
.
Объем
тела равен
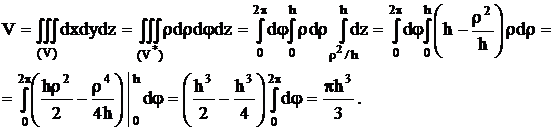
Координаты
центра масс тела вычисляются по формулам
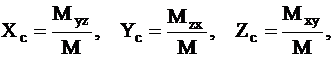 где
где
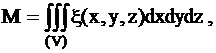

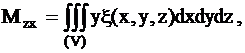
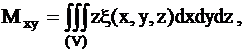
где
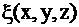 - плотность тела в точке (х,y,z).
Для однородного тела можно положить
- плотность тела в точке (х,y,z).
Для однородного тела можно положить 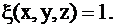
Находим:
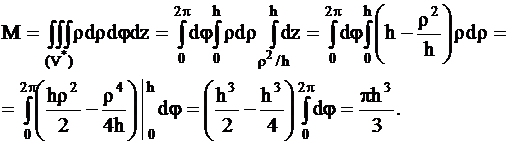
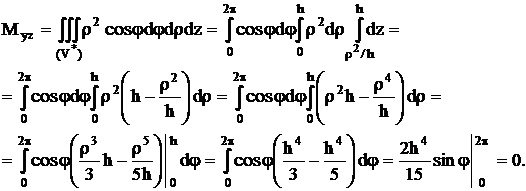
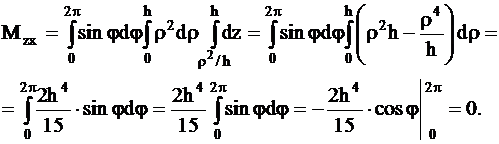
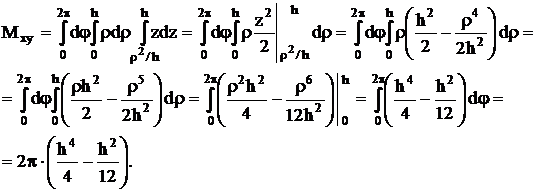
Таким
образом
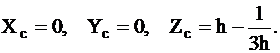
2.
Программная реализация задачи
2.1 Постановка задачи на разработку программы
Вычислить приближенные значения тройного интеграла по прямоугольной
области.
Язык программирования
Язык программирования Object Pascal разработан фирмой Inprise
International для использования в среде Delphi - мощном и популярном
современном средстве визуального программирования, позволяющем решать практически
любые задачи обработки данных и способном удовлетворить самые сложные запросы и
потребности программиста.
Его прародителем является язык Pascal, который был разработан швейцарским
математиком Николаусом Виртом в 1968 г. с целью использования его в качестве
инструмента для обучения компьютерному программированию как системной
дисциплине. В основу языка были положены основные идеи широко известного в 60-е
годы языка ALGOL-60. Благодаря чрезвычайной гибкости и удобству языка Pascal
были созданы многочисленные его диалекты, нашедшие свое воплощение в
программном обеспечении ЭВМ последующих поколений, что также способствовало его
популяризации. Теоретические основы языка, как выяснилось позже, оказались
настолько удачны, что помимо традиционных вычислительных задач язык оказался
пригоден для разработки более сложных программных структур - систем обработки
баз данных, компиляторов и даже операционных систем.
С внедрением персональных IBM-совместимых компьютеров в середине 80-х
годов фирмой Borland International была разработана новая версия языка,
получившая название Turbo Pascal. По сути Turbo Pascal стал даже не языком, а
системой, представляющей собой интегрированную (целостную) среду
программирования, включающую весь необходимый инструментарий для прохождения
программы через компьютер - от ее ввода до получения готового результата.
Наиболее удачные версии языка - Turbo Pascal 5.5, Turbo Pascal 6.0, Borland
Pascal 7.0 - относятся к 1986 - 1992 г.г. Принципиальными нововведениями Turbo
Pascal стали модульная технология конструирования программ и
объектно-ориентированные средства программирования. Эти новшества, в
особенности технология модульного программирования, позволили с небывалой
легкостью создавать не только традиционные вычислительные программы, но и очень
сложные информационно-вычислительные системы.
С появлением и развитием операционных систем Microsoft Windows, пришедших
на смену DOS, значение Turbo Pascal как среды программирования резко снизилось.
В настоящее время эта среда практически не применяется и используется для
внесения коррективов в ранее созданные и до сих пор работающие программы и базы
данных и/или в низкоресурсных компьютерах устаревших моделей.
Значение самого языка Turbo Pascal, напротив, не уменьшилось, т. к. на
смену вышеназванным DOS-средствам одноименного названия пришло новое, еще более
мощное и более удобное средство программирования - среда Delphi (Делфи или
Дельфи), основой которого является по-прежнему Turbo Pascal и который выступает
теперь под названием - Object Pascal.
Среда Delphi, в отличие от Turbo Pascal, является принципиально новым
средством программирования. Она построена на идее визуального способа
программирования. Сочетание визуализации программирования и преимуществ языка
сделало Delphi весьма популярным среди программистов из-за поразительной
простоты и наглядности в составлении компьютерных программ. Можно привести
примеры практически значимых программ на Delphi, составление которых вообще не
требует знания языка программирования, т. к. действия программиста в написании
таких программ выполняет сама Delphi! Такие программы она пишет на языке Object
Pascal. Эти примеры хотя и показательны, тем не менее не являются убедительным
доказатель-ством исключительных возможностей Delphi как абсолютной альтернативы
труду программиста. Образно говоря, Delphi является грандиозным складом
строительных материалов и технологий конструирования многообразных типовых
программ, что позволяет автоматизировать множество действий, которые необходимо
выполнить при написании программы. Однако она не может пока с присущей ей
легкостью конструировать программы для обработки ситуаций, которые наперед
неизвестны и которые тем не менее необходимо реализовать в таких программах.
Именно здесь необходимо знание языка Object Pascal для того, чтобы программист
смог сам написать с помощью этого языка необходимые программные коды для
Delphi, которые не предусмотрены стандартами ее аппарата. К их числу относятся,
например: а) обработка оригинальных событий; б) написание стилевых процедур,
которые заставляют компьютер выполнять некоторые действия в "фирменном
стиле" автора; в) написание процедур, обеспечивающих групповую обработку
ряда повторяющихся или подобных операций, которые могут порождаться
выработанной нестандартной или новой методикой решения конкретной задачи и др.и
Object Pascal с момента своего появления в 1995 году за короткий срок прошли
несколько этапов развития. Последовательно, с интервалом в один год, появились
новые версии Delphi 2, Delphi 3, Delphi 4, Delphi 5 и их промежуточные версии,
в которых так же оперативно появлялись новые средства удовлетворения
современных запросов программистов.
Сравнение с другими современными средствами программирования, например
Visual Basic или C++, показывает, что Delphi, благодаря ряду уникальных особенностей,
пользуется неизменной популярностью среди программистов и может быть
рекомендована к использованию в практике решения задач самого широкого спектра
приложения - от простых или сложных вычислений, обработки сигналов внешних
устройств, работы в Internet до ведения и обработки больших баз данных. С её
помощью можно создавать удобные экранные интерфейсы, печатные документы,
производить стыковку разрабатываемого программного продукта с популярными
фирменными интерфейсами и многое другое. В этой связи язык Object Pascal не
теряет своей актуальности и может быть рекомендован к изучению как важный и
перспективный компонент современных информационных технологий.
Наряду с достоинствами необходимо указать на один, однако весьма
существенный недостаток языка Object Pascal - слабые возможности языка для
обеспечения математических вычислений. В частности, в языке по непонятным
причинам полностью отсутствуют средства работы с комплексными числами. Между
тем математический комплексный анализ является важнейшей составной частью
исследований, которые нередко необходимо проводить в ряде расчетов, например в
области механики твердого тела или механики жидкости и газа. Особенно часто эти
расчеты необходимы при изучении динамического качества машин и механизмов, в
частности при изучении их динамической устойчивости к внешним возмущениям.
Заметим, что среди большого разнообразия средств программирования есть только
один язык, который позволяет выполнять любые математические операции, включая
обработку комплексных чисел. Это язык программирования Fortran.
Однако он также имеет свои недостатки. Например, он не может быть
использован при работе с базами данных, при создании удобных интерфейсов,
экранных и печатных форм и многое другое. В этом смысле Fortran отстал от
требований, предъявляемых к современному программному продукту, что снижает
привлекательность этого несомненно нужного языка в сравнении с Object Pascal,
тем более Delphi.
С появлением Delphi язык Object Pascal существенно изменился. Он обрел
много новых необходимых процедур и функций. При этом ряд старых процедур и
функций приобрели новые имена, а старые имена используются в новом контексте.
Произошли и другие изменения.
Системные требования
В данном разделе приведено описание примерных характеристик, которым
должен соответствовать компьютер для того, чтобы на нём могла использоваться
разработанная программа.
|
Декларируемые как
минимальные
|
Рекомендуемые
|
|
Процессор
|
233 MHz
|
300 MHz или выше
|
|
Оперативная память
|
64 Мб RAM (могут быть
ограничены некоторые возможности)
|
128 Мб RAM или выше
|
|
Видеоадаптер и монитор
|
VGA (640´480)
|
Super VGA (800´600) или выше
|
|
Свободное место на HDD
|
1.5 Гб
|
1.5 Гб или больше
|
|
Оптические накопители
|
CD-ROM (требуется для
установки)
|
CD-ROM или
DVD-ROM
|
|
Устройства взаимодействия с
пользователем
|
клавиатура
|
клавиатура
|
Минимальные системные требования - это набор условий, необходимых для
возможности запуска и работы программного продукта. Однако, наличие минимальных
системных требований не отменяет возможность запуска ПО на компьютерах, которые
по характеристикам слабее минимальных.
Рекомендуемые системные требования - набор характеристик, подразумевающих
оптимальную работу большей части возможностей продукта. Однако, даже если
компьютер и подходит под рекомендуемые системные требования, это не значит
высокой производительности ПО, например, в некоторых играх невозможно играть на
максимальных настройках графики.
2.2 Структура программы
Состав программы:_int3.pas -
главный программный модуль;.pas -
модуль проекта.
Процедуры и функции пользователя:
Функция f(x, y, z)
Вычисление подынтегральной функции.
Процедура INT3P(a1, a2, b1, b2, c1, c2, res)
Вычисление тройного интеграла по прямоугольной области.
Параметры:, a2 - пределы интегрирования по оси Ox;, b2 - пределы
интегрирования по оси Oy;, c2 - пределы интегрирования по оси Oz;- значение
тройного интеграла.P - процедура вычисления тройного интеграла по прямоугольной
области D = [a1, a2]´[b1, b2]´[c1, c2]
использует кубатурную формулу с 34 узлами и алгебраическим порядком точности
7., bb1, cc1, cc2 - коэффициенты кубатурной формулы;, s1, e1, e2 - узлы
кубатурной формулы.
Процедура cmdExitExecute
Закрытие главной формы.
Процедура cmdIntegrExecute
Расчет интегралов и вывод решения.
Диалог взаимодействия
После отладки программы и ее компиляции на диске будет создан выполняемый
файл с именем INT3.EXE. Для удобства работы его можно
поместить в отдельный каталог жесткого диска или любого сменного носителя.
Для запуска программы необходимо выполнить одно из следующих действий:
) Из Проводника. Щелкните правой кнопкой мыши на кнопке Пуск и выберите в
открывшемся меню пункт Проводник. На левой панели окна Проводника
разворачивайте вложенные папки, пока не найдете нужную. Откройте ее, и на
правой панели увидите значок созданного приложения. Оно запускается двойным
щелчком на значке.
) С помощью команды «Выполнить». Нажать кнопку Пуск и выбрать команду
Выполнить. Ввести в поле Открыть имя и путь к программе. Если точное
расположение и/или имя программы неизвестны, нажимается кнопка Обзор и
требуемое приложение выбирается из списка файлов в выбранной папке.
После этого на экране появляется главное окно приложения (рис. 2).
В верхней части окна находится инструментальная панель с двумя кнопками:
Вычислить - вычисление интеграла;
Выход - завершение работы с программой.
Среднюю часть окна занимает область ввода исходных данных пределов
интегрирования по осям координат.
Остальная часть окна служит для вывода результата.
Последовательность работы с программой:
§ ввести пределы интегрирования;
§ нажать кнопку Вычислить.
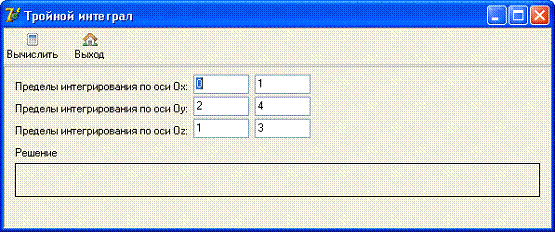
Окно программы
.3 Контрольный пример
В качестве контрольного примера проводилось вычисление интеграла
I = 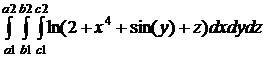 .
.
по
области D = [a1, a2]´[b1, b2]´[c1, c2].
Результат
решения приведен на рис. 3.
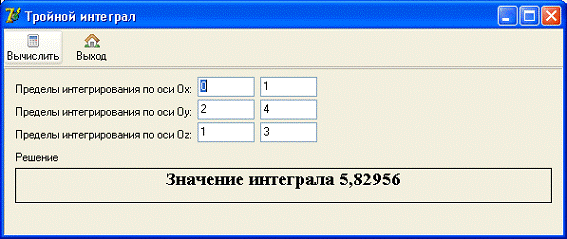
Результат выполнения программы
Заключение
В ходе работы мной была использована справочная и научная литературу.
Результатами исследования по данной теме курсовой работы являются:
) представление теоретического материала по данной теме
) введено понятия «кратных» и «тройных» интегралов
) рассмотрение применения кратных интегралов для вычисления площадей,
объемов, масс, моментов инерции, статистических моментов и координат центра
масс тела
) подробный разбор примеров на приложения кратных интегралов.
) разработка программы расчета тройных интегралов по прямоугольной
области.
В результате проведенной работы была изучена теория кратных интегралов и
разработана программа по теме: «Тройные интегралы».
Список использованной литературы
1. Берман Г.Н. Сборник задач по курсу математического
анализа: Учеб. пособие. -СПб: Профессия, 2003.-432 с.
2. Бронштейн И.Н., Семендяев К.А. Справочник по
математике для инженеров и учащихся втузов. -М.: Наука, 1959. -373 с.
. Бугров Я.С., Никольский С.М. Высшая математика. -М.:
Дрофа, 2003. -509 с.
. Данко П.Е. и др. Высшая математика в упражнениях и
задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова. -М.: ОНИКС
21 век, 2002. -416 с.
. Запорожец Г.И. Руководство к решению задач по
математическому анализу. -М.: Высш. шк., 1966. -294 с.
. Ильин В.А., Позняк Э.Г. Основы математического
анализа. Учеб. для вузов в 2-х частях.-М.: Физматлит, 2002. -646 с.
. Кудрявцев Л.Д. Курс математического анализа. Учеб.
для вузов: В 3-х томах. -М.: Дрофа, 2003. -703 с.
. Пискунов Н.С. Дифференциальное и интегральное
исчисление: Учеб. пособие: в 2-х т. -М.: Интеграл - Пресс, -2001. -415 с.
. Фихтенгольц Г.М. Курс дифференциального и
интегрального исчисления. Учеб. для вузов: в 3-х томах. -М.: Физматлит, 2001.
-697 с.
Приложение. Листинг программы
unit frm_int3;, Messages, SysUtils, Variants, Classes, Graphics,
Controls, Forms,, StdCtrls, Buttons, TeEngine, Series, ExtCtrls, TeeProcs,
Chart,, ActnList, ComCtrls, ToolWin, Menus, ImgList, XPMan;= class(TForm):
TImageList;: TToolBar;: TToolButton;: TToolButton;: TPanel;: TStaticText;:
TLabel;: TEdit;: TEdit;: TLabel;: TLabel;: TEdit;: TEdit;: TLabel;: TEdit;:
TEdit;cmdExitExecute(Sender: TObject);cmdIntegrExecute(Sender: TObject);
{ Private declarations }
{ Public declarations };: TForm1;
{$R *.dfm}f(x, y, z: real): real;
//подынтегральная функция;:= Ln(2 + Sqr(x * x) + Sin(y) + z);;INT3P(a1,
a2, b1, b2, c1, c2: real; var res: real);
//Вычисление ТРОЙНОГО интеграла по прямоугольной области
//a1,a2 - пределы интегрирования по оси Ox;
//b1,b2 - пределы интегрирования по оси Oy;
//c1,c2 - пределы интегрирования по оси Oz;
//res - значение тройного интеграла;
//INT3P - процедура вычисления тройного интеграла по прямоугольной
// области D=[a1,a2]x[b1,b2]x[c1,c2] использует кубатурную
//формулу с 34 узлами и алгебраическим порядком точности 7;
//aa1,bb1,cc1,cc2 - коэффициенты кубатурной формулы;
//v1,s1,e1,e2 - узлы кубатурной формулы.= 0.2957476;= 0.0941015;=
0.2247031;= 0.4123338; //коэффициенты кубатуры= 0.9258200;= 0.9258200;=
0.7341125;= 0.4067031; //узлы, y0, z0, dx, dy, dz, sum1, sum2, sum3, sum4:
real;, j, k, l, i3, j2, j5: integer;:= (a1 + a2) / 2;:= (b1 + b2) / 2;:= (c1 +
c2) / 2;:= (a2 - a1) / 2;:= (b2 - b1) / 2;:= (c2 - c1) / 2;:= f(x0 + dx *
v1,y0,z0) + f(x0 - dx * v1,y0,z0) +(x0,y0 + dy * v1,z0) + f(x0,y0 - dy * v1,z0)
+(x0,y0,z0 + dz * v1) + f(x0,y0,z0 - dz * v1);:= 0;:= 0;:= 0;j := 1 to 4 do(j
mod 2) = 0 then:= 1:= -1;:= i div 3;(i3 mod 2) = 0 then:= 1:= -1;:= sum2 + f(x0
+ i * dx * s1,y0 + k * dy * s1,z0) +(x0 + i * dx * s1, y0, z0 + k * dz * s1)
+(x0, y0 + i * dx * s1, z0 + k * dz * s1);;j := 1 to 8 do(j mod 2)=0 then:= 1:=
-1;:= (j + 1) div 2;(j2 mod 2)=0 then:= 1:= -1;:= j div 5;(j5 mod 2)=0 then:=
1:= -1;:= sum3 + f(x0 + i * dx * e1, y0 + k * dy * e1, z0 + l * dz * e1);:=
sum4 + f(x0 + i * dx * e2, y0 + k * dy * e2, z0 + l * dz * e2);;:= (aa1 * sum1
+ bb1 * sum2 + cc1 * sum3 + cc2 * sum4) * dx * dy *
dz;;TForm1.cmdExitExecute(Sender: TObject);
//Закрытие главной формы;;TForm1.cmdIntegrExecute(Sender: TObject);
//расчет интегралов и вывод решения, a2, b1, b2, c1, c2, res: real;:=
StrToFloat(Edit1.text);:= StrToFloat(Edit2.text);:= StrToFloat(Edit3.text);:=
StrToFloat(Edit4.text);:= StrToFloat(Edit5.text);:=
StrToFloat(Edit6.text);EConvertError do('Ошибка в записи исходных
данных!');;;;P(a1, a2, b1, b2, c1, c2, res);.Caption := 'Значение интеграла ' +
Format('%5.5f', [res]);;.