Аппроксимация функции к полиному n степени методом наименьших квадратов

Аппроксимация функции к полиному n степени методом наименьших квадратов

Введение

В настоящее время компьютеры способны облегчить работу человеку в любой сфере деятельности, так как с помощью вычислительных машин есть возможность автоматизировать многие задачи, тем самым сэкономить время на повторяющихся действиях. Компьютеры могут производить труднейшие для человека вычисления за секунды, а также исключают ошибки вычислений.

Огромное быстродействие вычислительных машин открывает новые широкие возможности для применения общих математических методов исследования в проблемах разных ветвей науки.

В данной курсовой работе рассматривается задача аппроксимации функции к полиному n степени методом наименьших квадратов с последующим нахождением корней этой функции. Вид формулы задается пользователем. Метод наименьших квадратов находит широкое применение при обработке экспериментальных данных.

В первом разделе рассмотрена математическая модель задачи нахождения полинома и расчета его корней, определяющая входные и выходные данные программы.

Во втором разделе рассмотрено проектирование программного модуля, также описана схема модуля и рассмотрен пользовательский интерфейс.

В третьем разделе рассмотрен тест программного модуля.

1. Постановка задачи

.1 Математическая модель задачи

Аппроксимация (или упрощение кривыми) - это процесс замены таблично заданной функции y(x) аналитическим выражением кривой g(x), которая необязательно совпадает с допустимой погрешностью. Одним из видов аппроксимации табличных функций является степенной ряд (полином). Для определения коэффициентов в аналитических выражениях используют метод наименьших квадратов, при котором коэффициенты определяются таким образом, что суммарная квадратичная ошибка

в узлах таблицы являются минимальными.

Рассмотрим задачу. Известна таблица (таблица 1) значений двух переменных x и y.

Таблица 1 - Значения x и y

Требуется найти зависимость между переменными в виде уравнения .

Предполагается, что каждое данное  измерено с некоторой неизвестной ошибкой , где  - истинное значение.

Если данные предположения (гипотеза Гаусса) выполняются, среди семейства параметрических кривых  наибольшую вероятность для данной совокупности данных  обеспечивает кривая, для которой минимальна сумма квадратов отклонений во всех точках :

.

Параметры эмпирической формулы  находятся из условия минимума функции , который определяется путем приравнивания нулю частных производных этой функции по всем ее переменным :

.

Полученные соотношения - система уравнений для определения параметров .

Очень часто в качестве эмпирической функции используется многочлен степени m:

.

Тогда

;

.

Приравнивая эти выражения нулю и собирая коэффициенты при неизвестных , получаем следующую систему уравнений:

,

где .

Далее подставив значения координат точек в систему уравнений запишем ее в более компактной форме:

,

где уже неизвестное - это . Решая эту систему линейных уравнений, получаем коэффициенты , которые являются искомыми параметрами эмпирической формулы. Для решения системы линейных уравнений воспользуемся методом Якоби. Для начала запишем систему уравнений в векторном виде

,

где

.

Предполагается, что матрица А неособенная, т. е. , и решение единственно.

Если все диагональные коэффициенты , то систему  можно представить в так называемом приведенном виде:

где

Введем обозначения

и перепишем систему (1) в виде одного матричного уравнения

 (2)

Здесь ax -произведение матрицы a на вектор x.

Последовательные приближения (итерации) найдем следующим образом. Возьмем в качестве начального приближения x(0) вектор β и подставим его в правую часть уравнения (2); получим x(1). Продолжая аналогичные вычисления, придём к векторной последовательности приближений:

Если существует придел ξ последовательности векторов x(k), то, переходя к пределу в равенстве  при k→∞, убеждаемся, что ξ является решением уравнения (2), т. е.

Достаточные условия сходимости итераций к решению содержит следующая теорема.

Теорема. Если какая либо норма матрицы меньше единицы: ||a||<1, то уравнение (2) имеет единственное решение ξ, к которому стремится последовательность итераций (3) при любом выборе начального приближения x(0).

В расчетах полагают x(0)=β. Погрешность приблеженного решения уравнения (2) на k-м шаге оценивают неравенством

Из неравенства (4) можно получить оценку числа итераций k, необходимых для обеспечения заданной точности ε.

Отклонение приближения x(k) от решения ξ по норме не будет превышать ε, если

Неравенство (5) дает обычно завышенную оценку числа итераций k. В оценках (4), (5) одновременно используются согласованные нормы для матриц и векторов (m- и l-нормы).

Из неравенства (5) видно, что условие, позволяющее принять приближение x(k) в качестве решения с точностью ε, можно представить в следующей удобной для вычислительного процесса форме:

Замечание. Достаточное условие сходимости для каждого уравнения системы  по m-норме можно представить в виде

Здесь модули диагональных коэффициентов для каждого уравнения системы  больше суммы модулей всех остальных коэффициентов. Естественно, что если условия (7) не выполнены, то следует применять условия сходимости по l- и k-нормам после приведения системы к виду (1) или непосредственно к неприведенной системе . Достаточное условие сходимости процесса итераций для неприведенной системы  по l-норме можно представить в виде

Если система (8) не решается методом Якоби, то в программе автоматически запускается решение методом Гаусса. Суть его в том, что систему мы преобразуем, исключив сначала неизвестную a1 из второго и последующих уравнений системы. Затем вычитаем уравнение из остальных. В результате получаем систему, в которой неизвестное a1 исключено из последующих уравнений.

Разделив второе уравнение на x2, затем умножив на xn в зависимости от уравнения из которого будим вычитать и так далее пака не получим нижнюю треугольную матрицу.

Таким же методом преобразуем матрицу к диагональному виду.

Итак, решение системы уравнений представляет собой вектор

Для нахождения корне полученного полинома воспользуемся методом простой итерации. Для начала приравняем полином n-ой степени к 0, т. е. пусть f(x)=0 - некоторое уравнение. Число ξ называется корнем или решением данного уравнения, если оно, будучи подставлено в уравнение, обращает его в равенство, т. е. f(ξ)=0. Число ξ называют нулем функции y=f(x).

Нахождение действительных корней с определенной точностью можно разбить на два этапа:

отделение корней, т. е. установление промежутков, в которых содержится один корень уравнения;

вычисление корня, принадлежащего выбранному промежутку, с заданной точностью.

Известно, что если функция f(x) непрерывна и принимает на концах отрезка [a,b] значения разных знаков, т. е. f(a)f(b)<0, то внутри этого промежутка

найдется нуль функции.

Пусть требуется решить уравнение, представленное в виде

где правая часть уравнения - непрерывная на отрезке [a,b] функция g(x). Суть метода простых итераций (метода последовательных приближений) состоит в следующем. Начиная с произвольной точки x(0), принадлежащей отрезку [a,b], последовательно получаем

Последовательность

называется последовательностью итераций для уравнения (8) с начальной точкой x(0). Если все точки (9) принадлежат отрезку [a,b] и существует предел то, перейдя к пределу в равенстве

получим

Следовательно, если существует предел последовательности итераций (9), то он является корнем уравнения (8). Достаточные условия сходимости последовательности итераций содержатся в следующей теореме.

Теорема. Пусть функция g(x) имеет на отрезке [a,b] непрерывную производную и выполнены два условия:

значение функции y=g(x) принадлежит отрезку [a,b] для любого .

Тогда при любом выборе начального приближения  процесс итераций сходится к единственному корню ξ уравнения (8) на отрезке .

Оценка погрешности k-го приближения x(k) к корню ξ такова:

где

1.2 Входные данные

Входными данными для решения поставленной задачи является количество точек m, значения координат точек x и y, а также значение степени полинома n. Для вычисления корней уравнения необходимо задать начало отрезка [a,b], на котором они вычисляются, конец же определяется программой.

Значения зависимости x от y вводятся с клавиатуры, либо из выбранного двоичного файла. Точность расчетов e вводится разработчиком программного модуля, или другим лицом при отладке программы. Входные данные в курсовом проекте приведены в таблице 2.

Таблица 2 - Входные данные

1.3 Выходные данные

Результатом работы программы является нахождение коэффициентов уравнения с последующим нахождением его корней на отрезке [a,b]. Также определяются значения полученной функции при введенных координатах точек x. Выходные данные представлены в таблице 3.

Таблица 3 - Выходные данные

1.4 Требования к надежности

Все ошибки, возникающие при выполнении программы, возможная реакция программы на них и методы их исправления представлены в таблице 4.

Таблица 4 - Требования к надежности

2. Проектирование программного модуля

.1 Структурная диаграмма программного модуля

Иерархическая структура алгоритма представлена на рисунке 1. Последовательность вызова функции выглядит следующим образом: в результате выполнения функции main вызывается функция menu. Из функции menu вызывается одна из трех функций: vvod, vivod либо quit. При работе функции vvod вызываются функции input или input_f. После выполнения функции input (или input_f) будет вызвана функция korek, после которой запустится функция zapis (или zapis2). Затем будет вызвана функция aproks, которая вызовет функции resalt и koren.

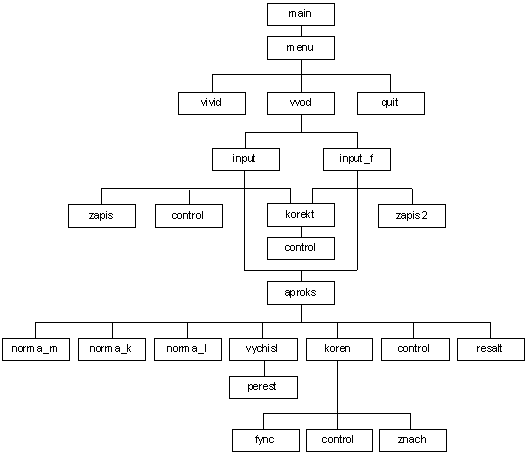
Рисунок 1. Структурная диаграмма программного модуля

int menu - вывод основного меню на экран и возврат номера выбранной функции.

void quit - выход из программы.

void vivod - вывод на экран содержимого двоичного файла.

void vvod - вывод на экран меню, содержащего способы ввода данных.

void input_f - ввод исходных данных из файла.

void input - ввод исходных данных с клавиатуры.

void apros - аппроксимация функции.

void korekt - корректировка данных.

void koren - нахождение значение корня функции.

double control - контроль формата вводимых значений.

void resalt - запись исходных и полученных данных в файл resalt.kr.

double norma_l - нахождение нормы l типа.

double norma_m - нахождение нормы m типа.

double norma_k - нахождение нормы k типа.

void vychisl - вычисление методом Гаусса.

void perest - переставляет местами строки матрицы.

double fync - вычисление значения функции.

double znach - вычисление значения k-той итерации.

2.2 Разработка схемы программного модуля и ее описание

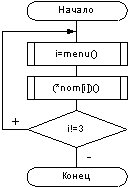
Рисунок 2. Блок-схема к функции main

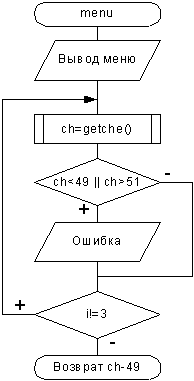
Рисунок 3. Блок-схема к функции menu

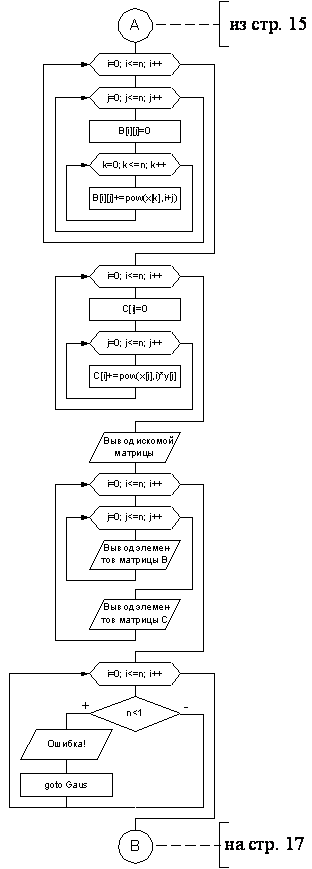
Рисунок 4. Лист 1 - Блок-схема к функции aproks

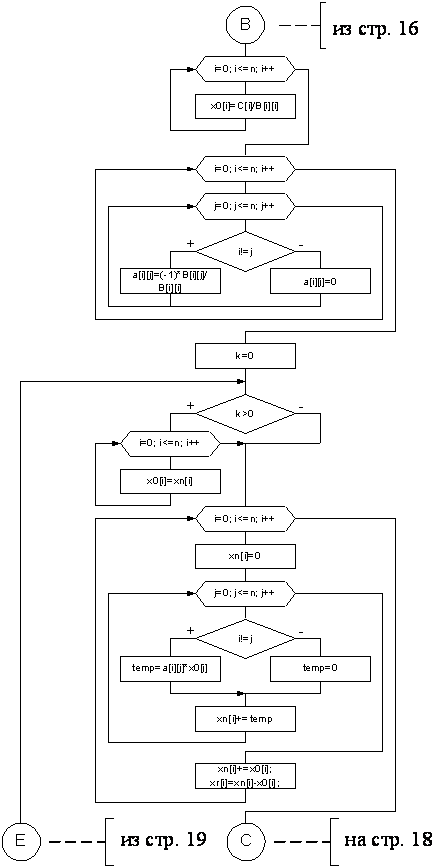
Рисунок 5. Лист 2 - Блок-схема к функции aproks

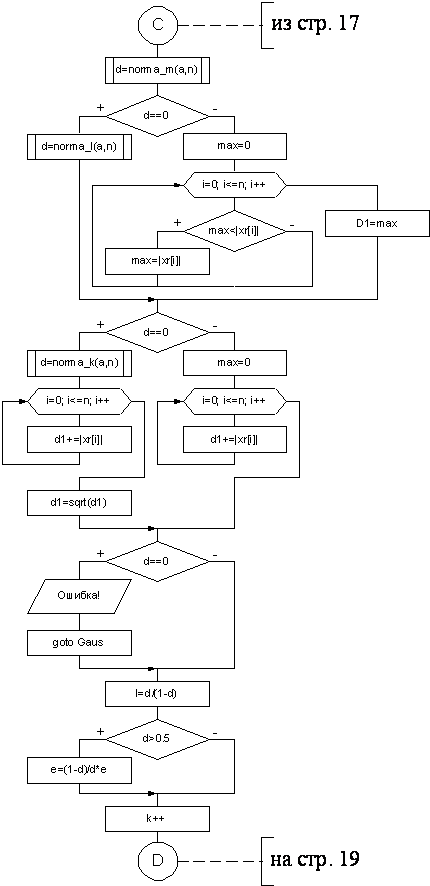
Рисунок 6. Лист 3 - Блок-схема к функции aproks

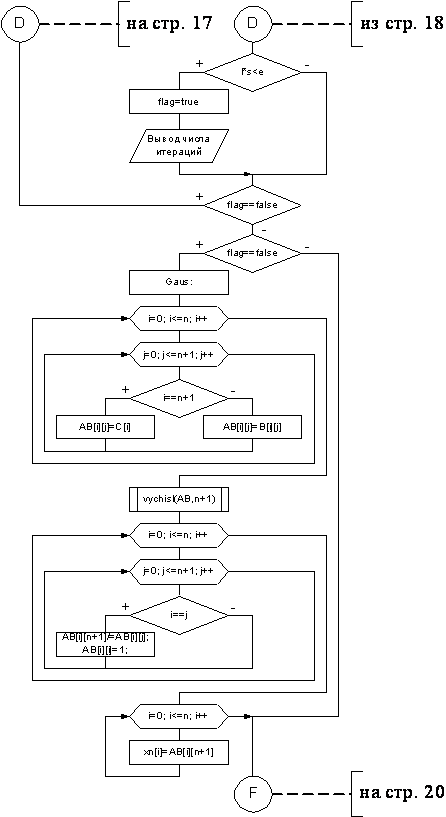
Рисунок 7. Лист 4 - Блок-схема к функции aproks

Рисунок 8. Лист 5 - Блок-схема к функции aproks

Рисунок 9. Лист 6 - Блок-схема к функции aproks

2.3 Разработка пользовательского интерфейса

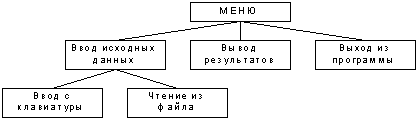
Рисунок 10. Иерархия меню

Пользовательский интерфейс представлен в виде меню, в котором пункты выбираются с помощью нажатия соответствующей клавиши. Главное меню имеет вид:

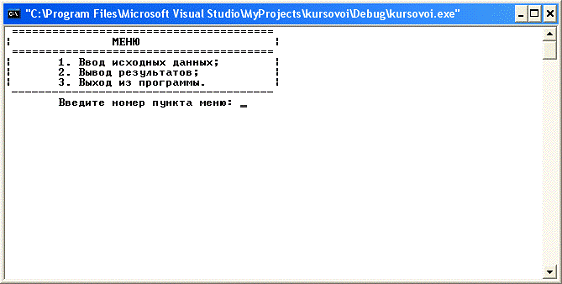
Рисунок 11. Пользовательское меню

При выборе пункта меню “Ввод исходных данных”, пользователь получит возможность выбора типов ввода, а при чтении данных из файл, увидит список доступных файлов. После ввода исходных данных будет предложена возможность откорректировать введенные (считанные) данные.

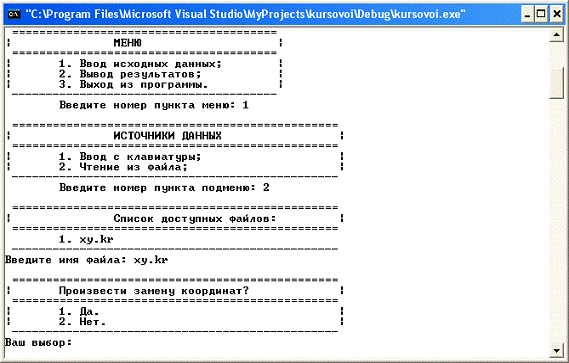
Рисунок 12. Ввод исходных данных

При вводе ошибочных данных программа будет повторять ввод до тех пор, пока не будут введены правильные данные. При выборе пункта меню “Вывод результатов”, пользователь увидит содержимое файла “result.txt”.

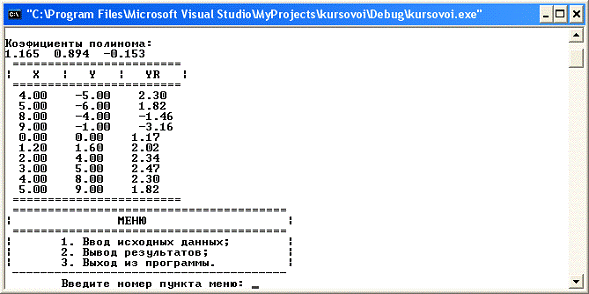
Рисунок 13. Результат выполнения программного модуля

3. Тестирование программного модуля

Тестирование разработанной программы представлено в таблице 5.

Таблица 5 - Тестирование программного модуля

Заключение

аппроксимация функция гаусс программа

В данном курсовом проекте была рассмотрена задача аппроксимации функции методом наименьших квадратов к полиному n степени с последующим нахождением значения корня функции на определенном интервале. Алгоритм программы реализован в среде Visual C++ 6.0. Выполнены все пункты задания. В программе предусмотрена обработка большого количества ошибок ввода.

Приложение 1

Код программы

Файл “kyrs.cpp”:

#include"menu.h"(*nom[])()={vvod,vivod,quit};main()

{ int i; do { =menu();

(*nom[i])(); } while(i!=3); return 0;

}

Файл “rus.h”:

#include <windows.h>buf[256];* rus(char* text)

{ CharToOem(text, buf); return buf;

}

Файл “menu.h”:

#include<stdio.h>

#include<iostream.h>

#include<stdlib.h>

#include<string.h>

#include<conio.h>

#include<math.h>

#include"rus.h"

#include"reshenie.h"korekt(double *x,double *y, int m) //коректировка данных

{ int num; char ch; printf("\n ================================================\n"); printf(rus("|\tПроизвести замену координат? |\n")); printf(" ================================================\n"); printf(rus("|\t1. Да. |\n")); printf(rus("|\t2. Нет. |\n")); printf(" ------------------------------------------------\n"); printf(rus("Ваш выбор: ")); ch=getche(); printf("\n"); do { (ch<49 || ch>50)

{

printf(rus("Такого пункта нет!\nВведите от 1 до 2: "));

ch=getche(); ("\n");

} } while(!strchr("12", ch)); ch-=48; if (ch==1)  

{

printf(rus("\nВведите номер точки: "));

num=(int)control(); ("\n"); (num>m || num<1)

{ (rus("Такой точки несуществует!\nВведите другую: ")); =(int)control(); ("\n");

} (rus("Текущее значение точки:(%.2lf,%.2lf)\n"),x[num-1],y[num-1]); (rus("Введите новое значение:\n"));

printf("x="); [num-1]=control(); ("y="); [num-1]=control(); (" ------------------------------------------------\n"); (rus("|\t1. Еще раз произвести замену. |\n"));

printf(rus("|\t2. Достаточно. |\n"));

printf(" ------------------------------------------------\n"); (rus("Ваш выбор: ")); =getche(); ("\n");

{ (ch<49 || ch>50)

{

printf(rus("Такого пункта нет!\nВведите от 1 до 2: "));

ch=getche();

printf("\n");

}

} (!strchr("12", ch)); =48;

} (ch!=2);

}zapis(double *x, double *y, int m) //запись кординат в файл

return; } fseek(fp,0,0); do { fgets(s,80,fp); if(!feof(fp)) {

s[strlen(s)-1]='\0';

if((strcmp(fn,s))==NULL)

{

while(strcmp(fn,s)==NULL)

{

printf(rus("Файл с таким именем уже сущ.,введите др.имя:\n"));

scanf("%s",fn); [strlen(s)-1]='\0';

}

fseek(fp,0,0);

}

} } while(!feof(fp)); fseek(fp,0,2); fprintf(fp,"%s\n",fn); if((fp1=fopen(fn,"wb"))==NULL) { (rus("Ошибка создания файла\n"));

return; } for(i=0;i<m;i++) { (&x[i],sizeof(double),1,fp1); (&y[i],sizeof(double),1,fp1); } fcloseall();

}zapis2(double *x, double *y, int m, char *file) //перезапись файла

{ FILE *fp; int i; if((fp=fopen(file,"wb"))==NULL) { (rus("Ошибка создания файла\n"));

return; } for(i=0;i<m;i++) { (&x[i],sizeof(double),1,fp); (&y[i],sizeof(double),1,fp); } fclose(fp);

}

void quit() //функция выхода

{ exit(0);

}input(double *x,double*y,int m) //ввод с клавиатуры

{ int i; printf(rus("Введите количество точек: ")); m=(int)control(); for(i=0;i<m;i++) { (rus("Введите координаты %d точки:\n"), i+1);

printf("x="); [i]=control(); ("y="); [i]=control(); ("\n"); } korekt(x,y,m); zapis(x,y,m);

printf(rus("Запуск решения...\n")); aproks(x,y,m);

}input_f(double*x,double*y,int m)//ввод из файла

{ FILE *fp; int i=0; char file[15]; double x1,y1; printf(" ================================================\n"); printf(rus("|\t\tСписок доступных файлов: |\n")); printf(" ================================================\n"); while((fp=fopen("list.kr","r"))==NULL) { (rus("Ошибка открытия файла!"));

printf(rus("Файл со списком не существует!")); } do {

fgets(file,80,fp); (!feof(fp))

{ ++; ("\t%d. %s",i,file);

} if(i==0)

{ (rus("|\tФайлы с координатами отсутствует! |\n")); (" ------------------------------------------------\n"); (rus("Введите координаты с клавиатуры!\n")); (x,y,m);

} } while(!feof(fp)); fclose(fp); printf(" ------------------------------------\n"); (rus("Введите имя файла: ")); scanf("%s",&file); while((fp=fopen(file,"rb"))==NULL) { (rus("Ошибка открытия файла!"));

printf(rus("Файл не существует, введите другое имя файла: "));

scanf("%s",&file); } i=0; while(fread(&x1,sizeof(double),1,fp)) { (&y1,sizeof(double),1,fp); [i]=x1; [i]=y1; ++; } m=i; fclose(fp); korekt(x,y,m); zapis2(x,y,m,file); printf(rus("Запуск решения...\n")); aproks(x,y,m);

}vvod() //меню ввода данных

{ int m=0; char ch; double *x=new double[m]; double *y=new double[m]; do { (" ================================================\n"); (rus("|\t\tИСТОЧНИКИ ДАННЫХ |\n")); (" ================================================\n"); (rus("|\t1. Ввод с клавиатуры; |\n")); (rus("|\t2. Чтение из файла; |\n"));

printf(" ------------------------------------------------\n");

printf(rus("\tВведите номер пункта подменю: "));

ch=getche(); ("\n\n");  

{

if(ch<49 || ch>50)

{

printf(rus("Такого пункта нет!\nВведите от 1 до 2: "));

ch=getche(); ("\n");

}

} (!strchr("12", ch)); } while(!strchr("12", ch)); ch-=48; if (ch==1) { (rus("Введите количество точек: "));

m=(int)control(); (x,y,m); } else _f(x,y,m);

}vivod()//вывод результатов

{ FILE *fp; int i; double x; char str[80]; while((fp=fopen("resalt.kr","r"))==NULL) { (rus("Ошибка открытия файла!"));

printf(rus("Фалы с результатами отсутствует!"));

printf(rus("Введите сначала данные!\n\n"));

return; } i=0; printf(rus("Коэфициенты полинома:\n")); fgets(str,80,fp); printf("%s",str); printf(" ========================\n"); printf("| X | Y | YR |\n"); printf(" ========================\n"); do {

if(!feof(fp))

{ (i==3)

{ ("\n"); =0;

} (fp,"%lf",&x); (" %.2lf ",x); ++;

} } while(!feof(fp)); printf("\n ========================\n");

}menu() //функция меню { char ch; printf(" =======================================\n"); printf(rus("| \t\tМЕНЮ |\n")); printf(" =======================================\n"); printf(rus("|\t1. Ввод исходных данных; |\n")); printf(rus("|\t2. Вывод результатов; |\n")); printf(rus("|\t3. Выход из программы. |\n")); printf(" ---------------------------------------\n"); printf(rus("\tВведите номер пункта меню: ")); do {

ch=getche(); ("\n\n"); (ch<49 || ch>51) (rus("Такого пункта нет!\nВведите от 1 до 3: ")); } while(!strchr("123", ch)); return ch-49;

}

Файл “reshenie.h”:resalt(double*x,double*y, double*xn, int m,int n)

{ FILE *fp; double *yr=new double[m]; double s=0; int i,j; for(i=0;i<m;i++) { (j=0;j<=n;j++) +=xn[j]*pow(x[i],j); [i]=s; =0; } while((fp=fopen("resalt.kr","w"))==NULL) { (rus("Ошибка открытия файла!"));

exit(0); } for(i=0;i<=n;i++) { (fp,"%.3lf ",xn[i]); } for(i=0;i<m;i++) { (fp,"\n"); (fp,"%lf ",x[i]); (fp,"%lf ",y[i]); (fp,"%lf",yr[i]); } fclose(fp);

}control() // контроль правильности ввода

{ char s[10]; int i,k=0,c,d,l,t=0,x,m=0; double f; c=0; do { ("%s",s); =strlen(s); (s[0]==45)

{ =1;

=1;

} (i=k;i<l;i++)

{ =s[i]; ((d>=48&&s[i]<=57)||s[i]==46)

{ =0; (s[i]==46) =i;

} { (rus("ОШИБКА! Неверный формат числа!\n"));

c=1; ;

}

} } while(c); f=0; if(t) {=t-l+1; (i=l-1;i>t;i--)

{+=(s[i]-48)*pow(10,x); ++;

} =0; (i=t-1;i>=k;i--)

{+=(s[i]-48)*pow(10,x); ++;

} } else { =0; (i=l-1;i>=k;i--)

{ +=(s[i]-48)*pow(10,x); ++;

} } if(m==1) *=-1; return f;

}perest(double*x,double*y,int n)

{ //функция переставляет местами строки int i; double buf; for(i=0;i<n;i++) { //перестановка происходит в цикле поэлементно

buf=x[i]; [i]=y[i]; [i]=buf; }

}vychisl(double**x,int n)

{ //вычисление методом Гаусса int i,j,k,nj; for(i=0;i<n-1;i++) { =0; (j=i;j<n;j++) (x[i][i]<x[j][i])

nj=j; //нахождение главного элемента

if(nj!=0)

perest(x[i],x[nj],n+1); //перестановка строк

for(k=0;k<n-1-i;k++) (j=n;j>=i;j--)

{

if(x[i][i]==0)

{

printf(rus("Нет результата")); exit(0); } //вычитание одной строки из другой

x[i+k+1][j]=x[i+k+1][j]-(x[i][j]/x[i][i])*(x[i+k+1][i]); } } for(i=n-1;i>0;i--) (k=0;k<i;k++) (j=n;j>i-k-1;j--)

{

if(x[i][i]==0)

{ //значит система несовместна

printf(rus("Бесконечное множество решений"));

exit(0);

} //вычитание одной строки из другой

x[i-1-k][j]=x[i-1-k][j]-(x[i][j]/x[i][i])*(x[i-1-k][i]);

}

}fync(double x,double *xn,int n)

{ int i; double s=0; for(i=0;i<=n;i++) +=xn[i]*pow(x,i); return s;

}znach(double x, double*xn,double M,int n)

{ double z; z=x-1./M*fync(x,xn,n);

return z;

}norma_m(double **a,int n) //функция поиска нормы m матрицы

{ int i,j; double s=0, max=0; for(i=0;i<=n;i++) { (j=0;j<=n;j++) (i!=j) +=fabs(a[i][j]); (s>a[i][i]) =0; (i==0) =s; if(s>max) =s; } s=max; return s;

}norma_k(double **a,int n) //функция поиска нормы k матрицы

{ int i,j; double s=0, max=0; for(i=0;i<=n;i++) (j=0;j<=n;j++) +=pow(a[i][j],2); s=sqrt(s); return s;

}norma_l(double **a,int n) //функция поиска нормы l матрицы

{ int i,j; double s=0, max=0; for(j=0;j<=n;j++) { (i=0;i<=n;i++) (i!=j) +=fabs(a[i][j]); (s>a[j][j]) =0; (j==0) =s; if(s>max) =s; } s=max; return s;

}

void koren(double*xn, int n) //---------Поиск корней методом простой итерации--------

{ int i=0; double l,lp,temp,m,M,a,b,e=0.0001; printf(rus("Введите начало интервала [a,b]: ")); a=(int)control(); printf("\n"); b=a+1; while((fync(a,xn,n)*fync(b,xn,n))>=0) //поиск конца отрезка {

b+=1; ++; (i>=1000)

{ (rus("Корней нет!!!\n")); ;

} } printf(rus("Тогда интервал принимает вид: [%.2lf,%.2lf]\n"),a,b); temp=fync(a,xn,n)/a-xn[0]; m=temp; M=temp; for(l=a+0.1;l<=b;l+=0.1) //проверка условия сходимости { (l==0) =xn[1]; =fync(l,xn,n)/l-xn[0]; (temp<0) *=(-1); (temp<m) =temp; if(temp>M) =temp; } if((temp=1-m/M)>1) { (rus("Корней нет!!!\n"));

return; } temp=(a+b)/2; i=0; printf(rus("Последователность итерациу:\n")); printf("x[%d]=%.6lf; ",i,temp); do //сами итерации {

l=znach(temp,xn,M,n); =temp; =l; ++; ("x[%d]=%.6lf; ",i,l); } while(fabs(l-lp)>=e); printf(rus("\nЗаданая точность достигнута на %d итерации.\n"),i); printf(rus("Итоговое значение корня: %.4lf"), l); printf("\n");

}aproks(double *x,double *y, int m) //функция апроксимации к полиному n степени

{ bool flag=false; int i,j,k,n=2; printf(rus("Введите степень полинома (от 1 до %d): "),m-1); n=(int)control(); do { if(n<1) { (rus("ОШИБКА!Нельзя вводить знач. меньше 1!\nВведите еще раз: "));

n=(int)control(); } else if(n>=m) { (rus("ОШИБКА!Ст-нь должна быть < кол-ва точек!\nВвед. еще раз:"));

n=(int)control(); } } while(n>=m || n<1); double **B=new double*[n]; for(i=0;i<=n;i++) [i]=new double[n]; double **a=new double*[n]; for(i=0;i<=n;i++) [i]=new double[n]; double *C=new double[n+1]; double temp,max,s=0,d,l,d1=0, e=0.001; double *xr=new double[n]; double *x0=new double[n]; double *xn=new double[n]; double **AB=new double*[n]; for(i=0;i<=n;i++) [i]=new double[n+1]; for(i=0;i<=n;i++) //заполнение матрицы B (j=0;j<=n;j++)

{ [i][j]=0; (k=0;k<m;k++) [i][j]+=pow(x[k],i+j);

} for(i=0;i<=n;i++) //заполнение матрицы С {

C[i]=0;

for(j=0;j<m;j++)

C[i]+=pow(x[j],i)*y[j]; } printf(rus("Исходная матрица системы:\n")); for(i=0;i<=n;i++) //вывод на экран аргументов полученой системы {

for(j=0;j<=n;j++) ("B[%d][%d]=%.2lf

",i,j,B[i][j]); ("C[i]=%.2lf\n",C[i]); }

//----------------Метод Якоби-----------------

for(i=0;i<=n;i++) if(B[i][i]==0) { (rus("Данная система мет. Якоби не реш-ся\nПрин-м извинения.\n"));

goto Gaus; }; for(i=0;i<=n;i++) [i]=C[i]/B[i][i]; // вектор B-та for(i=0;i<=n;i++) // формирование матрицы a (j=0;j<=n;j++)

{ (i!=j) [i][j]=(-1)*(B[i][j]/B[i][i]); a[i][j]=0;

}

k=0; do { (k>0) (i=0;i<=n;i++) [i]=xn[i]; (i=0;i<=n;i++)

{ [i]=0; (j=0;j<=n;j++)

{ (i!=j) =a[i][j]*x0[j]; temp=0; [i]+=temp;

} [i]+=x0[i]; [i]=xn[i]-x0[i];

{ =0; (i=0;i<=n;i++) (max<fabs(xr[i])) =fabs(xr[i]); =max;

} (d==0)

{ =norma_k(a,n); (i=0;i<=n;i++) +=fabs(xr[i]); =sqrt(d1);

}

{ (i=0;i<=n;i++) +=fabs(xr[i]);

} (d>1 || d==0)

{

printf(rus("Данная сис-ма метю Якоби не реш-ся\nПрин. извинения.\n"));

goto Gaus;

}=d/(1-d); (d>0.5) =(1-d)/d*e; ++; (l*s<e)

{

flag=true;

printf(rus("Заданая точность достигнута на %d итерации.\n"),k);

}

} while(flag==false); if(flag==false) //--------Метод Гауса---------- {: printf(rus("Применим метод Гауса! В итоге:\n")); (i=0;i<=n;i++) (j=0;j<=n+1;j++) (j==n+1) [i][j]=C[i]; [i][j]=B[i][j]; (AB,n+1); (i=0;i<=n;i++) (j=0;j<=n+1;j++) (i==j)

{ [i][n+1]/=AB[i][j]; [i][j]=1;

} for(i=0;i<=n;i++) [i]=AB[i][n+1];

} printf(rus("Получили следующие аргументы полинома %d степени:\n"),n); for(i=0;i<=n;i++) ("a%d=%.2lf ",i,xn[i]); printf("\n"); resalt(x,y,xn,m,n); //вызов функции записи в файл resalt.kr koren(xn,n); //вызов функции поиска корня

}

Приложение 2

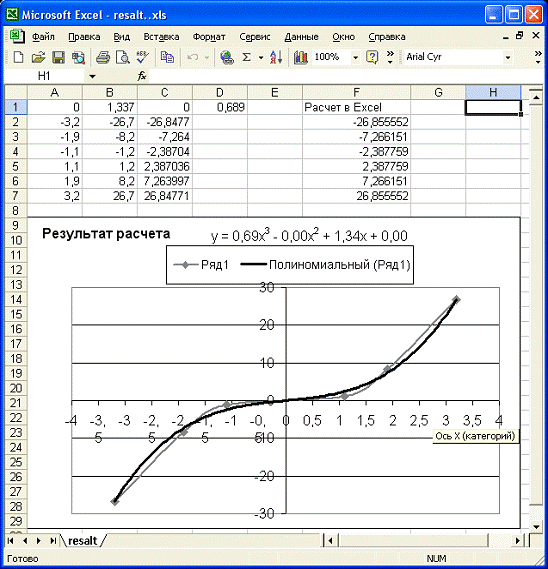
В данном приложении представлен график, построенный в редакторе Excel(рисунок 14), функции полученной в результате выполнения программы при введенных значениях X и Y. Столбец “Yr” содержит значения функции полученные в результате выполнения программы, столбец “Расчет в Excel” содержит значения функции полученные при расчете в Excel.

Рисунок 14. Результат расчета в Excel