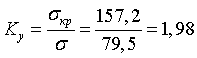Определение параметров вала и балки
1. Расчеты на прочность
статически определимых систем растяжения - сжатия
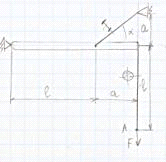
Дано:
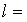 2 м,
2 м, 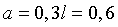 м,
м,
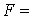 500
кН,
500
кН, 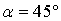 ,
,
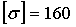 МПа,
МПа,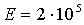 МПа.
МПа.
Решение:
1. Рассмотрим равновесие
каждого жесткого стержня в отдельности
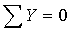 :
: 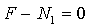 ,
, 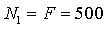 кН.
кН.
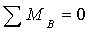 :
: 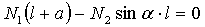 ,
,
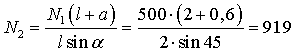 кН.
кН.
2. Подберем из условия
прочности сечения стержней
а) для стержня 1: 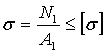 ,
где
,
где 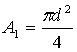 .
Тогда
.
Тогда
 м.
м.
Принимаем 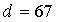 мм.
Уточненная площадь стержня 1
мм.
Уточненная площадь стержня 1
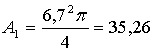 см2.
см2.
б) для стержня 2: 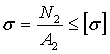 .
Тогда
.
Тогда 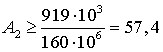 см2.
см2.
Принимаем двутавр №36 с 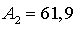 см2.
см2.
3. Определим изменение длины
каждого стержня.
а) удлинение стержня 1
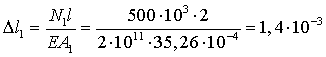 м=1,4 мм.
м=1,4 мм.
б) удлинение стержня 2
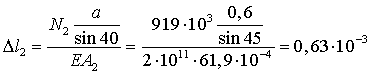 м=0,63 мм.
м=0,63 мм.
. Найдем
перемещение т.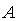 .
.
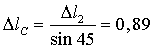 мм,
мм, 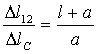 ,
, 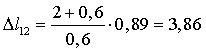 мм.
мм.
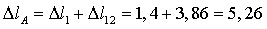 мм.
мм.
2. Геометрические
характеристики плоских сечений
Дано:
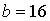 см
см
- Прямоугольник 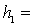 24
см,
24
см, 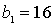 см.
см.
- Прямоугольник 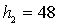 см,
см,
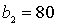 см.
см.
- Прямоугольный
треугольник 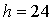 см,
см,
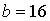 см.
см.
Решение:
1. Рассмотрим сложную фигуру,
состоящую из прямоугольника 1, прямоугольника 2 у которого удалили треугольник
3.
Выбираем вспомогательные
оси, совпадающие с центральными осями 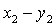 прямоугольника 2.
Определяем центр тяжести фигуры
прямоугольника 2.
Определяем центр тяжести фигуры
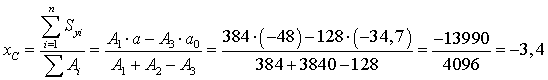 см.
см.
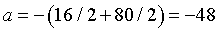 см.
см.
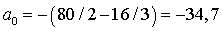 см.
см.
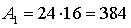 см2.
см2.
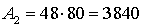 см2.
см2.
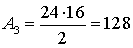 см2.
см2.
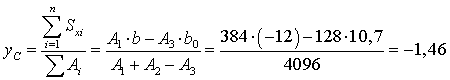 см.
см.
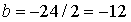 см,
см,
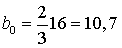 см.
см.
2. Определяем моменты инерции
относительно центральных осей
Осевые моменты:
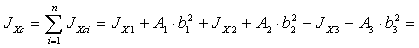
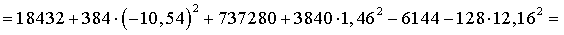 787015 см4
787015 см4
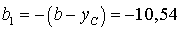 см,
см,
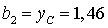 см,
см,
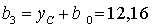 см,
см,
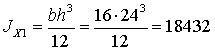 см4
см4
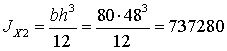 см4
см4
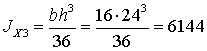 см4
см4
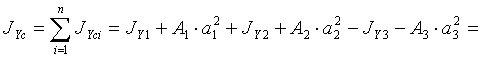
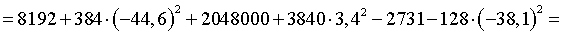 =2675883 см4
=2675883 см4
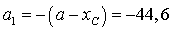 см,
см,
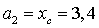 см,
см,
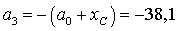 см.
см.
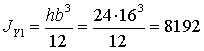 см4
см4
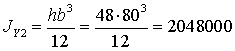 см4
см4
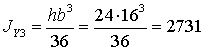 см4
см4
Центробежный момент:
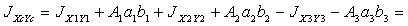
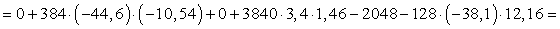
=256828 см4
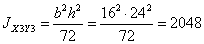 см4
см4
3. Определим угол поворота
главных осей относительно центральных.
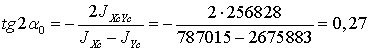
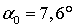
Ось х необходимо
повернуть против часовой стрелки на угол 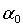 до совмещения с главной
осью U.
до совмещения с главной
осью U.
4. Рассчитаем моменты инерции
сложного сечения относительно главных центральных осей.
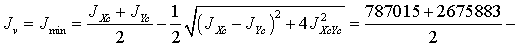
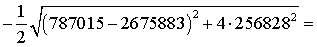 752717 см4
752717 см4
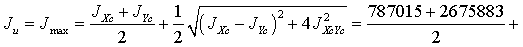
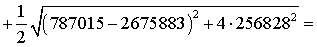 2710181 см4
2710181 см4
=3462898
Радиусы инерции:
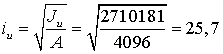 см,
см,
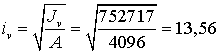 см.
см.
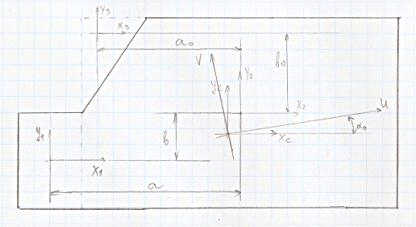
3. Анализ напряженного
состояния
Дано: 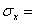 100
МПа,
100
МПа, 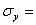 -65
МПа,
-65
МПа, 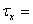 35
МПа,
35
МПа, 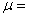 0,26,
0,26,
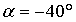 .
.
Решение:
1. Определим положение главных
площадок и величину действующих на них главных напряжений.
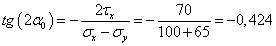
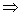
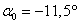 .
.
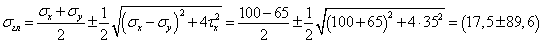 МПа
МПа
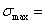 107,1 МПа,
107,1 МПа, 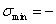 72,1МПа.
72,1МПа.
Из условия 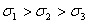
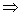
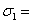 107,1
МПа,
107,1
МПа, 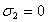 ,
,
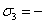 72,1
МПа.
72,1
МПа.
. Определим
напряжения на взаимно перпендикулярных площадках, повернутых относительно
исходных на угол 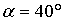 .
.
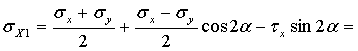
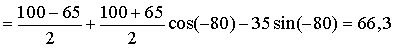 МПа,
МПа,
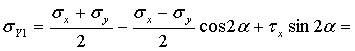
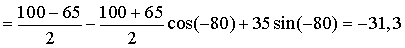 МПа,
МПа,
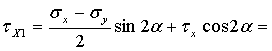
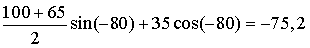 МПа.
МПа.
3. Определим максимальные
касательные напряжения.
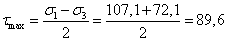 МПа.
МПа.
4. Определим главные
деформации.
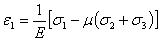
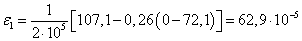
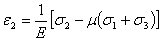
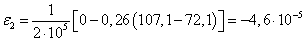
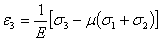
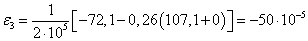
5. Вычислим относительное
изменение объема.
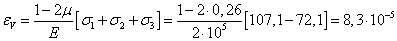
6. Вычислим эквивалентные
напряжения и определим коэффициент запаса прочности.
а) Пластичный материал.
По теории наибольших касательных
напряжений
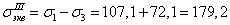 МПа
МПа 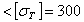 МПа.
МПа.
Коэффициент запаса 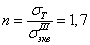
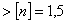 . Прочность детали
обеспечена
. Прочность детали
обеспечена
По теории потенциальной
энергии изменения формы
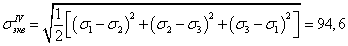 МПа
МПа 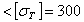 МПа.
МПа.
Коэффициент запаса 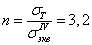
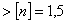 . Прочность детали
обеспечена.
. Прочность детали
обеспечена.
б) Хрупкий материал.
По теории наибольших
линейных деформаций
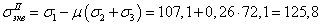 МПа
МПа 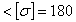 МПа.
МПа.
Коэффициент запаса 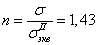
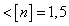 . Прочность детали не
обеспечена.
. Прочность детали не
обеспечена.
По теории Мора
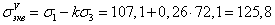 МПа
МПа 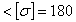 МПа
МПа
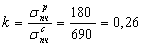 .
.
Коэффициент запаса 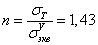
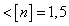 . Прочность детали не
обеспечена.
. Прочность детали не
обеспечена.
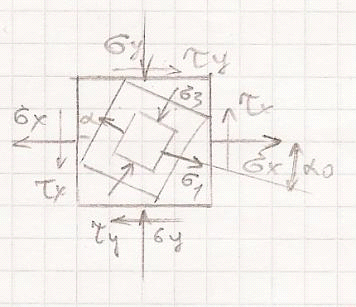
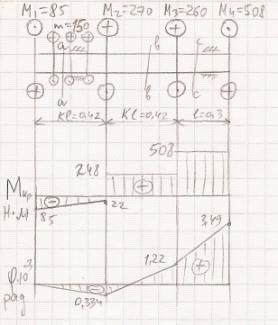
4. Расчет вала на
прочность и жесткость
Дано:
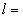 0,3 м,
0,3 м, 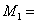 85
Н∙м,
85
Н∙м, 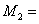 270
Н∙м,
270
Н∙м, 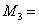 260
Н∙м,
260
Н∙м, 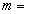 150
Н∙м/м,
150
Н∙м/м, 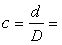 0,6,
0,6,
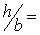 1,5,
1,5,
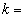 1,4,
1,4,
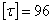 МПа,
МПа,
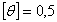 град/м.
град/м.
Решение:
. Определим из
условия равновесия вала крутящий момент 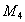
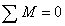 :
: 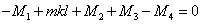 ,
,
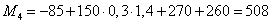 Н∙м.
Н∙м.
Рассчитаем значения
крутящихся моментов по участкам вала.
В сечение 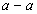 :
: 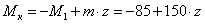 ,
,
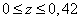 .
.
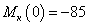 Н∙м,
Н∙м, 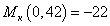 Н∙м.
Н∙м.
В сечение 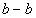 :
: 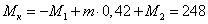 Н∙м.
Н∙м.
В сечение 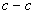 :
: 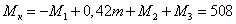 Н∙м.
Н∙м.
Наибольший крутящий
момент: 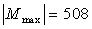 Н∙м.
Н∙м.
2. Определим диаметр вала из
условия прочности и жесткости.
Условие прочности 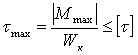 .
.
Условие жесткости 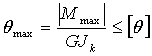 ,
,
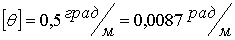 .
.
а) Круглое сплошное сечение
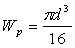 . Тогда
. Тогда 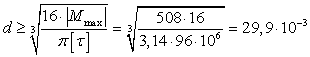 м.
м.
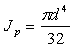 . Тогда
. Тогда 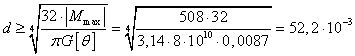 м.
м.
Наибольшее значение
диаметра получилось из условия жесткости. Из ряда нормальных линейных размеров
принимаем 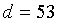 мм.
мм.
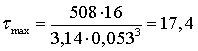 МПа.
МПа.
б) Прямоугольное сечение
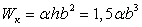 , где
, где 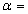 0,231.
0,231.
Тогда  м.
м.
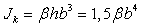 , где
, где 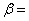 0,196.
0,196.
Тогда 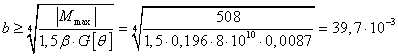 м.
м.
Наибольшее значение
диаметра получилось из условия жесткости. Из ряда нормальных линейных размеров
принимаем 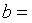 40
мм,
40
мм, 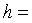 60
мм.
60
мм.
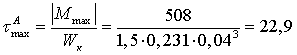 МПа,
МПа,
в) Трубчатое сечение
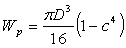 . Тогда
. Тогда 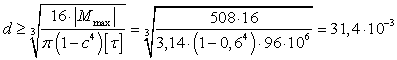 м.
м.
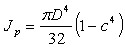 .
.
Тогда 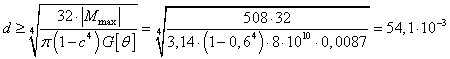 м.
м.
Наибольшее значение
диаметра получилось из условия жесткости. Из ряда нормальных линейных размеров
принимаем 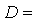 56
мм.
56
мм.
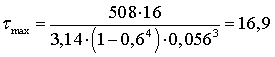 МПа.
МПа.
3. Оценим рациональность
сечений с позиции прочности и жесткости.
а) Круглое сечение
с позиции прочности 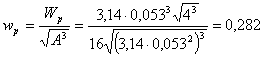 ,
,
с позиции жесткости 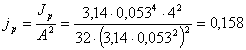 .
.
б) Прямоугольное сечение
с позиции прочности 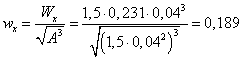 ,
,
с позиции жесткости 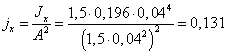 .
.
в) Трубчатое сечение
с позиции прочности 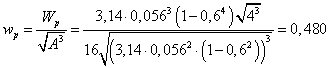 ,
,
с позиции жесткости 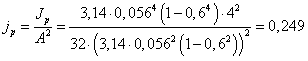 .
.
Наиболее рациональным
является трубчатое сечение, наименее - прямоугольное.
Отношение весов валов:
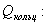
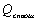
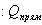
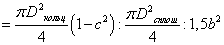
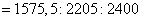
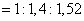
Вес вала с трубчатым
сечением в 1,14 раз легче вала с круглым сплошным сечением и в 1,52 раза легче
вала с прямоугольным сечением.
4. Рассчитаем значения углов
закручивания вала с трубчатым сечением.
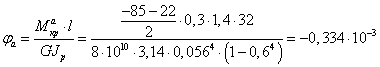 рад,
рад,
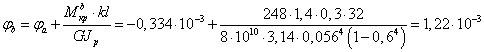 рад,
рад, 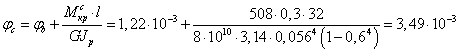 рад.
рад.
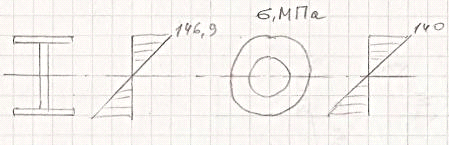
Эскиз опасного сечения вала и эпюра
касательных напряжений
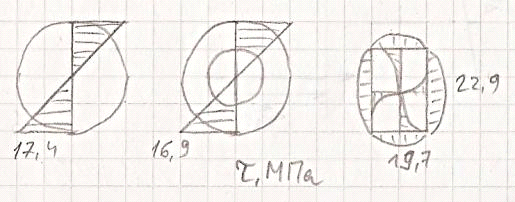
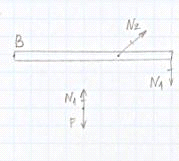
5. Расчет балки на
прочность по нормальным напряжениям
Дано:
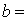 5,8 м,
5,8 м,  1,6
м,
1,6
м, 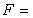 24
кН,
24
кН, 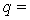 25
кН/м,
25
кН/м, 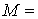 12
кН∙м,
12
кН∙м, 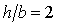 ,
,
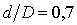 ,
,
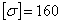 МПа.
МПа.
Решение:
1. Запишем уравнения статики и
определим опорные реакции:
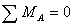 :
: 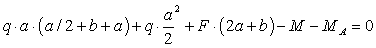 ,
,
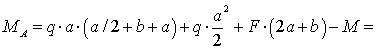
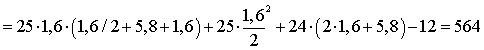 кН∙м.
кН∙м.
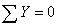 :
: 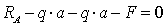 ,
,
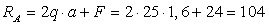 кН.
кН.
. Определим
внутренние усилия 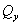 ,
,
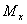 с
помощью метода сечений.
с
помощью метода сечений.
Запишем для каждого выделенного
участка балки выражения внутренних усилий и найдем их значения на границах
участков.
1. 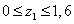 м.
м.
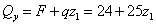 ,
, 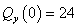 кН,
кН, 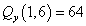 кН.
кН.
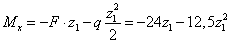 ,
,
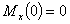 кН∙м,
кН∙м, 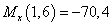 кН∙м.
кН∙м.
2. 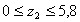 м.
м.
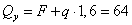 кН.
кН.
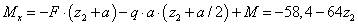 ,
,
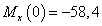 кН∙м,
кН∙м, 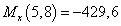 кН∙м.
кН∙м.
3. 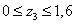 м.
м.
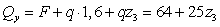 ,
, 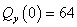 ,
, 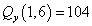 кН.
кН.
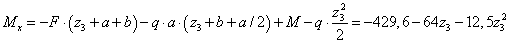 ,
,
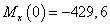 кН∙м,
кН∙м, 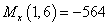 кН∙м.
кН∙м.
3. Дифференциальные
зависимости
На первом и третьем
участках действует распределенная нагрузка 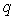 , поэтому поперечная
сила должна быть линейной функцией от координаты, а изгибающий момент должен
менять по закону квадратной параболы. Второй участок свободен от распределенной
нагрузки, поперечная сила постоянна на данном участке, а эпюра изгибающего
момента описывается прямой наклонной линией.
, поэтому поперечная
сила должна быть линейной функцией от координаты, а изгибающий момент должен
менять по закону квадратной параболы. Второй участок свободен от распределенной
нагрузки, поперечная сила постоянна на данном участке, а эпюра изгибающего
момента описывается прямой наклонной линией.
В сечениях А и D, где балка нагружена сосредоточенными внешними силами на эпюре 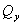 должно
скачком меняться значение ординаты на величину этой силы с учетом ее
направления. Аналогичные скачки имеются и на эпюре
должно
скачком меняться значение ординаты на величину этой силы с учетом ее
направления. Аналогичные скачки имеются и на эпюре 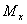 в
сечениях А и C.
в
сечениях А и C.
4. Определим размеры сечения
балки из условия прочности.
Наиболее опасным
является сечение 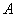 ,
в котором изгибающий момент достигает максимального по модулю значения
,
в котором изгибающий момент достигает максимального по модулю значения 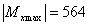 кН∙м.
кН∙м.
Из условия прочности при
изгибе 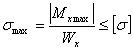 определим
максимальную величину момента сопротивления:
определим
максимальную величину момента сопротивления: 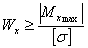 ,
, 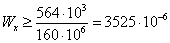 м3.
м3.
а) Двутавр
По ГОСТу 8239-89
выбираем двутавр №70 с моментом сопротивления 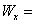 3840 см3 и
площадью сечения
3840 см3 и
площадью сечения 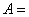 176
см2.
176
см2.
Определяем наибольшее
напряжение: 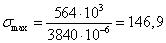 МПа
МПа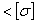 .
.
б) Прямоугольное сечение
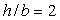 .
.
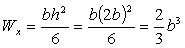 ,
, 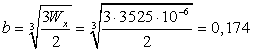 м=174
мм
м=174
мм
Принимаем 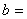 180
мм,
180
мм, 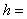 360
мм, площадь сечения
360
мм, площадь сечения 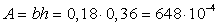 м2.
м2.
Определяем наибольшее
напряжение: 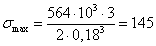 МПа
МПа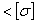 .
.
в) Квадратное сечение 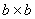 .
.
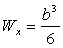 ,
, 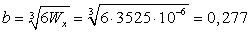 м=277
мм
м=277
мм
Принимаем 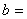 280
мм, площадь сечения
280
мм, площадь сечения 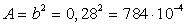 м2.
м2.
Определяем наибольшее
напряжение: 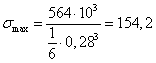 МПа
МПа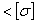 .
.
г) Круглое сечение 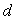 .
.
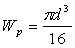 ,
, 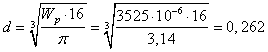 м=262
мм.
м=262
мм.
Принимаем 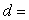 280
мм, площадь сечения
280
мм, площадь сечения
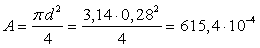 м2.
м2.
д) Кольцевое сечение 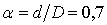 .
.
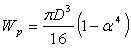 ,
, 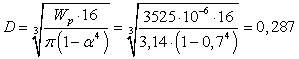 м=287
мм.
м=287
мм.
Принимаем 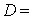 300
мм площадь сечения
300
мм площадь сечения
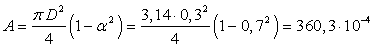 м2.
м2.
Определяем наибольшее
напряжение: 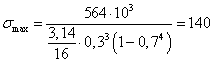 МПа
МПа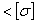 .
.
5. Оценим экономичность
подобранных сечений.
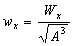
Двутавр: 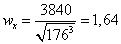 ,
,
Прямоугольник: 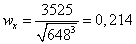 ,
,
Квадрат: 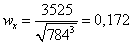 ,
,
Круг: 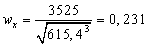 ,
,
Кольцо: 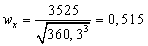 .
.
Наиболее рациональными
при изгибе являются тонкостенные сечения - двутавр, кольцевое сечение.
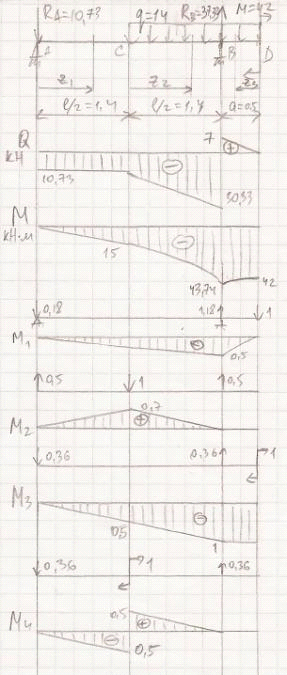
8. Определение
перемещения в балках
Дано:
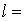 2,8 м,
2,8 м, 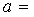 0,5
м,
0,5
м, 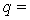 14
кН/м,
14
кН/м, 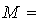 42
кН∙м,
42
кН∙м, 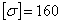 МПа.
МПа.
Решение:
1. Запишем уравнения статики и
определим опорные реакции:
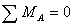 :
: 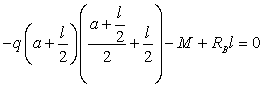 ,
,
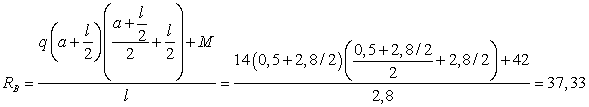 кН.
кН.
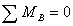 :
: 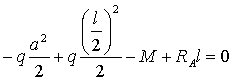 ,
,
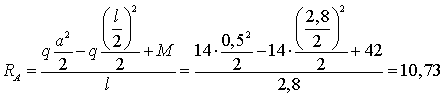 кН
кН
Проверка: 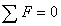 :
:
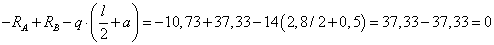 .
.
. Определим
внутренние усилия 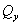 ,
,
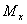 с
помощью метода сечений.
с
помощью метода сечений.
Запишем для каждого выделенного
участка балки выражения внутренних усилий и найдем их значения на границах
участков.
1) 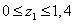 м.
м.
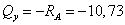 кН.
кН.
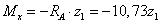 ,
, 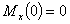 ,
, 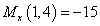 кН∙м.
кН∙м.
2) 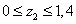 м.
м.
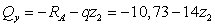 ,
, 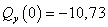 кН,
кН, 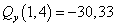 кН.
кН.
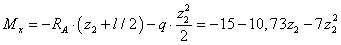 ,
,
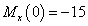 кН∙м,
кН∙м, 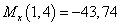 кН∙м,
кН∙м,
3) 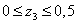 м.
м.
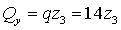 ,
, 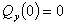 ,
, 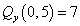 кН.
кН.
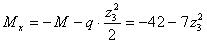 ,
,
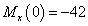 кН∙м,
кН∙м, 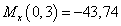 кН∙м.
кН∙м.
. Опасное сечение
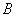 ,
где изгибающий момент принимает максимальное по модулю значение
,
где изгибающий момент принимает максимальное по модулю значение 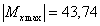 кН∙м.
кН∙м.
Из условия прочности при
изгибе 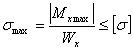 определим
максимальную величину момента сопротивления:
определим
максимальную величину момента сопротивления: 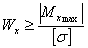 ,
,
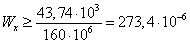 м3.
м3.
Принимаем двутавр №24 с 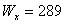 см3,
см3,
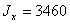 см4.
см4.
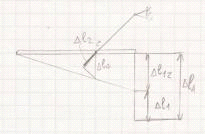
4. Определим перемещения на
конце консоли и посередине пролета методом Мора.
a. Составим схему единичного
нагружения, прикладывая к т D безразмерную силу.
Строим эпюру моментов (М1).
Записываем для каждого участка
выражения изгибающих моментов M1 от единичной нагрузки.
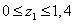 м
м 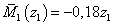 ,
, 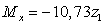 ,
,
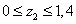 м
м 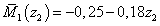 ,
, 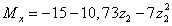 ,
,
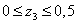 м
м 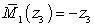 ,
, 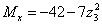 .
.
Записываем интегралы
Мора на каждом участке и, суммируя результаты, вычисляем прогиб сечения D.
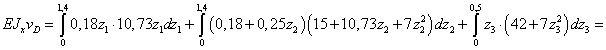
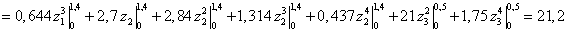 кН∙м3.
кН∙м3.
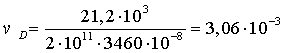 м.
м.
b. Составим схему единичного
нагружения, прикладывая к т С безразмерную силу. Строим эпюру моментов (М2).
Записываем для каждого участка
выражения изгибающих моментов M2 от единичной нагрузки.
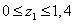 м
м 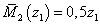 ,
, 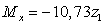 ,
,
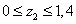 м
м 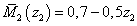 ,
, 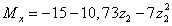 ,
,
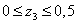 м
м 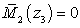 ,
, 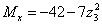 .
.
Записываем интегралы
Мора на каждом участке и, суммируя результаты, вычисляем прогиб сечения С.
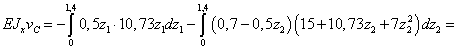
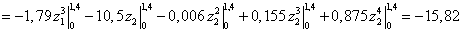 кН∙м3.
кН∙м3.
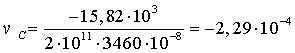 м.
м.
c. Составим схему единичного
нагружения, прикладывая к т D безразмерный момент.
Строим эпюру моментов (М3).
Записываем для каждого участка
выражения изгибающих моментов M3 от единичной нагрузки.
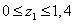 м
м 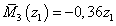 ,
, 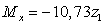 ,
,
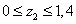 м
м 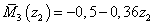 ,
, 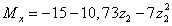 ,
,
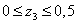 м
м 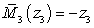 ,
, 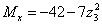 .
.
Записываем интегралы Мора на каждом
участке и, суммируя результаты, вычисляем прогиб сечения D.
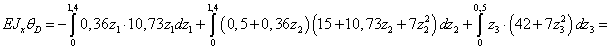
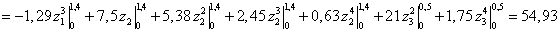 .
.
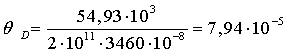 рад.
рад.
d. Составим схему единичного
нагружения, прикладывая к т С безразмерный момент. Строим эпюру моментов
(М4).
Записываем для каждого участка
выражения изгибающих моментов M4 от единичной нагрузки.
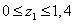 м
м 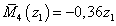 ,
, 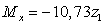 ,
,
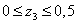 м
м 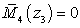 ,
, 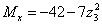 .
.
Записываем интегралы Мора на каждом
участке и, суммируя результаты, вычисляем прогиб сечения С.
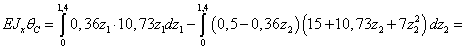
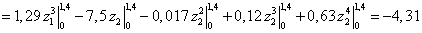 .
.
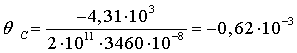 рад.
рад.
5. Определим перемещение на
конце консоли и посередине пролета способом Верещагина
На первом участке:
- треугольник 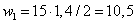 кН∙м2,
кН∙м2,
На втором участке эпюры
разбиваем на три фигуры:
- дуга 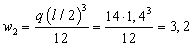 кН∙м2,
кН∙м2,
треугольник 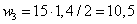 кН∙м2,
кН∙м2,
треугольник 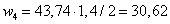 кН∙м2,
кН∙м2,
На третьем участке эпюры
разбиваем на три фигуры:
дуга 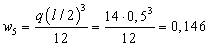 кН∙м2,
кН∙м2,
треугольник 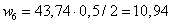 кН∙м2,
кН∙м2,
треугольник 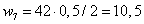 кН∙м2.
кН∙м2.
Составим схему единичного
нагружения, прикладывая к т D безразмерную силу.
Строим эпюру моментов (М1).
Значение ординат под
соответствующими площадями:
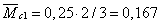 м,
м, 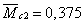 м,
м,
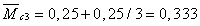 м,
м,
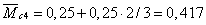 м,
м,
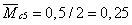 м,
м,
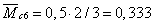 м,
м,
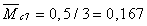 м.
м.
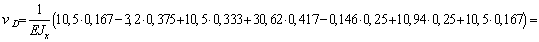
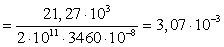 м.
м.
Составим схему
единичного нагружения, прикладывая к т С безразмерную силу. Строим эпюру
моментов (М2).
Значение ординат под
соответствующими площадями:
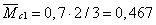 м,
м, 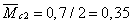 м,
м,
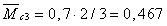 м,
м,
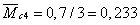 м,
м,
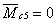 м,
м,
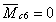 м,
м,
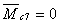 м.
м.
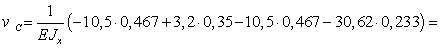
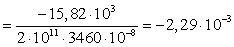 м.
м.
Составим схему
единичного нагружения, прикладывая к т D безразмерный момент. Строим эпюру моментов (М3).
Значение ординат под
соответствующими площадями:
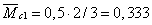 м,
м, 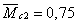 м,
м,
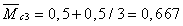 м,
м,
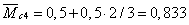 м,
м,
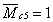 м,
м,
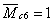 м,
м,
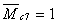 м.
м.
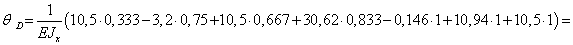
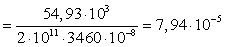 м.
м.
Составим схему
единичного нагружения, прикладывая к т С безразмерный момент. Строим
эпюру моментов (М4).
Значение ординат под
соответствующими площадями:
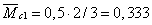 м,
м, 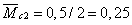 м,
м,
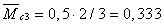 м,
м,
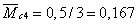 м,
м,
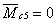 м,
м,
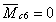 м,
м,
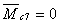 м.
м.
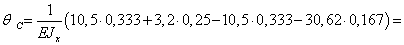
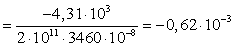 м.
м.
6. Проверим балку на жесткость
в пролете и на консоли
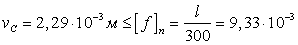 м. Условия прочности
выполнены.
м. Условия прочности
выполнены.
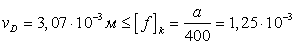 м. Условие прочности не
выполнено.
м. Условие прочности не
выполнено.
Необходимо подобрать другой двутавр.
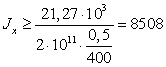 см4.
см4.
Выбираем №33 с 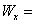 597
см3,
597
см3, 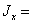 9840
см4
9840
см4
9. Расчет на
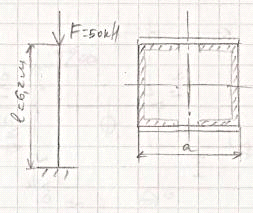
устойчивость центрально сжатого стержня
сечение вал балка
Дано:  6,2
м,
6,2
м, 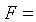 560
кН.
560
кН.
Решение: 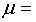 2.
2.
Первое приближение 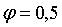
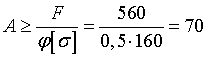 см2.
см2.
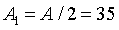 см2.
Принимаем швеллер №27 с
см2.
Принимаем швеллер №27 с 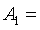 35,2
см2,
35,2
см2, 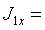 4160
см4.
4160
см4.
Момент инерции
относительно оси х составного стержня
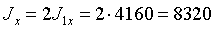 см4.
см4.
Радиус инерции
относительно оси х составного стержня
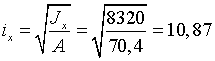 см.
см.
Гибкость относительно
оси х для составного стержня
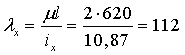 ,
, 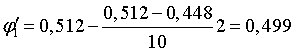
Допускаемое напряжение 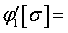 79,9
МПа.
79,9
МПа.
Действительное
напряжение 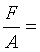 79,5
МПа.
79,5
МПа.
Профиль не догружен на 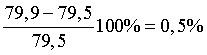 .
.
При ослаблении сечения
заклепками на 12% получаем 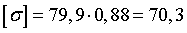 МПа.
МПа.
Перегрузка составляет 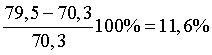 .
.
Необходимо усилить
сечение окончательно приминаем швеллер №30 с 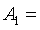 40,5 см2,
40,5 см2, 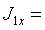 5810
см4,
5810
см4, 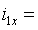 12 см,
12 см, 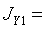 327
см4,
327
см4, 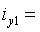 2,84
см,
2,84
см, 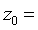 2,52
см.
2,52
см.
Найдем расстояние а.
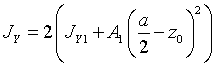 ,
, 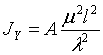
Получаем 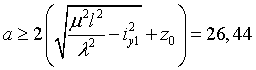 см.
см.
т.к. 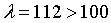 ,
то критическое напряжение для стали Ст. 3 можно определить как
,
то критическое напряжение для стали Ст. 3 можно определить как
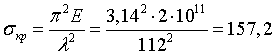 МПа.
МПа.
Фактический коэффициент
запаса