|
Преступник
2
|
|
Сознаться
|
Молчать
|
|
Преступник
1
|
-5;
-5
|
0; -10
|
|
Молчать
|
-10;
0
|
-1; -1
|
Здесь ситуация меняется таким образом, что если
преступник 1 сознается в совершении преступления, а преступник 2 промолчит, то
в таком случае преступник 1 выйдет на свободу, а преступник 2 получит 10 лет
тюремного заключения и наоборот. Результаты возможных стратегий преступников
указаны в таблице №2.
В этой игре доминирующая сторона каждого
преступника - сознаться, т.к. ни один из игроков не знает действий другого, но
прекрасно понимает, что если он даст возможность оппоненту признаться, то ему
дадут 10 лет, и тогда для минимизации ущерба ему необходимо будет признаться
тоже.
В игре «дилемма заключенных» следование каждым
игроком личной выгоде приводит к неэффективному для группы результату. Если бы
оба преступника молчали, то они были бы в лучшем положении - эффективным по
Парето. Здесь равновесие по Нэшу неэффективное, ведь преступники могли бы
получить по одному году, а получили по 5 лет.
В игре типа «Дилемма заключенных» можно
предположить, что трудность выбора максимально полезной стратегии заключается в
том, что преступники не смогли договориться, но даже в этом случае ни у одного
из них нет гарантии в том, что оппонент не изменил бы своего решения в последний
момент. Основная проблема в ситуациях такого типа - отсутствие надежного,
застуживающего доверия обязательства со стороны каждого из игроков.
Обязательство будет надежным, если одна из
сторон видит, что другая сторона лишена возможности нарушить это обязательство.[1,
с.20]
Институт, который позволяет достичь эффективного
для группы результата в ситуации «дилемма заключенных», содержит механизм
принуждения к соблюдению правил. Чтобы понять, что представляет собой этот
механизм принуждения, рассмотрим следующую игру.
Игра «Два пулеметчика».
Таблица 3. Игра «Два пулеметчика»
|
Пулеметчик
2
|
|
Сражаться
|
Дезертировать
|
|
Пулеметчик
1
|
Сражаться
|
1;
1
|
-2; 2
|
|
Дезертировать
|
2; -2
|
-1; -1
|
Два пулеметчика на двух изолированных постах
должны отразить атаку врага. Каждый должен выбрать одну из двух стратегий:
сражаться или дезертировать. Если оба пулеметчика останутся на своих постах и
будут сражаться, то атака врага будет отбита. Если оба пулеметчика дезертируют,
то враг сможет прорваться, и они попадут в плен. Если один из них останется на
посту, а другой дезертирует, то тот, кто будет сражаться, даст возможность
другому пулеметчику благополучно убежать, затем враг прорвется, и сражающийся
пулеметчик будет убит. Выигрыши обоих игроков представлены в матрице игры (таблица
3). Эта ситуация представляет собой классическую дилемму заключенных. Результат
игры - оба пулеметчика дезертируют и попадают в плен - неэффективен не только с
точки зрения интересов командования и страны, которую они защищали, но и с
точки зрения их собственных интересов.
В этой ситуации возможны следующие решения:) заминировать
подходы к постам, что изменит выигрыши в игре и взаимная солидарность будет
обеспечена;) ввести строжайшую дисциплину в подразделении, где служат
пулеметчики. Знание того, что подразделение дисциплинированное, создаст у
каждого солдата уверенность в другом игроке. Угроза наказания перевесит соблазн
дезертировать. В этом случае игра будет иметь такой же вид, как и в случае а);) иногда
наиболее эффективным механизмом принуждения может быть представление о чести,
которое есть у игроков. В данном случае действует внутренний механизм
принуждения и матрица игры принимает следующий вид (таблица 4).
Таблица 4. Игра «Два пулеметчика»
|
Пулеметчик
2
|
|
Сражаться
|
Дезертировать
|
|
Пулеметчик
1
|
Сражаться
|
1;
1
|
-1;
-2
|
|
Дезертировать
|
-2;
-1
|
-2;
-2
|
При таком раскладе дезертир, даже если ему
удастся сбежать, обесчестит свое имя, поэтому его выигрыш 2 в таблице 3 здесь
будет проигрышем -2, а оставшийся пулеметчик погибнет, но станет героем,
поэтому его выигрыш уже будет -1. Если же они дезертируют вдвоем, то они мало
того, что попадут в плен, так еще и обесчестят свое имя и выигрыш каждого из
них составит -2.
. Ситуация координации. [1,
с.24]
Самым простым примером института, который
возникает в ситуации координации, являются правила дорожного движения. На
примере именно этого института мы и будем рассматривать ситуацию типа
«Координационная игра».
Таблица 5. «Координационная игра»
|
Водитель
2
|
|
Правая
|
Левая
|
|
Водитель
1
|
Правая
|
1;
1
|
0;
0
|
|
Левая
|
0;
0
|
1;
1
|
Если автомобили движутся по разным сторонам
дороги, то для того чтобы разъехаться, водителям нужно останавливаться и вести
переговоры, чреватые издержками, поэтому в этом случае их выигрыши равны нулю.
Если оба выбирают правую сторону дороги или оба водителя выбирают левую, то их
выигрыши составляют по единице. Интересы водителей в этом игре не противоречат
друг другу, они совпадают, поэтому здесь нет необходимости в принуждении. Но
проблема в этой игре возникает в связи с тем, что здесь появляются два
равноценных равновесия по Нэшу, и трудность заключается в том, чтобы
осуществить выбор из этих двух равноценных результатов. Для того чтобы игроки
скоординировали свой выбор, нужен какой-то знак, сигнал, который приведет их в
фокальную точку. В качестве такого знака и возникает социальная норма
правостороннего (или левостороннего) движения, которая представляет собой
простейшую форму института. Каким образом возникает этот институт? Возможны два
основных пути его появления:
1. установление
института в централизованном порядке путем указа. Примером может служить
декрет, изданный после Французской революции 1789 года, который предписывал
экипажам, запряженным лошадьми, ездить по правой стороне дороги. До этого
декрета действовало правило левостороннего движения: экипажи ездили по левой
стороне дороги, а пешеходы ходили по правой стороне. Изменение правила имело
символический смысл: ездить по левой стороне было политически некорректным,
потому что это ассоциировалось с привилегированными классами, движение по правой
стороне было привычным для простого человека, поэтому считалось более
демократичным.
2. эта
социальная норма может возникнуть эволюционным путем. В Англии не было
какого-либо заметного события, которое породило бы господствующую норму
левостороннего движения. Эта норма возникла как местный обычай, а потом
распространялась от одного региона к другому. Иными словами, в периодически
повторяющейся координационной игре найденное удачное решение, которое затем
повторяется, становится нормой. В данном случае фокальная точка является
результатом некоторого жизненного опыта. При этом нельзя сказать заранее, какая
из норм возникнет. Но чем больше игроков следуют этой норме, тем более
укоренившейся она становится.
Итак, мы видим, что в ситуации координации институт
необходим вследствие множественности возможных равновесий. Институт,
возникающий в этой ситуации, не нуждается в специальном механизме принуждения,
людям нужен лишь знак, сигнал о том, какое из равновесий им выбрать, ведь в
ситуации координации они заинтересованы в нахождении единого решения.
3. Ситуация
неравенства. [1, с.27]
Для того чтобы выяснить суть ситуации
неравенства и институтов, возникающих в ней, представим себе некое аграрное
общество до установления в нем прав собственности.
В этом обществе живут два пастуха - А и В, и
есть два пастбища - 1 и 2. Пастбище 1 - более плодородное, чем пастбище 2.
Расстояние от жилищ обоих пастухов до каждого из пастбищ одинаковое. Каждую
весну перед пастухами встает дилемма: на какое пастбище гнать свои стада. Оба
пастуха предпочитают пасти овец на более плодородном пастбище 1, но в этом
случае пастбище быстро истощается, и результат будет хуже, чем в том случае,
если пастухи пасли бы свои стада на разных пастбищах. Следовательно, наибольший
выигрыш пастухи получают, если пасут овец на разных пастбищах. Выигрыши
пастухов представлены в матрице игры (таблица 6).
Таблица 6. Ситуация неравенства
|
Пастух
В
|
|
Пастбище
1
|
Пастбище
2
|
|
Пастух
А
|
Пастбище
1
|
2;
2
|
8;
4
|
|
Пастбище
2
|
4;
8
|
1;
1
|
Для решения возникшей проблемы вводится институт
прав собственности. Пастух А получает в свою собственность пастбище 1, а пастух
В - пастбище 2. Оба пастуха выигрывают от передачи пастбищ в частную
собственности, однако пастух А выигрывает в большей степени, чем пастух В,
поскольку первое пастбище более плодородное. При решении проблемы координации
возникает неравенство между пастухами.
Право собственности функционирует, с одной
стороны, в качестве информации, указывающей, на каком пастбище каждый из
пастухов должен пасти свое стадо. Но этим функции института собственности не
исчерпываются. Право собственности выполняет не только функции координации, они
служат также сохранению неравенства. Предположим, что оба пастуха умерли, и
наследники В не согласны с существующим неравенством. Они могут привести свое
стадо на пастбище 1 в надежде, что наследники А уведут свое стадо на другое
пастбище. Но если социальный институт собственности развит в достаточной
степени, то эта попытка не удастся, поскольку этот институт предусматривает
наказание за неправильное поведение.
. решают проблему координации действий
людей;
. сохраняют существующее неравенство.
К. Маркс в связи с этим выдвинул довольно
сильное утверждение о том, что сам институт государства и вся общественная
система и институты, которые ее поддерживают, являются институтами, служащими
сохранению неравенства, и все они нацелены на то, чтобы защитить положение и
собственность власть имущих. Однако институт частной собственности выполняет не
только функцию сохранения неравенства, но и является необходимым условием для
взаимовыгодного обмена, поскольку позволяют людям координировать свою
производственную деятельность и не тратить ресурсы на перераспределение богатства.
Выводы
Экономисты с течением времени очень часто
сталкиваются с такой проблемой, как неэффективность применения теоретических
основ экономики без их проверки практической деятельностью. Но данный факт
вовсе не означает, что экономическая теория не имеет смысла вообще. Для того,
чтобы теоретические аспекты или институты экономической науки были эффективны
на практике, необходимо максимально представлять ситуации, в которых они могут
быть применены.
Главный аргумент в пользу того, чтобы строить модели
институтов с помощью теории игр, заключается в интересе теории игр к ситуациям
взаимозависимости действий индивидов, проблемам координации и согласования
действий. Ведь именно институты призваны решить эти проблемы.
Необходимость в социальных институтах возникает
в тех ситуациях, когда имеется несколько равновесий (проблема координации),
неэффективность равновесия (дилемма заключенных) или несправедливость
равновесия (ситуация неравенства) в тех типах взаимодействий людей, которые
ведут к их возникновению.
Итак, можно обобщить представленный выше анализ,
указав на два положительных эффекта существования институтов-правил.
Координационный эффект заключается в том, что они обеспечивают состыковку
планов, т. е. создают предпосылки для осуществления правильного выбора в
отношении того, что, как, кому и для кого нужно делать в хозяйственной жизни,
при котором имеет место эффективное размещение ресурсов. На языке теории игр
данная состыковка планов может возникать, в частности, благодаря обеспечению
предсказуемости поведения людей друг для друга через формирование
эволюционно-стабильных стратегий. Мотивационный эффект состоит в обеспечении
ими состыковки стимулов, т. е. институты-правила делают выгодным для индивидов
осуществление правильного экономического выбора. Разрешение дилеммы заключенных
связано со стимулированием сотрудничества между людьми, тогда как достижение
равновесия Нэша посредством смешанных стратегий означает отсутствие стимулов к
стратегическому поведению, что выступает в качестве возможных иллюстраций
данного эффекта. Таким образом, значение этих двух эффектов заключается в том,
что благодаря существованию институтов-правил индивиды могут и хотят делать
выбор, обеспечивающий эффективное размещение ресурсов.
Кроме того, имеется также и распределительный
эффект, состоящий в том, что любой набор правил определяет структуру прав
собственности, которая может быть более выгодна одним членам общества в ущерб
другим.
игра жизнь человек экономический
ГЛАВА 2. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРИИ ИГР
.1 РАЗНООБРАЗИЕ СИТУАЦИЙ И СФЕР ЖИЗНИ
ЧЕЛОВЕКА, В КОТОРЫХ ПРИМЕНИМА ТЕОРИЯ ИГР
В жизни известно немало примеров столкновения
противоположных сторон, принимающих форму конфликта с двумя действующими
сторонами, преследующими противоположные интересы.
Такие ситуации возникают, например, тогда, когда
речь идет о доверии. Соответствие действий контрагента ожиданиям становится
особенно важным в тех ситуациях, когда риск принимаемых индивидом решений
определен действиями контрагента. Модели теории игр служат лучшей иллюстрацией
сказанному: выбор игроком той или иной стратегии зависит от действий другого
игрока. Доверие заключается в «ожидании определенных действий окружающих,
которые влияют на выбор индивида, когда индивид должен начать действовать до
того, как станут известными действия окружающих». Подчеркнем связь сделок на
рынке с доверием в деперсонифицированной форме (доверия в качестве нормы,
регулирующей отношения между индивидами), так как круг участников сделок не
должен быть ограничен лично знакомыми людьми. Убедиться в необходимости
существования доверия в деперсонифицированной форме для осуществления
простейшей рыночной сделки с использованием предоплаты помогает следующая
модель (рис.2).

Рисунок 2
Предположим, что покупателю противостоит
множество продавцов и он из своего предыдущего делового опыта знает вероятность
обмана (1 - р). Рассчитаем такую величину p,
чтобы сделка состоялась, т. е. «делать предоплату» была эволюционно-стабильной
стратегией. EU (делать предоплату) = 10р - 5(1 - р) = 15p
- 5, EU(не делать предоплату) = 0,15p
- -5 > 0, р>1/3. Иначе говоря, при уровне доверия покупателя к продавцам
меньше 33,3% сделки с предоплатой при заданных условиях становятся
невозможными. Иными словами, р= 1/3 является критическим, минимально
необходимым уровнем доверия.
Для обобщения результатов заменим конкретные
величины выигрыша (10) и проигрыша (-5) покупателя символами G и L. Тогда при
прежней структуре игры сделка состоится при р/1-р> L/G: чем выше величина
проигрыша относительно выигрыша, тем выше должен быть уровень доверия между
участниками сделки. Джеймс Коулмен следующим образом изобразил зависимость
потребности в доверии от условий заключаемой сделки (рис. 3).
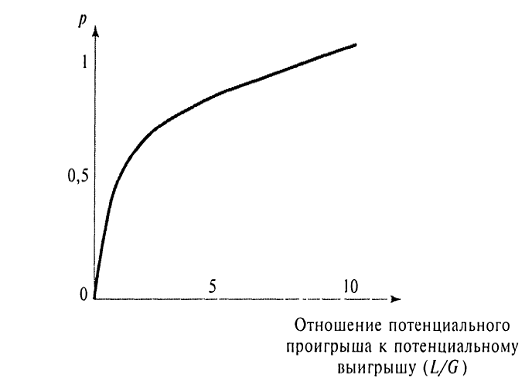
Рисунок 3
Расчетные данные о минимально необходимом уровне
доверия подтверждаются эмпирически. Так, уровень деперсонифицированного доверия
в странах с развитой рыночной экономикой, измеренный с помощью ответа на
вопрос: «Исходя из Вашего личного опыта, считаете ли Вы, что окружающим людям
можно доверять? », составлял 94% в Дании24, 90 - в ФРГ, 88 - в Великобритании,
84 - во Франции, 72 - на севере Италии и 65% - на юге. Показателен низкий
уровень доверия на юге Италии, где традиционно сильна мафия. Не случайно один
из исследователей мафии - Д. Гамбетта объясняет ее возникновение критически
низким уровнем доверия в южных регионах Италии и, следовательно, потребностью в
заменителе доверия, принимающего форму вмешательства «третьей стороны», которой
доверяют оба участника сделки.
Еще один яркий пример теории игр - контракты
между инвестором и государством на разработку месторождений полезных
ископаемых.
Для иллюстрации этого примера возьмем контракт о
купле-продаже стульев с учетом того, что наличие в них зашитых сокровищ, находится
под вопросом [8, с. 231]. Изображать пример будем с учетом того, что в рамках
теории игр внешние по отношению к намерениям сторон контракта факторы
учитываются с помощью введения в игру с двумя участниками третьего игрока,
«природы» (рис. 4).
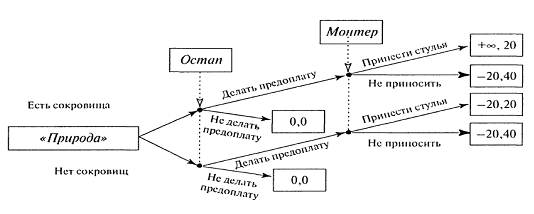
Рисунок 4
Как следует из представления игры в развернутой
форме, вместо четырех исходов их в игре шесть. И если проблема зависимости
выигрыша Остапа от действий машиниста сцены находит свое решение при наличии
любого отличного от нуля уровня доверия Остапа, то проблема зависимости
выигрыша Остапа от наличия в стульях сокровищ остается неразрешимой, что,
впрочем, и подтверждает финал романа.
.2 ВОЗМОЖНЫЕ СТРАТЕГИИ В ПОВТОРЯЮЩИХСЯ
ИГРАХ
. Смешанные стратегии. [8, с.83]
Когда игроки попадают в определенную ситуацию
выбора неоднократно, то их взаимодействие существенным образом усложняется. Они
могут позволить себе комбинировать стратегии, максимизируя общий выигрыш.
Покажем это с помощью модели, описывающей отношения между Центральным банком
(ЦБ) и экономическим агентом в связи с проводимой ЦБ кредитно-денежной
политикой.
ЦБ ориентируется либо на жесткую
кредитно-денежную политику, стремясь поддержать инфляцию на фиксированном
уровне (π0),
либо на эмиссию и, следовательно, повышение темпов инфляции (π1).
В свою очередь, экономический агент действует на основе своих инфляционных
ожиданий πе (устанавливает
цены на свою продукцию, решает вопросы о приобретении товаров и услуг и т.д.),
которые могут либо подтверждаться, либо не подтверждаться в результате
проводимой ЦБ политики. В случае если π1
> πе,
ЦБ получает прибыль от сеньоража и от инфляционного налога. Если πе
= π1,
то в проигрыше оказывается и ЦБ из-за сокращения поступлений от сеньоража, и
экономические агенты, которые продолжают нести тяжесть инфляционного налога.
Если πе
= π0,
то сохраняется статус-кво и в проигрыше никто не оказывается. Наконец, если πе
> π0,
то проигрывают только экономические агенты: производители - из-за потери спроса
на необоснованно подорожавшую продукцию, потребители - из-за создания
неоправданных запасов.
В предложенной модели при однократном
взаимодействии у агентов нет доминирующих стратегий, отсутствует и равновесие
по Нэшу. При повторяющемся многократно взаимодействии, а именно такое
взаимодействие и характерно для реальных ситуаций, оба участника могут
использовать и ту, и другую имеющуюся у них в распоряжении стратегии. Позволяет
ли игрокам чередование стратегий в определенной последовательности
максимизировать свою полезность, т. е. достичь равновесия по Нэшу в смешанных
стратегиях: исхода, при котором ни один участник не может увеличить свой
выигрыш, изменяя в одностороннем порядке свою стратегию? Предположим, что ЦБ
проводит жесткую кредитно-денежную политику с вероятностью Р1 (в P1
% случаев), а с вероятностью (1 - Р1) - инфляционную политику. Тогда при выборе
экономическим агентом неинфляционных ожиданий (πe
= π0)
ЦБ может рассчитывать на получение выигрыша, равного EU(ЦБ) = Р1 0+, 1 (1 - Р1)
= 1- -P1 В случае
инфляционных ожиданий у экономического агента выигрыш ЦБ составит EU(ЦБ) = Р10
+ (1 - Р1)(-2) = 2Р1 - 2. Теперь допустим, что экономический агент имеет
неифляционные ожидания с вероятностью Р2 (в Р2 % случаев), а инфляционные
ожидания - с вероятностью (1 - Р2). Отсюда ожидаемая полезность ЦБ составит
EU(ЦБ) = Р2(1 - Р1) + (1 - Р2)(2Р1-2) = =ЗР2-ЗР1 Р2+2Р1 - 2 (рис. 5).
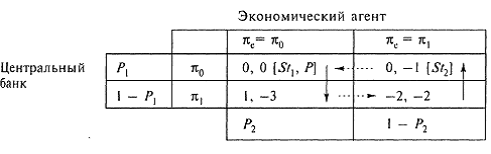
Рисунок 5
Аналогичные расчеты для экономического агента
дадут EU (э.а.) =
Р1(Р2- 1) + (1 - Р1)(-Р2-2) = 2Р1Р2 + Р1- Р2-2. Если мы перепишем данные
выражения в следующей форме EU(ЦБ)
= Pl(2-3P2)
+ ЗР2-2 и EU(э.a.)=
=Р2(2Р1-1) +Р1-2, то нетрудно заметить, что при Р2= 2/3 выигрыш ЦБ не зависит
от его собственной политики, а при Р1= 1/2 выигрыш экономического агента не
зависит от его ожиданий.
Иными словами, равновесием по Нэшу в смешанных
стратегиях будет формирование экономическим агентом в 2/3 случаев
неинфляционных ожиданий и проведение ЦБ в половине случаев жесткой
кредитно-денежной политики. Найденное равновесие достижимо при условии, что
экономические агенты формируют ожидания рациональным образом, а не на основе
инфляционных ожиданий в предыдущий период, скорректированных на ошибку прогноза
предыдущего периода8. Следовательно, изменения в политике ЦБ влияют на
поведение экономических агентов только в той степени, в которой они неожиданны
и непредсказуемы. Стратегия ЦБ в 50% случаев проводить жесткую
кредитно-денежную политику, а в 50% - мягкую как нельзя лучше соответствует
созданию атмосферы непредсказуемости.
. Эволюционно-стабильная стратегия.
Эволюционно-стабильная стратегия - такая
стратегия, что если ее использует большинство индивидов, то никакая
альтернативная стратегия не может ее вытеснить посредством механизма
естественного отбора, даже если последняя более эффективна по Парето.
Разновидностью повторяющихся игр являются
ситуации, когда индивид многократно попадает в определенную ситуацию выбора, но
его контрагент не постоянен, а в каждом периоде индивид взаимодействует с новым
визави. Поэтому вероятность выбора контрагентом той или иной стратегии будет
зависеть не столько от конфигурации смешанной стратегии, сколько от
предпочтений каждого из контрагентов. В частности, предполагается, что из
общего числа N потенциальных контрагентов n
(n/N%) всегда выбирают стратегию А, а m
(m/N%) - стратегию Б. Тем самым создаются предпосылки для достижения нового
типа равновесия, эволюционно-стабильных стратегий. Эволюционно-стабильной (ESS
- Evolutionary
Stable Strategy)
становится та стратегия, при которой если все члены определенной популяции
используют ее, то никакая альтернативная стратегия не может ее вытеснить
посредством механизма естественного отбора. Рассмотрим в качестве примера
простейший вариант проблемы координации: разъезд на узкой дороге двух
автомобилей. Предполагается, что в данной местности лево- и правосторонний
стандарты движения равноправны (или же Правила дорожного движения просто не
всегда выполняются). Автомобилю А движутся навстречу несколько автомобилей, с
которыми ему нужно разъехаться. Если оба автомобиля принимают влево, въезжая на
левую обочину по ходу движения, то они разъезжаются без проблем. То же самое
происходит, если оба автомобиля принимают вправо. Когда же один автомобиль
принимает вправо, а второй - влево и наоборот, то разъехаться они не смогут
(рис.6).

Рисунок 6
Итак, автомобилисту А известен приблизительный
процент автомобилистов Б, систематически принимающих влево (Р), и процент
автомобилистов Б, принимающих вправо (1 - Р). Условие для того, чтобы стратегия
«принять вправо» стала для автомобилиста А эволюционно-стабильной,
формулируется следующим образом: EU(вправо) > EU(влево), или 0P+
1(1 - Р) > 1Р+ 0(1 - Р), откуда Р< 1/2. Таким образом, при превышении
доли автомобилистов во встречном потоке, принимающих вправо, уровня 50%
эволюционно-стабильной стратегией становится «принять вправо» - сворачивать на
правую обочину при каждом разъезде.
В общем виде требования к эволюционно-стабильной
стратегии записываются следующим образом. Стратегия I, используемая
контрагентами с вероятностью p,
является эволюционно-стабильной для игрока тогда и только тогда, когда
выполняются следующие условия
(I,
p) > EU{J, p), что тождественно
pU(I,
I) + (l
-p)U(I,J)>pU(J,I)
+ (1 -p)U(J,J)
Из чего следует:
U(I, I)> U(J, I) или(I,
I) = U(J, I ) и U(I, J) > U(J,
J),
где - U(I,
I) выигрыш игрока
при выборе стратегии I,
если контрагент выбирает стратегию I;
U(J,
I) - выигрыш игрока
при выборе стратегии J,
если контрагент выбирает стратегию I,
и т. д.
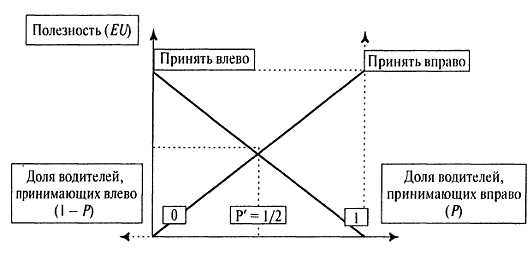
Рисунок 7
Можно представить эти условия и в графической
форме. Отложим по вертикальной оси ожидаемую полезность выбора той или иной
стратегии, а по горизонтальной - долю индивидов в общей популяции игроков,
выбирающих обе стратегии. Тогда мы получим следующий график (значения взяты из
модели разъезда двух автомобилей), изображенный на рис. 7.
Из рисунка следует, что и «принять влево», и
«принять вправо» имеют равные шансы на то, чтобы стать эволюционно-стабильной
стратегией до тех пор, пока ни одна из них не охватила больше половины
«популяции» водителей. Если же стратегия перешагивает этот рубеж, то она
постепенно, но неизбежно вытеснит другую стратегию и охватит всю популяцию
водителей. Дело в том, что, если стратегия перешагивает рубеж 50%, для любого
водителя становится выгодным использовать ее в маневрах, что, в свою очередь,
еще больше увеличивает привлекательность данной стратегии для остальных
водителей. В строгой форме данное утверждение будет выглядеть следующим образом
/dt = G [EU(I, p) - EU(J, p)],
G'>0
Главным результатом анализа повторяющихся игр
является увеличение числа точек равновесия и решение на этой основе проблем
координации, кооперации, совместимости и справедливости. Даже в дилемме
заключенных, переход к повторяющемуся взаимодействию позволяет достичь
оптимального по Парето результата («отрицать вину»), не выходя за рамки нормы
рациональности и запрета на обмен информацией между игроками. Именно в этом
смысл «всеобщей теоремы»: любой исход, устраивающий индивида индивидуально,
может стать при переходе к структуре повторяющейся игры равновесным. В ситуации
дилеммы заключенных равновесным исходом при определенных условиях может стать и
простая стратегия «не признавать», и множество смешанных стратегий. В числе
смешанных и эволюционных стратегий, отметим следующие: Tit-For-Two-Tats
- начинать с отрицания вины и признавать вину, только если в два предшествующих
периода кряду контрагент признавал вину; DOWING - стратегия, исходящая из
предположения о равновероятном использовании контрагентом стратегий «отрицать
вину» и «признавать» в самом начале игры. Далее каждое отрицание вины со
стороны контрагента поощряется, а каждое признание - наказывается выбором
стратегии «признавать вину» в следующий период; TESTER - начинать с признания
вины, и если контрагент тоже признает вину, то в следующем периоде отрицать
вину.
ЗАКЛЮЧЕНИЕ
В заключение данной работы можно сделать вывод о
необходимости использования теории игр в современных экономических условиях.
В условиях альтернативы (выбора) очень часто
нелегко принять решение и выбрать ту или иную стратегию. Исследование операций
позволяет с помощью использования соответствующих математических методов
принять обоснованное решение о целесообразности той или иной стратегии. Теория
игр, имеющая в запасе арсенал методов решения матричных игр, позволяет
эффективно решать указанные задачи несколькими методами и из их множества
выбрать наиболее эффективные, а также упрощать исходные матрицы игр.
В данной работе были проиллюстрированы
практическое применение основных стратегий теории игр и сделаны соответствующие
выводы, изучены самые используемые и часто применяемые стратегии и основные
понятия.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Институциональная
экономика Одинцова М.И Уч. пос. изд. ГУ ВШЭ, 2007.
2. Мак-Кинси
Дж. Введение в теорию игр. М.: Гос. изд-во физмат литературы, 1960.
. Институциональная
экономика: теория и практика А.В. Виноградова Учебно-методическое пособие. -
Нижний Новгород: Нижегородский госуниверситет, 2012.
. С.Г.
Коковин Лекции по теории игр - вводный уровень, 2010.
. Норт
Д. Институты, институциональные изменения и функционирование экономики. Москва,
1997.
. К.Л.
Самаров. Математика. Учебно-методическое пособие по разделу «Элементы теории
игр», ООО «Резольвента»,2009.
. А.Н.
Олейник. Институциональная экономика. Учебное пособие, Москва ИНФРА-М, 2002.